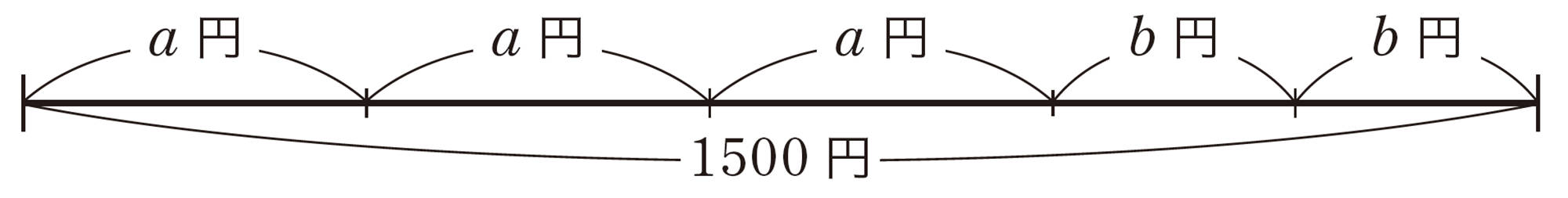<1年p.95>
３章 Chapter 3 一次方程式
1節 方程式
2節 1次方程式の利用
クリップ3個
1円玉2枚
クリップ1個
1円玉10枚
天びんは，つりあっているね。クリップの重さがわかるかな。
1円玉1枚が1g だから…。
両方の皿から1円玉を2枚取っても，天びんはつり合ったままになりそうだね。
それでも，まだクリップの重さはわかりそうにないな…。
？ 文字にあてはまる数はどうしたら求められるかな？
<1年p.96>
1節 方程式
2つの数量の関係は？
クリップと1円玉が箱の中に入っています。拓真さん，大和さん，美月さん，真央さんの4人は，箱の中から適当にクリップと 1円玉をつかみ取ると，それぞれ次のような個数になりました。
クリップ3個
1円玉2枚
クリップ5個
1円玉3枚
美月さん
クリップ2個
1円玉4枚
真央さん
クリップ1個
1円玉10枚
<1年p.97>
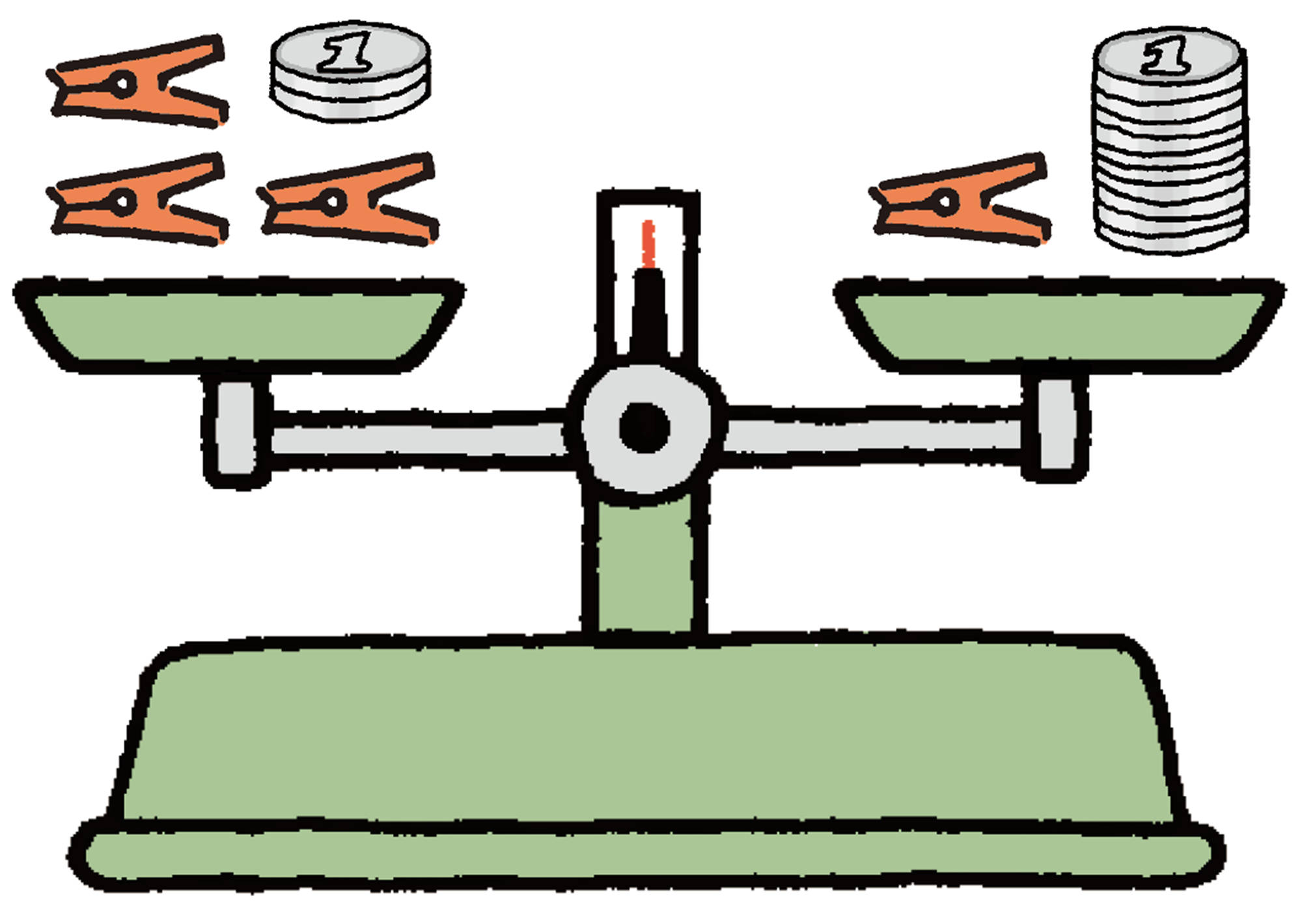
【１】 4人が持っているクリップと1円玉の重さを天びんで比べると，次の❶ 〜❸ のような状態になりました。このことから，4人の中では誰のものがもっとも重いといえるでしょうか。また，誰のものがもっとも軽いといえるでしょうか。
❶
拓真さん
大和さん
❷
拓真さん
真央さん
❸
大和さん
美月さん
もっとも軽いのが誰のものか，これでわかるのかな。
クリップ1個の重さがわかれば，計算でわかるよ。
【２】 【１】では，誰のものがもっとも軽いかがわかりませんでした。4人の持っているクリップと1円玉の重さを比べるには，どうすればよいでしょうか。
【３】 1円玉1枚の重さは1 g です。クリップ1 個の重さを求めるには，どうすればよいでしょうか。
クリップ1個の重さをxg として，計算すればいいよ。
一人ひとりの重さは文字式で表せるけど，2つの数量の関係をどう表せばいいのかな。
次の課題へ！
2つの数量の関係を，文字を使った式で表すにはどうすればいいのかな？
P.98
次の課題へ！
クリップ1個の重さは，どうすれば求められるのかな？
P.102，104
<1年p.98>
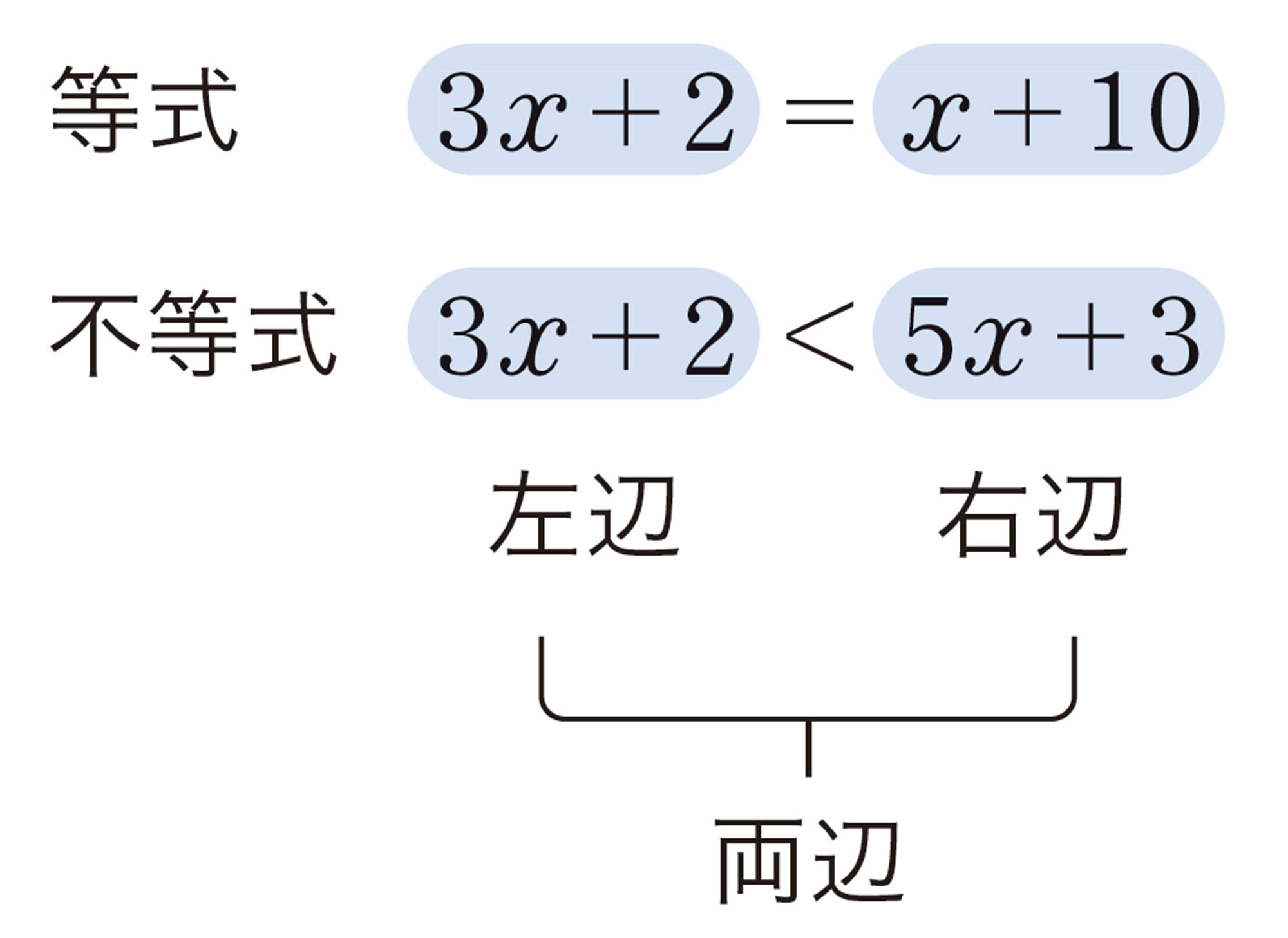
１ 等式と不等式
Q Question
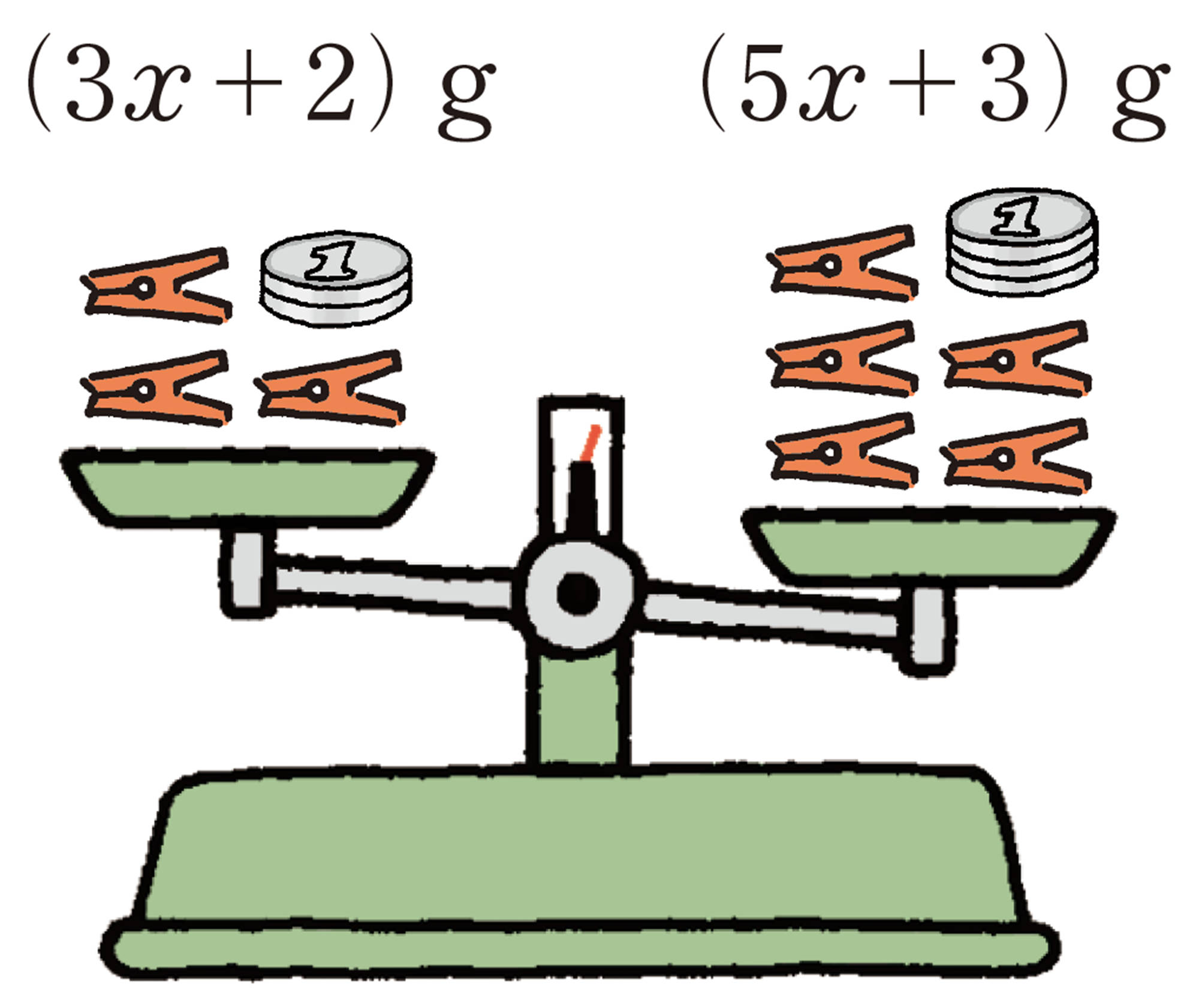
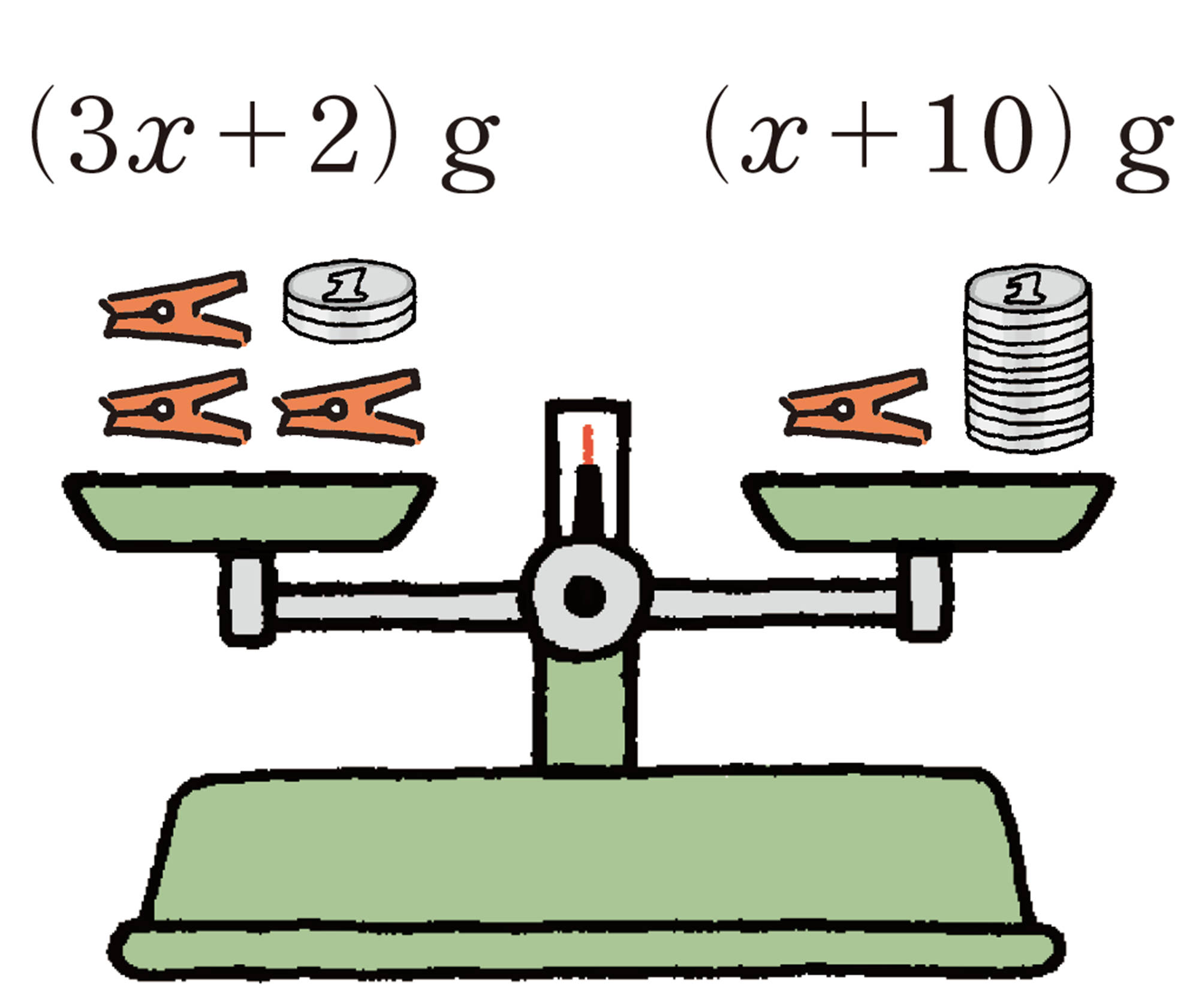
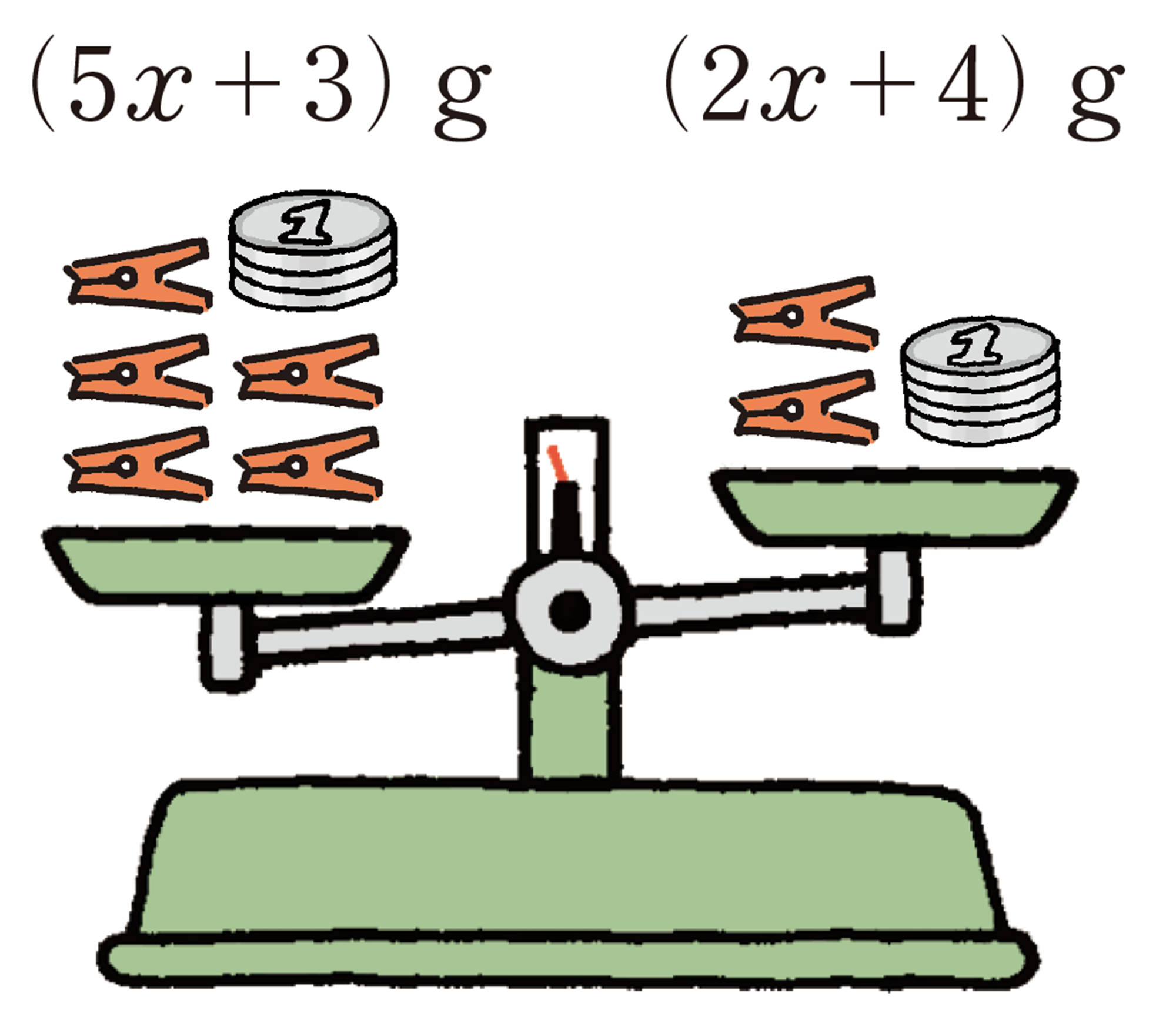
前ページの【１】 ❶ ，❷の天びんについて，2つの数量の重さの関係を式で表すにはどうしたらよいか考えてみましょう。クリップ1個の重さをxg，1円玉1枚の重さを1g として考えてみましょう。
2つの数の関係は，等号や不等号を使って表したね。
2つの数量の関係も，等号や不等号を使って表せるのかな。
見方・考え方
数量の関係も，数と同じように式で表せるかな。
目標 ▷ 2つの数量の関係を式で表そう。
右の図は，前ページの【１】 ❶の天びんを示したものである。
左側の重さは，[mathjax]\((3x+2)\)g，
右側の重さは，[mathjax]\((5x+3)\)g
となる。このとき，右側の方が重いから，左右の重さの関係は，
[mathjax]\(3x+2 \lt 5x+3\)
と表すことができる。
[mathjax]\(3x+2<5x+3\)
( クリップ1 個…[mathjax]\(x\)g ，1 円玉1 枚…1 g )
このように，不等号を使って数量の関係を表した式を 不等式 という。
また，前ページの【１】 ❷の天びんは，
左側の重さは，[mathjax]\((3x+2)\)g，
右側の重さは，[mathjax]\((x+10)\)g
となる。このとき，左右がつり合っているから，左右の重さの関係は，
[mathjax]\(3x+2=x+10\)
と表すことができる。
[mathjax]\(3x+2=x+10\)
このように，等号を使って数量の関係を表した式を 等式 という。
<1年p.99>
問 １ 97ページの【１】❸の関係を， 不等式で表しなさい。
等式や不等式で，等号や不等号の左側の式を 左辺 ，右側の式を 右辺 ，左辺と右辺を合わせて 両辺 という。
例 １ 入館料が，大人1人a円，子ども1人b円 の科学館に行きました。次の⑴，⑵の数量の関係を，等式や不等式で表すと，次のようになる。
⑴ 「大人1人と子ども2人の入館料を払うと，1000円でおつりがあった。」
このことを図に表すと，
[mathjax]\((\text{大人}1\text{人の入館料})+(\text{ 子ども2人の入館料})\lt 1000\text{円}\)
したがって，[mathjax]\(a+2b \lt 1000\) と表すことができる。
⑵ 「大人3人と子ども2人の入館料の合計は1500円だった。」このことを図に表すと，
[mathjax]\((\text{大人}3\text{人の入館料})+(\text{ 子ども2人の入館料})= 1500\text{円}\)
したがって，[mathjax]\(3a+2b=1500\)と表すことができる。
<1年p.100>
問 ２ 次の数量の関係を，等式や不等式で表しなさい。
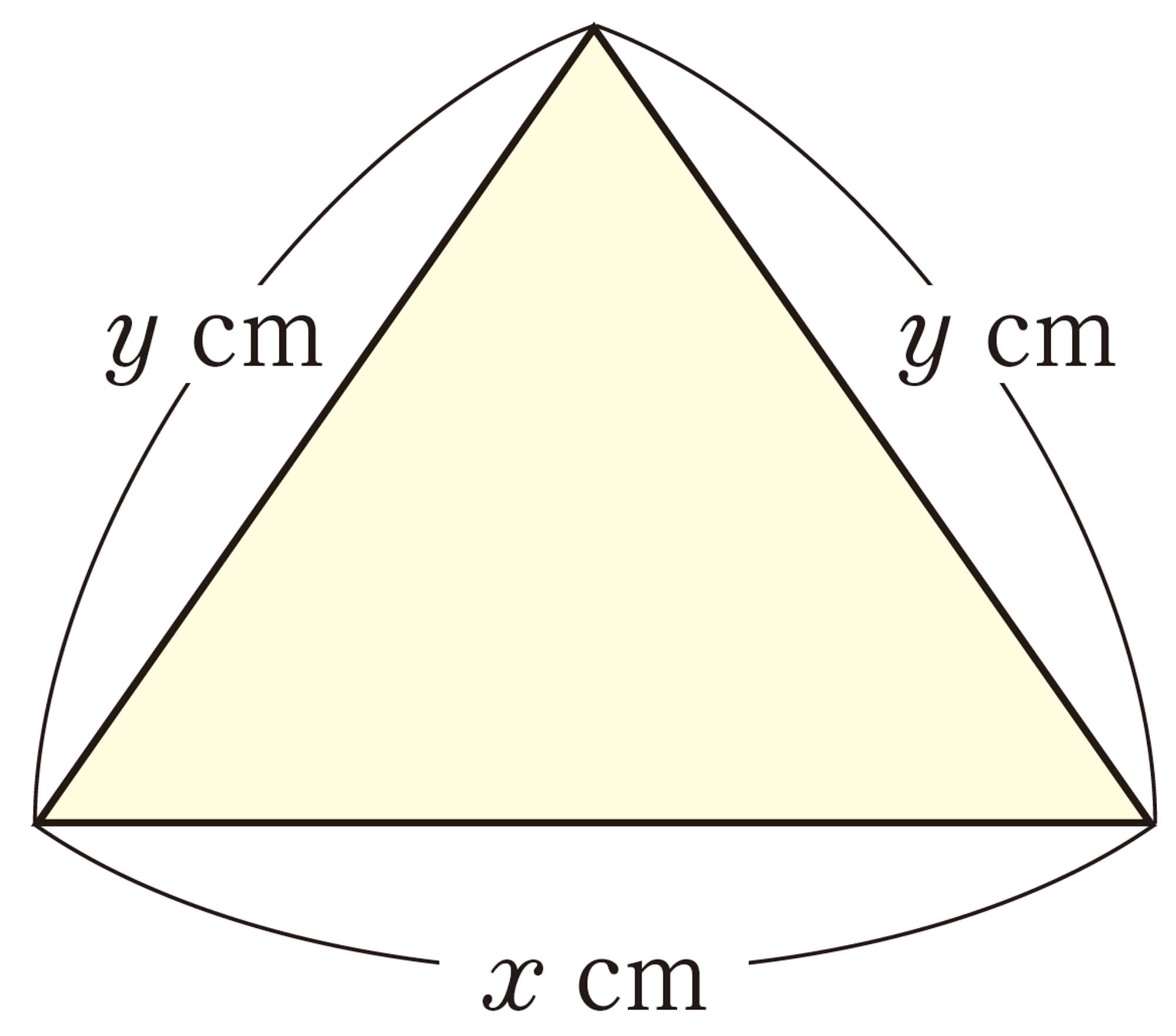
⑴ 1本a円の鉛筆3本と1個b円の消しゴム2個の代金の合計は，300円より高い。
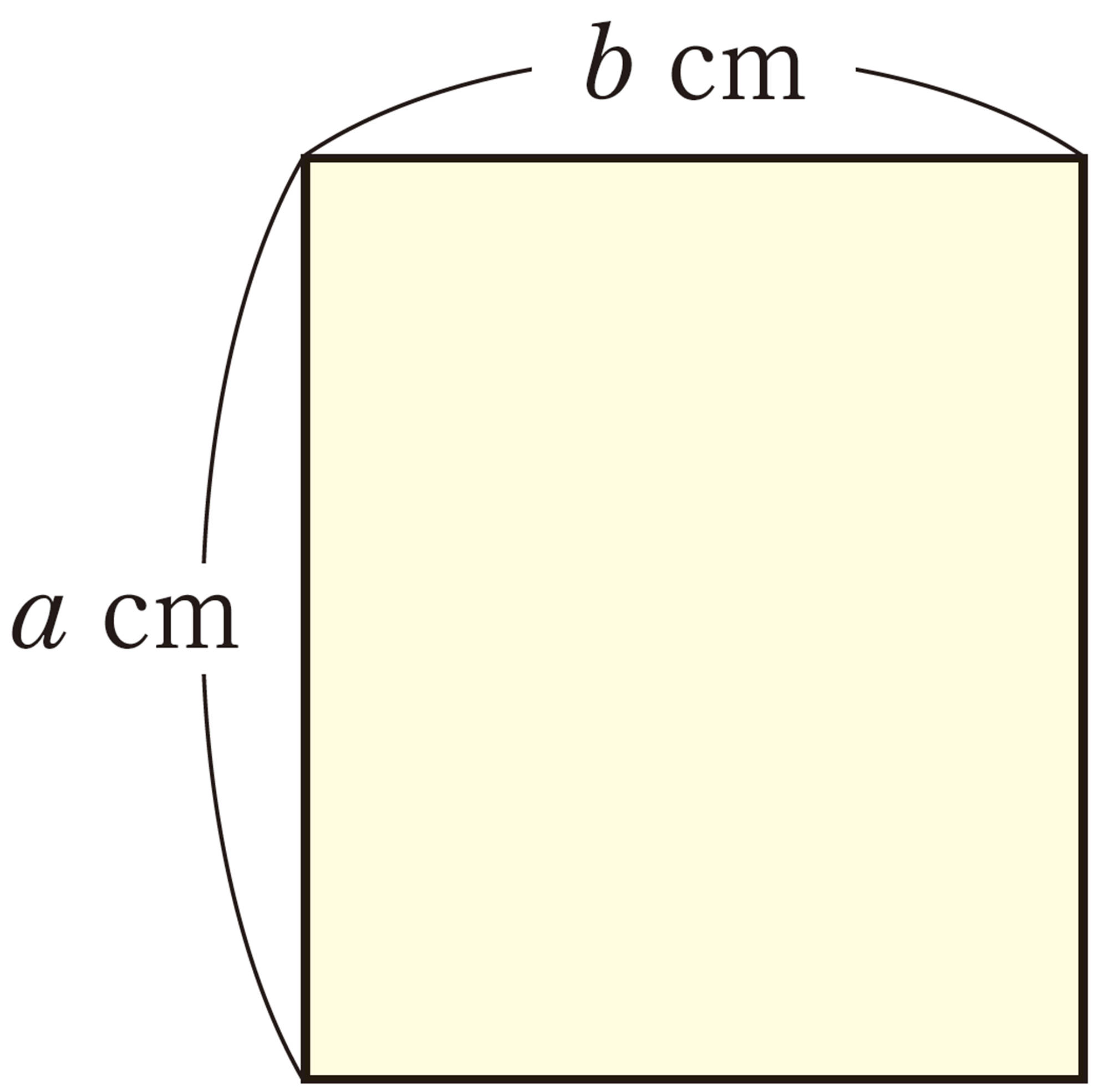
⑵ 1個3 kg の荷物a個と1個5 kg の荷物b個の重さの合計は，40 kg である。
⑶ 3600 m の道のりを分速x m で走ると，かかった時間は15分未満だった。
⑷ ある数xの3倍に5を加えると，17になる。
ふりかえり 小学校4年
a未満 … aより小さい。
数量の関係が，
「aはb以上」であることを，[mathjax]\(a \geqq b\)，
「cはd以下」であることを，[mathjax]\(c \leqq d\)
と表す。記号 [mathjax]\(\geqq\)，[mathjax]\(\leqq\) も不等号といい，これらの記号を使って数量の関係を表した式も不等式という。
ふりかえり 小学校4年
a以上 … ちょうどa， またはaより大きい。
a以下 … ちょうどa，またはaより小さい。
注意 [mathjax]\(a \geqq b\)は，[mathjax]\(a \gt b\)または[mathjax]\(a=b\)を1つにまとめたもの，[mathjax]\(c \leqq d\)は，[mathjax]\(c \lt d\)または[mathjax]\(c=d\)を1つにまとめたものである。
例 ２
⑴ 1年生で野球のチームをつくるために，1組からa人，2組からb人を選び，人数の合計が9人以上となるように
する。このことは，
[mathjax]\(a+b \geqq 9\)
と表すことができる。
⑵ 体重60 kg の人が1個20 kg の荷物 a個とともにエレベーターに乗り，重さの合計が制限重量の300 kg 以下となるようにする。このことは，
[mathjax]\(20a+60 \leqq 300\)
と表すことができる。
<1年p.101>
問 ３ 次の数量の関係を，不等式で表しなさい。
⑴ 男子a人と女子b人の人数の合計は，30人以上であった。
⑵ 1本40円の鉛筆 a本と1冊180円のノート1冊を買ったときの代金の合計が，500円以下であった。
⑶ 長さx m の紙テープを5等分したところ，1本分の長さは2 m 以上になった。
⑷ a人の参加者のうち25人が帰ったので，残った人数は10人以下になった。
等式や不等式の表している数量
例 ３ 右の図のような底辺がx cm， 等しい2辺がy cm の二等辺三角形がある。このとき，
[mathjax]\(2y \gt x\)
は，等しい2辺の長さの和が，底辺の長さよりも長いことを表している。
問 ４ ある植物園の入園料は，大人1人がx円，中学生1人がy円です。このとき，次の等式や不等式がどんな数量の関係を表しているか答えなさい。
⑴ [mathjax]\(2x+y=1250\)
⑵ [mathjax]\(3x \gt 5y\)
問 ５ 縦a cm，横b cm の長方形があります。このとき，次の等式や不等式は，この長方形について，どんな数量の関係を表していますか。ことばで説明しなさい。
⑴ [mathjax]\(a \gt b\)
⑵ [mathjax]\(ab=48\)
⑶ [mathjax]\(2(a+b) \leqq 32\)
どんなことがわかったかな
数の大小関係を等号や不等号を用いて表したように，文字式で表された2つの数量の大小関係も，等号や不等号を用いて表すことができます。
