<1年p.65>
２章 Chapter 2 文字式
1節 文字式
2節 式の計算
ストロー4本で正方形をx個つくると，ストローは[mathjax]\((4 \times x)\)本必要だね。
ストロー3 本で正三角形をx 個つくると， ストローは[mathjax]\((3\times x)\)本必要だよ。
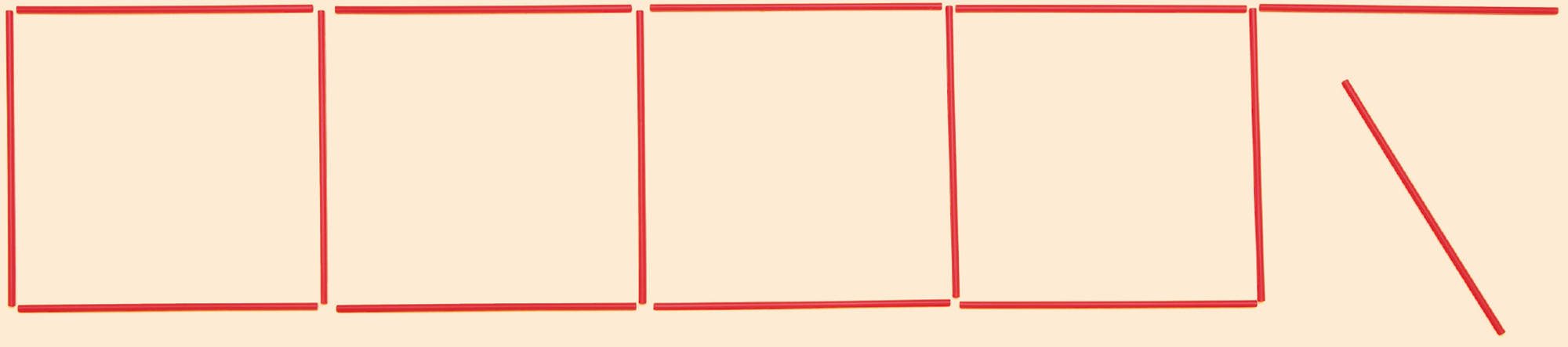
ストローで，正方形と正三角形を，それぞれx 個つくると，ストローは[mathjax]\((4 \times x)+(3 \times x)\)本必要だね。
ストローで，正方形と正三角形を1個ずつつくると，7本必要だから，それぞれx個つくると，[mathjax]\((7 \times x)\)本必要だよ。2つの式は，同じになるはずだよね。
？ 文字の入った式をたすことはできるのかな？
<1年p.66>
1節 文字式
ストローは何本必要？
同じ長さのストローを使って，正方形を横につないだ形をつくります。正方形を100個つくるとき，ストローは何本必要でしょうか。
1個つくるのに4本いるから，[mathjax]\(4 \times 100\)で，400本必要だと思う。
それだと2個のとき，[mathjax]\(4 \times 2\)で 8本になるけどいいのかな。
正方形の数が，もっと少ない場合で考えてみよう。
【１】 真央さんは，正方形の数とストローの本数を次の図のようにまとめました。□にあてはまる数を入れましょう。
<1年p.67>
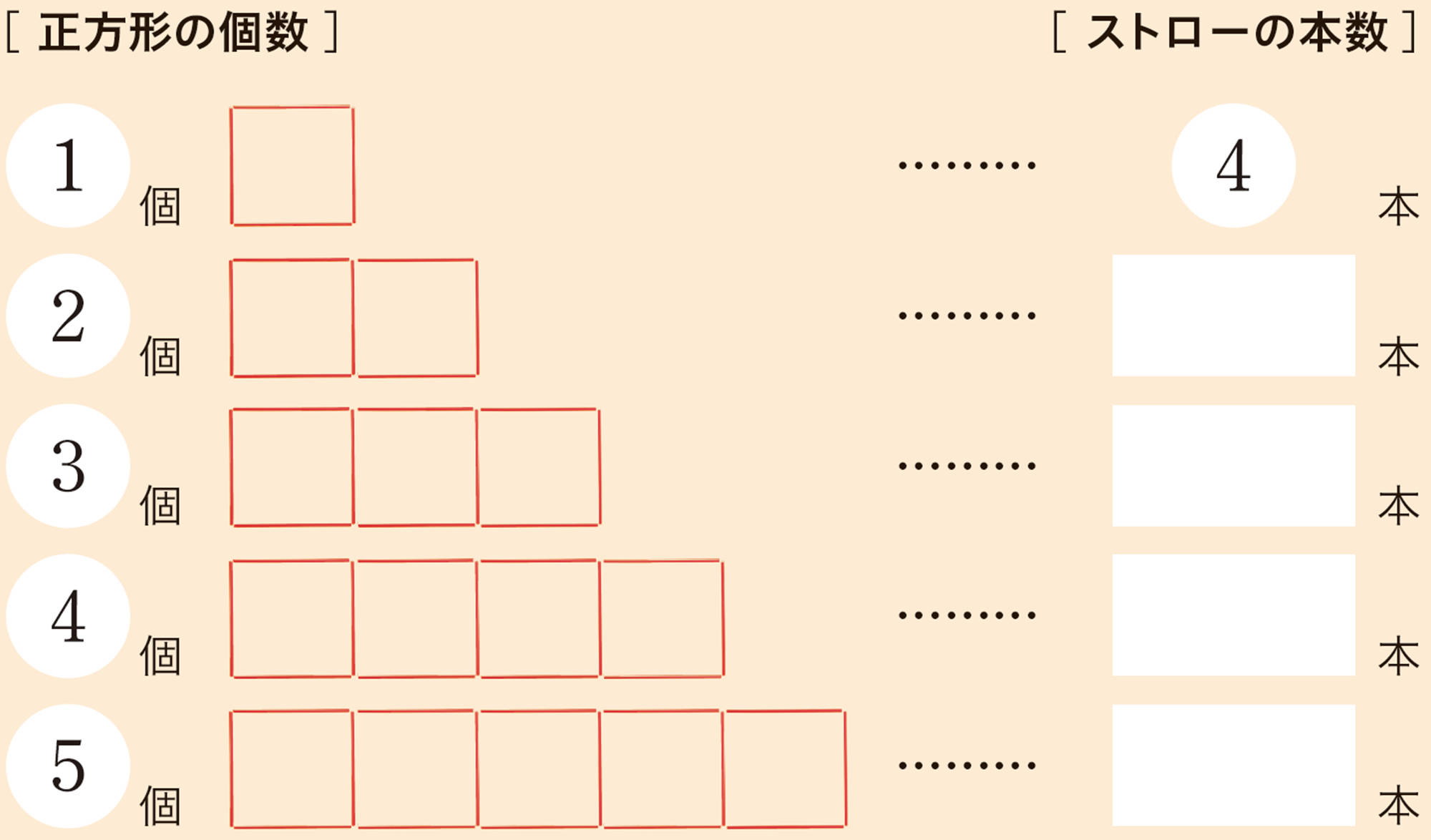
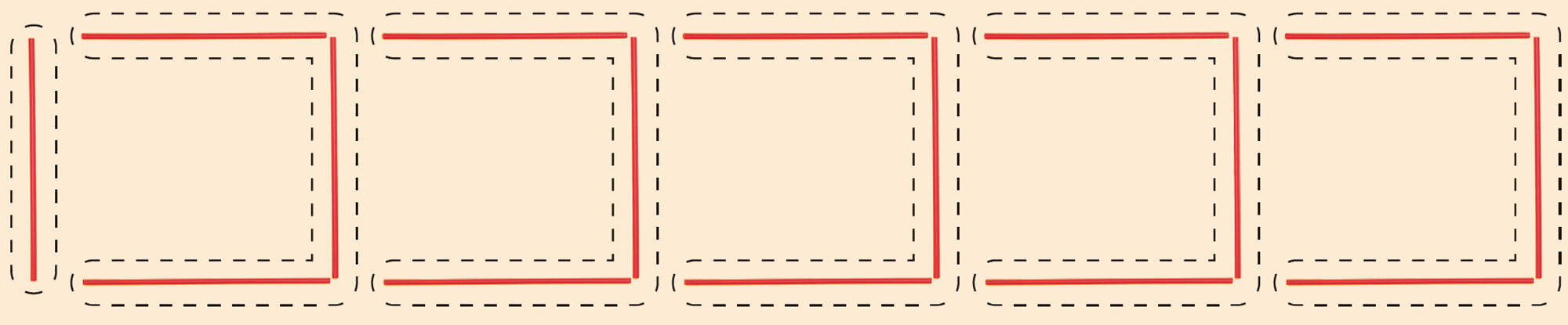
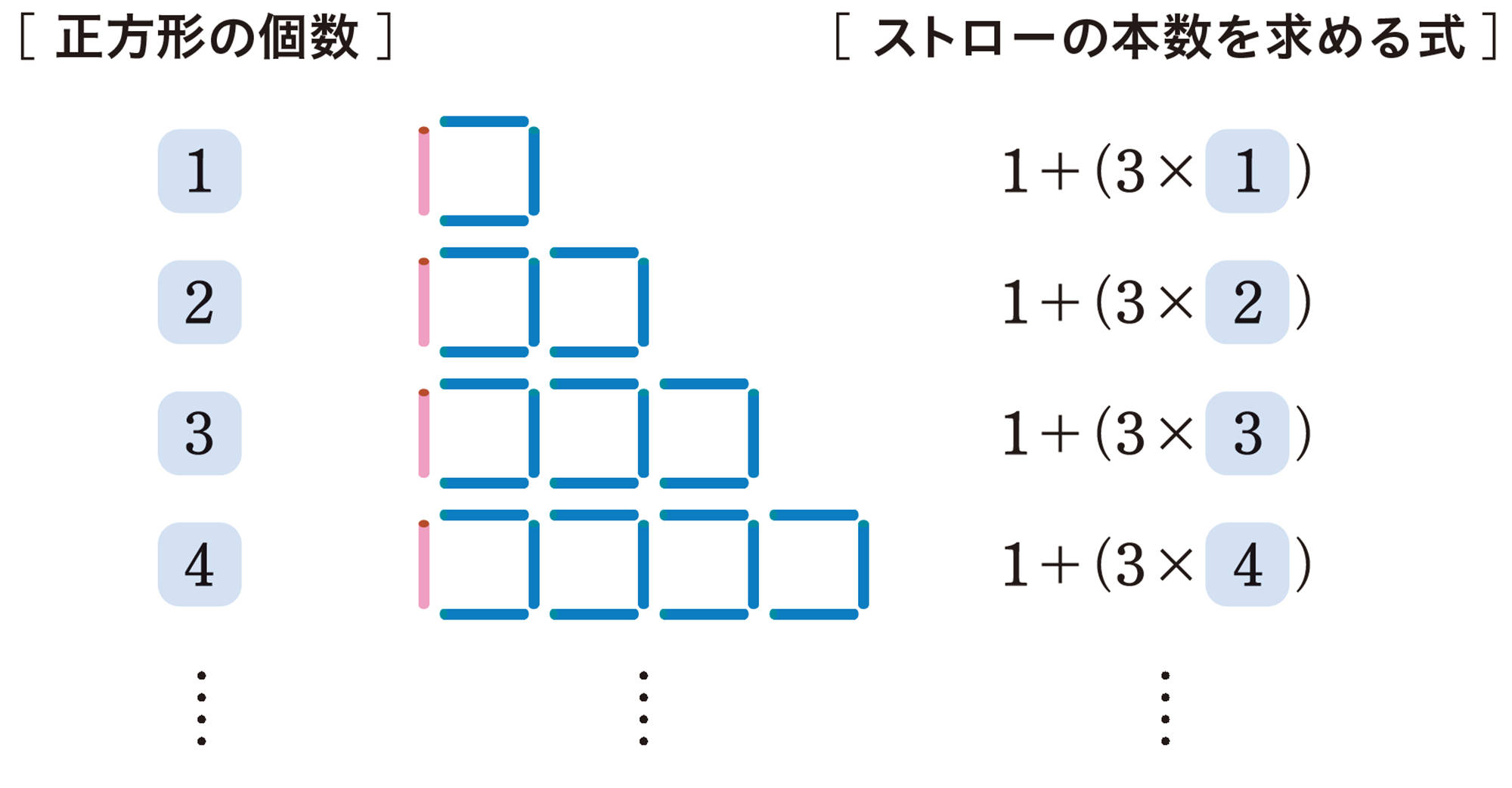
【２】 美月さんは，正方形が5個のときのストローの本数を求めるために，次の図のように考えて式をつくりました。美月さんの考えを説明してみましょう。
[mathjax]\(1+3 \times 5\)
[mathjax] \(1\)，[mathjax] \(3\)，[mathjax] \(5\)は，それぞれ何を表しているのかな。
【３】 美月さんの考え方で，正方形が6個のとき，ストローの本数を求める式はどうなるでしょうか。また，正方形が10個のときはどうなるでしょうか。
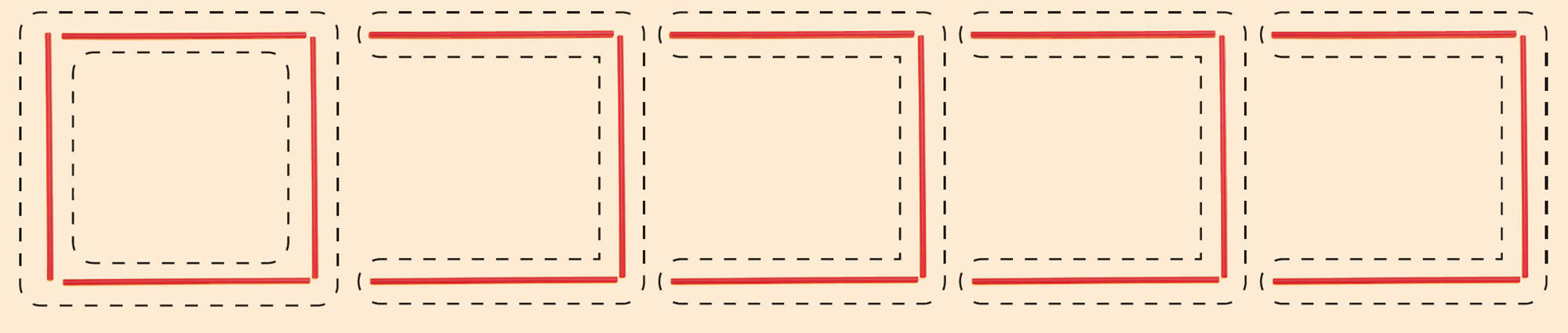
【４】 拓真さんは，正方形が5個のときのストローの本数を求めるために，次の図のように考えて式をつくりました。拓真さんの考えを説明してみましょう。
[mathjax]\(4 +3\times (5-1)\)
【５】 美月さんと拓真さんの式で，正方形の数が変わるとどこの数値が変わるでしょうか。また，それぞれの考え方で，正方形が100個のときのストローの本数を求める式を書いてみましょう。
【６】 美月さんや拓真さんとは別の考え方で，ストローの本数を求める式をつくりましょう。また，その考え方を説明してみましょう。
次の課題へ！
上の考え方を使って，正方形が何個のときでも，ストローの本数を求める式がつくれないかな？
P.68
次の課題へ！
同じ答えを求める式なのに，ちがう式ができるのはどうしてかな？
P.85
<1年p.68>
１ 文字を使った式
Q Question
[mathjax] \(66\)，[mathjax] \(67\)ページの問題で，正方形の個数を増やしていくとき，ストローの本数を求める式はどうなるでしょうか。美月さんの考え方を使って考えてみましょう。
見方・考え方
いろいろな個数の場合で考えられるかな。
正方形の個数が変わると，式の中で数が変わるところがあるね。
小学校のとき，変わる数はどのように表したかな。
目標 ▷ ストローの本数を求める式について考えよう。
【Q】で考えたように，ストローの本数は，いつでも，
[mathjax]\(1+3 \times\)(正方形の個数)
という式で求めることができる。
正方形の個数は，[mathjax] \(1\)，[mathjax] \(2\)，[mathjax] \(3\)，[mathjax] \(4\)，…といろいろな値をとるが，それを文字aで表せば，ストローの本数を求める式は，
[mathjax]\(1+3 \times a\)
と表すことができる。
このように，文字を使って表した式を文字式 という。
<1年p.69>
問 １ 前ページのストローの本数を求める式で，正方形が20個，30個のときのストローの本数を，それぞれ求めなさい。
式の中の文字を数でおきかえることを，文字にその数を 代入する といい，代入して計算した結果を，その 式の値 という。
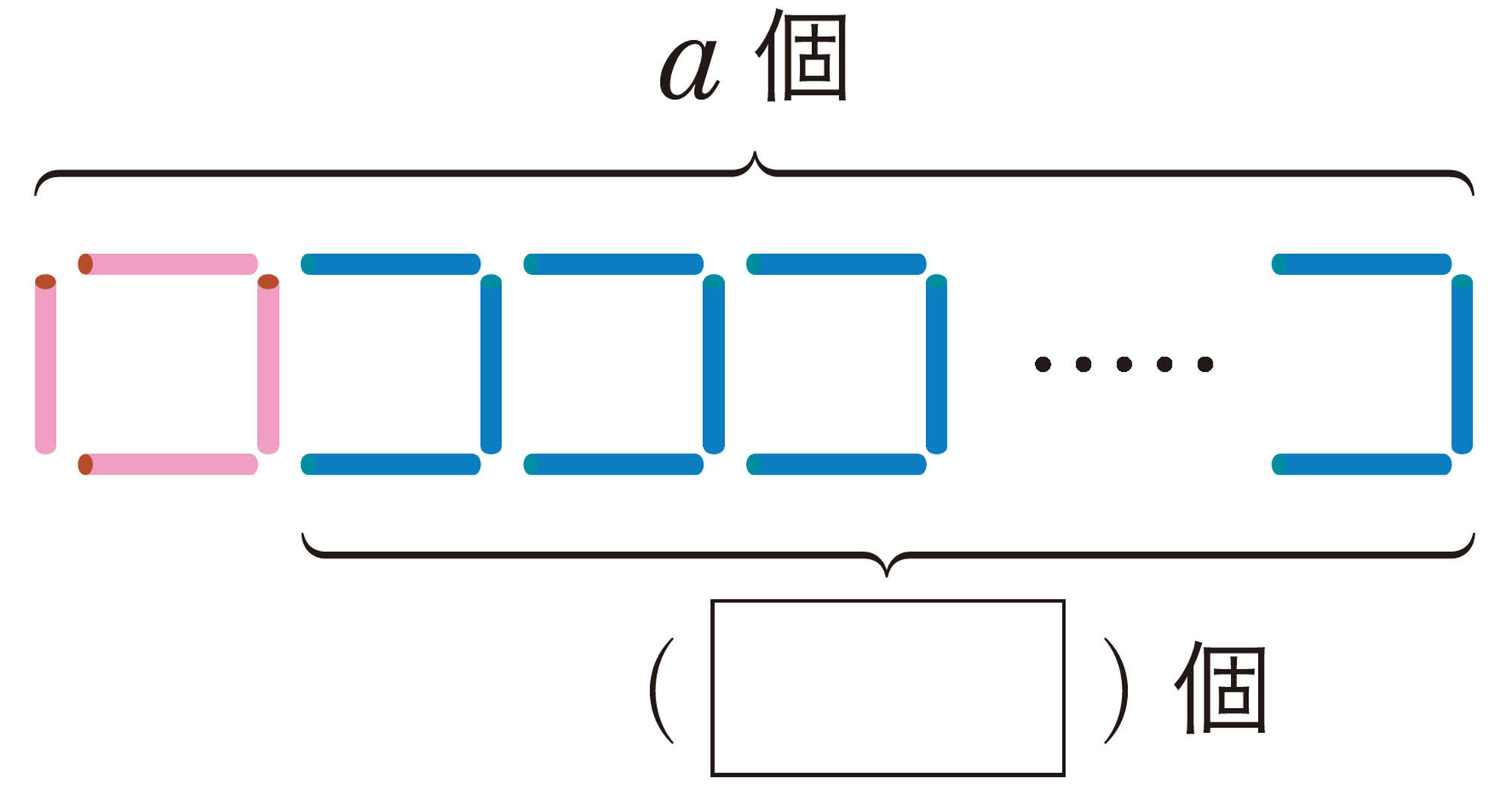
問 ２ [mathjax] \(66\)，[mathjax] \(67\)ページの問題で，拓真さんの考え方を使うと，正方形がa個のときのストローの本数を求める式は[mathjax]\(4+3 \times (a-1)\)となります。次の[mathjax]\(\boxed{\phantom{000}}\)にあてはまる数や式を入れて，説明を完成させなさい。
最初の正方形はストローが[mathjax]\(\boxed{\phantom{00}}\)本必要であるが，2番目の正方形からはストローを[mathjax]\(\boxed{\phantom{00}}\)本ずつ加えていけばよい。正方形は全部でa個であるから，最初の1個を除いた正方形の個数は([mathjax]\(\boxed{\phantom{000}}\))個である。したがって，ストローの本数を求める式は，[mathjax]\(4+3 \times (a-1)\)
問 ３ 問2の式で，正方形が20個，30個のときのストローの本数を，それぞれ求めなさい。また，問1で求めた値と比べなさい。
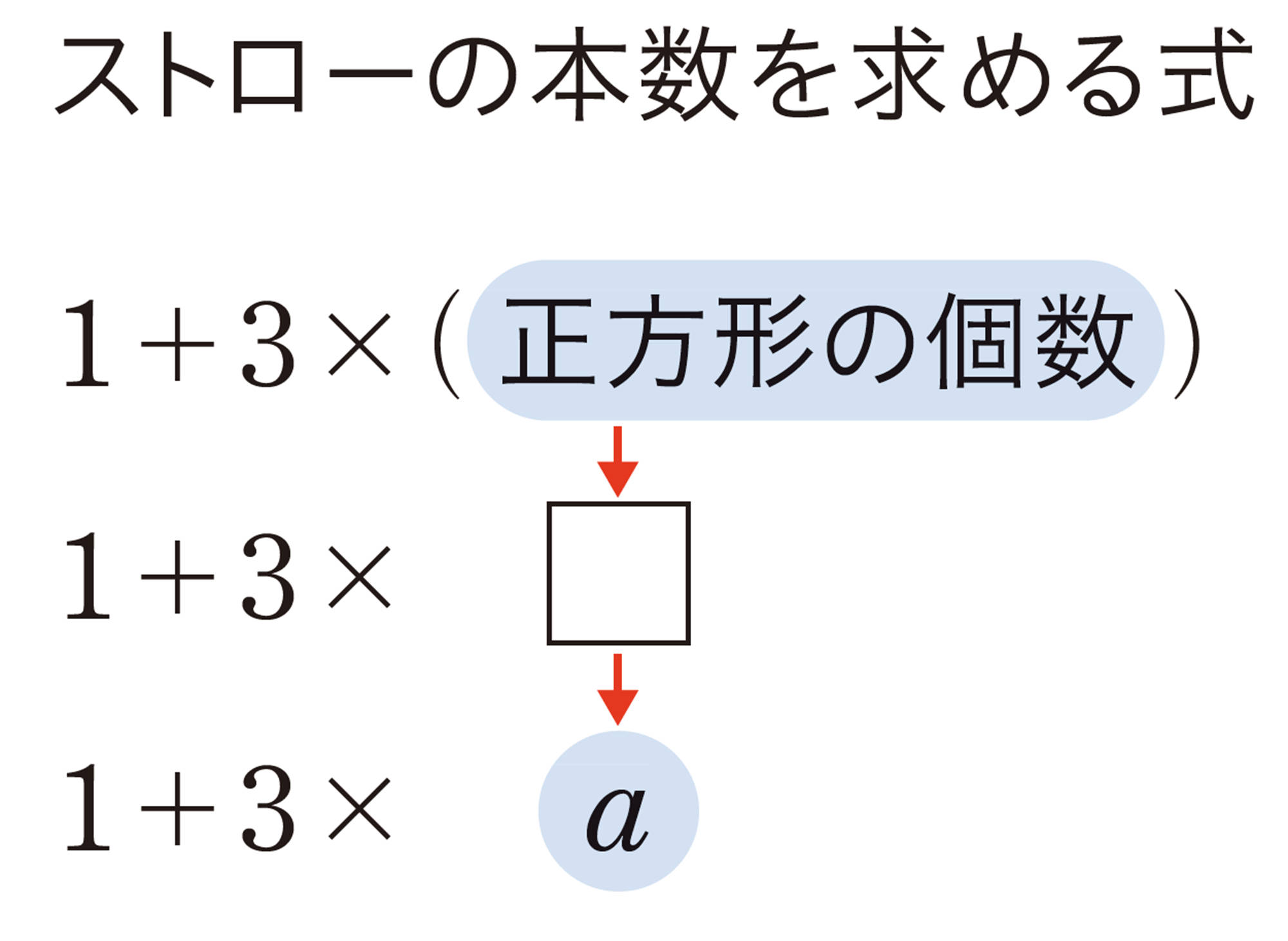
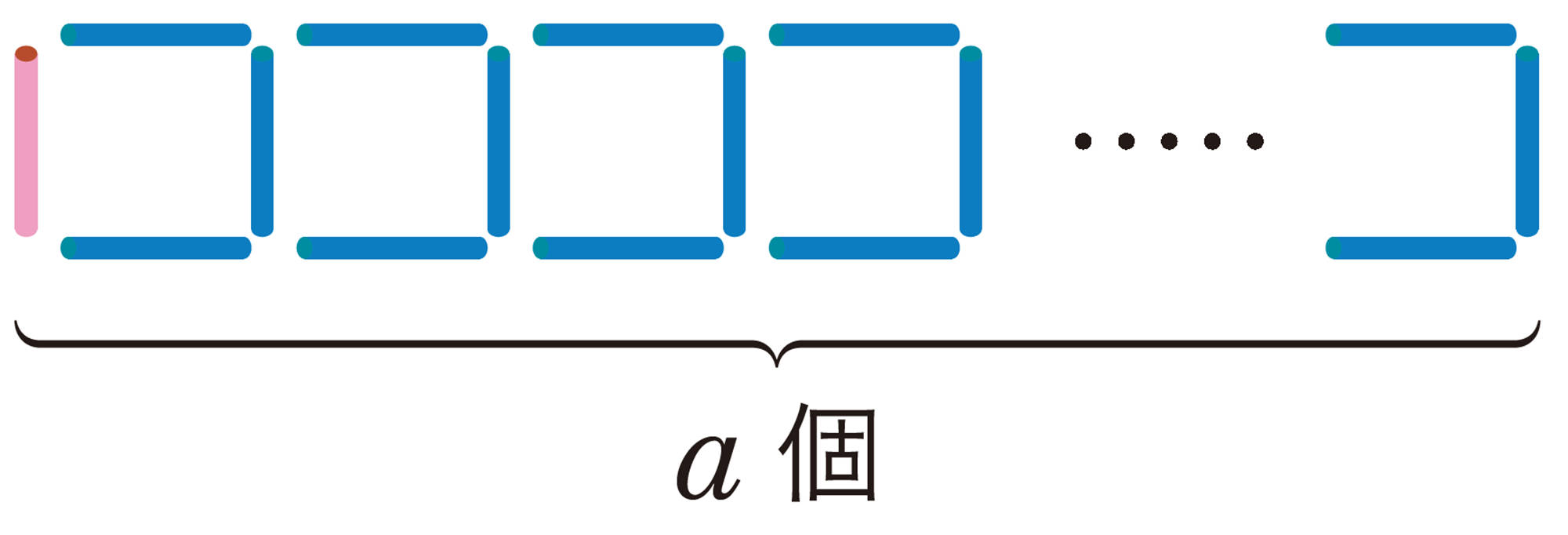
前ページの【Q】の考え方で，正方形がa個のとき，ストローの本数を求める式は，[mathjax]\(1+3 \times a\)と表すことができる。また，そのときのストローの本数は，[mathjax]\((1+3 \times a)\)本と表すことができる。すなわち，文字を使って表した式は，ストローの本数の求め方を表すと同時に，求めた結果を表している。
問 ４ 問2の考え方で，正方形がa個のとき，ストローの本数は何本と表すことができますか。また，[mathjax]\(a=100\)のときの式の値を求めなさい。このとき，求めた式の値は何を表していますか。
<1年p.70>
いろいろな数量を文字式で表してみよう。
例 １ 1個akg の荷物5個の重さは，
[mathjax]\((a \times 5)\)kg
と表すことができる。
問 ５ 例1で，荷物が1個12kg のときの重さの合計を求めなさい。
問 ６ 次の数量を，文字式で表しなさい。
⑴ 1個x円の品物8個を買ったときの代金
⑵ 千円札1枚でa円の品物を買ったときのおつり
⑶ 長さxm のテープを4等分したときの1本分の長さ
解答
1本60円の鉛筆a本の代金は， [mathjax] \( 60\times a\)円
1冊100円のノートb冊の代金は，[mathjax] \( 100\times b\)円
したがって， 代金の合計は，
[mathjax] \( (60\times a+100\times b)\) 円
と表すことができる。
答 [mathjax] \((60\times a+100\times b)\) 円
問 ７ 例2で，[mathjax] \(a=5\)，[mathjax] \(b=3\)のときの式の値を求めなさい。また，それはどんなことを表していますか。
問 ８ 次の数量を，文字式で表しなさい。
⑴ 80円の色鉛筆x本と30円の画用紙y枚を買ったときの代金の合計
⑵ 1個ag のおもり3個と1個bg のおもり1個の重さの合計
どんなことがわかったかな
文字を使うと，いろいろな数量を文字式で表すことができます。
次の課題へ！
文字式で表すとき，どんな表し方をすればいいのかな？
P.71
