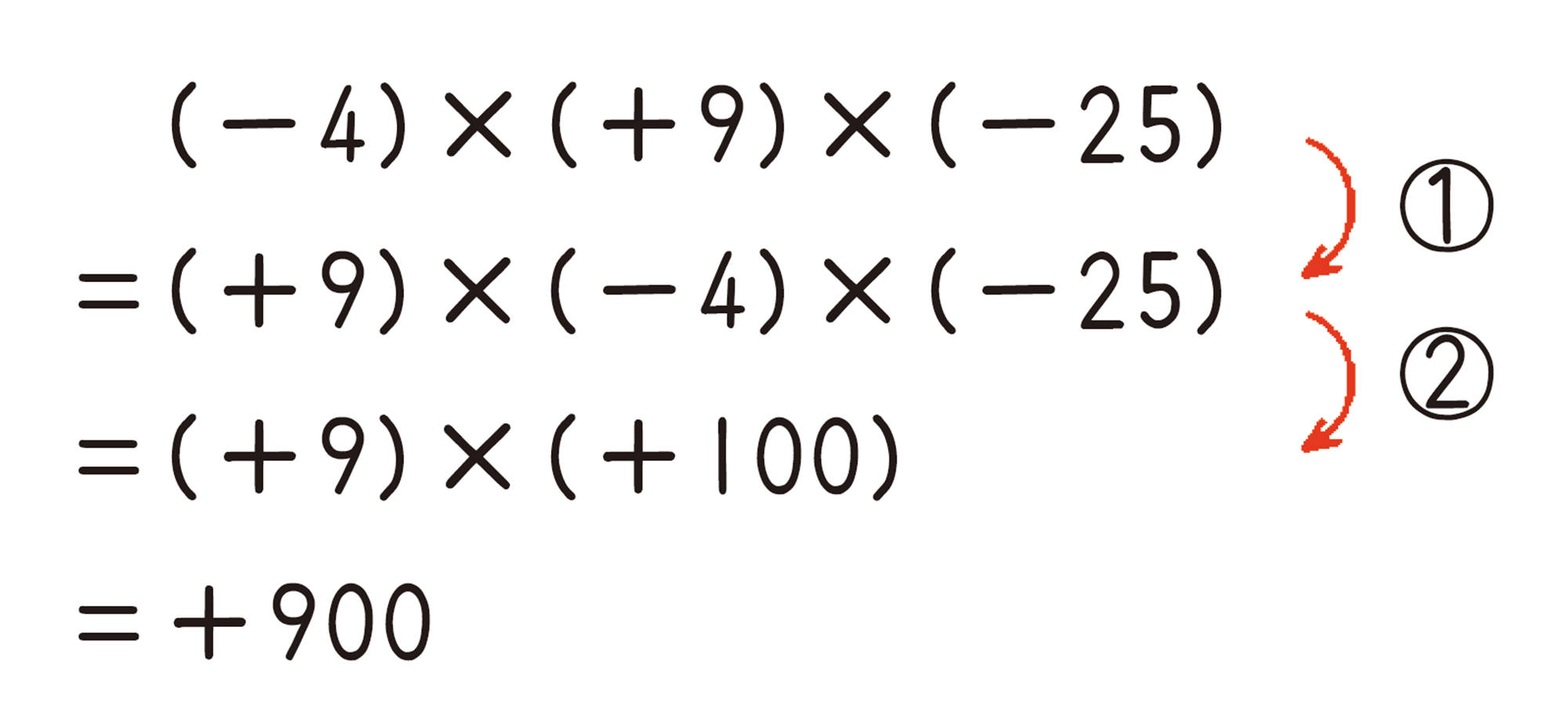<1年p.35>
３節 乗法・除法
負の数のかけ算もできるのかな？
次のような正の数と負の数の加法と減法の計算ができるようになりました。
⑴
⑵
⑶
⑷
正の数と負の数のかけ算やわり算の計算ができるか考えてみましょう。
まず，かけ算について考えてみよう。
速さ，時間，道のりの関係で考えてみよう。
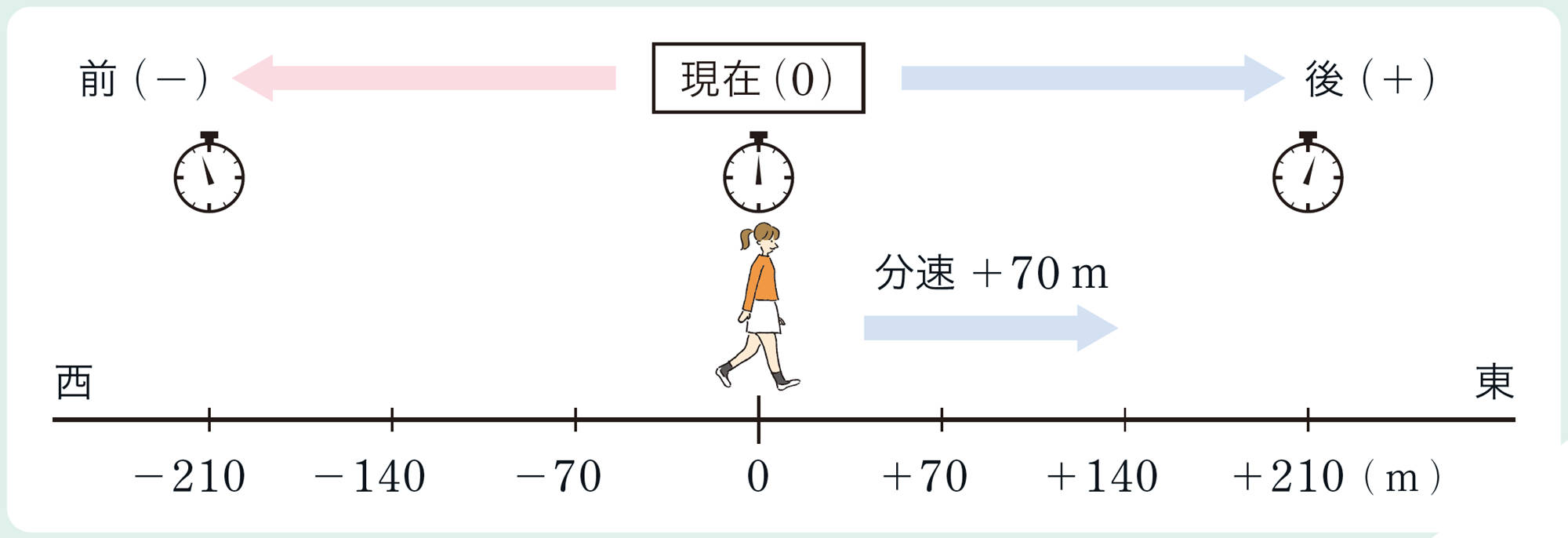
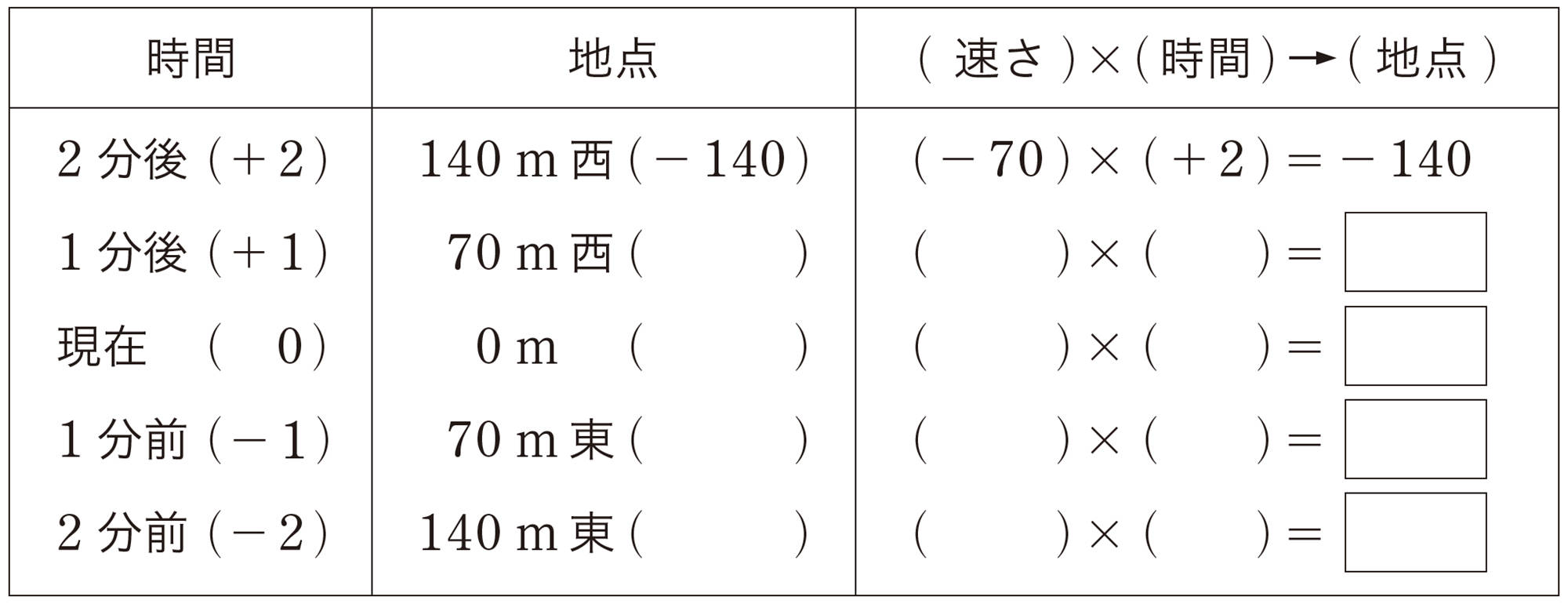
【1】 結菜さんは，東に向かって分速70m で歩いています。現在の地点を0m とし，東の方向を正の方向とします。また，1分後を+1分とします。結菜さんは，1分後，2分後にはどの地点にいるでしょうか。次の図に矢印↓で示してみましょう。
速さ，時間，道のりの関係だから，速さ[mathjax]\(\times\)時間[mathjax]\(=\)道のりの式で考えられると思う。
1分前，2分前にはどの地点にいたかな。
次の課題へ！
正の数，負の数のかけ算も，加法，減法と同じようにできるのかな？
P.36
<1年p.36>
１ 乗法
Q Question
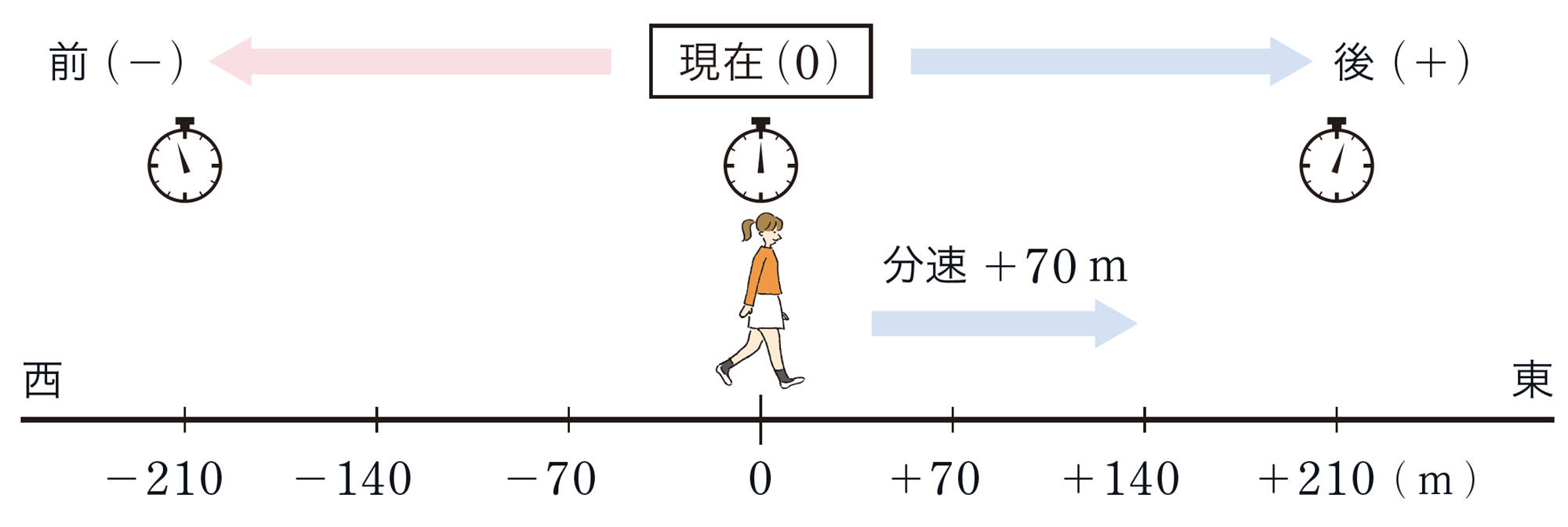
前ページの【１】で，次の問題に答えましょう。
⑴ 結菜さんは，1分前，2分前にはどの地点にいましたか。次の図に矢印[mathjax]\(\downarrow\)で示してみましょう。
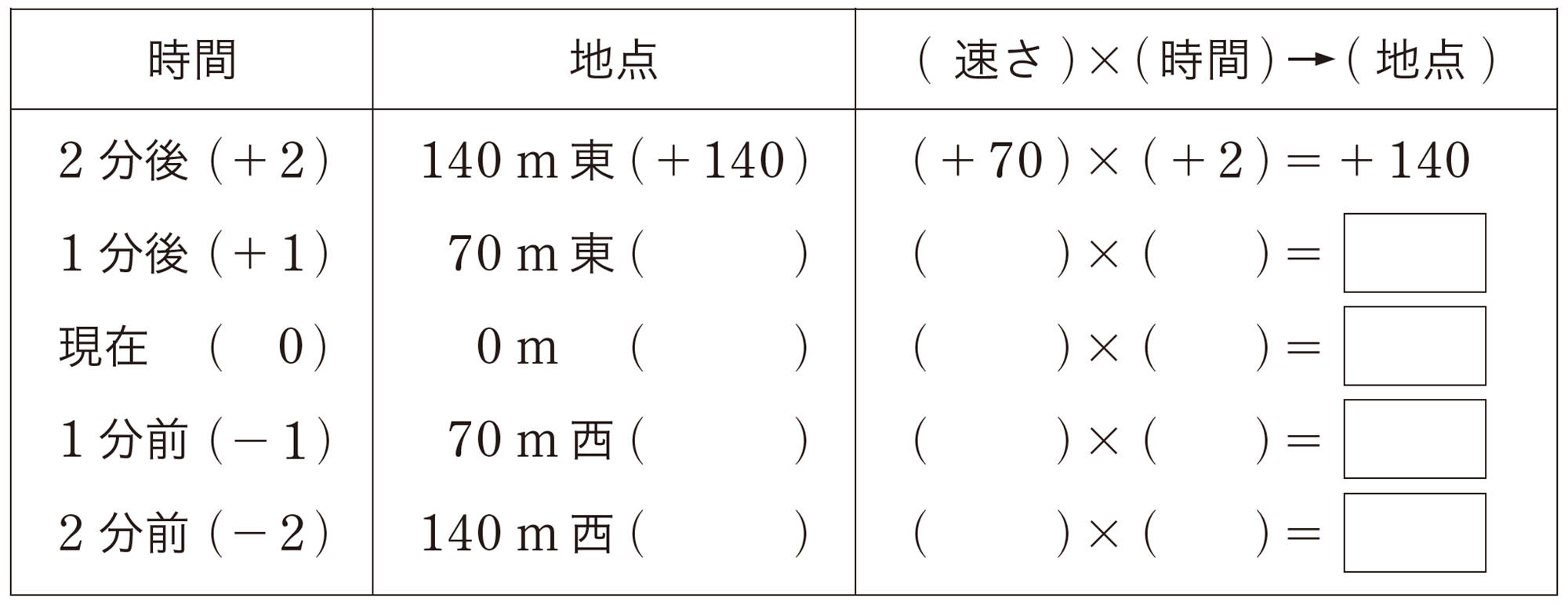
⑵ 前ページや⑴をもとに，次の表の( )や [mathjax]\(\boxed{\phantom{000}}\) にあてはまる数を入れて，結菜さんのいる地点を式で表してみましょう。
見方・考え方
具体的な場面を式に表せるかな。
時間が負の数でも，かけ算の式で表せるのかな。
かけ算のきまりを使って考えられるかな。
目標 ▷ 正の数，負の数のかけ算を考えよう。
問 １ 【Q】 で，結菜さんは，5分後，10分前には，それぞれどの地点にいますか。また，その地点を式で表しなさい。
<1年p.37>
Q Question
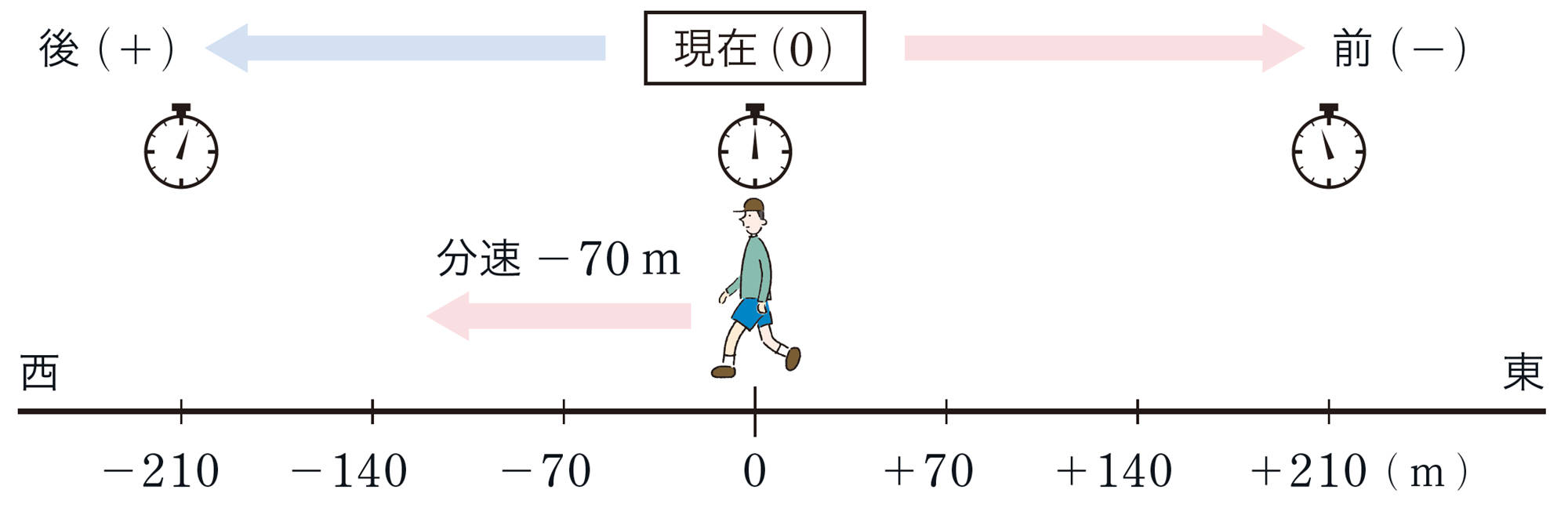
陸さんは，西に向かって分速70m で歩いています。現在の地点を0m とし，東の方向を正の方向とします。また，1分後を[mathjax] \(+1\)分とします。
⑴ 陸さんは，1分後，2分後にはどの地点にいますか。また，1分前，2分前はどの地点にいましたか。次の図に矢印↓で示してみましょう。
⑵ 次の表の( )や[mathjax]\(\boxed{\phantom{000}}\)にあてはまる数を入れて，陸さんのいる地点を式で表してみましょう。
見方・考え方
速さが正の数のときと同じように考えられるかな。
時間が負の数でも，かけ算の式で表せたね。
速さが負の数でも，同じようにかけ算で考えられるかな。
問 ２ 【Q】で，陸さんは，5分後，10分前には，それぞれどの地点にいますか。また，その地点を式で表しなさい。
かけ算のことを 乗法 という。その結果が積である。
問 ３ 前ページの【Q】や上の【Q】で，かける数が1増えるごとに，その積はどのように変化していますか。また，そのちがいについて話し合いなさい。
<1年p.38>
符号や絶対値に着目した乗法
Q Question
正の数，負の数の乗法では，積の符号や絶対値は，かけ合わせる2数の符号や
絶対値とどんな関係があるでしょうか。36ページの【Q】 や前ページの【Q】 の表をもとに話し合ってみましょう。
符号が同じときとちがうときに分けられそうだね。
何か共通していることがあるかな。
見方・考え方
符号と絶対値に着目すると，どんなきまりを見つけられるかな。
例 １ 同符号の2数の積
⑴
[mathjax]\((+) \times (+) \rightarrow (+)\)
⑵
[mathjax]\((-) \times (-) \rightarrow (+)\)
例 ２ 異符号の2数の積
⑴
[mathjax]\((+)\times (-) \rightarrow(-)\)
⑵
[mathjax]\((-) \times (+) \rightarrow (-)\)
問 ４ 次の計算をしなさい。
⑴ [mathjax]\((+6)\times (+5)\)
⑵ [mathjax]\((-7) \times (-8)\)
⑶ [mathjax]\((+12)\times (-3)\)
⑷ [mathjax]\((-2)\times (+10)\)
正の数，負の数の乗法について，次のようにまとめることができる。
正の数，負の数の乗法
<1年p.39>
問 ５ 次の計算をして，気づいたことをいいなさい。
⑴ [mathjax]\((+14) \times (+1)\)
⑵ [mathjax]\((-6) \times (+1)\)
⑶ [mathjax]\((+14) \times (-1)\)
⑷ [mathjax]\((-6)\times (-1)\)
⑸ [mathjax]\((-8) \times 0\)
⑹ [mathjax]\(0 \times (-8)\)
例 ３
⑴
⑵
問 ６ 次の計算をしなさい。
⑴ [mathjax]\((+0.5) \times (-2)\)
⑵ [mathjax]\((-3.6) \times (-1.4)\)
⑶ [mathjax]\(\require{physics} \left(-\dfrac{2}{3}\right) \times (-9)\)
⑷ [mathjax]\(\require{physics} \left(-\dfrac{4}{7}\right) \times \require{physics} \left(+ \dfrac{7}{8}\right)\)
乗法の交換法則・結合法則
Q Question
次の㋐，㋑の計算をして，その結果を比べましょう。
どんなことがわかるでしょうか。
⑴ ㋐ [mathjax]\((+4) \times (-3)\)
㋑ [mathjax]\((-3) \times (+4)\)
⑵ ㋐ [mathjax]\(\{(+2) \times (-4)\} \times (-5)\)
㋑ [mathjax]\((+2)\times \{(-4) \times (-5)\}\)
小学校では，かける順序を変えても積は変わらなかったね。
正の数，負の数が混じった乗法でも，同じことがいえるのかな。
見方・考え方
負の数をふくむ乗法も，小学校のときと同じように計算のきまりが成り立つかな。
<1年p.40>
正の数，負の数の乗法でも，次のことが成り立つ。
乗法の交換法則 [mathjax]\(a \times b = b \times a\)
乗法の結合法則 [mathjax]\((a \times b) \times c = a \times (b \times c)\)
乗法では，交換法則や結合法則を使って，数の順序や組み合わせを変えて計算することができる。
問 ７ 美月さんは，[mathjax]\((-4) \times (+9) \times (-25)\)の計算を，右のように行いました。①，②の計算の手順を，それぞれ説明しなさい。また，計算の順序を変えた理由を説明しなさい。
問 ８ 計算しやすい方法を考えて，次の計算をしなさい。
⑴ [mathjax]\((-50) \times (+17) \times (-2)\)
⑵ [mathjax]\((+9)\times (-4.5)\times (+2)\)
⑶ [mathjax]\(\require{physics} \left(-\dfrac{1}{8}\right) \times (+3.6) \times (-8)\)
⑷ [mathjax]\(\require{physics} \left(+\dfrac{1}{3}\right) \times (-10) \times \require{physics} \left(- \dfrac{3}{5}\right)\)
いくつかの数の積の符号
Q Question
かける数が増えると，積の符号が変わるね。
かける数はすべて負の数だけど，そのことと関係はあるのかな。
見方・考え方
符号に着目して，どんなきまりがあるか見つけられるかな。
<1年p.41>
ある数に正の数をいくつかけても積の符号は変わらないが，負の数を1つかけるごとに積の符号が変わる。
つまり，積の符号は，かけ合わせる負の数の個数によって決まってくる。
例 ４
⑴
⑵
問 ９ 次の計算をしなさい。
⑴ [mathjax]\((-5) \times (-6) \times (+2)\)
⑵ [mathjax]\((-7) \times \require{physics} \left(-\dfrac{3}{14}\right) \times \require{physics} \left(-\dfrac{4}{3}\right)\)
いくつかの数の積について，次のようにまとめることができる。
積の符号と絶対値
乗法では，式の中や答えの正の符号[mathjax]\(+\)を省くことができる。また，式の最初の数のかっこを省くことがある。
問 10 次の計算をしなさい。
⑴ [mathjax]\(4 \times (-2) \times 6\)
⑵ [mathjax]\(-5 \times 2 \times (-7)\)
⑶ [mathjax]\((-3.5) \times (-2) \times 9\)
⑷ [mathjax]\(- \dfrac{1}{3} \times 6 \times (-4) \times (-9)\)
⑸ [mathjax]\(8 \times (-3) \times \dfrac{1}{6} \times \require{physics} \left(-\dfrac{1}{4}\right)\)
⑹ [mathjax]\((-5) \times (-5) \times (-5)\)
<1年p.42>
累乗
前ページの問10 ⑹のように，同じ数をいくつかかけ合わせたものを，その数の 累乗 という。
[mathjax]\(5 \times 5\)を[mathjax] \(5²\)と表して，「5の 2乗 」，[mathjax]\(5 \times 5 \times 5\)を[mathjax] \(5³\)と表して，「5の 3乗 」と読む。また，いくつかけ合わせたかを示す数を，累乗の 指数 という。
注意 2乗を平方，3乗を立方ということがある。
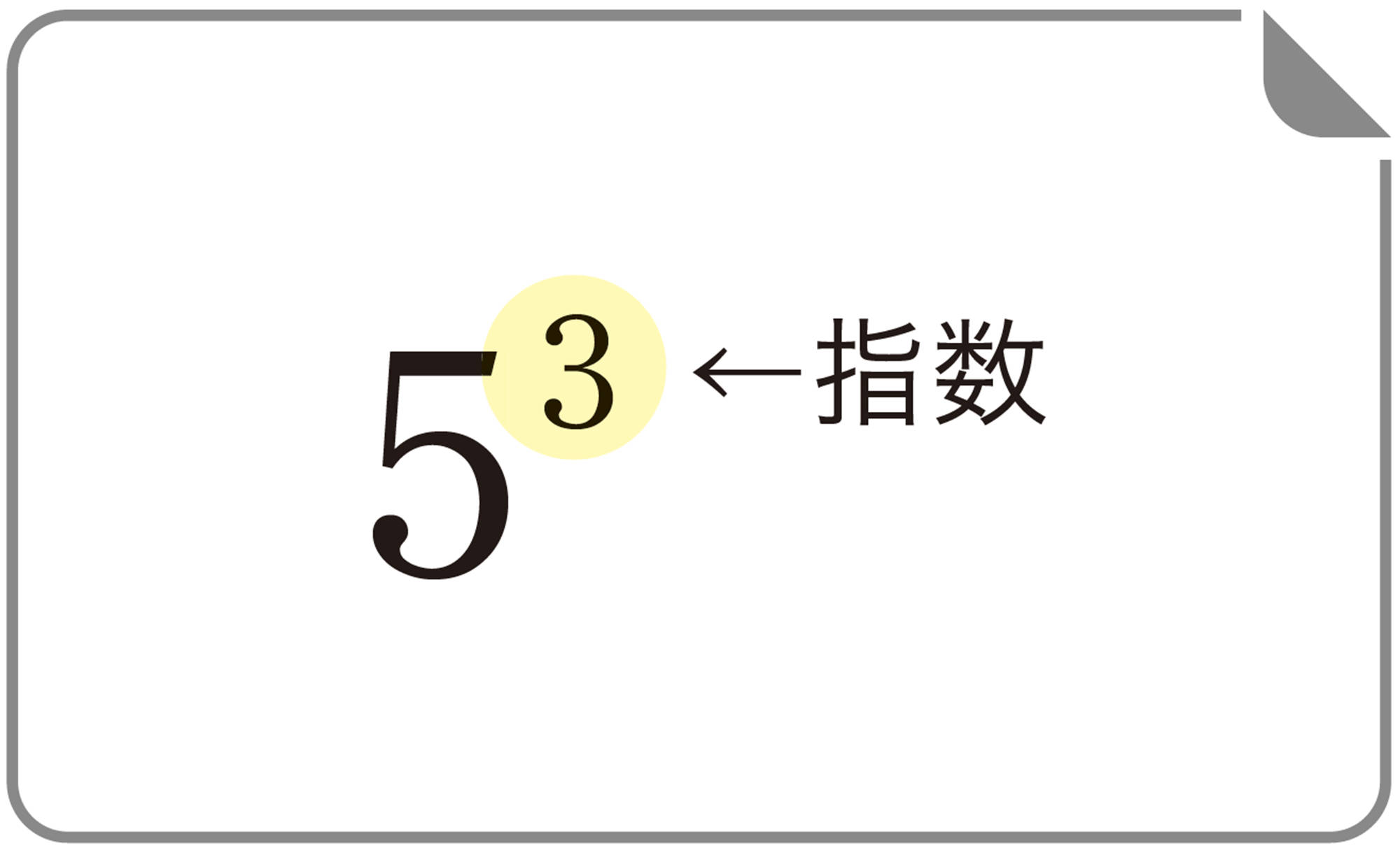
例 ５
⑴
⑵
問 11 次の式を，累乗の指数を使って表しなさい。
⑴ [mathjax]\(2 \times 2 \times 2\)
⑵ [mathjax]\((-4) \times (-4)\)
⑶ [mathjax]\(\require{physics} \left(-\dfrac{3}{5}\right)\times \require{physics} \left(-\dfrac{3}{5}\right)\)
問 12 1辺5 cm の正方形の面積や1辺5 cm の立方体の体積を，累乗の指数を使って表しなさい。また，それぞれの単位について考えなさい。
例 ６
⑴
⑵
[mathjax] \((-3)²\)と[mathjax] \(-3²\)は，式の意味がちがうね。
問 13 次の計算をしなさい。
⑴ [mathjax]\((-8)²\)
⑵ [mathjax]\( -8²\)
⑶ [mathjax]\(\require{physics}\left(-\dfrac{4}{7}\right)^{2}\)
⑷ [mathjax] \(0.3²\)
⑸ [mathjax] \((-2)³\)
⑹ [mathjax] \(-2³\)
P.53
どんなことがわかったかな
正の数，負の数の乗法は，積の符号に注意すれば，小学校のかけ算と同じようにできます。また，乗法の交換法則，結合法則が成り立ちます。
次の課題へ！
正の数，負の数のわり算も，乗法と同じようにできるのかな？
P.43
