<1年p.25>
２ 減法
Q Question
巻末①のカードゲームで，健太さんは2回目が終わったとき[mathjax] \(+5\)の位置にいました。
⑴ 1回目に出たカードが[mathjax] \(+2\)だったとき，
2回目に出たカードは何でしょうか。
⑵ 1回目に出たカードが[mathjax] \(-1\)だったとき，
2回目に出たカードは何でしょうか。
2回目の動きは，結果と1回目の動きの差になるね。
負の数があっても，ひき算で表していいのかな。
見方・考え方
具体的な場面を式に表せるかな。
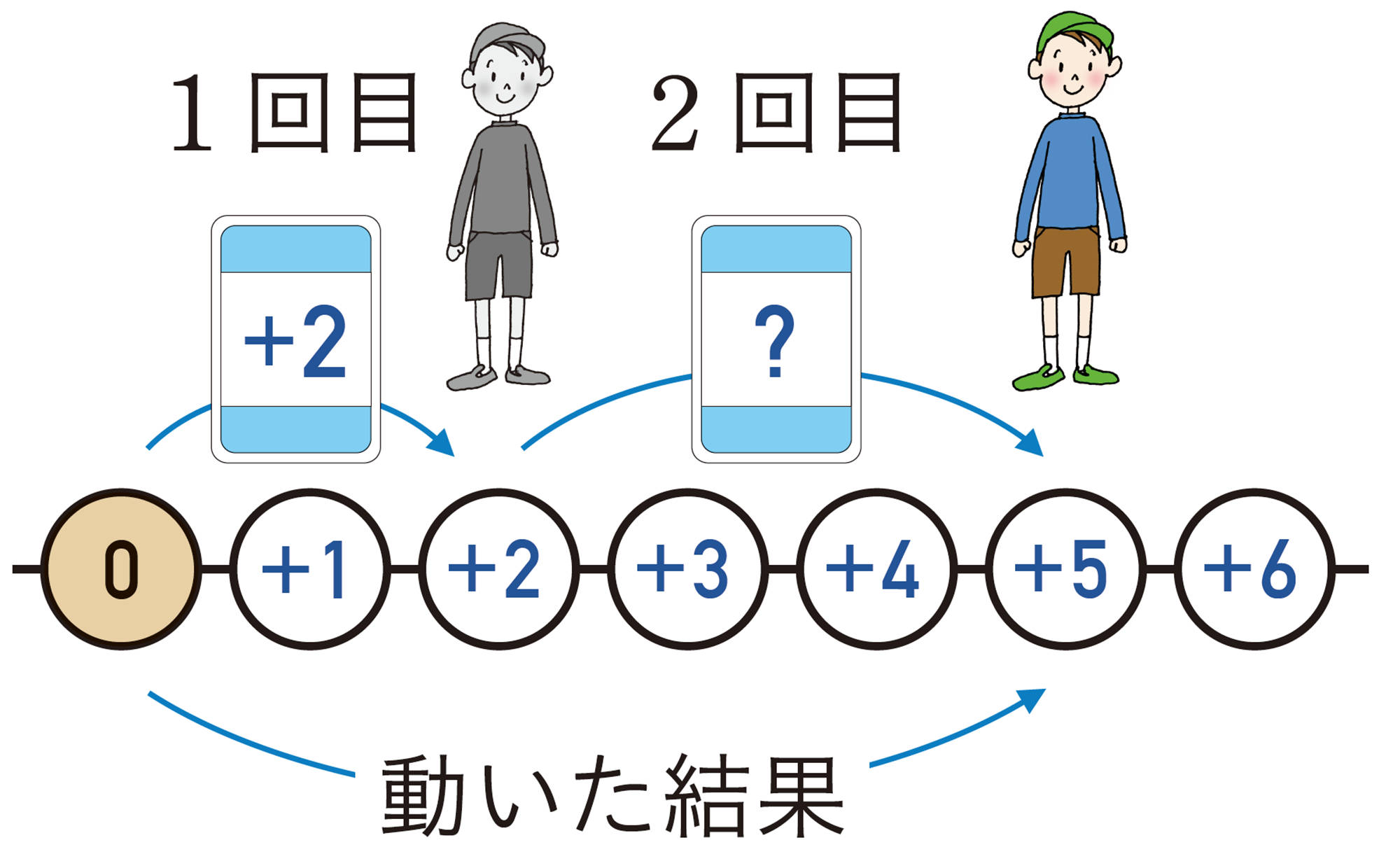
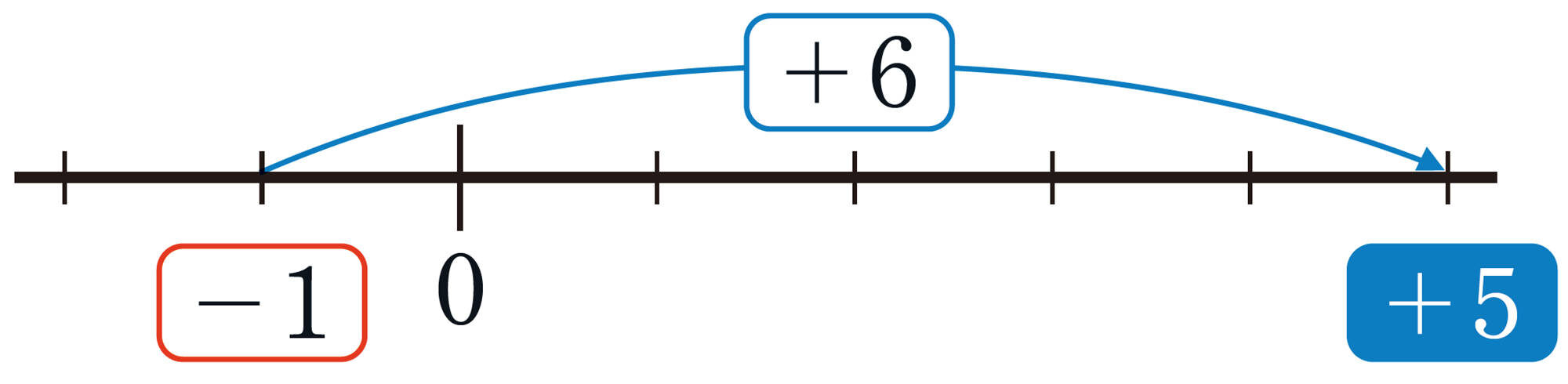
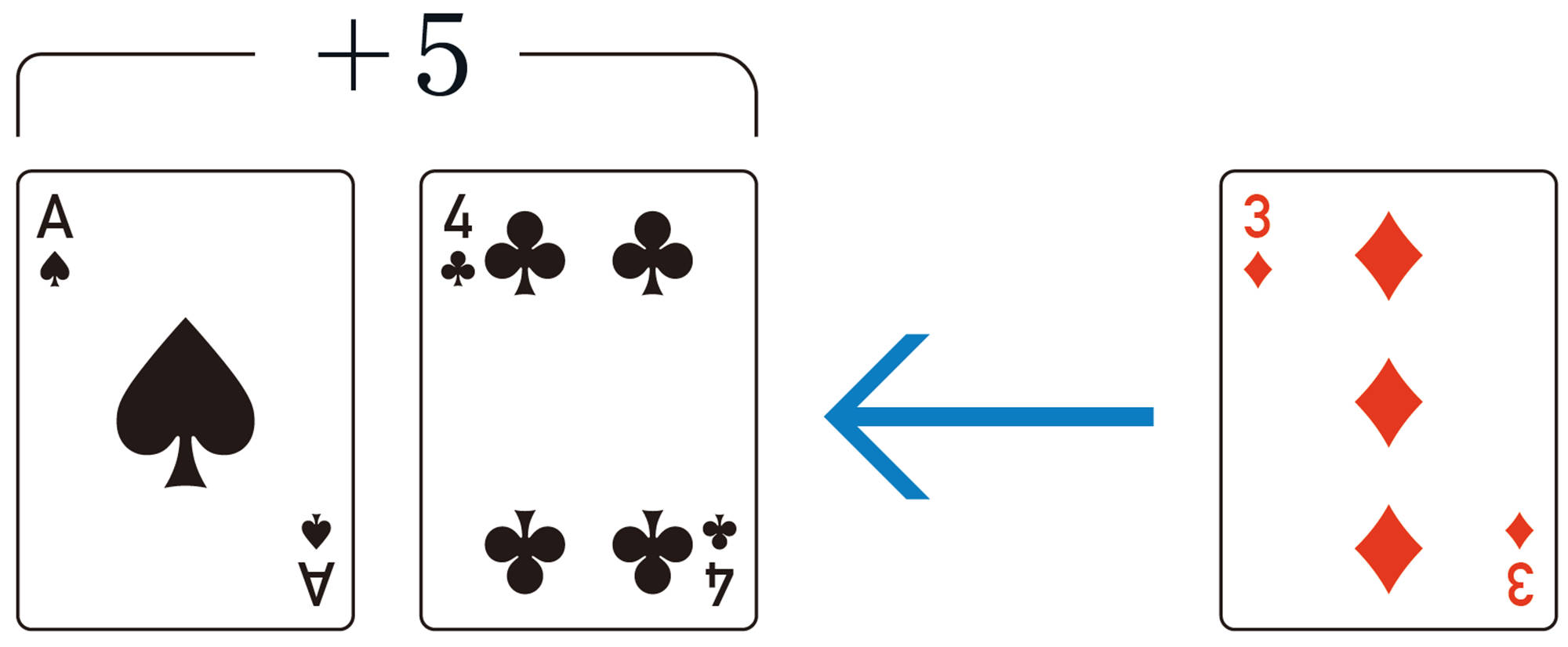
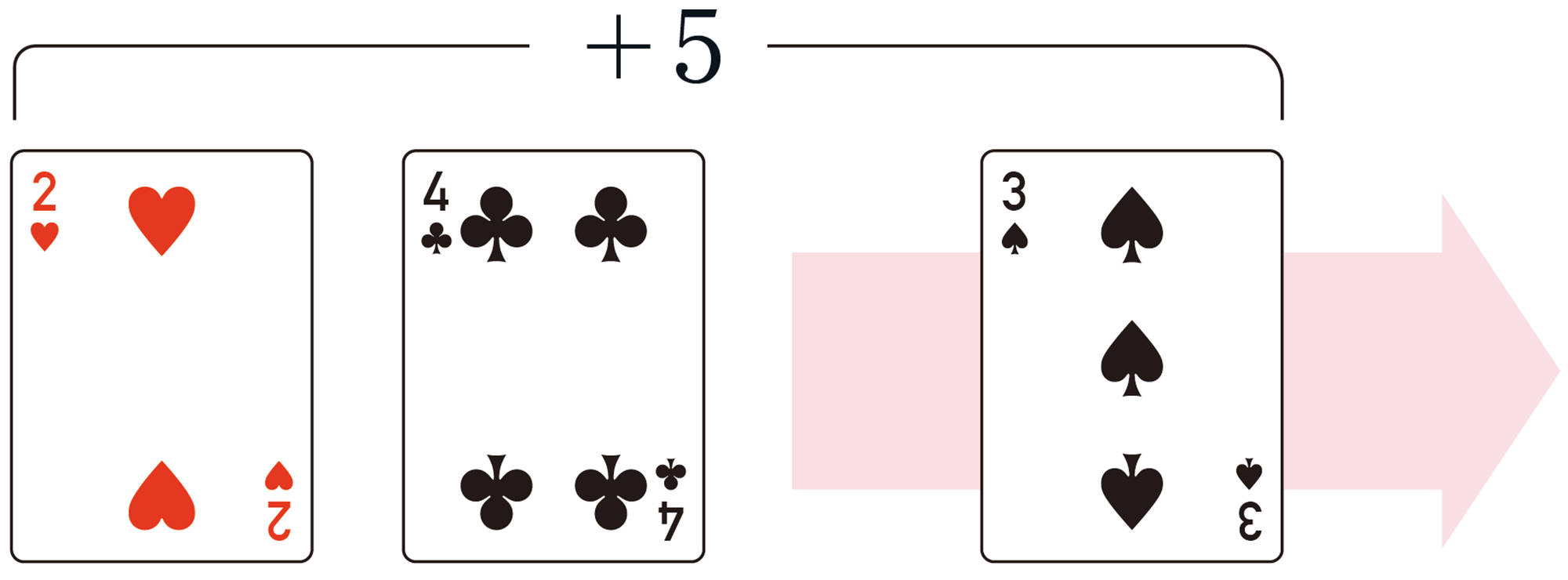
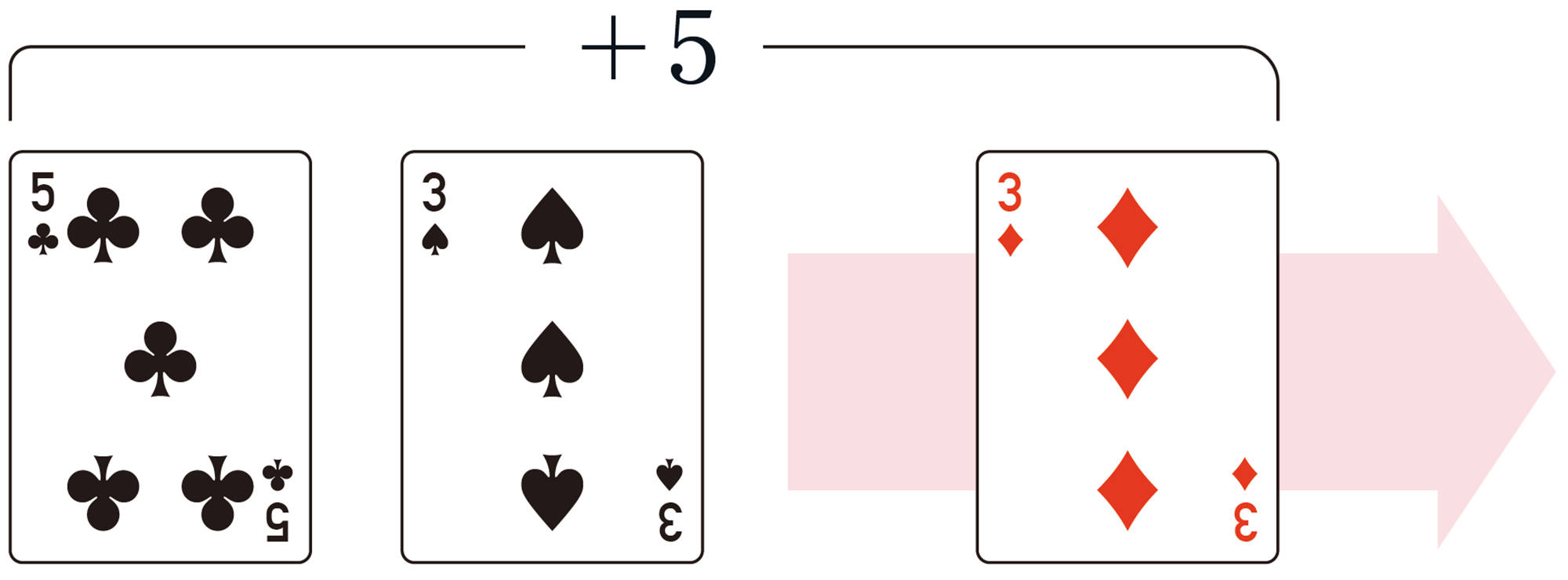
【Q】⑴について，2回目に出たカードを[mathjax]\(\boxed{\phantom{000}}\)とすると， 健太さんのコマが2回目に[mathjax]\(\boxed{\phantom{000}}\)動いて[mathjax] \(+5\)の位置にあるから，健太さんのコマの動きについて，次のような加法の式をつくることができる。
[mathjax]\((+2) + (\boxed{\phantom{000}}) = +5\)
( 1回目の動き) [mathjax] \(+\) ( 2回目の動き) [mathjax] \(=\) (動いた結果)
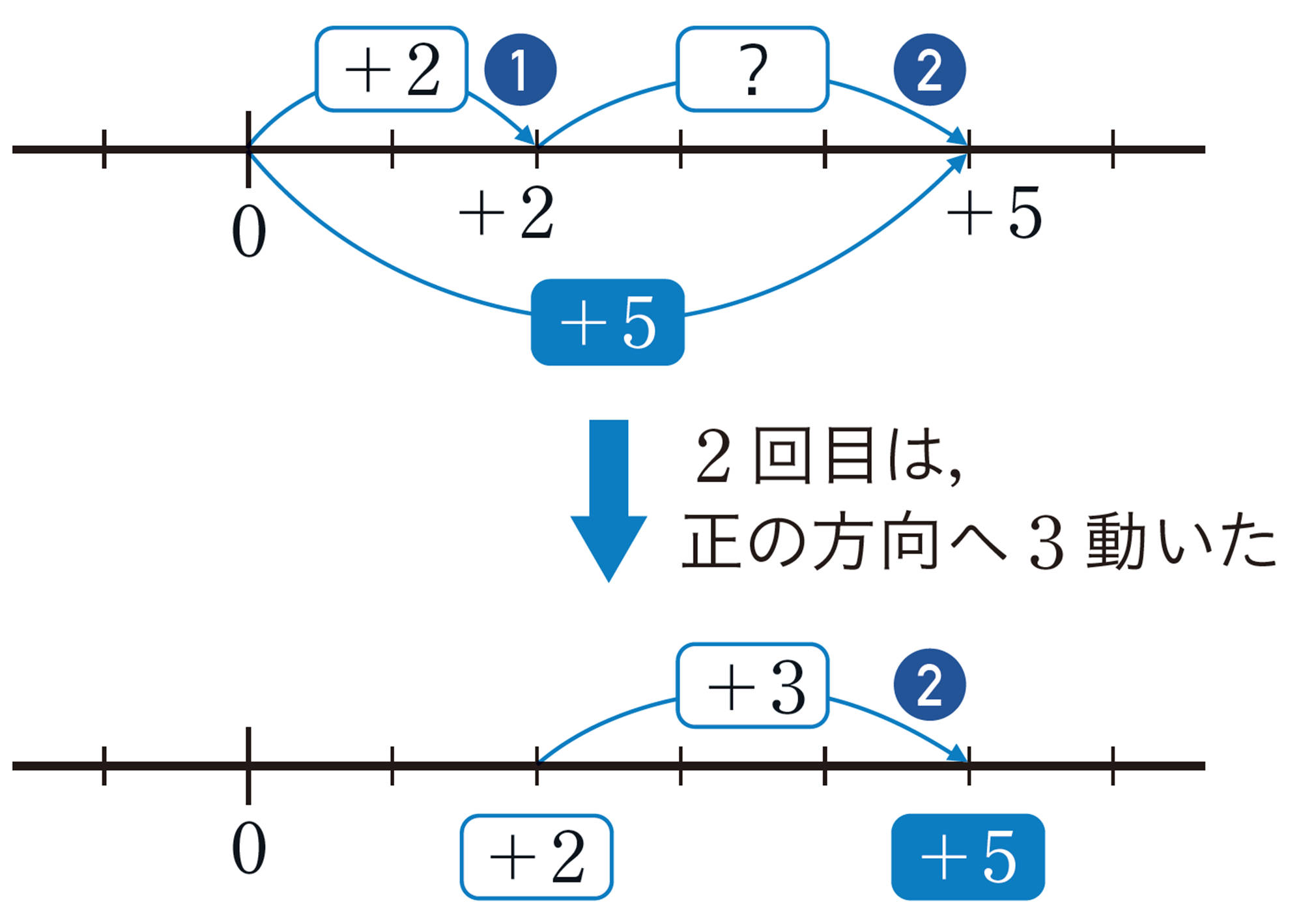
したがって，[mathjax]\(\boxed{\phantom{000}}\)にあてはまる数を求めるには，次のようなひき算の式を考えればよい。
[mathjax]\((+5)-(+2)=\boxed{\phantom{000}}\)
(動いた結果) [mathjax]\(-\) ( 1回目の動き) [mathjax]\(=\) ( 2回目の動き)
目標 ▷ 正の数，負の数のひき算を考えよう。
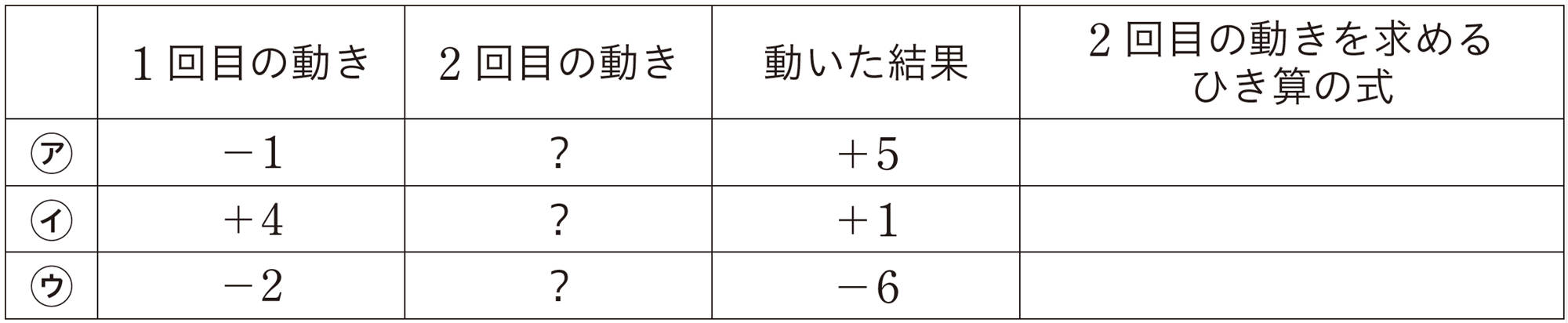
問 １ 【Q】のカードゲームで，次の表の㋐，㋑，㋒の場合について，2回目の動きを求めるひき算の式を書き入れなさい。
<1年p.26>
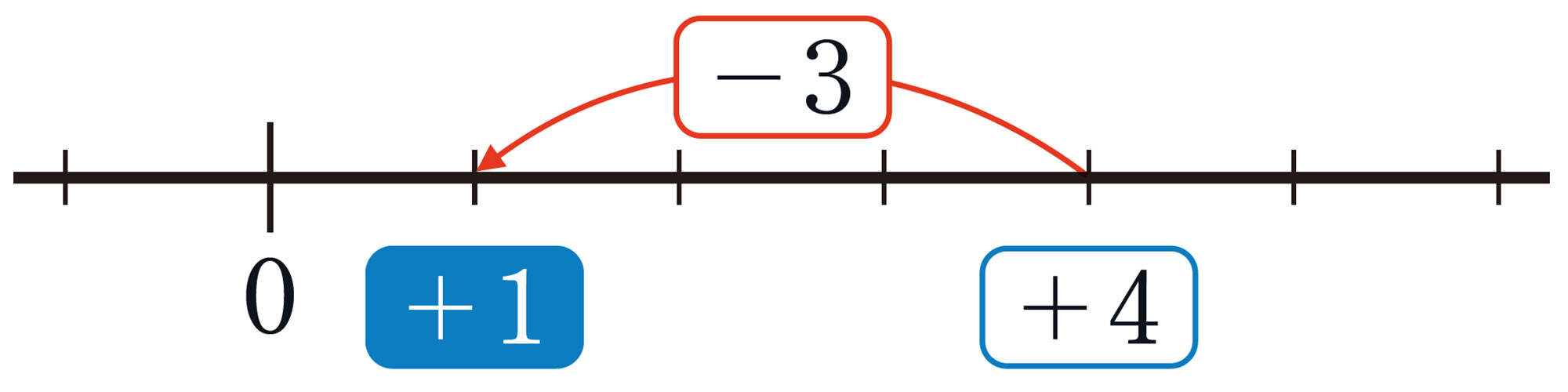
前ページでつくったひき算の式の計算を，数直線を使って考えてみよう。
ひき算を数直線上で考えると，[mathjax] \(+5\)は，[mathjax] \(+2\)から正の方向へ3動いた位置にあるから，2回目の動きは[mathjax] \(+3\)であることがわかる。
つまり，次のようになる。
[mathjax]\((+5)-(+2)=+3\)
例 １
⑴ [mathjax]\((+5)-(-1)\)
[mathjax]\((+5)-(-1)=+6\)
[mathjax] \(+5\)は，[mathjax] \(-1\)から正の方向へ6動いた位置にあるから，2回目の動きは[mathjax] \(+6\)である。
⑵ [mathjax]\((+1)-(+4)\)
[mathjax]\((+1)-(+4)=-3\)
[mathjax] \(+1\)は，[mathjax] \(+4\)から負の方向へ3動いた位置にあるから，2回目の動きは[mathjax] \(-3\)である。
問 ２ 数直線を使って，[mathjax]\((-6)-(-2)\)の計算を説明しなさい。
⑴ [mathjax]\((+2)-(+4)\)
⑵ [mathjax]\((+3)-(-6)\)
⑶ [mathjax]\((-1)-(+3)\)
⑷ [mathjax]\((-4)-(-5)\)
ひき算のことを 減法 という。その結果が差である。
<1年p.27>
減法と加法の関係
Q Question
次の⑴〜⑷の4つの減法と答えが同じになる式を，①〜④の加法から選び，[mathjax]\(\boxed{\phantom{000}}\)にその式を書き入れてみましょう。また，その結果から，気づいたことを話し合ってみましょう。
見方・考え方
具体的な式から，これまで学んだことを使って，きまりを見つけられるかな。
⑴ [mathjax]\((+3)-(+5)=\boxed{\phantom{00000000}}\)
⑵ [mathjax]\((+3)-(-5)=\boxed{\phantom{00000000}}\)
⑶ [mathjax]\((-3)-(+5)=\boxed{\phantom{00000000}}\)
⑷ [mathjax]\((-3)-(-5)=\boxed{\phantom{00000000}}\)
① [mathjax]\((+3)+(+5)\)
② [mathjax]\((+3)+(-5)\)
③ [mathjax]\((-3)+(+5)\)
④ [mathjax]\((-3)+(-5)\)
符号がちがうけど，同じ数字が並んでいるね。
答えが同じになる式には，どんな関係があるのかな。
【Q】から，次のことがわかる。
「[mathjax] \(+5\)をひく」ことは，「[mathjax] \(-5\)を加える」ことと同じである。
「[mathjax] \(-5\)をひく」ことは，「[mathjax] \(+5\)を加える」ことと同じである。
例 ２
⑴
⑵
⑶
⑷
問 ４ 次の減法を，加法に直して計算しなさい。
⑴ [mathjax]\((+5)-(+12)\)
⑵ [mathjax]\((+3)-(-8)\)
⑶ [mathjax]\((-15)-(+10)\)
⑷ [mathjax]\((-7)-(-7)\)
<1年p.28>
正の数，負の数の減法について，次のようにまとめることができる。
問 ５ 次の計算をしなさい。
⑴ [mathjax]\(0-(+3)\)
⑵ [mathjax]\(0-(-5)\)
0からある数をひくと，差はひく数の符号を変えた数になる。また，[mathjax]\((+8)-0=+8\)，[mathjax]\((-1)-0=-1\)のように，ある数から0をひいても，差はもとの数のままである。
⑴ [mathjax] \((+8)-(+2)\)
⑵ [mathjax] \((+3)-(+7)\)
⑶ [mathjax] \((+5)-(-4)\)
⑷ [mathjax] \((-12)-(+9)\)
⑸ [mathjax] \((-26)-(-18)\)
⑹ [mathjax] \((-16)-(-16)\)
⑺ [mathjax] \((+38)-(-12)\)
⑻ [mathjax] \((-10)-0\)
⑼ [mathjax] \(0-(-24)\)
問 ７ 11ページの各地の最高気温について，札幌，仙台の前日の最高気温を求める式をつくり，答えを求めなさい。
小数や分数の減法
例 ３
⑴
⑵
問 ８ 次の計算をしなさい。
⑴ [mathjax] \((-2.7)-(-3.4)\)
⑵ [mathjax] \((-1)-(+0.8)\)
⑶ [mathjax] \(\require{physics} \left(+\dfrac{1}{5}\right) – \require{physics} \left(-\dfrac{4}{5}\right)\)
⑷ [mathjax] \(\require{physics} \left(-\dfrac{3}{4}\right) – \require{physics} \left(+\dfrac{1}{2}\right)\)
⑸ [mathjax] \(\require{physics} \left(-\dfrac{7}{4}\right) -(+2)\)
⑹ [mathjax] \((-0.75)-\require{physics} \left(-\dfrac{3}{4}\right)\)
<1年p.29>
トライ 九州新幹線の鹿児島中央駅から熊本駅までに停車駅が全部で6つあります。次の表は，鹿児島中央駅を基準とし，熊本駅の方向を正の方向として，各駅までの距離を示したものです。
出水駅を基準とした場合，それぞれの距離は，正の数，負の数を使ってどのように表せるでしょうか。次の表にあてはまる数を入れてみよう。
どんなことがわかったかな
正の数，負の数の減法は，ひく数の符号を変えて加法に直して計算できます。
次の課題へ！
これまでに学んだことをもとにして，加法と減法が混じった計算を考えることができるかな？
P.30
トランプゲームで計算しよう Tea Break
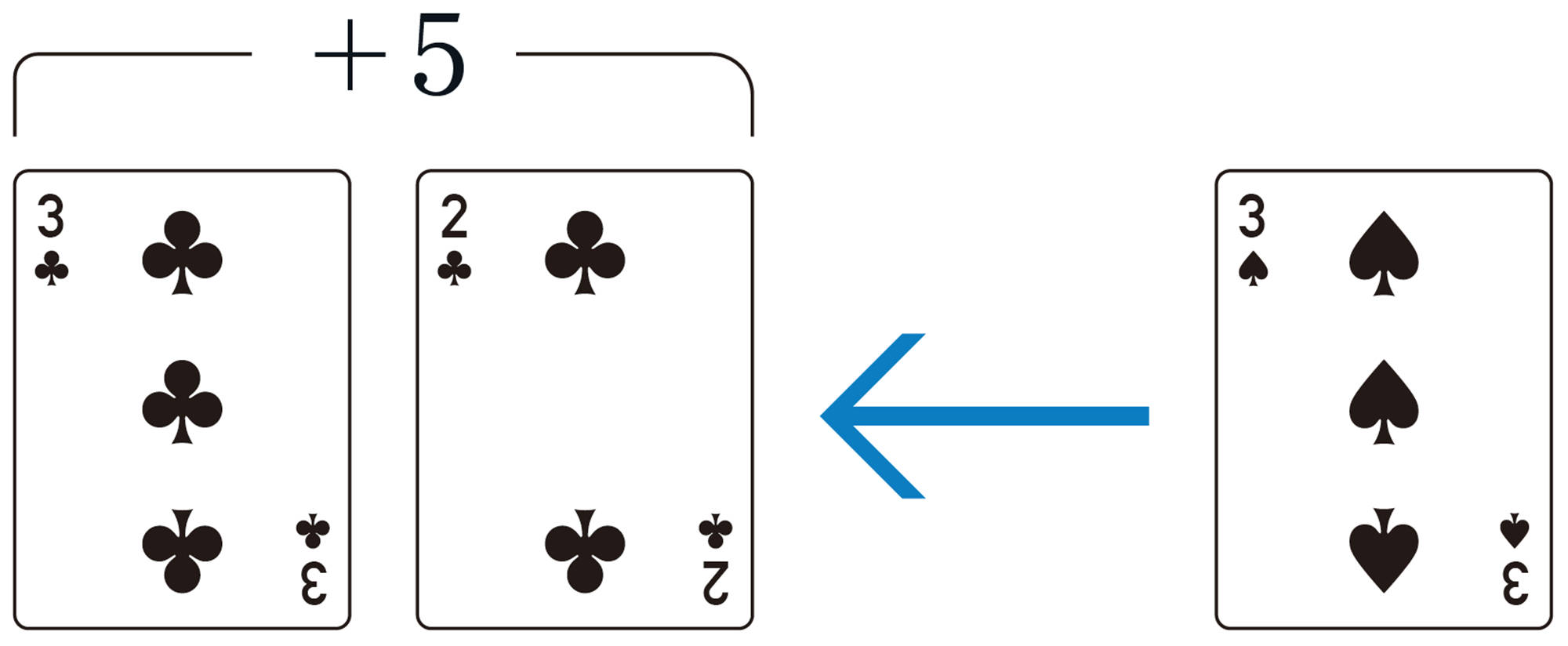
黒(♠，♣)のカードの数を正の得点，赤(♥，♦)のカードの数を負の得点として，トランプゲームをしました。次の①〜④の合計得点は，それぞれ何点になるでしょうか。
①持ち点が[mathjax] \(+5\)点のとき，黒の3をとった。
[mathjax]\((+5)+(+3)=\boxed{\phantom{000}}\)
②持ち点が[mathjax] \(+5\)点のとき，赤の3をとった。
[mathjax]\((+5)+(-3)=\boxed{\phantom{000}}\)
③持ち点が[mathjax] \(+5\)点のとき，黒の3をとられた。
[mathjax]\((+5)-(+3)=\boxed{\phantom{000}}\)
④持ち点が[mathjax] \(+5\)点のとき，赤の3をとられた。
[mathjax]\((+5)-(-3)=\boxed{\phantom{000}}\)
ゲームのルールを決めて，やってみましょう。
