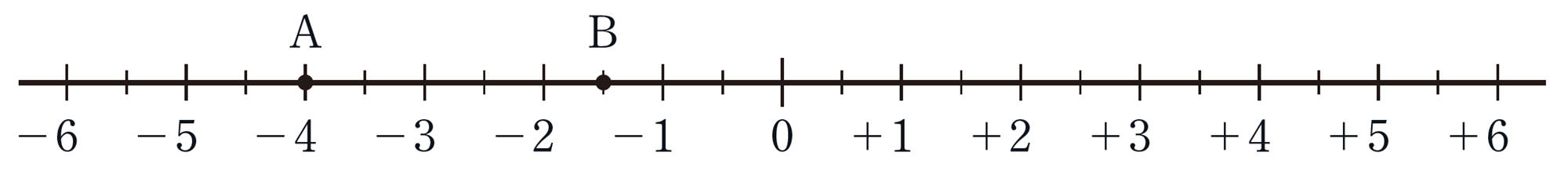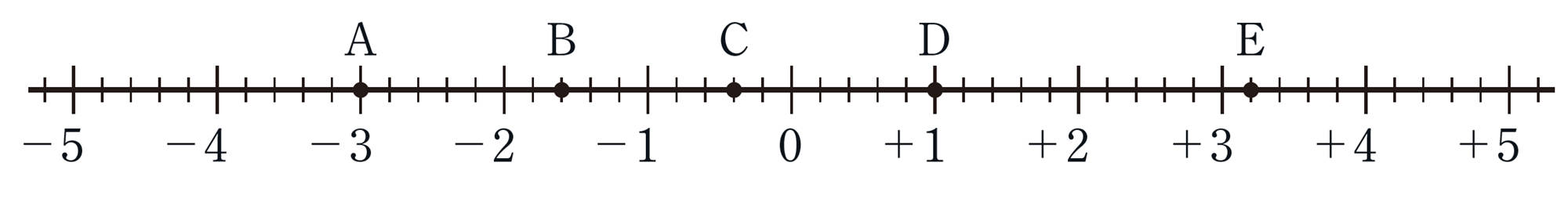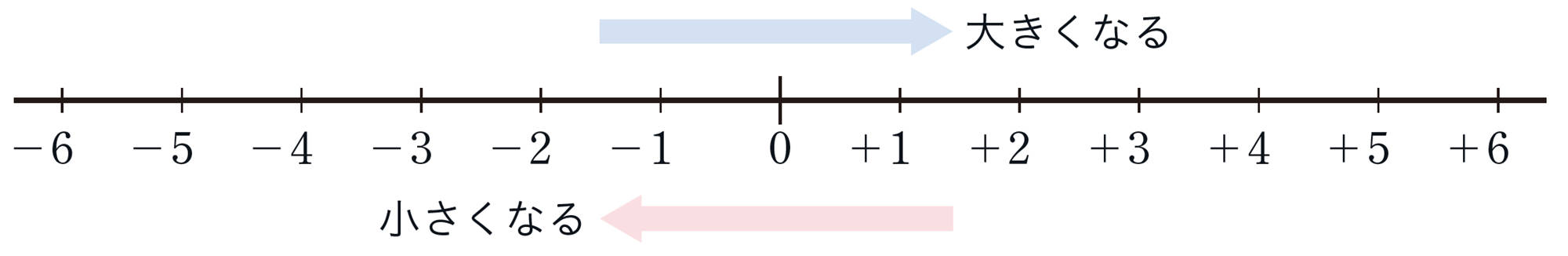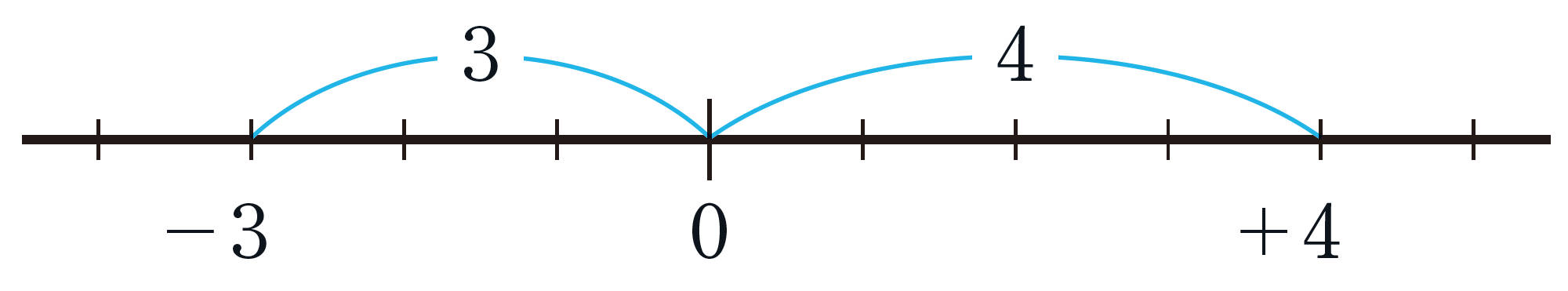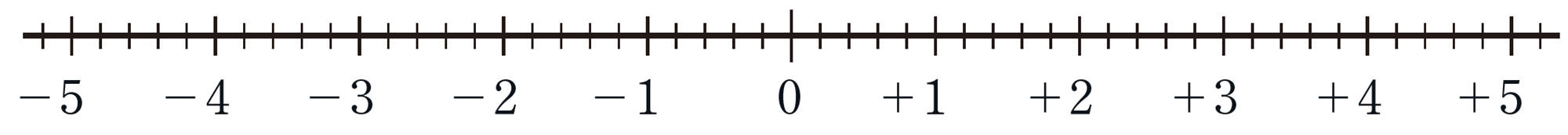<1年p.15>
２ 数の大小
Q Question
数直線について，次の問いに答えましょう。
⑴ 次の数直線上に，[mathjax]\(2\)，[mathjax]\(3.5\)，[mathjax]\(\dfrac{1}{2}\)に対応する点をかき入れてみましょう。また，その大小を比べてみましょう。
⑵ 負の数を数直線上に表すには，どんな数直線にすればよいでしょうか。上の数直線を使ってかいてみましょう。
正の数と同じように考えればいいのかな。
見方・考え方 負の数を表す数直線が考えられるかな。
目標 ▷ 正の数，負の数の大小を数直線を使って比べよう。
負の数は，【Q】⑴の数直線を0より左の方向へのばして，もとの数直線と同じ間隔で目盛りをとり，その直線上の点に数を対応させる。
次の数直線で，点Aは[mathjax] \(-4\)，点Bは[mathjax] \(-1.5\)に対応している。
数直線で，0に対応する点を 原点 といい，数直線の右の方向を 正の方向，左の方向を 負の方向 という。
問 １ 数直線をかき，次の数に対応する点をとりなさい。
[mathjax] \(+4\)，[mathjax] \(+0.5\)，[mathjax] \(-2\)，[mathjax] \(-5\)，[mathjax] \(-3.5\)，[mathjax] \(-\dfrac{3}{2}\)
問 ２ 次の数直線上の点 A，B，C，D，E に対応する数をいいなさい。
<1年p.16>
負の数をふくむ数を数直線上に表したとき，正の数と同じように，右にある数ほど大きく，左にある数ほど小さい。
例 １ [mathjax] \(-2\)と[mathjax] \(-5\)では，数直線上で，[mathjax] \(-2\)は[mathjax] \(-5\)より右にあるから，[mathjax] \(-2\)の方が[mathjax] \(-5\)より大きい。
[mathjax] \(-5 \lt -2\) または [mathjax] \(-2 \gt -5\)
ふりかえり 小学校3年
例 ２ [mathjax] \(-2\)，[mathjax] \(+3\)，[mathjax] \(-4\)を数直線上に表すと，右の図のようになる。
小さい数から順に並べると，[mathjax] \(-4 \lt -2 \lt +3\)
[mathjax]\(-2 \lt +3 \gt -4\)と表さないのはなぜかな。
問 ３ 次の各組の数の大小を，不等号を使って表しなさい。
⑴ [mathjax] \(+3\)，[mathjax] \(+4\)
⑵ [mathjax]\(-4\)，[mathjax]\(-6\)
⑶ [mathjax]\(+0.1\)，[mathjax]\(-0.2\)
⑷ [mathjax] \(-\dfrac{2}{3}\)，[mathjax] \(-\dfrac{1}{3}\)
⑸ [mathjax]\(+1\)，[mathjax]\(-3\)，[mathjax]\(0\)
⑹ [mathjax]\(-2\)，[mathjax]\(+5\)，[mathjax]\(-5\)
絶対値
Q Question
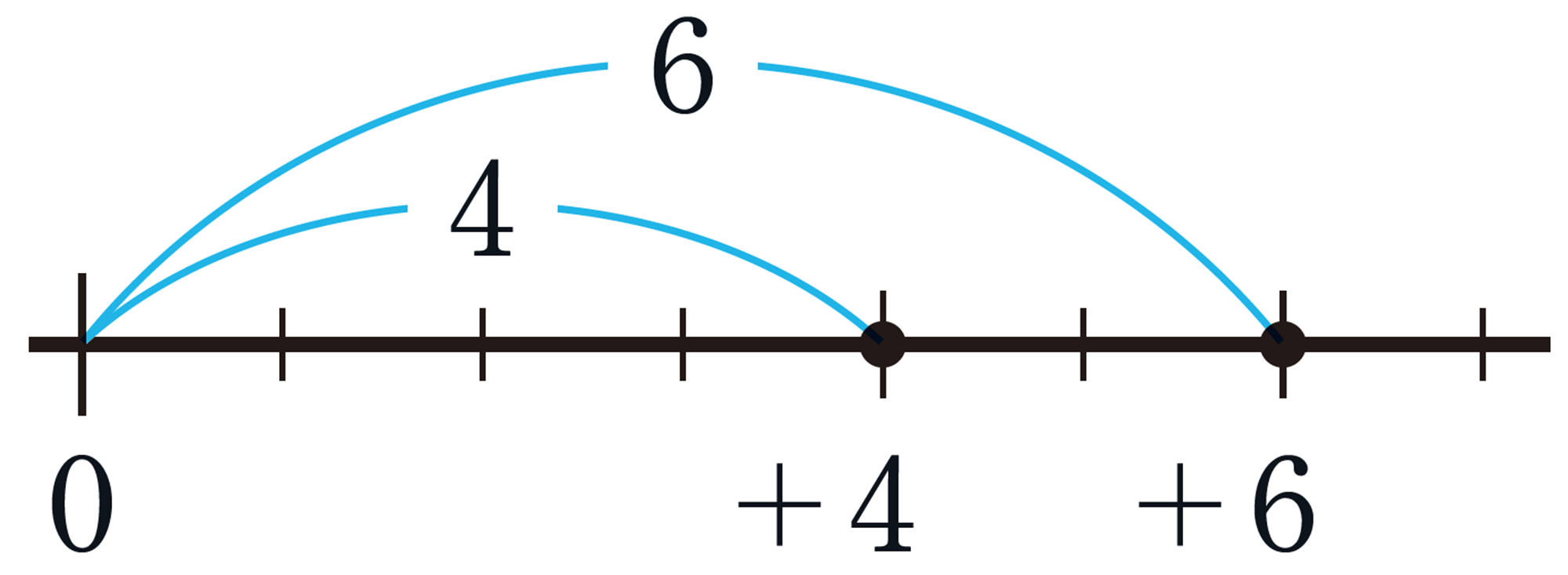
[mathjax] \(+4\)と[mathjax] \(+6\)を数直線上に表したとき，その大小を原点からの距離で説明してみましょう。[mathjax] \(-4\)と[mathjax] \(-6\)についても同じように説明してみましょう。
正の数では，原点から離れるほど大きくなるね。
負の数だとどうなるのかな。
見方・考え方 数直線上の点の位置に着目して考えられるかな。
<1年p.17>
数直線上で，ある数に対応する点と原点との距離を，その数の絶対値 という。たとえば，[mathjax] \(+4\)の絶対値は4，[mathjax] \(-3\)の絶対値は3である。
0の絶対値は0である。
2つの正の数[mathjax] \(+4\)と[mathjax] \(+6\)を比べると，絶対値は[mathjax] \(+6\)の方が大きく，数直線上では[mathjax] \(+6\)の方が右にある。
このように，2つの正の数では，絶対値の大きい数の方が大きい。
問 ４ 2つの負の数の大小について，絶対値で比べるとどんなことがいえますか。例をあげて，「数直線」，「絶対値」ということばを使って説明しなさい。
問 ５ [mathjax] \(-7\)，[mathjax] \(+5.2\)の絶対値を，それぞれいいなさい。
問 ６ 絶対値が10である数，[mathjax] \(\dfrac{2}{3}\) である数を，それぞれいいなさい。
2つの正の数[mathjax] \(+4\)と[mathjax] \(+6\)を比べると，絶対値は[mathjax] \(+6\)の方が大きく，数直線上では[mathjax] \(+6\)の方が右にある。
このように，2つの正の数では，絶対値の大きい数の方が大きい。
2数の大小
① 正の数は0より大きく，負の数は0より小さい。 また，正の数は負の数より大きい。
② 2つの正の数では，絶対値の大きい数の方が大きい。
③ 2つの負の数では，絶対値の大きい数の方が小さい。
どんなことがわかったかな
負の数も，正の数と同じように，数直線上に表して大小を比べることができます。
次の課題へ！
正の数，負の数の計算は，小学校のときの計算と同じようにできるのかな？
P.19
<1年p.18>
確かめよう １節 正の数・負の数
□ いろいろな数量を正の符号，負の符号を使って表すことができる。「[mathjax] \(-\)」のついたいろいろな数量P.13問2，問3
１ 数量を正の符号，負の符号を使って表すとき，次の問いに答えなさい。
⑴ A地点を基準0km として，「A から北へ3km」の地点を[mathjax] \(+3\)km と表すとき，「Aから南へ5km」の地点は，どのように表すことができますか。
⑵ 「200円の損失」を[mathjax] \(-200\)円と表すとき，[mathjax] \(+300\)円はどんなことを表していますか。
□ 正の数，負の数について理解している。 正の数・負の数P.14問6
２ 次の数について，下の問いに答えなさい。
[mathjax] \(-12\)， [mathjax] \(+7\)， [mathjax] \(0\)， [mathjax] \(+0.6\)， [mathjax] \(-3\)， [mathjax] \(+25\)，[mathjax]\(-\dfrac{8}{3}\)
⑴ 正の数はどれですか。また，負の数はどれですか。
⑵ 整数はどれですか。また，自然数はどれですか。
⑶ 正の数でも負の数でもない数はどれですか。
３ 下の数直線上に，次の数に対応する点をとりなさい。
[mathjax] \(-4\)， [mathjax] \(+3\)， [mathjax] \(-2.8\)，[mathjax]\(+\dfrac{3}{5}\)
４ 次の各組の数の大小を，不等号を使って表しなさい。
⑴ [mathjax] \(-3\)，[mathjax] \(+5\)
⑵ [mathjax] \(0\)，[mathjax] \(-7\)
⑶ [mathjax] \(-1.6\)，[mathjax] \(-2.4\)
⑷ [mathjax] \(+1\)，[mathjax] \(-3\)，[mathjax] \(-2\)
５ [mathjax] \(+16\)，[mathjax]\(-\dfrac{9}{7}\) の絶対値を，それぞれいいなさい。
また，絶対値が9である数，0である数を，それぞれいいなさい。
