<1年p.211>
２ 直線や平面の位置関係
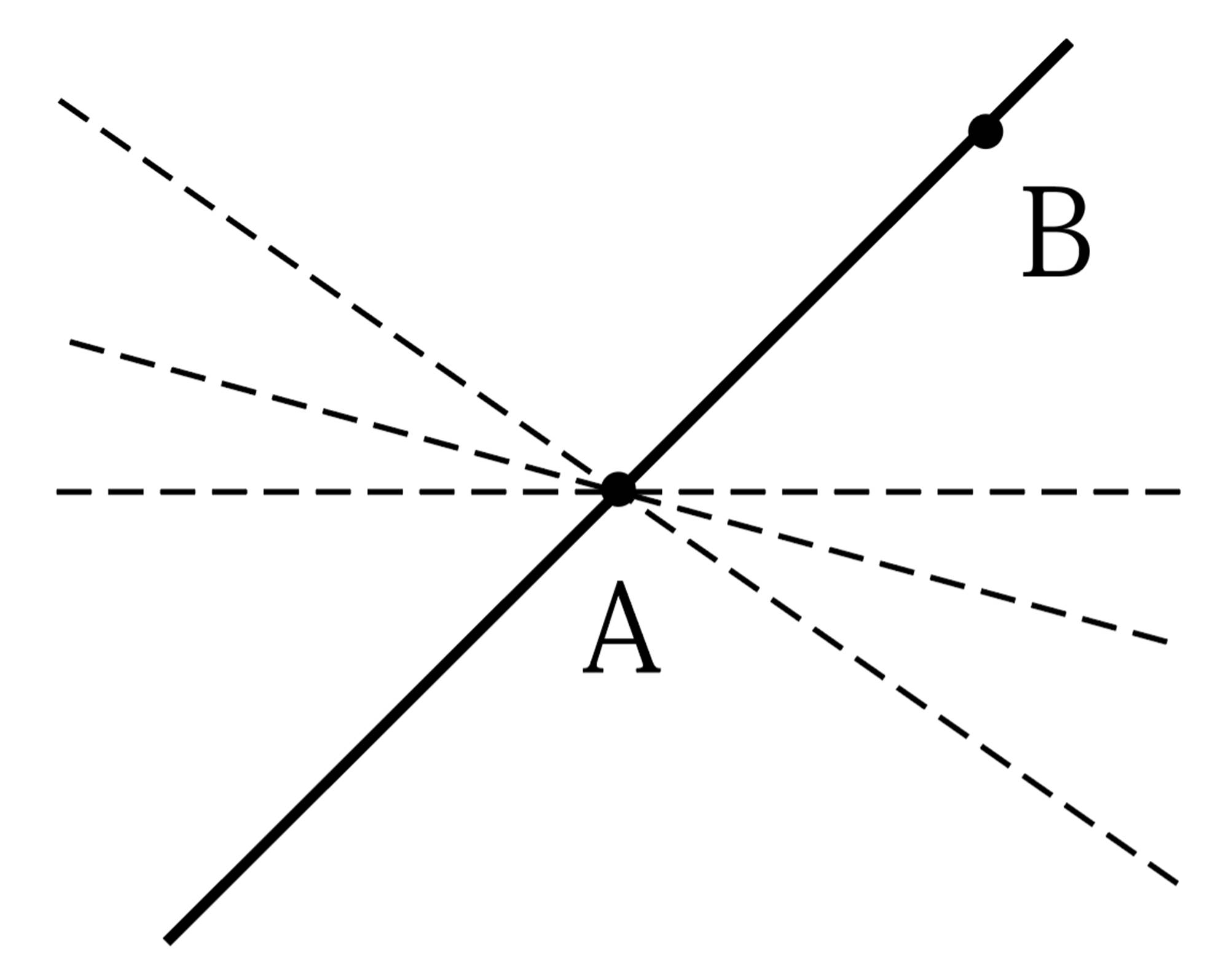
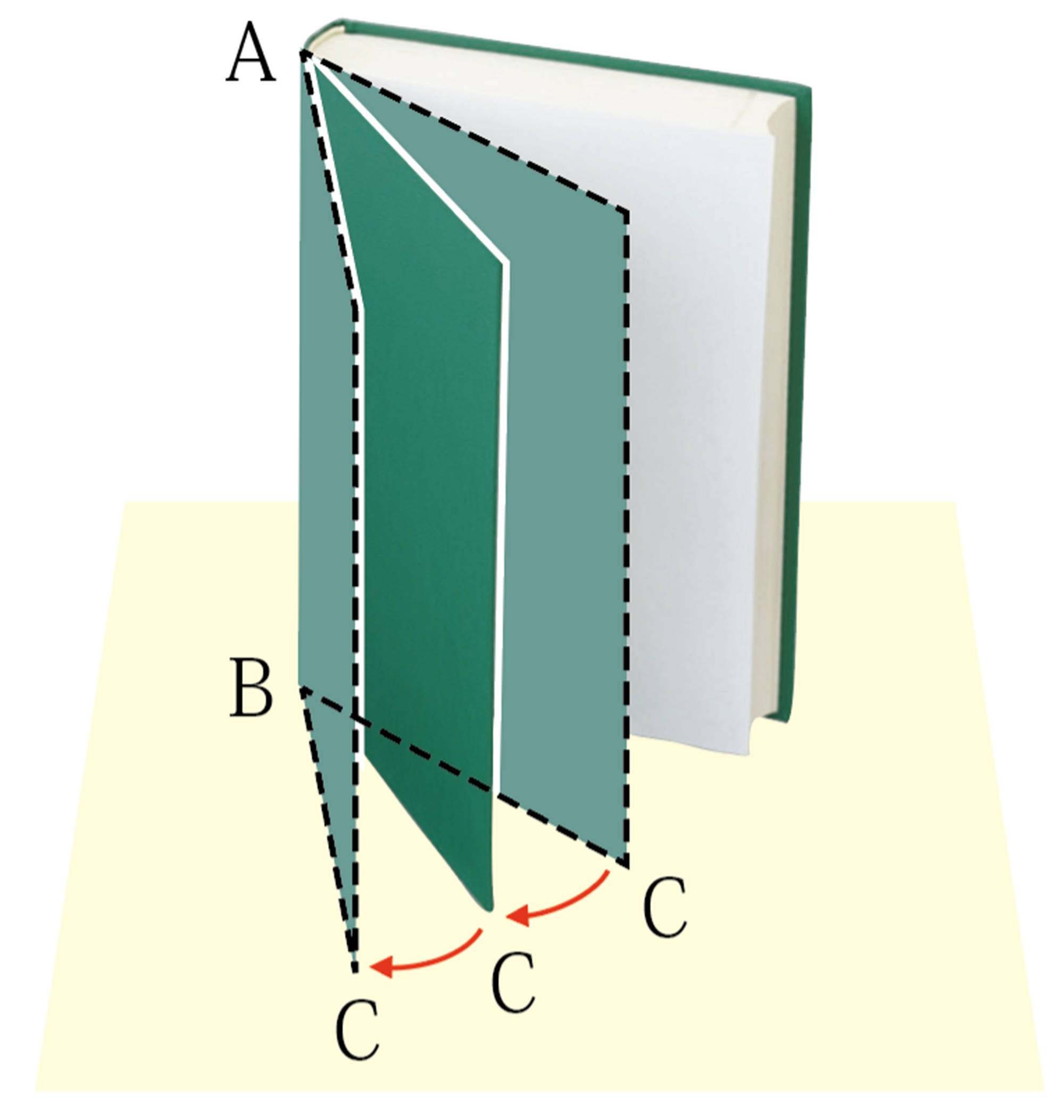
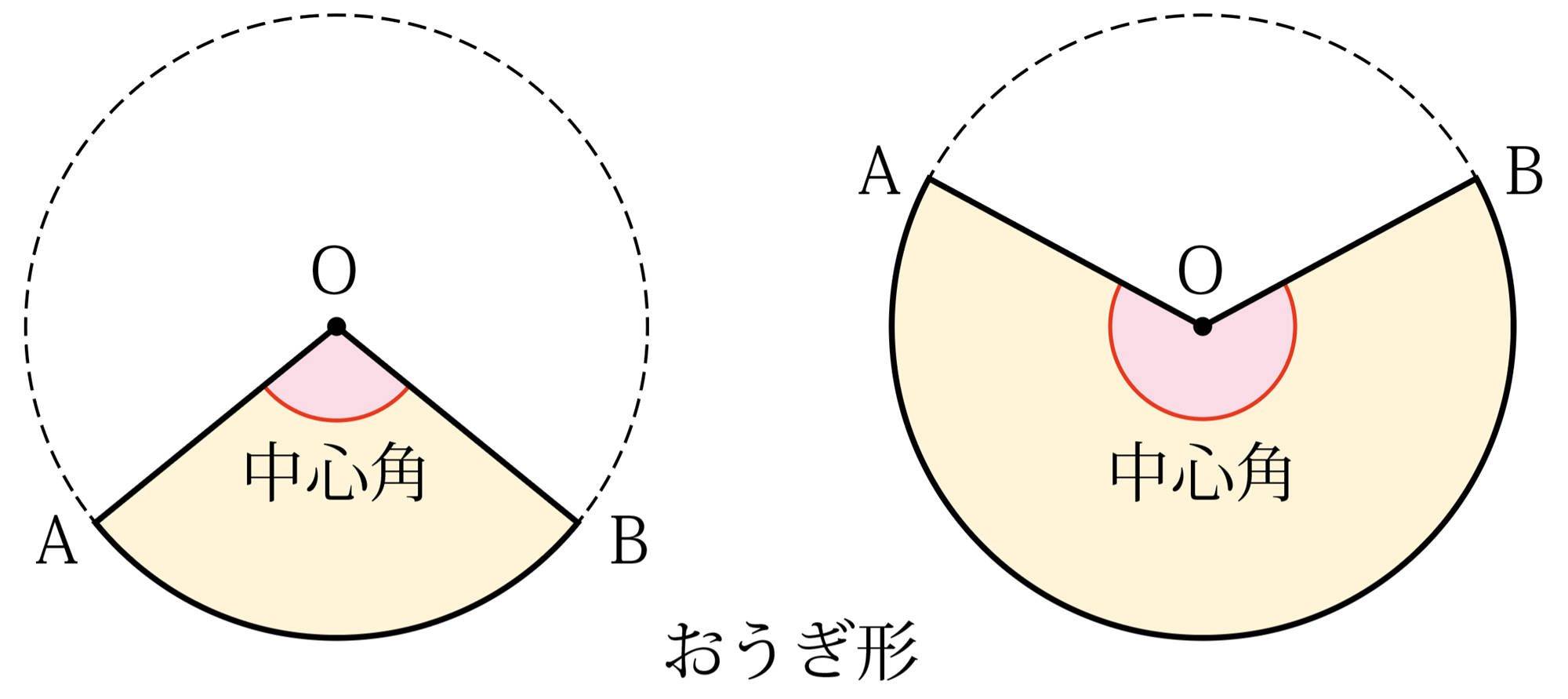
平面の決定
Q Question
平面を1 つに決めるには，どうしたらよいか考えてみましょう。
2点を通る直線は1 本に決まったね。
2点を通る平面は，たくさんありそうだね。
見方・考え方
いろいろな場合を調べて考えられるかな。
平面は，どの方向にも限りなく広がっているものと考える。
平面[mathjax] \( P \) 上に2 点[mathjax] \( A \) ， [mathjax] \( B \) があるとき，直線[mathjax] \( AB \) は，[mathjax] \( P \)にふくまれる。[mathjax] \( AB \)をふくむ平面は無数にあるが，[mathjax] \( AB \)と[mathjax] \(AB \)上にない点[mathjax] \( C \) をふくむ平面は，ただ 1 つしかない。
つまり，一直線上にない3 点をふくむ平面は1 つに決まる。
注意 平面は記号をつけて，平面[mathjax] \( P \)などと表す。
目標 ▷ 直線や平面を決定する条件などをもとにして，空間内における位置関係について調べよう。
<1年p.212>
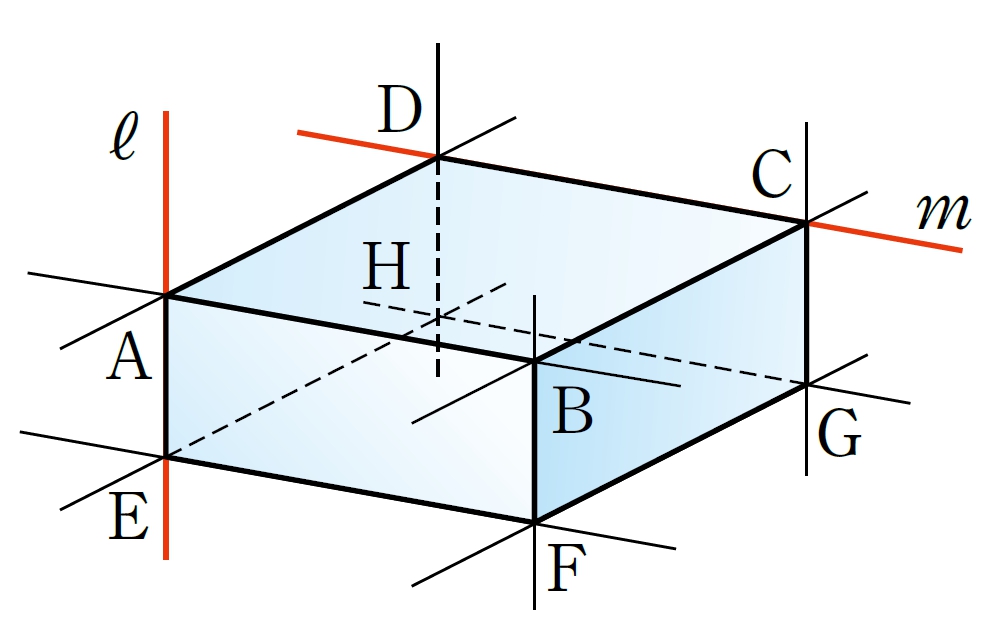
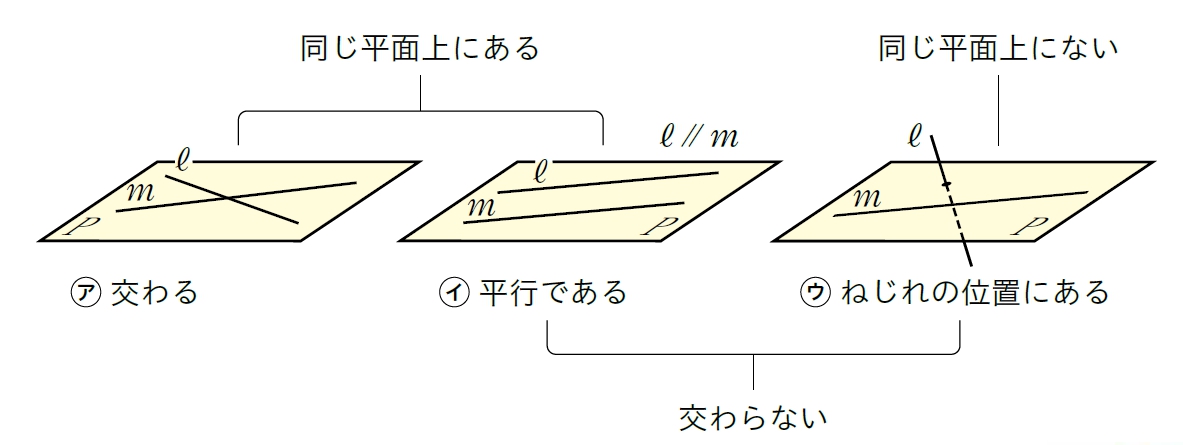
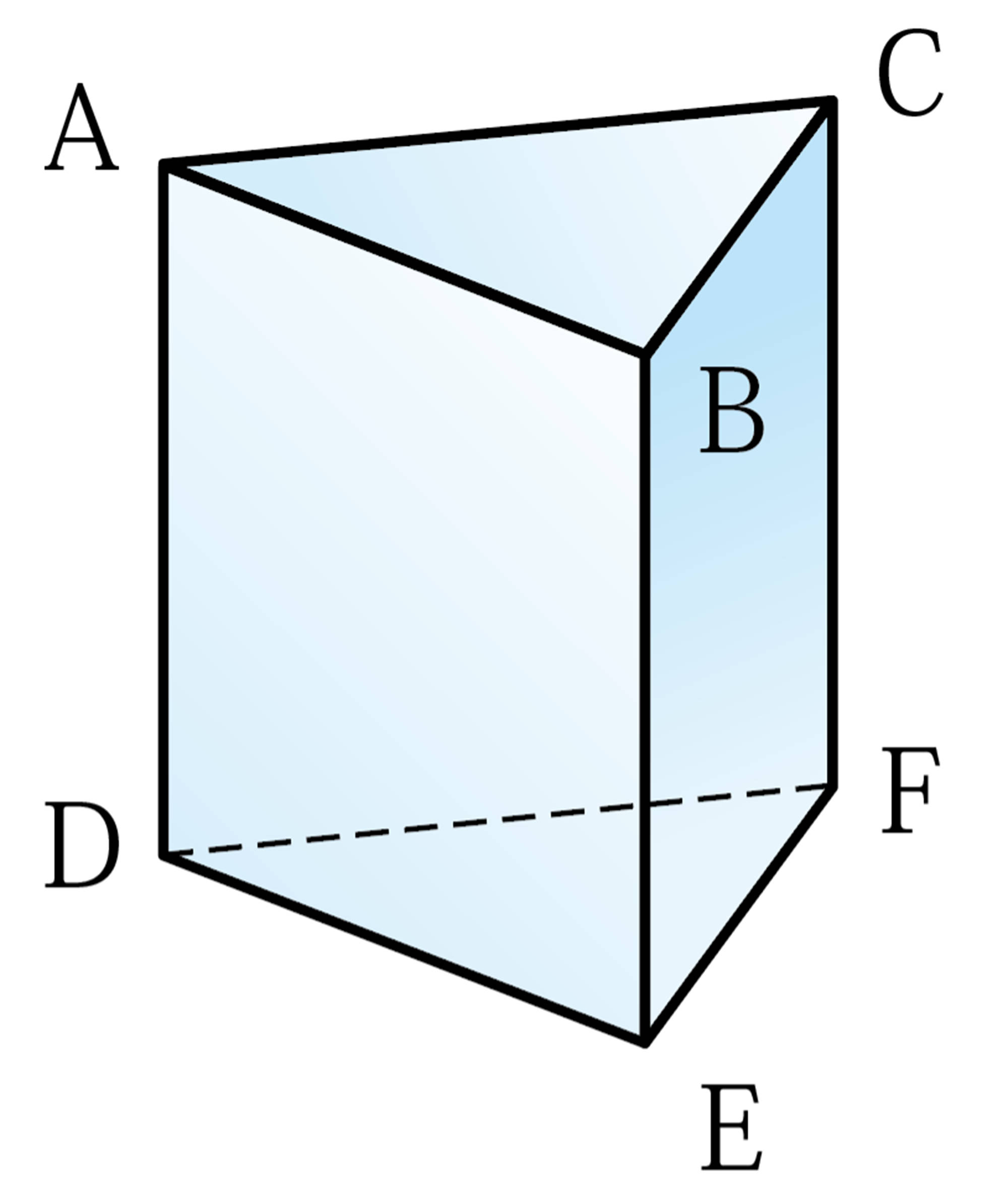
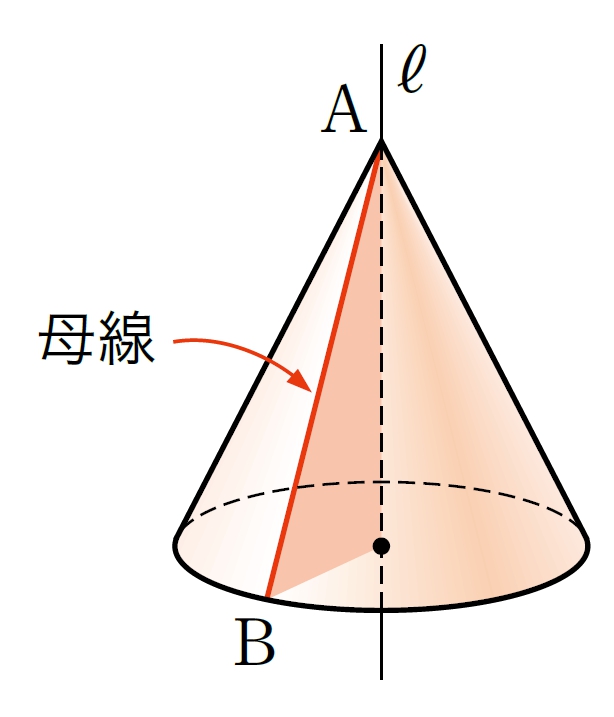
直線と直線
Q Question
右の図の直方体で，すべての辺を直線と考えたとき，2 直線の位置関係について調べてみましょう。
⑴ 直線 [mathjax] \( ℓ \) と平行な直線はどれでしょうか。また，直線[mathjax] \( ℓ \)と垂直に交わる直線はどれでしょうか。
⑵ 直線[mathjax] \( ℓ \)と平行ではなく，しかも交わらない直線はあるでしょうか。
見方・考え方
直方体の辺におきかえて考えられるかな。
同じ平面上にある2 直線は，平行になるか，交わるね。
同じ平面上にない場合を考えればいいのかな。
空間内では，上の図の直線 [mathjax] \( ℓ \)と直線[mathjax] \( m \) のように，平行ではなく，しかも交わらない2 直線がある。これらの2 直線は，【ねじれの位置】にあるという。ねじれの位置にある2 直線は，同じ平面上にはない。
空間内の2 直線の位置関係には，次の3 つの場合がある。
問 １ 【Q】で，直線[mathjax] \( EF \)とねじれの位置にある直線はどれですか。
問 ２ 身のまわりから，ねじれの位置にあるものを探しなさい。
<1年p.213>
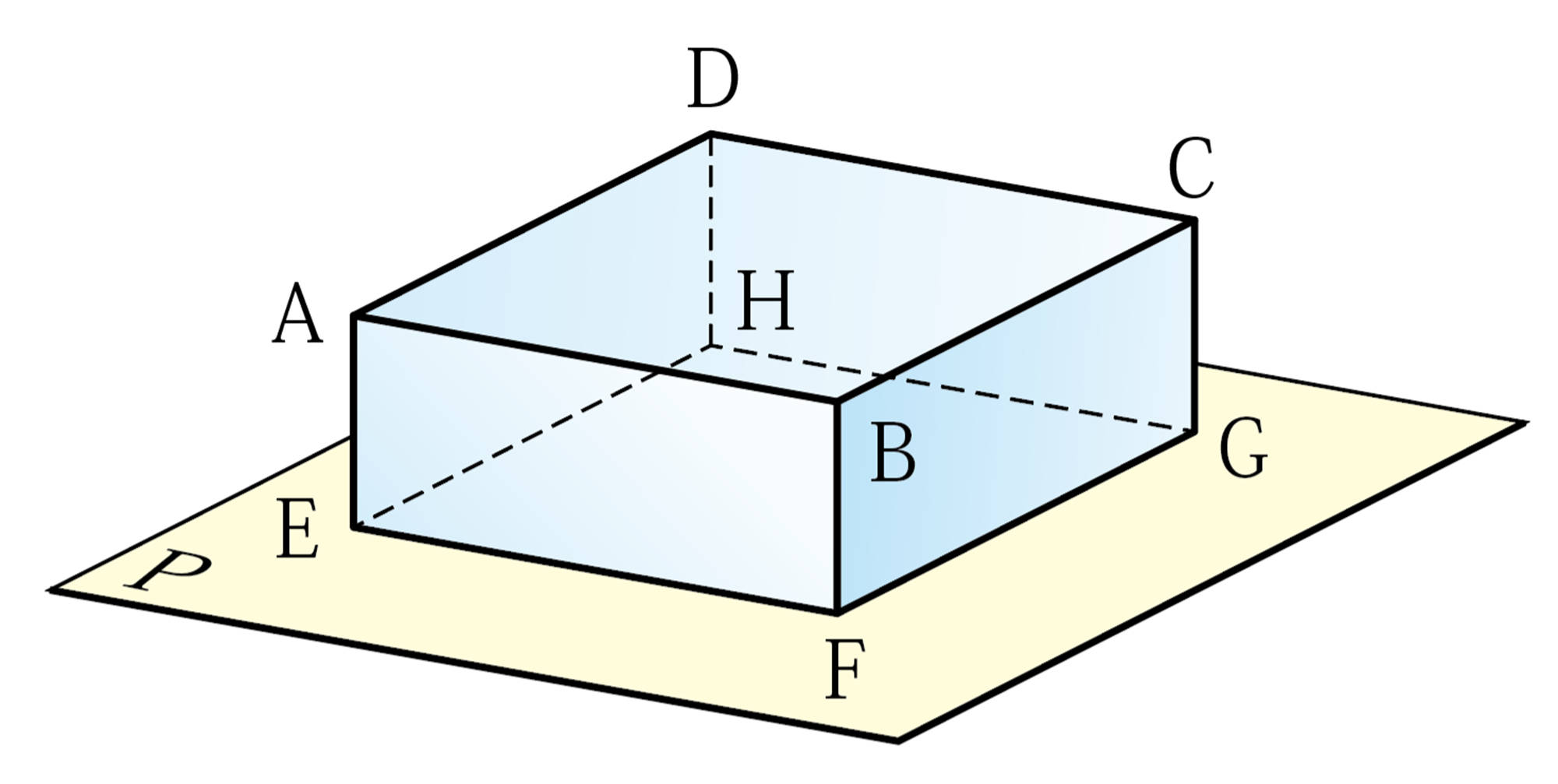
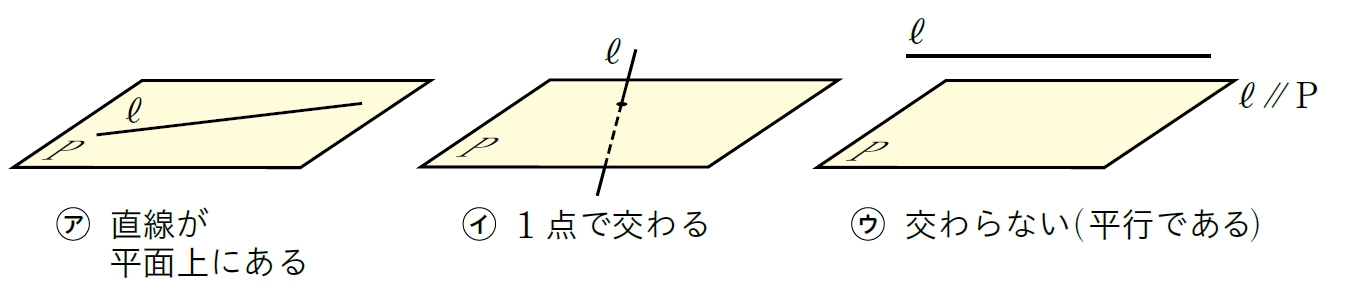
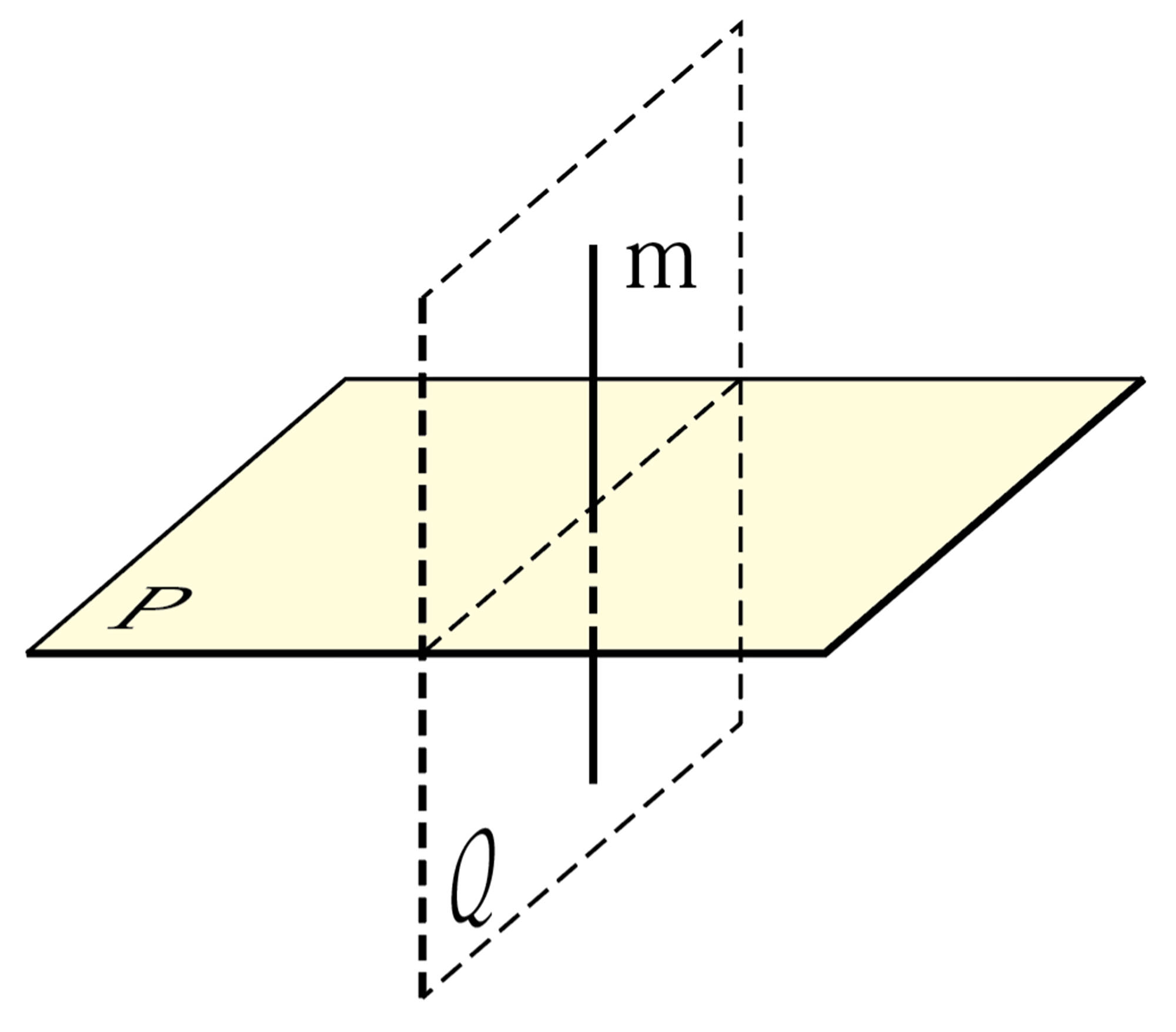
直線と平面
Q Question
右の図の直方体で， すべての辺を直線 ，すべての面を平面と考えたとき，平面 [mathjax] \( P\) とそれぞれの直線との位置関係を調べてみましょう。また， その位置関係によって，直線を分類してみましょう。
見方・考え方
直方体の辺と面におきかえて考えられるかな。
直線が平面上にあるかどうかで分けられるかな。
平面と交わるか，交わらないかで分けられるかな。
直線 [mathjax] \( ℓ \) と平面[mathjax] \( P\) が交わらないとき， 直線[mathjax] \( ℓ \) と平面[mathjax] \( P\)は平行であるといい， [mathjax] \( ℓ /\!/P\) と表す。
空間内の直線と平面の位置関係には，次の3 つの場合がある。
問 ３ 右の図のように本を机の上に立て，表紙を開いたとき，辺 [mathjax] \( AB \)と辺 [mathjax] \( BC\)はどんな位置関係になっていますか。
直線 [mathjax] \( ℓ \)が平面[mathjax] \( P\)と点 [mathjax] \(O\)で交わり，[mathjax] \(O\) を通る[mathjax] \( P \) 上 のすべての直線と垂直であるとき，直線 [mathjax] \( ℓ \)と平面[mathjax] \( P \)は垂直であるといい， [mathjax] \( ℓ \bot P\) と表す。
このとき，直線 [mathjax] \( ℓ \) を平面[mathjax] \( P \)の垂線という。
<1年p.214>
問 ４ 右のように，カメラを一脚に固定して撮影しています。一脚は，地面に垂直に立てられているといえますか。
直線 [mathjax] \( ℓ \)が平面[mathjax] \( P\)と点 [mathjax] \( O \) で交わり， [mathjax] \( O \) を通る [mathjax] \( P \) 上の2 直線と垂直であるとき，直線 [mathjax] \( ℓ \) と平面 [mathjax] \( P \) は垂直である。
問 ５ 右の図の三角柱で， 面 [mathjax] \( ADEB \) と平行な辺はどれですか。また， 辺 [mathjax] \( BE \) と垂直な面はどれですか。
問 ６ 身のまわりから， 平面と直線の位置関係が，平行になっているものと垂直になっているものを， それぞれ探しなさい。
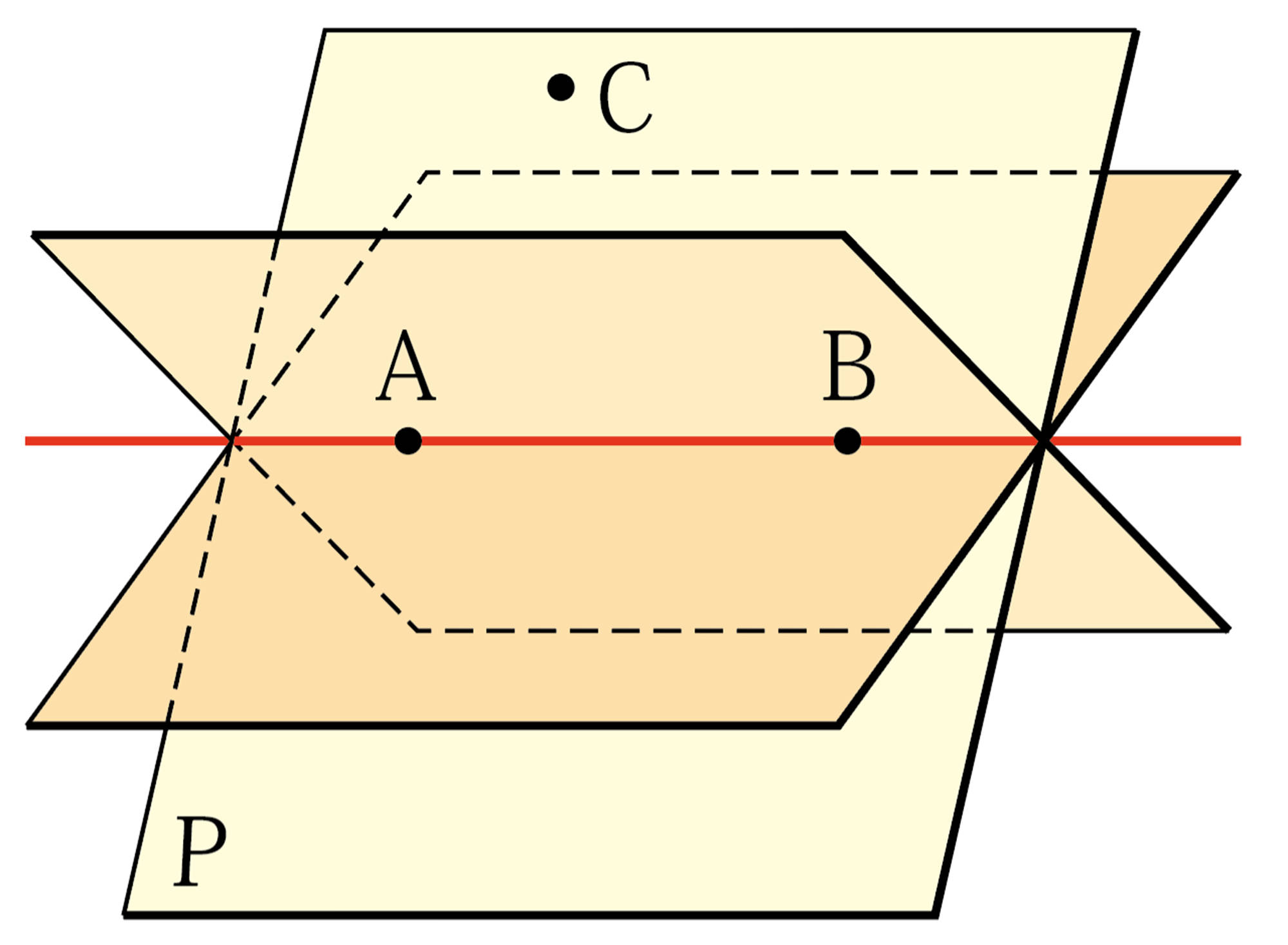
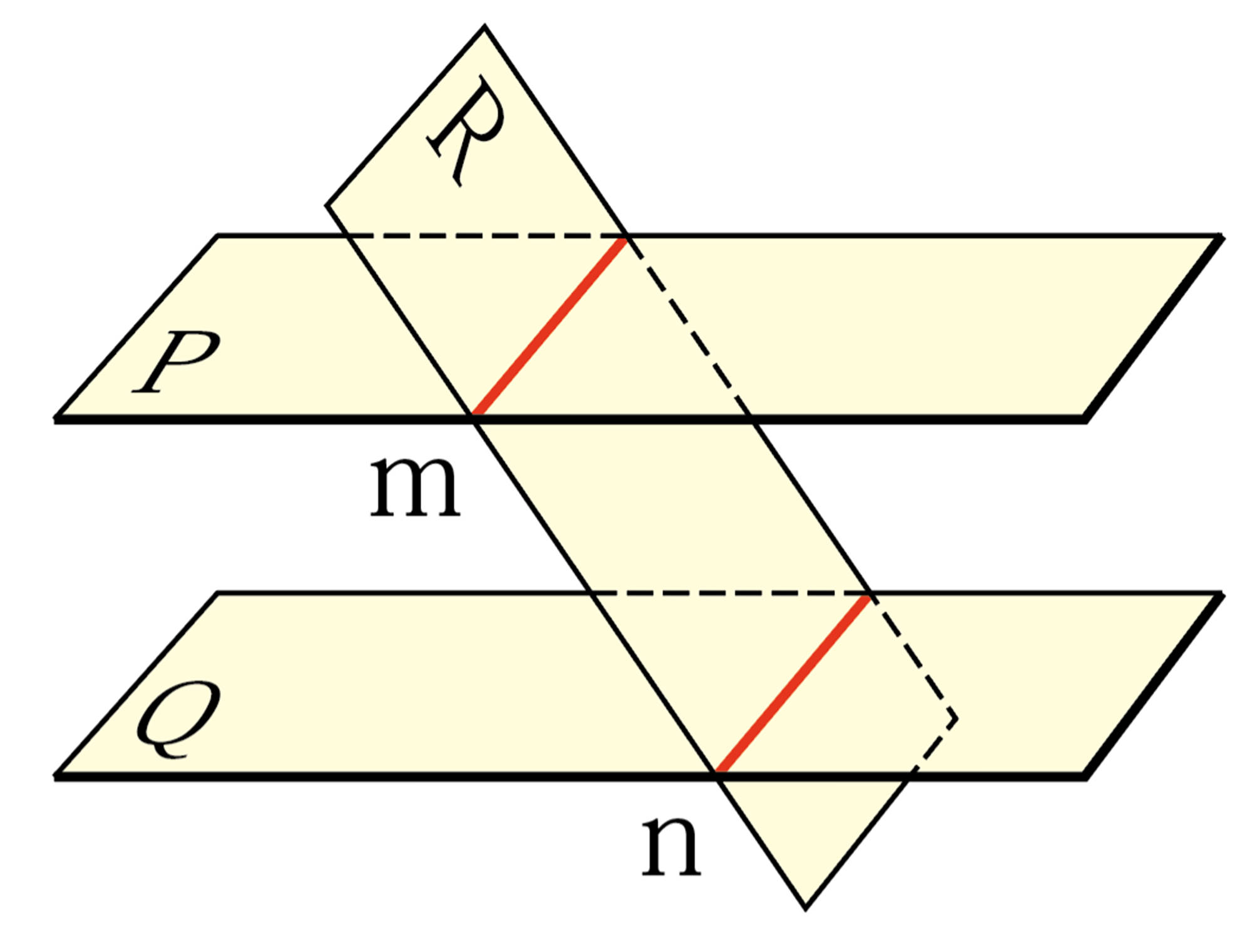
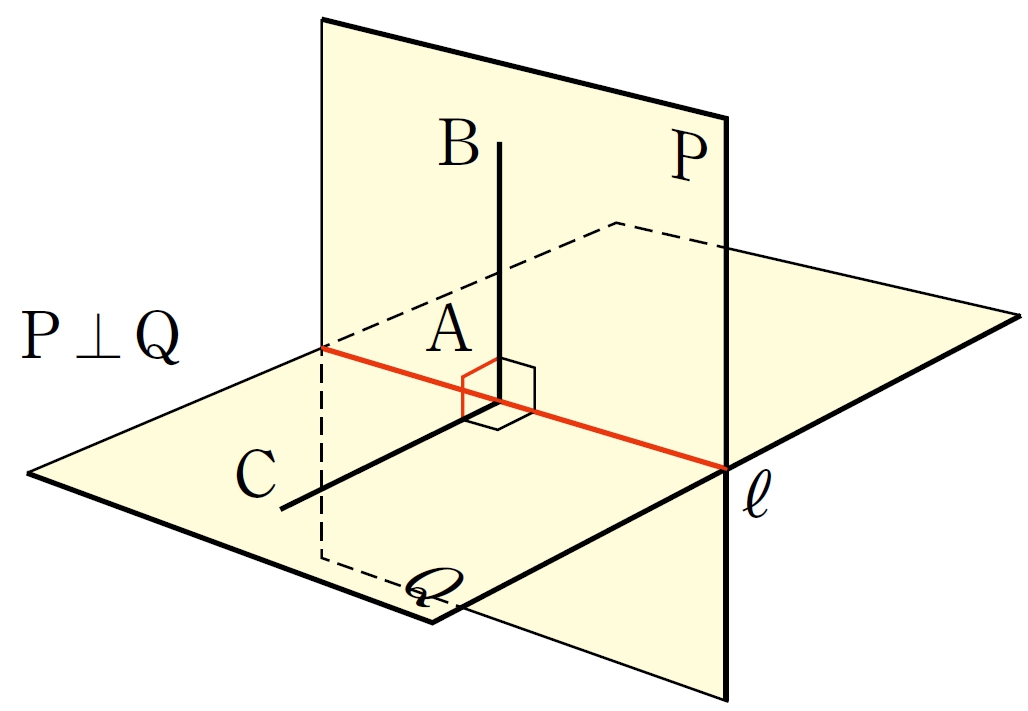
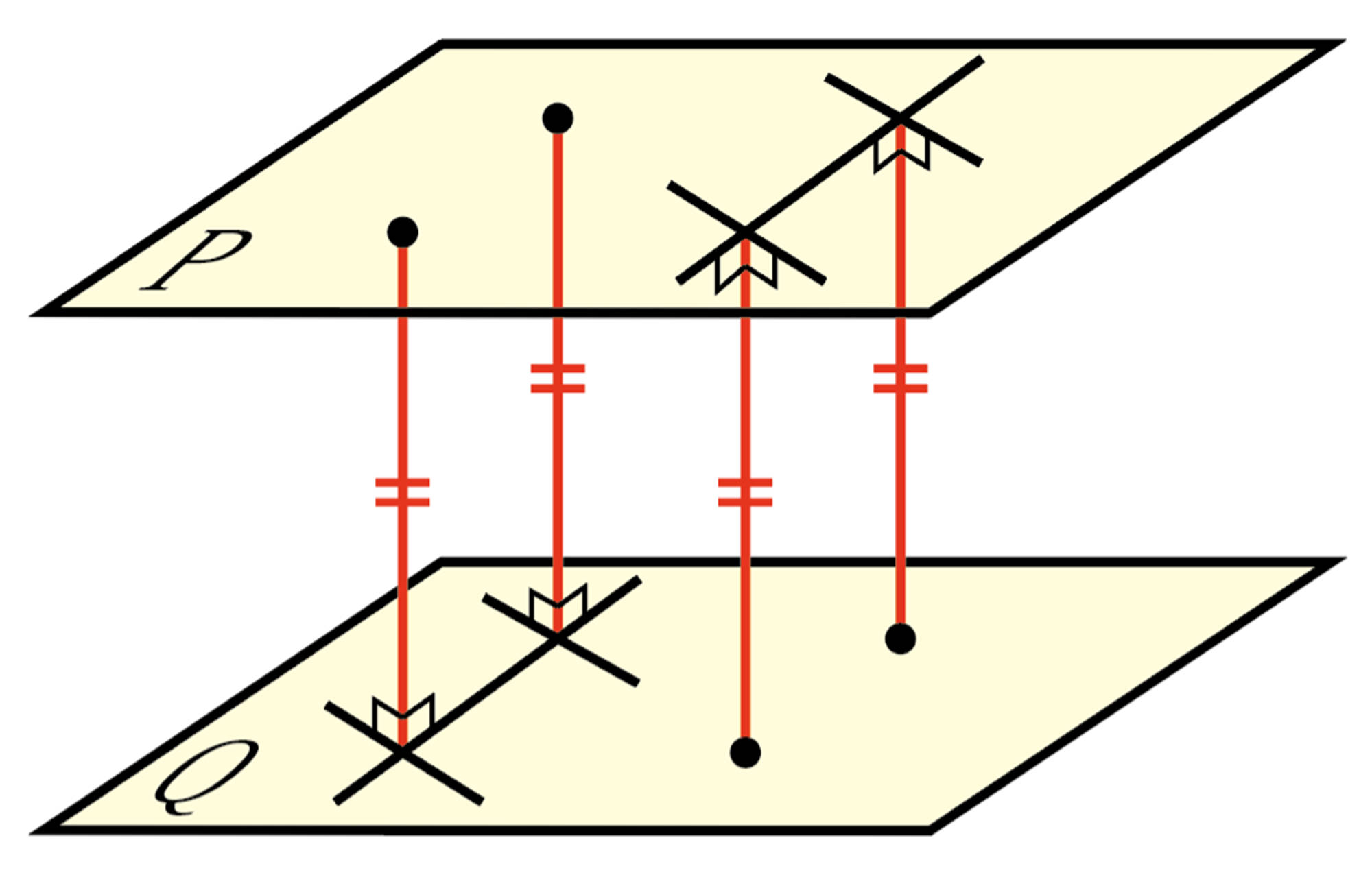
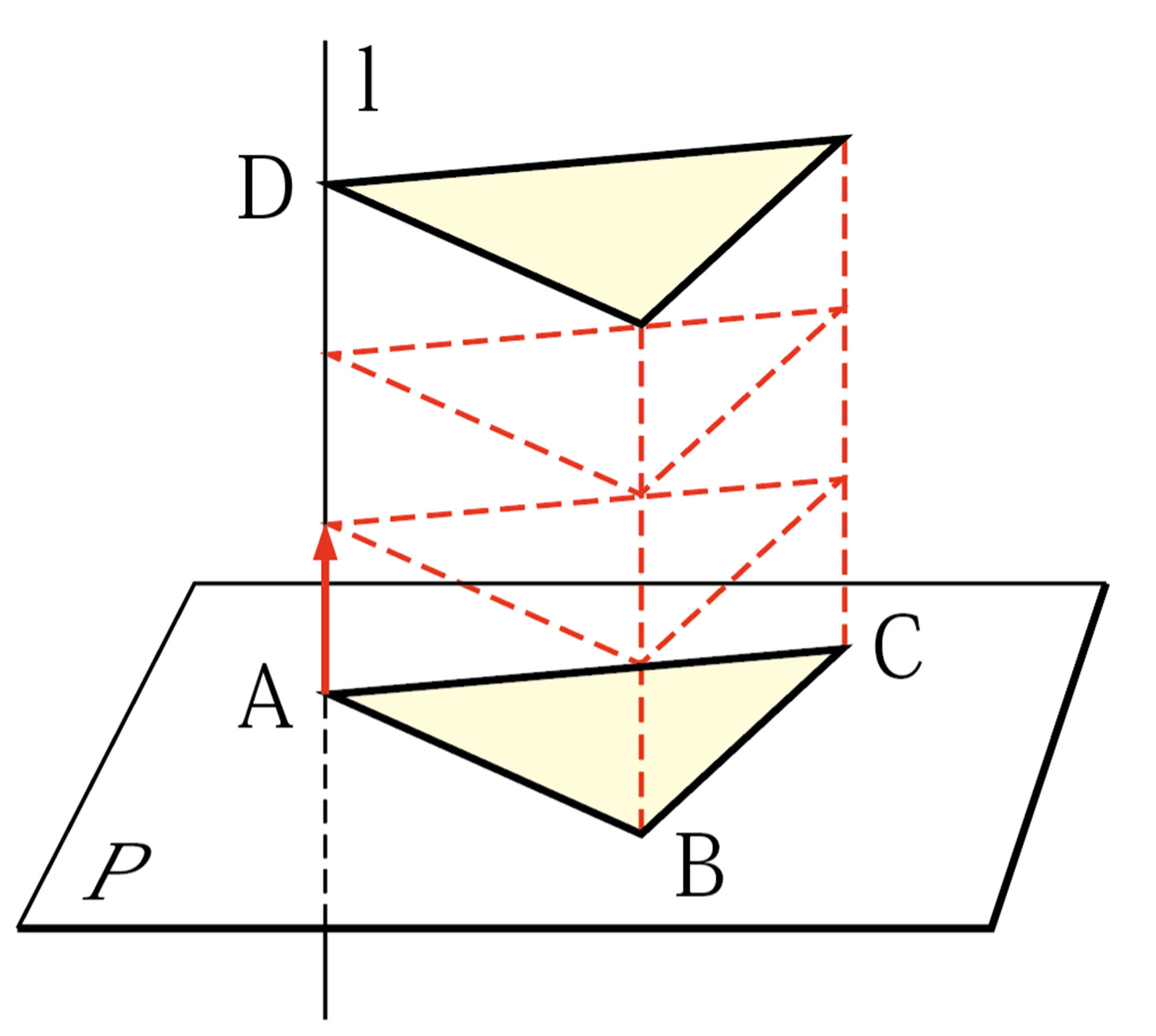
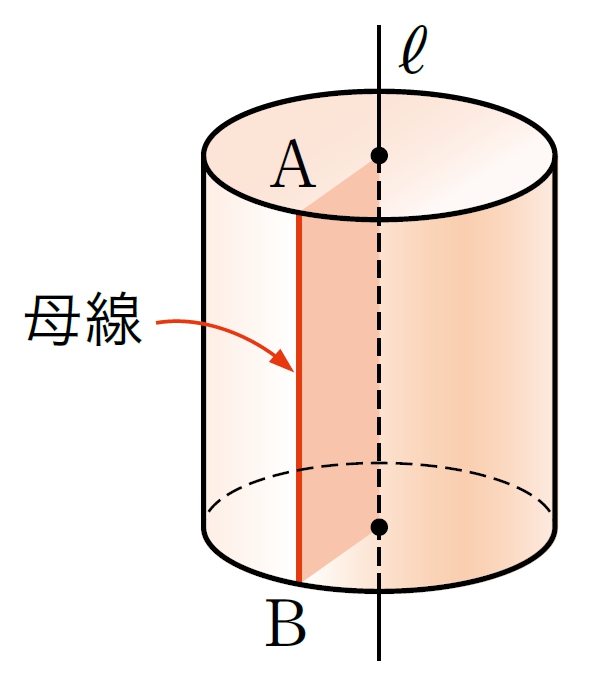
平面と平面
Q Question
空間内に，2 つの平面 [mathjax] \( P\) ， [mathjax] \( Q \) があるとき，この 2 平面の位置関係には，どのような場合があるか調べてみましょう。
どんな分類のしかたがあるかな。
交わるか，交わらないかの2 つになるのかな。
見方・考え方
2 直線のときと同じように，いくつかの場合に分けて考えられるかな。
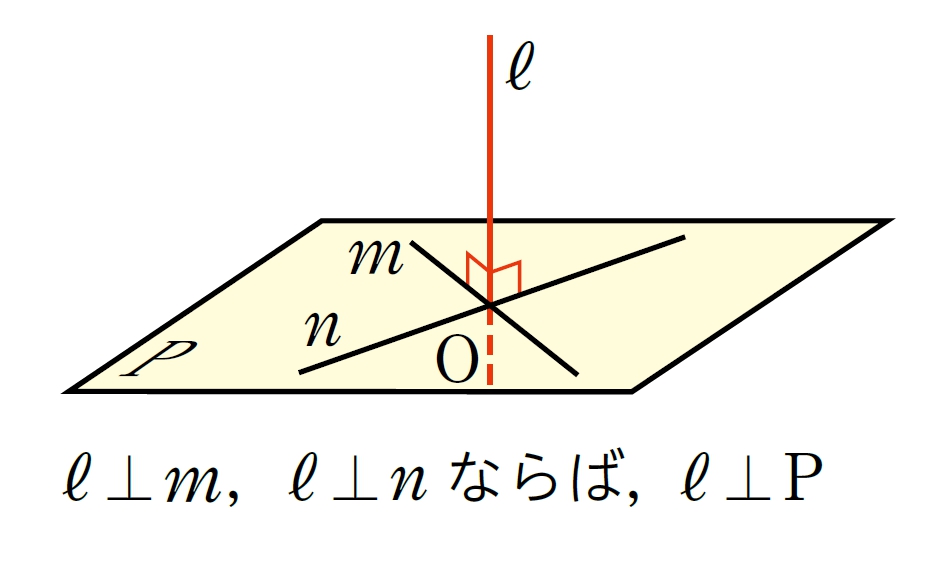
2 平面 [mathjax] \( P \) ， [mathjax] \( Q\) が交わらないとき，平面[mathjax] \( P \) と平面[mathjax] \( Q \)は平行であるといい， [mathjax] \( P/\!/Q\) と表す。
<1年p.215>
空間内の2 平面の位置関係には，次の2 つの場合がある。
2 平面 [mathjax] \( P \)， [mathjax] \( Q\) が交わるとき，その交わりは直線で，その直線を【交線】という。
問 ７ 右の図のように，平行な2 平面 [mathjax] \( P \)，[mathjax] \( Q \) に別の平面 [mathjax] \( R\)が交わってできる2 つの交線 [mathjax] \( m\) ， [mathjax] \( n \)は，どんな位置関係になっていますか。
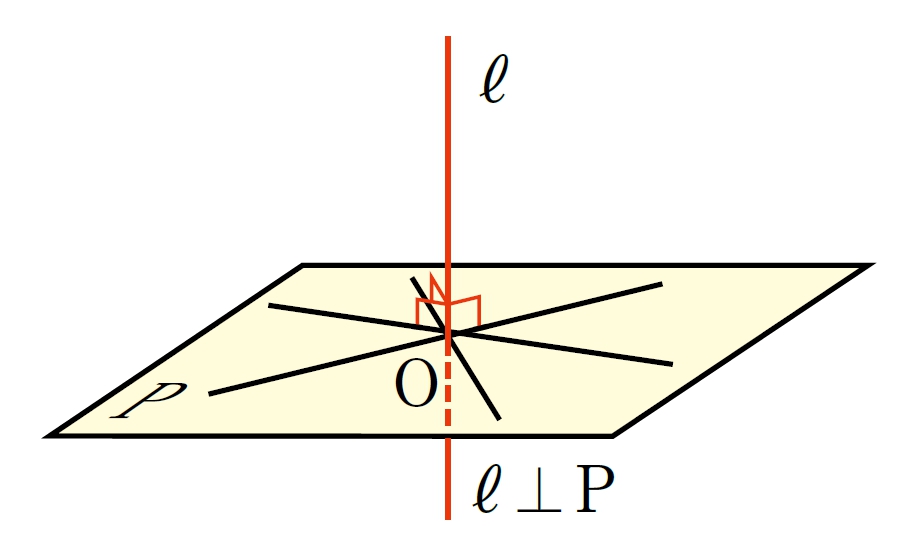
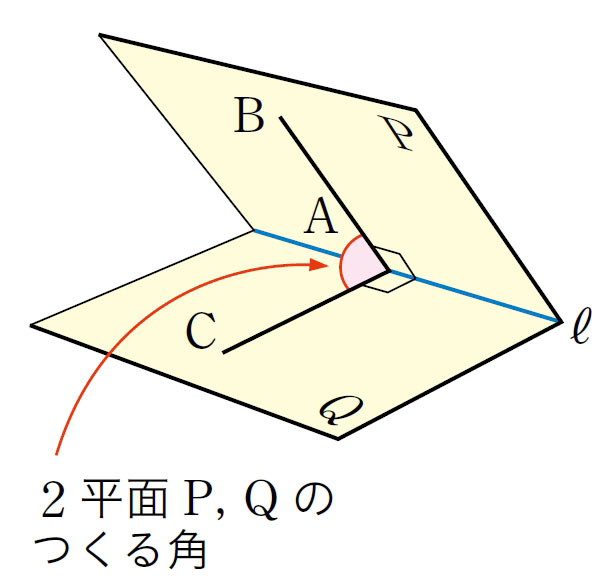
平面と平面のつくる角
2 平面 [mathjax] \(P\)，[mathjax] \( Q\)が交わるとき，その交線 [mathjax] \( ℓ \)上に点[mathjax] \( A\) をとり，右の図のように，
[mathjax] \( P \) 上に [mathjax] \( AB\bot ℓ \) ，
[mathjax] \( Q \) 上に [mathjax] \( AC\bot ℓ \)
となる半直線 [mathjax] \( AB \)， [mathjax] \( AC \) を引く。
このとき，[mathjax] \( \angle BAC\)を2 平面 [mathjax] \( P \) ， [mathjax] \(Q\) のつくる角という。
また， [mathjax] \( \angle BAC=90^{\circ}\) のとき， 平面 [mathjax] \(P\) と平面 [mathjax] \(Q\) は垂直であるといい，[mathjax] \( P \bot Q\)と表す。
問 ８ 右の図で， 直線 [mathjax] \(m\) は平面 [mathjax] \(P\) の垂線です。直線[mathjax] \( m\)をふくむ平面を [mathjax] \( Q \)とするとき， [mathjax] \(P\) と [mathjax] \(Q\) はどんな位置関係になっていますか。
<1年p.216>
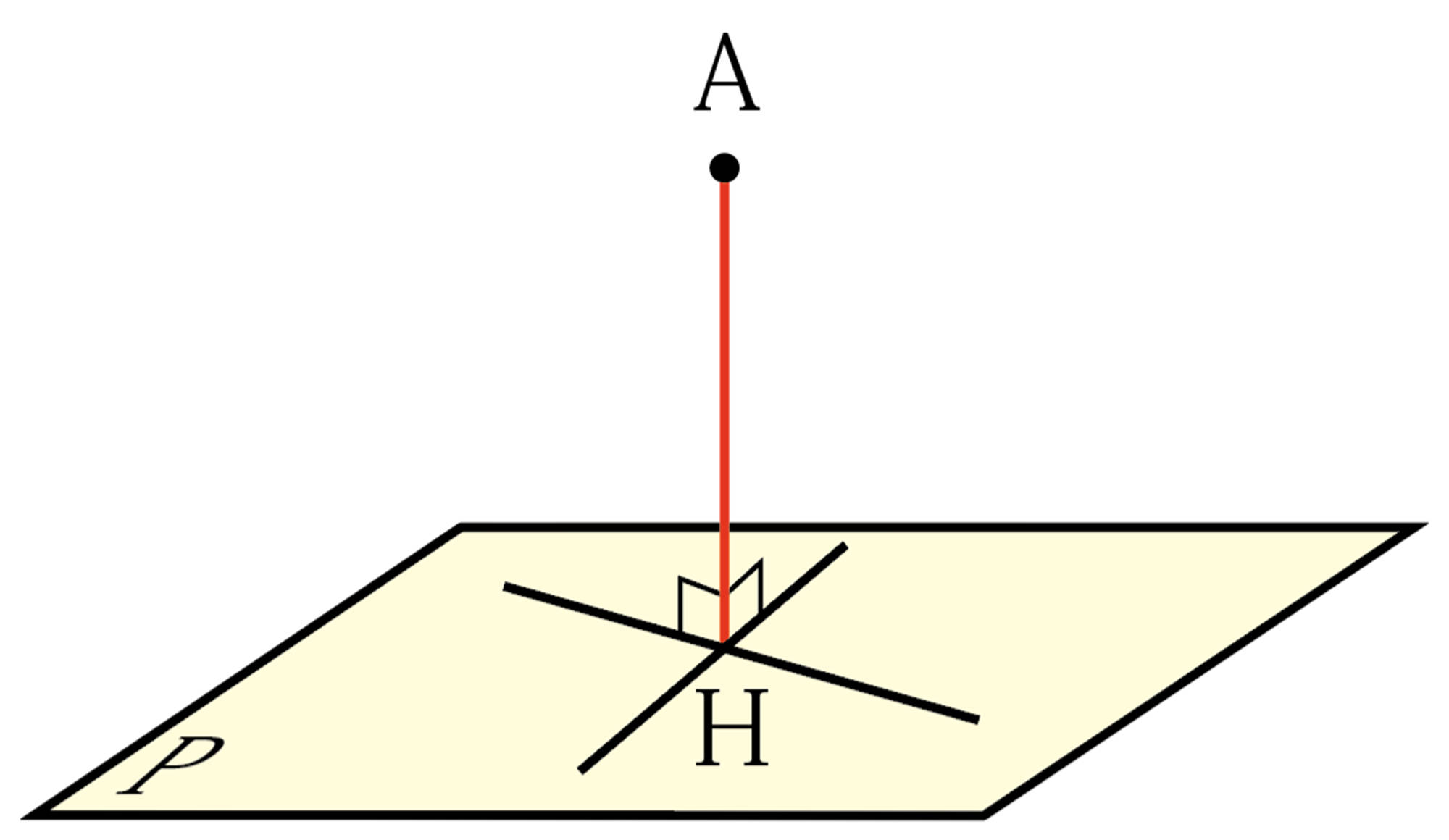
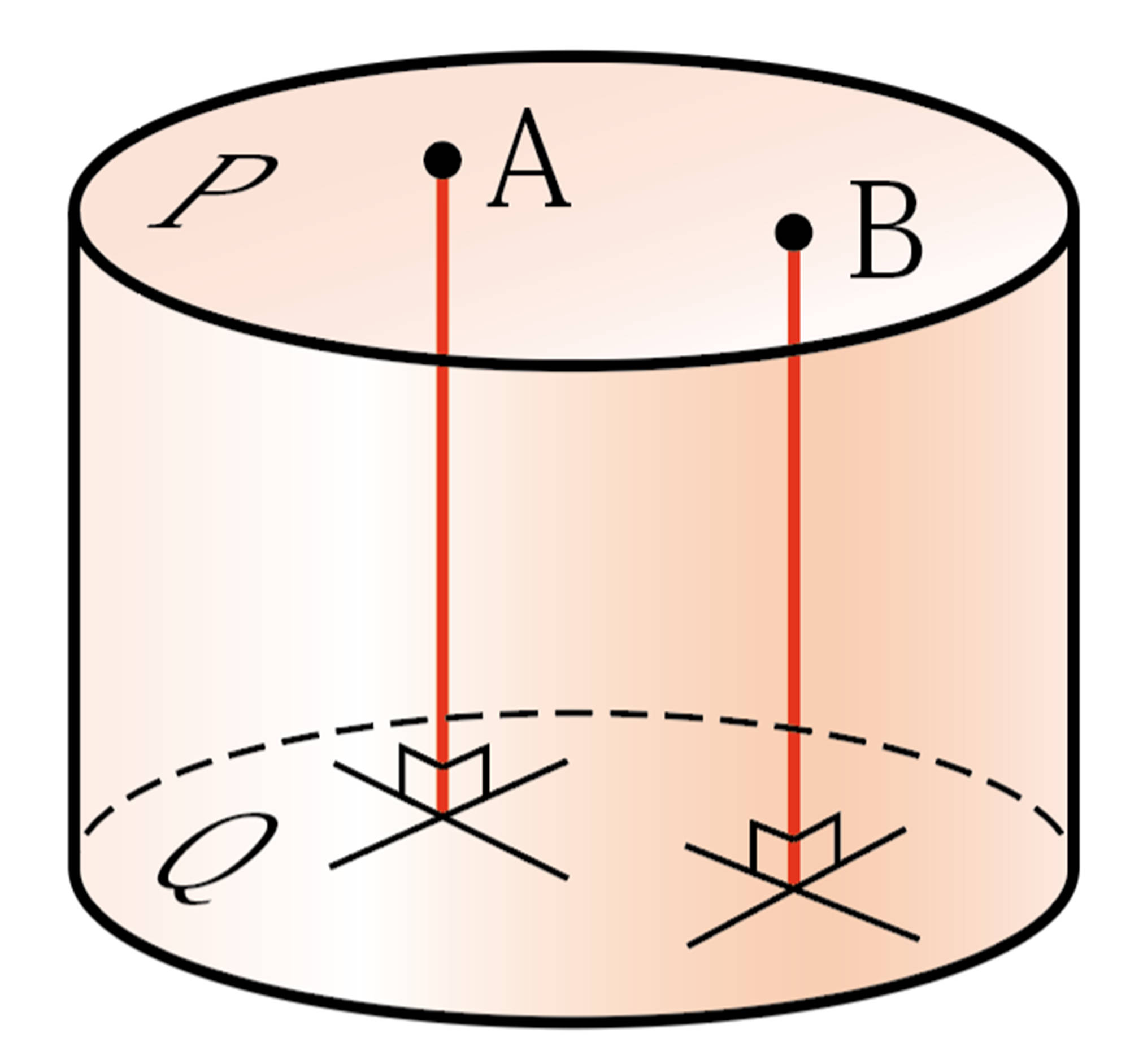
空間内での距離
Q Question
右の図は，身長を測っているところです。どこの長さを測っているのでしょうか。説明してみましょう。
頭のてっぺんから，足の裏までの長さを測ればいいね。
平面のときの点と直線の距離は，点から直線に垂直に引いた線分の長さで表したね。
見方・考え方
具体的な場面で考えられるかな。
平面 [mathjax] \( P \) 上にない点 [mathjax] \( A \) から [mathjax] \( P \) へ引いた垂線 [mathjax] \( AH \) の長さは，[mathjax] \( A \)と [mathjax] \( P \) 上のほかのどの点を結ぶ線分の長さよりも短くなる。この垂線AHの長さを，点[mathjax] \( A \)と平面 [mathjax] \( P \) との距離という。
問 ９ 右の図の円柱で，点 [mathjax] \( A \) ，[mathjax] \( B \) は底面 [mathjax] \( P \) 上の点です。それぞれの点と底面 [mathjax] \( Q \)との距離を比べなさい。
2平面[mathjax] \( P \)，[mathjax] \( Q \)が平行であるとき，一方の平面上の点と他方の平面との距離はすべて等しい。この距離を，平行な2平面 [mathjax] \( P \)，[mathjax] \( Q \)間の距離という。
角柱や円柱では，2つの底面間の距離を，その角柱や円柱の高さという。
また，角錐や円錐では，頂点と底面との距離を，その角錐や円錐の高さという。
どんなことがわかったかな
空間内での直線や平面の位置関係は，立体の辺や面をもとに考えることができます。
<1年p.217>
３ 面が動いてできる立体
次の図のように，点が動くと線が，線が動くと面が，面が動くと立体ができる。
Q Question
次の㋐～㋓の立体は，ある平面図形を動かしてできたものです。それぞれ，どのような平面図形をどのように動かしてできた立体といえるでしょうか。
底面を重ねていくと，角柱や円柱ができるね。
重ねることは，底面がどのように動いたといえるのかな。
見方・考え方
立体をこれまでと異なる見方で見ることができるかな。
目標 ▷ いろいろな立体は，どのような平面図形が動いてできているか調べよう。
角柱や円柱は，それぞれの底面の多角形や円が，底面と垂直な方向に動いてできた立体とみることができる。
問 １ [mathjax] \( \triangle ABC\)が，この三角形をふくむ平面 [mathjax] \(P\) の垂線 [mathjax] \( ℓ \) にそって平行に，点 [mathjax] \(A\) から点 [mathjax] \(D\) まで動きます。
⑴ [mathjax] \( \triangle ABC \) が動いてできる立体は何ですか。
⑵ 線分 [mathjax] \(AD\) の長さは，その立体の何を表していますか。
<1年p.218>
回転体
例 １ 右の図のように，直角三角形 [mathjax] \( ABC \) を，辺 [mathjax] \( AC \) を軸として1回転すると，底面の半径が [mathjax] \( BC \) ，高さが [mathjax] \( AC \) の円錐になる。
平面図形を，同じ平面上の直線 [mathjax] \( ℓ \)を軸として1回転してできる立体を【回転体】という。
円錐は直角三角形からできる回転体，円柱は長方形からできる回転体とみることができる。
また，右の図の円錐や円柱で，側面をえがく線分 [mathjax] \( AB \) を，円錐や円柱の【母線】という。
問 ２ 次の問いに答えなさい。
⑴ 半円を，直径をふくむ直線 [mathjax] \( ℓ \) を軸として1回転してできる立体は何ですか。
⑵ 右の図の長方形㋐を，直線 [mathjax] \( ℓ \) を軸として1回転してできる立体の見取図をかきなさい。
▲トライ 身のまわりから，回転体とみることができるものを探してみよう。
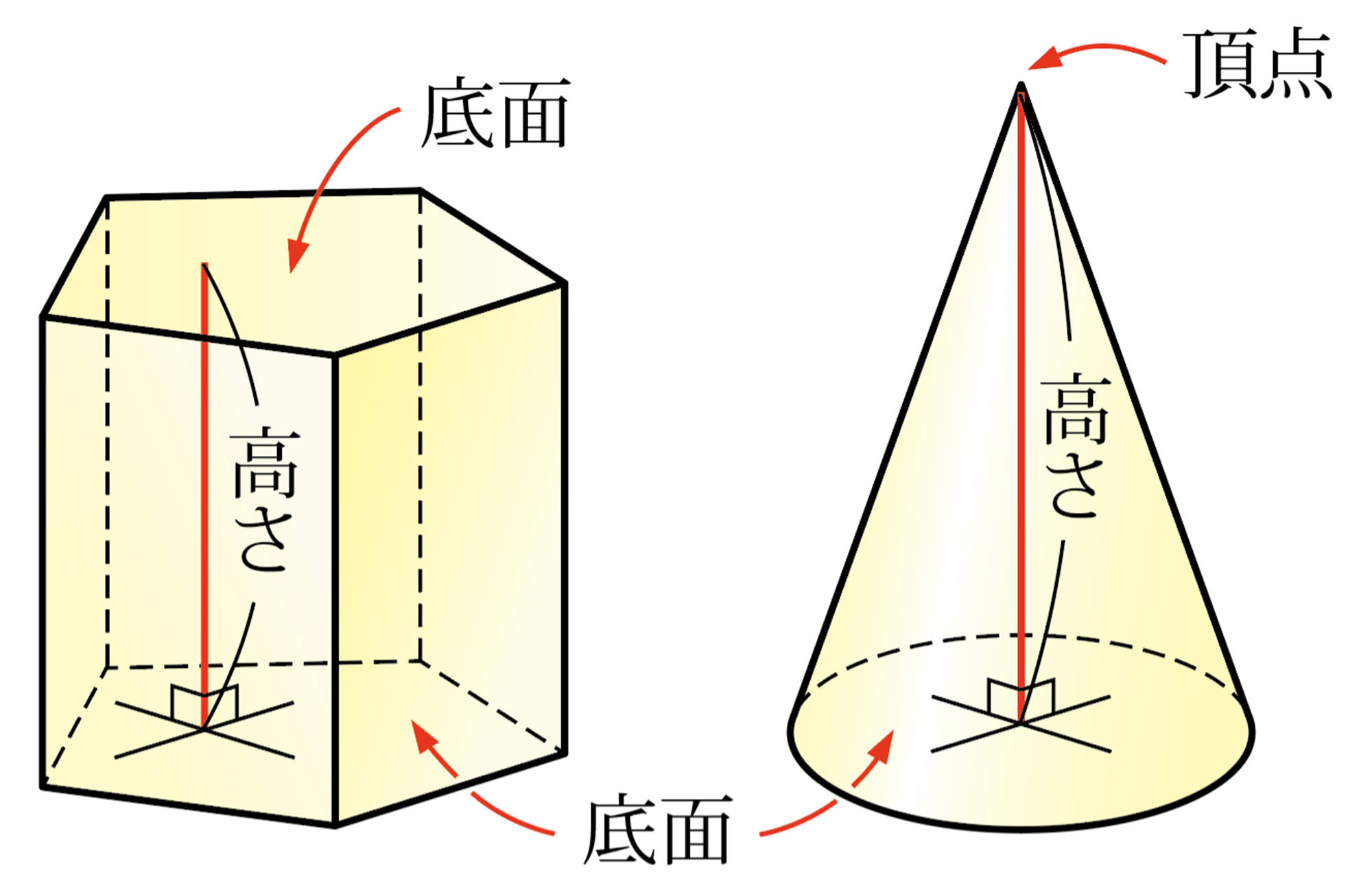
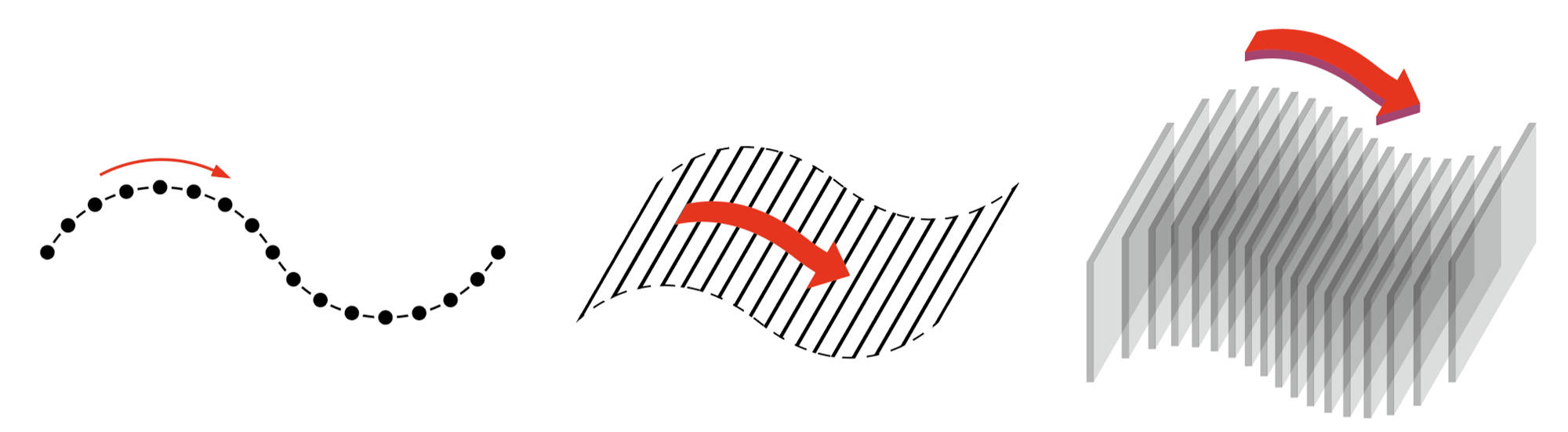
どんなことがわかったかな
立体には，多角形や円が，底面と垂直な方向に動いたり，回転したりしてできる図形とみることができるものがあります。
次の課題へ！
立体を展開図で表す方法があるけど，いろいろな立体を展開図で表せるのかな？
↓P.219
<1年p.219>
４ 立体の展開図
Q Question
次のような正四角錐，円錐の展開図はどのようになるか考えてみましょう。
⑴ 正四角錐
⑵ 円錐
角柱や円柱の展開図は，かいたことがあるよ。
四角錐は側面の形がわかるけど，円錐の側面はどんな形になるのかな。
見方・考え方
角柱や円柱と同じようにかけるかな。
目標 ▷ 角錐や円錐の展開図について調べよう。
角錐，円錐の展開図
問 １ 右の図は，【Q】⑴の正四角錐の展開図です。正四角錐のどの辺にそって切り開いたものですか。また，ほかの辺で切り開いた展開図をかきなさい。
【Q】⑵の円錐の側面を母線で切り開くと，次の図のような円の一部分になる。
<1年p.220>
円錐の側面の展開図のように，2つの半径と弧で囲まれた図形を【おうぎ形】という。おうぎ形で2つの半径のつくる角を【中心角】という。
問 ２ 前ページの円錐の展開図について，次の問いに答えなさい。
⑴ おうぎ形の半径は，もとの円錐のどの部分の長さと等しいですか。
⑵ [mathjax] \( \stackrel{\huge\frown}{AB} \)の長さは，もとの円錐のどの部分の長さと等しいですか。
問 ３ 大和さんは，次の①〜④の展開図をつくりました。㋐〜㋒のどの円錐の展開図だと考えられますか。また，円錐ができないものはありますか。
①
②
③
④
㋐
㋑
㋒
どんなことがわかったかな
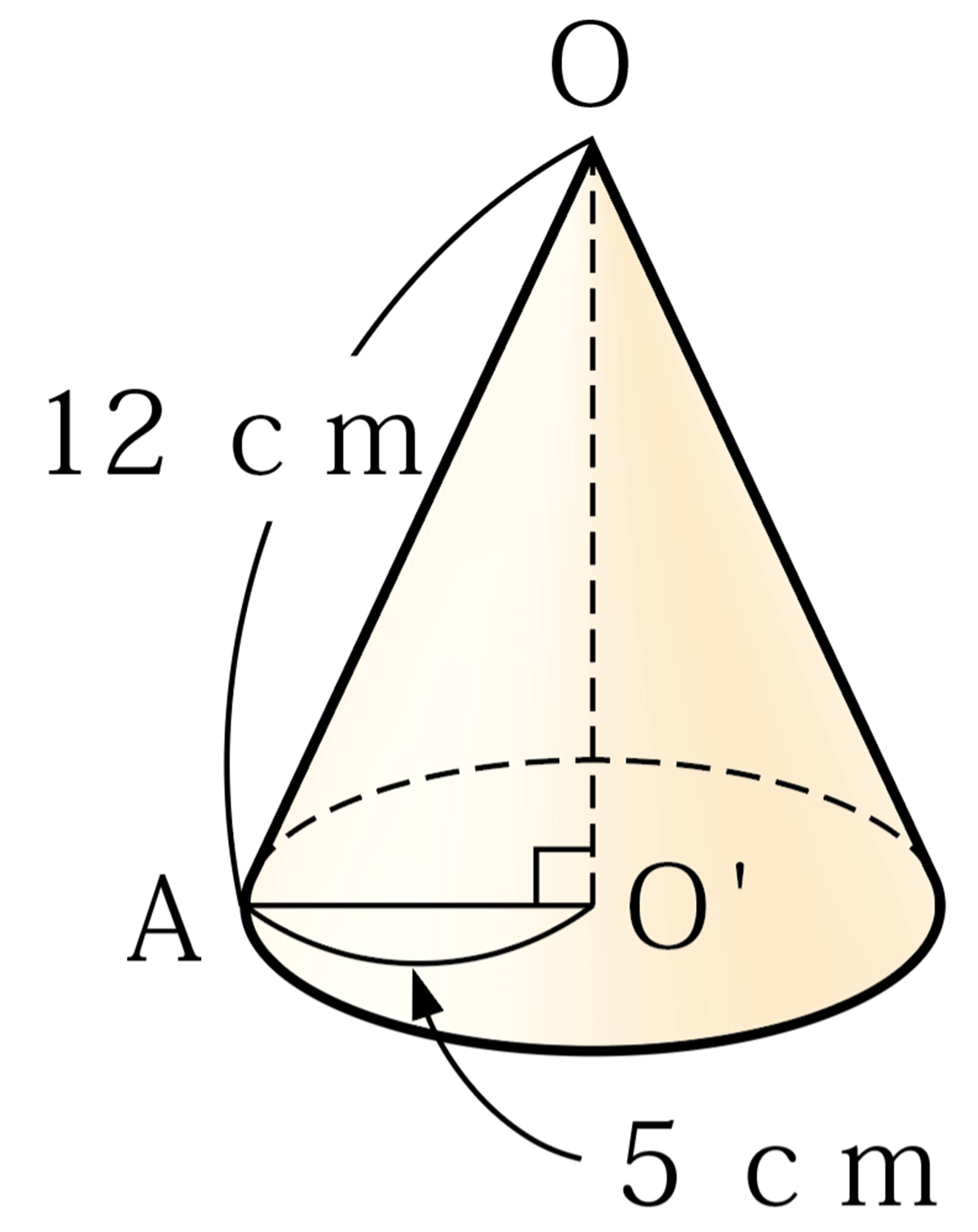
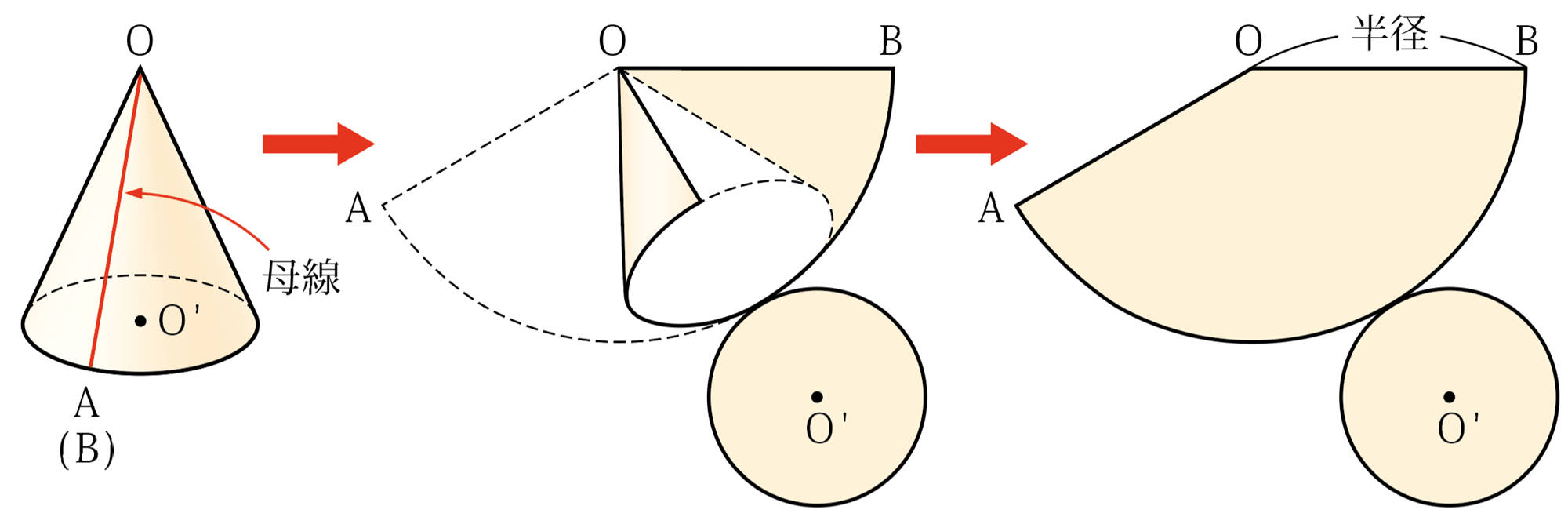
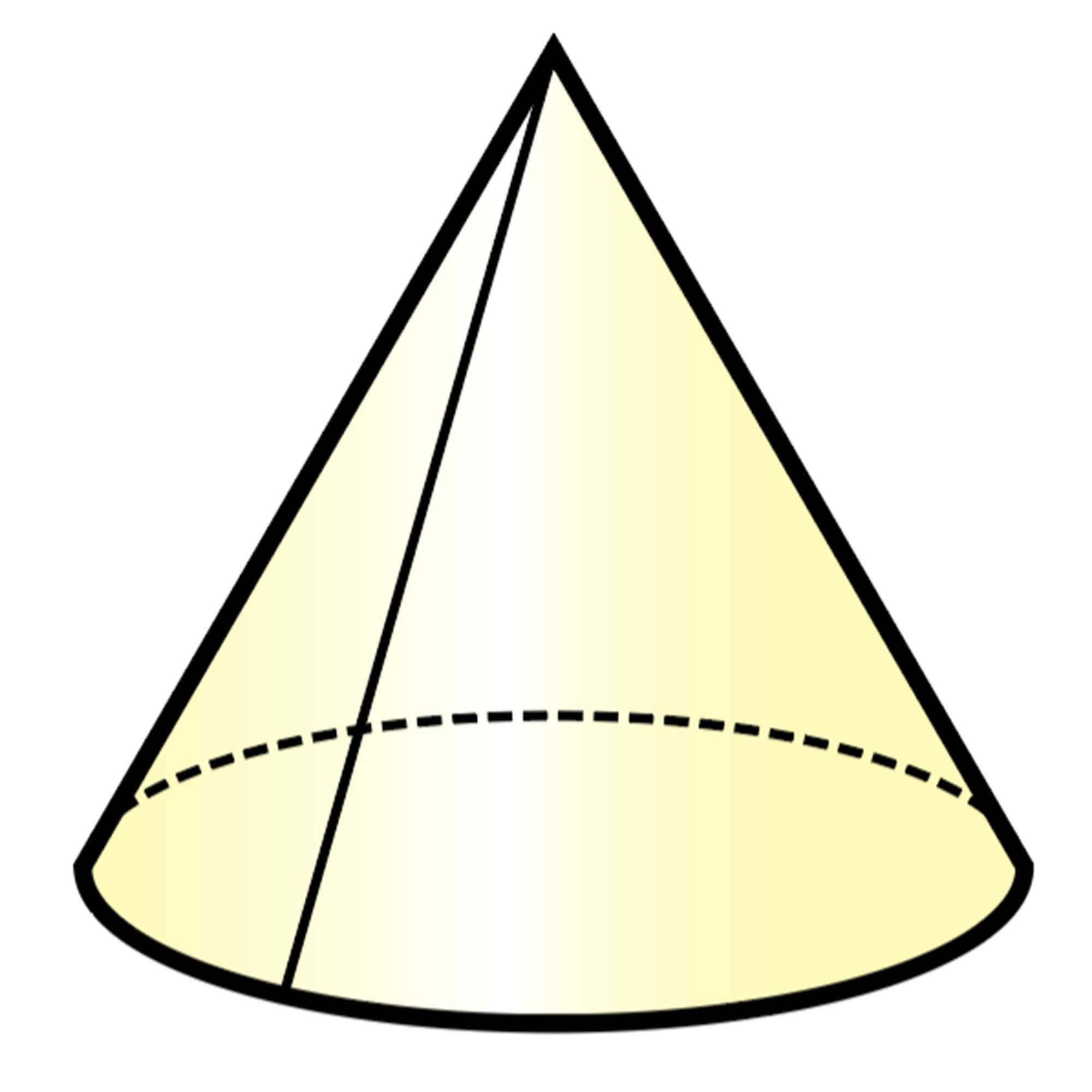
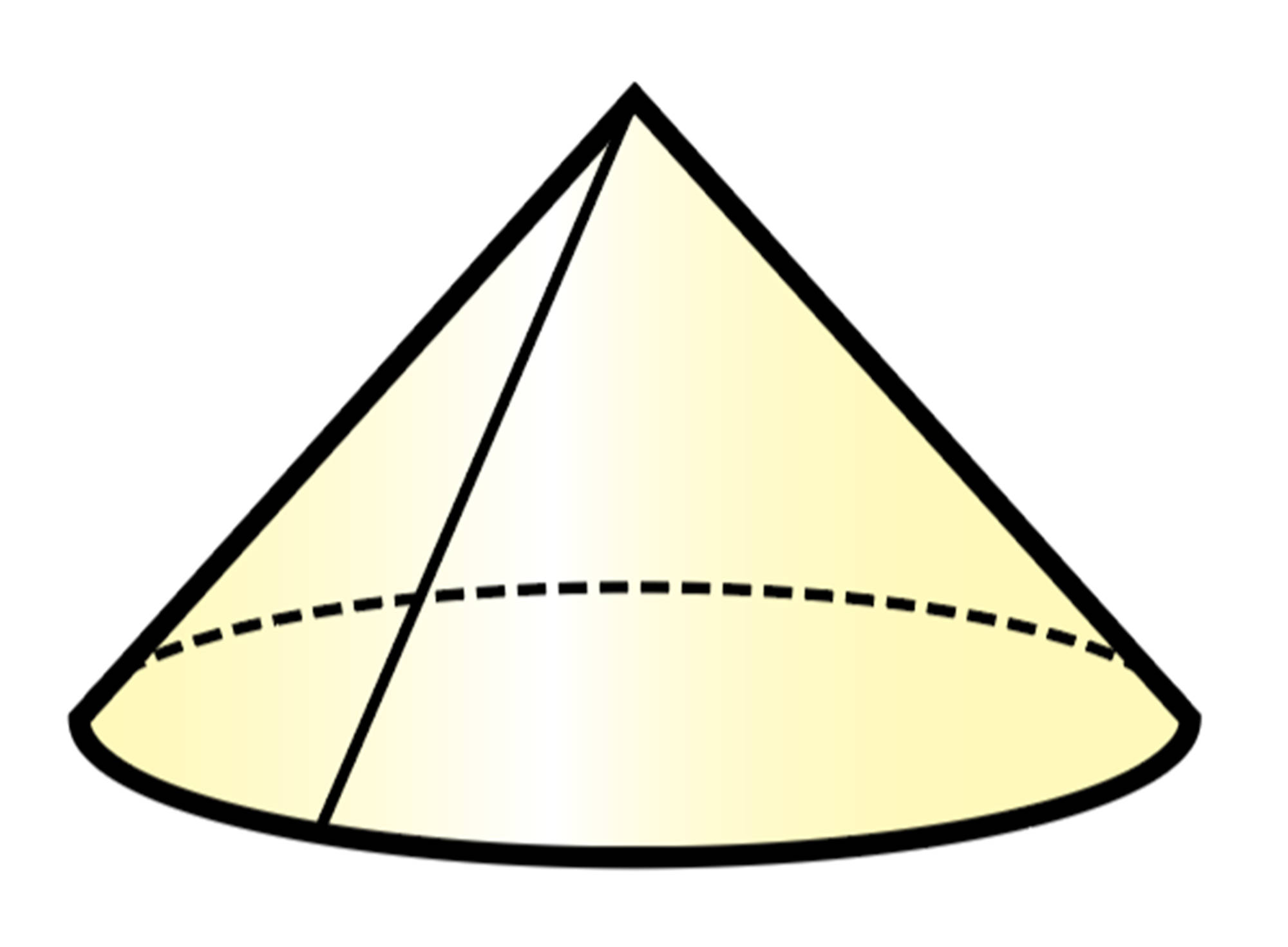
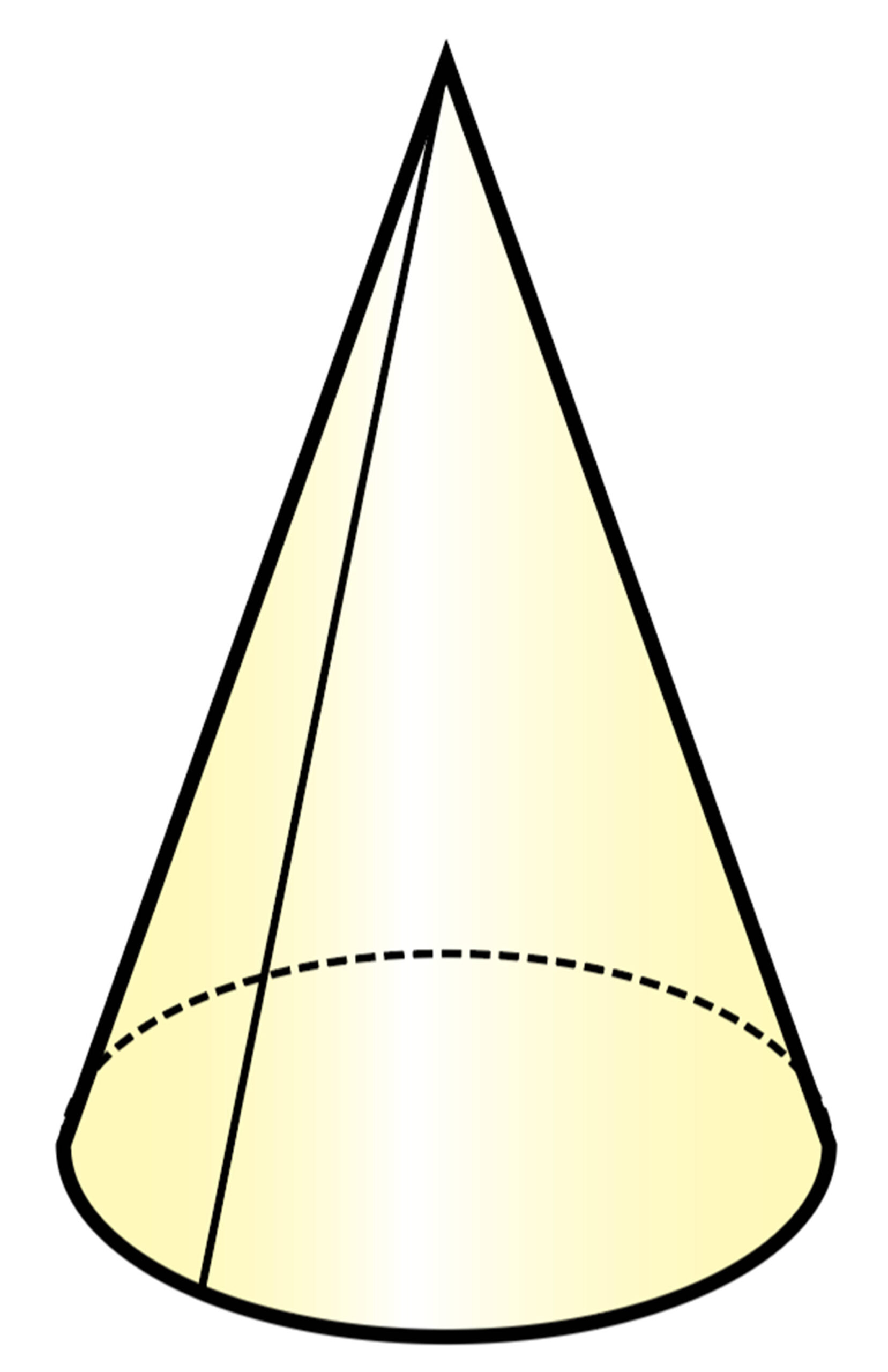
角錐の展開図では，角錐の側面はいくつかの三角形で表すことができます。また，円錐の展開図では，円錐の側面はおうぎ形で表すことができます。
おしえて！
P.222
正多面体の展開図はどんな形かな？
<1年p.221>
確かめよう １節 空間図形の見方
１ 右の㋐，㋑，㋒の立体について，次の問いに答えなさい。
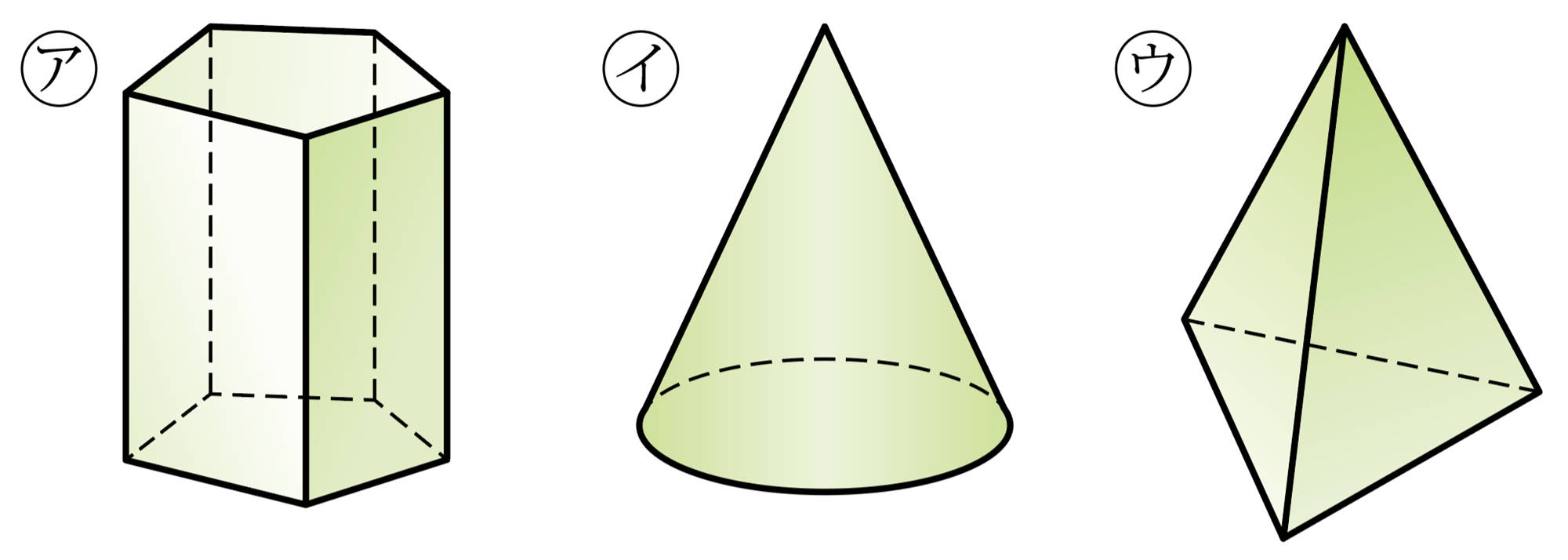
⑴ それぞれの立体の名称をいいなさい。
⑵ 多面体はどれですか。
２ 右の図の正四角錐について，次の問いに答えなさい。
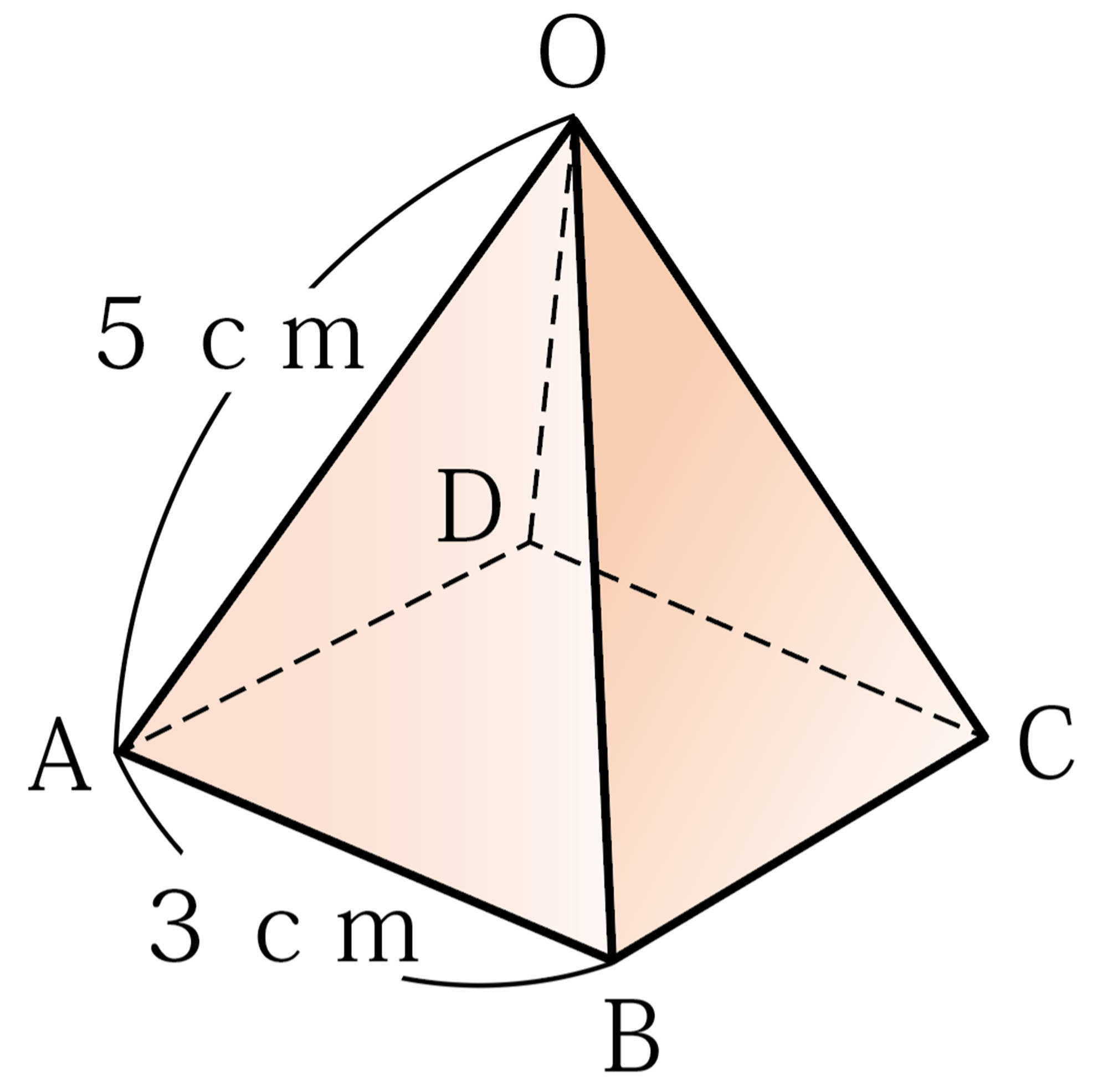
⑴ 辺 [mathjax] \( AB \) とねじれの位置にある辺はどれですか。
⑵ 面 [mathjax] \( OAB \) と辺 [mathjax] \( CD \) の位置関係をいいなさい。
⑶ この正四角錐の高さを示す線分 [mathjax] \( OH \) を，右の図にかき入れなさい。
３ 右の図は，ある立体の展開図です。この立体の名称をいいなさい。また，この立体の見取図，投影図をかきなさい。
正多面体の双対性 Tea Break
右の図のように，正六面体の各面の中心を頂点とする多面体は正八面体になり，正八面体の各面の中心を頂点とする多面体は正六面体になる。正六面体と正八面体は，双対の関係にあるという。
正十二面体と正二十面体も双対の関係にあり，正四面体は自分自身と双対の関係にある。
<1年p.222>
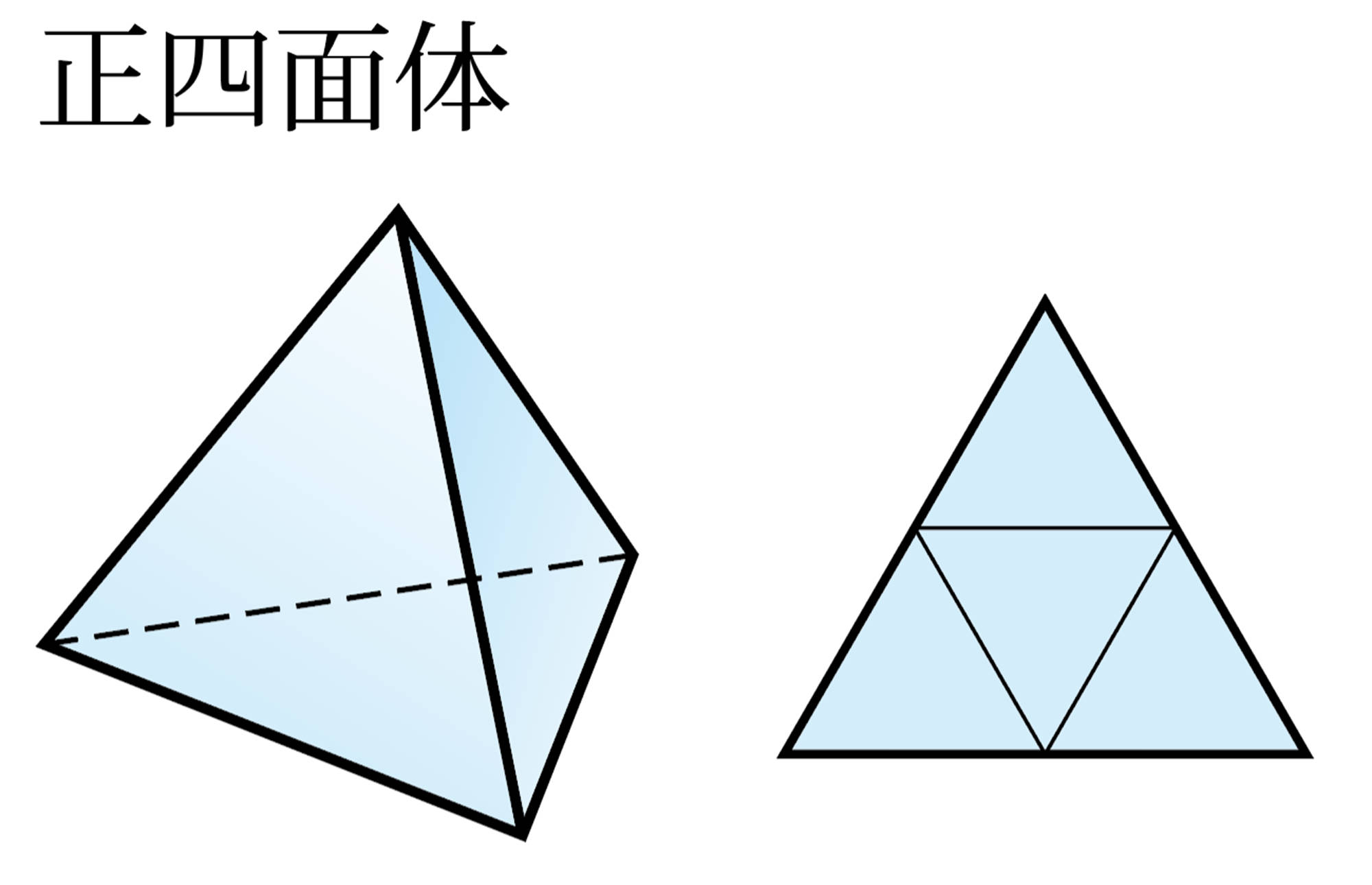
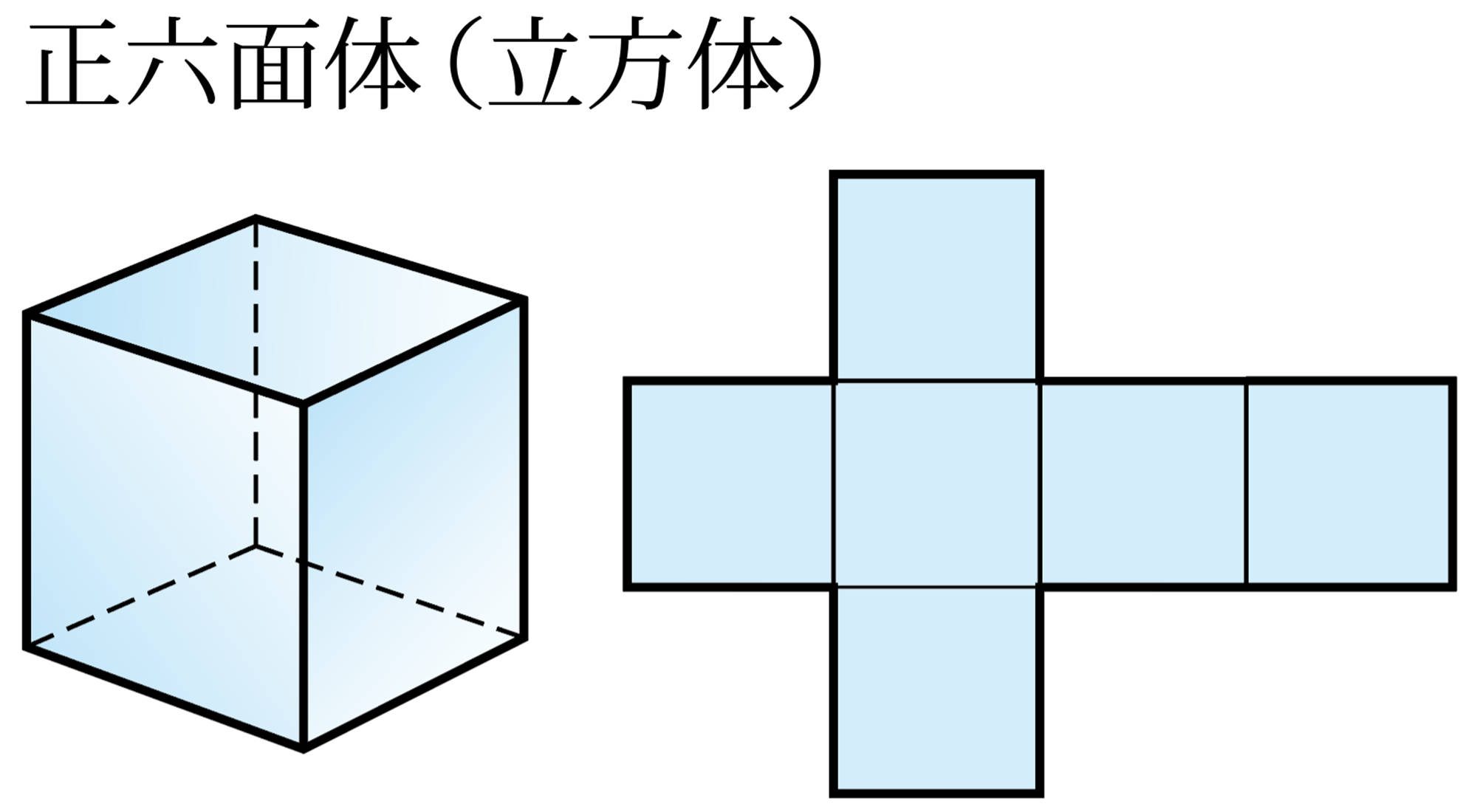
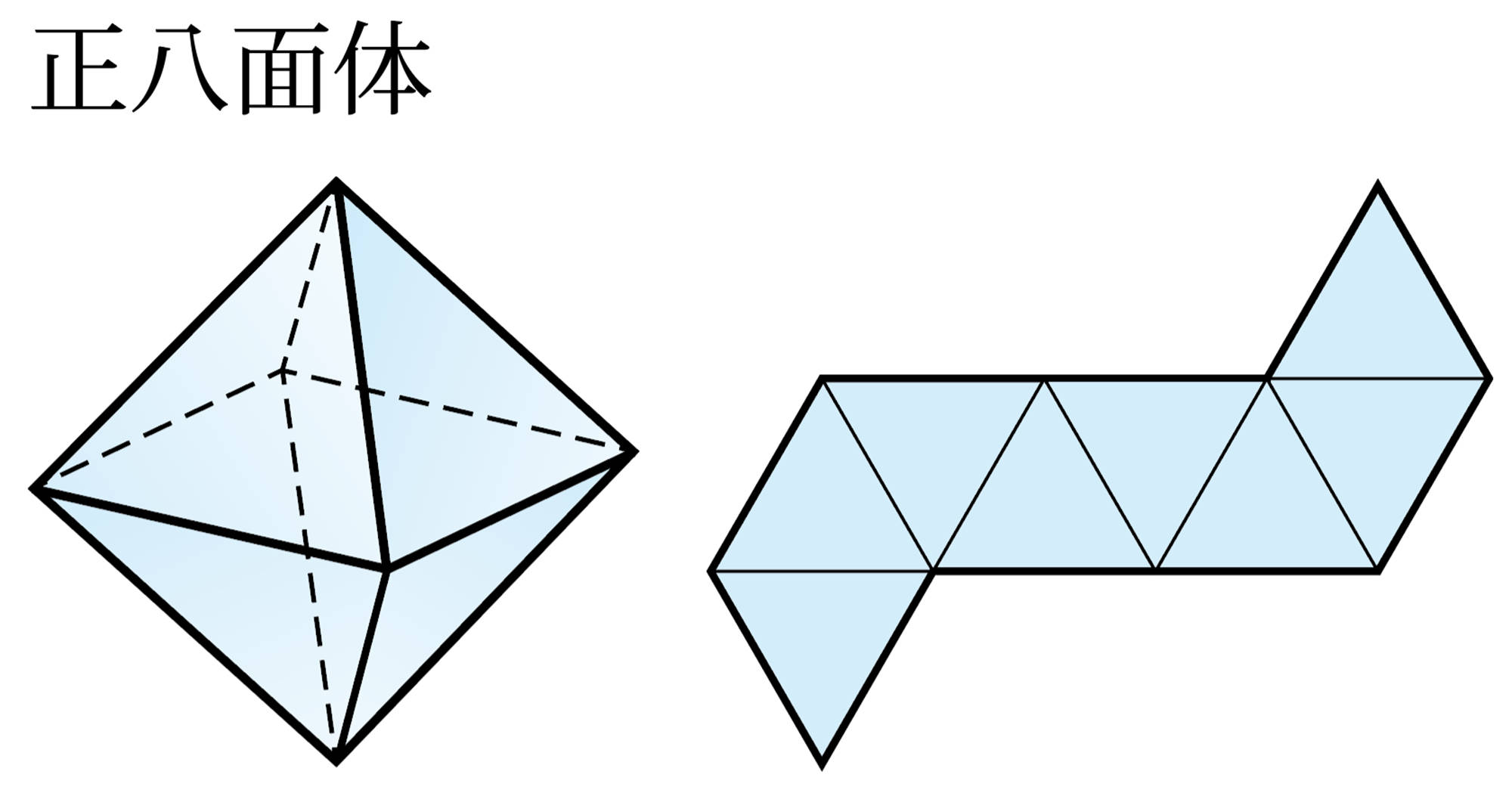
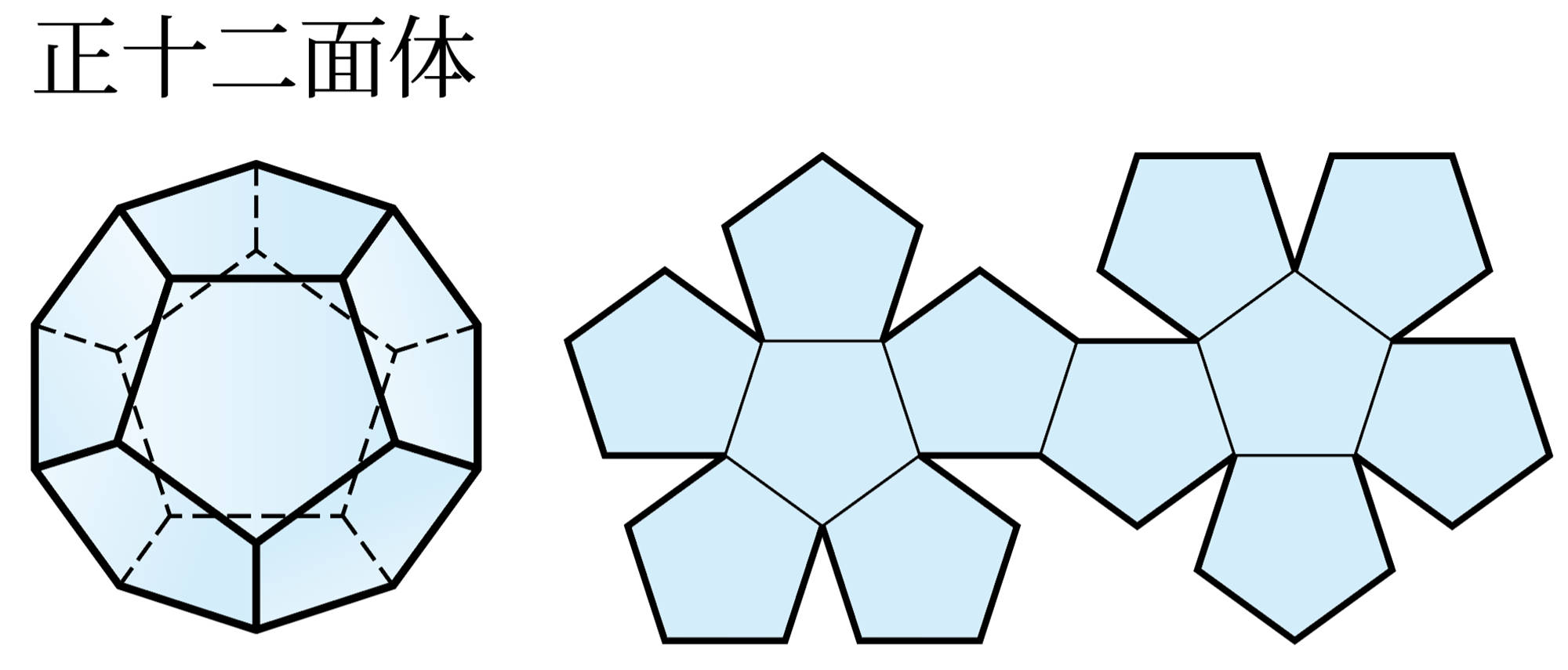
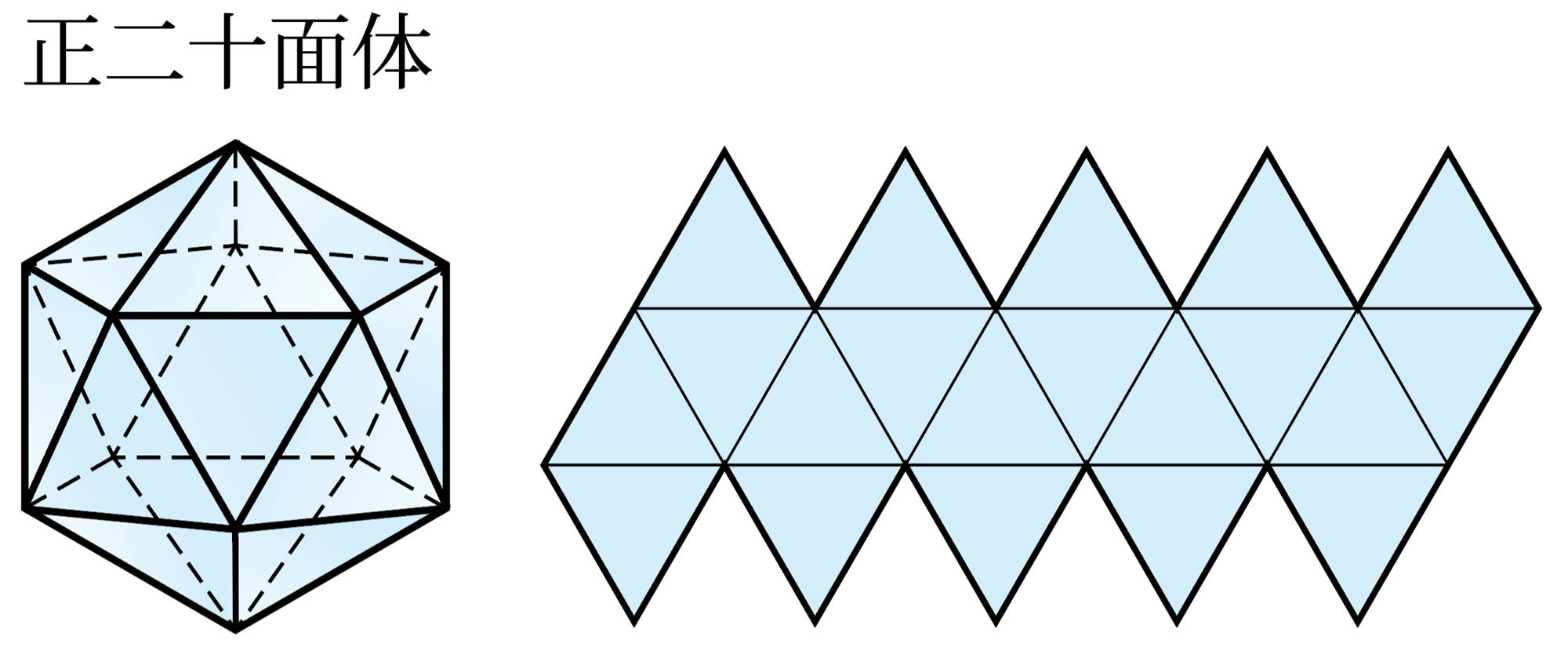
正多面体 Tea Break
１ 次の表は，正多面体の面についてまとめたものです。
⑴ 1つの頂点に，正三角形を6個集めて立体をつくることができるでしょうか。
⑵ 1つの頂点に，正方形や正五角形を4個以上集めて立体をつくることができるでしょうか。
⑶ 1つの頂点に，正六角形を何個か集めて立体をつくることができるでしょうか。
⑷ ⑴〜⑶をもとに，正多面体が5種類しかない理由を考えてみましょう。
２ 次の図は，5種類の正多面体とその展開図です。
正六面体は11通りの展開図がかけます。
