<3年p.300>
1章 式の計算 [解答]
計算力を高めよう１ P.22
１
⑴ [mathjax]\(2x²+8x\)
⑵ [mathjax]\(3x²-6x\)
⑶ [mathjax]\(-10a²+16a\)
⑷ [mathjax]\(-28x²+8x\)
⑸ [mathjax]\(-3a²+15ab-3a\)
⑹ [mathjax]\(9a²+6a\)
⑺ [mathjax]\(2x-9\)
⑻ [mathjax]\(5a+b\)
⑼ [mathjax]\(4a-b\)
⑽ [mathjax]\(-4x-3y\)
⑾ [mathjax]\(9y-6\)
２
⑴ [mathjax]\(ab+2a+8b+16\)
⑵ [mathjax]\(xy+6x-7y-42\)
⑶ [mathjax]\(2a²-17a+8\)
⑷ [mathjax]\(6x²+14x+4\)
⑸ [mathjax]\(-2a²+17ab-30b²\)
⑹ [mathjax]\(-49x²+7xy+6y²\)
⑺ [mathjax]\(ax-ay+5a+bx-by+5b\)
⑻ [mathjax]\(ax+2ay-3a-2bx-4by+6b\)
⑼ [mathjax]\(x²-y²-3x+3y\)
⑽ [mathjax]\(2a²+5ab-3b²-4a-12b\)
３
⑴ [mathjax]\(x²+10x+21\)
⑵ [mathjax]\(x²-9x+20\)
⑶ [mathjax]\(x²-x-90\)
⑷ [mathjax]\(x²+5x-6\)
⑸ [mathjax]\(x²+8x+16\)
⑹ [mathjax]\(x²-20x+100\)
⑺ [mathjax]\(x²+ \dfrac{2}{3} x + \dfrac{1}{9}\)
⑻ [mathjax]\(x²-1\)
⑼ [mathjax]\(a²-81\)
⑽ [mathjax]\(36-x²\)
⑾ [mathjax]\(x²- \dfrac{25}{16}\)
４
⑴ [mathjax]\(4x²-49\)
⑵ [mathjax]\(9a²+30a+25\)
⑶ [mathjax]\(25x²-20xy+4y²\)
⑷ [mathjax]\(4a²+18a+18\)
⑸ [mathjax]\(x²-2xy+y²-64\)
⑹ [mathjax]\(a²+2ab+b²-7a-7b+10\)
⑺ [mathjax]\(a²-b²+8b-16\)
⑻ [mathjax]\(4x-9\)
⑼ [mathjax]\(a²\)
⑽ [mathjax]\(11x+8\)
⑾ [mathjax]\(8ab\)
計算力を高めよう2 P.31
１
⑴ [mathjax]\(x(y+4)\)
⑵ [mathjax]\(a(5x-8y+2)\)
⑶ [mathjax]\(x(x+7)\)
⑷ [mathjax]\(xy(2x-3y)\)
⑸ [mathjax]\(3a(2a+3b)\)
⑹ [mathjax]\(5x(2x-5y+1)\)
２
⑴ [mathjax]\((x+1)(x+5)\)
⑵ [mathjax]\((x+3)(x+7)\)
⑶ [mathjax]\((x-1)(x-6)\)
⑷ [mathjax]\((x-3)(x-9)\)
⑸ [mathjax]\((x+4)(x-2)\)
⑹ [mathjax]\((x+2)(x-5)\)
⑺ [mathjax]\((x+1)(x-2)\)
⑻ [mathjax]\((x+9)(x-5)\)
⑼ [mathjax]\((x+7)²\)
⑽ [mathjax]\((x+8)²\)
⑾ [mathjax]\((x-5)²\)
⑿ [mathjax]\((x-10)²\)
⒀ [mathjax]\((x+1)(x-1)\)
⒁ [mathjax]\((x+8)(x-8)\)
３
⑴ [mathjax]\((2x+3)²\)
⑵ [mathjax]\((3x-1)²\)
⑶ [mathjax]\((x-y)²\)
⑷ [mathjax]\((x+4y)²\)
⑸ [mathjax]\((10x+7)(10x-7)\)
⑹ [mathjax]\((4+5x)(4-5x)\)
⑺ [mathjax]\((2x+7y)(2x-7y)\)
⑻ [mathjax]\(\require{physics} \left(x+ \dfrac{y}{3}\right)\require{physics} \left(x- \dfrac{y}{3}\right)\)
⑼ [mathjax]\(a(x+y)(x-y)\)
⑽ [mathjax]\(a(x+1)²\)
⑾ [mathjax]\(3(x-3y)²\)
⑿ [mathjax]\(2y(x+5)(x-3)\)
⒀ [mathjax]\((x+6)(x-3)\)
⒁ [mathjax]\((x-3)(x-4)\)
⒂ [mathjax]\((x+3)²\)
⒃ [mathjax]\((x+3)(x-6)\)
⒄ [mathjax]\((x-4)(x-7)\)
⒅ [mathjax]\((a-b)(x+y)\)
⒆ [mathjax]\((x+6)(x-1)\)
⒇ [mathjax]\(x(x-10)\)
（21） [mathjax]\((x+1)(y-5)\)
（22） [mathjax]\((x+1)(2y-3)\)
トライ P.37
道の3つの曲線部分を合わせると半径aの円になる。
道の直線部分全体の中央線の長さを[mathjax]\(ℓ₁\)，面積を[mathjax]\(S₁\)，曲線部分全体の中央線の長さを[mathjax]\(ℓ₂\)，面積を[mathjax]\(S₂\)とすると，
[mathjax]\(S₁=aℓ₁\)，[mathjax]\(S₂=aℓ₂\)
したがって，
1章のまとめの問題 P.39〜41
１
⑴ [mathjax]\(6a²-12a\)
⑵ [mathjax]\(-2xy+5y²\)
⑶ [mathjax]\(-4x+3y\)
⑷ [mathjax]\(6b+8\)
２
⑴ [mathjax]\(ax+ay-bx-by\)
⑵ [mathjax]\(3x²+5x+2\)
⑶ [mathjax]\(x²-x-6\)
⑷ [mathjax]\(y²-12y+36\)
⑸ [mathjax]\(a²-9b²\)
⑹ [mathjax]\(4x²+12x+9\)
３
⑴ [mathjax]\(3a²-2a+1\)
⑵ [mathjax]\(2x\)
４
⑴ [mathjax]\(2ab(2a-3b)\)
⑵ [mathjax]\((x+3)(x+4)\)
⑶ [mathjax]\((x-3)²\)
⑷ [mathjax]\((12+x)(12-x)\)
⑸ [mathjax]\((x+7)(x-5)\)
⑹ [mathjax]\((2x+3y)²\)
⑺ [mathjax]\(y(x-3)(x-6)\)
⑻ [mathjax]\((x+1)(x+3)\)
５
連続する3つの整数は，nを整数とすると，[mathjax]\(n-1\)，n，[mathjax]\(n+1\) と表される。
したがって，連続する3つの整数では，もっとも大きい数の2乗からもっとも小さい数の2乗をひいた差は，中央の数の4倍になる。
<3年p.301>
６
[mathjax]\(2\pi ab\)
応用
１
⑴ [mathjax]\(x²-\dfrac{3}{2}x-1\)
⑵ [mathjax]\(a²-49b²\)
⑶ [mathjax]\(x²+4xy+4y²-18x-36y+81\)
⑷ [mathjax]\(a²-b²+2b-1\)
２
⑴ [mathjax]\((x+5)(x-3)\)
⑵ [mathjax]\(x(x+1)\)
⑶ [mathjax]\((x+a)(x-1)\)
⑷ [mathjax]\((x-2)(y-3)\)
３
[mathjax]\((7a-15)\) m²大きくなる，10 m
４
2つの奇数は，m，nを整数とすると，[mathjax]\(2m+1\)，[mathjax]\(2n+1\)と表される。
[mathjax]\(2mn+m+n\) は整数だから，
[mathjax]\(2(2mn+m+n)+1\)は奇数である。
したがって，2つの奇数の積は奇数になる。
５
25
６
⑴ [mathjax] \(-80\)
⑵ [mathjax]\(48.99\)
７
⑴ [mathjax]\(ℓ= \dfrac{\pi (2r+h)}{3}\)
⑵ 芝生の面積をSm²とすると，
⑴より，[mathjax]\(ℓ= \dfrac{\pi (2r+h)}{3}\)であるから，
[mathjax]\(S=hℓ\) したがって，芝生の面積はhℓm²となる。
活用
１
⑴ ㋐ 40 ㋑ 36
⑵ 113
⑶ 8n
⑷ n枚目のページ番号a，b，c，dを，それぞれnを使って表すと，[mathjax]\(a=8n-3\)， [mathjax]\(b=8n-4\)，[mathjax]\(c=8n\)，[mathjax]\(d=8n-7\)
したがって，n枚目のページ番号で，[mathjax]\(ab-cd=12\)の関係が成り立つ。
簡単に計算する方法 P.42
① 略
② ⑴ 9801 ⑵ 9025 ⑶ 8464
③ ⑴ 10201 ⑵ 10609 ⑶ 11664
2章 平方根 [解答]
計算力を高めよう3 P.67
１
⑴ [mathjax]\(\sqrt{26}\)
⑵ [mathjax]\(\sqrt{6}\)
⑶ 12
⑷ 5
⑸ [mathjax]\(8 \sqrt{10}\)
⑹ [mathjax]\(-12 \sqrt{5}\)
⑺ [mathjax]\(\dfrac{15 \sqrt{2}}{2}\)
⑻ [mathjax]\(3 \sqrt{3}\)
⑼ [mathjax]\(2 \sqrt{6}\)
⑽ [mathjax]\(2 \sqrt{3}\)
２
⑴ [mathjax]\(7 \sqrt{5}\)
⑵ [mathjax]\(-5 \sqrt{7}\)
⑶ [mathjax]\(4 \sqrt{2}\)
⑷ [mathjax]\(-3 \sqrt{2} + 5 \sqrt{6}\)
⑸ [mathjax]\(4 \sqrt{7}\)
⑹ [mathjax]\(2 \sqrt{2}\)
⑺ [mathjax]\(0 \)
⑻ [mathjax]\(5 \sqrt{5}\)
⑼ [mathjax]\(5 \sqrt{2}\)
⑽ [mathjax]\(- \sqrt{6}\)
⑾ [mathjax]\(2 \sqrt{15}\)
⑿ [mathjax]\(7 \sqrt{2}\)
３
⑴ [mathjax]\(3 \sqrt{6}\)
⑵ [mathjax]\(3 \sqrt{3}\)
⑶ [mathjax]\(5 \sqrt{6}-2\)
⑷ [mathjax]\(3- \sqrt{7}\)
⑸ [mathjax]\(17+7 \sqrt{7}\)
⑹ [mathjax]\(53+ \sqrt{3}\)
⑺ [mathjax]\(11-7 \sqrt{5}\)
⑻ [mathjax]\(-71\)
⑼ 6
⑽ 3
⑾ [mathjax]\(16+6 \sqrt{7}\)
⑿ [mathjax]\(8-4 \sqrt{3}\)
⒀ [mathjax]\(8+6 \sqrt{3}\)
⒁ [mathjax]\(43-30 \sqrt{2}\)
⒂ 22
⒃ [mathjax]\(\dfrac{7}{3}\)
⒄ [mathjax]\(2 \sqrt{2}\)
⒅ [mathjax]\(-3- \sqrt{2}\)
⒆ 6
2章のまとめの問題 P.69〜71
１
⑴ [mathjax]\(\pm 5\)
⑵ [mathjax]\(\pm \sqrt{19}\)
⑶ [mathjax]\(0\)
⑷ [mathjax]\(\pm 0.4\)
２
⑴ 7
⑵ 正しい
⑶ 2
⑷ 大きい
３
⑴ [mathjax]\(4 \sqrt{3} \lt 7\)
⑵ [mathjax]\(- \sqrt{17} \gt -3 \sqrt{2}\)
４
⑴ [mathjax]\(6 \sqrt{7}\)
⑵ [mathjax]\(\dfrac {2 \sqrt{6}}{3}\)
⑶ [mathjax]\(4 \sqrt{3}\)
⑷ [mathjax]\(\sqrt{3}+5 \sqrt{2}\)
⑸ [mathjax]\(6 \sqrt{5}\)
⑹ [mathjax]\(3 \sqrt{6}\)
⑺ [mathjax]\(20+6 \sqrt{11}\)
⑻ 17
５
⑴ [mathjax]\(2 \sqrt{21}\)cm
⑵ 8個
⑶ [mathjax]\(8 \sqrt{3}\)
応用
１
[mathjax]\(\dfrac{ \sqrt{3}}{7} \lt \dfrac{3}{7} \lt \sqrt{\dfrac{3}{7}} \lt \dfrac{3}{ \sqrt{7}}\)
２
⑴ [mathjax]\(\dfrac{\sqrt{6}+ \sqrt{2}}{2}\)
⑵ [mathjax]\(\dfrac{5 \sqrt{2}- \sqrt{10}}{5}\)
３
⑴ [mathjax]\(10 \sqrt{3}\)
⑵ 30
<3年p.302>
⑶ [mathjax]\(\sqrt{3}\)
⑷ [mathjax]\(-5+2\sqrt{7}\)
⑸ [mathjax]\(2 \sqrt{3}\)
４
⑴ [mathjax]\(n=6\)
⑵ 13
⑶ 5
⑷ [mathjax]\(1-\sqrt{5}\)
５
[mathjax]\((18 – 12 \sqrt{2})\)cm²
活用
１
[mathjax]\(2 \sqrt{2}\)倍
２
F2
丸太からとれる角材は？ ◁P.72
① 4cm9mm
② 正方形の1辺は，丸太の直径の[mathjax]\(\dfrac{1}{\sqrt{2}}\)倍だから，角目の目盛りの数値がそのまま正方形の1辺の長さになる。
3章 2次方程式 [解答]
トライ ◁P.85
[mathjax]\(\require{physics} \left(x+\dfrac{5}{2}\right)^{2}=\dfrac{33}{4}\)から，[mathjax]\(x=\dfrac{-5\pm \sqrt{33}}{2}\)
トライ ◁P.89
根号の中の[mathjax]\((b²-4ac)\)の値が0になる場合に， 解が1つになる。
計算力を高めよう4 ◁P.90
１
⑴ [mathjax]\(x=3\)，[mathjax]\(x=-9\)
⑵ [mathjax]\(x=-1\)，[mathjax]\(x=-5\)
⑶ [mathjax]\(x=3\)，[mathjax]\(x=-8\)
⑷ [mathjax]\(x=-3\)，[mathjax]\(x=-8\)
⑸ [mathjax]\(x=3\)，[mathjax]\(x=5\)
⑹ [mathjax]\(x=-4\)
⑺ [mathjax]\(x=6\)
⑻ [mathjax]\(x=7\)，[mathjax]\(x=-6\)
⑼ [mathjax]\(x=0\)，[mathjax]\(x=-1\)
⑽ [mathjax]\(x=\pm 6\)
⑾ [mathjax]\(x=7\)，[mathjax]\(x=-5\)
⑿ [mathjax]\(x=5\)
⒀ [mathjax]\(x=2\)，[mathjax]\(x=3\)
⒁ [mathjax]\(x=4\)，[mathjax]\(x=-1\)
⒂ [mathjax]\(x=6\)，[mathjax]\(x=-1\)
⒃ [mathjax]\(x=4\)，[mathjax]\(x=7\)
⒄ [mathjax]\(x=\pm 1\)
⒅ [mathjax]\(x=6\)，[mathjax]\(x=-7\)
２
⑴ [mathjax]\(x=\pm 2\sqrt{3}\)
⑵ [mathjax]\(x=\pm \dfrac{9}{2}\)
⑶ [mathjax]\(x=\pm \sqrt{7}\)
⑷ [mathjax]\(x=\pm 3\)
⑸ [mathjax]\(x=\pm 2\sqrt{5}\)
⑹ [mathjax]\(x=-6\pm \sqrt{11}\)
⑺ [mathjax]\(x=5\)，[mathjax]\(x=13\)
⑻ [mathjax]\(x=3\pm 3\sqrt{2}\)
⑼ [mathjax]\(x=-1\)，[mathjax]\(x=-4\)
⑽ [mathjax]\(x=5\)，[mathjax]\(x=-1\)
３
⑴ [mathjax]\(x=\dfrac{-7\pm \sqrt{41}}{2}\)
⑵ [mathjax]\(x=\dfrac{5\pm \sqrt{17}}{4}\)
⑶ [mathjax]\(x=2\)，[mathjax]\(x=-\dfrac{1}{3}\)
⑷ [mathjax]\(x=\dfrac{1}{2}\)，[mathjax]\(x=-\dfrac{5}{2}\)
⑸ [mathjax]\(x=-1\pm \sqrt{5}\)
⑹ [mathjax]\(x=- 3\pm 2\sqrt{2}\)
⑺ [mathjax]\(x=\dfrac{-1\pm \sqrt{5}}{2}\)
⑻ [mathjax]\(x=\dfrac{4\pm \sqrt{10}}{3}\)
⑼ [mathjax]\(x=\dfrac{1\pm \sqrt{97}}{12}\)
⑽ [mathjax]\(x=\dfrac{1}{2}\)，[mathjax]\(x=-\dfrac{1}{3}\)
⑾ [mathjax]\(x=\dfrac{3\pm \sqrt{29}}{5}\)
⑿ [mathjax]\(x=2\)，[mathjax]\(x=-\dfrac{5}{2}\)
3章のまとめの問題 ◁P.96〜98
１
㋑，㋒
２
⑴ [mathjax]\(x=\pm \dfrac{5}{2}\)
⑵ [mathjax]\(x=5\pm \sqrt{6}\)
⑶ [mathjax]\(x=\dfrac{9}{2}\)，[mathjax]\(x=-\dfrac{7}{2}\)
⑷ [mathjax]\(x=-2\)，[mathjax]\(x=-6\)
⑸ [mathjax]\(x=6\)，[mathjax]\(x=- 5\)
⑹ [mathjax]\(x=\dfrac{7\pm 3\sqrt{5}}{2}\)
⑺ [mathjax]\(x=1\)，[mathjax]\(x=6\)
⑻ [mathjax]\(x=\dfrac{3\pm \sqrt{3}}{2}\)
⑼ [mathjax]\(x=5\)
⑽ [mathjax]\(x=0\)，[mathjax]\(x=7\)
３
[mathjax]\(a=2\)，[mathjax]\(x=-5\)
４
⑴ [mathjax]\(x²-2x=35\)
⑵ [mathjax]\(x=7\)，[mathjax]\(x=-5\)
xは自然数であるから，[mathjax]\(x=7\)
答 7
５
道の幅をxmとすると，[mathjax]\((15-2x)²=144\)
これを解くと，[mathjax]\(x=\dfrac{3}{2}\)，[mathjax]\(x=\dfrac{27}{2}\)
[mathjax]\(0 \lt x \lt \dfrac{15}{2}\)であるから，[mathjax]\(x=\dfrac{3}{2}\)
答 [mathjax]\(1.5\) m
応用
１
⑴ [mathjax]\(x=4\)，[mathjax]\(x=-3\)
⑵ [mathjax]\(x=4\)，[mathjax]\(x=6\)
⑶ [mathjax]\(x=1\pm \sqrt{7}\)
⑷ [mathjax]\(x=-\dfrac{1}{3}\)
２
⑴ [mathjax]\(a=2\)，[mathjax]\(b=4\)
⑵ ㋐ [mathjax]\(x=6\) ㋑ [mathjax]\(x=-4\)
３
連続する3つの自然数のうち，中央の数をxとすると，
[mathjax]\((x-1)(x+1)-2x=47\)
これを解くと，[mathjax]\(x=8\)，[mathjax]\(x=-6\)
xは自然数であるから，[mathjax]\(x=8\)
答 [mathjax] \(7\)，[mathjax] \(8\)，[mathjax] \(9\)
４
もとの厚紙の縦の長さをx cmとすると，
[mathjax]\(2(x-4)(x+3-4)=80\)
これを解くと，[mathjax]\(x=9\)，[mathjax]\(x=-4\)
[mathjax]\(x \gt 4\) であるから，[mathjax]\(x=9\)
答 9cm
５
点P，Qが出発してからx秒後に[mathjax]\(\triangle PBQ\)の面積が8cm²になるとすると，
[mathjax]\(\dfrac{1}{2}x(10-x)=8\)
<3年p.303>
これを解くと，[mathjax]\(x=2\)，[mathjax]\(x=8\)
答 2秒後，8秒後
活用
１
⑴ 四角形…2本，五角形…5本
六角形…9本，七角形…14本
⑵ 1つの頂点からは，それ自身ととなり合う頂点を除き，[mathjax]\((n-3)\)本の対角線が引ける。
頂点はn個あるので，[mathjax]\(n(n-3)\)本となるが，2回重複して数えることになるので，それに[mathjax]\(\dfrac{1}{2}\)をかけると，対角線の総数は，[mathjax]\(\dfrac{1}{2}n(n-3)\)本となる。
⑶ 20本，十角形
2次方程式のおもしろい解き方 ◁P.99
①
答 同じになる
② ⑴
a，bを次のようにおきかえる。
③，④を②に代入して，mについて解く。
[mathjax]\(+\sqrt{5}\)の方を③，④に代入する。
方程式[mathjax]\(x²+4x-1=0\)は，[mathjax]\(\{x+(2+\sqrt{5})\}\{x+(2-\sqrt{5})\}=0\)と変形できる。したがって，方程式の解は，
[mathjax]\(x=-2 \pm \sqrt{5}\)
⑵
a，bを次のようにおきかえる。
③，④を②に代入して，mについて解く。
[mathjax]\(+\sqrt{3}\)の方を③，④に代入する。
方程式[mathjax]\(x²+2x-2=0\)は，[mathjax]\(\{x+(1+\sqrt{3})\}\{x+(1-\sqrt{3})\}=0\)と変形できる。したがって，方程式の解は，
[mathjax]\(x=-1 \pm \sqrt{3}\)
4章 関数[mathjax]\(y=ax²\) [解答]
トライ ◁P.120
1秒後 ～[mathjax]\(1.1\)秒後 [mathjax]\(10.29\) m/s
1秒後 ～[mathjax]\(1.01\)秒後 [mathjax]\(9.849\) m/s
1秒後 ～[mathjax]\(1.001\)秒後 [mathjax]\(9.8049\) m/s
となり，時間の幅を短くしていくと，平均の速さは[mathjax]\(9.8\) m/sに近づいていく。このことから，1秒後の瞬間の速さは[mathjax]\(9.8\) m/sと考えられる。
トライ ◁P.132
⑴ 表の左から順に，2，4，8，16，32
⑵ 略
⑶ 1024枚
4章のまとめの問題 ◁P.134〜136
１
⑴ ㋐，㋑，㋔，㋕
⑵ ㋐，㋓，㋔
⑶ ㋑，㋕
２
⑴ [mathjax]\(y=2x-1\)
⑵ [mathjax]\(y=x²\)
⑶ 100枚
３
⑴ [mathjax]\(a=-\dfrac{1}{2}\)
⑵ 最小値…[mathjax] \(-8\)，最大値…0
⑶ [mathjax] \(-3\)
応用
１
⑴ [mathjax]\(a=\dfrac{1}{4}\)
⑵ [mathjax]\(a=-1\)
⑶ [mathjax]\(a=\dfrac{1}{3}\)
２
⑴ [mathjax]\(y=10 \pi x²\)
⑵ [mathjax]\(5.64\)cm
３
⑴ A[mathjax] \((-2，2)\)
⑵ [mathjax]\(a=\dfrac{1}{2}\)
⑶ 12
４
⑴ [mathjax]\(y=x²\)
⑵ [mathjax]\(y=4x\)
活用
１
⑴ ③，[mathjax]\(y=\dfrac{5}{16}x²\)
⑵ (例)⑴で求めた式に[mathjax]\(y=4000\)を代入すると，[mathjax]\(x=113.13…\)
答 約113m
<3年p.304>
スピードと停止距離の関係は？ ◁P.137〜139
①②③ 略
④ [mathjax]\(y=0.28x\)
⑤ [mathjax]\(y=0.0072x²\)
⑥ 空走距離…28m，制動距離…72m，停止距離…100m
⑦ グラフは略
(例)時速が増すほど制動距離の差が大きくなる。
⑧ 最低でも18m手前
⑨ ブレーキをかけるようにうながすため
5章 相似な図形 [解答]
トライ ◁P.163
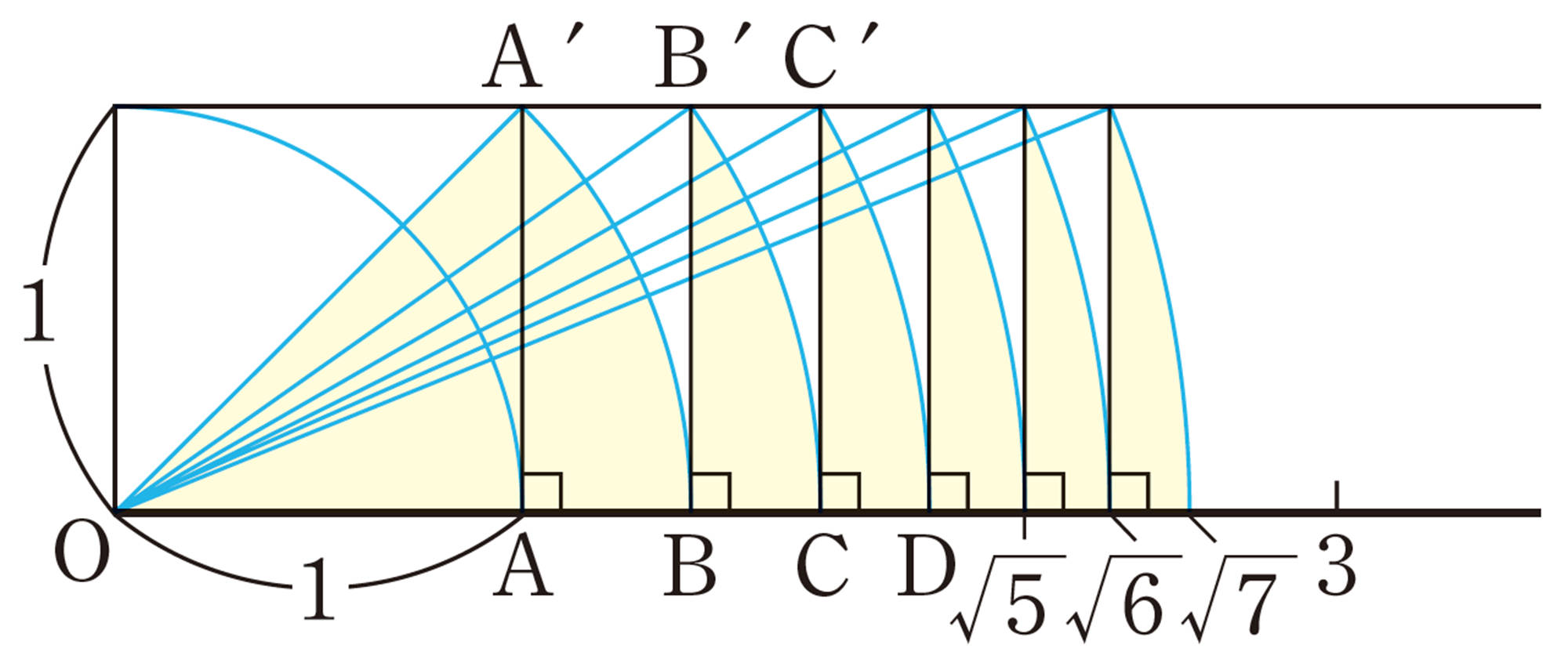
[mathjax]\(1:a=a:x\)より，[mathjax]\(x=a²\)
トライ ◁P.171
略
5章のまとめの問題 ◁P.183〜185
基本
１
⑴ [mathjax]\(\triangle ABC \backsim \triangle EBD\)，2組の角がそれぞれ等しい
⑵ [mathjax]\(\triangle ABC \backsim \triangle AED\)，2組の辺の比とその間の角がそれぞれ等しい
２
⑴ [mathjax]\(x=2\)
⑵ [mathjax]\(x=\dfrac{18}{5}\)
３
[mathjax]\(\triangle APO\)と[mathjax]\(\triangle BQO\)において，
仮定から，[mathjax]\(\angle APO=\angle BQO=90^{\circ} \quad \cdots \cdots\mathsf{①}\)
対頂角は等しいから，
[mathjax]\(\hspace{35pt}\angle AOP=\angle BOQ \hspace{42pt}\cdots \cdots\mathsf{②}\)
①，②より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle APO \backsim \triangle BQO\)
４
⑴ 6cm
⑵ [mathjax]\(\dfrac{27}{125}\)倍
応用
１
[mathjax]\(BQ=6\)cm，[mathjax]\(PQ=3.6\)cm
２
⑴ [mathjax]\(\triangle CAB\)において，点H，Eはそれぞれ辺CA，CBの中点であるから，
[mathjax]\(HE/\!/AB\)，[mathjax]\(HE=\dfrac{1}{2}AB \quad\quad\cdots \cdots\mathsf{①}\)
[mathjax]\(\triangle DAB\)において，同様にして，
[mathjax]\(FG/\!/AB\)，[mathjax]\(FG=\dfrac{1}{2}AB \ \quad\quad\cdots \cdots\mathsf{②}\)
①，②から，[mathjax]\(HE/\!/FG\)，[mathjax]\(HE=FG\)
1組の対辺が平行で等しいから，四角形FGEHは平行四辺形である。
⑵ ひし形
３
[mathjax]\(\triangle ADQ\)と[mathjax]\(\triangle QCP\)において，
[mathjax]\(\hspace{16pt}\angle D=\angle C=90^{\circ} \hspace{80pt}\cdots \cdots\mathsf{①}\)
②，③から，[mathjax]\(\angle DAQ=\angle CQP \hspace{32pt}\cdots\cdots\mathsf{④}\)
①，④より，2組の角がそれぞれ等しいから，
[mathjax]\(\hspace{16pt}\triangle ADQ \backsim \triangle QCP\)
４
[mathjax]\(\triangle AFD\)と[mathjax]\(\triangle DEC\)において，
[mathjax]\(\hspace{34pt}AD=DC \hspace{50pt}\cdots \cdots\mathsf{①}\)
仮定から[mathjax]\(DF=CE \hspace{51pt}\cdots \cdots\mathsf{②}\)
[mathjax]\(\hspace{19pt}\angle ADF=\angle DCE=90^{\circ} \hspace{8pt}\cdots \cdots\mathsf{③}\)
①，②，③より，2組の辺とその間の角がそれぞれ等しいから，
[mathjax]\(\hspace{17pt}\triangle AFD \equiv \triangle DEC \hspace{33pt}\cdots \cdots\mathsf{④}\)
[mathjax]\(\triangle ADH\)と[mathjax]\(\triangle DFH\)において，
④より，合同な三角形の対応する角は等しいから，
[mathjax]\(\hspace{17pt}\angle DAH=\angle FDH \hspace{33pt}\cdots \cdots\mathsf{⑤}\)
また，
⑤より，
[mathjax]\(\hspace{18pt}\angle HDA=\angle HFD \hspace{32pt}\cdots \cdots\mathsf{⑥}\)
⑤，⑥より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle ADH \backsim \triangle DFH\)
活用
１
約410mL
２
① 体積，[mathjax] \(729\)，[mathjax] \(1000\)，[mathjax] \(219\)
② [mathjax] \(160\)，[mathjax] \(200\)，体積，[mathjax] \(729\)，[mathjax] \(1000\)
問題づくりにチャレンジ！ ◁P.186
①② 略
6章 円 [解答]
トライ ◁P.193
点Pを通る直径PQを引く。
[mathjax]\(OP=OA\) から，
[mathjax]\(\hspace{15pt}\angle OPA=\angle OAP\)
よって，
<3年p.305>
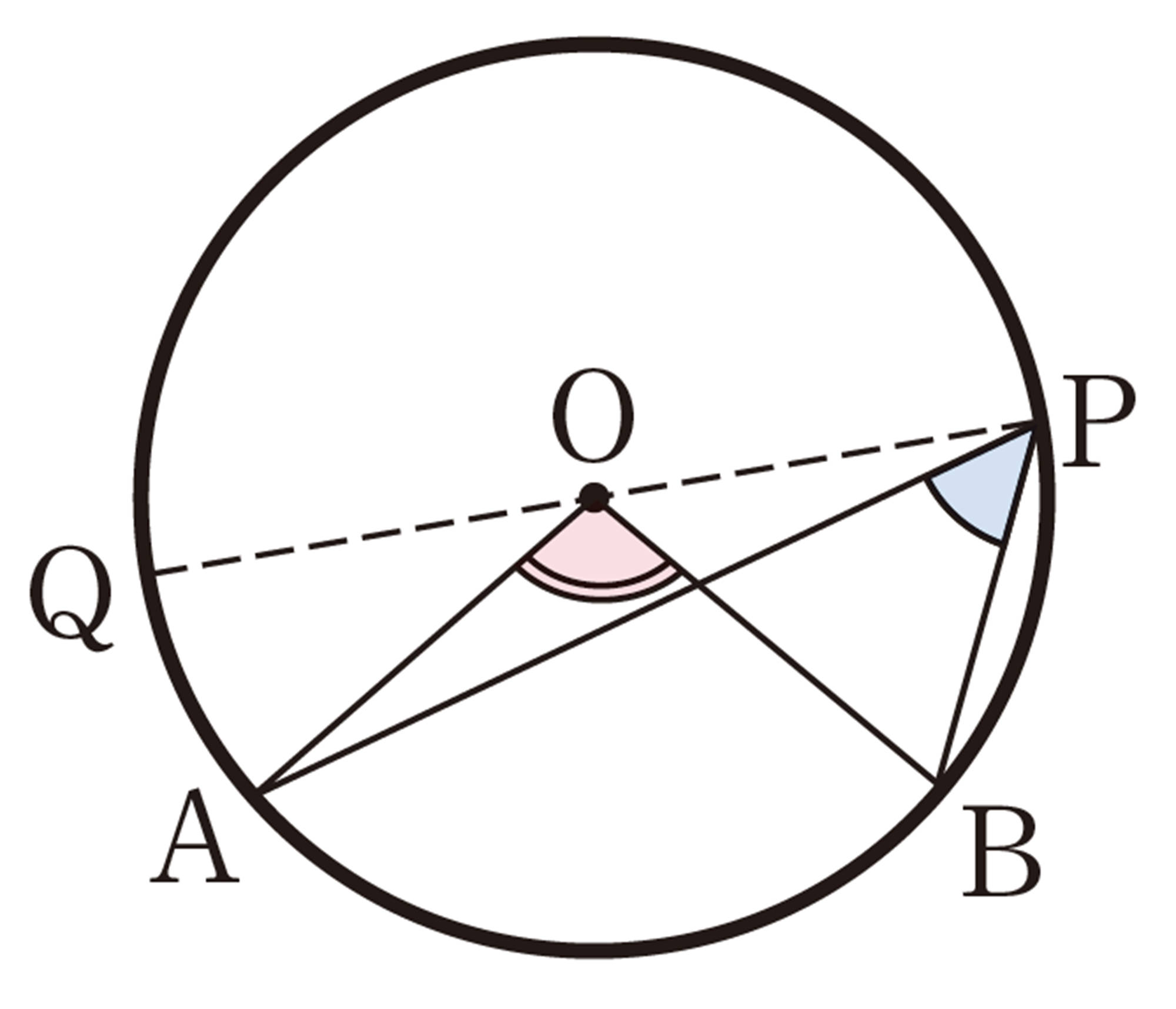
したがって，[mathjax]\(\angle AOQ= 2\angle APQ\quad \cdots \cdots\mathsf{①}\)
同様にして，[mathjax]\(\angle BOQ= 2\angle BPQ\quad \cdots \cdots\mathsf{②}\)
①，②から，
したがって，[mathjax]\(\angle APB=\dfrac{1}{2} \angle AOB\)
トライ ◁P.195
(例) 次の図で，[mathjax]\(\angle AOC=2 \angle AOB\)とすると，
[mathjax]\(AC \lt AB + BC\)つまり，[mathjax]\(AC \lt 2AB\)
であり，中心角の大きさが 2倍になっても，弦の長さは 2倍にならない。
したがって，中心角の大きさと弦の長さは比例しない。
トライ ◁P.204
(例1) [mathjax]\(\triangle ACP\)と[mathjax]\(\triangle DBP\)において，[mathjax]\(\triangle ACP \backsim \triangle DBP\)であるから，
[mathjax]\(AP:DP=CP:BP\)
したがって，[mathjax]\(AP\times BP=CP\times DP\)
(問3) [mathjax]\(\triangle ADP\)と[mathjax]\(\triangle CBP\)において，[mathjax]\(\triangle ADP \backsim \triangle CBP\)であるから，
[mathjax]\(AP:CP=DP:BP\)
したがって，[mathjax]\(AP\times BP=CP\times DP\)
6章のまとめの問題 ◁P.209〜211
１
⑴ [mathjax]\(\angle x = 110^{\circ}\)
⑵ [mathjax]\(\angle x = 32^{\circ}\)
⑶ [mathjax]\(\angle x = 58^{\circ}\)
⑷ [mathjax]\(\angle x = 35^{\circ}\)
⑸ [mathjax]\(\angle x = 80^{\circ}\)
⑹ [mathjax]\(\angle x = 20^{\circ}\)
２
⑴ [mathjax]\(\triangle ABD\)と[mathjax]\(\triangle PBA\)において，
半円の弧に対する円周角は[mathjax]\(90^{\circ}\)であるから，[mathjax]\(\angle ADB = 90^{\circ}\)
円の接線は，接点を通る半径に垂直であるから，[mathjax]\(\angle PAB = 90^{\circ}\)
したがって，[mathjax]\(\angle ADB = \angle PAB \quad \cdots \cdots\mathsf{①}\)
また，[mathjax]\(\angle B\)は共通 [mathjax]\(\hspace{61pt}\cdots \cdots \mathsf{②}\)
①，②より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle ABD \backsim \triangle PBA\)
⑵ 5cm
３
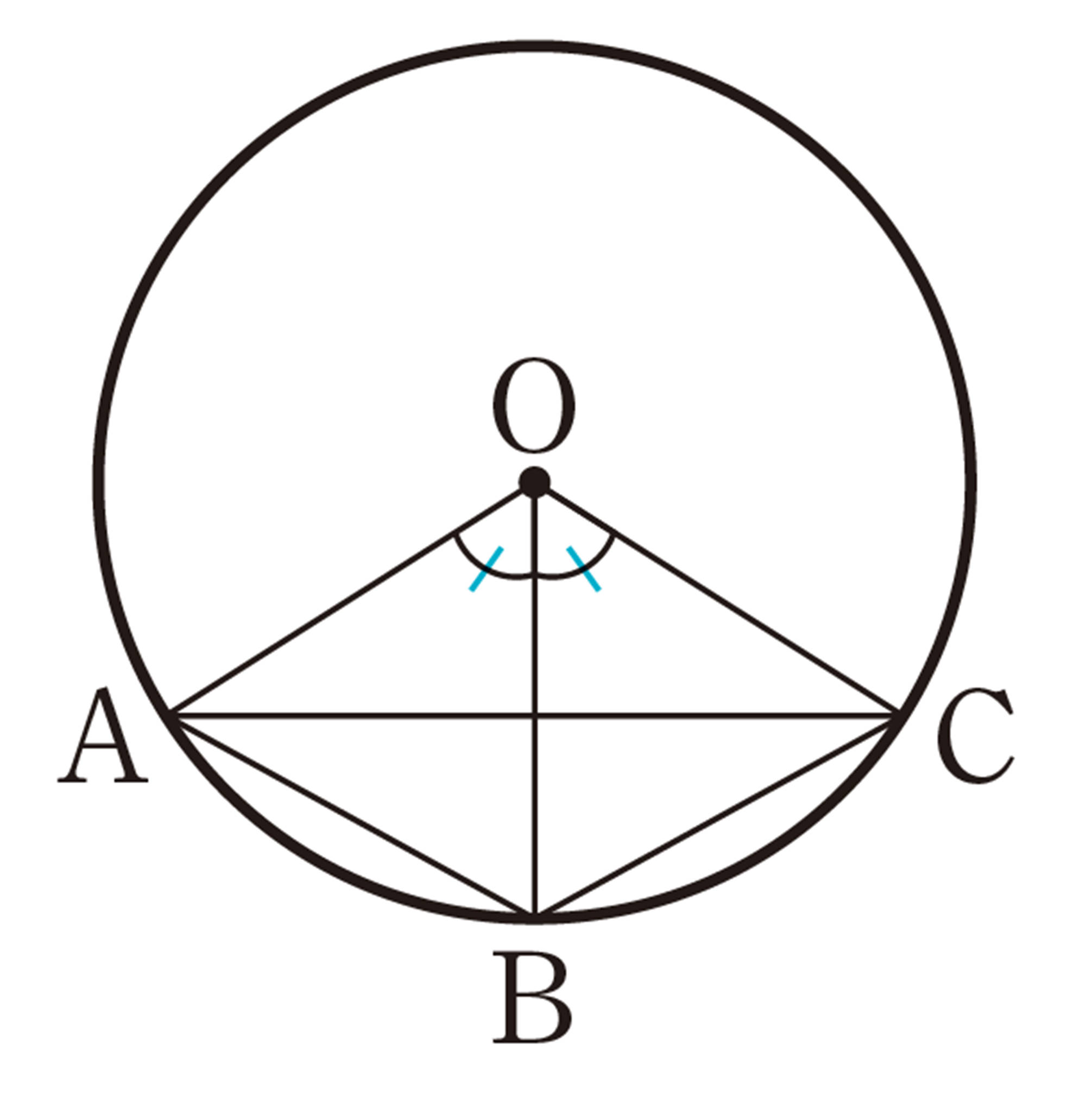
⑴ [mathjax]\(\triangle DBC\)と[mathjax]\(\triangle ECB\)において，[mathjax]\(\triangle ABC\)は二等辺三角形であるから，
[mathjax]\(\angle DBC =\angle ECB\quad\cdots\cdots\mathsf{①}\)
仮定から，[mathjax]\(BD=CE \quad \cdots \cdots \mathsf{②}\)
また，BCは共通[mathjax]\(\cdots\cdots\mathsf{③}\)
① ，②，③より，2 組の辺とその間の角が それぞれ等しいから，[mathjax]\(\triangle DBC \equiv \triangle ECB\)
⑵ 2点D，Eは，直線BCに対して同じ側にある。
また，⑴から，[mathjax]\(\angle BDC = \angle CEB\)
したがって，4点D，B，C，Eは1つの円周上にある。
応用
１
⑴ [mathjax]\(\angle x = 35^{\circ}\)
⑵ [mathjax]\(\angle x = 130^{\circ}\)
⑶ [mathjax]\(\angle x = 100^{\circ}\)
２
[mathjax]\(\stackrel{\huge\frown}{AE}:\stackrel{\huge\frown}{EC}＝35:25＝7:5\)
３
[mathjax]\(\triangle ABE\)と[mathjax]\(\triangle ACD\)において，
仮定から，[mathjax]\(\angle AEB = 90^{\circ}\)
半円の弧に対する円周角は[mathjax]\(90^{\circ}\)であるから，
[mathjax]\(\angle ADC = 90^{\circ}\)
したがって，[mathjax]\(\angle AEB = \angle ADC \quad \cdots \cdots\mathsf{①}\)
[mathjax]\(\stackrel{\huge\frown}{AD}\)に対する円周角は等しいから，
[mathjax]\(\angle ABE = \angle ACD \hspace{50pt} \cdots \cdots\mathsf{②}\)
①，②より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle ABE\backsim\triangle ACD\)
４
[mathjax]\(\triangle ABD\)と[mathjax]\(\triangle BFC\)において，
[mathjax]\(\stackrel{\huge\frown}{AB}\)に対する円周角は等しいから，
[mathjax]\(\angle ADB = \angle BCF \hspace{52pt} \cdots \cdots\mathsf{①}\)
[mathjax]\(\stackrel{\huge\frown}{BD} = \stackrel{\huge\frown}{CE}\)より，等しい弧に対する円周角は
等しいから，[mathjax]\(\angle BAD = \angle FBC \quad \cdots \cdots\mathsf{②}\)
①，②より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle ABD \backsim \triangle BFC\)
活用
１
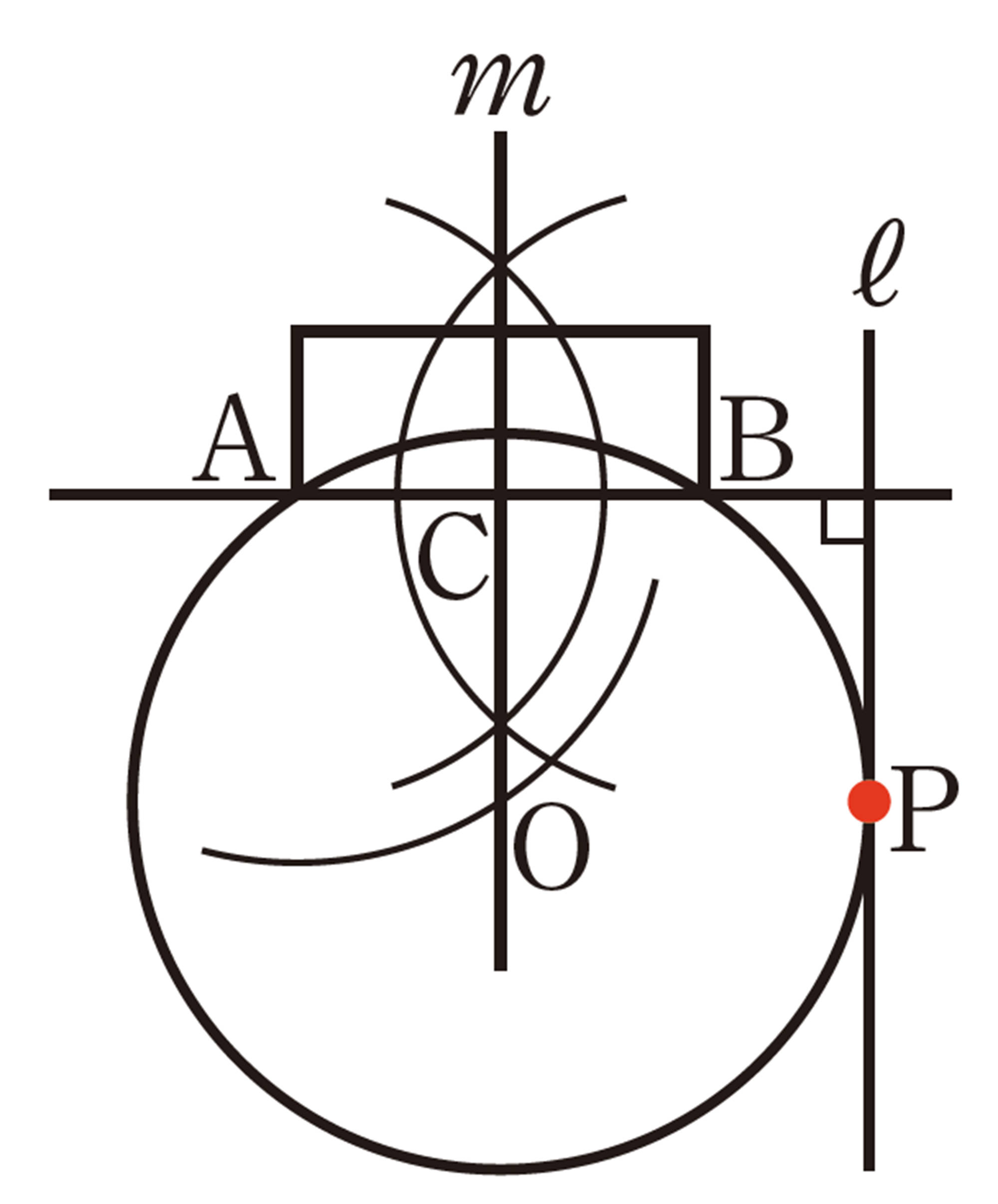
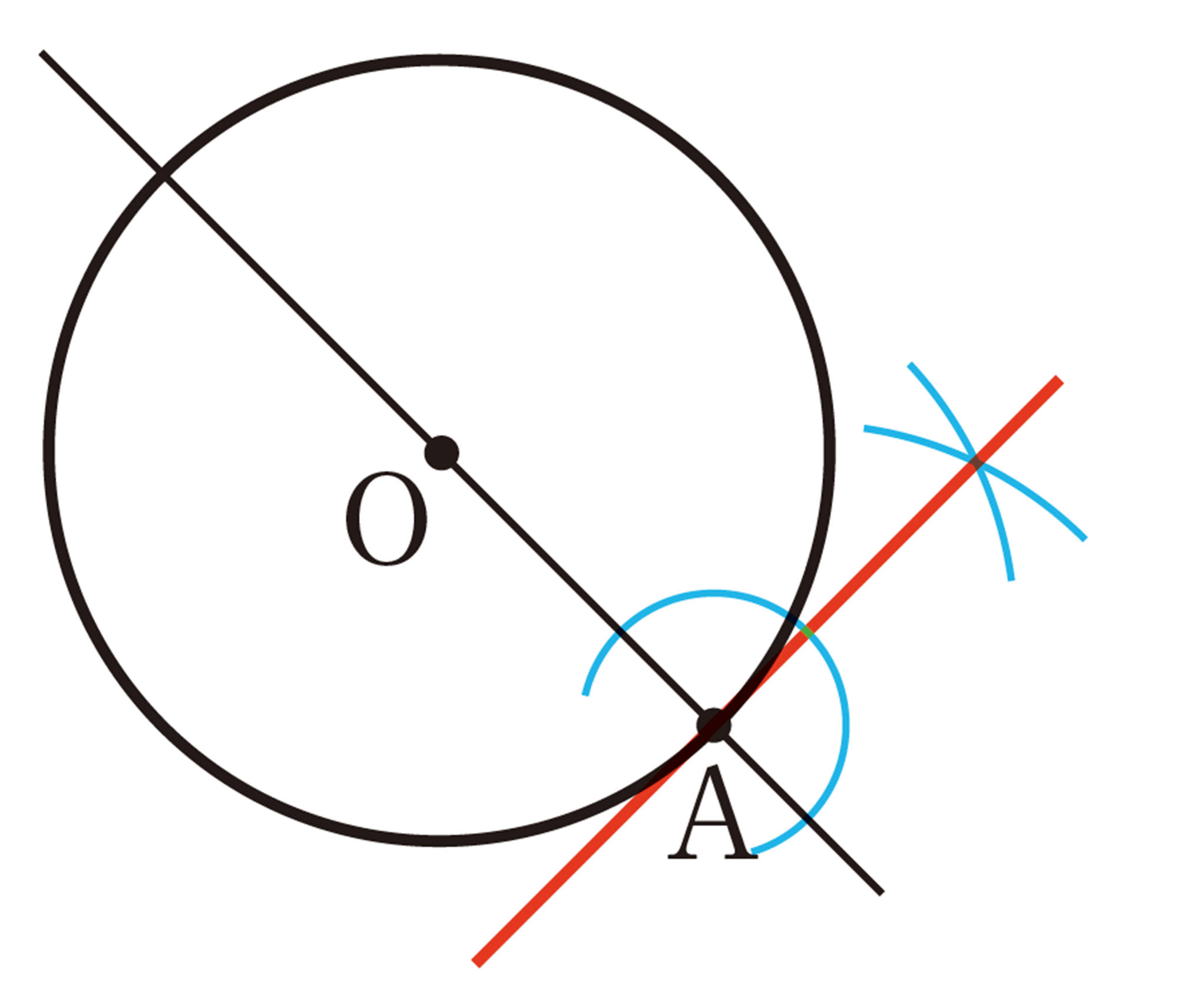
⑴ ① ABの垂直二等分線mを引き，ABとの交点をCとする。
② Aを中心として，Cとℓの距離を半径とした円をかき，mとの交点をOとする。
③ Oを中心として，半径AOの円をかいたとき，ℓとの接点がPとなる。
⑵ 点P以外のℓ上の点Qは，円の外側の点になるので，[mathjax]\(\angle AQB\)は，⑴でかいた円Oの[mathjax]\(\stackrel{\huge\frown}{AB}\)に対する円周角[mathjax]\(\angle APB\)より小さくなる。
よって，ゴールに入る確率がもっとも高い場所は，ゴールの両端A，Bを通る円のうち，直線ℓと接する円の接点Pになる。
<3年p.306>
動かして考えよう ◁P.212
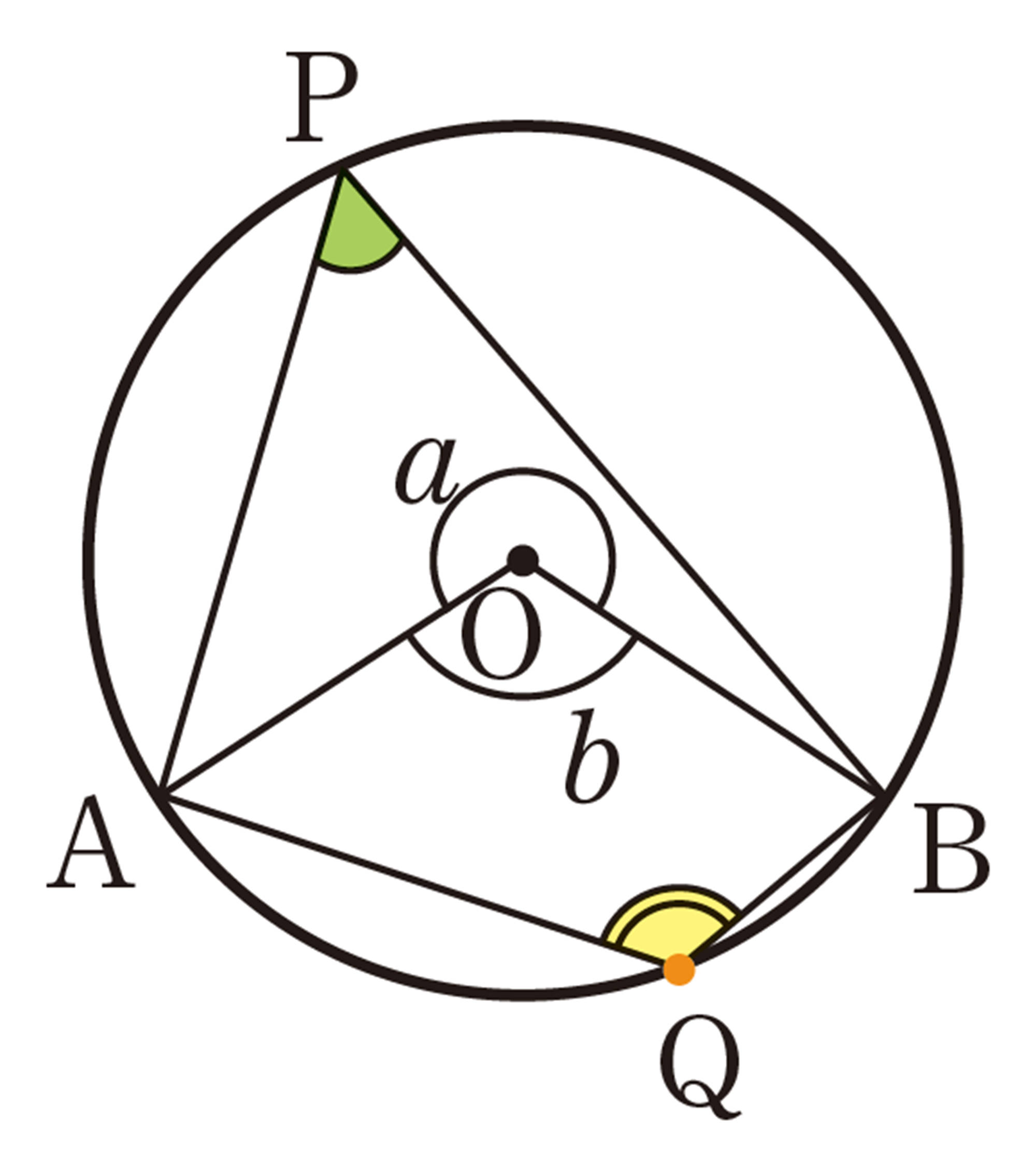
① [mathjax]\(\angle APB = \angle AQC\)
② [mathjax]\(\angle APB + \angle AQB = 180^{\circ}\)
③（例）AとO，BとOをそれぞれ結ぶ。
右の図のように，円周角が[mathjax]\(\angle Q\)のときの弧に対する中心角を[mathjax]\(\angle a\)，円周角が[mathjax]\(\angle P\)のときの弧に対する中心角を[mathjax]\(\angle b\)とすると，
[mathjax]\(\angle Q = \dfrac{1}{2} \angle a\)，[mathjax]\(\angle P = \dfrac{1}{2} \angle b\)
[mathjax]\(\angle a + \angle b = 360^{\circ}\)であるから，
7章 三平方の定理 [解答]
トライ ◁P.220
略
トライ ◁P.229
略
7章のまとめの問題 ◁P.236〜238
基本
１
⑴ [mathjax]\(c=\sqrt{17}\)
⑵ [mathjax]\(b=2 \sqrt{3}\)
２
⑴ いえる
⑵ いえない
⑶ いえない
⑷ いえる
３
[mathjax]\(AB=\sqrt{13}\)，[mathjax]\(BC=\sqrt{13}\)，[mathjax]\(CA=\sqrt{26}\)
([mathjax]\(\angle B = 90^{\circ}\)の)直角二等辺三角形
４
⑴ 高さ…[mathjax]\(\sqrt{7}\)cm，体積…[mathjax]\(12\sqrt{7}\)cm³
⑵ 84cm²
５
⑴ 点B…直角三角形[mathjax] \(OAA´\)をかき，斜辺[mathjax] \(OA´\)と等しい長さでOBをとる。
点C…直角三角形[mathjax] \(OBB´\)をかき，斜辺[mathjax] \(OB´\)と等しい長さでOCをとる。
⑵ 2
⑶
応用
１
[mathjax]\(12\sqrt{3}\)cm²
２
[mathjax]\(\dfrac{7}{8}\)cm
３
340 m
４
⑴ 12cm
⑵ [mathjax]\(\triangle ABH\)と[mathjax]\(\triangle ADC\)において，仮定から，[mathjax]\(\angle AHB = 90^{\circ}\)
半円の弧に対する円周角は[mathjax]\(90^{circ}\)だから，
[mathjax]\(\angle ACD = 90^{\circ}\)
したがって，[mathjax]\(\angle AHB = \angle ACD \quad \cdots \cdots\mathsf{①}\)
[mathjax]\(\stackrel{\huge\frown}{AC}\)に対する円周角は等しいから，
[mathjax]\(\angle ABH = \angle ADC \hspace{50pt} \cdots \cdots\mathsf{②}\)
①，②より，2組の角がそれぞれ等しいから，
[mathjax]\(\triangle ABH \backsim \triangle ADC\)
⑶ [mathjax]\(\dfrac{65}{8}\)cm
活用
１
① ㋐，㋑の長さを測定し，三平方の定理を使って，[mathjax]\(a=\sqrt{AC²-CB²}\)として求める。
② ㋐，㋑，㋒の長さを測定し，三平方の定理を使って， [mathjax]\(b=\sqrt{AE²-ED²}+\sqrt{EB²-ED²}\)として求める。
２
⑴ 約[mathjax]\(6.9\)m
⑵ 約[mathjax]\(6.9\)m
３
㋐，㋑，㋒の長さを測定し，三平方の定理を使って，[mathjax]\(c=\sqrt{AE²-ED²}-\sqrt{GE²-ED²}\)として求める。
約[mathjax]\(2.3\)m
釣瓶岳から富士山が撮影できた？ ◁P.239
① 約233km
② 約113m
8章 標本調査 [解答]
8章のまとめの問題 ◁P.254〜255
１
適切であるとはいえない。
(理由) インターネットのあるサイトを利用した調査であり，サイトにアクセスする人の男女比や年齢層などの分布が，日本国民の分布と同じであるとはいえないため。
２
推定した値は略。実際の母平均は，[mathjax]\(7.715\)秒より，約[mathjax]\(7.7\)秒
<3年p.307>
応用
１
① びんの中から適当な数の大豆を取り出し，印をつけてからびんにもどす。
② 十分にびんの中の大豆を混ぜてから，再び適当な数の大豆を取り出し，その中にある印のついた大豆の数を数える。
③ ①と②から，大豆の総数を推定する。
２
約240個
活用
１
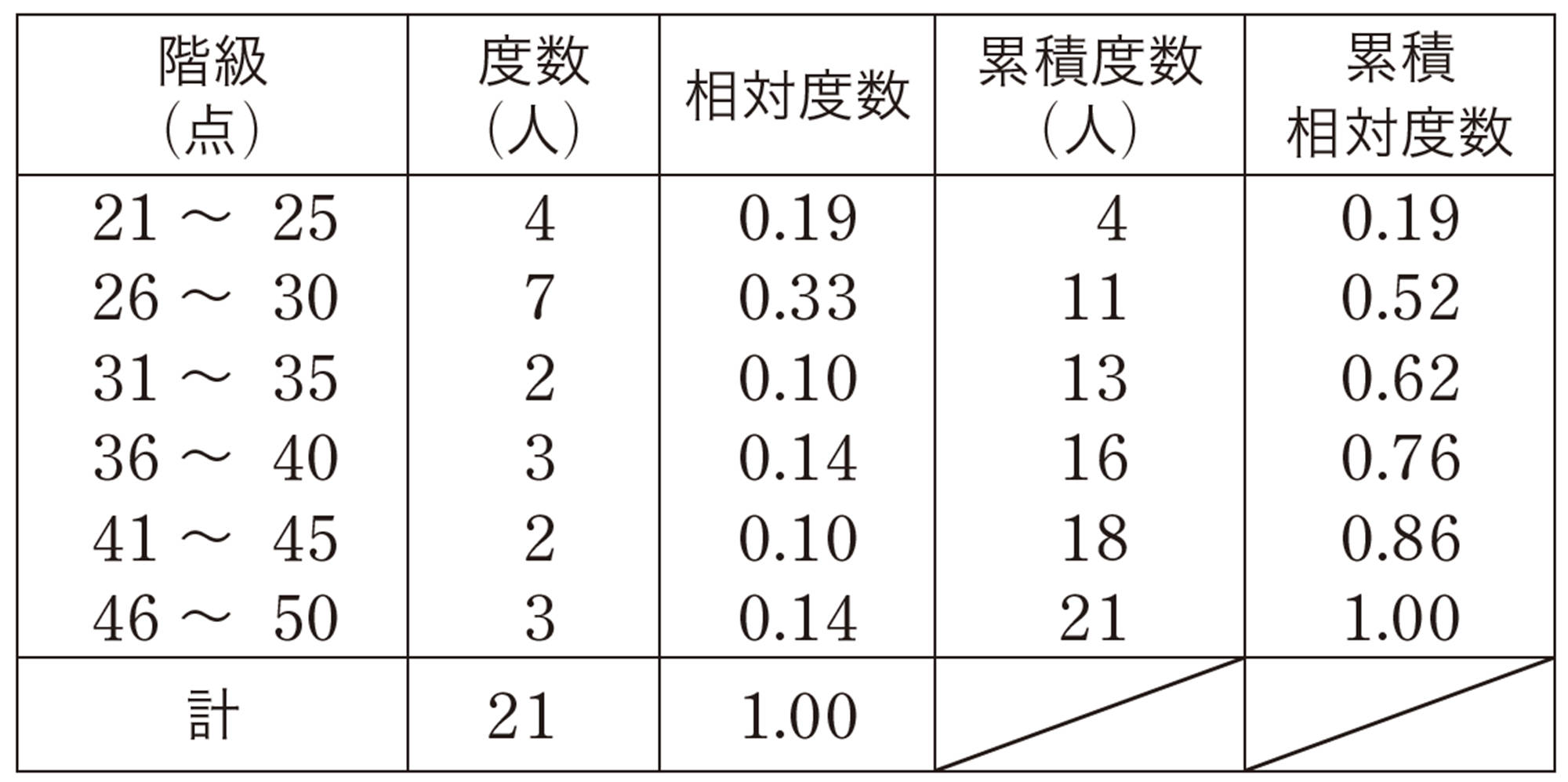
⑴ 約107g
⑵ 上から，[mathjax] \(0.20\)，[mathjax] \(0.41\)，[mathjax] \(0.29\)，[mathjax] \(0.10\)，計[mathjax]\(1.00\)
⑶ 約31個
⑷ できる
(理由) 収穫できるみかんの個数は，[mathjax]\((\textsf{全体の重さ}) \div (\textsf{平均の重さ})\) より，約20万個。そのうち，2Lサイズのみかんの個数は約2万個である。2Lサイズのみかん5kg入りの箱には約31個入るから，箱は約645箱できる。
久山町研究 ◁P.258
① （例）久山町住民は全国平均とほぼ同じ年齢・職業分布をしていて，偏りがほとんどない平均的な日本人の住民になっているため。
②③ 略
１・２，３年の復習・総合問題 [解答]
数と式 ◁P.284〜285
1
⑴ [mathjax] \(-13\)
⑵ 11
⑶ [mathjax] \(-6\)
⑷ [mathjax] \(-2\)
⑸ [mathjax]\(\dfrac{5}{12}\)
⑹ [mathjax]\(1.4\)
⑺ [mathjax] \(-48\)
⑻ [mathjax] \(-4\)
⑼ 28
⑽ 16
⑾ [mathjax] \(-6\)
⑿ 39
⒀ 16
2
⑴ [mathjax] \(-10x\)
⑵ [mathjax]\(3a-7\)
⑶ [mathjax]\(-\dfrac{1}{12}x + 5\)
⑷ 35x
⑸ [mathjax]\(-2a+3\)
⑹ [mathjax]\(\dfrac{3}{4}a\)
⑺ 9x
⑻ [mathjax]\(-11x-3\)
3
⑴ [mathjax]\(-2x-5y\)
⑵ [mathjax]\(-x²-5x+10\)
⑶ [mathjax]\(2x²-x-3\)
⑷ [mathjax]\(2x+13y\)
⑸ [mathjax]\(\dfrac{-a-b}{15}\)
⑹ [mathjax]\(\dfrac{-3x+13y}{18}\)
⑺ [mathjax] \(-24ab\)
⑻ 2x
⑼ [mathjax]\(\dfrac{2a²}{3b}\)
⑽ [mathjax] \(12x²\)
4
⑴ [mathjax]\(x=-8\)
⑵ [mathjax]\(x=4\)
⑶ [mathjax]\(x=-12\)
⑷ [mathjax]\(x=2\)
⑸ [mathjax]\(x=-4\)
⑹ [mathjax]\(x=-\dfrac{5}{2}\)
⑺ [mathjax]\(x=7\)
⑻ [mathjax]\(x=3\)
⑼ [mathjax]\(x=-9\)
⑽ [mathjax]\(x=-17\)
⑾ [mathjax]\(x=10\)
⑿ [mathjax]\(x=8\)
⒀ [mathjax]\(x=13\)
⒁ [mathjax]\(x=-3\)
5
⑴
⑵
⑶
⑷
⑸
⑹
6
⑴ 13
⑵ [mathjax] \(-9\)
⑶ 2
7
[mathjax]\(a=2\)，[mathjax]\(b=3\)
8
3
9
[mathjax]\((17x+y)\)人
10
4800m
11
35
12
男性…133人，女性…243人
関数，データの活用 ◁P.286〜287
1
⑴ [mathjax]\(y=-6x\)，[mathjax]\(y=30\)
⑵ [mathjax]\(y= \dfrac{36}{x}\)，[mathjax]\(y=12\)
2
⑴ [mathjax]\(y=-3x+7\)
⑵ [mathjax]\(y=2x+5\)
⑶ [mathjax]\(y=\dfrac{1}{2}x-4\)
3
⑴ A…3回転，B…[mathjax]\(\dfrac{12}{5}\)回転，C…2回転
⑵ [mathjax]\(y= \dfrac{180}{x}\)
⑶ [mathjax]\(y= \dfrac{240}{x}\)，A…20回転，B…16回転，C…[mathjax]\(\dfrac{40}{3}\)回転
4
⑴ [mathjax]\(y=8x\)
⑵ [mathjax]\(0 \leqq x \leqq 6\)，[mathjax]\(0 \leqq y \leqq 48\)
⑶ 3秒後
5
⑴ A[mathjax]\((3，4)\)，B[mathjax]\((1，0)\)，D[mathjax]\((9，0)\)
⑵ 16
<3年p.308>
6
⑴
⑵ 10％
⑶ 62％
⑷ 第1四分位数…28点
第2四分位数…30点
第3四分位数…41点
四分位範囲…13点
⑸
7
[mathjax]\(\dfrac{5}{12}\)
8
⑴ [mathjax]\(\dfrac{7}{15}\)
⑵ [mathjax]\(\dfrac{4}{5}\)
図形 ◁P.288〜289
1
2
[mathjax]\(\triangle ACP\)，[mathjax]\(\triangle ABP\)
3
4
⑴ [mathjax]\(\triangle DEO\)
⑵
(例)▷BOを対称の軸として対称移動し，点Bから点Oの方向にBOの長さだけ平行移動する。
▷点Bから点Oの方向にBOの長さだけ平行移動し，OEを対称の軸として対称移動する。
5
⑴ 辺AE，CG，DH
⑵ 辺AB，AE，DC，DH
⑶ 辺AE，BF，EH，FG
⑷ 辺DC，DH，CG，HG
⑸ 辺AB，EF，HG，DC
6
表面積…[mathjax]\(144 \pi\)cm²，体積…[mathjax]\(288 \pi\)cm³
7
⑴ [mathjax]\(288^{\circ}\)
⑵ [mathjax]\(144 \pi\)cm²
⑶ [mathjax]\(128 \pi\)cm³
8
⑴ [mathjax]\(\angle x=63^{\circ}\)
⑵ [mathjax]\(\angle x=34^{\circ}\)
⑶ [mathjax]\(\angle x=26^{\circ}\)
9
[mathjax]\(\triangle ABP\)と[mathjax]\(\triangle CAQ\)において，
仮定から， [mathjax]\( \ \ AB=CA \hspace{51pt}\cdots \cdots \mathsf{①}\)
[mathjax]\(\hspace{35pt}\angle BPA = \angle AQC = 90^{\circ} \hspace{8pt} \cdots \cdots\mathsf{②}\)
また，[mathjax]\(\quad \angle BAP = 90^{\circ}- \angle CAQ\)
三角形の内角の和は[mathjax]\(180^{\circ}\)だから，
よって，[mathjax]\( \ \angle BAP = \angle ACQ \hspace{34pt} \cdots \cdots\mathsf{③}\)
① ，② ，③より，直角三角形の斜辺と1つの鋭角がそれぞれ等しいから，
[mathjax]\( \ \hspace{31pt}\triangle ABP \equiv \triangle CAQ\)
したがって，[mathjax]\(BP=AQ\)
10
①，②より，1組の対辺が平行で等しいから，四角形EBGFは平行四辺形である。
11
<3年p.309>
1章 式の計算 ◁P.290
1
⑴ [mathjax]\(-8a²+28a\)
⑵ [mathjax]\(10xy+6y²\)
⑶ [mathjax]\(12a²+6ab\)
⑷ [mathjax]\(-3x+2\)
⑸ [mathjax]\(3a-2b\)
⑹ [mathjax]\(16x-4y\)
2
⑴ [mathjax]\(6x²+xy-15y²\)
⑵ [mathjax]\(2a²-5ab-5a-3b²+15b\)
⑶ [mathjax]\(x²-3x-40\)
⑷ [mathjax]\(a²+10a+25\)
⑸ [mathjax]\(x²-4xy+4y²\)
⑹ [mathjax]\(y²- \dfrac{1}{4}\)
⑺ [mathjax]\(4a²-4ab+b²-10a+5b-6\)
⑻ [mathjax]\(x²-2xy+y²-8x+8y+16\)
3
⑴ [mathjax]\(-17x+60\)
⑵ [mathjax]\(-9x+23\)
4
⑴ [mathjax]\(x(a-2b)\)
⑵ [mathjax]\(xy(4x+3y-1)\)
⑶ [mathjax]\((x+2)(x-7)\)
⑷ [mathjax]\((x-2)(x-4)\)
⑸ [mathjax]\((x-4y)²\)
⑹ [mathjax]\((2x+5)²\)
⑺ [mathjax]\((4a+7b)(4a-7b)\)
⑻ [mathjax]\(\require{physics} \left(\dfrac{x}{3}+\dfrac{y}{4}\right)\require{physics} \left(\dfrac{x}{3}-\dfrac{y}{4}\right)\)
⑼ [mathjax]\(3(x+1)(x+3)\)
⑽ [mathjax]\(-3x(y+2)(y-2)\)
⑾ [mathjax]\((x+4)(x-3)\)
⑿ [mathjax]\((a+b)(x-2)\)
⒀ [mathjax]\((a-4)(b-4)\)
5
73
6
⑴ 100
⑵ [mathjax]\(0.9996\)
7
nを整数とすると，3の倍数より1大きい数は[mathjax]\(3n+1\)，同じ3の倍数より1小さい数は[mathjax]\(3n-1\)と表される。
したがって，3の倍数より1大きい数の2乗から，同じ3の倍数より1小さい数の2乗をひいた差は，12の倍数になる。
2章 平方根 ◁P.291
1
⑴ [mathjax]\(\pm 7\)
⑵ [mathjax]\(\pm \sqrt{13}\)
⑶ [mathjax]\(\pm \dfrac{3}{8}\)
⑷ [mathjax]\(\pm 0.6\)
2
⑴ 11
⑵ [mathjax] \(-5\)
⑶ [mathjax]\(0.16\)
⑷ 7
3
⑴ [mathjax]\(-\sqrt{20}\)，[mathjax] \(-4\)，[mathjax]\(-\sqrt{15}\)，[mathjax]\(\sqrt{24}\)，5
⑵ 有理数…[mathjax]\(\sqrt{144}\)，[mathjax]\(-\sqrt{\dfrac{1}{4}}\)，[mathjax]\(\dfrac{5}{2}\)
無理数…[mathjax]\(-\sqrt{13}\)，[mathjax]\(\dfrac{\pi}{2}\)
4
⑴ [mathjax]\(2\sqrt{3}\)
⑵ [mathjax]\(40\sqrt{2}\)
⑶ [mathjax]\(3\sqrt{5}\)
⑷ [mathjax]\(\dfrac{2\sqrt{6}}{3}\)
5
⑴ [mathjax]\(26.46\)
⑵ [mathjax]\(83.67\)
⑶ [mathjax]\(0.8367\)
⑷ [mathjax]\(15.876\)
6
⑴ [mathjax]\(13\sqrt{13}\)
⑵ [mathjax]\(7\sqrt{6}-6\sqrt{2}\)
⑶ [mathjax]\(-2\sqrt{3}\)
⑷ [mathjax]\(\sqrt{6}\)
⑸ [mathjax]\(2\sqrt{5}\)
⑹ [mathjax]\(7\sqrt{2}\)
7
⑴ [mathjax]\(\sqrt{15}\)
⑵ [mathjax]\(12\sqrt{2}+6\)
⑶ [mathjax]\(9-6\sqrt{2}\)
⑷ [mathjax]\(-3+2\sqrt{7}\)
8
[mathjax]\(4\sqrt{5}\)cm
3章 2次方程式 ◁P.292
1
⑴ [mathjax]\(x=1\)，[mathjax]\(x=-8\)
⑵ [mathjax]\(x=0\)，[mathjax]\(x=-4\)
⑶ [mathjax]\(x=3\)，[mathjax]\(x=-9\)
⑷ [mathjax]\(x=3\)，[mathjax]\(x=6\)
⑸ [mathjax]\(x=8\)，[mathjax]\(x=-5\)
⑹ [mathjax]\(x=9\)
⑺ [mathjax]\(x=\pm \dfrac{5}{3}\)
⑻ [mathjax]\(x=-2\)，[mathjax]\(x=-3\)
⑼ [mathjax]\(x=2\)，[mathjax]\(x=-8\)
⑽ [mathjax]\(x=5\)，[mathjax]\(x=-7\)
2
⑴ [mathjax]\(x=\pm 3\sqrt{2}\)
⑵ [mathjax]\(x=\pm 5\)
⑶ [mathjax]\(x=\pm \dfrac{\sqrt{3}}{3}\)
⑷ [mathjax]\(x=\pm \dfrac{2\sqrt{2}}{3}\)
⑸ [mathjax]\(x=-3\pm 2\sqrt{7}\)
⑹ [mathjax]\(x=6\pm 2\sqrt{6}\)
3
⑴ [mathjax]\(x=\dfrac{-3\pm \sqrt{5}}{2}\)
⑵ [mathjax]\(x=3\pm \sqrt{6}\)
⑶ [mathjax]\(x=\dfrac{3\pm \sqrt{41}}{8}\)
⑷ [mathjax]\(x=\dfrac{1}{2}\)，[mathjax]\(x=-1\)
⑸ [mathjax]\(x=\dfrac{-2\pm \sqrt{10}}{3}\)
⑹ [mathjax]\(x=\dfrac{3}{2}\)，[mathjax]\(x=-3\)
4
花だんの幅をxmとすると，
[mathjax]\((18-x)(30-2x)=18 \times 30 \times \dfrac{2}{3}\)
これを解くと，[mathjax]\(x=3\)，[mathjax]\(x=30\)
[mathjax]\(0 \lt x \lt 15\)であるから，[mathjax]\(x=3\)
答 3m
5
P，Qが出発してからx秒後に四角形APQCの面積が52cm²になるとすると，
[mathjax]\(\dfrac{1}{2} \times 16 \times 8-\dfrac{1}{2}(8-x) \times 2x=52\)
これを解くと，[mathjax]\(x=2\)，[mathjax]\(x=6\)
答 2秒後，6秒後
4章 関数[mathjax]\(y=ax²\) ◁P.293
1
⑴ [mathjax]\(y=\dfrac{1}{4}x²\)，[mathjax]\(y=9\)
⑵ [mathjax]\(a=-\dfrac{2}{3}\)
⑶ [mathjax]\(y=4x²\)
⑷ [mathjax]\(0 \leqq y \leqq 18\)
2
⑴ [mathjax] \(-6\)
⑵ [mathjax]\(a=3\)
3
[mathjax]\(a=-9\)
4
⑴ 約1m
⑵ 約4秒
⑶ 約8m
<3年p.310>
5章 相似な図形 ◁P.294
1
⑴ [mathjax]\(x=4\)，[mathjax]\(y=15\)
⑵ [mathjax]\(x=\dfrac{16}{5}\)，[mathjax]\(y=15\)
2
⑴ [mathjax]\(\triangle DBA\)，[mathjax]\(\triangle DAC\)，[mathjax]\(\triangle EBF\)
⑵ [mathjax]\(\triangle ABC\)と[mathjax]\(\triangle EBF\)
⑶ EF…15 cm，AD…30 cm，FC…[mathjax]\(37.5\) cm
3
[mathjax]\(157.35 \leqq a \lt 157.45\)
誤差の絶対値は[mathjax]\(0.05\) cm以下
4
[mathjax]\(\triangle ABC\)において，点E，Fは，それぞれ辺AB，ACの中点であるから，
[mathjax]\(EF/\!/ BC\)，[mathjax]\(EF= \dfrac{1}{2}BC \quad \cdots \cdots\mathsf{①}\)
[mathjax]\(\triangle DBC\)において，同様にして，
[mathjax]\(GH /\!/ BC\)，[mathjax]\(GH=\dfrac{1}{2}BC \quad \cdots \cdots\mathsf{②}\)
①，②から，[mathjax]\(EF/\!/ GH\)，[mathjax]\(EF=GH\)
1組の対辺が平行で等しいから，四角形EGHFは平行四辺形である。
5
⑴ 10cm²
⑵ 540cm³
6章 円 ◁P.295
1
⑴ [mathjax]\(\angle x=52^{\circ}\)
⑵ [mathjax]\(\angle x=116^{\circ}\)
⑶ [mathjax]\(\angle x=20^{\circ}\)
⑷ [mathjax]\(\angle x=68^{\circ}\)
⑸ [mathjax]\(\angle x=87^{\circ}\)
⑹ [mathjax]\(\angle x=32^{\circ}\)
2
平行四辺形の対角は等しいから，
[mathjax]\(\angle ABC=\angle D \quad\quad\quad \cdots \cdots\mathsf{①}\)
[mathjax]\(\stackrel{\huge\frown}{AC}\)の円周角は等しいから，
[mathjax]\(\angle ABC=\angle AED \ \ \quad \cdots \cdots\mathsf{②}\)
①，②から，[mathjax]\(\angle D=\angle AED\)
2つの角が等しいから，[mathjax]\(\triangle AED\)は二等辺三角形である。
3
30cm²
7章 三平方の定理 ◁P.296
1
⑴ [mathjax]\(x=4\sqrt{2}\)
⑵ [mathjax]\(x=7\)
⑶ [mathjax]\(x=3\sqrt{13}\)
2
[mathjax]\(AH…4\sqrt{3}\)cm，[mathjax]\(AC…4\sqrt{6}\)cm，[mathjax]\(BC \dots (4+4\sqrt{3})\)cm
3
[mathjax]\(3\sqrt{5}\)
4
[mathjax]\(8\sqrt{3}\)cm
5
体積…[mathjax]\(\dfrac{32\sqrt{7}}{3}\)cm³
表面積…[mathjax]\((16+32\sqrt{2})\) cm²
8章 標本調査 ◁P.297
1
⑴ 全数調査
⑵ 標本調査
⑶ 標本調査
⑷ 全数調査
⑸ 標本調査
2
約165cm
3
約300個
4
約330匹
総合問題 ◁.298〜299
1
⑴ オリジナルTシャツを3枚追加して購入金額が2400円増えているため，1枚当たりの値段は800円になるから。
⑵ 注文したオリジナルTシャツをx枚，無地のTシャツをy枚とすると，
これを解くと，
答 オリジナルTシャツ62枚，無地のTシャツ38枚
2
⑴ ① [mathjax]\(y=900+60x\)
② [mathjax]\(y=150x\)
⑵ 7m³…1320円，18m³…2700円
3
⑴ [mathjax]\(96\sqrt{5}\)cm³
⑵ [mathjax]\(\dfrac{36}{5}\)cm
4
⑴ ㋓
⑵ 99cm²
5
⑴ [mathjax]\(\dfrac{1}{12}\)
⑵ [mathjax]\(\dfrac{1}{6}\)
⑶ [mathjax]\(\dfrac{7}{36}\)
6
⑴ [mathjax]\(4\sqrt{6}\)cm
⑵ [mathjax]\(20\sqrt{3}\)cm²
<3年p.⑧>
数学の力
～ものづくりの哲学～
独立時計師ということばを聞いたことがありますか？
企業に属さず個人で時計を作る職人です。スイスに独立時計師協会という団体があり，私も2013 年から正会員として所属しています。協会には，様々な国籍の会員が約30 名ほど所属しており，それぞれの時計師が独自の世界観や哲学をもって，大量生産品の時計とは一味ちがった魅力のある時計を作っています。
時計作りに役に立っている工作機械の1 つが彫刻機です。彫刻機とは，小さいものを削けずるための機械です。現在では，コンピュータ制御で刃物を動かす彫刻機や刃物を使わないレーザー彫刻機などが登場しています。しかし，私が使っている彫刻機は旧式のもので，文字や模様の原図をなぞると，それらを縮小して彫刻します。作りたい部品の拡大した原図を機械にセットして，自分の手で原図をなぞるようにアームを動かすことで回転する刃物が材料を削っていきます。
なぜ古い機械を使うかというと，五感を働かせて「ものづくり」をしたいからです。自動の彫刻機は便利ですが，部品1 つを作る一瞬一瞬に自分が関わって制作する方が，作り手もそれを手にする人も喜びを感じられると思っているからです。
彫刻機が相似な形を彫刻できるしくみの要はパンタグラフです。パンタグラフとは，三角形の比と相似を応用した製図用具で，今から約400 年前に発明されました。1800 年代前半には，彫刻機として実用化されて時計作りにも使われていたようです。
私は学生時代，数学が苦手で，数学を学ぶことが何の役に立つのかわかっていませんでした。しかし，現在，私の時計作りの大きな助けとなっている機械が，相似を応用したものだと知り，数学の知識を応用して，便利なものや新しいものを生み出すことも，数学の一部なのだと思いました。
みなさんが興味や関心をもっていることにもきっと数学が関わっていますよ。
