<3年p.284>
1・2年の復習
数と式
1 次の計算をしなさい。
⑴ [mathjax]\((-5)+(-8)\)
⑵ [mathjax]\(7-(-4)\)
⑶ [mathjax]\(6-9-3\)
⑷ [mathjax]\(2-(-4)+(-8)\)
⑸ [mathjax]\(\dfrac{2}{3}+\require{physics} \left(-\dfrac{1}{4}\right)\)
⑹ [mathjax]\(-1.2-(-2.6)\)
⑺ [mathjax]\(8 \times (-6)\)
⑻ [mathjax]\(28 \div (-7)\)
⑼ [mathjax]\(4-8 \times (-3)\)
⑽ [mathjax]\(3 \times \{2+(-5)\}+(-5)²\)
⑾ [mathjax]\(-54 \div (-3²)-12\)
⑿ [mathjax]\(12-(-8²) \div \require{physics} \left(\dfrac{4}{3}\right)^{3}\)
⒀ [mathjax]\(\{(-2)³-3 \times (-4)\} \div \require{physics} \left(\dfrac{1}{2}-1\right)^{2}\)
2 次の計算をしなさい。
⑴ [mathjax]\(-8x-2x\)
⑵ [mathjax]\(-4a+2+7a-9\)
⑶ [mathjax]\(\require{physics} \left(\dfrac{1}{6}x+4\right)-\require{physics} \left(\dfrac{1}{4}x-1\right)\)
⑷ [mathjax]\((-7x) \times (-5)\)
⑸ [mathjax]\(\dfrac{1}{3}(-6a+9)\)
⑹ [mathjax]\(-9a \div (-12)\)
⑺ [mathjax]\(15x \div \dfrac{5}{3}\)
⑻ [mathjax]\(-8(4x-3)+3(7x-9)\)
3 次の計算をしなさい。
⑴ [mathjax]\(-7x+3y+5x-8y\)
⑵ [mathjax]\((x²-4x+3)+(-2x²-x+7)\)
⑶ [mathjax]\(x²+2x-3-(3x-x²)\)
⑷ [mathjax]\(2(6x-y)+5(-2x+3y)\)
⑸ [mathjax]\(\dfrac{1}{3}(a-2b)-\dfrac{1}{5}(2a-3b)\)
⑹ [mathjax]\(-\dfrac{3x-2y}{9}+\dfrac{x+3y}{6}\)
⑺ [mathjax]\(8a \times (-3b)\)
⑻ [mathjax]\((-14xy) \div (-7y)\)
⑼ [mathjax]\(a² \times 6a \div 9ab\)
⑽ [mathjax]\(3x \times (-2x)² \div x\)
4 次の方程式や，比例式を解きなさい。
⑴ [mathjax]\(6x=-48\)
⑵ [mathjax]\(x-7=-3\)
⑶ [mathjax]\(\dfrac{5}{6}x=-10\)
⑷ [mathjax]\(1-4x=-7\)
⑸ [mathjax]\(5x-17=8x-5\)
⑹ [mathjax]\(7(x+2)=x-1\)
⑺ [mathjax]\(6x-3(x+5)=6\)
⑻ [mathjax]\(1.8x-2.6=0.6x+1\)
⑼ [mathjax]\(\dfrac{2}{3}x-2=\dfrac{5}{6}x-\dfrac{1}{2}\)
⑽ [mathjax]\(\dfrac{2x-5}{3}=\dfrac{3x-1}{4}\)
⑾ [mathjax]\(4:x=6:15\)
⑿ [mathjax]\(9:12=(x-2):8\)
⒀ [mathjax]\(\dfrac{3x+6}{5}-\dfrac{7-x}{3}=\dfrac{4x-1}{6}+\dfrac{5}{2}\)
⒁ [mathjax]\((x+10):\dfrac{6-x}{3}=7:3\)
<3年p.285>
5 次の連立方程式を解きなさい。
⑴
⑵
⑶
⑷
⑹
6 次の問いに答えなさい。
⑴ [mathjax]\(a=-5\)，[mathjax]\(b=3\)のとき，[mathjax]\(-2a+b\)の値を求めなさい。
⑵ [mathjax]\(x=-2\)，[mathjax]\(y=\dfrac{1}{2}\)のとき，[mathjax]\(12x²y \div (-2x)² \times 6xy\)の値を求めなさい。
⑶ [mathjax]\(x=5\)，[mathjax]\(y=-\dfrac{1}{2}\)のとき，[mathjax]\(\dfrac{3x+4y}{2}- \dfrac{2x-7y}{3}\)の値を求めなさい。
7
連立方程式
の解が
であるとき，a，bの値を求めなさい。
8 432にできるだけ小さい自然数をかけて，その積がある自然数の2乗になるようにします。どんな数をかければよいですか。
9 長いすが18脚あります。この長いすに生徒がx人ずつすわっていくと，最後の18脚目だけはy人になりました。生徒の人数をx，yを使って表しなさい。
10 A地点から峠までの道を分速50 mで登るのと，峠からA地点まで同じ道を分速75 mで下るのでは，かかる時間が32分ちがいます。A地点から峠までの道のりは何mか求めなさい。
11 2桁の自然数があります。その自然数の十の位の数は一の位の数より2小さく，十の位の数と一の位の数を入れかえてできる自然数ともとの自然数の和は88です。もとの自然数を求めなさい。
12 ある美術館の今日の入館者数は376人でした。これを昨日の入館者数と比べると，男性は[mathjax]\(5\%\)減り，女性は [mathjax]\(8\%\)増え，合計では11人増えています。この美術館の今日の男性と女性の入館者数を，それぞれ求めなさい。
<3年p.286>
関数，データの活用
1 次の問いに答えなさい。
⑴ yはxに比例し，[mathjax]\(x=8\)のとき[mathjax]\(y=-48\)です。yをxの式で表しなさい。また，[mathjax]\(x=-5\)のときのyの値を求めなさい。
⑵ yはxに反比例し，[mathjax]\(x=-9\)のとき[mathjax]\(y=-4\)です。yをxの式で表しなさい。また，[mathjax]\(x=3\)のときのyの値を求めなさい。
2 次の直線の式を求めなさい。
⑴ 2点[mathjax]\((5，-8)\)，[mathjax]\((-2，13)\)を通る直線
⑵ 点[mathjax]\((-7，-9)\)を通り，直線[mathjax]\(y=2x-5\)に平行な直線
⑶ 点[mathjax]\((6，-1)\)を通り， 直線[mathjax]\(y=3x-4\)とy軸上で交わる直線
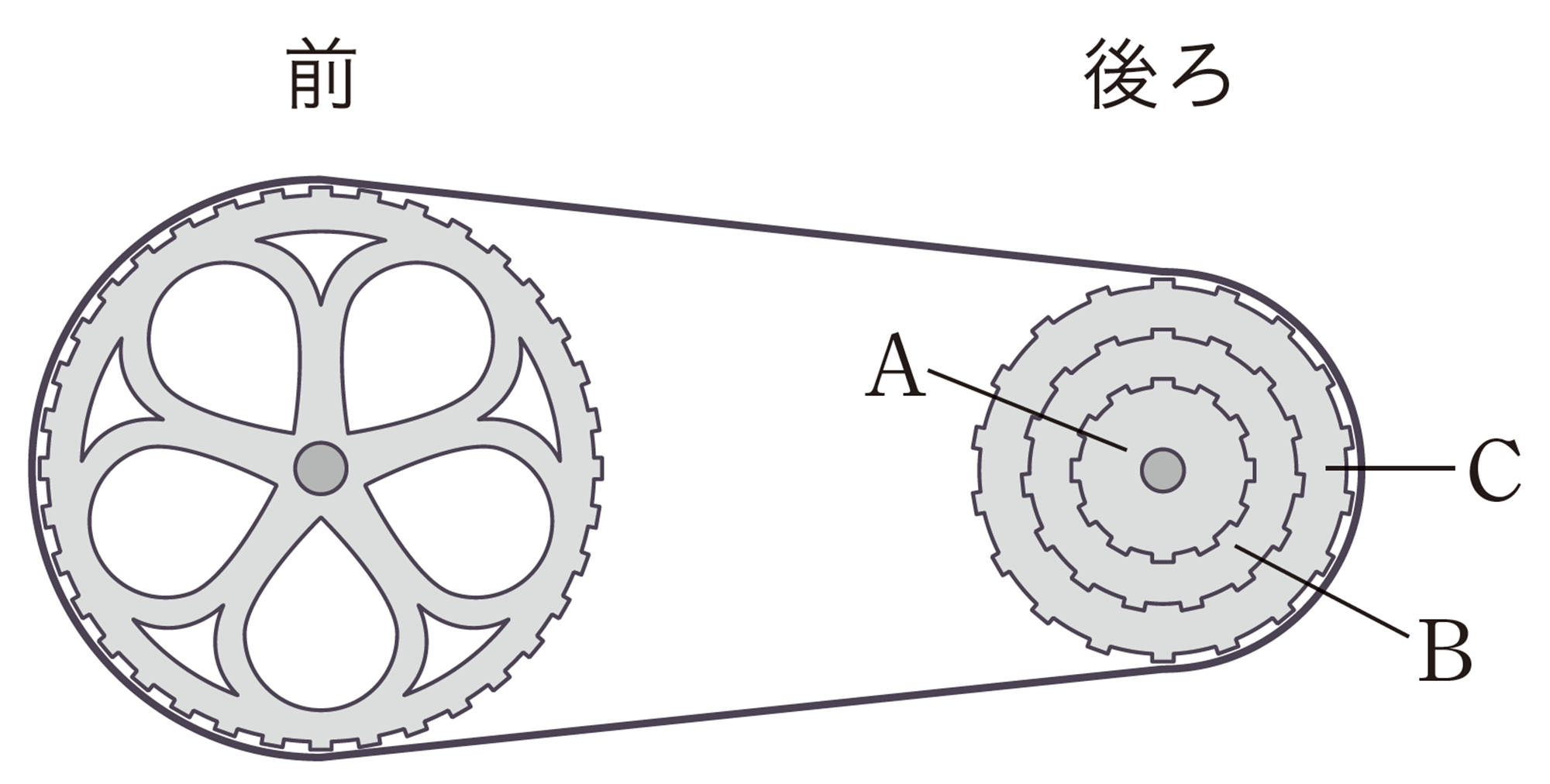
3 3段変速の自転車で，ペダルについている前のギアの歯の数と，後ろのギアA，B，Cの歯の数を調べたところ，前…36，A…12，B…15，C…18でした。次の問いに答えなさい。
⑴ チェーンがギアAにあるとき，ペダルを1回転させると，Aは何回転しますか。また，チェーンがギアB，Cにあるとき，B，Cはそれぞれ何回転しますか。
⑵ 後ろのギアの歯の数をxとし，ペダルを5回転させたときの後ろのギアの回転数をyとします。このとき，yをxの式で表しなさい。
⑶ ⑵において，前のギアの歯の数を48に変えたとき，yをxの式で表しなさい。また，このとき，チェーンがギア A，B，C にある場合のA，B，Cの回転数をそれぞれ求めなさい。
4 右の図のような長方形ABCDがあります。点PはCを出発して，秒速2cmで辺CD上をDまで動きます。点PがCを出発してからx秒後の[mathjax]\(\triangle PBC\)の面積をycm²とするとき，次の問いに答えなさい。
⑴ yをxの式で表しなさい。
⑵ xの変域とyの変域を求めなさい。
⑶ [mathjax]\(\triangle PBC\)の面積が24cm²になるのは，点PがCを出発してから何秒後か求めなさい。
<3年p.287>
5 右の図で，直線ℓの式は[mathjax]\(y=2x-2\)，直線mの式は[mathjax]\(y=-\dfrac{2}{3}x+6\)です。ℓ，mの交点を A，ℓとx軸，y軸との交点をそれぞれB，C，mとx軸，y軸との交点をそれぞれD，Eとするとき，次の問いに答えなさい。
⑴ 点A，B，Dの座標を求めなさい。
⑵ [mathjax]\(\triangle ABD\)の面積を求めなさい。
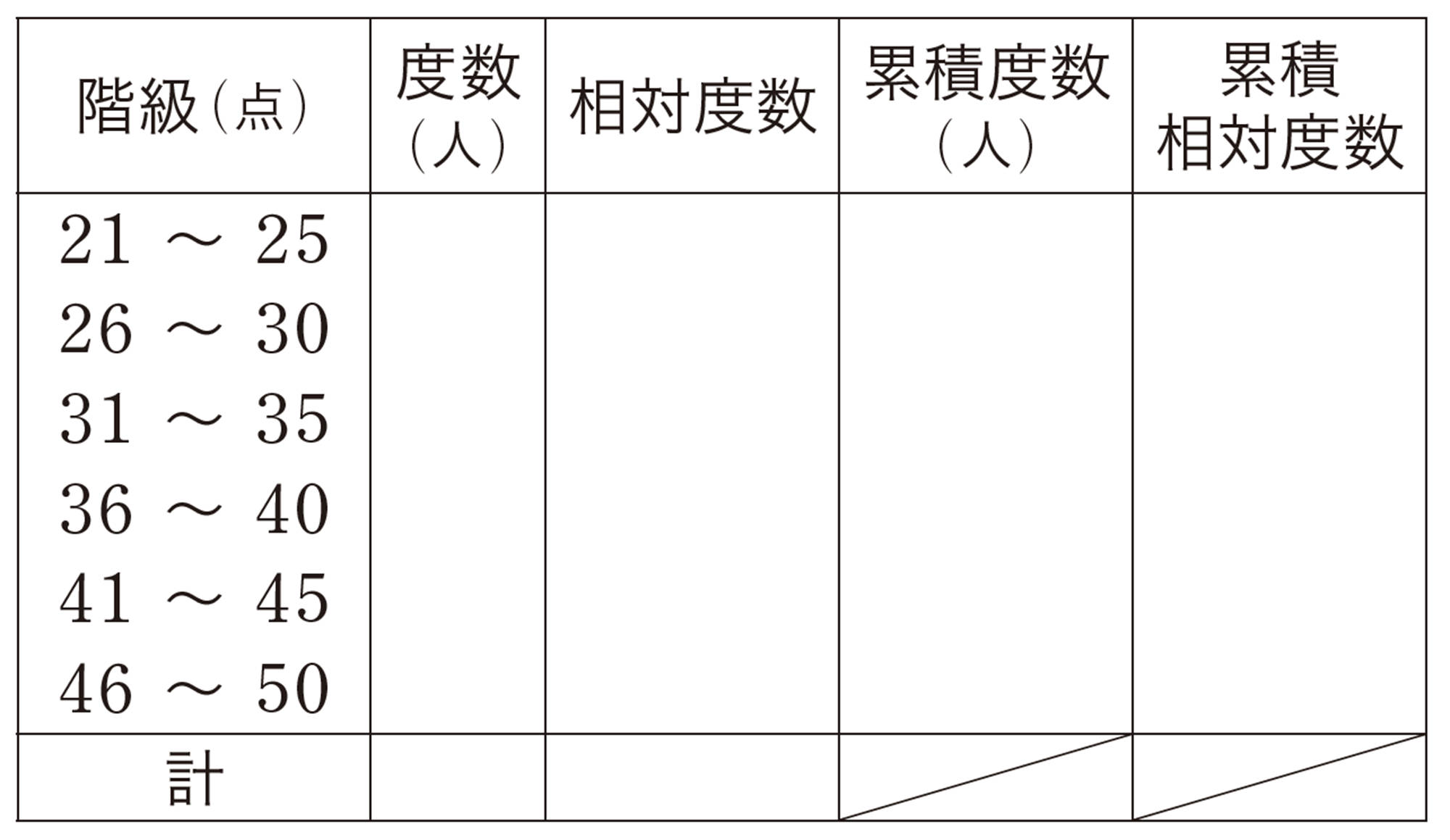
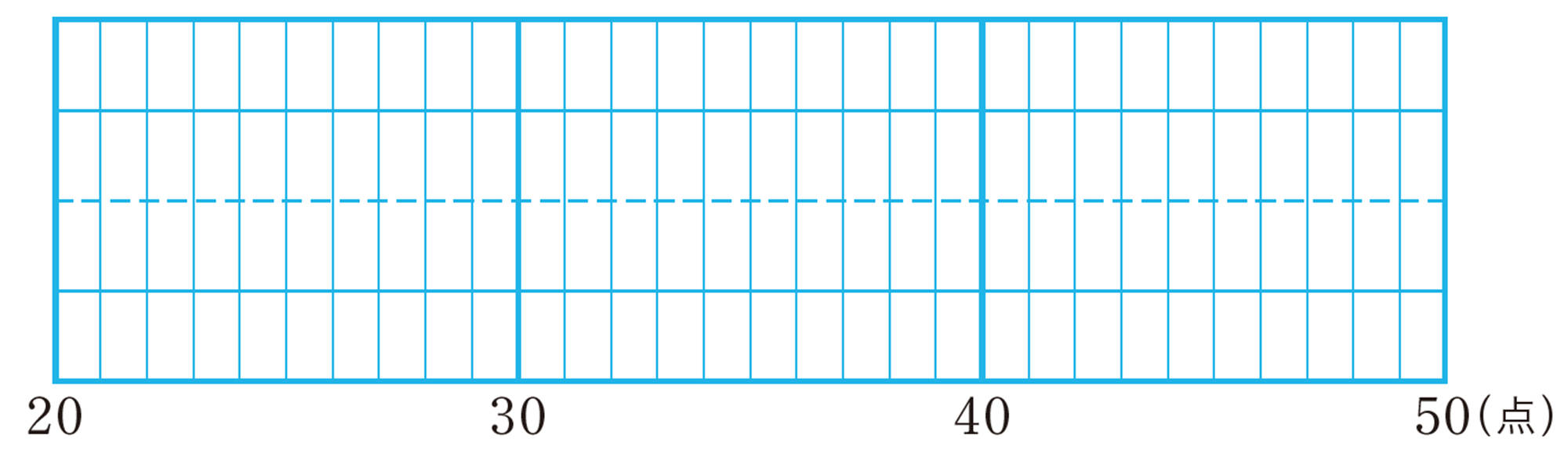
6 ある21人のクラスで50点満点のテストをしたところ，右のような結果になりました。次の問いに答えなさい。
⑴ 右の表を完成させなさい。ただし，相対度数，累積相対度数は，小数第二位まで求めなさい。
⑵ テストの点が31点から35点の生徒は全体の何%ですか。
⑶ テストの点が35点以下の生徒は全体の何%ですか。
⑷ 四分位数と四分位範囲をそれぞれ求めなさい。
⑸ 右の図に箱ひげ図をかきなさい。
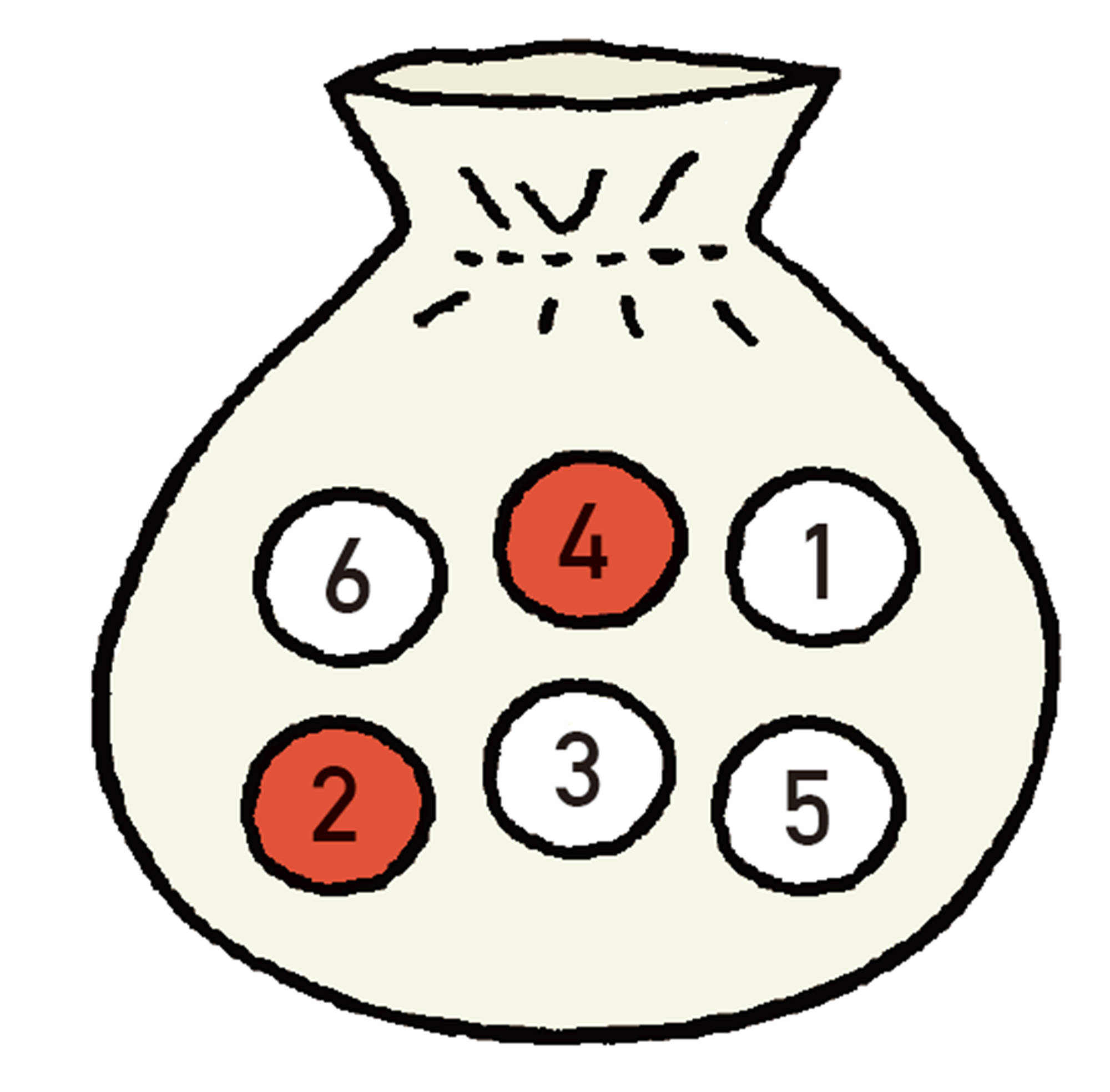
7 大小2つのさいころを同時に投げるとき，出る目の和が素数になる確率を求めなさい。
8 袋の中に[mathjax] \(1\)，[mathjax] \(3\)，[mathjax] \(5\)，[mathjax] \(6\)の数字が1つずつ書かれた4個の白玉と，[mathjax] \(2\)，[mathjax] \(4\)の数字が1つずつ書かれた2個の赤玉が入っています。この袋から同時に2個の玉を取り出すとき，次の確率を求めなさい。
⑴ 2個とも同じ色の玉である確率
⑵ 取り出した玉に書かれた数の積が偶数である確率
<3年p.288>
図形
1 右の図のような線分ABがあります。[mathjax]\(\angle CBA = 45^{\circ}\)となる半直線BCを作図しなさい。
2 ▱ABCDの辺 AD 上の点 P から，対角線 AC に平行な直線を引き，辺CDとの交点をQとし，PとB，PとC，AとQをそれぞれ結びます。このとき，[mathjax]\(\triangle ACQ\) と面積が等しい三角形をすべて答えなさい。
3 右の図のような円Oにおいて，円周上の点Aを通る接線を作図しなさい。
4 右の図は，6つの合同な正三角形を，すき間なく並べたものです。次の問いに答えなさい。
⑴ [mathjax]\(\triangle ABO\)を，点Oを回転の中心として点対称移動したとき，重なる図形はどれですか。
⑵ [mathjax]\(\triangle ABO\)を，2回の移動で[mathjax]\(\triangle DOE\)に重ねるためには，どのように移動すればよいですか。2通りの方法を答えなさい。
5 右の図の直方体について，次の辺を答えなさい。
⑴ 辺BFと平行な辺
⑵ 辺ADと垂直な辺
⑶ 辺DCとねじれの位置にある辺
⑷ 面AEFBと平行な辺
⑸ 面BFGCと垂直な辺
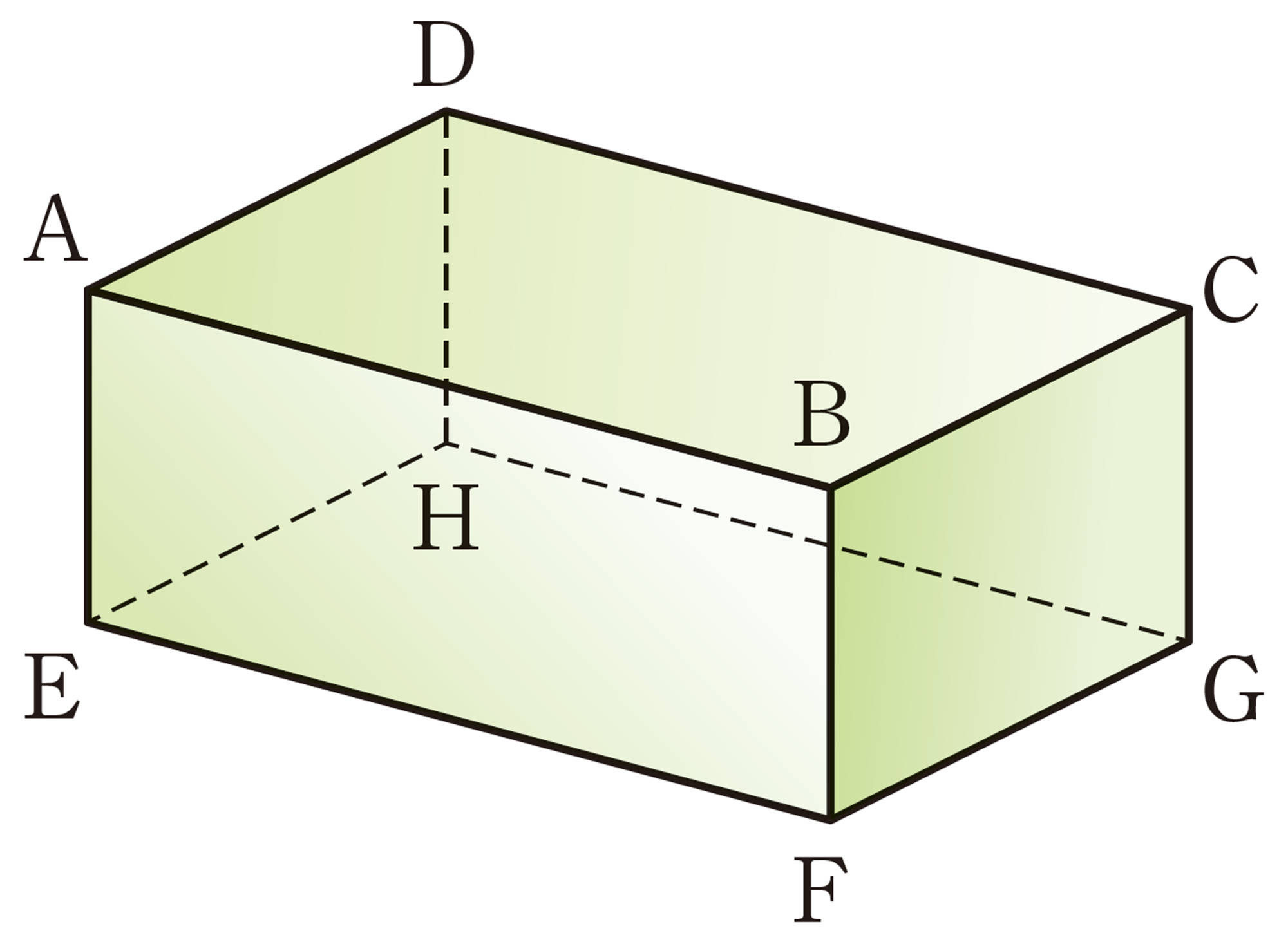
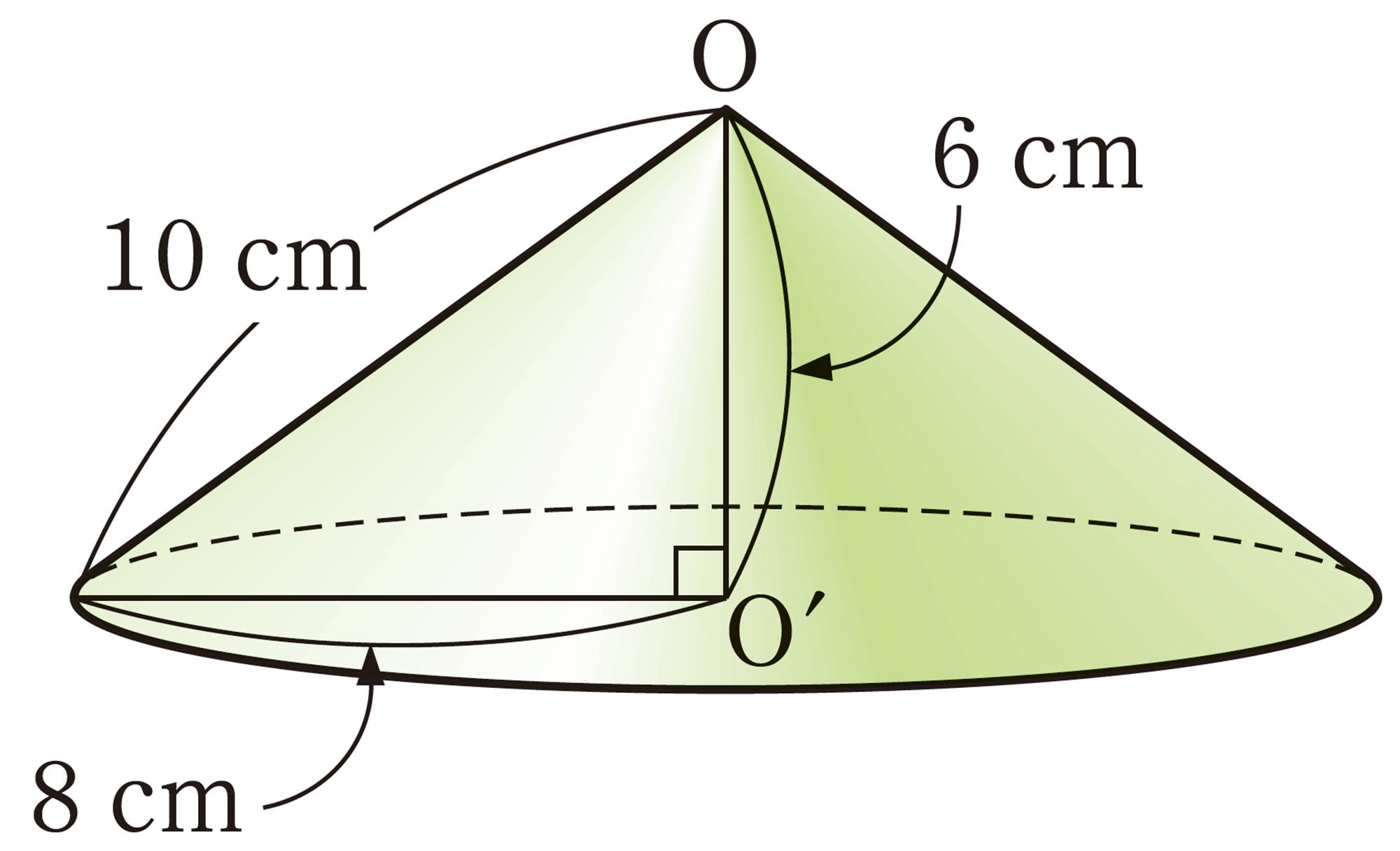
6 半径6cmの球の表面積と体積を求めなさい。
<3年p.289>
7 右の図のような，底面の半径が8cm，母線の長さが10cm，高さが6cmの円錐があります。次の問いに答えなさい。
⑴ 側面のおうぎ形の中心角を求めなさい。
⑵ この円錐の表面積を求めなさい。
⑶ この円錐の体積を求めなさい。
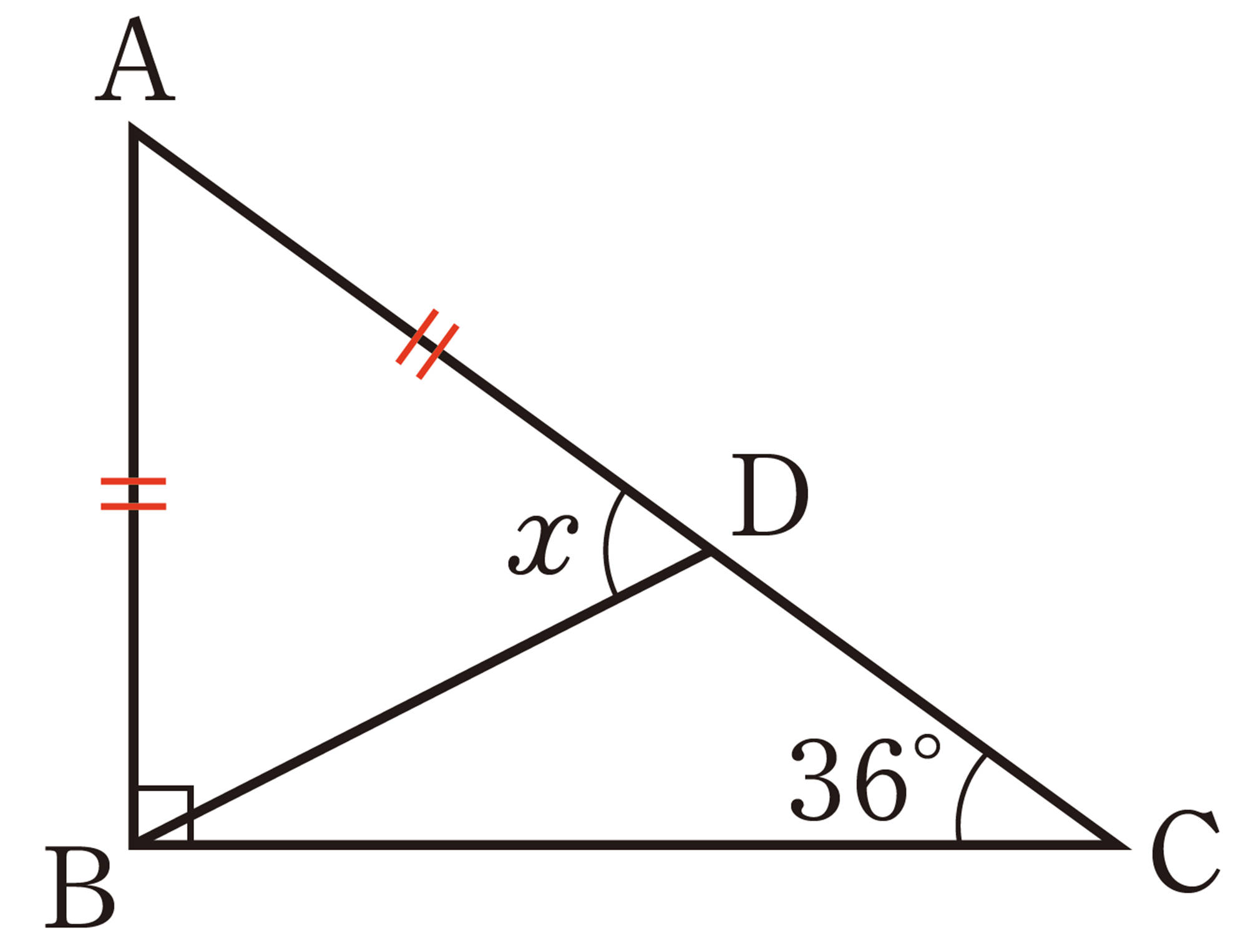
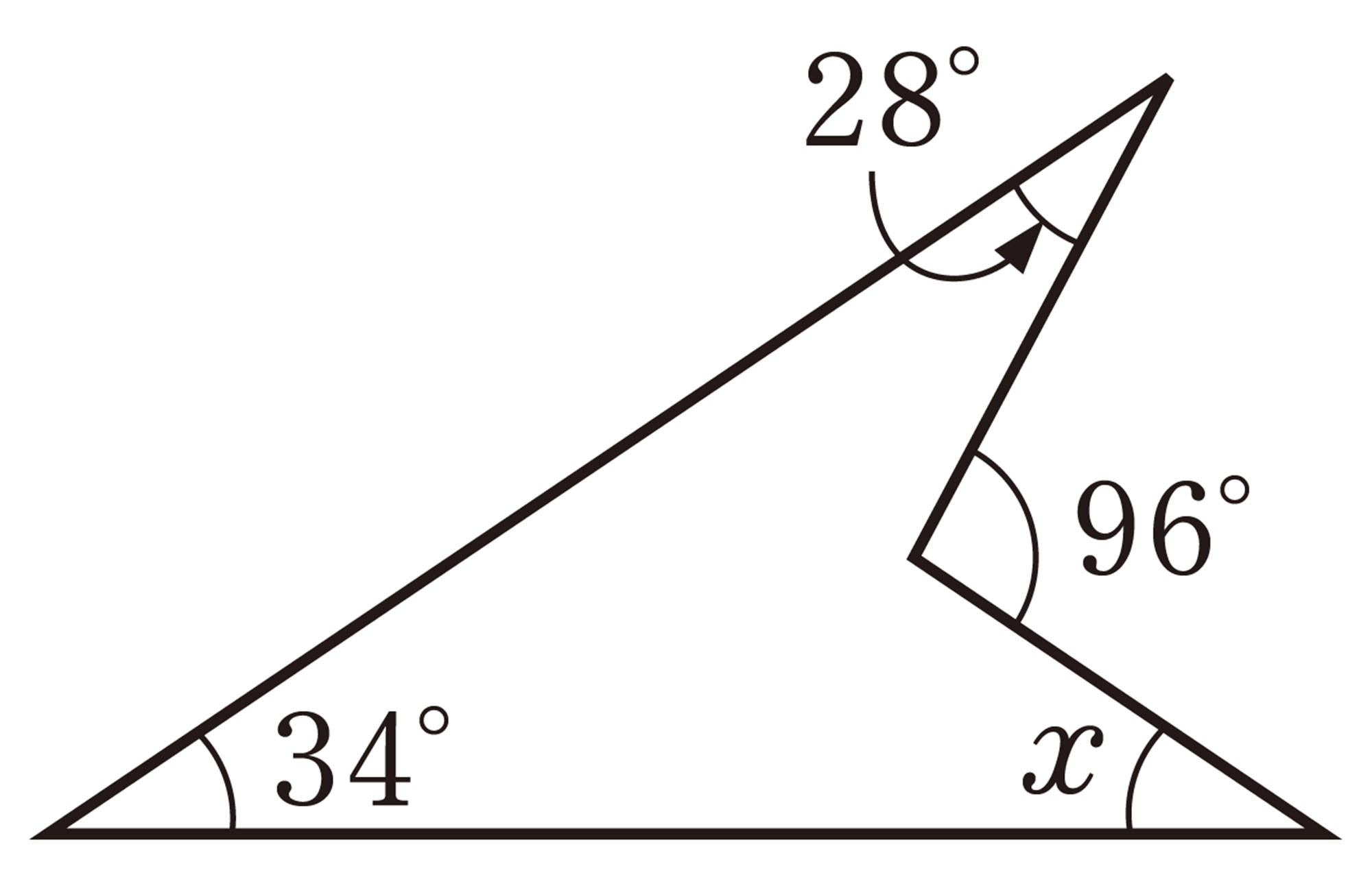
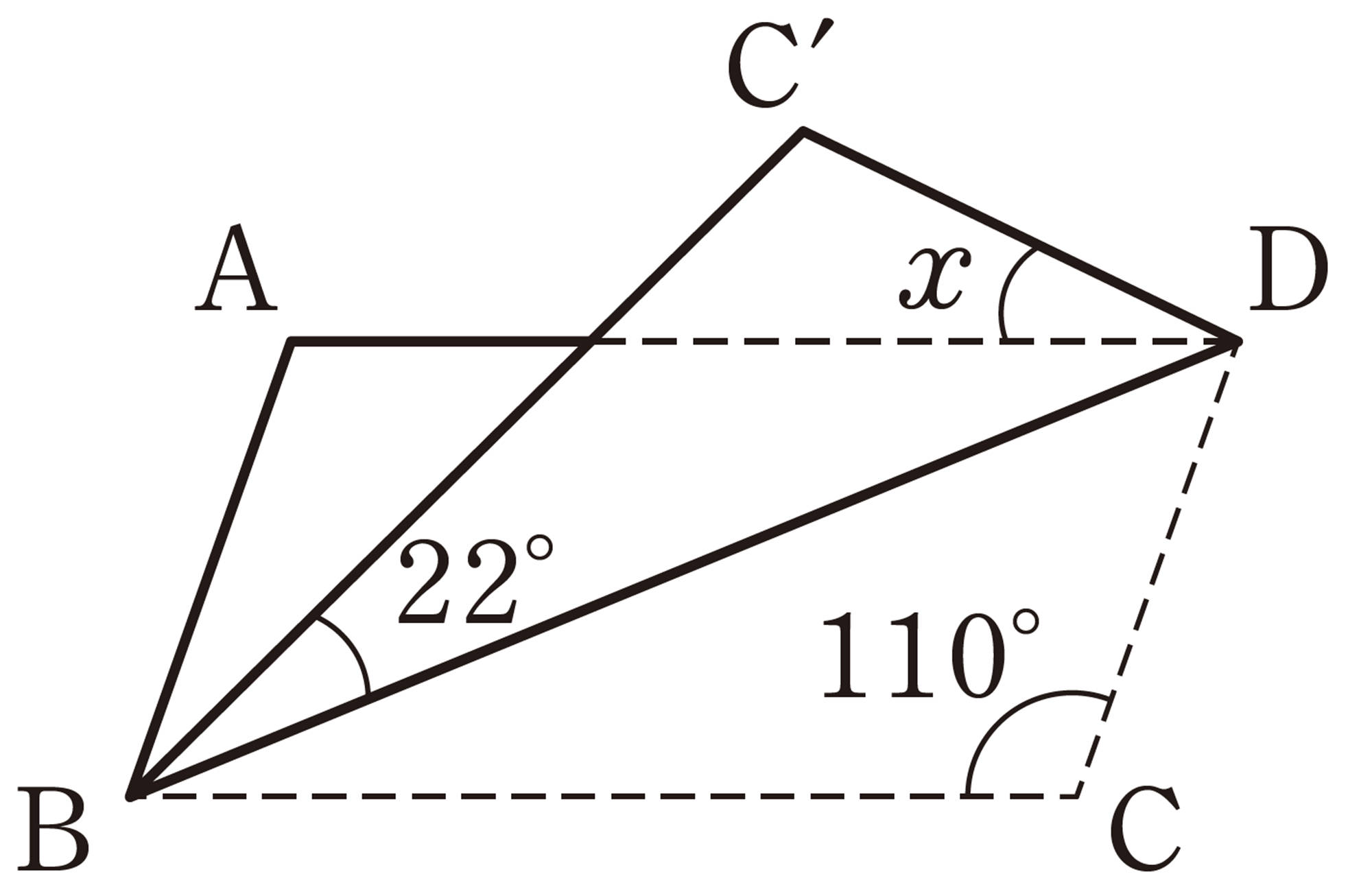
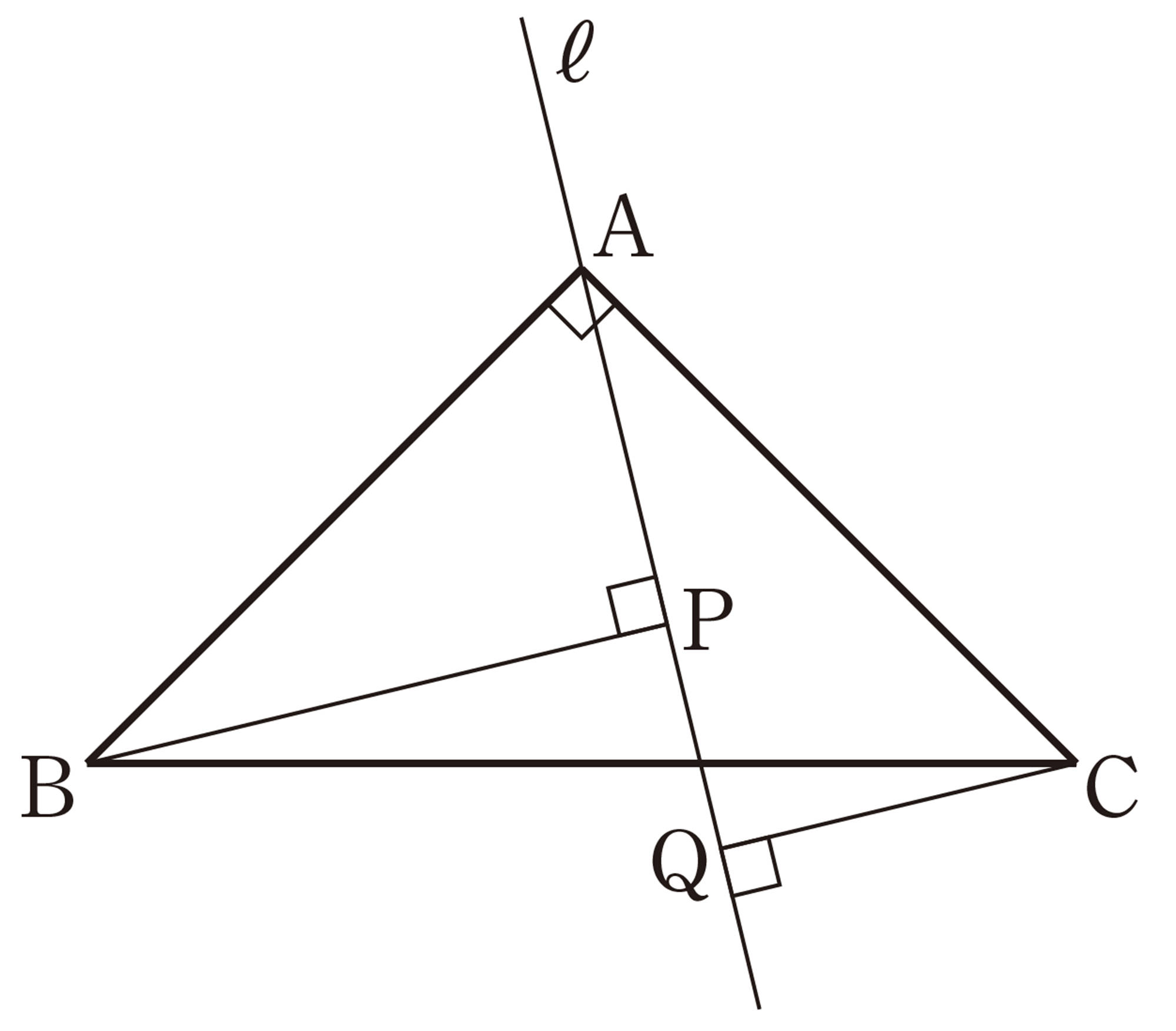
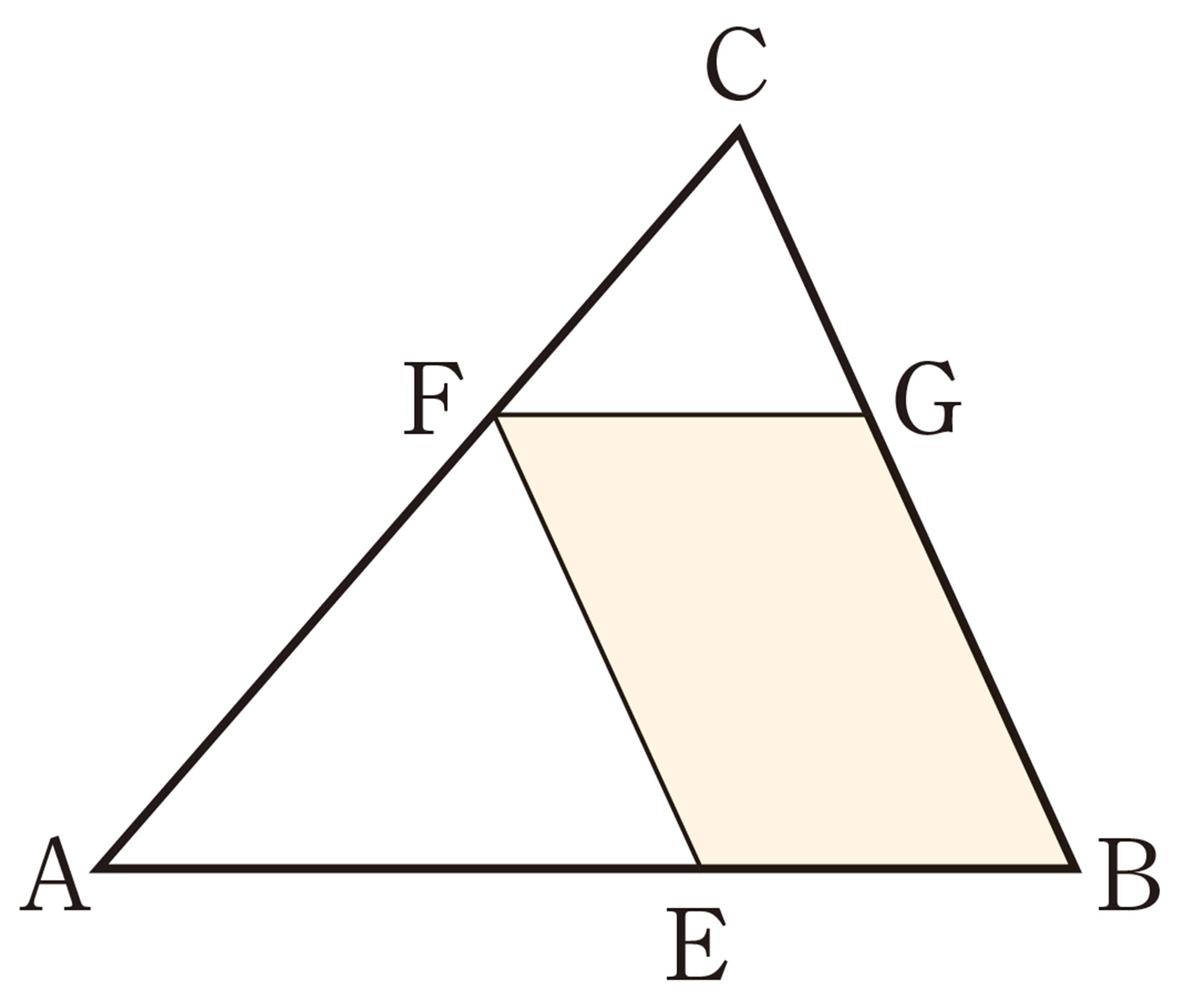
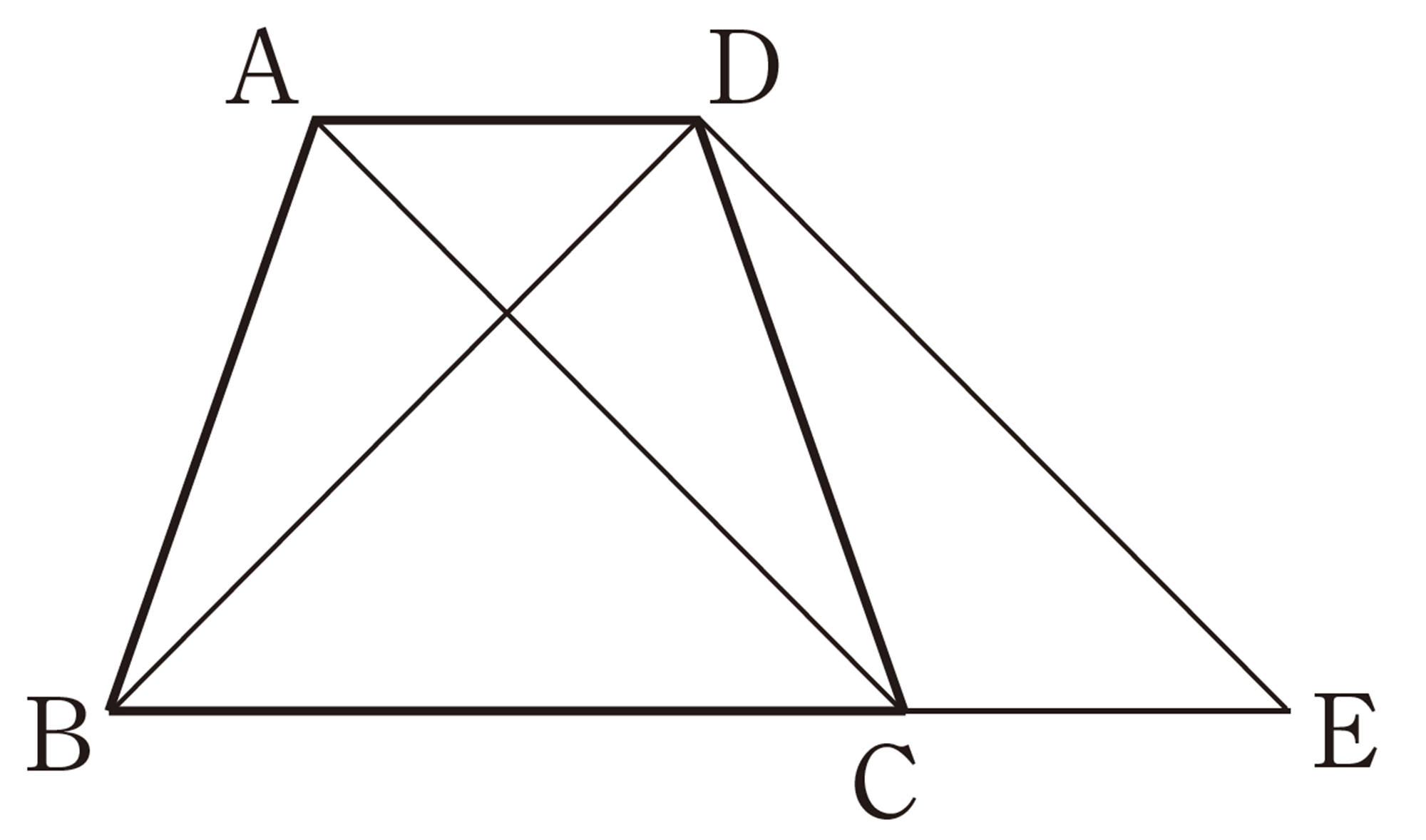
8 次の図で，[mathjax]\(\angle x\)の大きさを求めなさい。
⑴ [mathjax]\(\angle B = 90^{\circ}\)，[mathjax]\(AB=AD\)
⑵
⑶ ▱ABCDを対角線BDで折り返した図
9 [mathjax]\(\angle A = 90^{\circ}\)の直角二等辺三角形ABCの頂点Aを通る直線ℓに，頂点 B，C からそれぞれ垂線BP，CQを引くとき，[mathjax]\(BP=AQ\)であることを証明しなさい。
10 右の図の[mathjax]\(\triangle ABC\)は，[mathjax]\(AB=AC\)の二等辺三角形です。点E，F，Gはそれぞれ辺AB，AC，BC上の点で，[mathjax]\(AE=AF\)，[mathjax]\(FG=FC\)です。このとき，四角形EBGFは平行四辺形であることを証明しなさい。
11 [mathjax]\(AD/\!/BC\)，[mathjax]\(AC=DB\)である台形ABCDがあります。辺BCの延長上に[mathjax]\(AC/\!/DE\)となる点Eをとります。このとき，[mathjax]\(AB=DC\)であることを証明しなさい。
