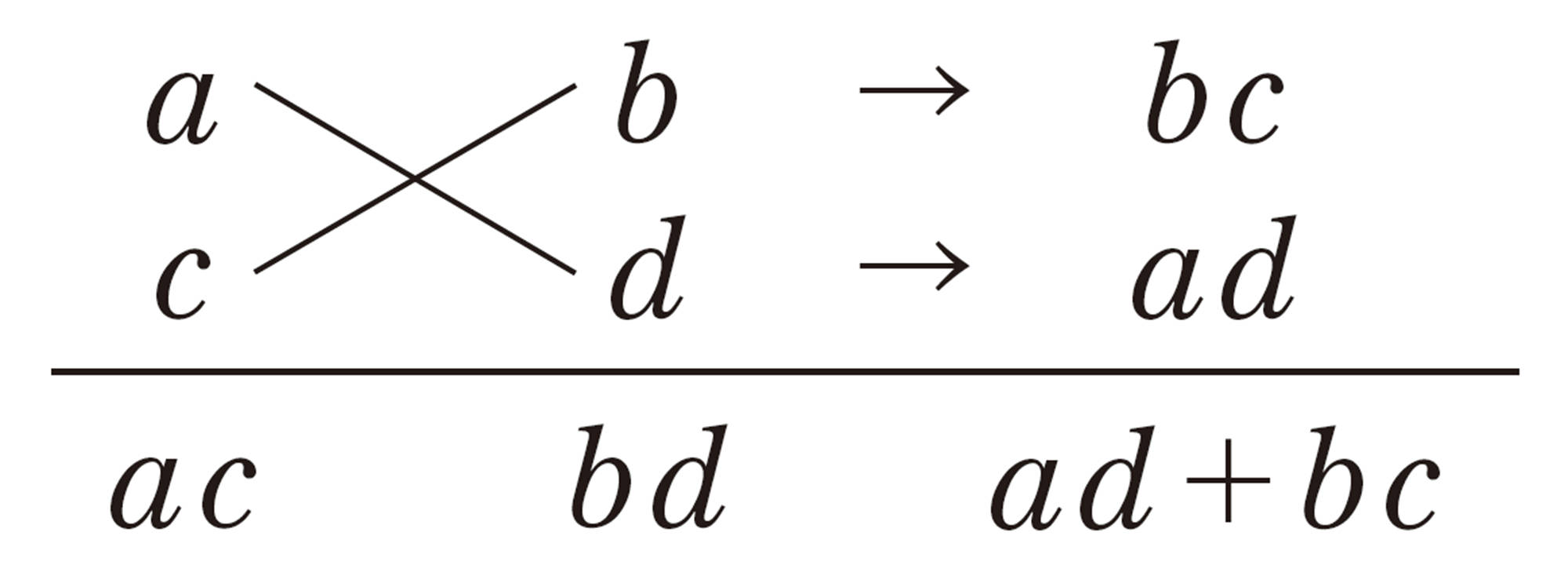<3年p.270>
Theme 疑問を考えよう
黄金比って何？
日本では白銀比が好まれると学んだね。
黄金比ってことばを聞いたことがあるけど，似ているのかな。
① 右の図で，長方形ABCDから正方形ABEFの部分を取り去った残りの長方形ECDFは，もとの長方形ABCDと相似になっています。長方形ABCDと長方形ECDFが相似であることをもとにして，[mathjax]\(AB＝1\)，[mathjax]\(BC＝x\)として比例式をつくり，それを解いてみましょう。
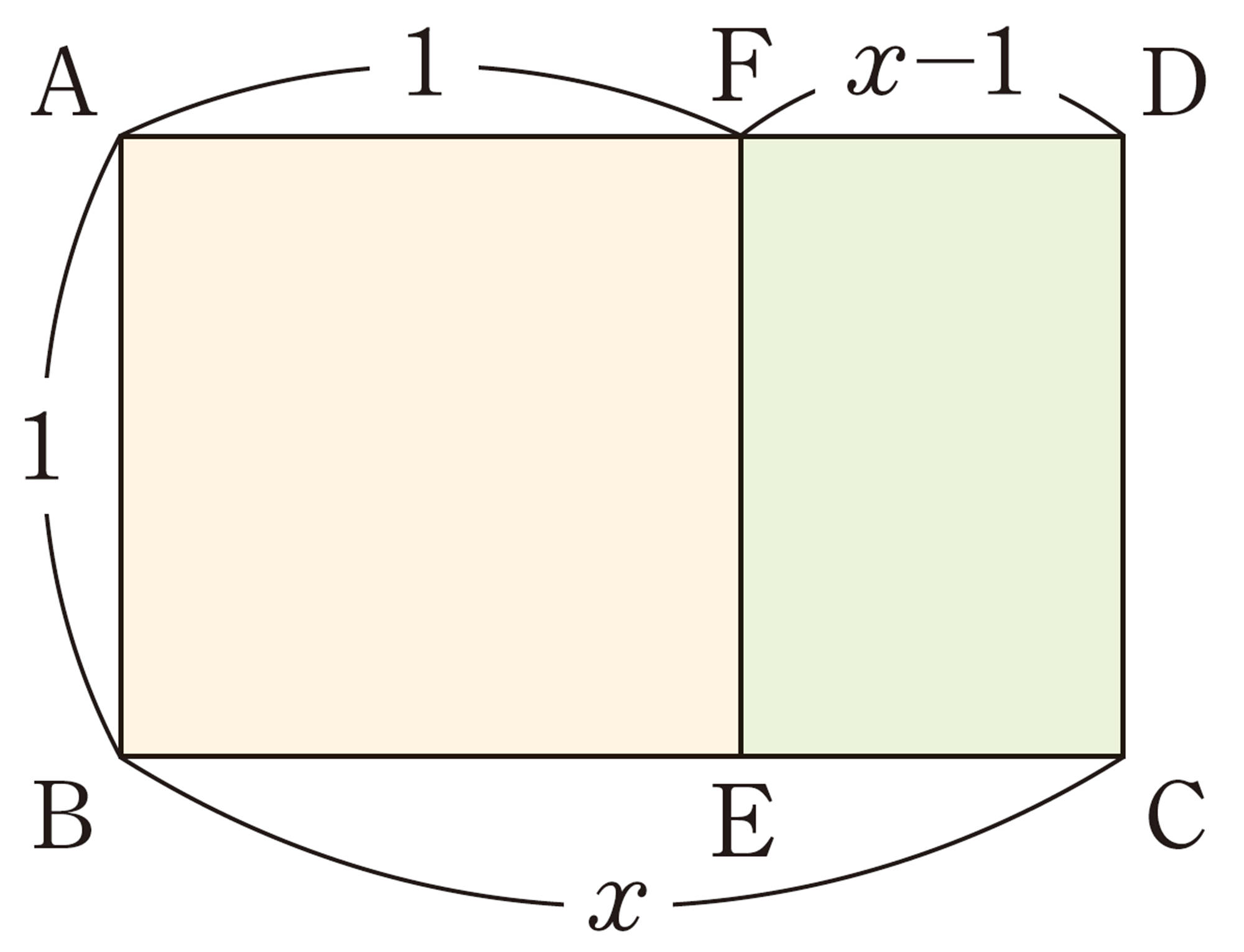
1から[mathjax]\(\dfrac{1+ \sqrt{5}}{2}\)が得られます。したがって，長方形ABCDの縦と横の長さの比が [mathjax]\(1:\dfrac{1+ \sqrt{5}}{2}\) ，およそ [mathjax]\(1:1.62\) であることがわかります。
この長方形は，ヨーロッパで昔からもっとも美しい長方形として親しまれてきました。そのため，この比は，黄金比（golden ratio）と呼ばれています。
黄金比は，ミロのビーナスやパルテノン神殿など，美術作品や建築物の中にも取り入れられています。
江戸時代の画家である葛飾北斎（1760〜1849）は，早くから洋画に関心をもち，その技法を取り入れていました。北斎の作品『冨嶽三十六景 神奈川沖浪裏』の構図にも，黄金比が使われています。
正五角形の1辺の長さと対角線の長さの比は，黄金比になっているんだって。
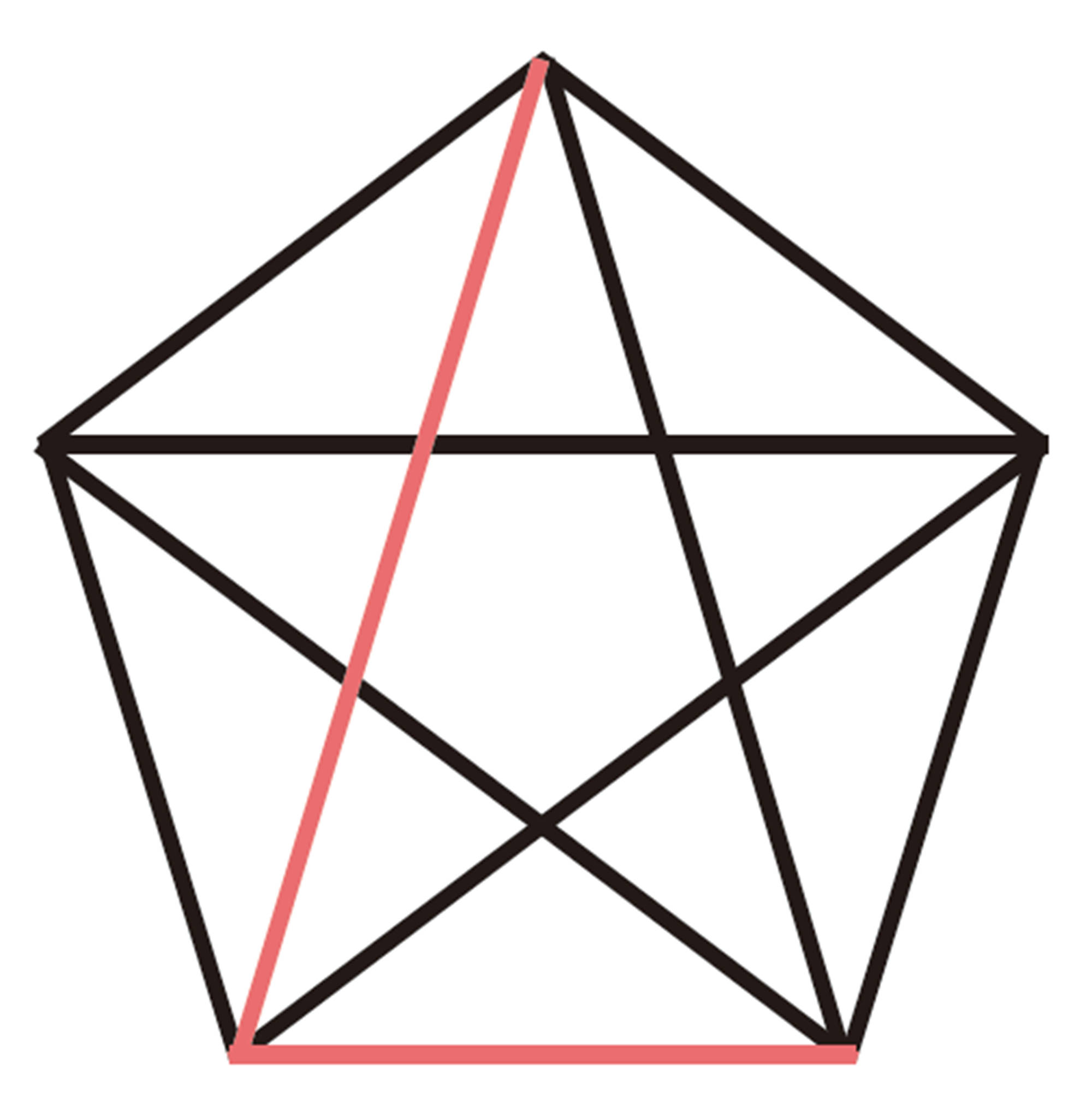
② 正五角形の中からほかに黄金比になっている場所を探してみましょう。
<3年p.271>
「三平方の定理の逆」の証明はほかにもある？
三平方の定理の逆
[mathjax]\(\triangle ABC\)の3辺の長さa，b，cの間に
[mathjax]\(a²+b²=c²\)
の関係が成り立てば，[mathjax]\(\angle C = 90^{\circ}\)である。
三平方の定理の逆を学んだね。
ほかにも証明のしかたはあるのかな。
① 仮定である[mathjax]\(a²+b²=c²\)の式を，a²について解いたあと，右辺を因数分解しましょう。次に，右のことを参考にしながら比例式に表してみましょう。
[mathjax]\(P² = Q \times R\)のとき，
[mathjax]\(Q:P=P:R\)
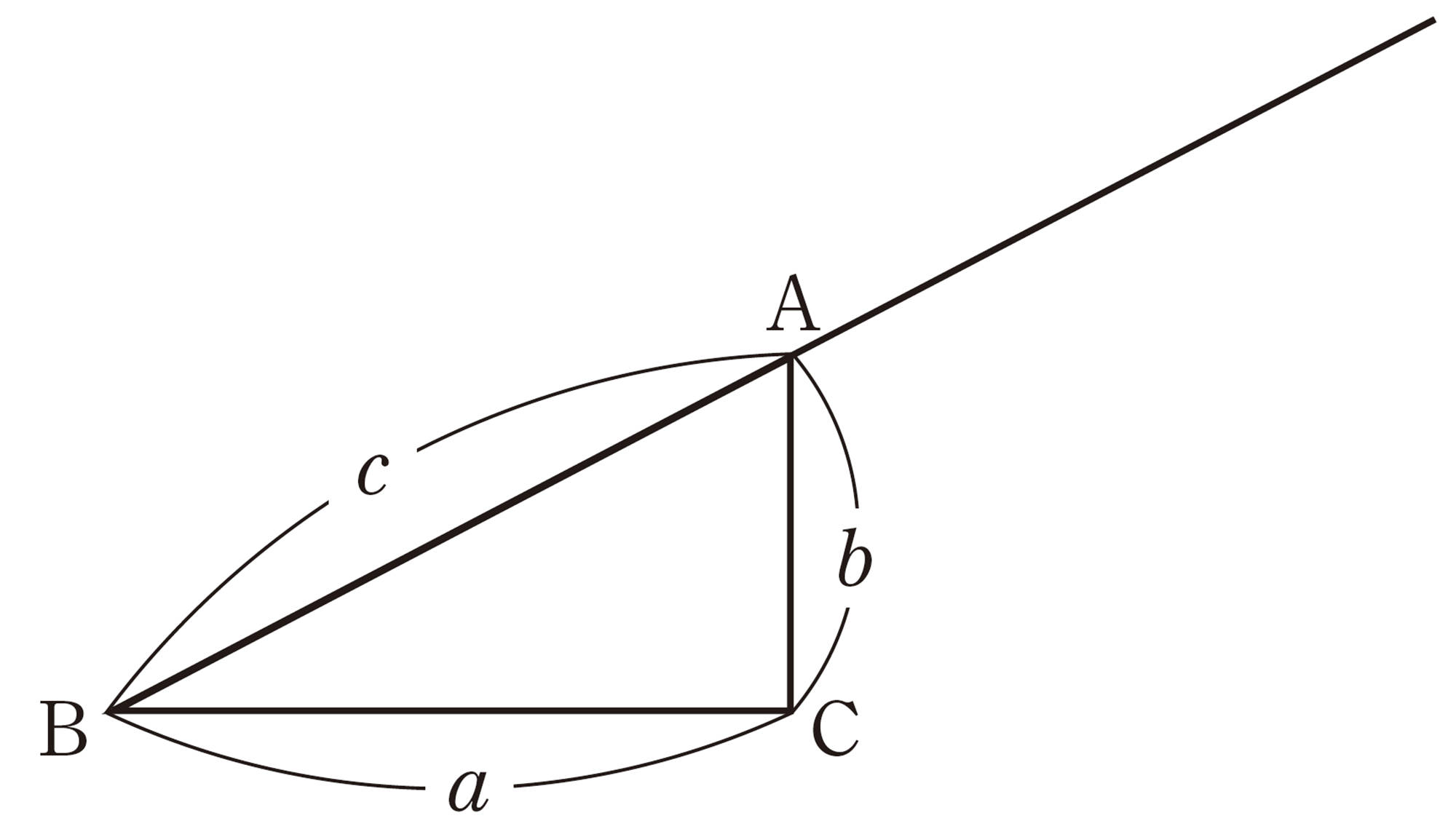
② 次の図の点Aを中心に，半径bの円をかき，半直線 BA上に[mathjax]\(BD=c+b\)となる点D，[mathjax]\(BE=c-b\)となる点Eをとり，CとD，CとEをそれぞれ結んだ図を作図してみましょう。
③ ②で作図した図の中に相似な三角形があります。 ①で導いた式を利用して，2つの三角形が相似であることを証明してみましょう。
④ ③で証明した相似な三角形と，②で作図した図の中にある2つの二等辺三角形に着目して，[mathjax]\(\angle ACB = 90^{\circ}\)を証明してみましょう。
<3年p.272>
放物線はみな相似？ 発展
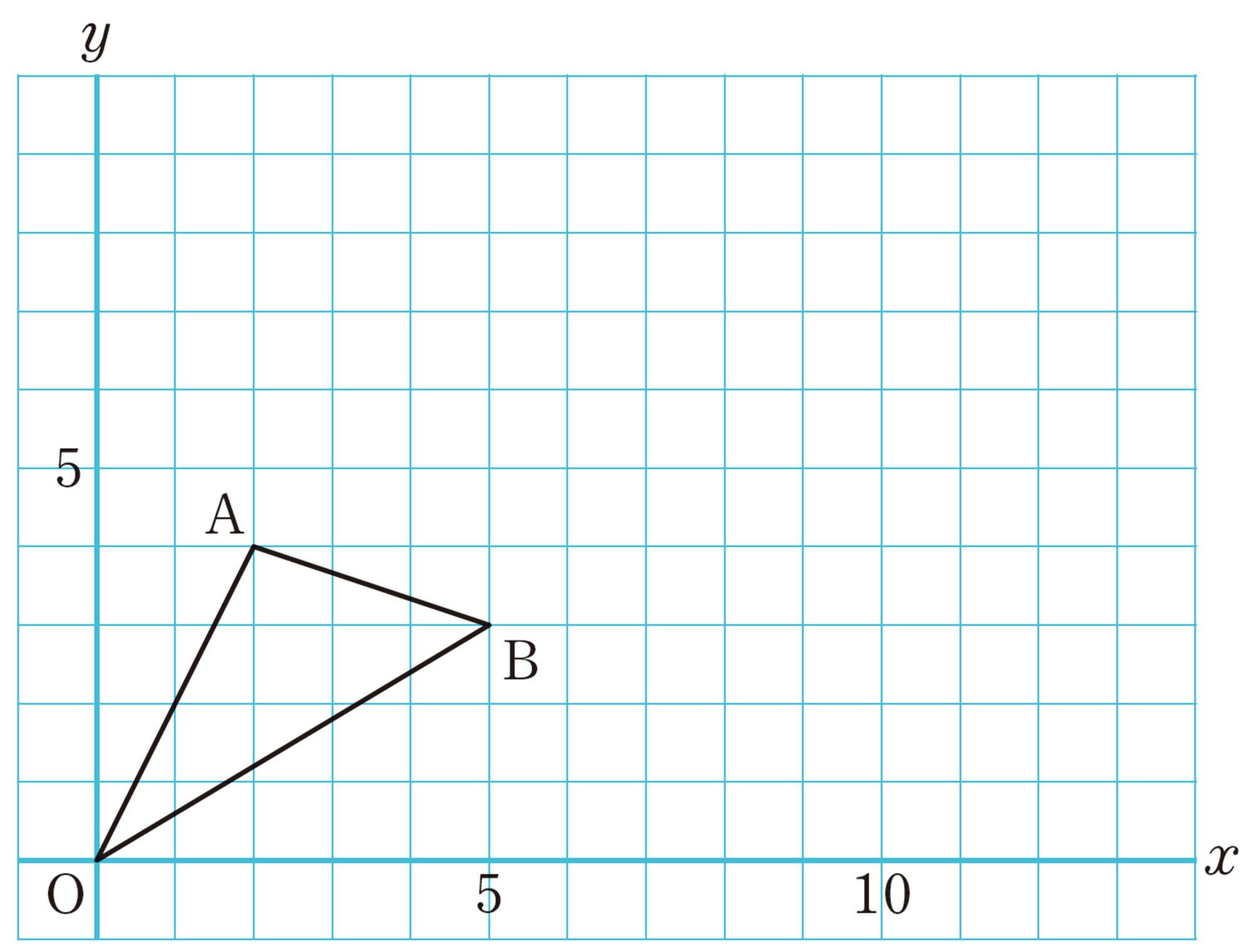
① 次の図は，座標を使って[mathjax]\(\triangle AOB\)をかいたものです。原点Oを相似の中心として，[mathjax]\(\triangle AOB\)を2倍に拡大した[mathjax]\(\triangle A´OB´\)を，次の図にかき入れてみましょう。
①のように，平面上では，図形の各点のx，y座標をそれぞれ2倍にすれば，原点Oを相似の中心として，2倍の拡大図をかくことができます。
曲線でもこの方法でかけるのかな。
放物線で考えてみたいな。
放物線[mathjax]\(y=x²\)を2倍に拡大してみましょう。
② 表計算ソフトに，右のようにxと[mathjax]\(y=x²\)の値を入力して，放物線[mathjax]\(y=x²\)をかいてみましょう(表1，図1)。また，x，yの値をそれぞれ2倍して，その放物線を2倍に拡大してみましょう(表2，図2)。
③ 表2や図2から，放物線[mathjax]\(y=x²\)を2倍に拡大した放物線の式を求めてみましょう。
<3年p.273>
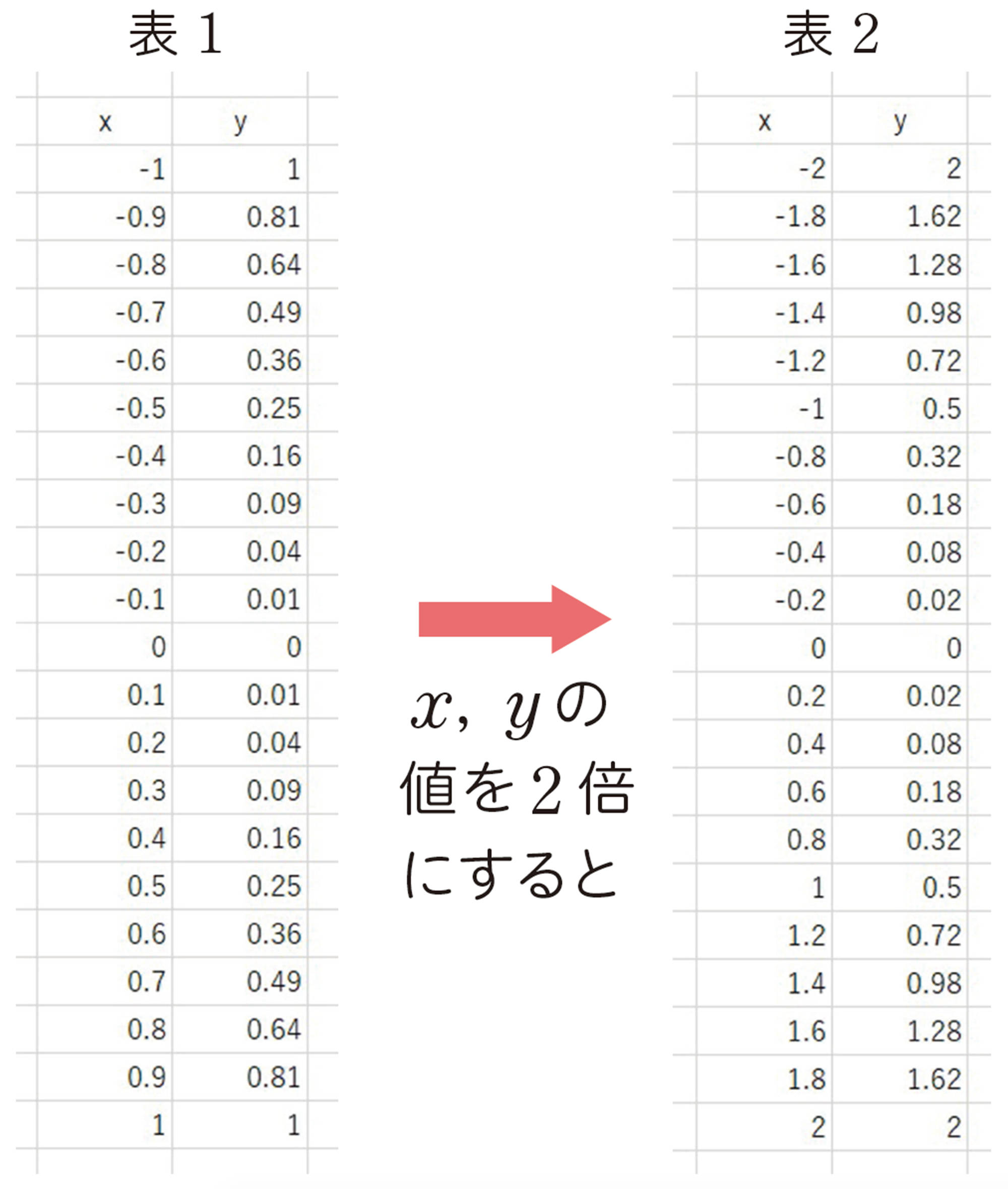
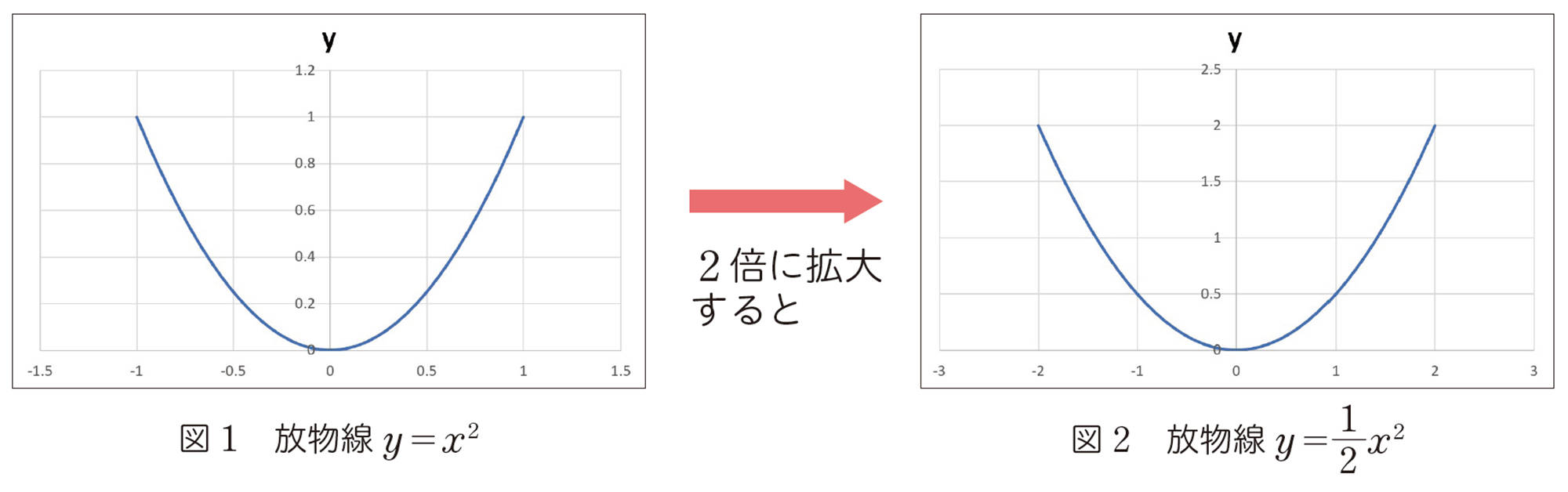
これまで調べたことから，放物線[mathjax]\(y=x²\)を2倍に拡大すると，放物線[mathjax]\(y=\dfrac{1}{2}x²\)になることがわかります。
このことは，次のように説明できます。
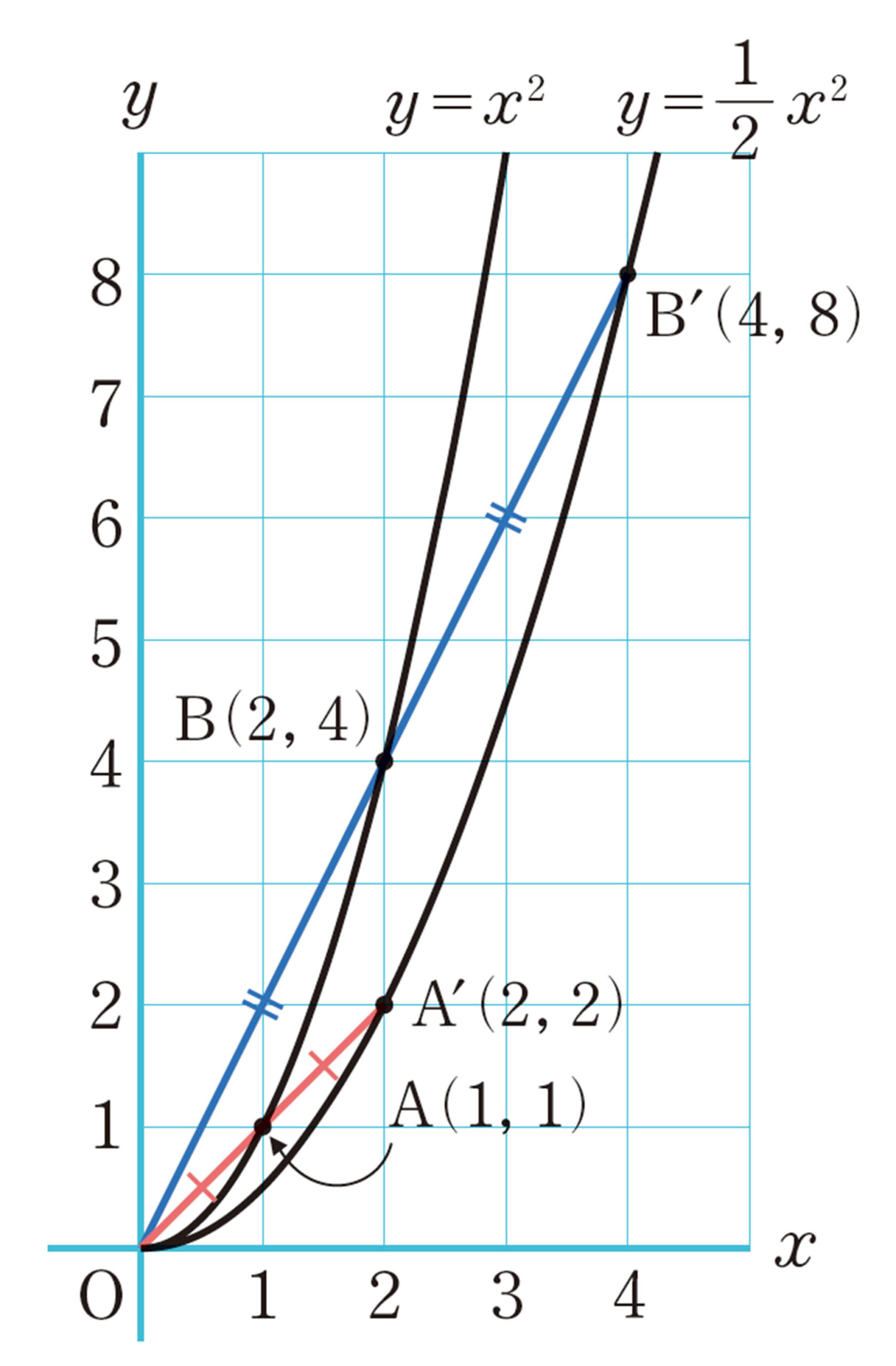
右の図のように，放物線[mathjax]\(y=x²\)上の点[mathjax]\( A(1，1)，B(2，4) \)を原点から2倍の距離に遠ざけると，それぞれ，[mathjax]\( A´(2,2)，B´(4,8) \)となります。これらの点はA´[mathjax]\(\require{physics} \left(2,\dfrac{1}{2} \times 2²\right)\)，B´[mathjax]\(\require{physics} \left(4,\dfrac{1}{2} \times 4²\right)\)と表すことができるので，それぞれ放物線[mathjax]\(y=\dfrac{1}{2}x²\)上の点であることがわかります。
④ 放物線[mathjax]\(y=x²\)上のほかの点についても，同じことを調べてみましょう。
⑤ 前ページの表1のx，yの値をそれぞれ[mathjax]\(\dfrac{1}{2}\)倍して，放物線をかいてみましょう。また，その放物線はどんな式になるでしょうか。
⑥ 放物線[mathjax]\(y=x²\)を3倍，[mathjax]\(\dfrac{1}{3}\)倍にしたとき，その放物線の式はどうなるでしょうか。また，それらのことから，放物線についてどんなことがわかるでしょうか。
ほかの放物線でも同じように考えてみたいな。
<3年p.274>
ドローンを使った撮影範囲は？
ドローンは，農業や林業，水産業，工業，商業などのあらゆる産業で利用されるだけでなく，新しい仕事を生み出しています。ドローンを使って空撮するときに相似の考えを使って，飛行高度に応じた撮影範囲を求めることができます。
カメラはイメージセンサーと呼ばれる部分に光を取り込むことで写真を撮影します。
右の図のように，イメージセンサーの大きさをセンサーサイズ（AB）といい，イメージセンサーとレンズの中心（O）との距離を焦点距離といいます。飛行高度とは地表からドローンまでの高さのことをいいますが，ここではレンズの中心から地表までの距離とします。
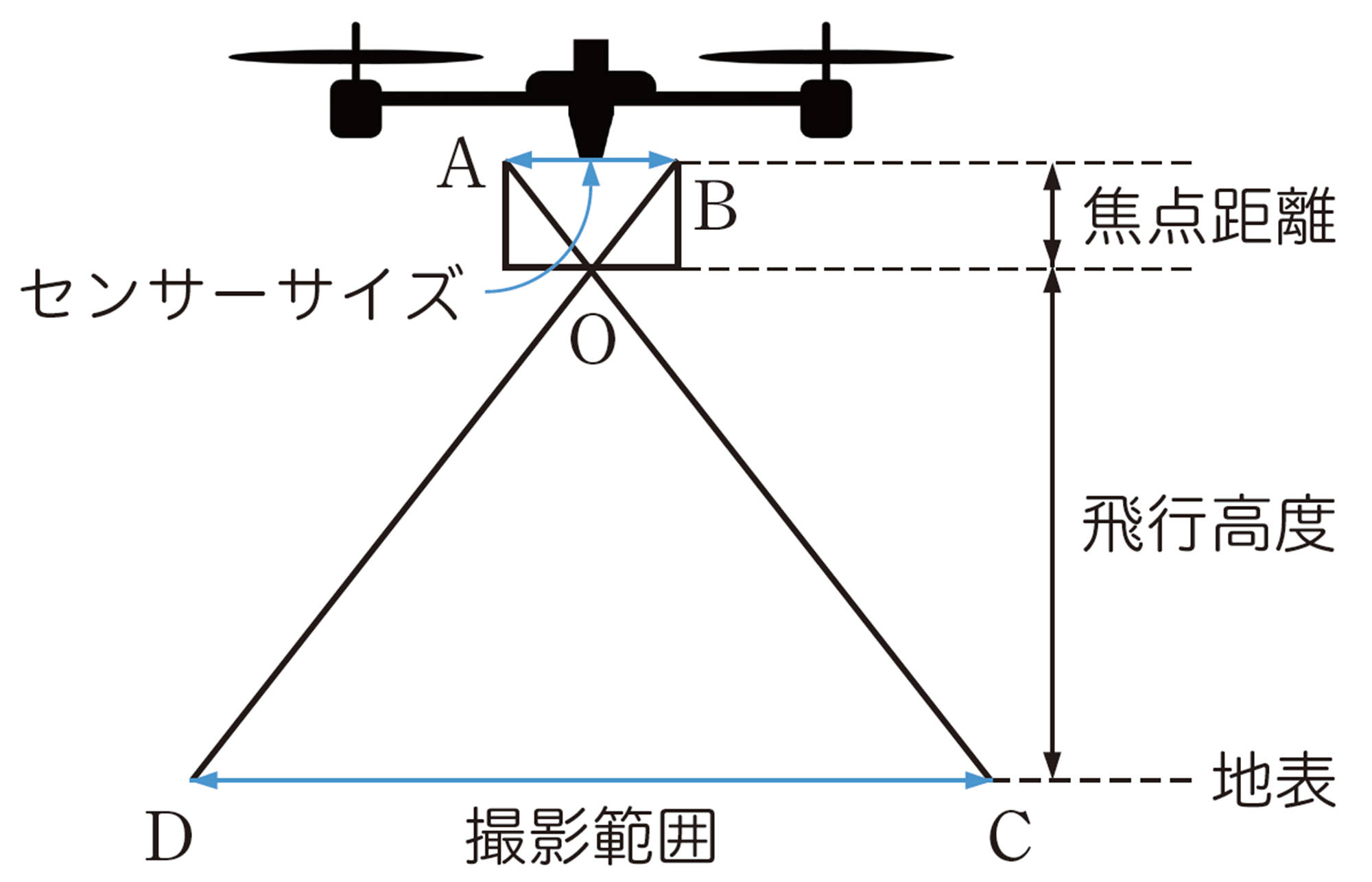
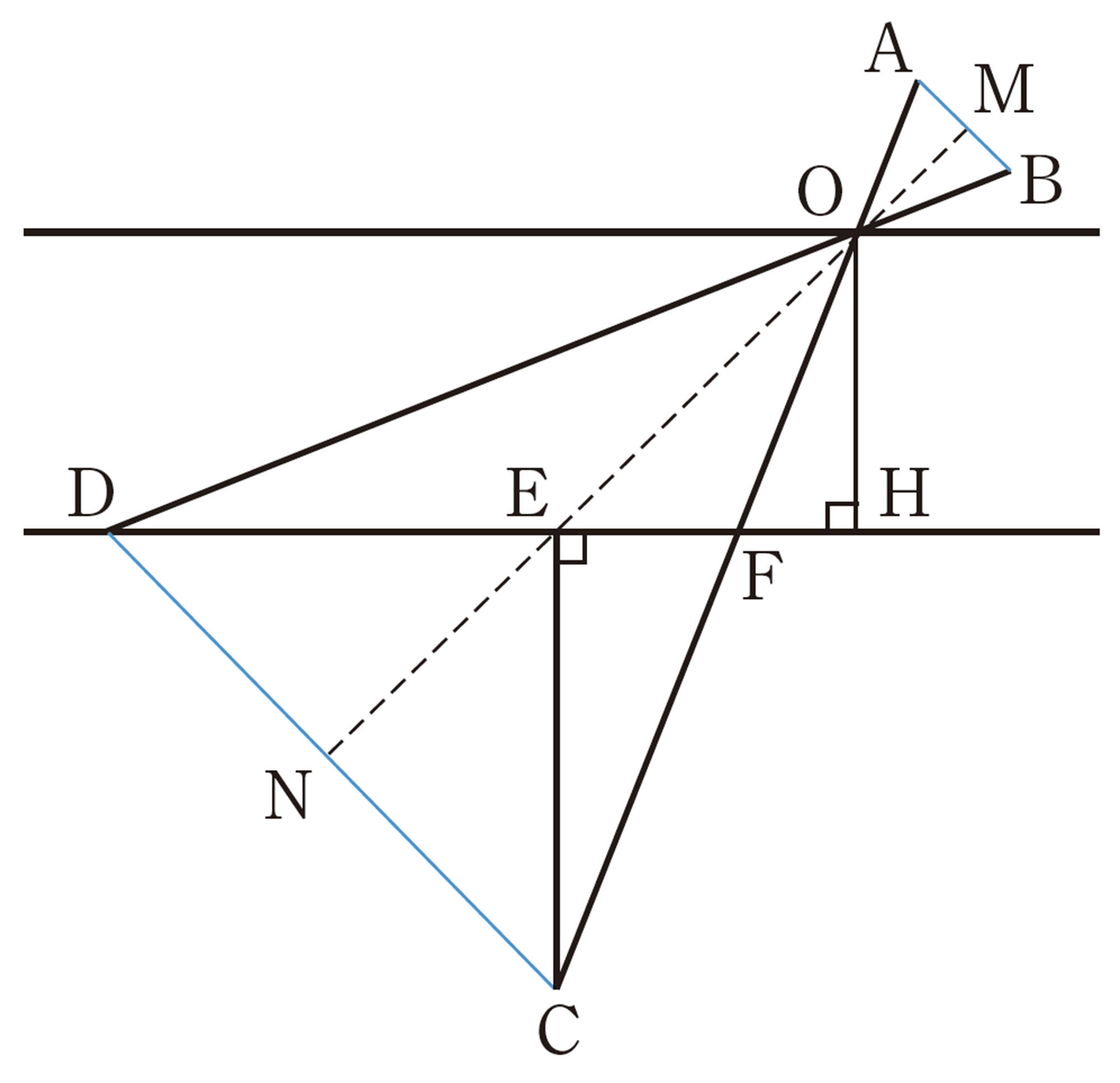
右の図のように，ドローンのカメラが地面に対して垂直方向を向いているときは，[mathjax]\(\triangle AOB\)と[mathjax]\(\triangle COD\)は相似と考えられるから，
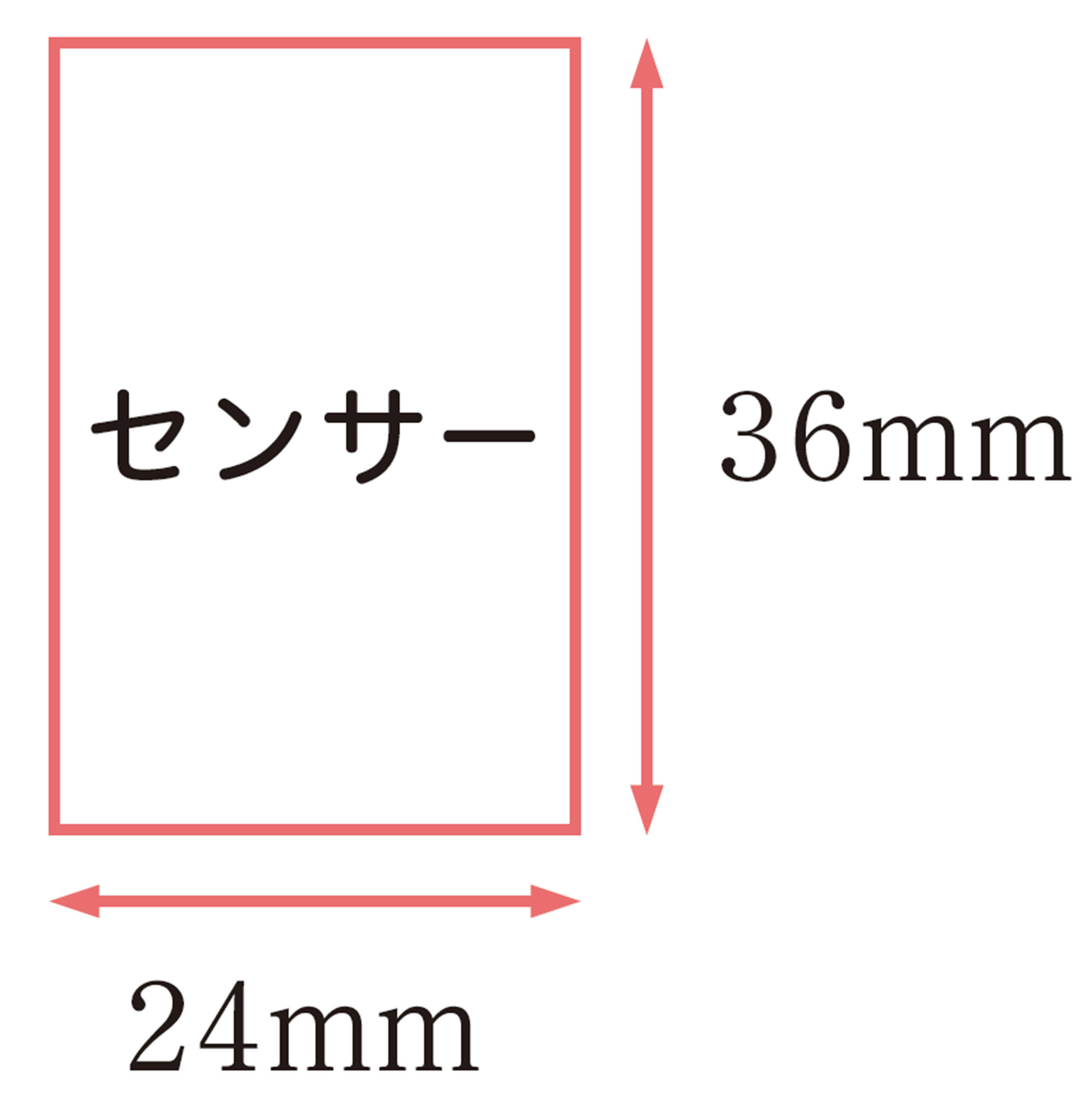
撮影範囲[mathjax]\(:\)センサーサイズ[mathjax]\(=\)飛行高度[mathjax]\(:\)焦点距離
が成り立ちます。
このことを利用すると，カメラの性能による撮影可能な範囲や必要となる高度を事前に判断することが可能になります。
① カメラのセンサーサイズが[mathjax]\(13.2\)mm，焦点距離が[mathjax]\(8.8\)mm，ドローンの飛行高度が50mのときの撮影範囲を求めてみましょう。
<3年p.275>
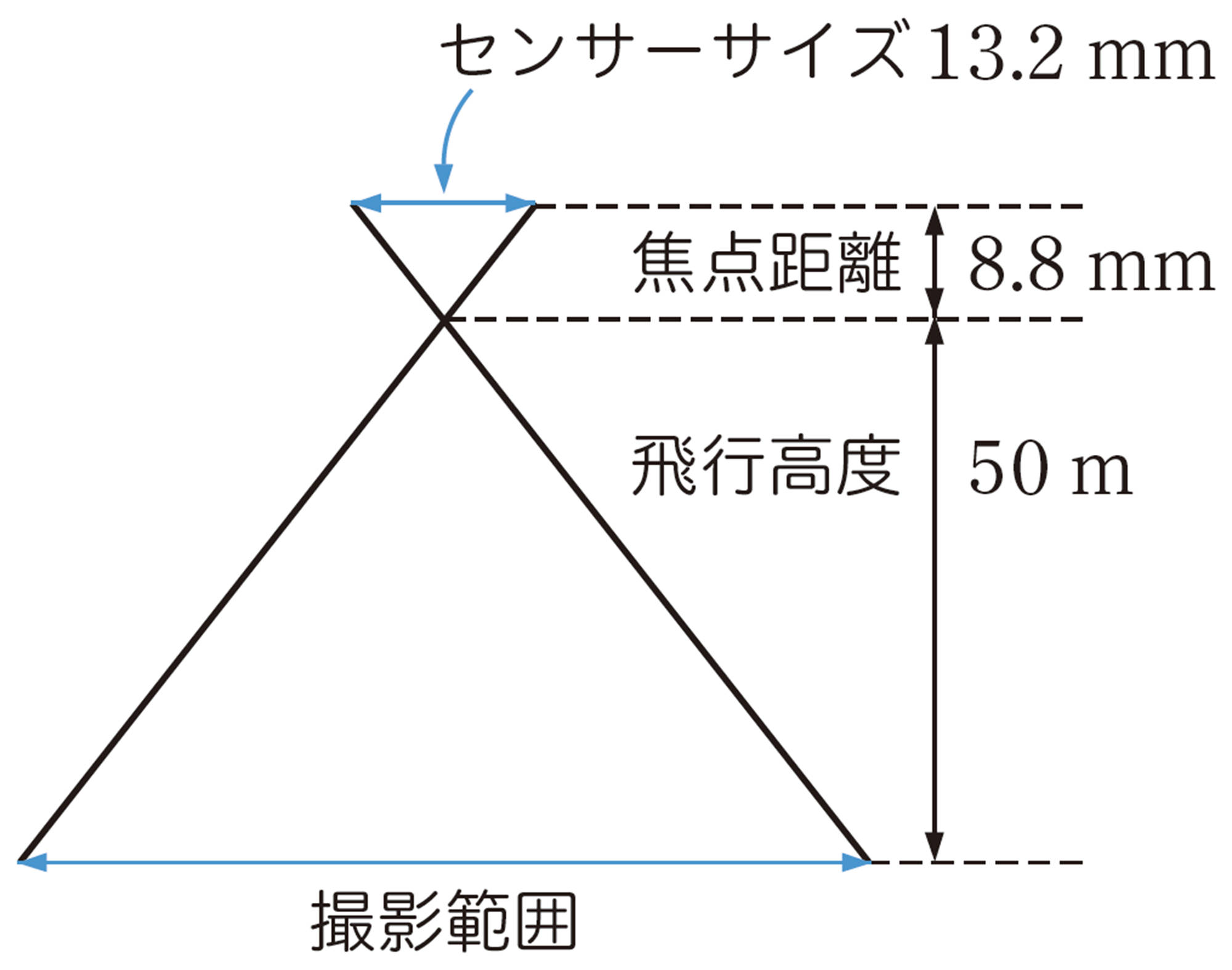
② カメラのセンサーサイズが24mm，焦点距離が24mm，撮影したい範囲が48mのとき，ドローンの飛行高度を求めてみましょう。また，焦点距離が15mmの場合の飛行高度を求めてみましょう。
③ ここまでは一方向だけを考えましたが，実際には縦方向，横方向の撮影範囲を考えます。センサーサイズが縦36mm，横24mm，焦点距離15mmのカメラを使って，縦250m，横150mの長方形の区画をドローンで撮影したいと思います。飛行高度は何m以上必要か求めてみましょう。
縦方向と横方向の両方を調べないとだめだね。
ドローンは，使えない場所や飛行高度に制限があるよ。
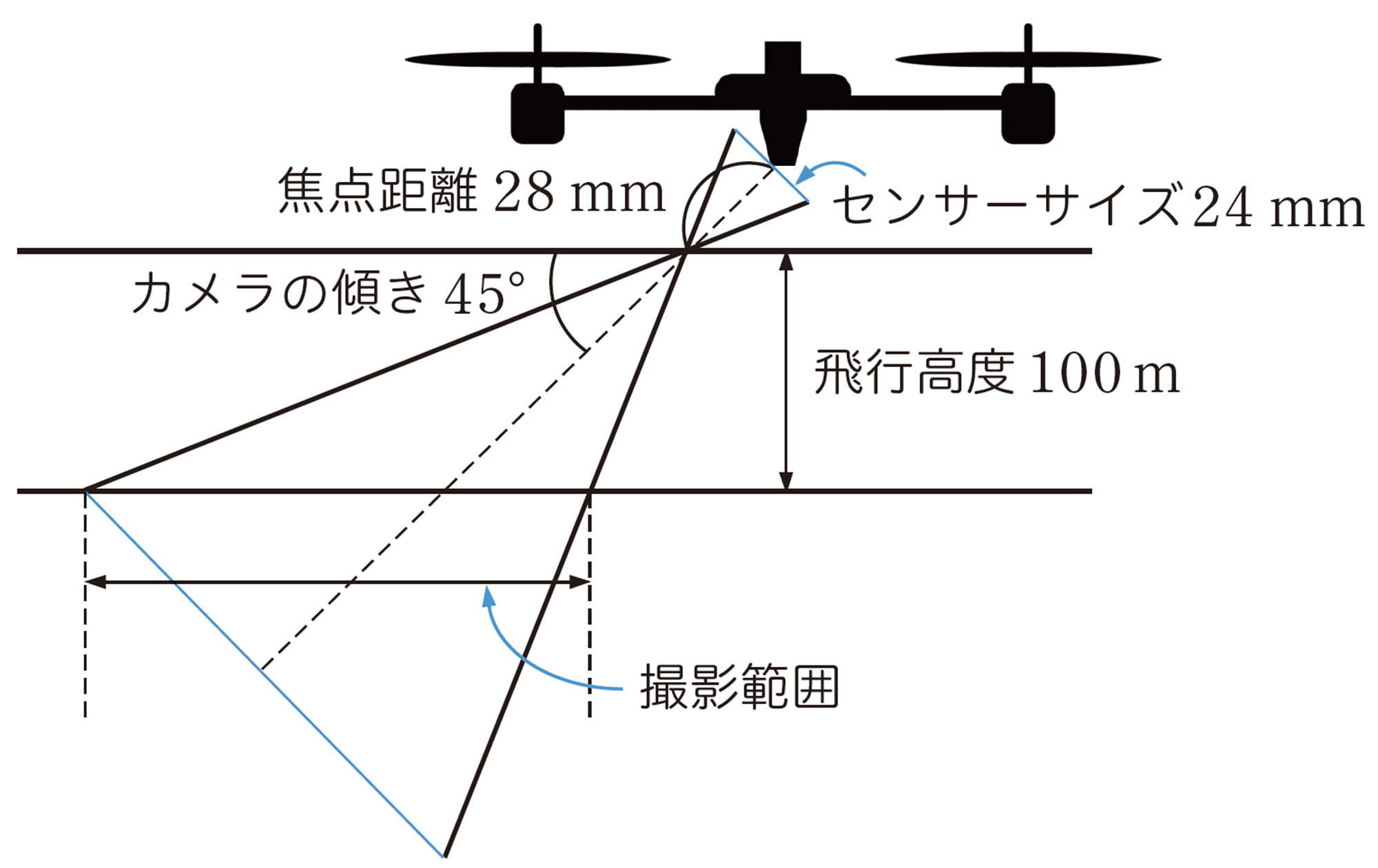
④ ドローンに搭載されているカメラは，角度を変えて撮影することができます。下の図のように，カメラのセンサーサイズが24mm，焦点距離が28mm，飛行高度が100m，カメラの傾きが45°のときの撮影範囲を考えてみましょう。
ヒント
❶縮図をかいて撮影範囲の長さを測る。
❷相似な三角形を利用して撮影範囲を計算で求める。
①
②
<3年p.276>
震源の位置を特定できる？
地震が起こったときのゆれの伝わり方を「地震波」という波として表現します。
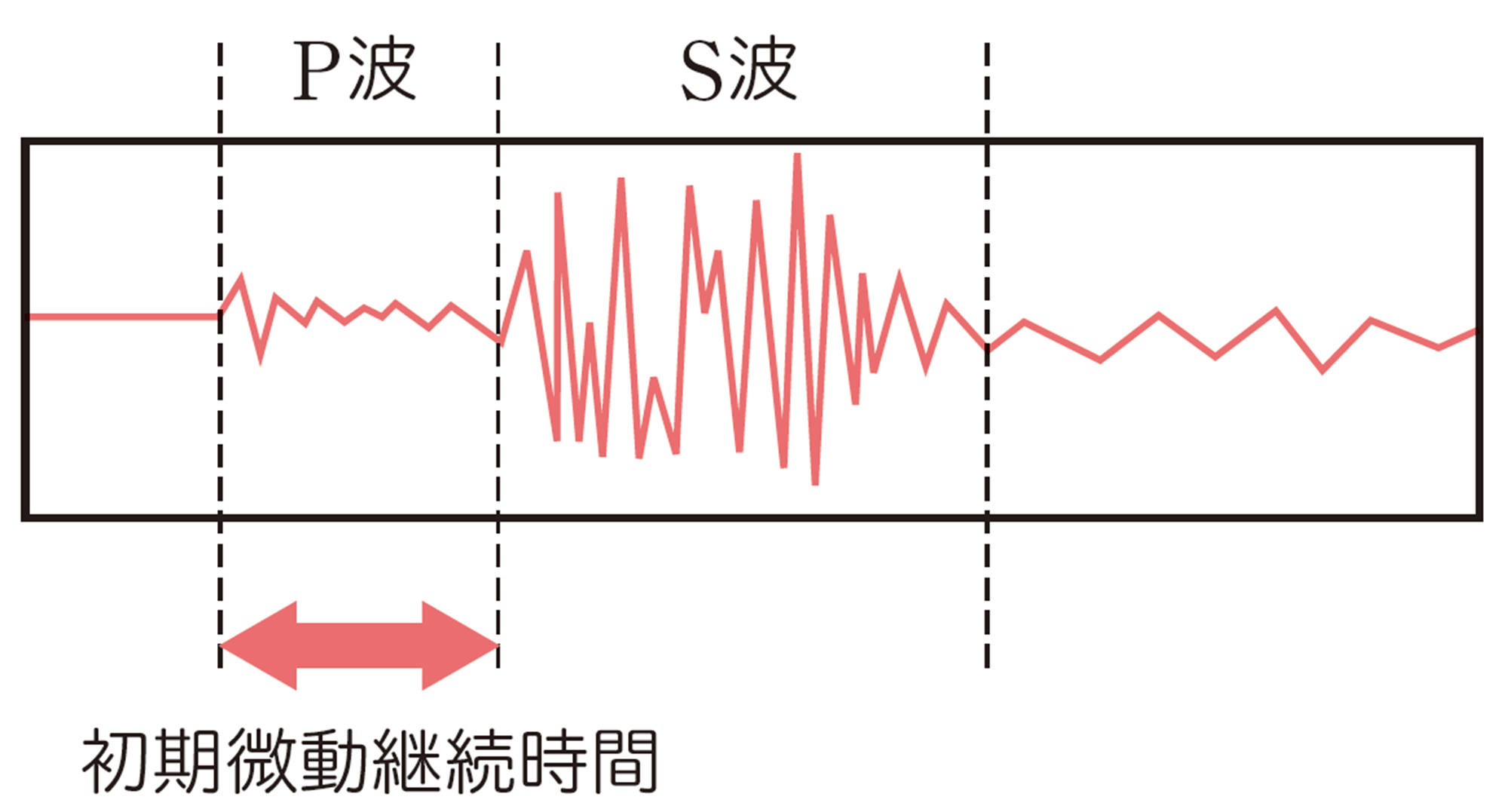
地震波には「P波」と「S波」の2種類が存在します。P波とは，地震発生時に最初に到達する地震波で，初期微動と呼ばれるゆれを起こします。P波のあとには，地震の主なゆれを起こすS波がきます。私たちが感じる強いゆれは，このS波です。P波が到達してからS波が到達するまでの初期微動が続く時間のことを初期微動継続時間と呼びます（図１）。
初期微動継続時間をt秒，震源までの距離をdkm とすると，次の関係が成り立ちます。
[mathjax]\(d=kt\)（kは6～8）
この式は，大森公式と呼ばれています。ここでは，[mathjax]\(k＝7.5\)とします。
地震があると，震源が発表されるね。
大森公式を使うと，震源が特定できるのかな。
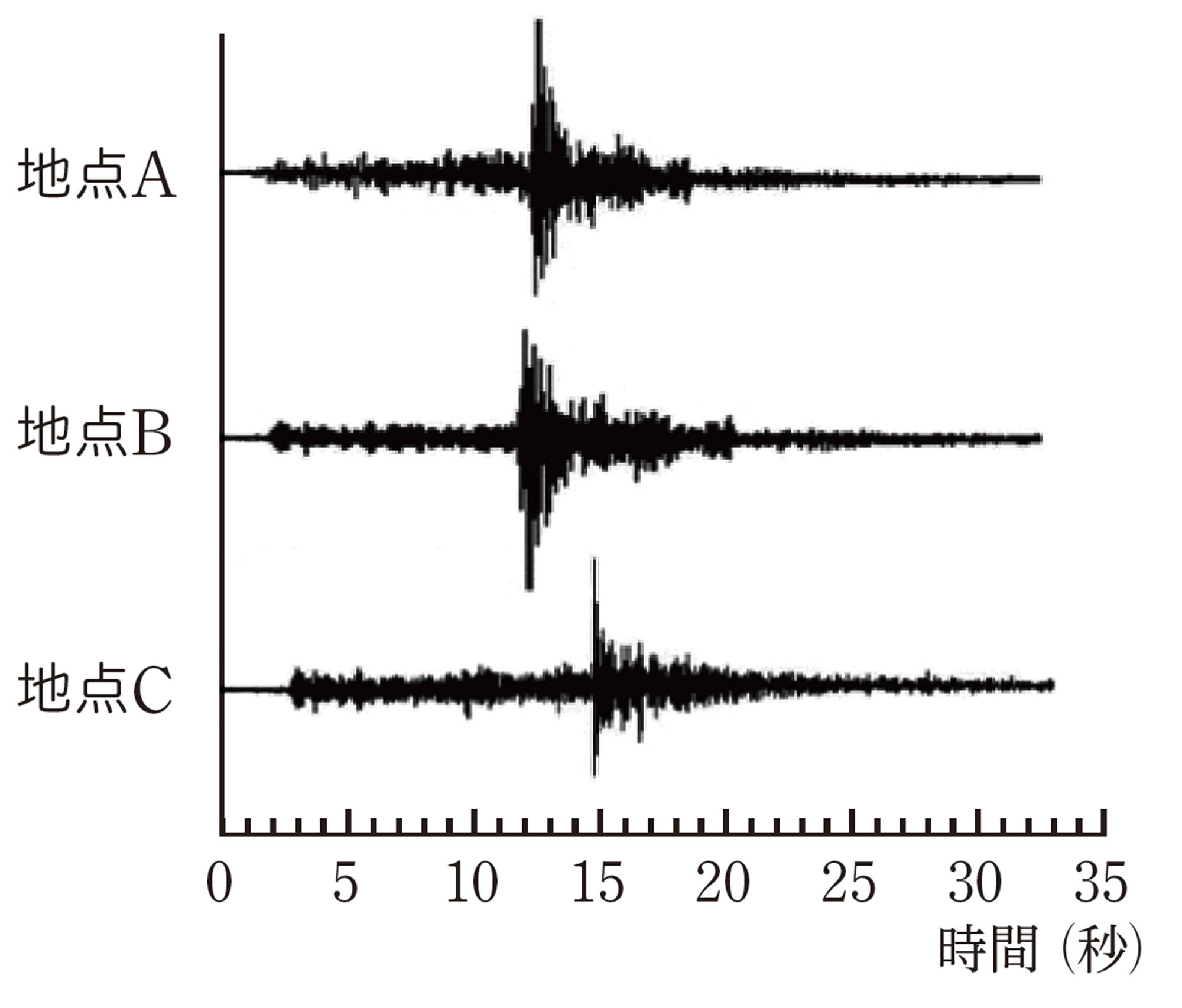
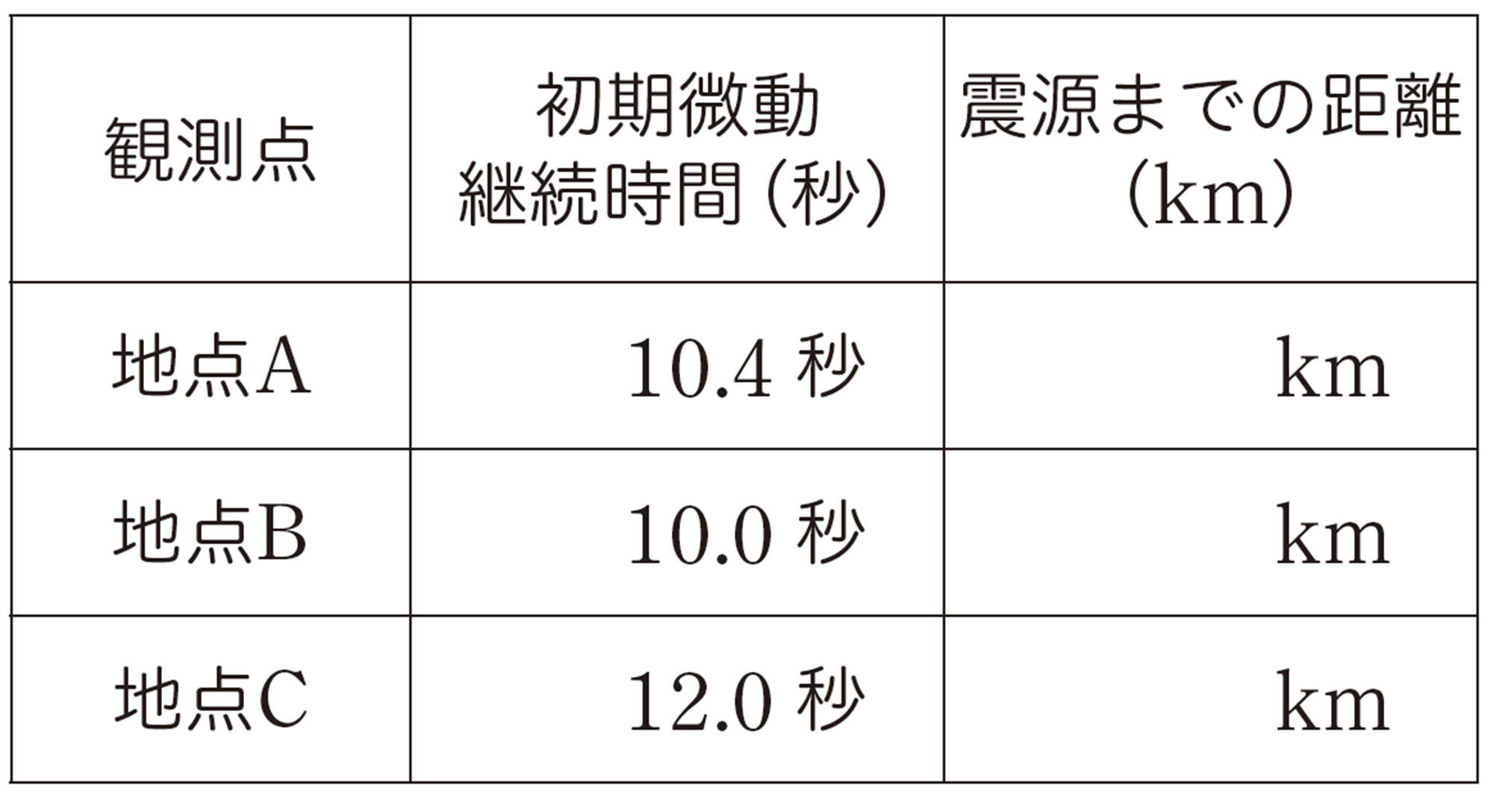
① ある地震について，図2は地点A，B，Cにおける地震計の記録です。地点 A，B，Cにおける初期微動継続時間は，右の表の通りでした。
大森公式を用いて，各地点から震源までの距離を求めましょう。
<3年p.277>
震源までの距離はわかったけど，これで震源が特定できるのかな。
ニュースを見ていると，震源の深さは何kmといっているね。深さも考えないと。
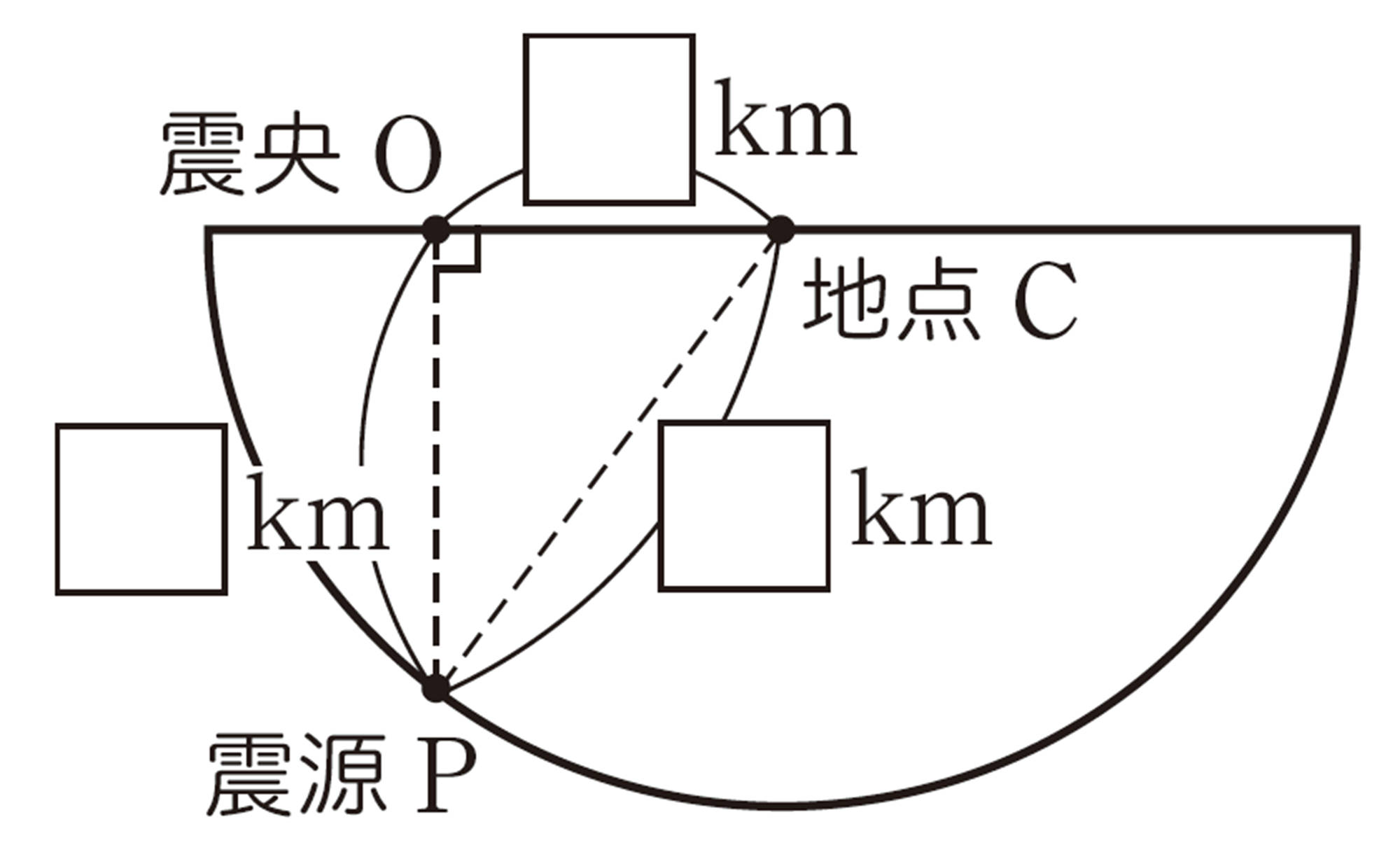
震源の真上の地表の点を「震央」と呼びます。震央の位置は，以下の作図によって特定することができます。
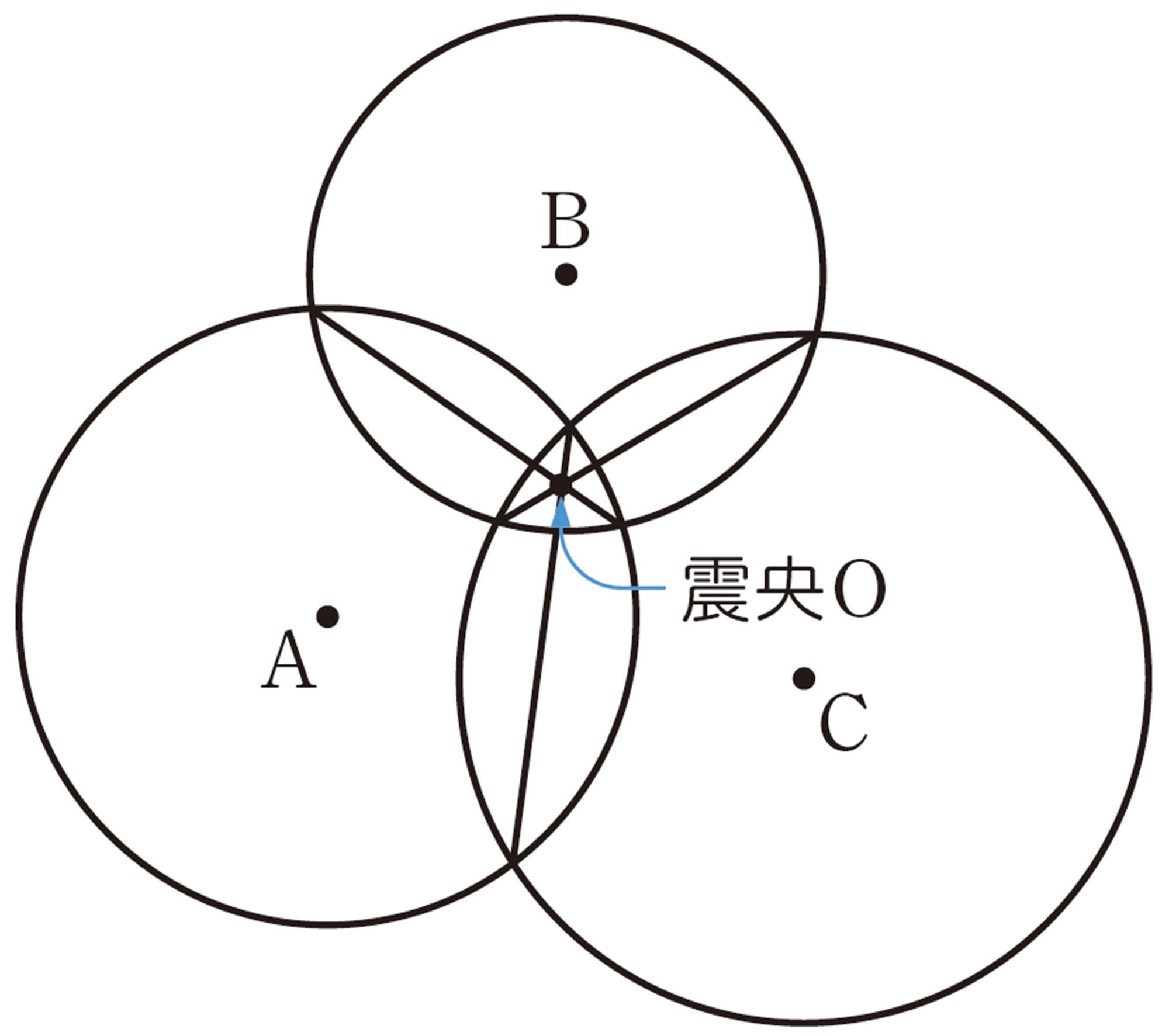
作図1：各地点を中心に，震源までの距離を半径とする円をかく。
作図2：2つの円の交点をそれぞれ結ぶと，それら3つの直線が一点で交わる。この点が震央である。
② 巻末②の地図は，地点 A，B，Cの位置を示しています。上の説明を参考にして，各地点から震源までの距離を半径とする円をかき，震央Oの位置を求めましょう。
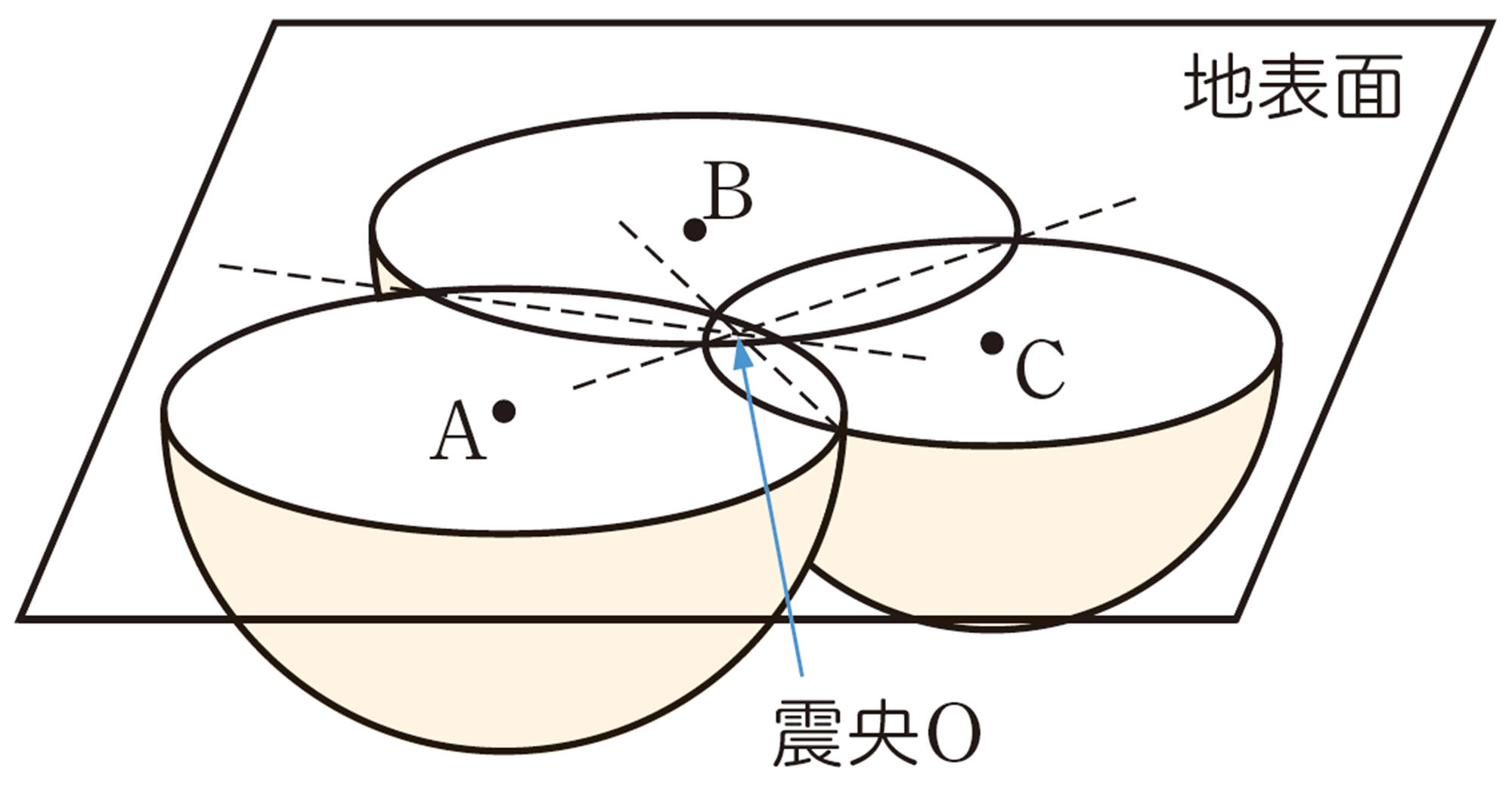
震央の位置はわかったね。
震央の真下が震源になるから，どうしたらいいかな。
③ 地図上で，震央Oと地点Cとの距離を定規で測り，震央までの実際の距離を求めましょう。また，震源Pの深さを求めましょう。
地点C，震央O，震源Pを図に表すと，右のようになるから…。
④ 地点 A，B でも，③と同じようにして，震源Pの深さを求めてみましょう。
<3年p.278>
Theme 数学の歴史の話
地球の測り方
①地球の大きさを測る
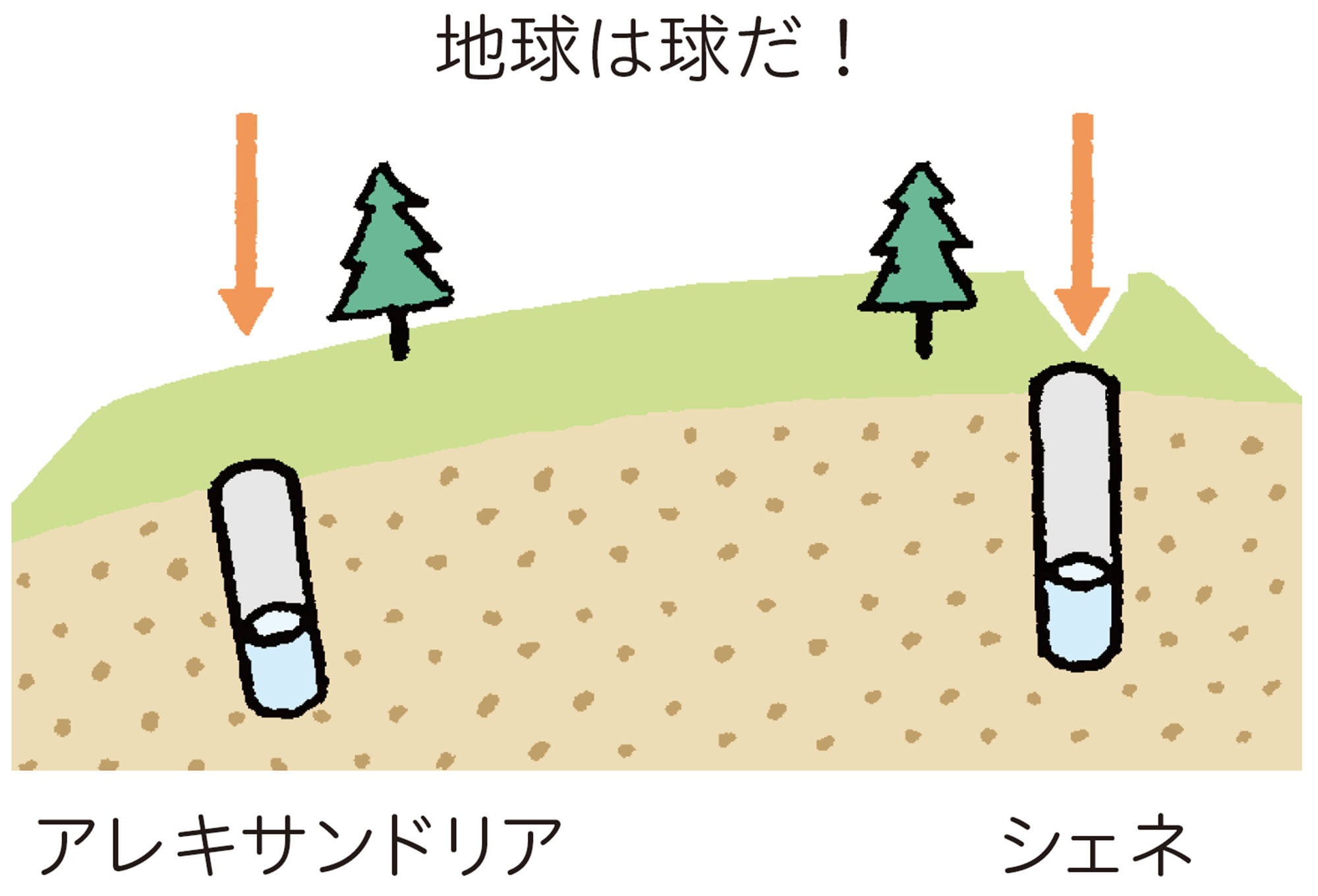
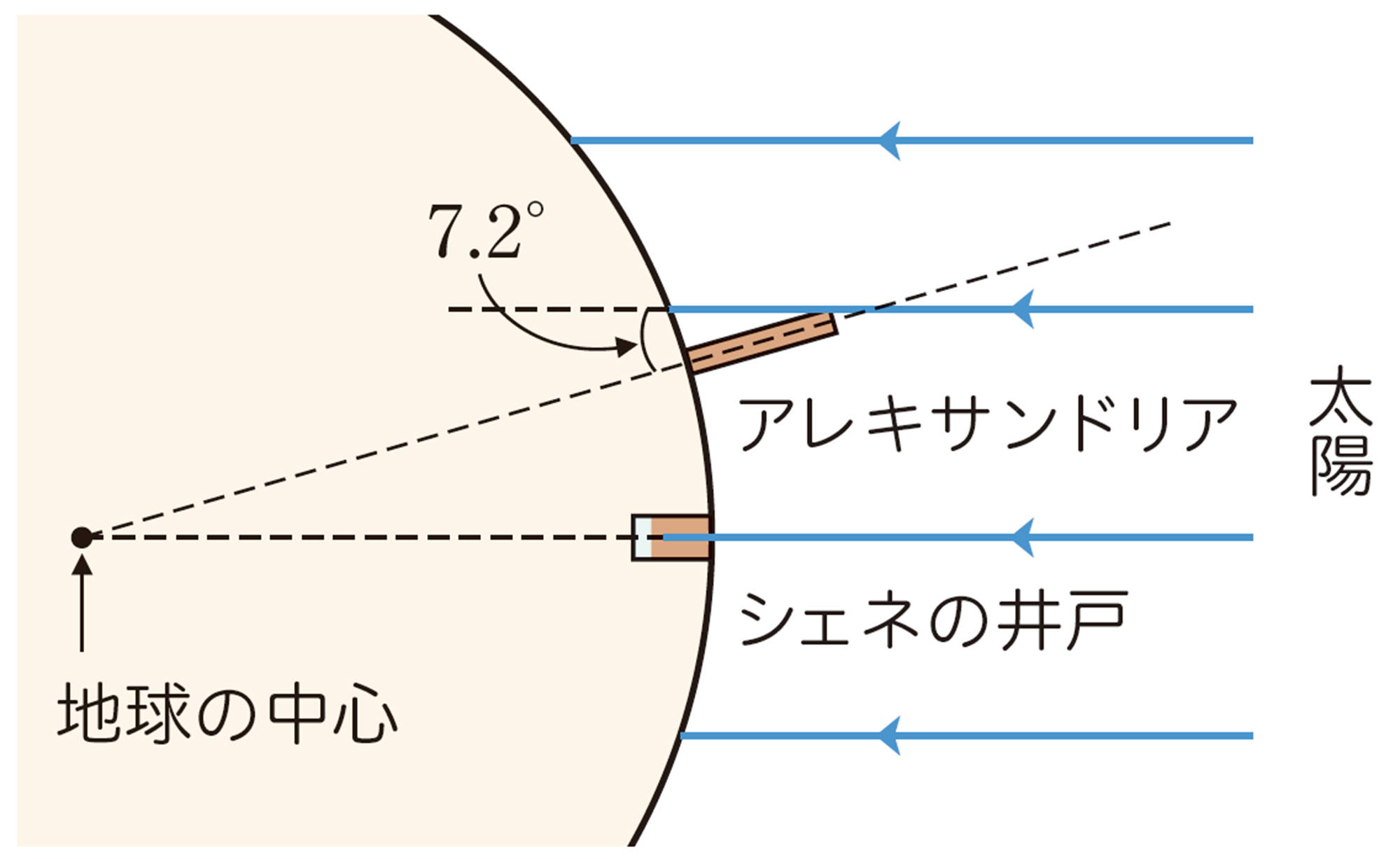
古代ギリシャの学者エラトステネスは，毎年夏至の日の正午になると，エジプト南部のシェネでは井戸の真上から太陽の光が差し込み，井戸の底まで照らしているのに対し，シェネから数百km北にあるアレキサンドリアでは，このようなことは起こらないことを知りました。このことから，地球が球形であることに気づいたといわれています。
エラトステネスは，地球が球であるならば，その大きさはどのくらいなのかを知ろうと思い，夏至の日の正午にアレキサンドリアで棒を垂直に立て，太陽の光と棒の角度が[mathjax]\(7.2^{circ}\)であることを測りました。
① アレキサンドリアで，太陽の光と棒の角度が[mathjax]\(7.2^{circ}\)であることから，シェネとアレキサンドリアの距離は地球のまわりの長さの何分の一であるといえますか。上の図をもとに，考えてみましょう。
② シェネとアレキサンドリアの距離は約785kmです。このことから，地球のまわりの長さを求めてみましょう。また，実際の地球のまわりの長さ(約40000km)と比べてみましょう。
これまで調べたように，エラトステネスの方法でも，かなり正確な値が得られます。当時は，角度や距離の測定に誤差がありましたが，エラトステネスは，かなり精度の高い計算をしたといわれています。
<3年p.279>
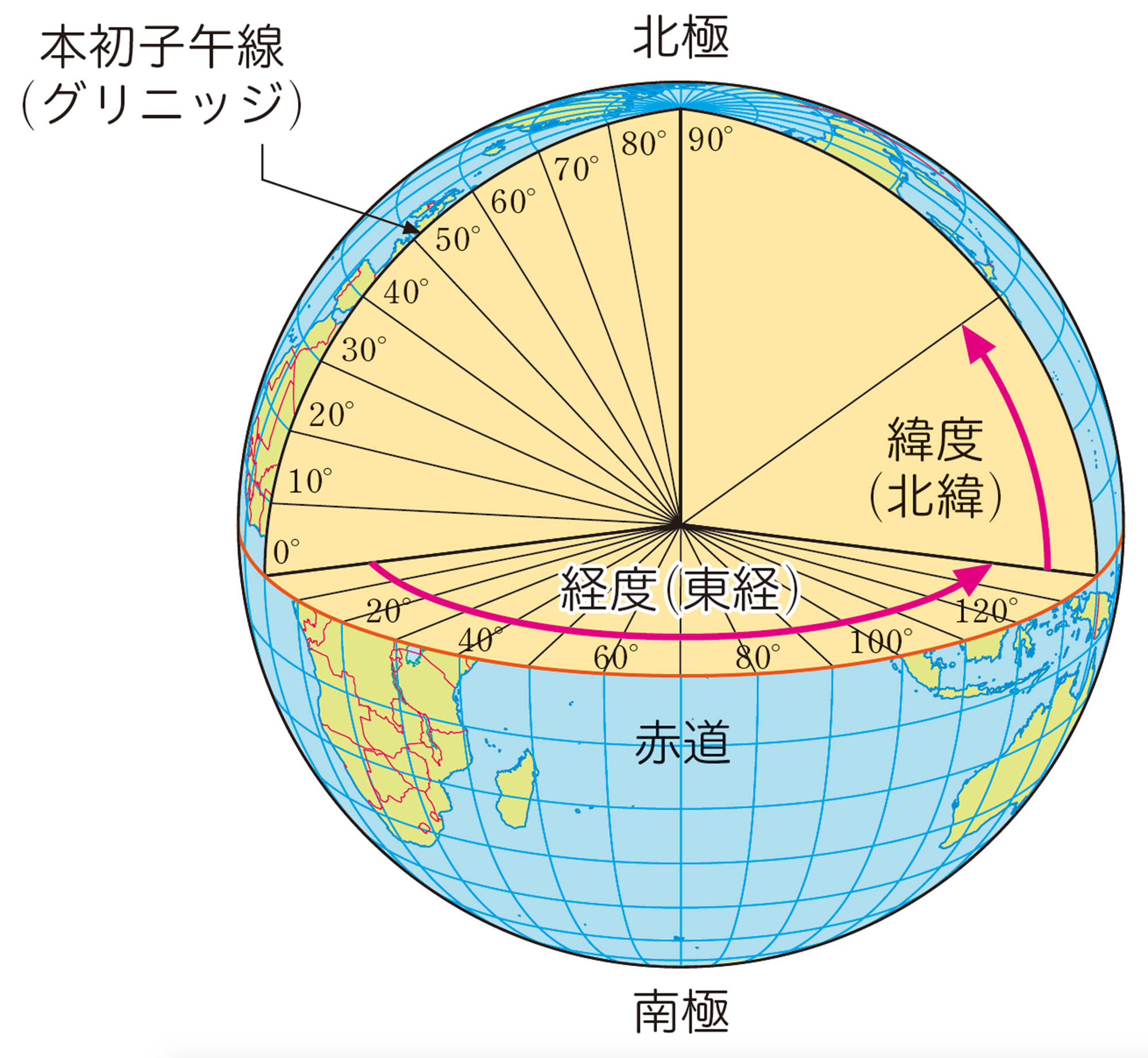
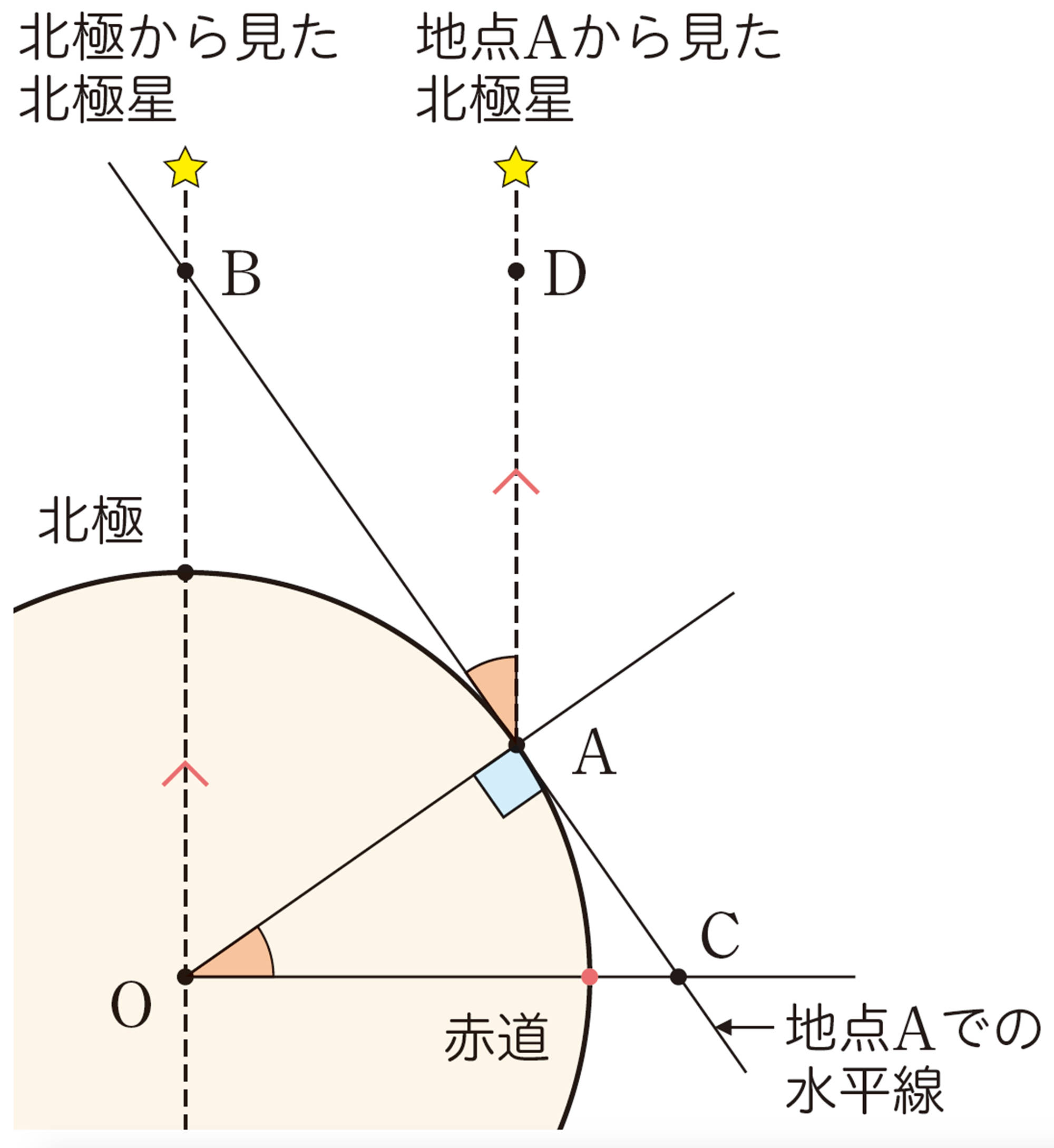
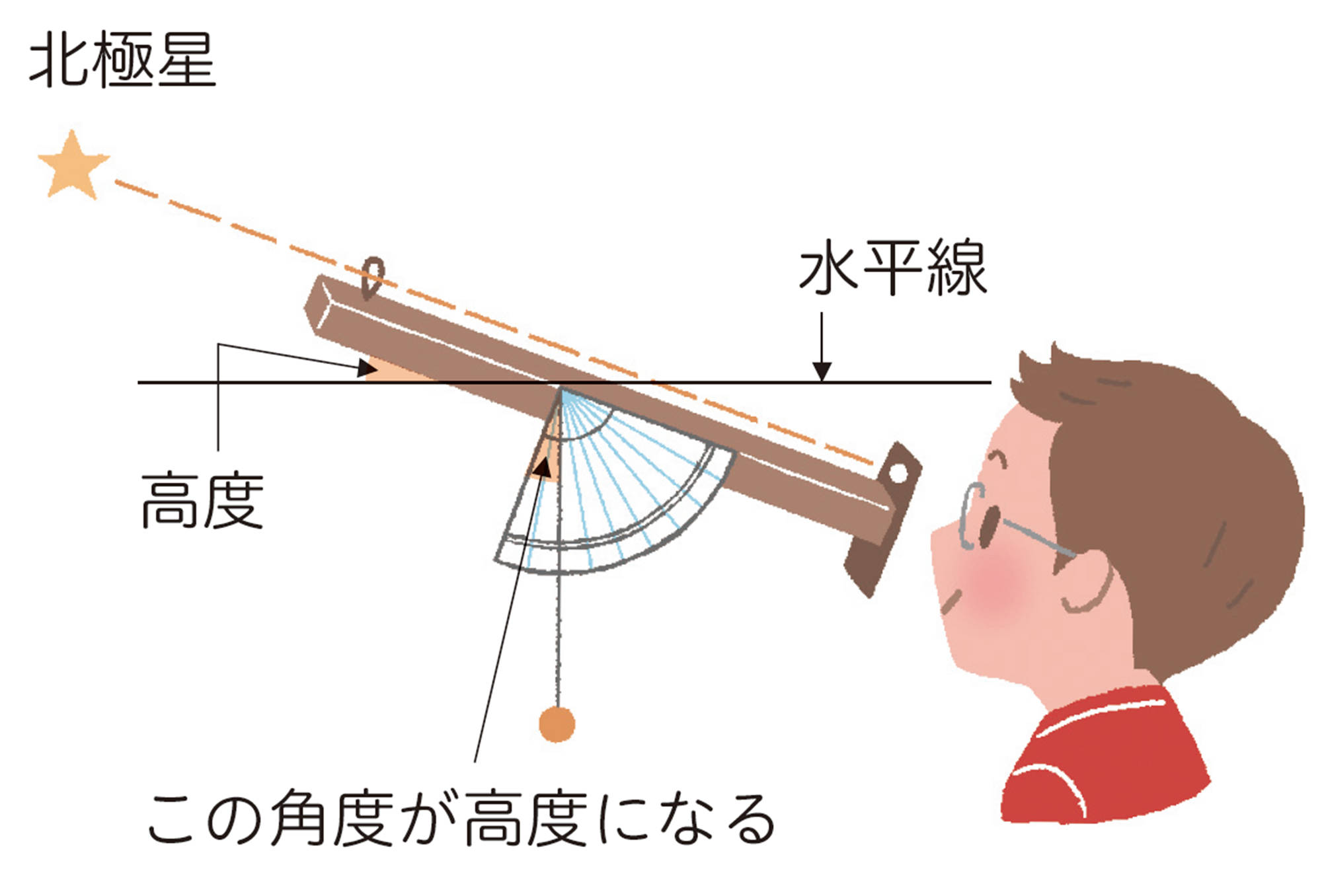
②緯度を求める
地球の緯度とは，右の図のように，赤道上を [mathjax]\(0^{\circ}\)としたときの地球の中心からの角度のことです。
自分のいる場所の緯度は，どのようにすれば求めることができるでしょうか。
右の図は，地点Aの緯度([mathjax]\(\angle AOC\))が，北極星の高度([mathjax]\(\angle DAB\))によって求められることを示した図です。
北極星は北極の頂点上に見える星で，地球からは非常に遠いので，地球上ではどこからでも同じ方向に見ることができます。右の図の直線BCは，点Aにおける円Oの接線で，地点Aでの水平線を示しています。
① 上の図で，[mathjax]\(\triangle BOC \backsim \triangle OAC\)であることを証明してみましょう。
② 1を利用して，地点Aの緯度は北極星の高度[mathjax]\(\angle DAB\)に等しいことを証明してみましょう。
③ 北極星の高度を測定し，自分の住んでいる場所の緯度を調べてみましょう。
札幌は北緯[mathjax]\(43^{circ}\)，那覇は北緯[mathjax]\(26^{circ}\)だね。
<3年p.280>
精密な日本地図を最初につくった人物
伊能忠敬(1745～1818)は，江戸時代に，実測による精密な日本地図を最初につくった人物です。
忠敬は，佐原(現在の千葉県香取市)の名主でしたが，50歳になってから，江戸に出て当時の天文学の第一人者であった高橋至時のもとで天文学や暦学を学びました。
その中で，忠敬は，正確な暦をつくるために地球の正確な大きさが問題になっていることを知りました。そこで，2地点で北極星の高度を比較することで緯度のちがいがわかり，2地点の距離を正確に測れば，地球の大きさを求めることができると考えました。その2地点は遠いほど誤差が小さくなるため，江戸と蝦夷地(北海道)を比較したいと考え，日本の正確な地図を作成するという名目で幕府から蝦夷地へ行く許可を得て，長い測量の旅が始まりました。
56歳から72歳までの足かけ17年かけて，日本全国約4万kmを踏破して測量が行われました。
最初は歩幅で距離を測定していましたが，のちに長さ一尺の鉄線を60本つないだくさりを使用するなど，誤差を減らすためにさまざまな測定法を活用しています。
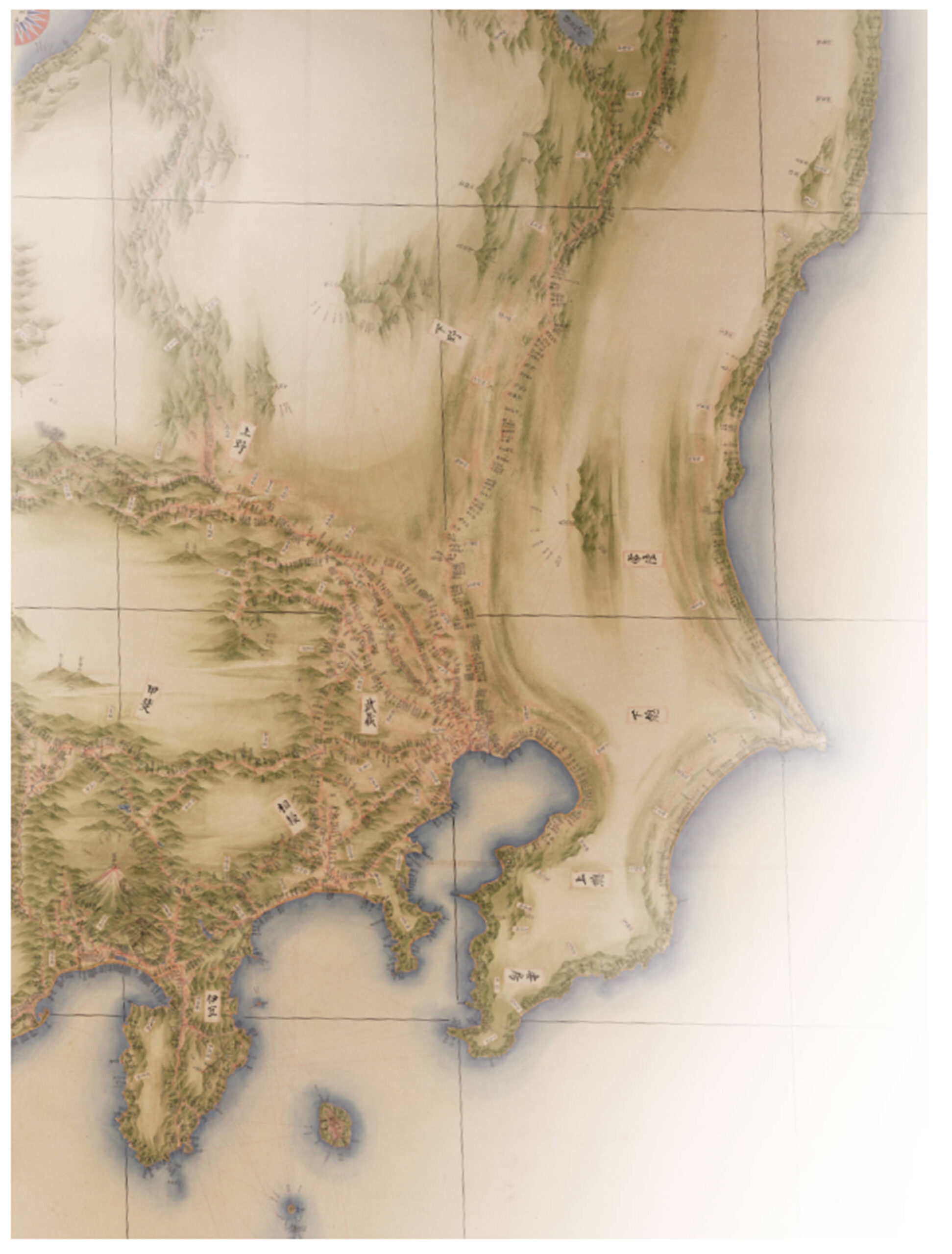
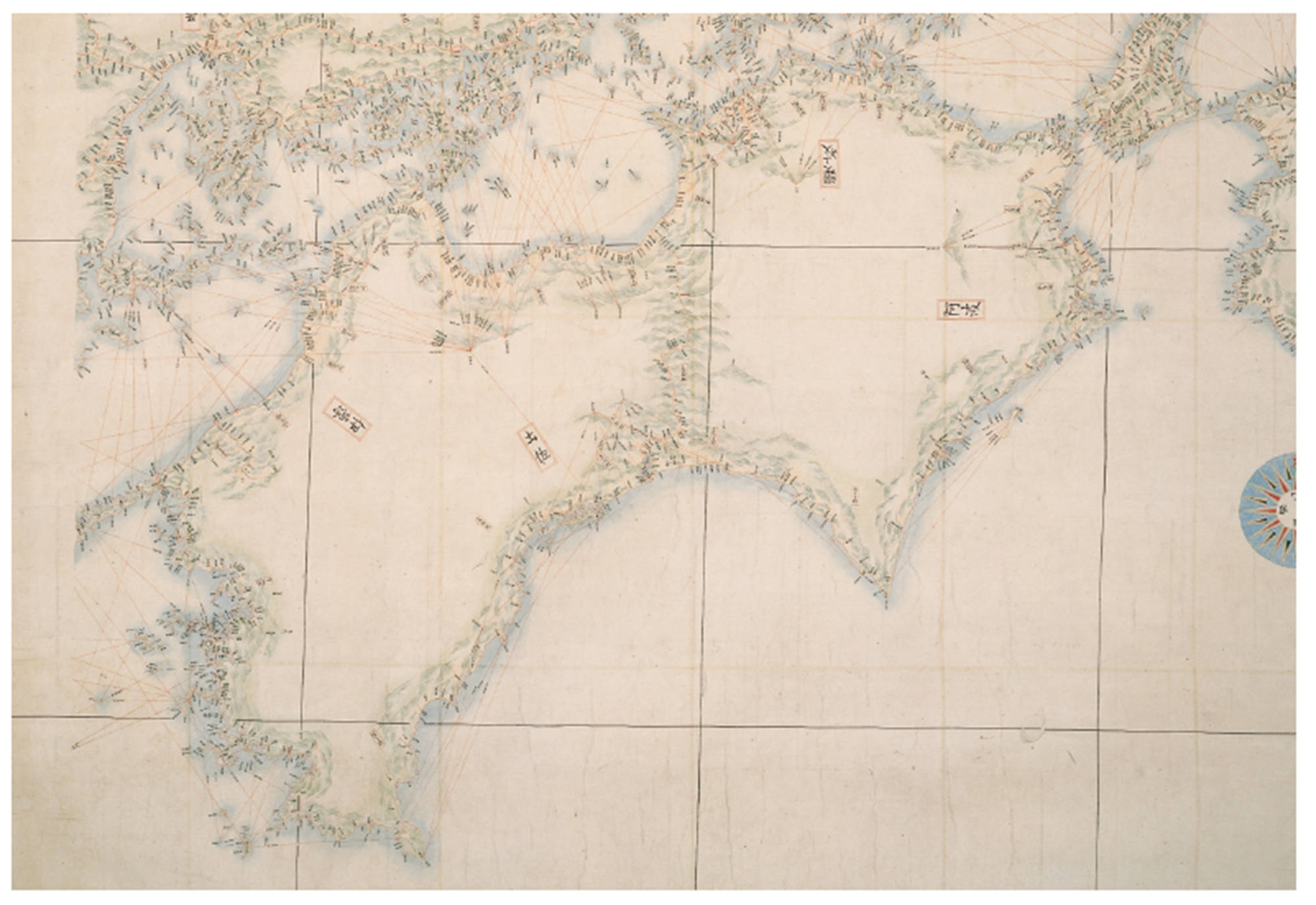
こうして集めた全国の測量データを用いて，日本地図の作成が始まりました。すべての地図，「大日本沿海輿地全図」が完成したのは，忠敬の死から3年がたった1821年のことでした。この地図は，当時の西洋の器具や技術を使っていないにもかかわらず，正確に描かれています。
<3年p.281>
三平方の定理の証明
三平方の定理の証明は，217ページで学んだ以外にもあります。
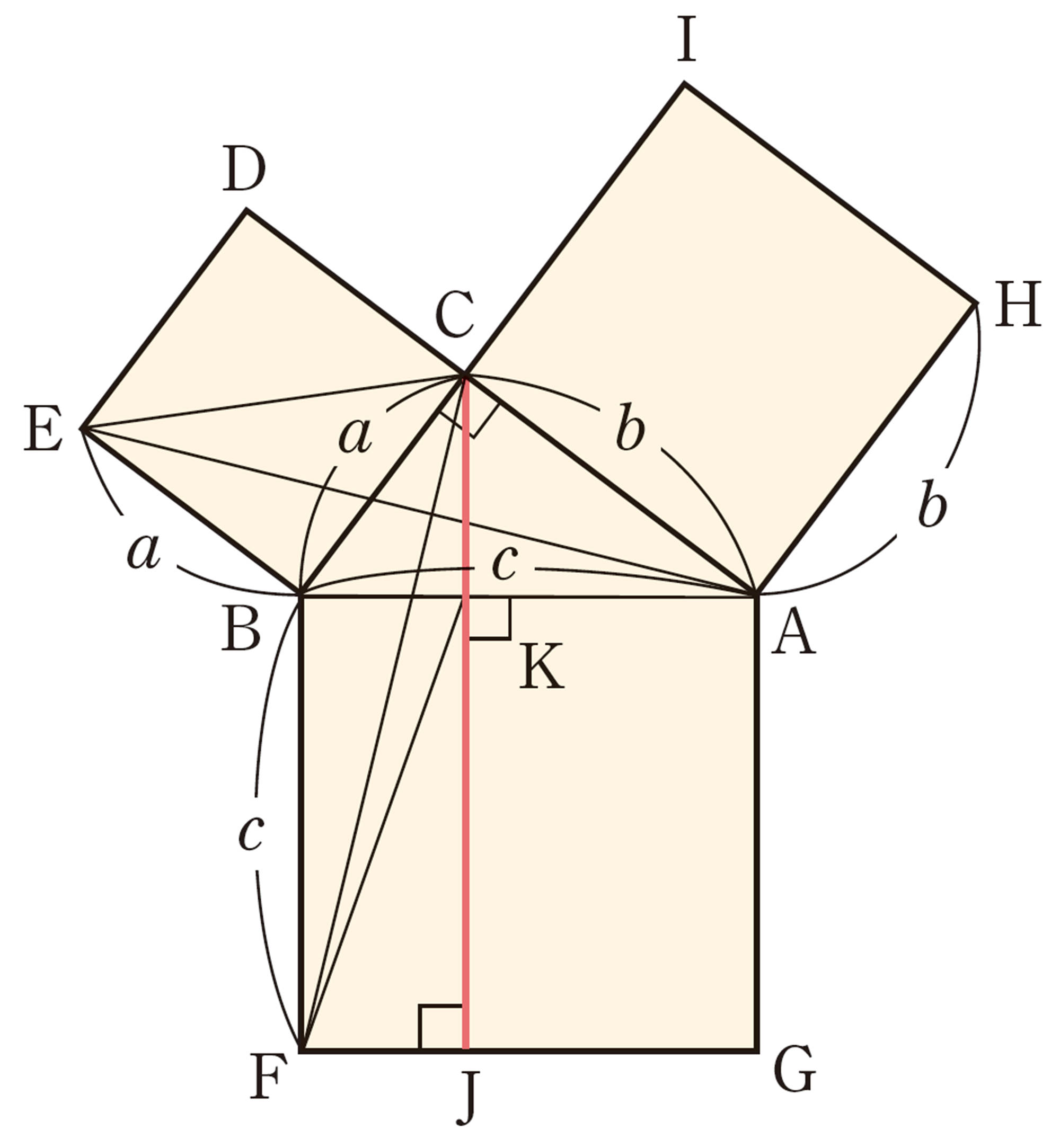
①ユークリッドによる証明
右の図は，古代ギリシャの数学者ユークリッド(紀元前3世紀頃)が 『原論』 の中で証明に使った図です。どのように証明したのか考えてみましょう。
ヒント
① [mathjax]\(\triangle EBC = \triangle EBA\)を示す。
② [mathjax]\(\triangle EBA = \triangle CBF\)を示す。
③ [mathjax]\(\triangle CBF = \triangle KBF\)を示す。
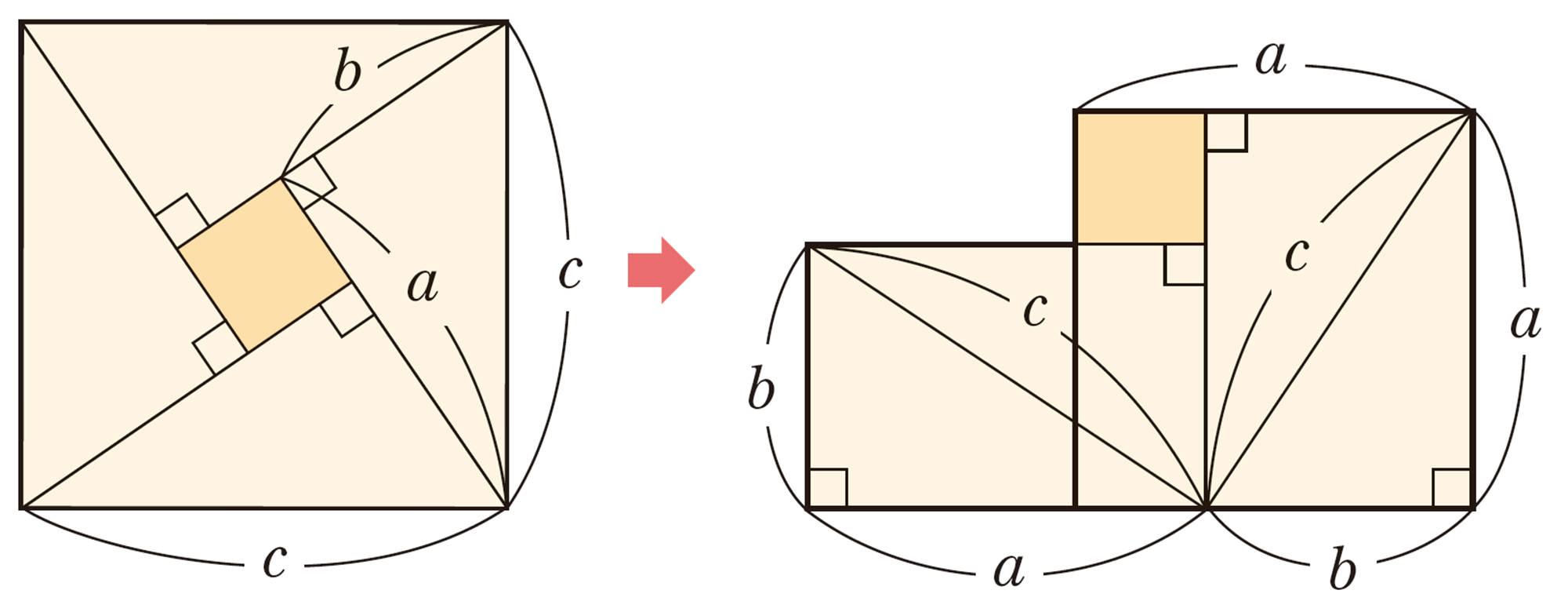
②バースカラによる証明
次の図は，インドの数学者バースカラ(1114～1185)が示した図です。どのように証明したのか考えてみましょう。
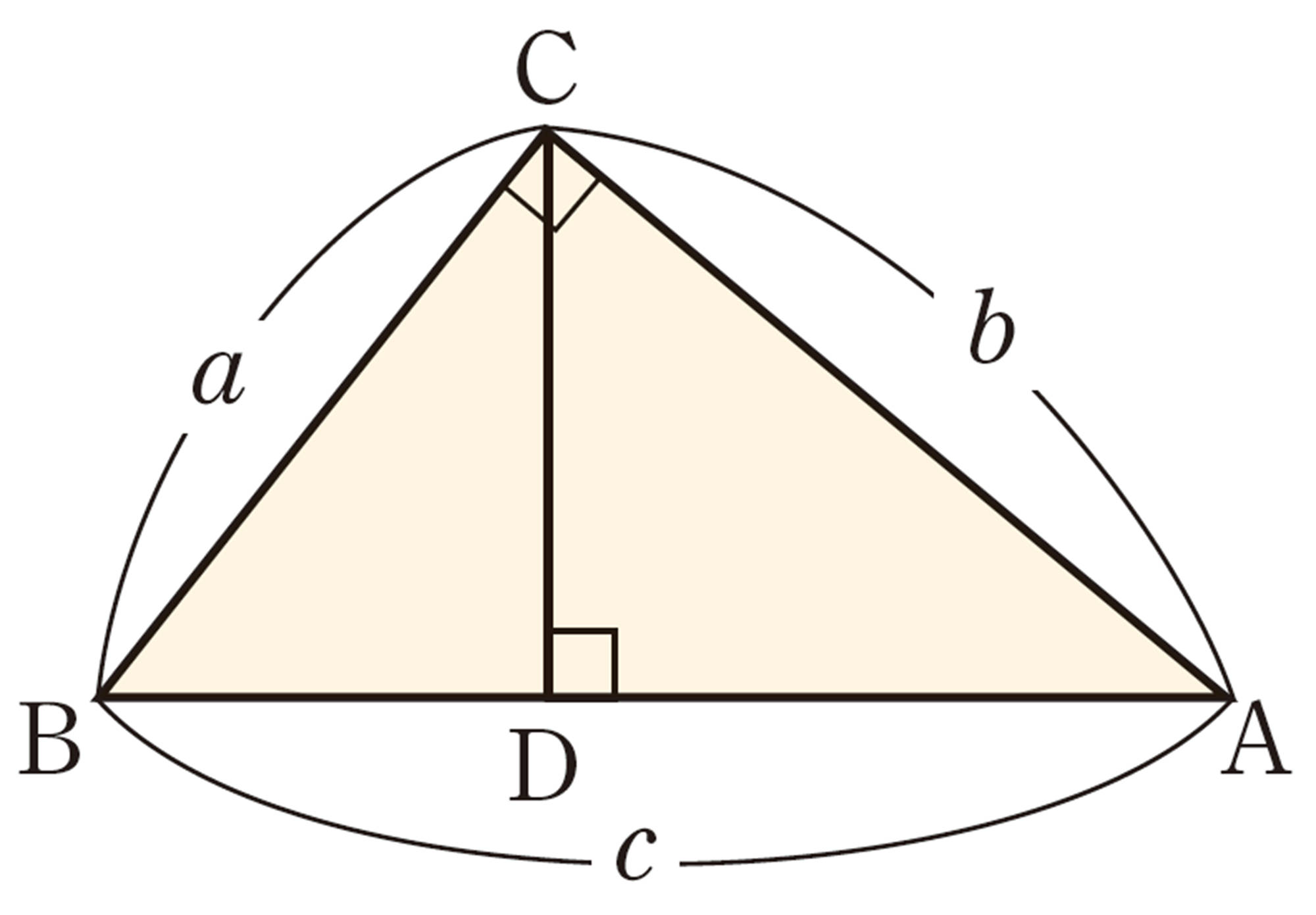
③アインシュタインによる証明
右の図は，ドイツの物理学者アルベルト・アインシュタイン(1879～1955)が証明に使った図です。どのように証明したのか考えてみましょう。
ヒント
① [mathjax]\(\triangle ABC \backsim \triangle CBD\)を利用して，BDの長さを，a，cを使って表す。
② [mathjax]\(\triangle ABC \backsim \triangle ACD\)を利用して，ADの長さを，b，cを使って表す。
ほかにも，さまざまな証明があります。インターネットを利用して，どんな証明の方法があるか調べてみましょう。
<3年p.282>
Theme 高校へのかけ橋 発展 高等学校
中学校での数学の学習はこれで終了です。しかし，まだ解決できていない疑問はありませんでしたか。それらの疑問はこれからさらに学習を進めていくと，少しずつ解決していくことができます。ここでは，高校で学習するいくつかの例を紹介します。ここで紹介した例以外でも，疑問に思ったことを調べてみましょう。
[mathjax]\(2x²+7x+3\)は因数分解できるかな？
「次の多項式の因数分解はできるかな。」
⑴ [mathjax]\(2x²+4x+2\)
⑵ [mathjax]\(4x²+12x+9\)
⑶ [mathjax]\(2x²+7x+3\)
「⑴は，2をくくり出せばできるし，⑵は，公式を利用してできるけど，⑶は共通な因数もないし，公式も使えないよ…。」
悠さんは，[mathjax]\(2x²+7x+3\)が因数分解できると仮定して，
[mathjax]\((ax+b)(cx+d)=acx²+(ad+bc)x+bd\)
の式をつくり，次のように考えました。
から，[mathjax]\(ac=2\)，[mathjax]\(ad+bc=7\)，[mathjax]\(bd=3\) になるa，b，c，dを見つければよい。
[mathjax]\(ac=2\)から，[mathjax]\(a=2\)，[mathjax]\(c=1\)と考えると，b，dについて，次の4通りが考えられる。
この中で[mathjax]\(ad+bc=7\)になるものは，[mathjax]\(b=1\)，[mathjax]\(d=3\)のときだけであるから，
[mathjax]\(2x²+7x+3=(2x+1)(x+3)\)
悠さんが求めた式を展開して，もとの式になるかどうか確かめてみましょう。
高校では，右のように，[mathjax]\(acx²+(ad+bc)x+bd\)の係数だけを抜き出して因数分解をすることがあります。この方法を「たすき掛け」による因数分解といいます。
<3年p.283>
関数[mathjax]\(y=x²+1\)のグラフはかけるかな？
「1次関数[mathjax]\(y=x+1\)のグラフは，比例[mathjax]\(y=x\)のグラフをもとにして考えたね。」
「それなら，[mathjax]\(y=x²\)のグラフをもとにして，[mathjax]\(y=x²+1\)のグラフもかけるのかな。」
咲良さんは，関数[mathjax]\(y=x²+1\) のグラフについて，次のように考えました。
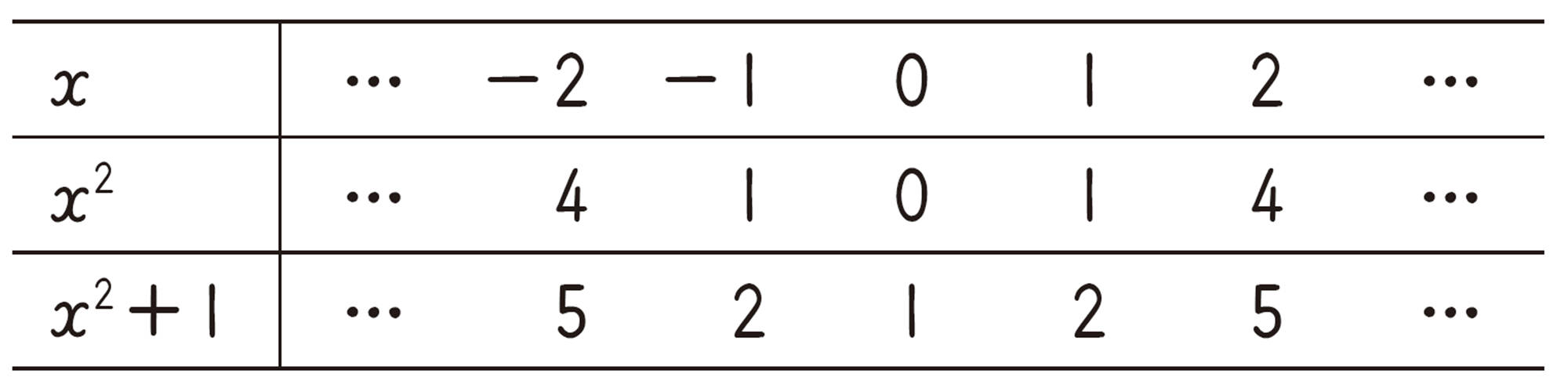
[mathjax]\(y=x²+1\)のxとx²，[mathjax]\(x²+1\)の関係を表に表すと，次のようになる。
表から，[mathjax]\(x²+1\)の値は，x²の値よりつねに1大きい。
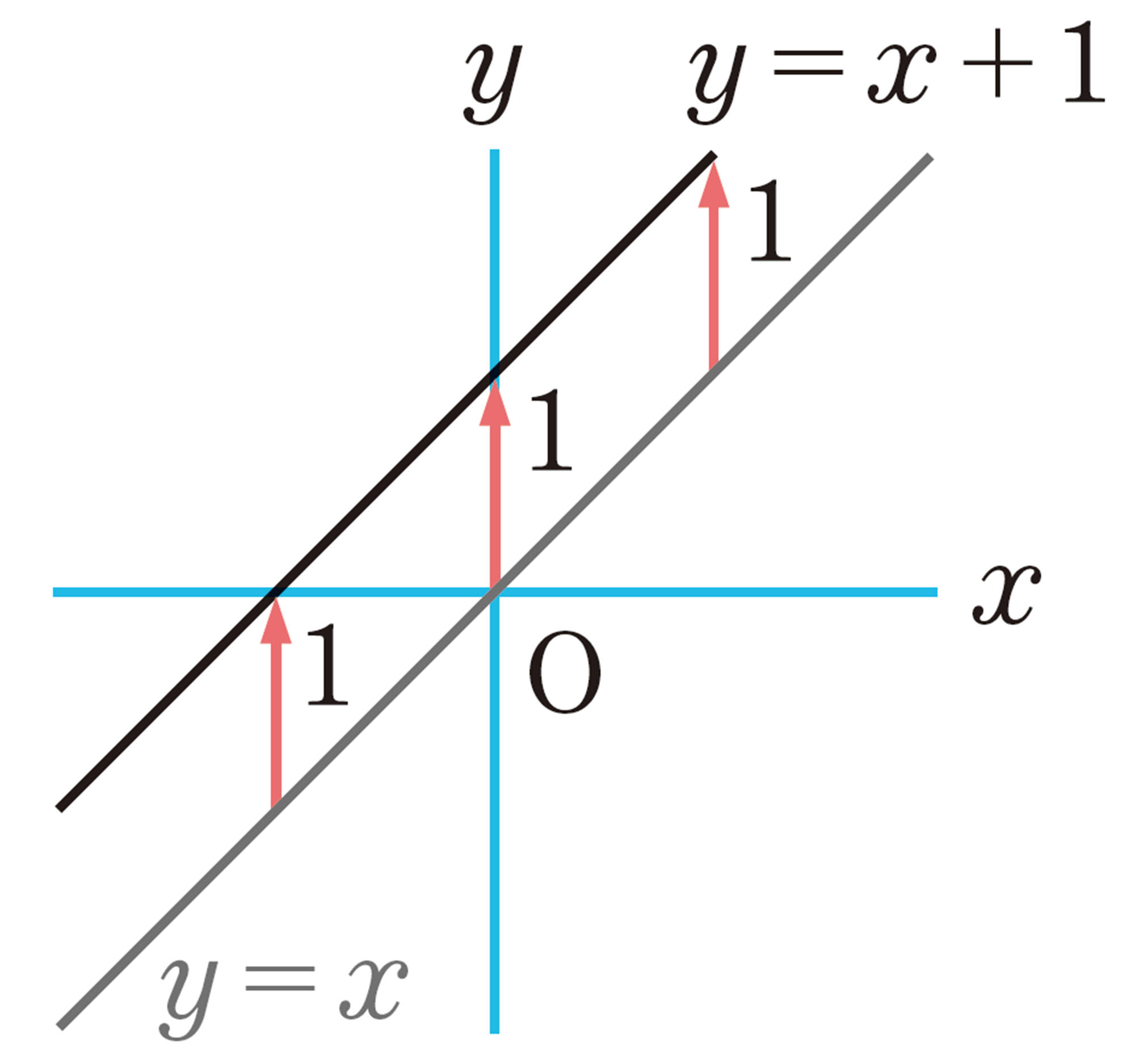
したがって，[mathjax]\(y=x²+1\)のグラフは，[mathjax]\(y=x²\)のグラフをy軸方向に1だけ平行移動した放物線になる。
咲良さんの考えを使って，関数[mathjax]\(y=x²+q\)のqにいろいろな数を入れて，グラフをかいてみましょう。
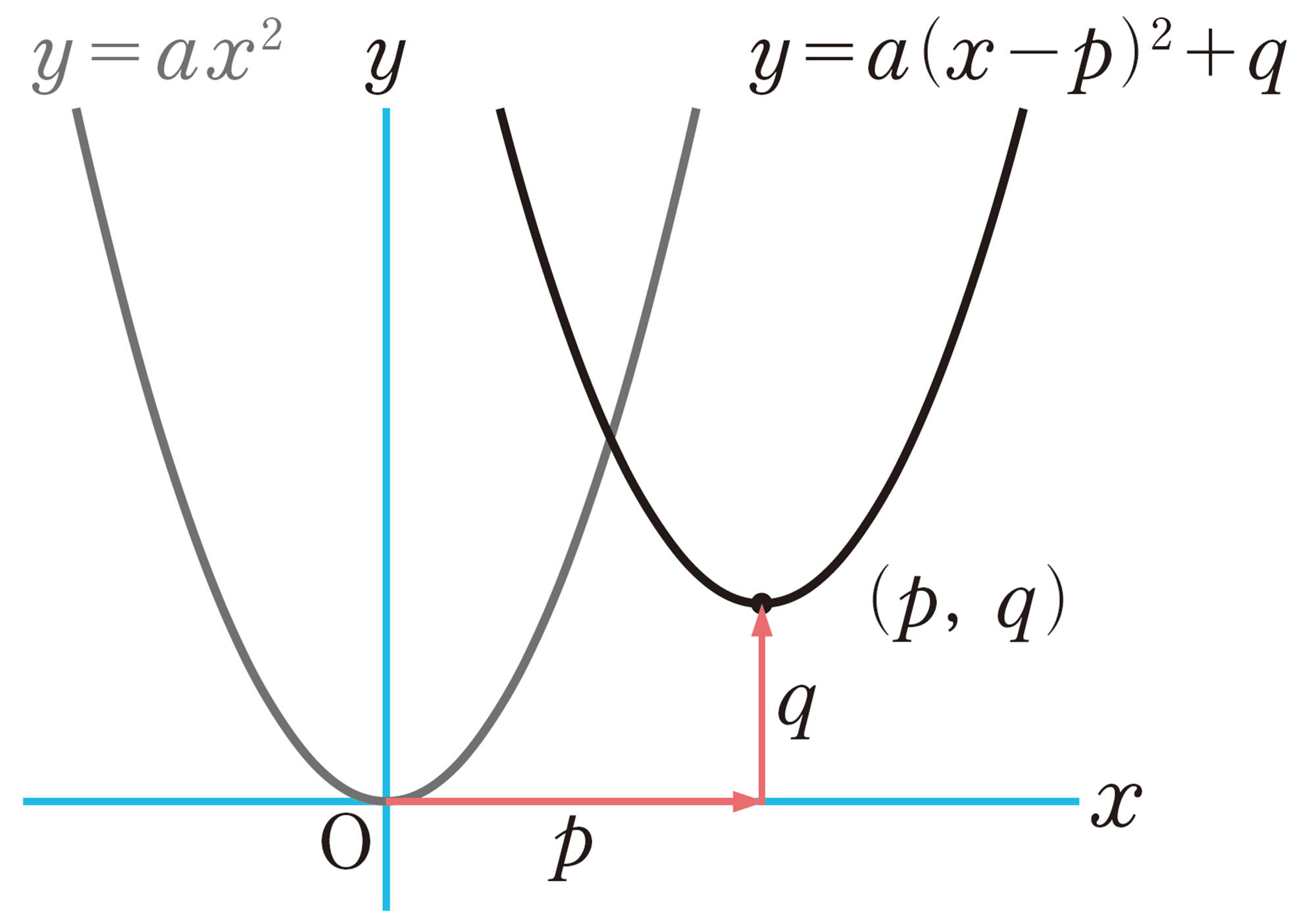
関数[mathjax]\(y=(x-1)²\)のグラフについて，どんなグラフになるか考えてみましょう。
yがxの関数で，[mathjax]\(y=ax²+bx+c(a \neq 0)\)の形で表されるとき，yはxの2次関数であるといいます。関数[mathjax]\(y=ax²\)や，上で考えた[mathjax]\(y=x²+1\)，[mathjax]\(y=(x-1)²\)も2次関数です。
以上のことから，2次関数[mathjax]\(y＝a(x-p)²+q\)のグラフは，右のような[mathjax]\(y=ax²\)のグラフをx軸方向にp，y軸方向にqだけ平行移動したグラフになります。
したがって，2次関数[mathjax]\(y=ax²+bx+c\)を[mathjax]\(y=a(x-p)²+q\)の形に直せば，グラフの頂点の位置がわかり，グラフをかくことができます。
