<3年p.240>
ふりかえり
データの傾向を調べるのに，箱ひげ図は大まかな傾向は比べやすいけど，ヒストグラムの方がくわしいことがわかったね。
【度数分布表】
階級と度数でデータの分布を示している表を度数分布表という。
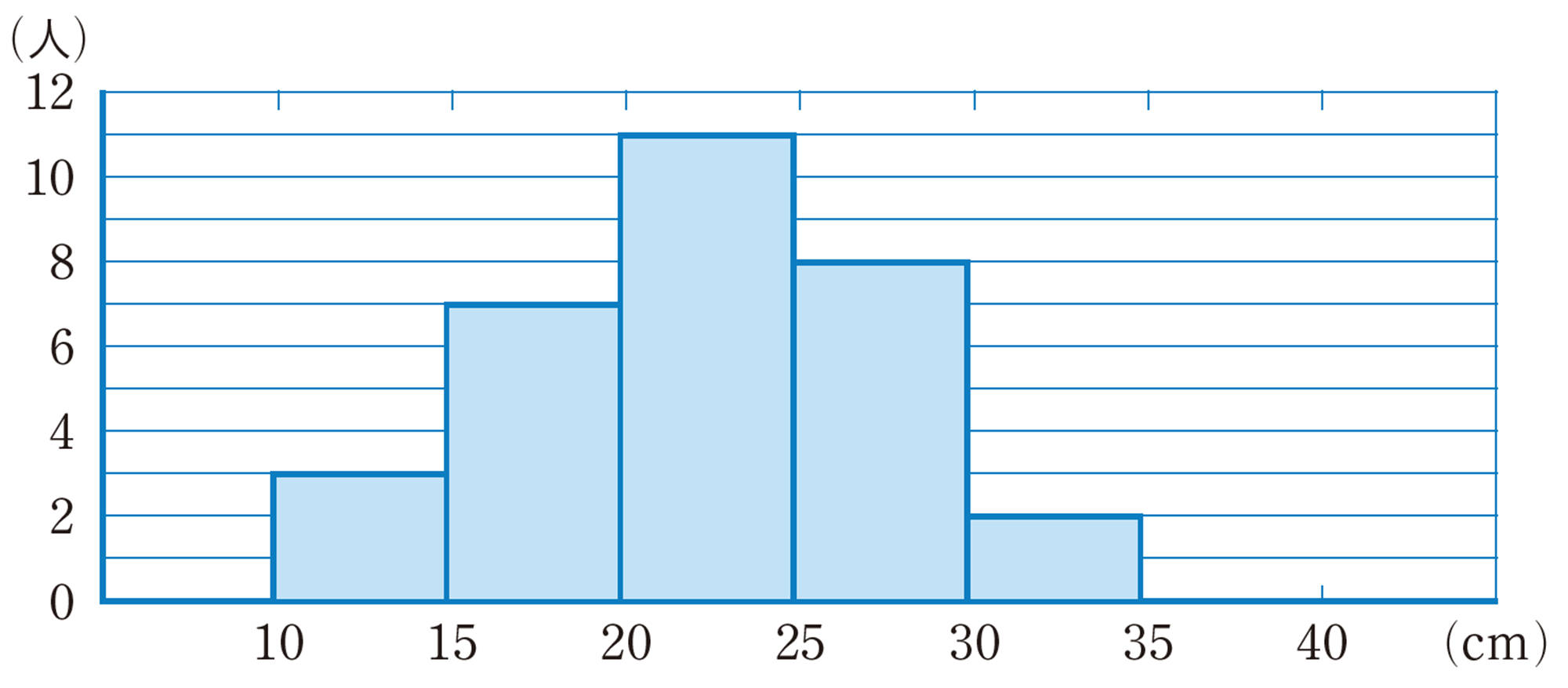
ルーラーキャッチのデータ
【ヒストグラム】
度数分布表を用いて，階級の幅を横，度数を縦とする長方形を順に並べてかいたグラフをヒストグラムという。
【四分位数】
あるデータを小さい順に並べたとき，そのデータを4等分したときの3つの区切りの値を小さい方から順に，第1四分位数，第2四分位数（中央値），第3四分位数といい，これらをまとめて四分位数という。
【四分位範囲】
第3四分位数と第1四分位数の差を，四分位範囲という。
【箱ひげ図】
箱ひげ図は，次の図のように，最小値，第1四分位数，第2四分位数，第3四分位数，最大値を使って表されている。
また，ひげの端から端までの長さは範囲，箱の幅は四分位範囲を表している。
調べたいことによって，まとめ方が変わってくるね。
身のまわりのデータを整理して傾向を調べると，いろいろなことの判断材料になるね。
<3年p.241>
８章 Chapter ８ 空間図形
1節 標本調査
中学生が家で勉強する時間は，1日平均90分です。
平均90分だって。
ぼくは，そんなにやっていないな。
どうやって，調べたのかな。
ぼくは聞かれていないから，中学生全員を調べたわけではなさそうだね。
？ 実際の調査はどんな調べ方をしたのかな？
<3年p.242>
1節 標本調査
この調査は有効か？
体育委員会では，中学校最後の思い出に，球技大会を行うことにしました。
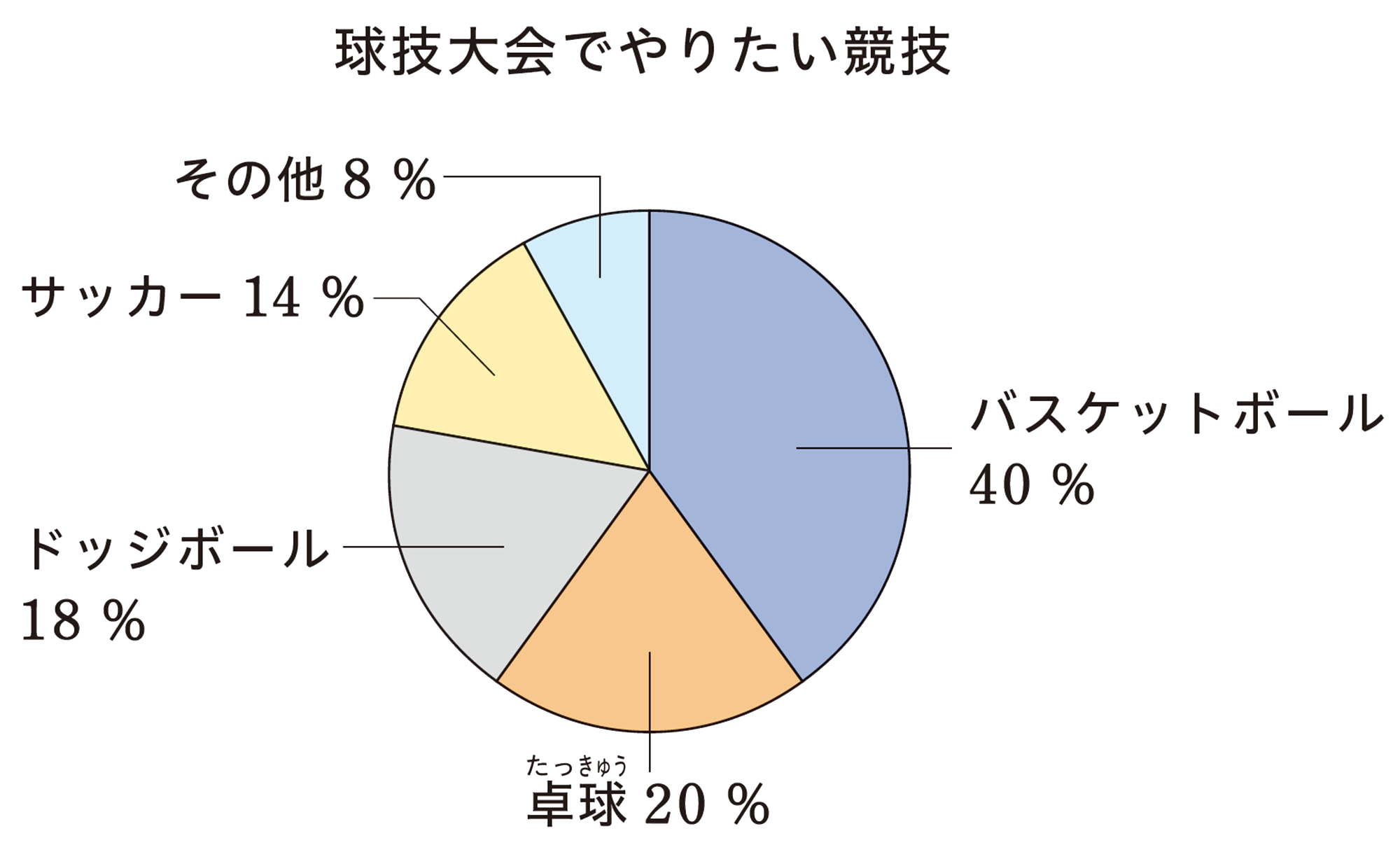
生徒にアンケートをして，球技大会の競技を決めます。全校生徒600人に1人ずつ聞いていくのはたいへんなので，昼休みに体育館に来た50人に「球技大会でやりたい競技は何ですか」というアンケートをとり，その結果を円グラフにまとめました。
この球技大会の競技についてのアンケートのとり方は，有効だといえるでしょうか。そう考えた理由を話し合ってみましょう。
バスケットボールがいちばん多いね。
ぼくのクラスでは，サッカーが人気だったよ。
室内の競技が多くなっているみたいだよ。
もっとたくさんの人に聞かなくてもいいのかな。
<3年p.243>
身のまわりでは，いろいろな調査が行われています。その調査結果は，テレビや新聞で報道されるものもたくさんあります。
【２】 次の①～⑤の調査は，テレビや新聞で報道されたり，よく目にしたりする調査です。これらの調査は，どのように行われているのか，それぞれ予想してみましょう。
次の課題へ！
それぞれどのように調べているのかな？
P.244
<3年p.244>
１ 全数調査と標本調査
Q Question
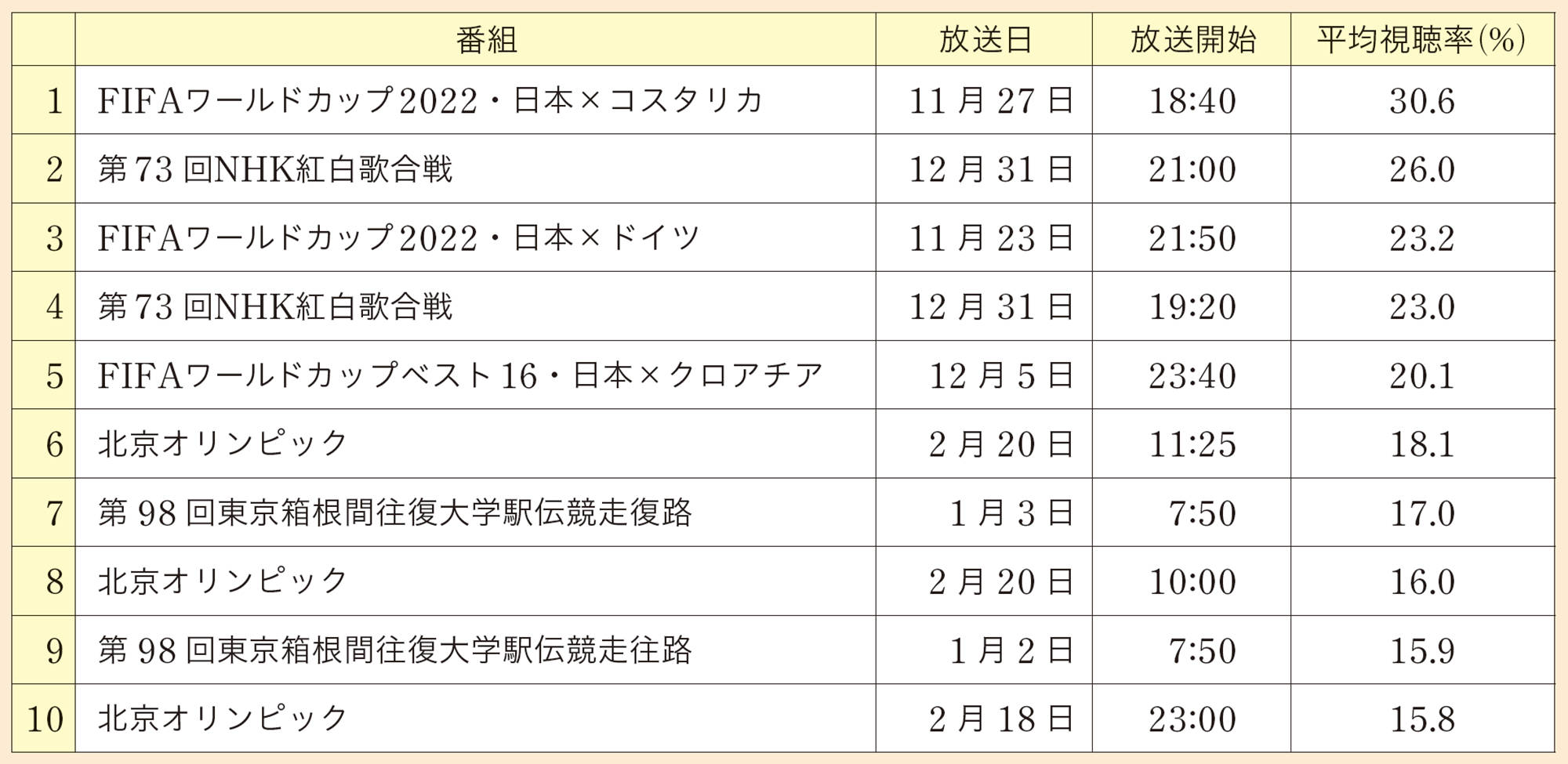
新聞に，国勢調査やテレビ番組の視聴率調査について掲載されていました。これらの調査は，どのように行われているのか調べてみましょう。
何かを調査するときは，全員を調べていると思う。
本当に全員を調べないとわからないのかな。
見方・考え方
調査のしかたにはどんなちがいがあるかな。
目標 ▷ 集団の性質を調査するために，どんな方法が用いられているか調べよう。
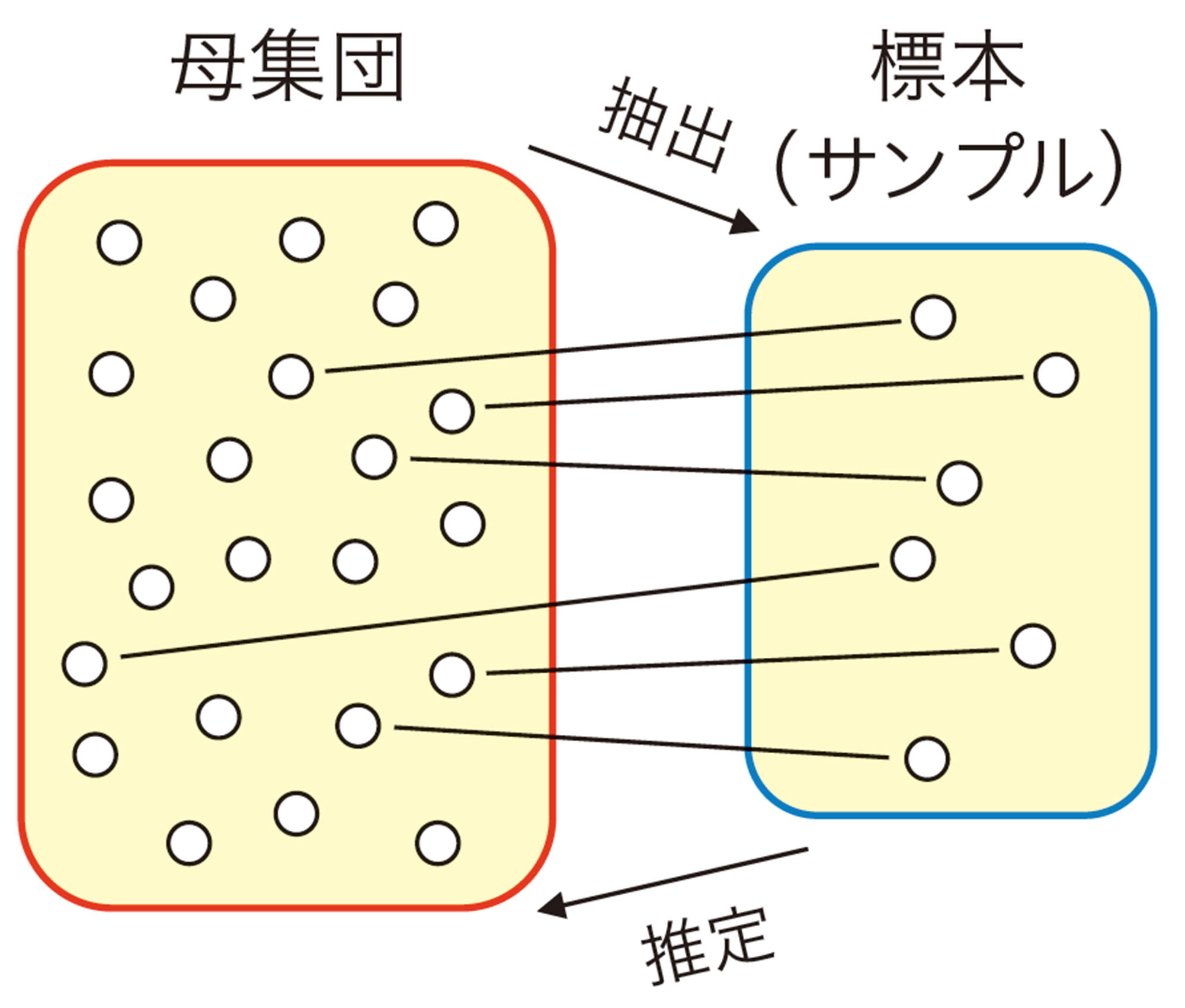
国勢調査のように，対象となる集団のすべてのものについて行う調査を全数調査という。これに対して，テレビ番組の視聴率調査のように，対象となる集団の中から一部を取り出して調べ，もとの集団全体の性質を推測する方法がある。このような調査を標本調査という。
問 １ 次の調査では，全数調査と標本調査のどちらが適していると考えられますか。また，そう判断した理由も説明しなさい。
⑴ 学校で行う新体力テスト
⑵ 川の水質調査
⑶ 飛行機に乗るときの手荷物検査
⑷ 世論調査
全数調査ができない場合や，全数調査を行うと時間や労力がかかりすぎる場合などには，標本調査が用いられる。
全数調査ができない場合とは，どんな場合なのかな。
どんなことがわかったかな
集団の性質の調査には，全数調査や標本調査が用いられています。
次の課題へ！
標本調査で，対象となる集団の中の一部は，どのように選べばいいのかな？
P.245
<3年p.245>
２ 標本調査による推定
標本の抽出
Q Question
美月さんは，自分の中学校の3年生90人の睡眠時間の平均値が何時間くらいか調べるために，10人の生徒から聞きとりを行おうと考えています。このとき，どの生徒も等しい確率で選ぶには，どんな選び方をすればよいでしょうか。
学校の近くに住んでいる10人に聞いてみようかな。
遠くに住んでいる生徒も同じように選ぶ必要はないのかな。
見方・考え方
具体的な場面で考えられるかな。
標本調査を行うとき，調査する対象となるもとの集団を母集団といい，母集団から取り出した一部分を標本またはサンプルという。
また，母集団から標本を取り出すことを標本の抽出といい，標本から母集団の性質を推測することを推定という。
問 １ 【Q】で，母集団をいいなさい。また，標本をいいなさい。
目標 ▷ 標本調査で，かたよりなく標本を抽出する方法について調べよう。
標本調査には，いろいろな抽出方法がある。その中の１つに，標本が母集団の性質をよく表すように，かたよりなく抽出する無作為抽出という方法がある。標本を無作為抽出することにより，その標本は母集団から等しい確率で取り出されたものと考えることができる。
どうしたら，無作為抽出できるのかな。
<3年p.246>
前ページの【Q】で，標本を無作為抽出するには，次のような方法がある。はじめに，90人の生徒に1 ～ 90までの番号をつけておくものとする。
方法①
くじ引きを用いる方法
1～90までの番号を書いた90枚のカードを用意し，裏返しにしてよく混ぜてから10枚取り出し，その番号の生徒10人を標本とする。
方法②
乱数表を用いる方法
乱数 とは，0～9までが等しい確率で不規則に出てくる数字の並びである。これから2桁の数をつくりまとめたものが乱数表である。この乱数表を用い，00と91以上を除いて標本を抽出する。
乱数表の一部
方法③
乱数さいを用いる方法
乱数さいは，正二十面体の各面に0～9までの数字が2回ずつ書かれたさいころである。この乱数さいを2個用いて2桁の数をつくり，00と91以上を除いて標本を抽出する。
方法④
コンピュータを用いる方法
コンピュータの表計算ソフトで乱数を発生させることができる。このソフトを用いて標本を抽出する。
関連 ▷ P.256，257
<3年p.247>
標本平均と母平均
問 ２ 箱の中に50個のみかんが入っています。次の表は，箱の中のすべてのみかんに番号をつけ，それぞれの重さを調べたものです。この表から，10個のみかんを標本として無作為抽出し，それらの重さの平均値を求めなさい。
みかん50個の重さ (単位:g)
問2の場合，50個のみかん全部が母集団，無作為抽出されたみかんが標本である。標本として抽出したデータの個数のことを，標本の大きさといい，標本の大きさは10である。また，母集団の平均値を母平均，標本の平均値を標本平均という。
問 ３ 問2の表から，みかん50個の重さの母平均を求めなさい。また，母平均と，問2で求めた標本平均との差を求めなさい。
母集団の中から無作為抽出された標本をもとに，母平均を推定することができる。また，一般的には，標本平均と母平均には誤差がある。
どんなことがわかったかな
無作為抽出することによって，母集団の性質を推定することができます。
次の課題へ！
どうすれば，標本平均と母平均の誤差を小さくできるのかな？
P.248
<3年p.248>
標本の大きさと標本平均
Q Question
前ページの問2で，標本の大きさを20個にした場合の標本平均を求め，標本の大きさが10個の場合の標本平均と比べてみましょう。
標本の大きさを大きくすると，標本平均は母平均に近づきそうだね。
1回調べるだけでいいのかな。
見方・考え方
標本の大きさを変えると，標本平均はどうなるかな。
目標 ▷ 標本平均と母平均の関係について調べよう。
問 ４ 次のデータAは，18人の生徒が前ページの問2の表から，それぞれ10個のみかんを標本として無作為抽出して求めた標本平均です。また，データBは，18人の生徒がそれぞれ20個のみかんを標本として無作為抽出して求めた標本平均です。次の問いに答えなさい。
A (単位:g)
B (単位:g)
⑴ AとBについて，小さい順に並べかえて，四分位数を求めなさい。
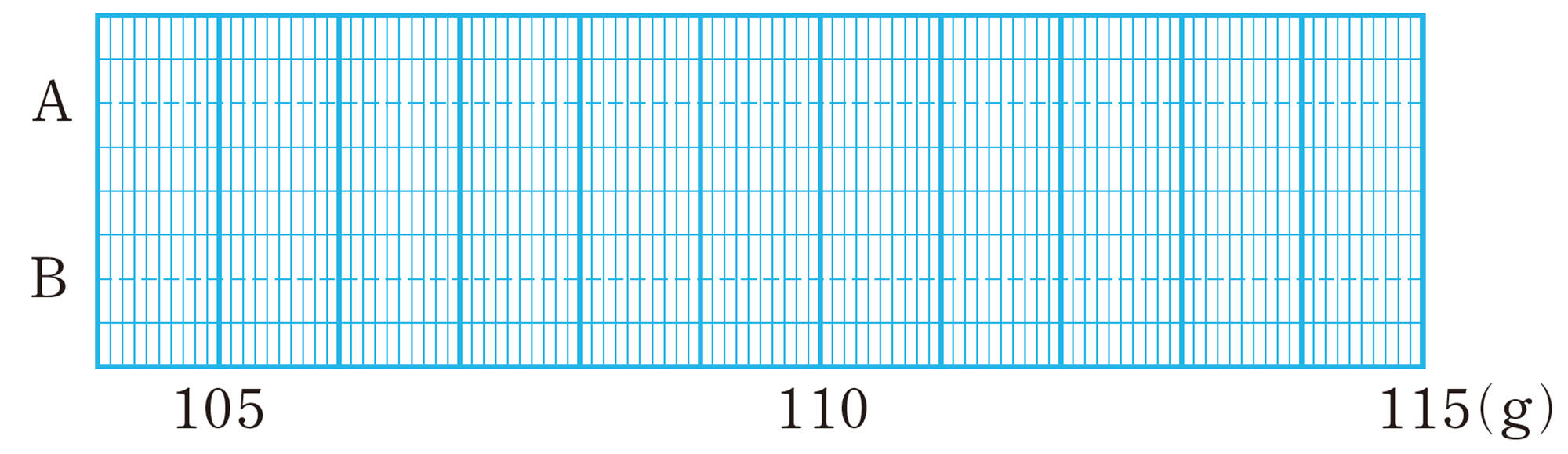
⑵ AとBについて，次の図に箱ひげ図をかきなさい。
⑶ AとBの標本平均の分布について，気づいたことをいいなさい。
<3年p.249>
一般に，標本の大きさが大きいほど，標本平均は母平均に近い値をとることが多くなる。
ただし，実際に標本調査を行う場合には，標本の大きさが大きいほど調査に時間や労力がかかるので，場面に応じて適切な標本の大きさを考える必要がある。
どんなことがわかったかな
標本の大きさが大きいほど，標本平均は母平均に近い値をとることが多くなり，母集団の性質を推定しやすくなります。
次の課題へ！
標本調査は，どんなところで使えるのかな？
P.250
無作為抽出できている？ Tea Break
A県の県庁健康増進課では，県内の中学校に通う生徒の休日の過ごし方についてアンケート調査をするために，県内の全中学校から20校を選んで協力をお願いしようと考えています。20校をどのように選べば，母集団の性質をより読み取りやすくなるでしょうか。話し合ってみましょう。
調査票を渡しに行きやすいから，「県庁から近い中学校から20校を選ぶ」という方法はどうかな。
場所がかたよってしまうから，よくないんじゃないかな。
「それぞれの学校に番号をつけ，思いついた番号を20個書き出して20校選ぶ」というのはどうかな。
でも，思いついた番号はかたよりがあるかもしれないよ。20個の選び方に何かくふうができないかな。
これまで学習したことをもとに，自分のアイデアを友だちに説明してみよう。友だちとの話し合いを通して，よりよいアイデアを考えよう。
