<3年p.228>
2 空間図形での利用
目標 ▷ 三平方の定理を使って,空間図形のいろいろな長さを求めよう。
Q Question
フェルマーの最終定理 Tea Break
三平方の定理[mathjax]\(a² + b² = c²\)を成り立たせる3つの自然数の組をピタゴラス数といいます。では,この式で指数の2を,3や4などに変えたときも,その式を成り立たせる3つの自然数の組はあるのでしょうか。これについて,次のようなフェルマーの最終定理と呼ばれる定理があります。
「3以上の自然数nについて,[mathjax]\(xⁿ + yⁿ = zⁿ\)となる自然数x,y,zは存在しない」
これは,フランスの数学者ピエール・ド・フェルマー(1607~1665)が,ディオファントスの著書『算術』の余白に書いた予想で,彼は「驚くべき証明を得たが,その証明を書くには余白がたりない」と書き残しました。
その後,名だたる数学者が証明に挑みましたが,証明することはできませんでした。しかし,1993年,イギリスの数学者アンドリュー・ワイルズ(1953~)が証明を発表しました。ただこの証明には誤りがあることがわかり,あきらめずに研究を続けた結果,翌1994年,ついに証明を完成させました。1995年にその証明に誤りがないことが確認され,実に300年以上にわたる歴史に終止符を打ちました。
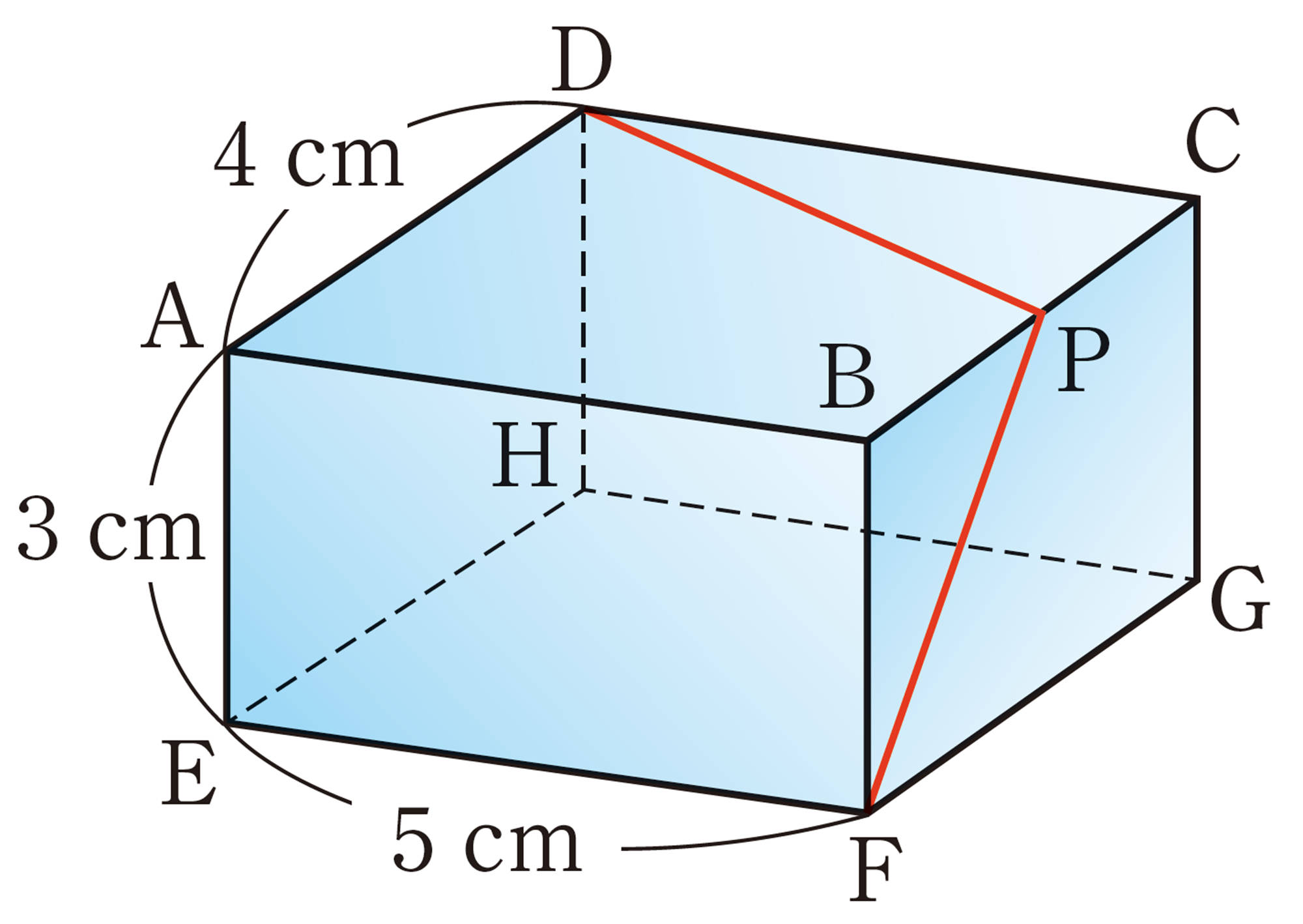
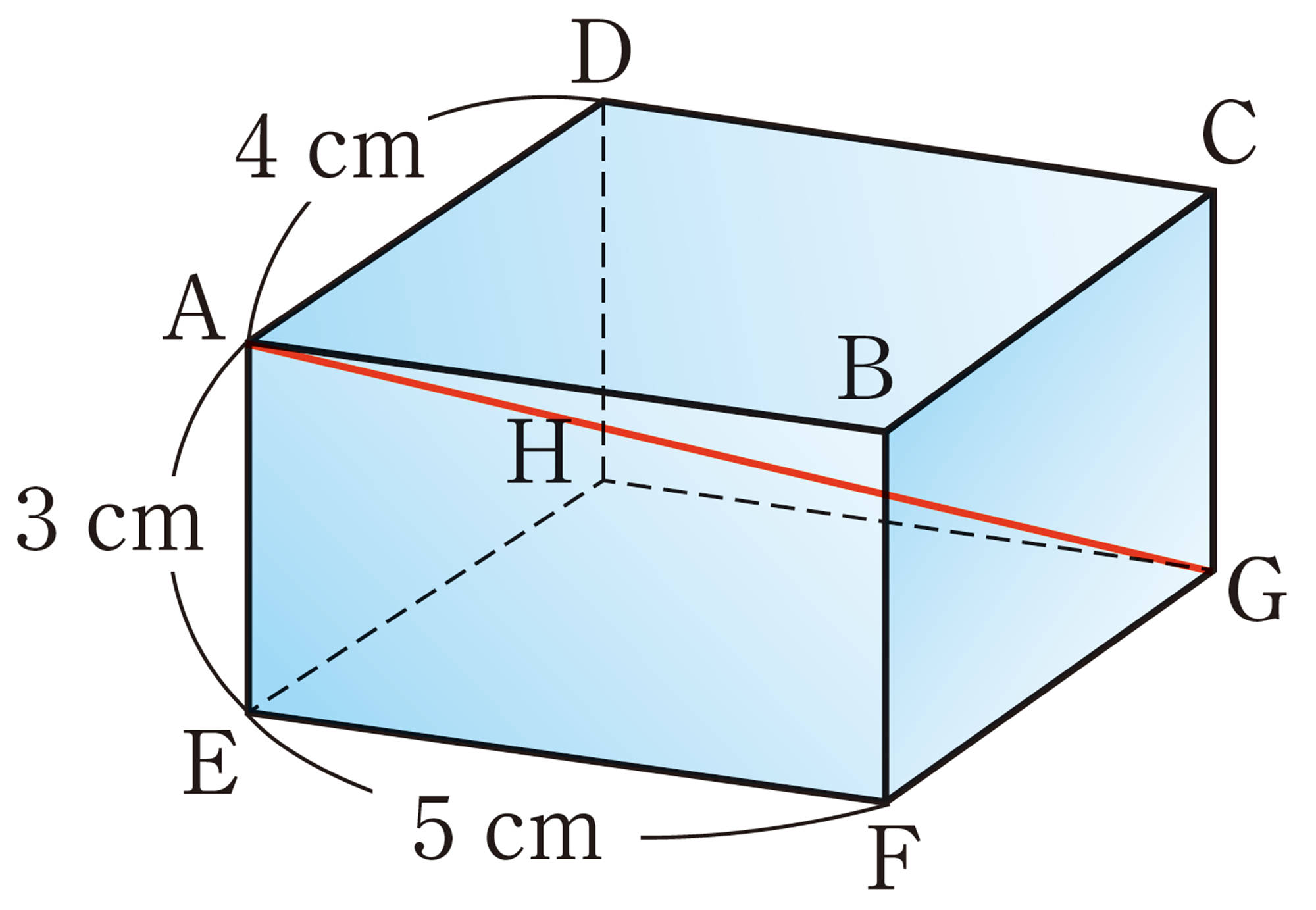
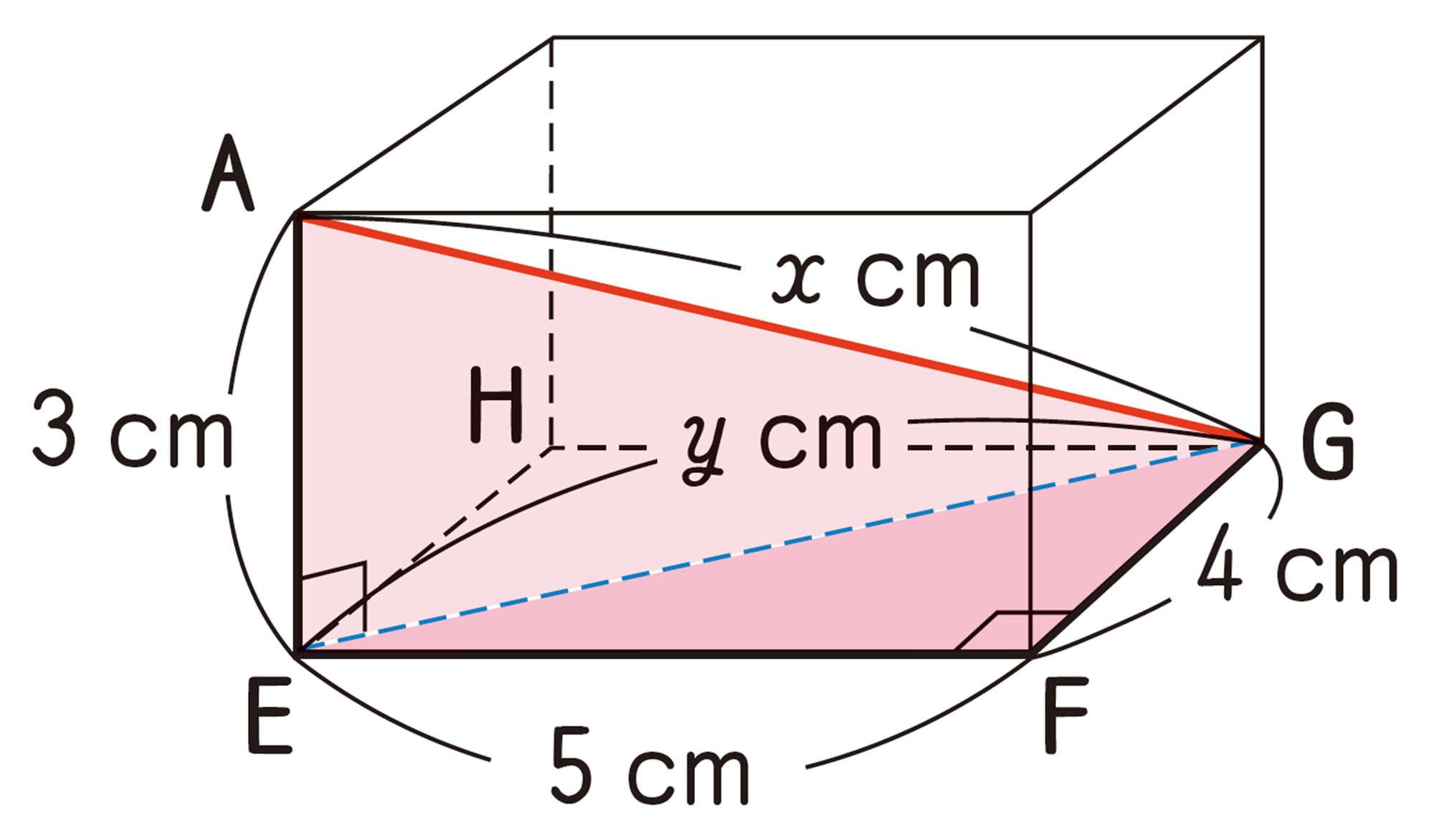
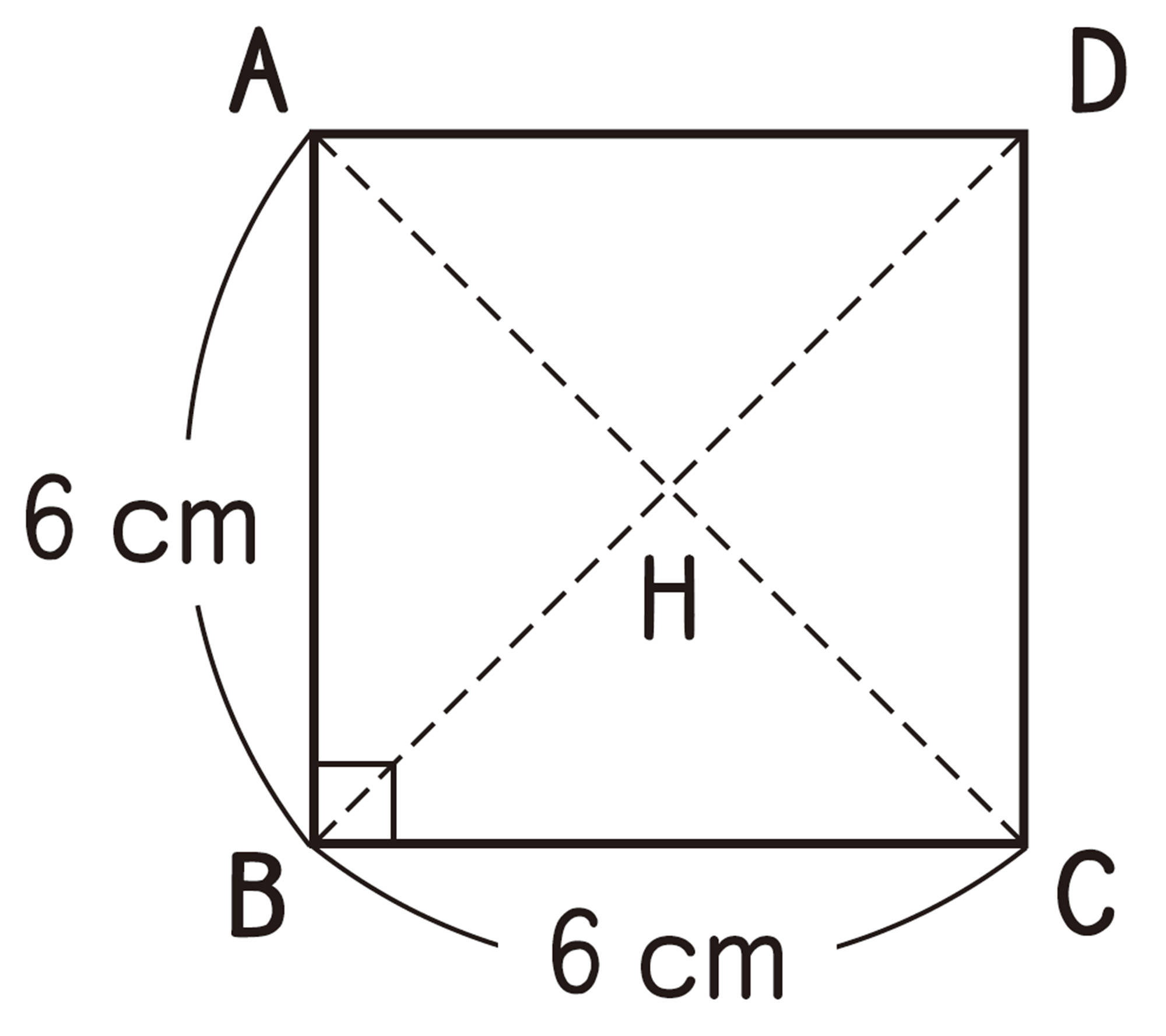
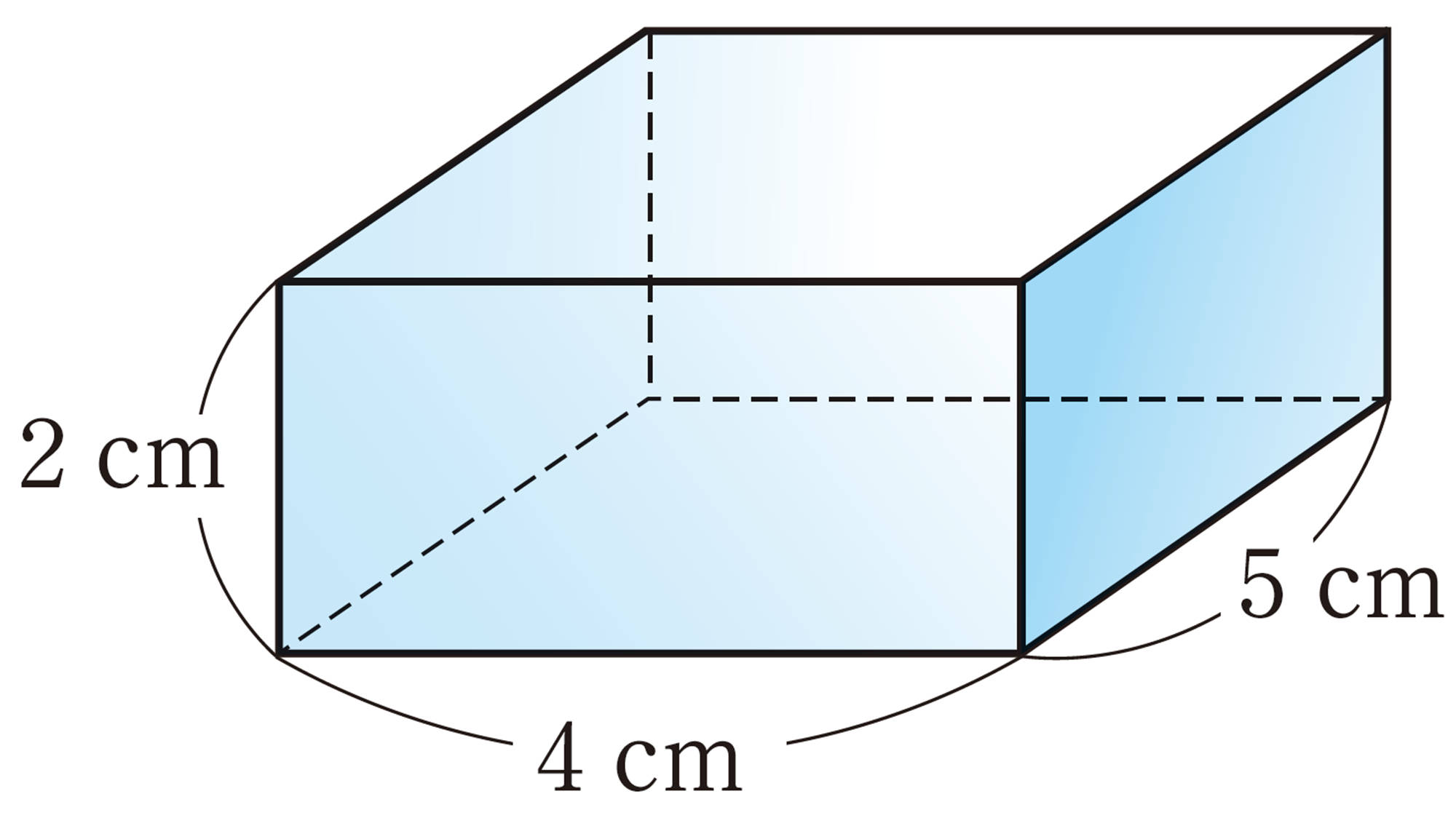
例 1 上の図の直方体で,対角線AGの長さを求めなさい。
考え方 AGを斜辺とする直角三角形AEGを使って,対角線の長さを求める。
解答
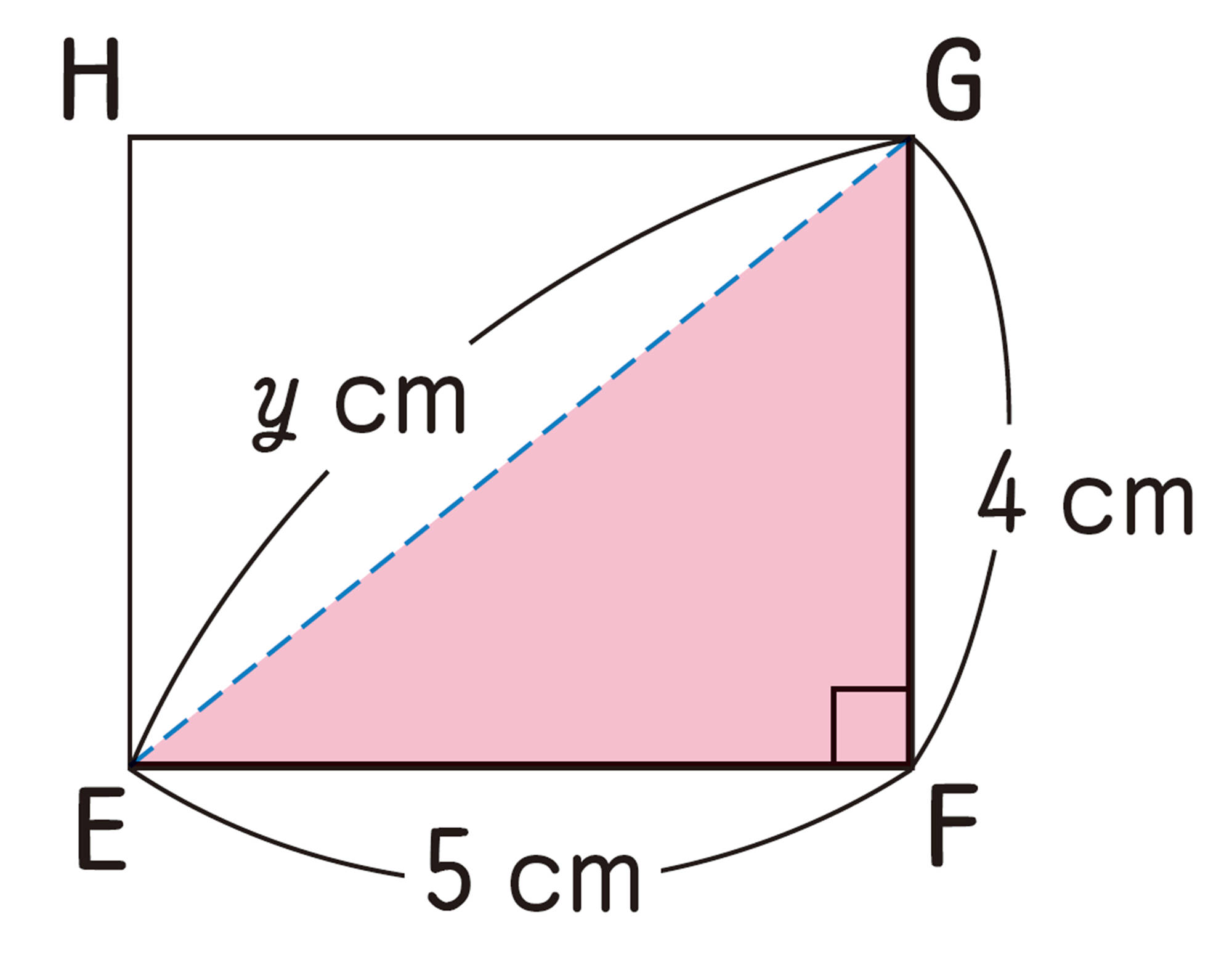
EとGを結び,[mathjax]\(AG=x\)cm,[mathjax]\(EG=y\)cmとする。
直角三角形EFGにおいて,
[mathjax]\(\hspace{71pt}y²=4²+5²\quad \cdots \cdots\mathsf{①}\)
直角三角形AEGにおいて,
答 [mathjax]\(5\sqrt{2}\) cm
<3年p.231>
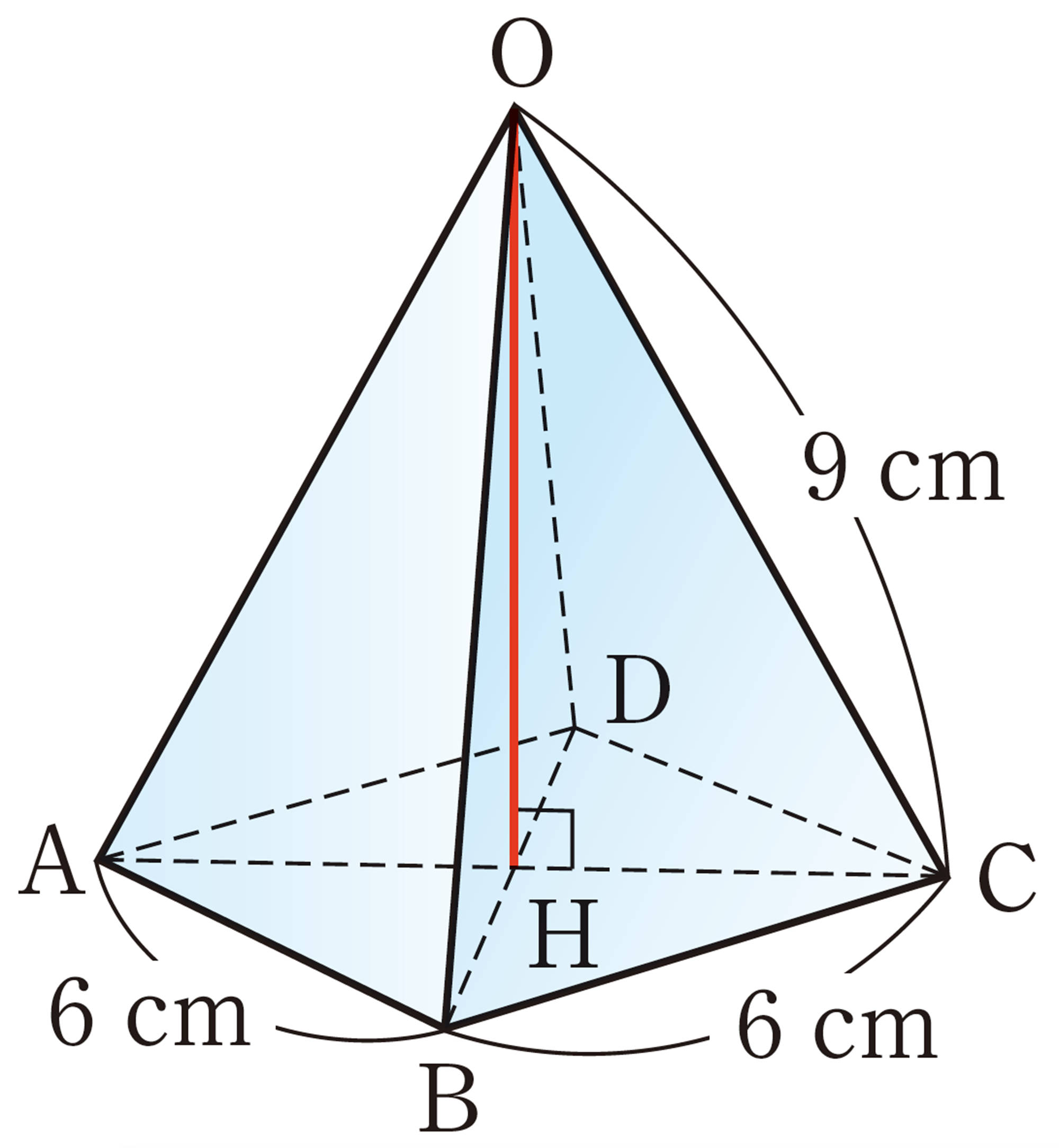
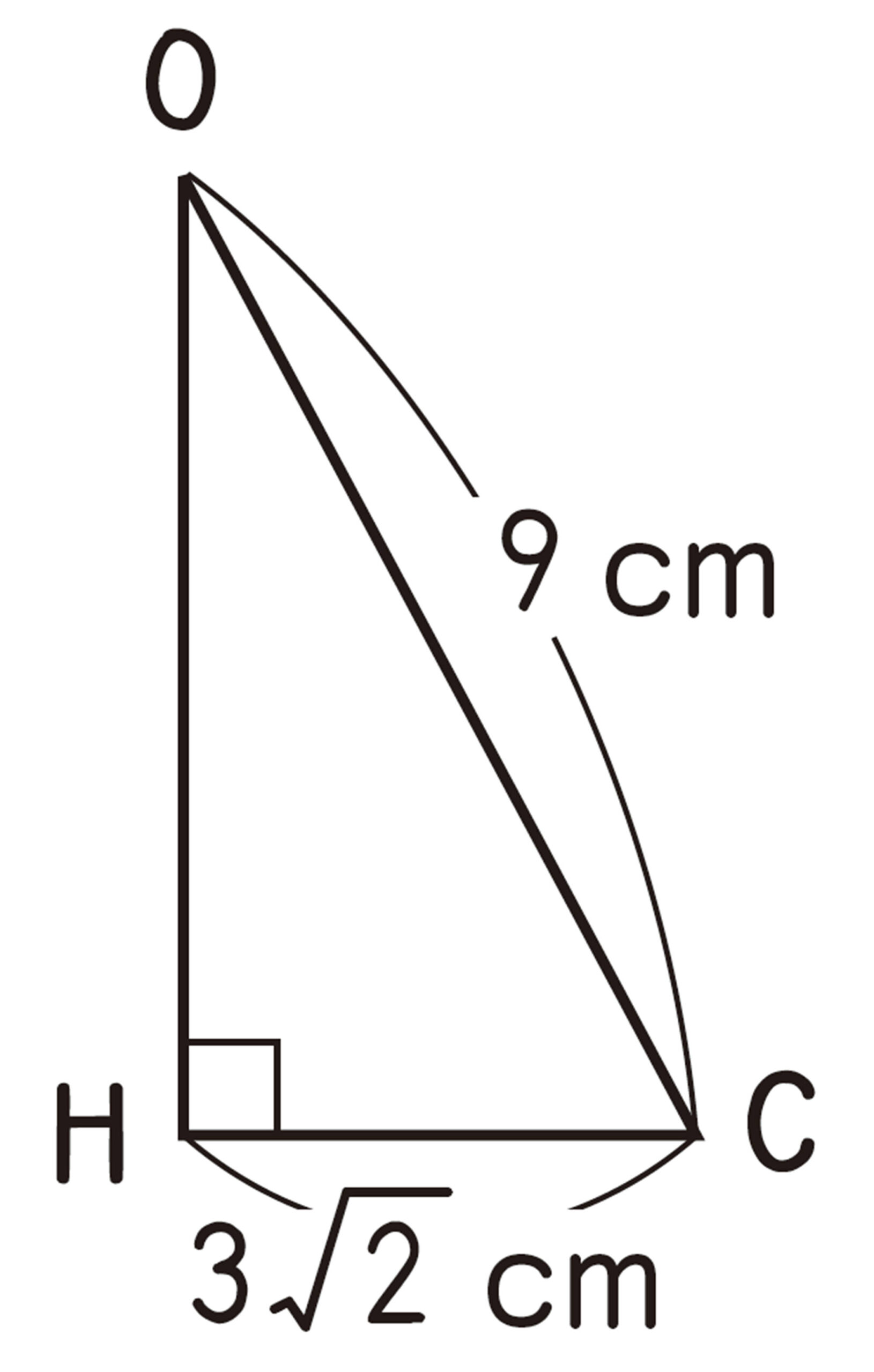
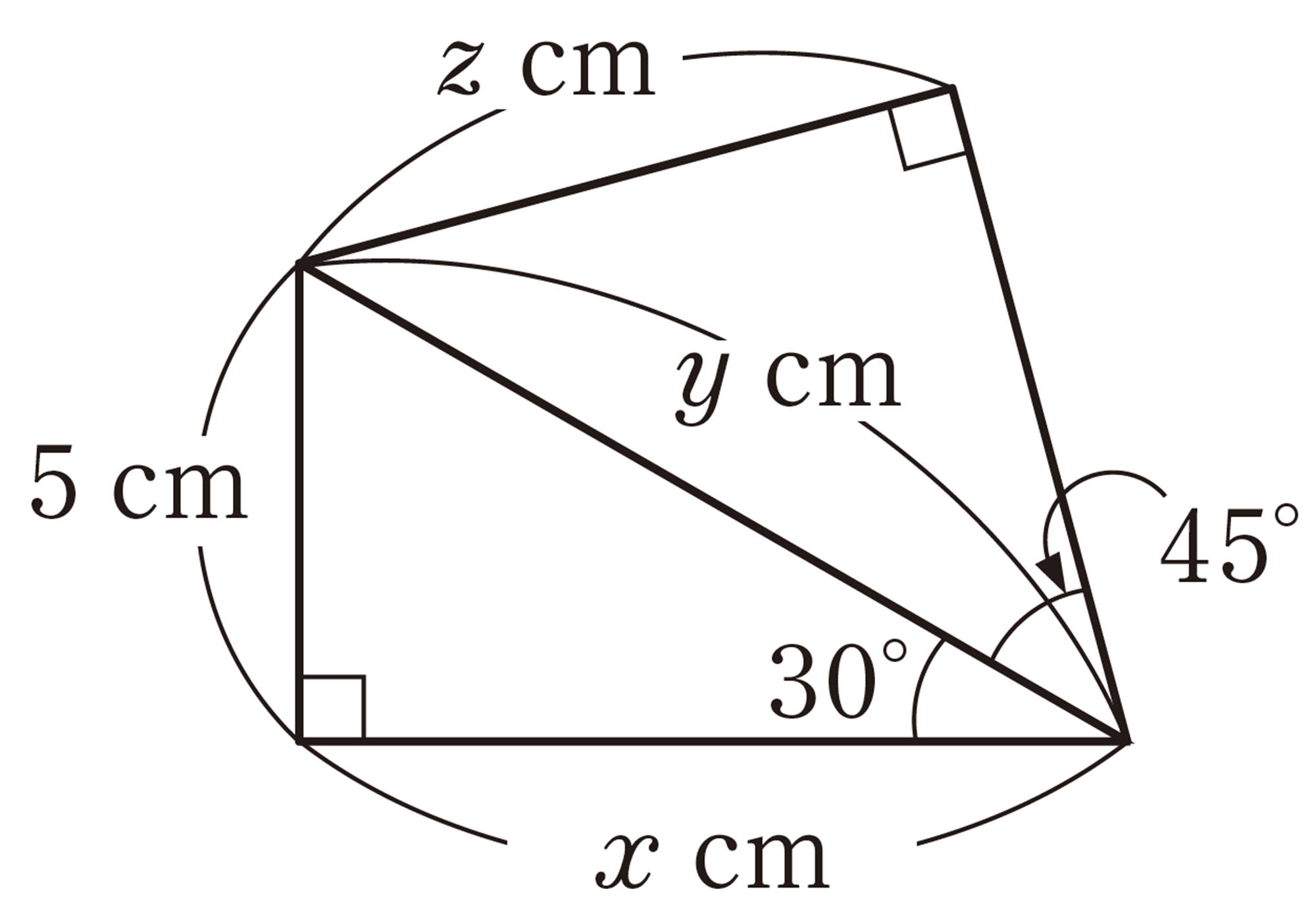
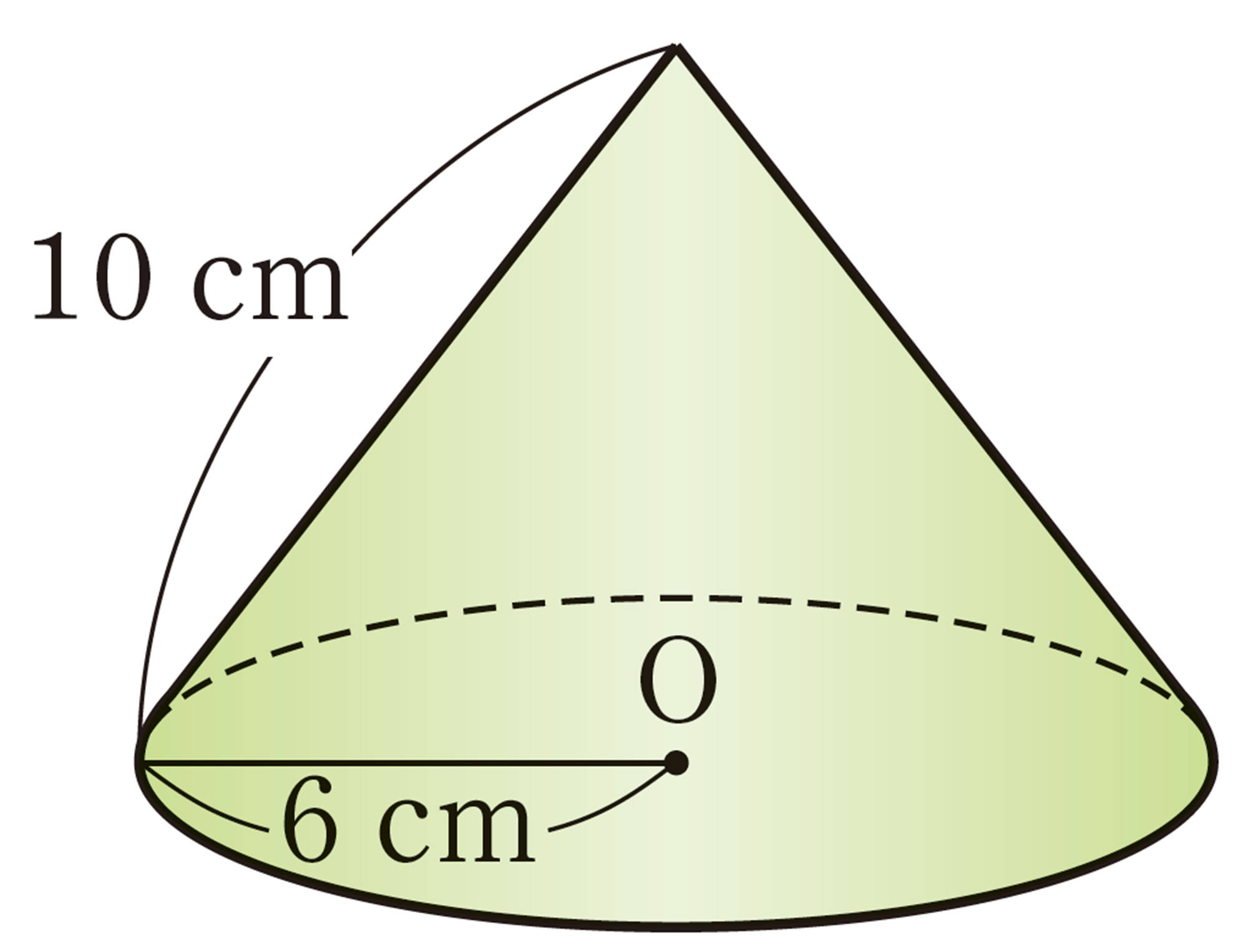
角錐・円錐の高さ
解答
[mathjax]\(\triangle ABC\)において,[mathjax]\(AB:AC=1: \sqrt{2}\)
よって,[mathjax]\(AC=6\sqrt{2}\)cm
したがって,対角線AC,BDの交点をHとすると,
[mathjax]\(CH=\dfrac{1}{2}AC\)であるから,[mathjax]\(CH=3\sqrt{2}\)cm
また,[mathjax]\(\triangle OHC\)は,[mathjax]\(\angle OHC=90^{\circ}\)の直角三角形であるから,
[mathjax]\(OH \gt 0\)であるから,[mathjax]\(OH=3\sqrt{7}\) cm
答 [mathjax]\(3\sqrt{7}\)cm
問 5 例2の正四角錐の体積を求めなさい。
問 6 例2の正四角錐で,辺ABの中点をMとして,OMの長さを求めなさい。また,この正四角錐の表面積を求めなさい。
問 7 底面の半径が5cm,母線の長さが13cmの円錐の高さと体積を求めなさい。
Q Question
<3年p.233>
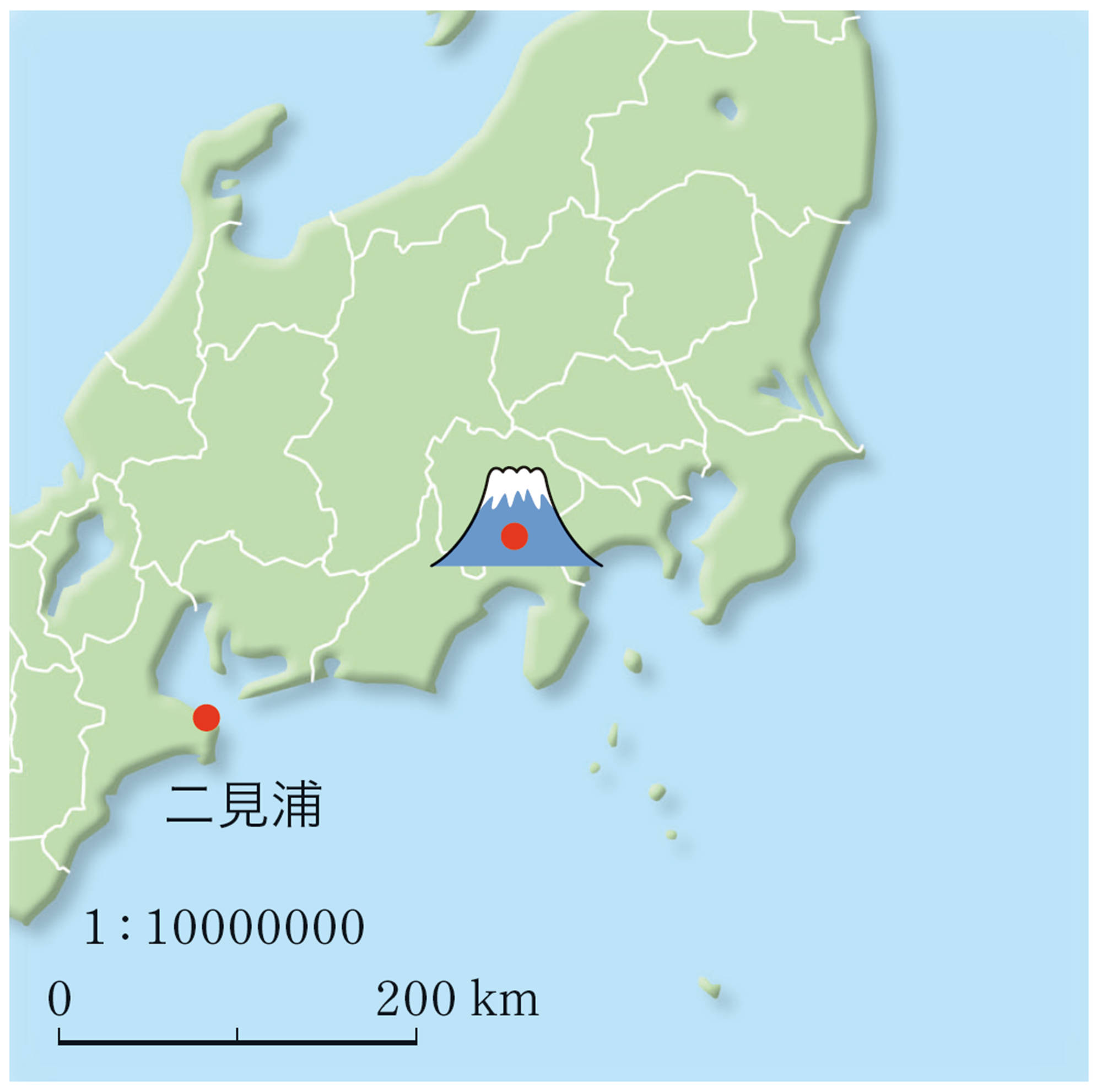
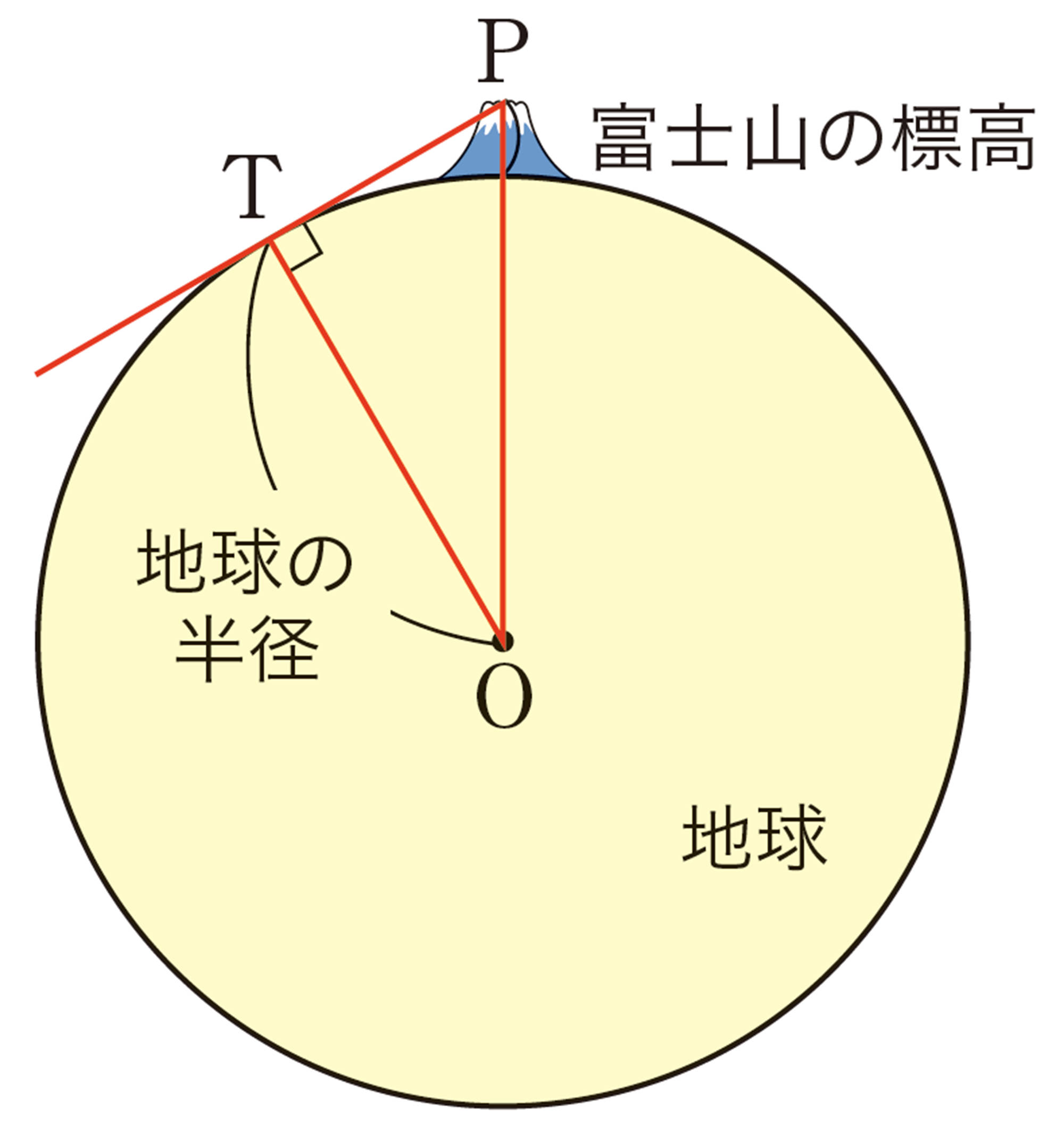
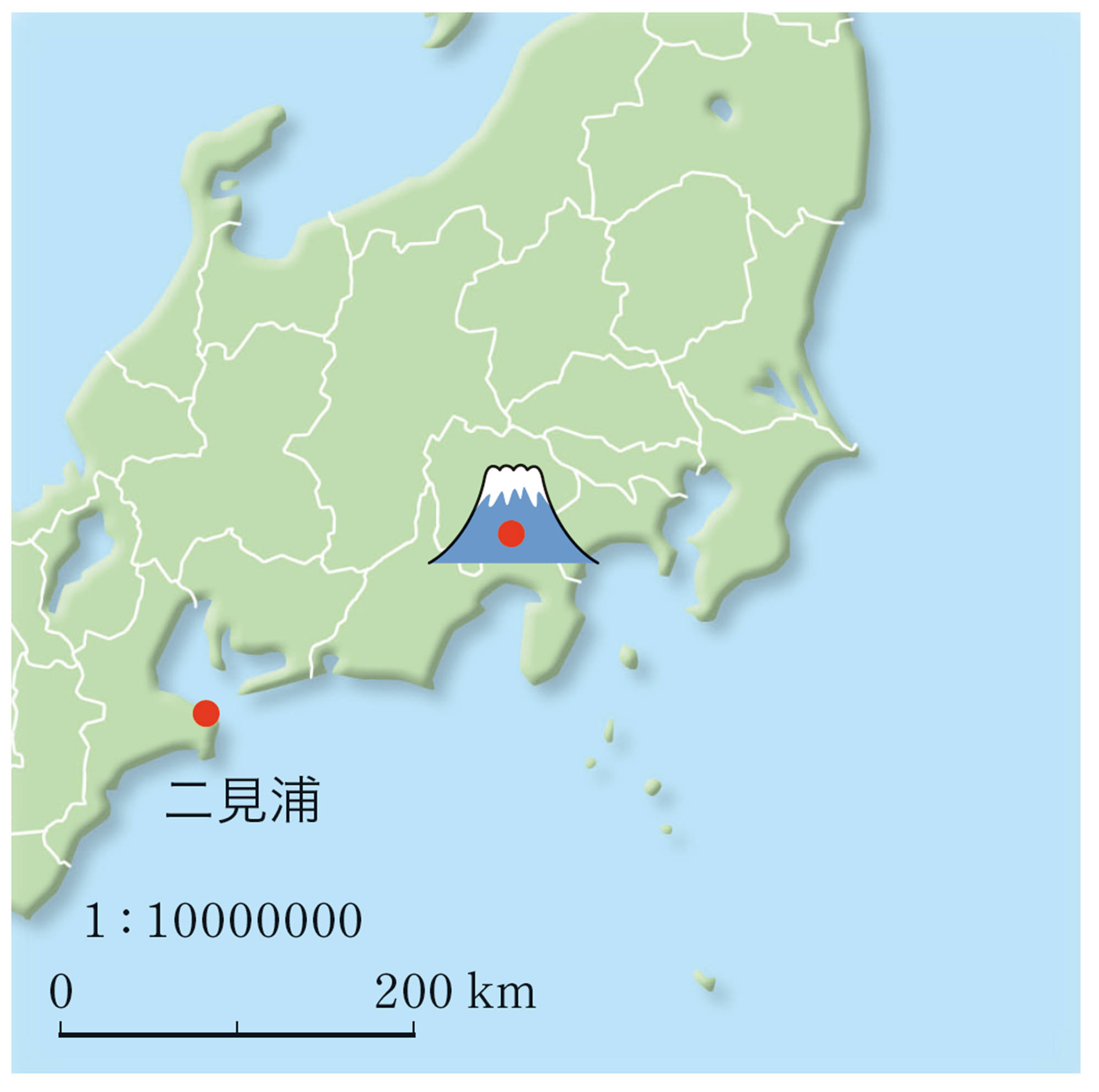
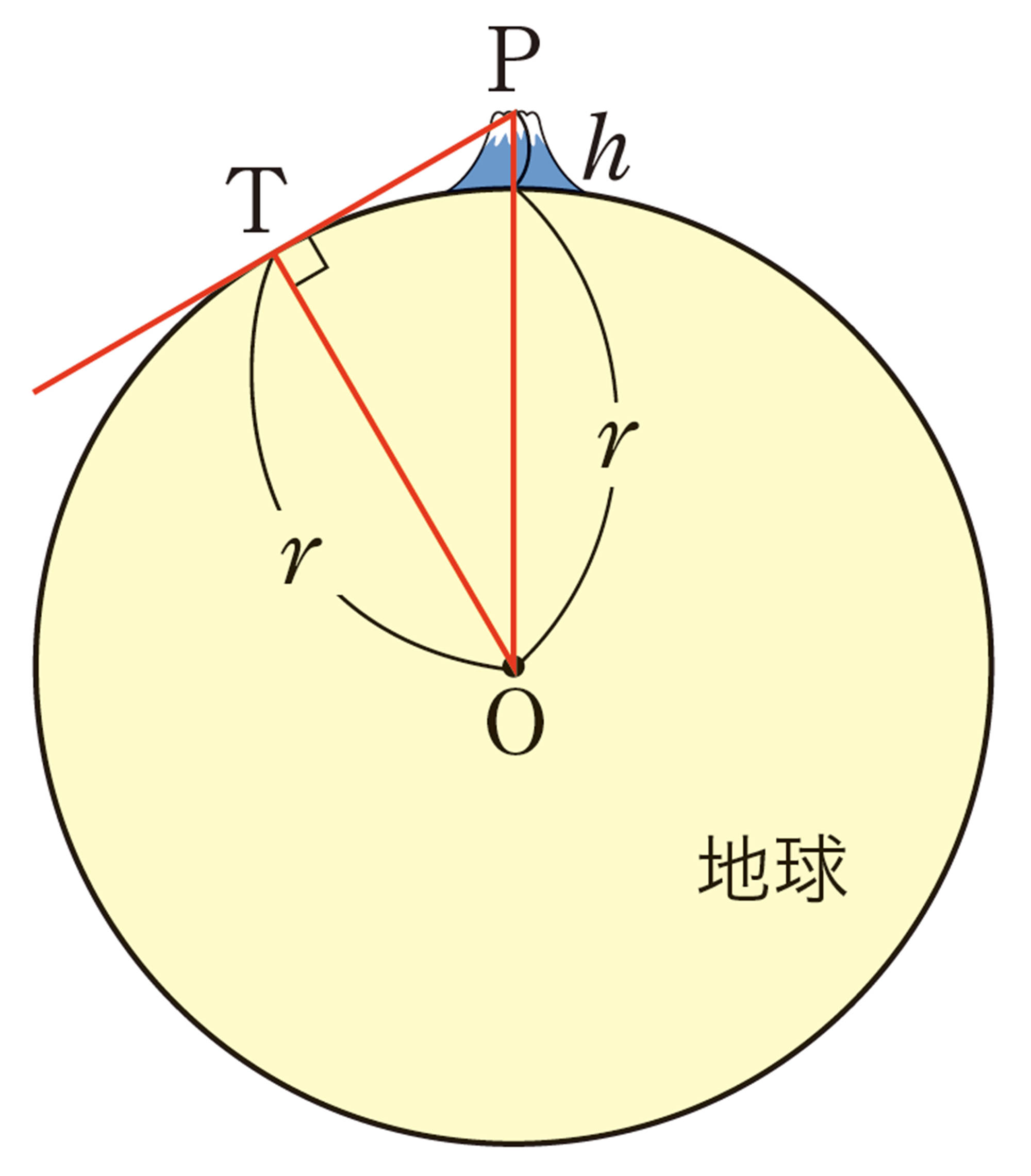
4 上の結果を利用して,自分の住んでいる地域の山や建物などが見える範囲を求めてみましょう。

この前,富士山から257km離れた滋賀県の釣瓶岳から撮影された富士山の写真を見たよ。
上の結果より離れているのに,どうして撮影できたのかな。

関連 ▷ P.239
どんなことがわかったかな
三平方の定理を利用すると,直方体の対角線の長さや角錐・円錐の高さなど,2点間の距離を求めることができます。
<3年p.234>
確かめよう 2節 三平方の定理の利用
□ 三平方の定理を利用して,対角線などの長さを求めることができる。 ▷対角線の長さや三角形の高さ ・P.222 例1 ・P.223 例2
1 次の問いに答えなさい。
⑴ 1辺7cmの正方形の対角線の長さを求めなさい。
⑵ 1辺10cmの正三角形の高さと面積を求めなさい。
4 2点 [mathjax]\(A(-3,2)\),[mathjax]\(B(3,6)\)間の距離を求めなさい。
<3年p.235>
7章 「三平方の定理」を学んで
できるようになったこと 身のまわりの課題へ ▷P.238,239
直角三角形では,三平方の定理が成り立ち,それを使って,直角三角形の辺の長さを求めることができる。
三平方の定理の逆を使って,3辺の長さがわかっている三角形が直角三角形かどうか判断することができる。
身のまわりや数学の中から見つけた問題を,三平方の定理や三平方の定理の逆を使って解決することができる。
さらに学んでみたいこと
これからもっと学んでみたいことや,疑問に思ったことを書いておこう。
数学へのいざない 三四五
いまから数千年前のエジプトでは,ナイル川の洪水で境界線がわからなくなった土地の分配や建築をするための測量を仕事としている人がいました。彼らは3辺の長さの比が [mathjax]\(3:4:5\) の直角三角形をもとに直角をつくったという説があります。当時建てられたピラミッドは,底面が正確な正方形になっています。
日本でも,大工が土地の測量のために,「おおがね」と呼ばれる道具をつくって直角を測ることがあります。おおがねにも,3辺の長さの比が [mathjax]\(3:4:5\) の直角三角形が利用されています。大工たちはこの方法を「三四五」と呼んで直角の確認に利用していました。
関連する職業・仕事 測量士,大工