<3年p.195>
等しい弧と円周角
Q Question
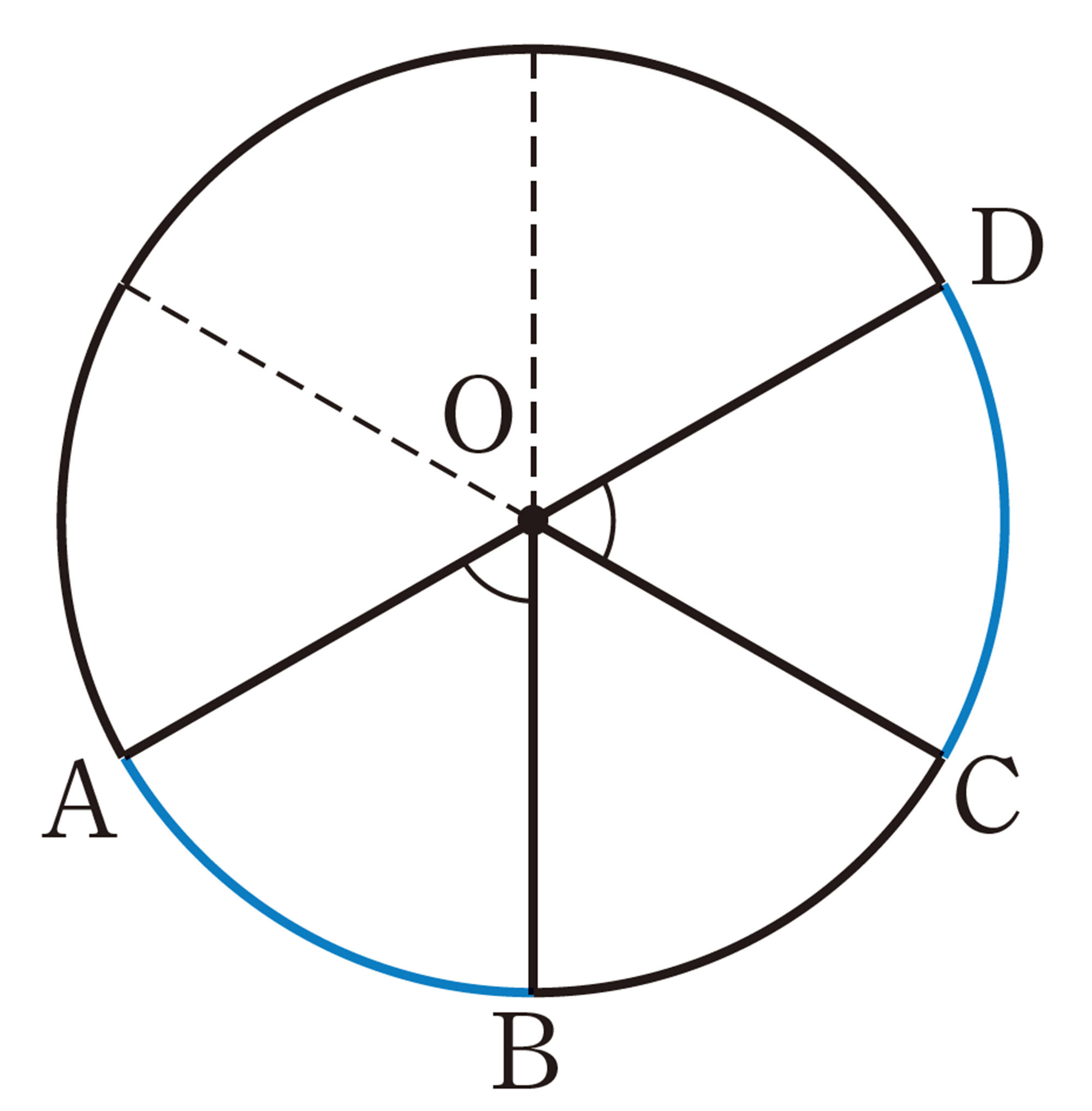
右の図で，[mathjax]\(\stackrel{\huge\frown}{AB}\)，[mathjax]\(\stackrel{\huge\frown}{CD}\)と，それぞれの中心角[mathjax]\(\angle AOB\)，[mathjax]\(\angle COD\)の関係について調べてみましょう。
⑴ [mathjax]\(\angle AOB = \angle COD\)のとき，[mathjax]\(\stackrel{\huge\frown}{AB}\)と[mathjax]\(\stackrel{\huge\frown}{CD}\)の長さはどんな関係にあるでしょうか。
⑵ [mathjax]\(\stackrel{\huge\frown}{AB} = \stackrel{\huge\frown}{CD}\)のとき，[mathjax]\(\angle AOB\)と[mathjax]\(\angle COD\)の大きさはどんな関係にあるでしょうか。
具体的な図を使って確かめられるかな。
注意 [mathjax]\(\stackrel{\huge\frown}{AB}\)と書いて，その弧の長さを表すことがある。
見方・考え方
弧の長さと中心角の大きさの間にはどんなきまりがあるかな。
目標 ▷ 長さの等しい弧と中心角や円周角の大きさの関係について調べよう。
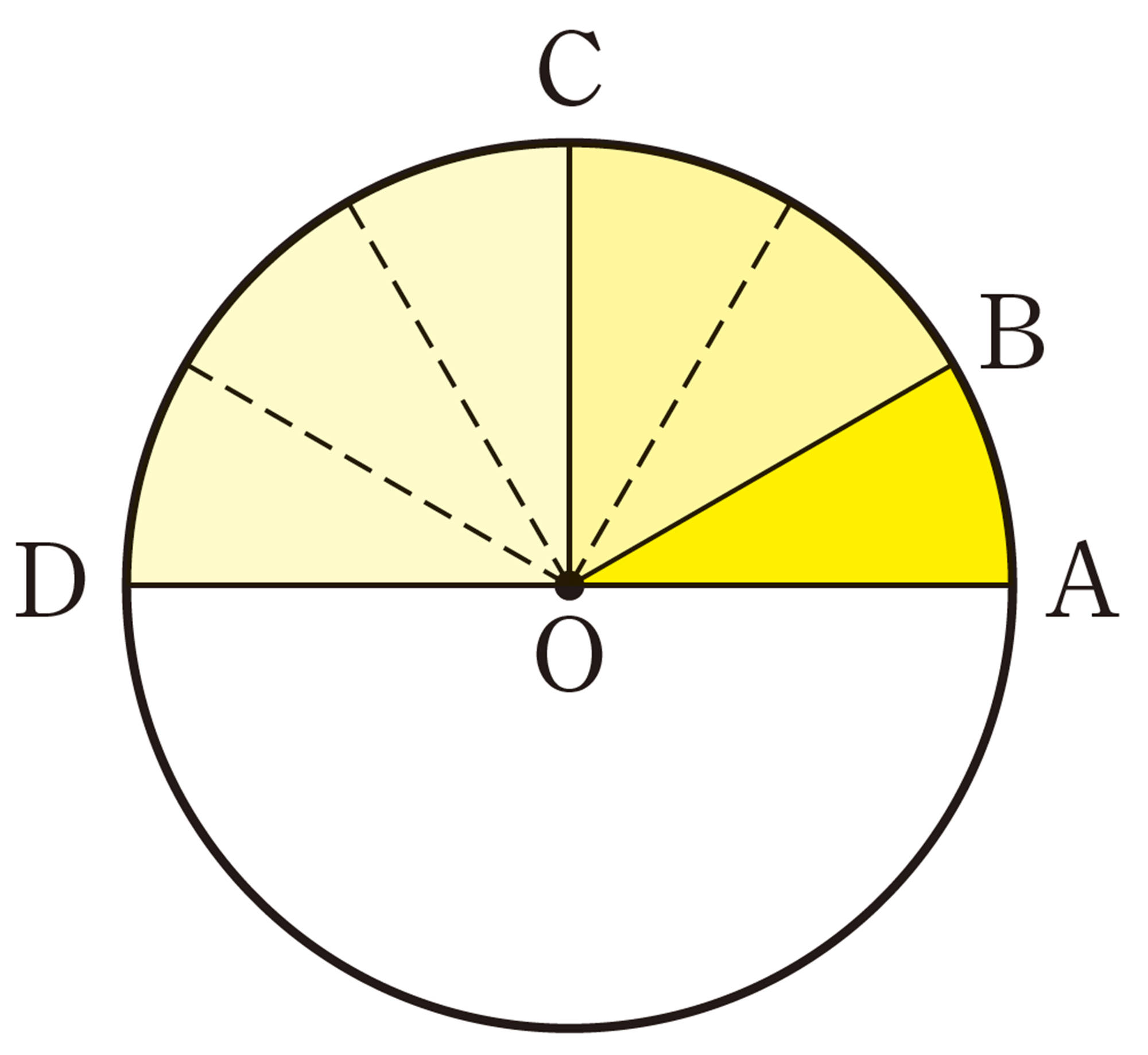
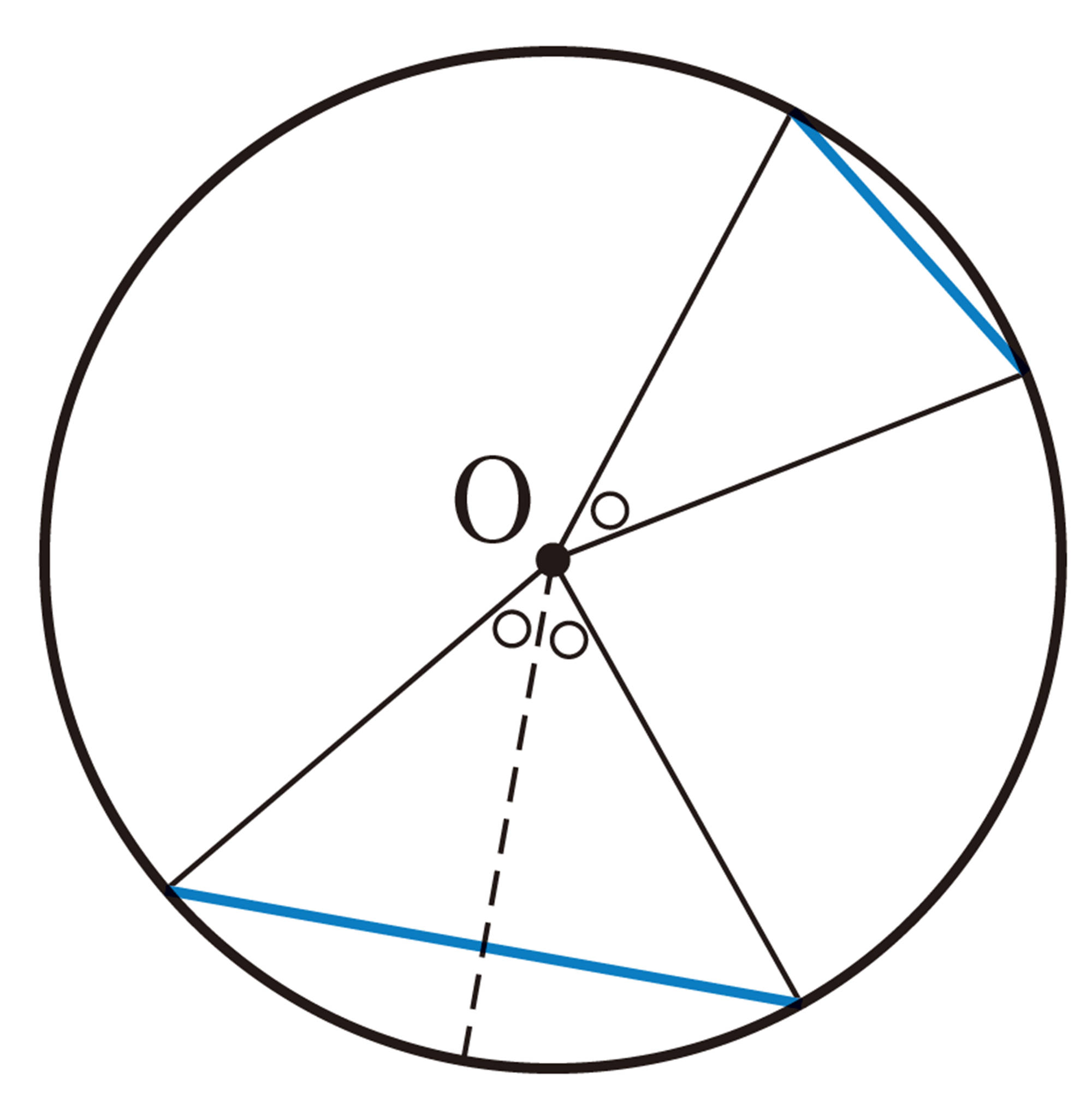
1つの円において，弧の長さが等しい2つのおうぎ形は，一方を移動してもう一方に重ねることができる。同様にして，中心角が等しい2つのおうぎ形も，ぴったり重ねることができる。
これらのことから，次のことがいえる。
1つの円において，
① 等しい弧に対する中心角は等しい。
② 等しい中心角に対する弧は等しい。
問 ５ 右の図のように，おうぎ形OABの中心角の大きさを2倍，3倍にしておうぎ形OBC，OCDをつくるとき，[mathjax]\(\stackrel{\huge\frown}{BC}\)，[mathjax]\(\stackrel{\huge\frown}{CD}\)の長さは，それぞれ[mathjax]\(\stackrel{\huge\frown}{AB}\)の長さの何倍になりますか。
問5で調べたように，1つの円において，弧の長さは中心角の大きさに比例する。
▲トライ 1つの円において，中心角の大きさと弦の長さは比例しないことを，反例をあげて説明してみよう。
<3年p.196>
前ページで調べたことをもとにして，長さの等しい弧に対する円周角の大きさが等しいことを証明してみよう。
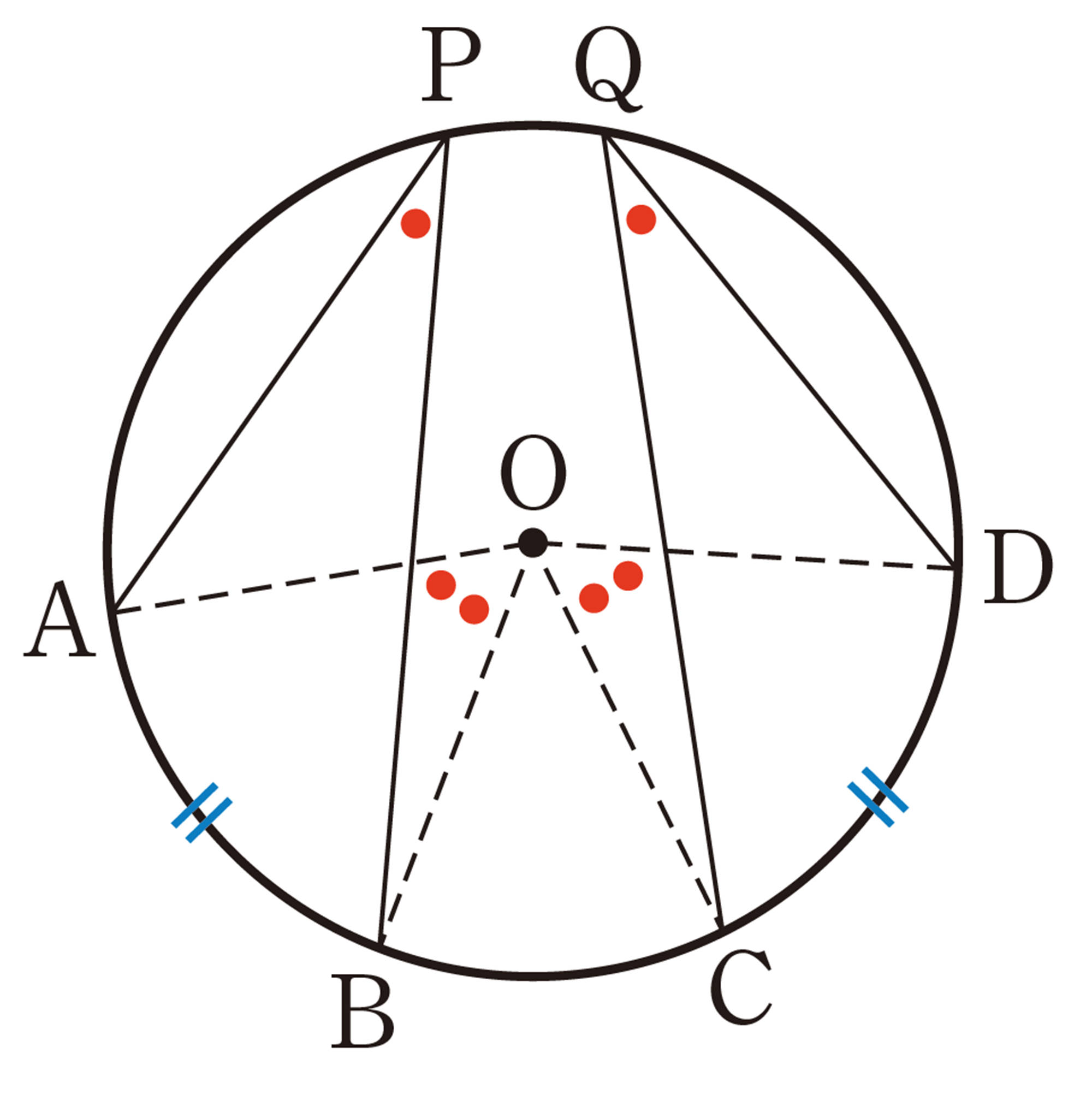
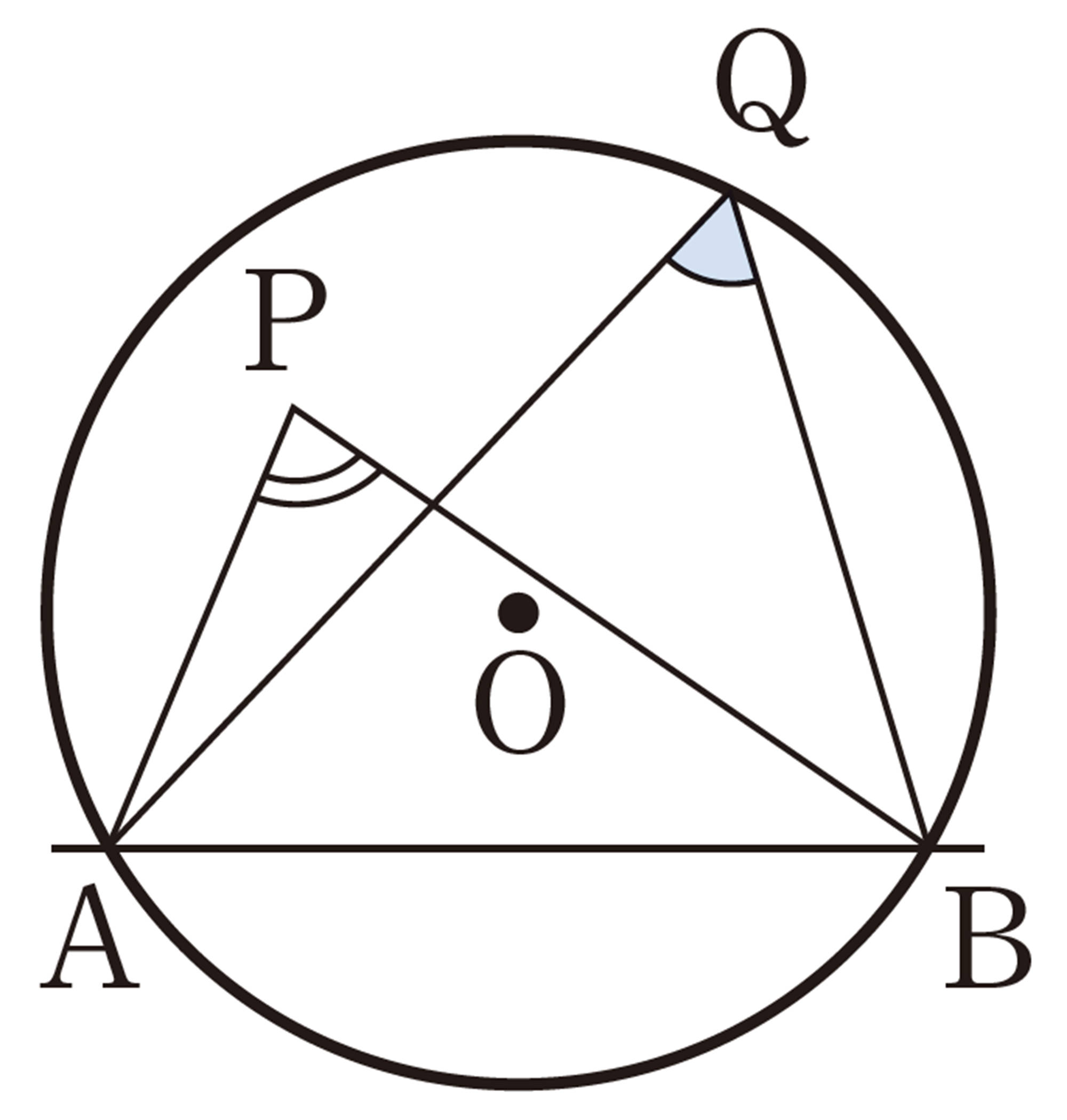
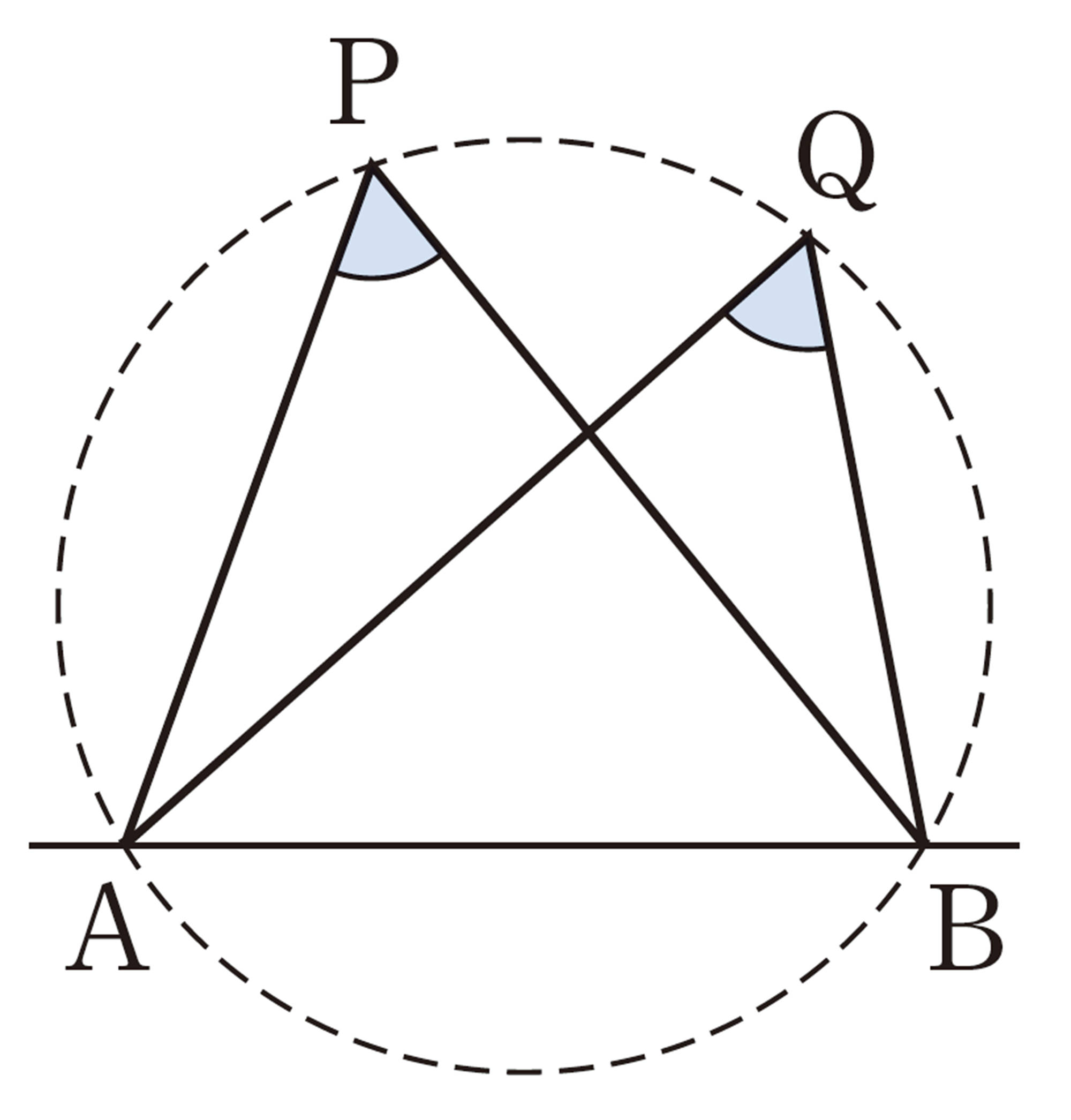
問 ６ 右の図のような円Oで，[mathjax]\(\stackrel{\huge\frown}{AB}\)，[mathjax]\(\stackrel{\huge\frown}{CD}\)に対する円周角を，それぞれ[mathjax]\(\angle APB\)，[mathjax]\(\angle CQD\)とするとき，[mathjax]\(\stackrel{\huge\frown}{AB} = \stackrel{\huge\frown}{CD}\)ならば，[mathjax]\(\angle APB = \angle CQD\)であることを，次のように証明しました。 [mathjax]\(\boxed{\phantom{000}}\) をうめて，証明を完成させなさい。
［証明］
1つの弧に対する円周角は，その弧に対する[mathjax]\(\boxed{\phantom{000}}\)の半分であるから，
仮定より，[mathjax]\(\stackrel{\huge\frown}{AB} = \stackrel{\huge\frown}{CD}\)であるから，
[mathjax]\(\hspace{15pt}\angle AOB = \angle \boxed{\phantom{000}} \quad \quad \cdots \cdots \mathsf{③}\)
①，②，③から，[mathjax]\(\angle APB = \angle CQD\)
問 ７ 問6で証明したことがらの逆をいいなさい。また，それが成り立つことを証明しなさい。
これまで調べたことは，次のように定理としてまとめることができる。
定理
弧と円周角
1つの円において，
❶ 等しい弧に対する円周角は等しい。
❷ 等しい円周角に対する弧は等しい。
<3年p.197>
問 ８ 次の図で，[mathjax]\(\angle x\)の大きさを求めなさい。
⑴ [mathjax]\(\stackrel{\huge\frown}{AB} = \stackrel{\huge\frown}{BC}\)
⑵ [mathjax]\(\stackrel{\huge\frown}{AB} = \stackrel{\huge\frown}{BC}\)
1つの円において，中心角の大きさと弧の長さが比例することから，円周角の大きさと弧の長さも比例することがわかる。
例 ２ 右の図で，[mathjax]\(\stackrel{\huge\frown}{AB}\)の長さが2cm，[mathjax]\(\stackrel{\huge\frown}{BC}\)の長さがxcmのとき，xの値を求めなさい。
解答
円周角の大きさと弧の長さは比例するから，
答 [mathjax]\(x=6\)
問 ９ 次の図で，xの値を求めなさい。
⑴ [mathjax]\(\stackrel{\huge\frown}{AB} = x\)cm
[mathjax]\(\stackrel{\huge\frown}{CD} = 6\)cm
⑵ [mathjax]\(\stackrel{\huge\frown}{AB} = 3\)cm
[mathjax]\(\stackrel{\huge\frown}{CD} = 4\)cm
⑶ [mathjax]\(\stackrel{\huge\frown}{AB} = 1\)cm
[mathjax]\(\stackrel{\huge\frown}{BC} = 3\)cm
[mathjax]\(\stackrel{\huge\frown}{CA} = 2\)cm
どんなことがわかったかな
1つの円において，等しい弧に対する中心角や円周角は等しくなります。
次の課題へ！
円周上以外にも，円周角と同じ大きさになる点はあるのかな？
P.198
<3年p.198>
２ 円周角の定理の逆
Q Question
右の図のように，円周上以外の点をP，円周上の点をQとします。円周角[mathjax]\(\angle AQB\)が[mathjax]\(60^{\circ}\)のとき，[mathjax]\(\angle APB = 60^{\circ}\)になる点Pがあるか探してみましょう。ただし，点Pと点Qは直線ABについて同じ側にあるものとします。
円周上以外の点には，どんな場合があるのかな。
点Pが円Oの内部と外部にあるときを調べればいいのかな。
見方・考え方
いろいろな場合を調べて，どんな性質があるか見つけられるかな。
【Q】で調べたことから，次の㋐，㋑，㋒のようになることが予想できる。
㋐ 点Pが円Oの内部にあるとき，[mathjax]\(\angle APB \gt \angle AQB\)
㋑ 点Pが円Oの円周上にあるとき，[mathjax]\(\angle APB = \angle AQB\)
㋒ 点Pが円Oの外部にあるとき，[mathjax]\(\angle APB \lt \angle AQB\)
目標 ▷ 円周上以外に点をとったときの角の大きさについて調べよう。
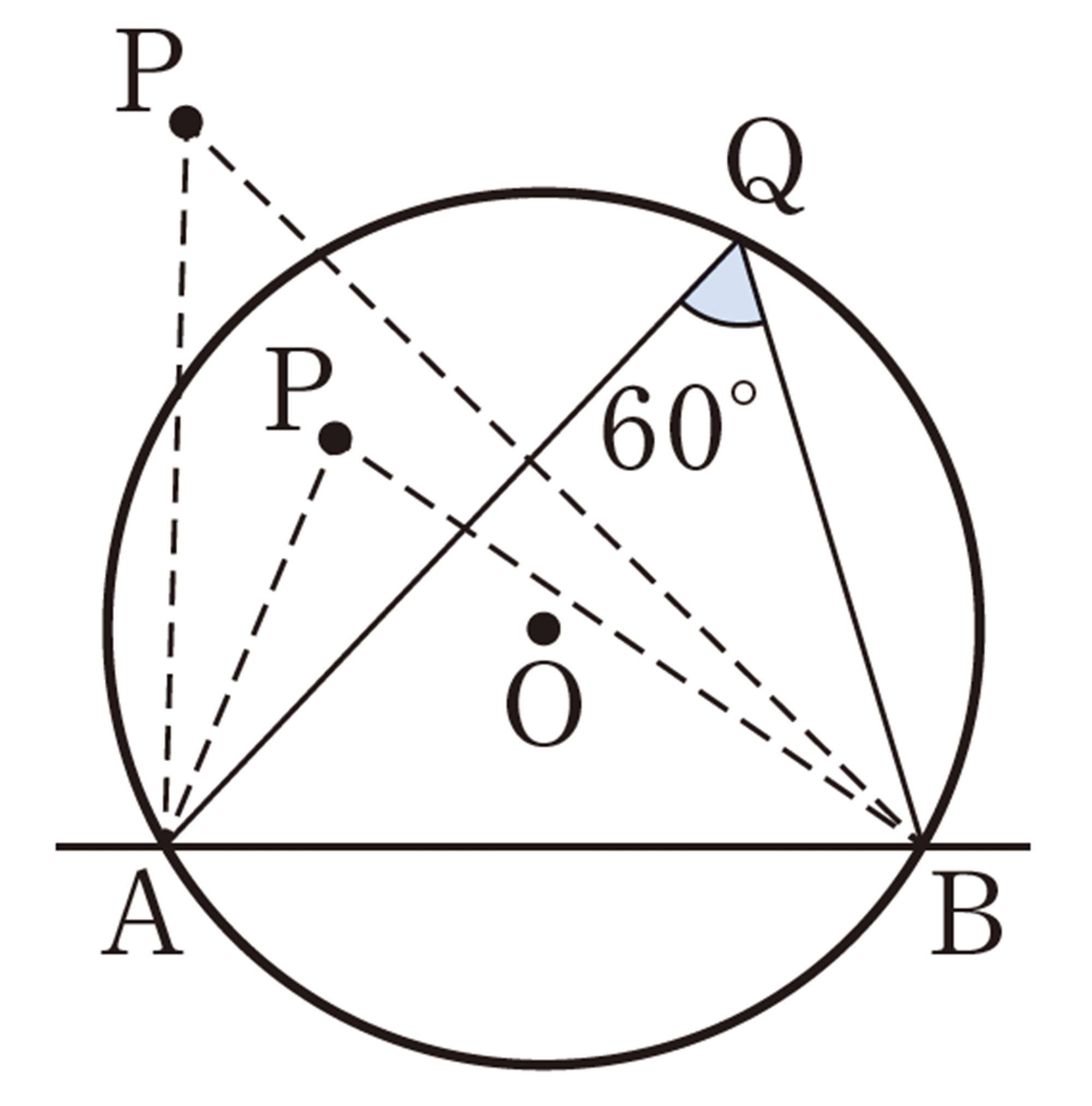
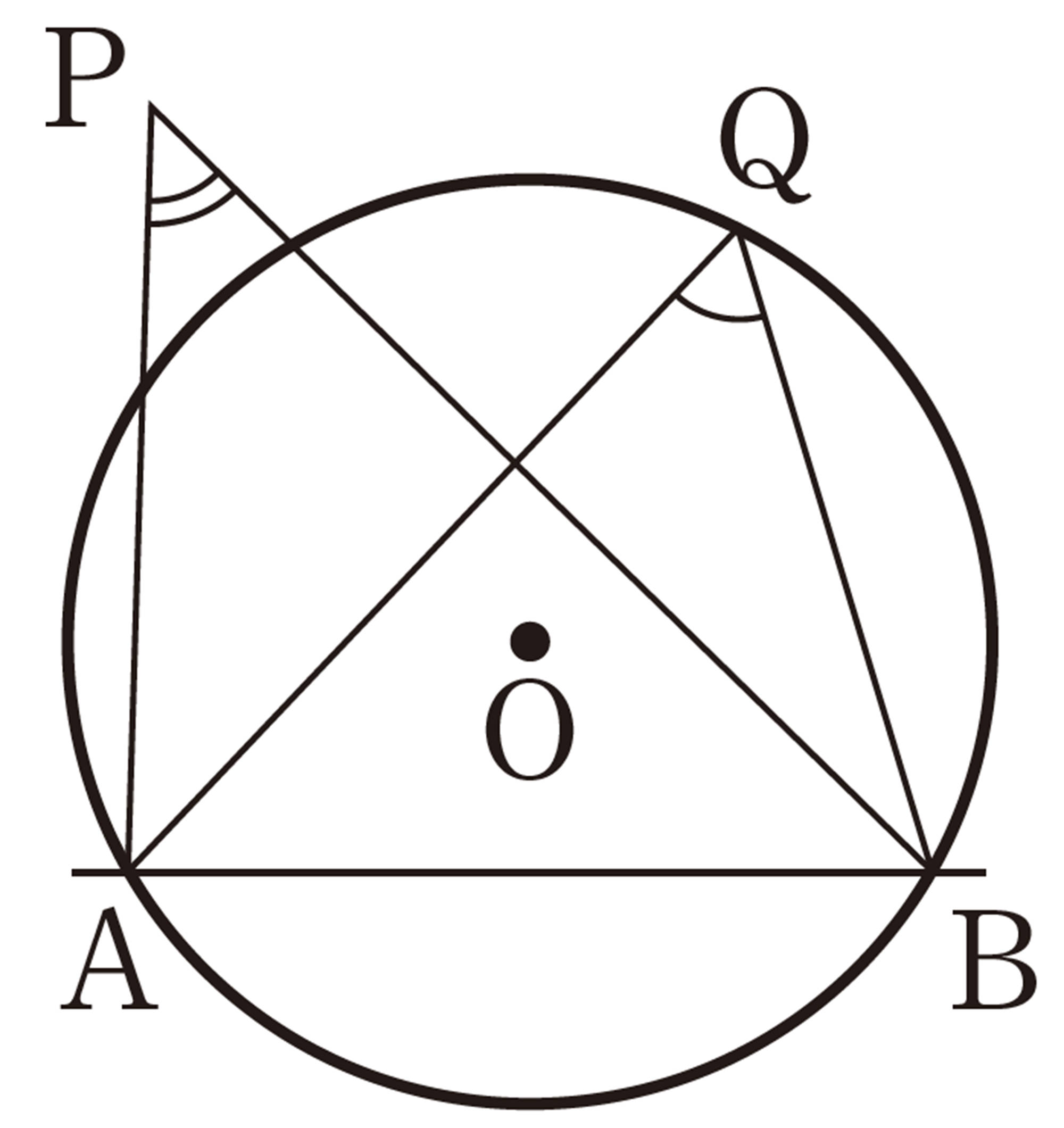
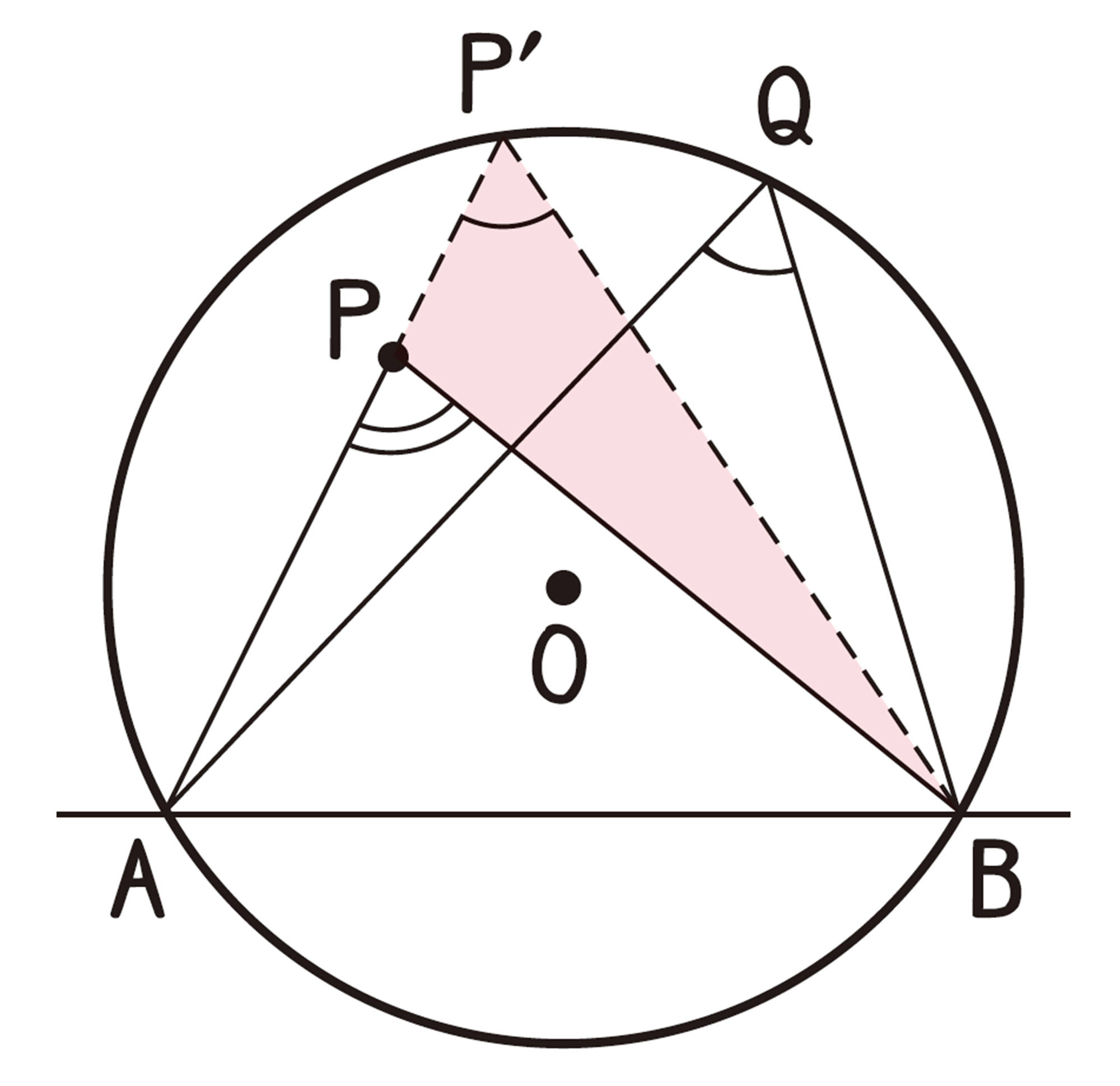
例 １ 上の㋐で，点Pが円Oの内部にあるとき，[mathjax]\(\angle APB \gt \angle AQB\)であることを証明しなさい。
証明
APを延長し，円Oとの交点を[mathjax]\(P´\)とする。
[mathjax]\(\angle APB\)は[mathjax]\(\triangle P´PB\)の外角であるから，
[mathjax]\(\hspace{25pt}\angle APB = \angle AP´B + \angle P´BP\)
したがって，[mathjax]\(\angle APB \gt \angle AP´B \quad \cdots \cdots\mathsf{①}\)
[mathjax]\(\stackrel{\huge\frown}{AB}\)に対する円周角は等しいから，
[mathjax]\(\hspace{25pt}\angle AP´B = \angle AQB \hspace{33pt}\cdots \cdots\mathsf{②}\)
①，②から，[mathjax]\(\angle APB \gt \angle AQB\)
<3年p.199>
問 １ 前ページの㋒で，点Pが円Oの外部にあるとき，[mathjax]\(\angle APB \lt \angle AQB\)であることを証明しなさい。
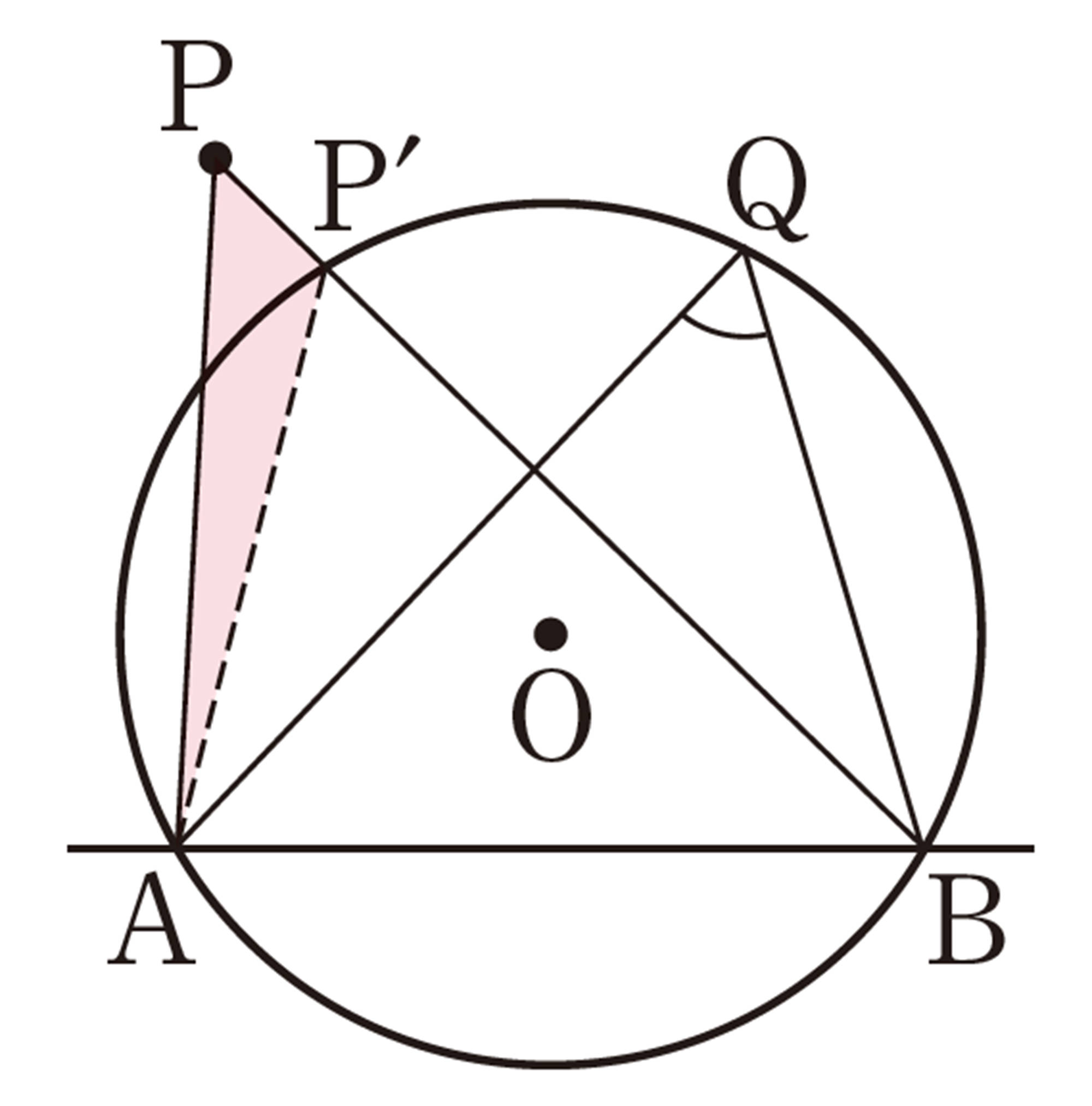
前ページの㋑については，円周角の定理によって，成り立つことがわかる。したがって，これまで調べたことから，[mathjax]\(\angle APB = \angle AQB\)となるのは，点Pが円Oの円周上にある場合に限られることがわかる。
このことから，次の定理が成り立つことがわかる。
定理
円周角の定理の逆
2点P，Qが直線ABについて同じ側にあるとき，
[mathjax]\(\angle APB = \angle AQB\)
ならば，4点 A，P，Q，B は1つの円周上にある。
円周角の定理❷の逆になっているね。
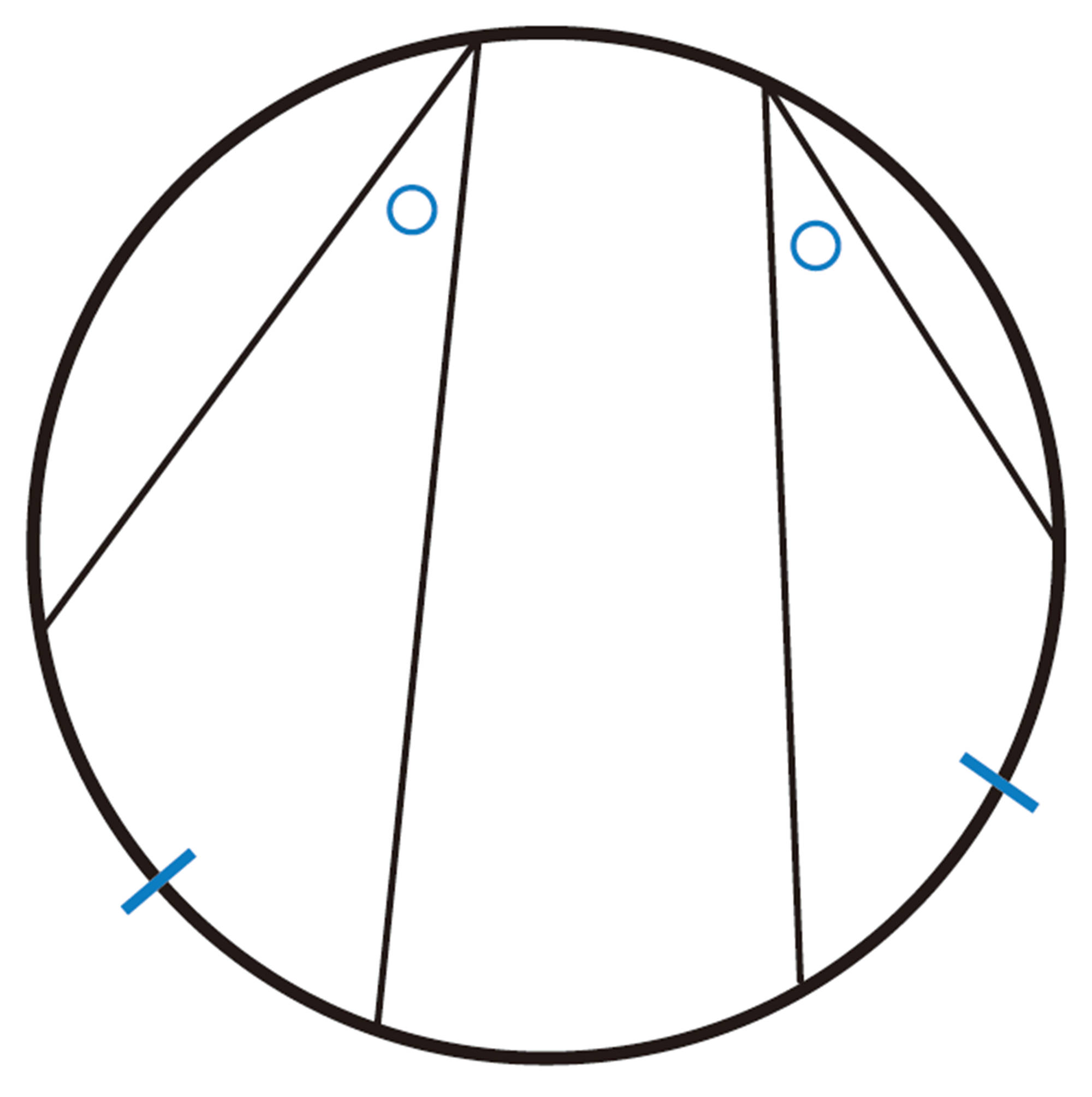
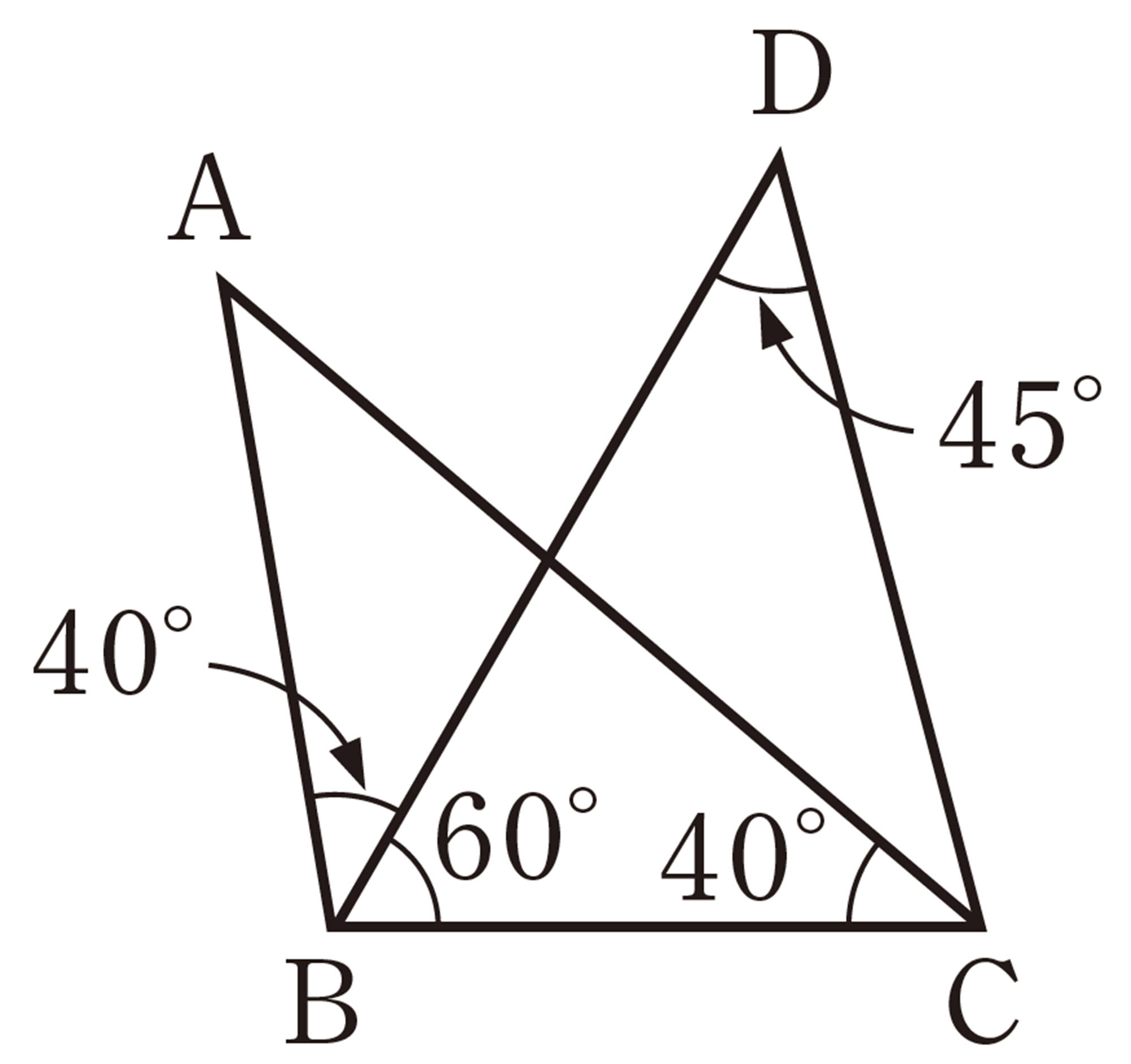
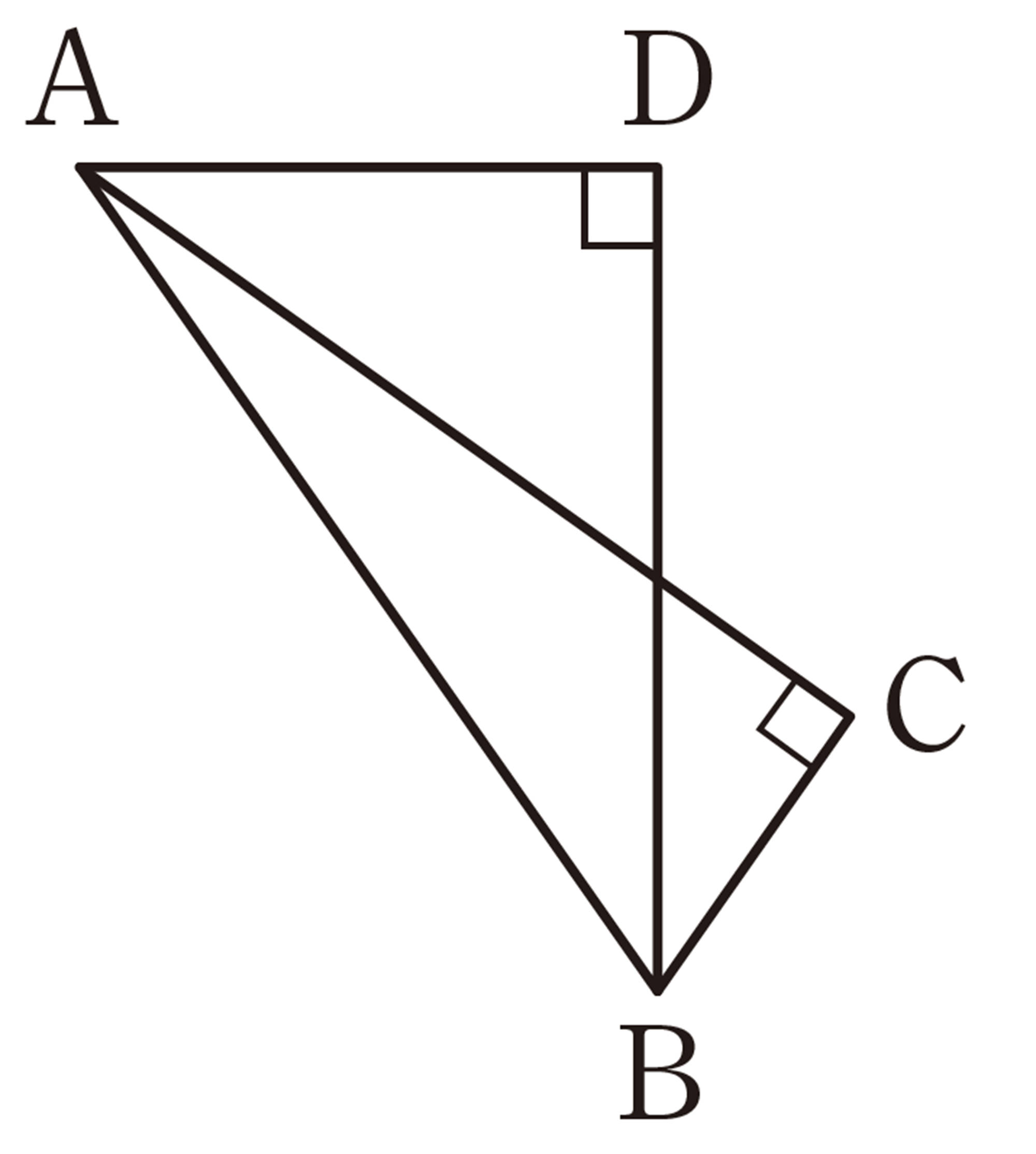
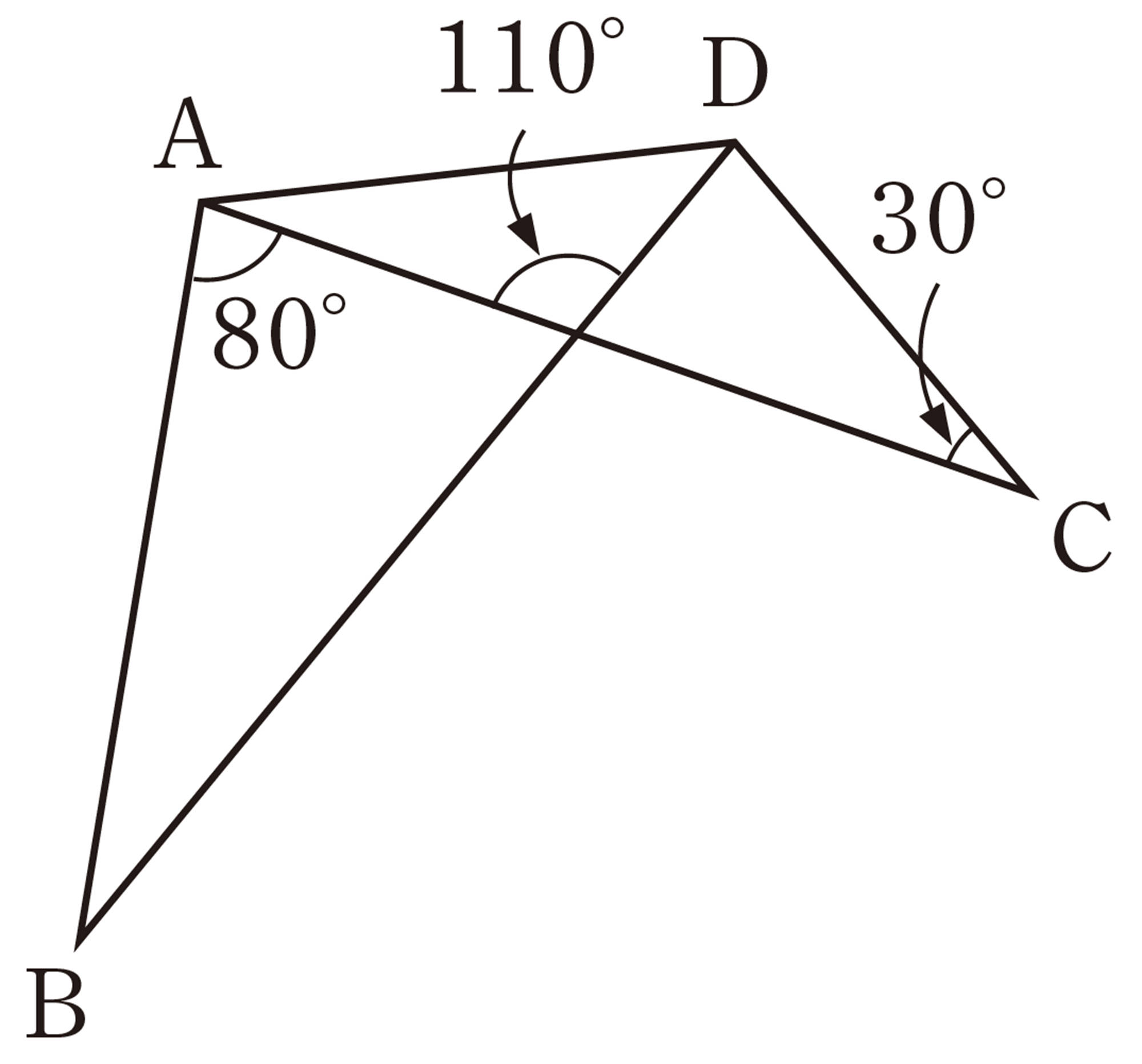
問 ２ 次の図で，4点A，B，C，Dが1つの円周上にあるのはどれですか。
㋐
㋑
㋒
どんなことがわかったかな
円周角の定理の逆が成り立つことから，4点が円周上にあるかどうかを調べることができます。
次の課題へ！
これまでに学んだ円と角の関係は，どんなところで使えるのかな？
P.201
<3年p.200>
確かめよう 1節 円周角と中心角
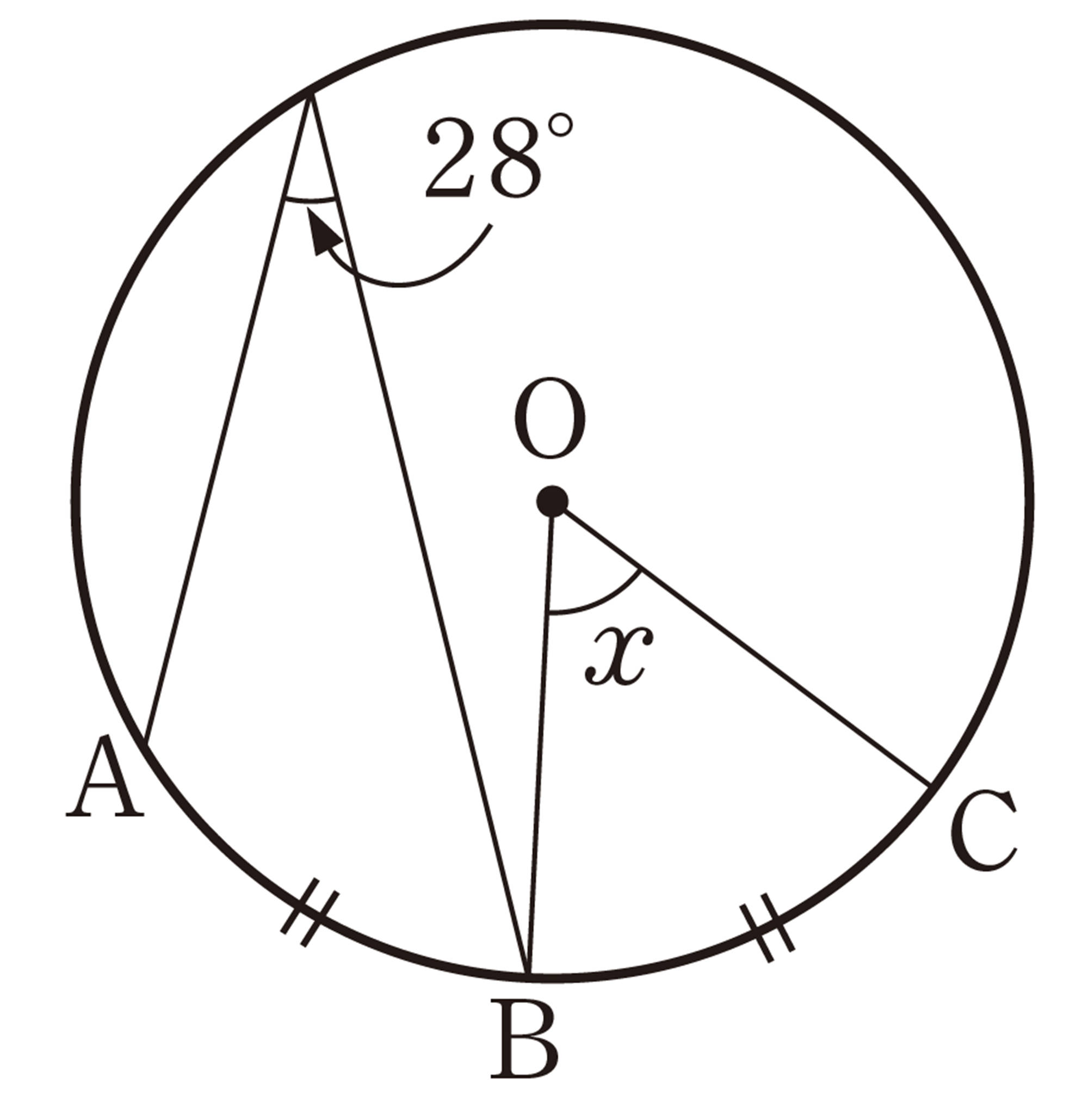
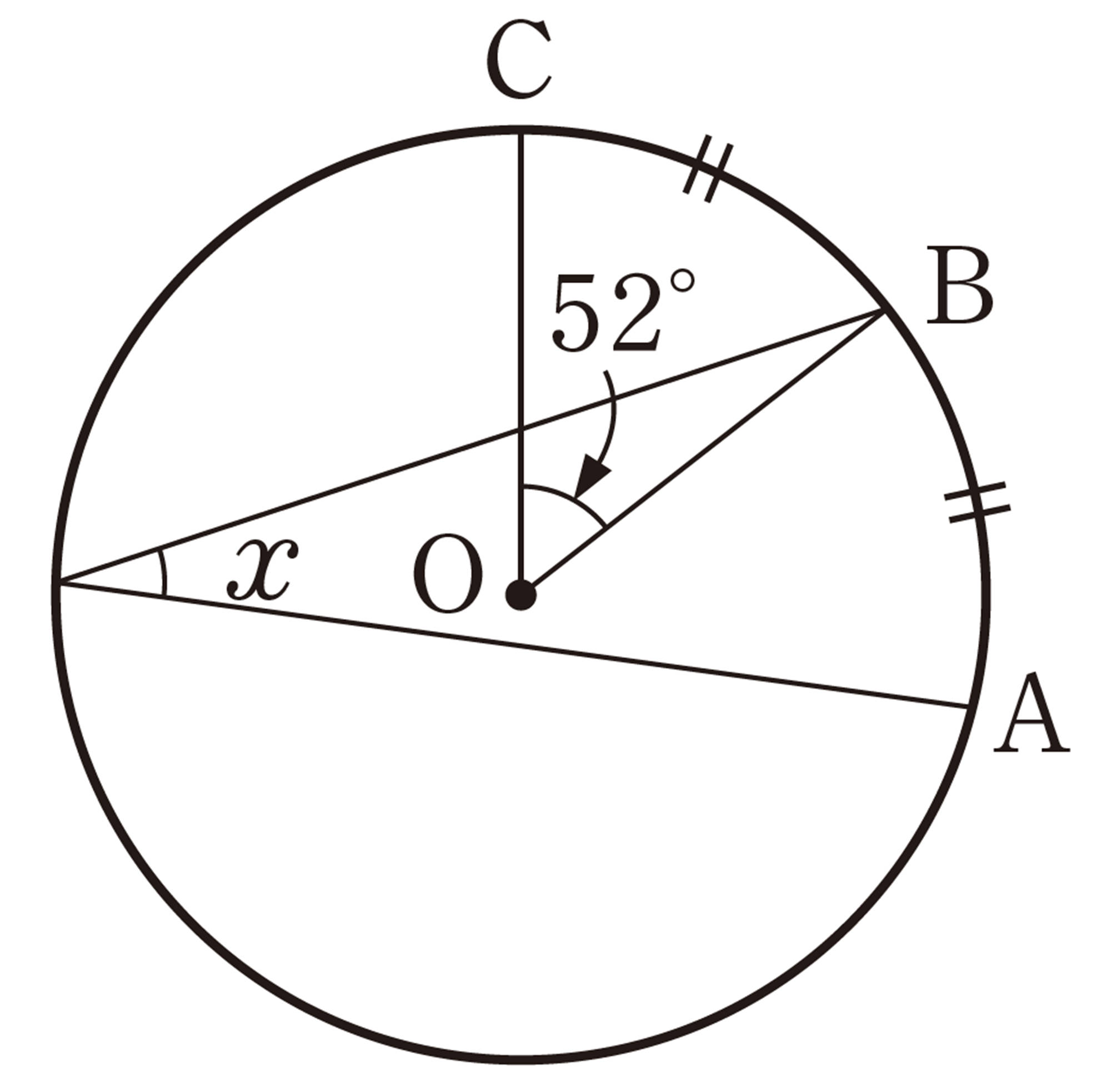
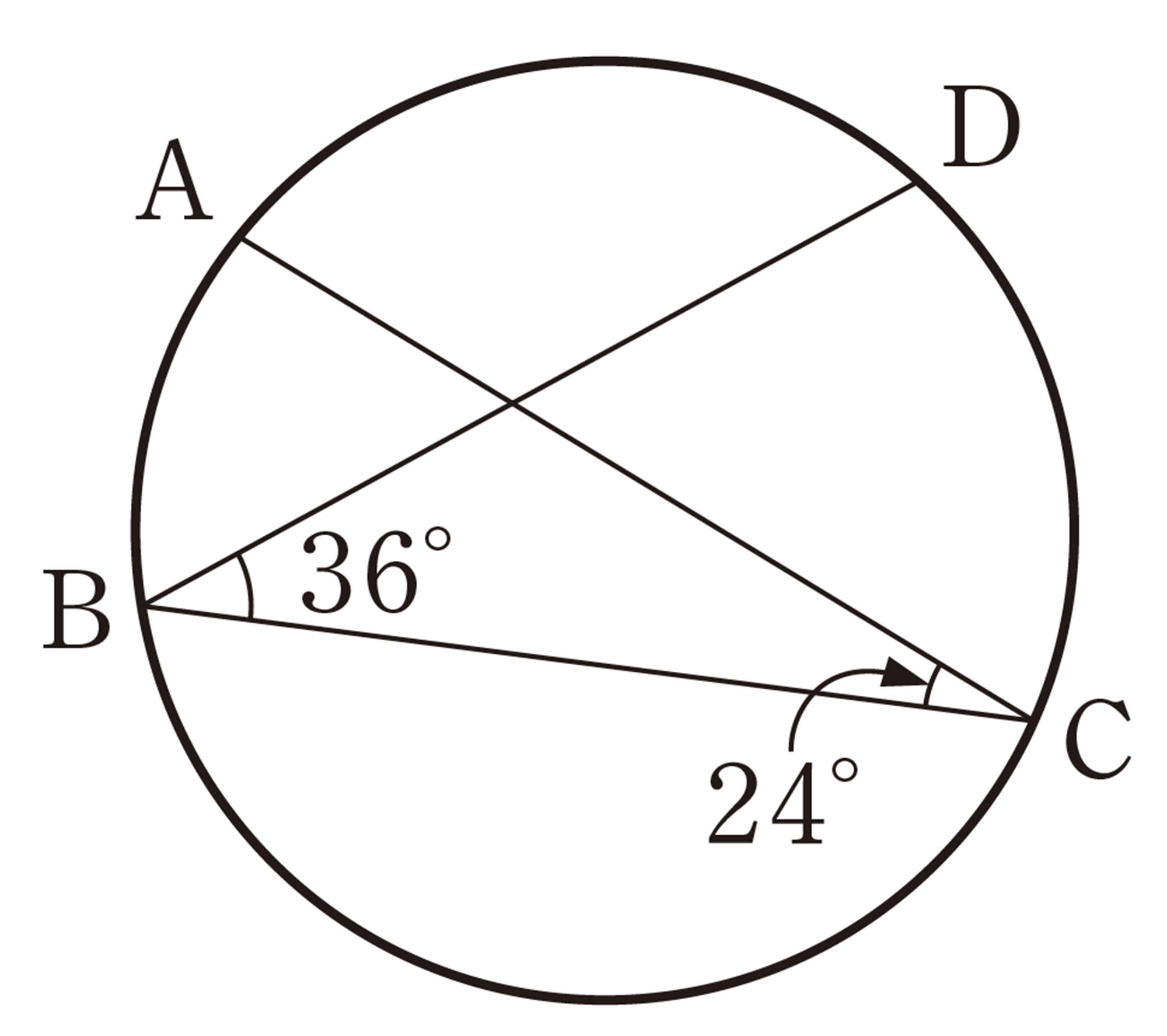
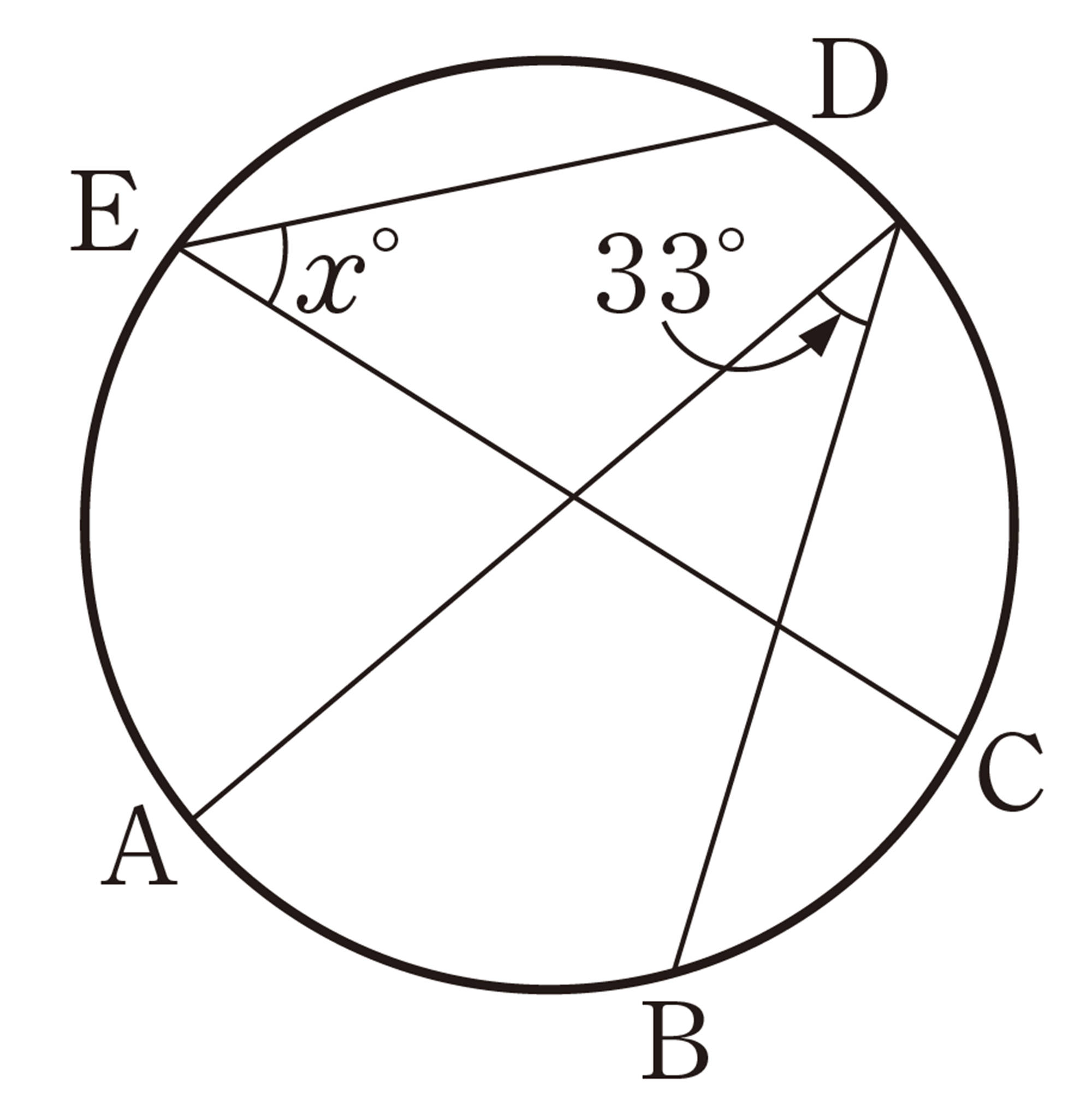
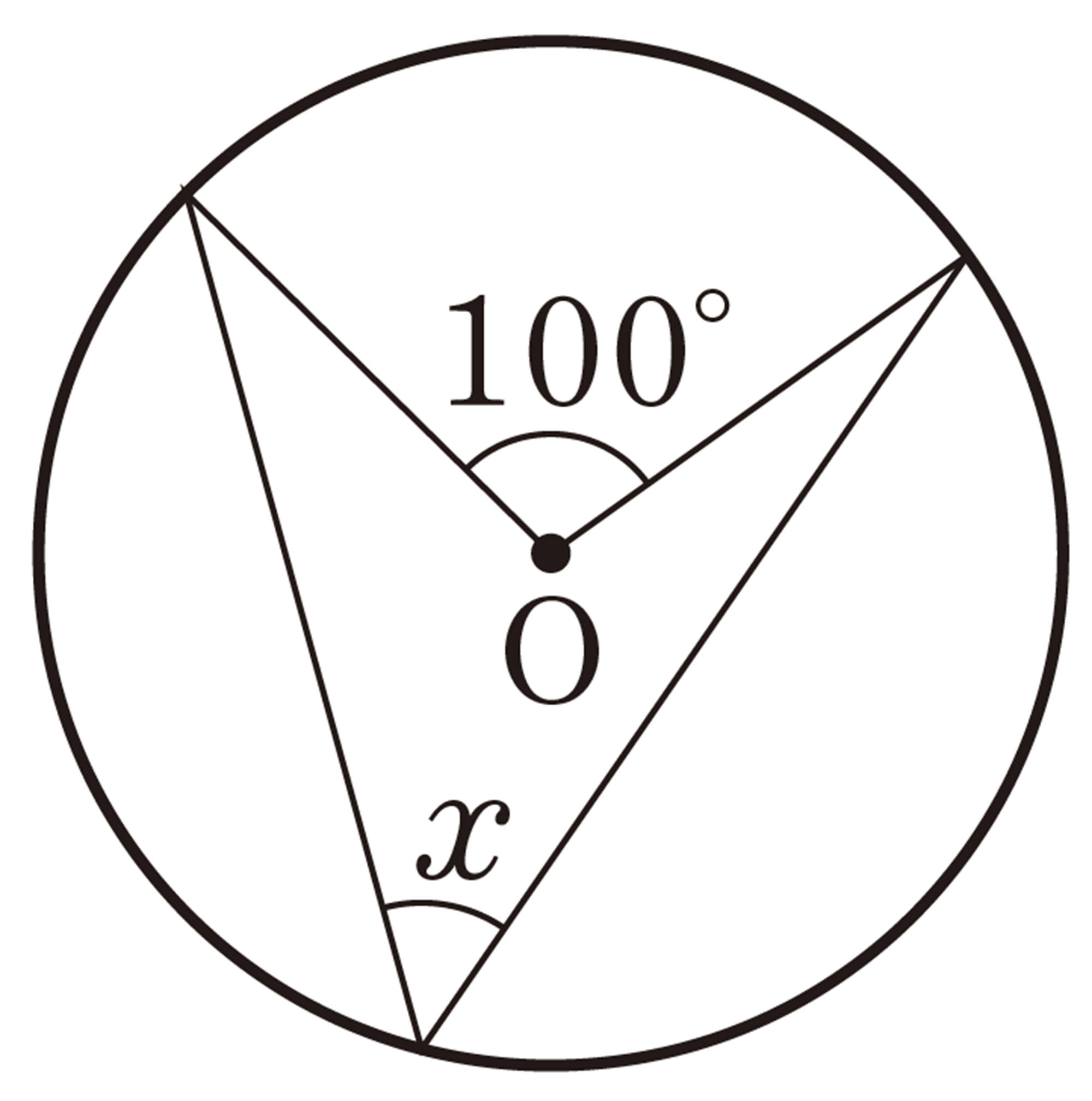
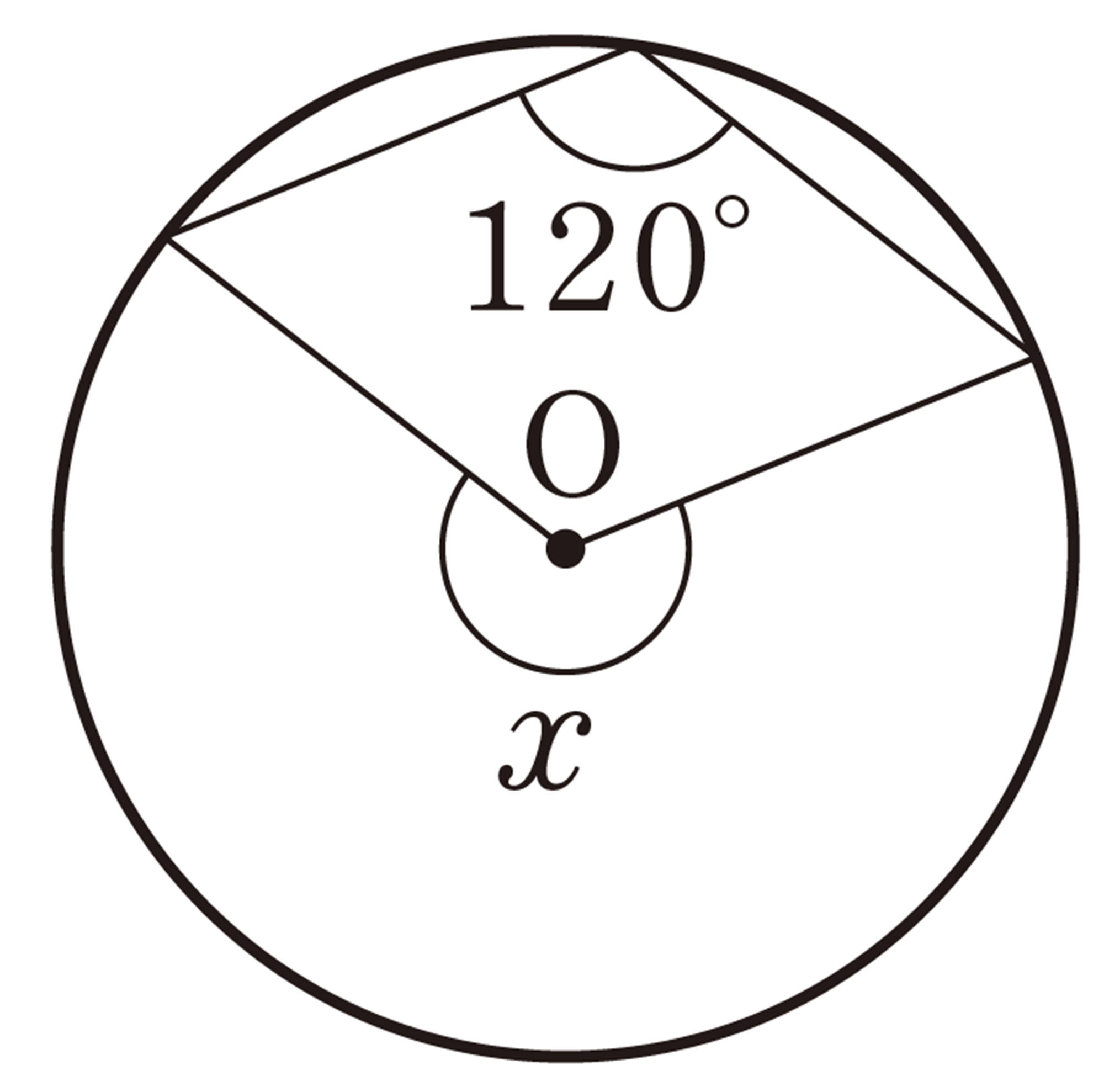
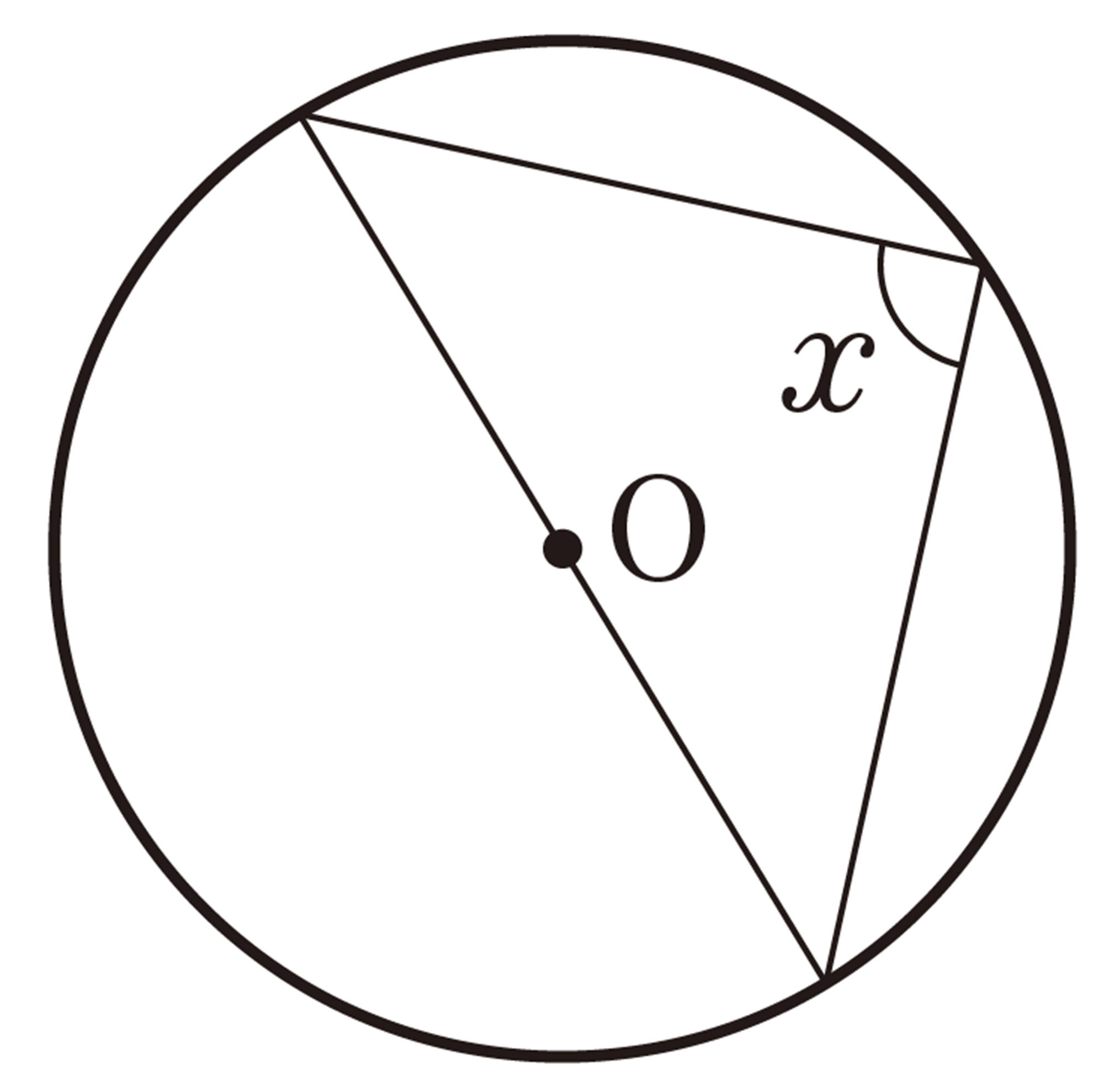
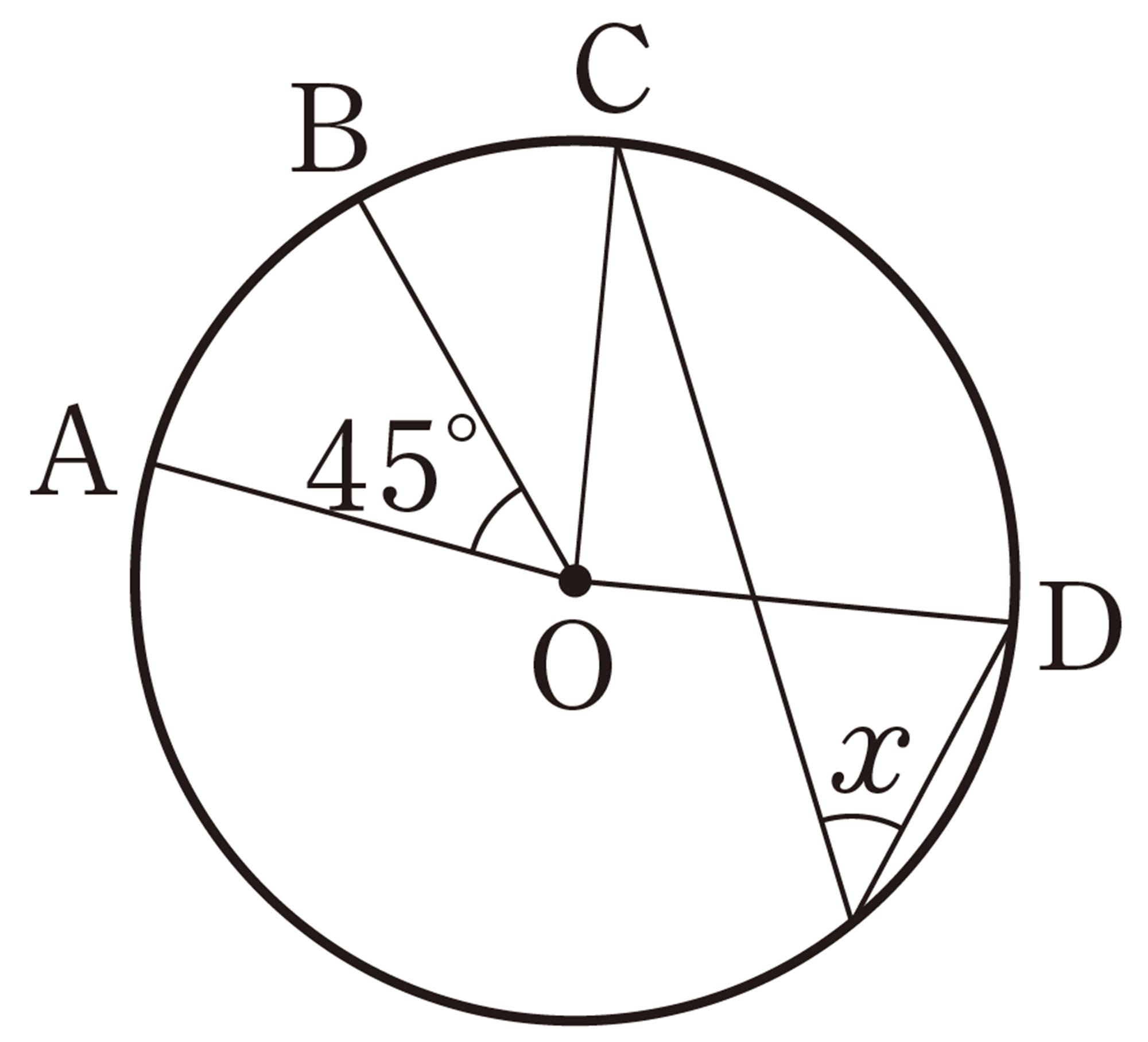
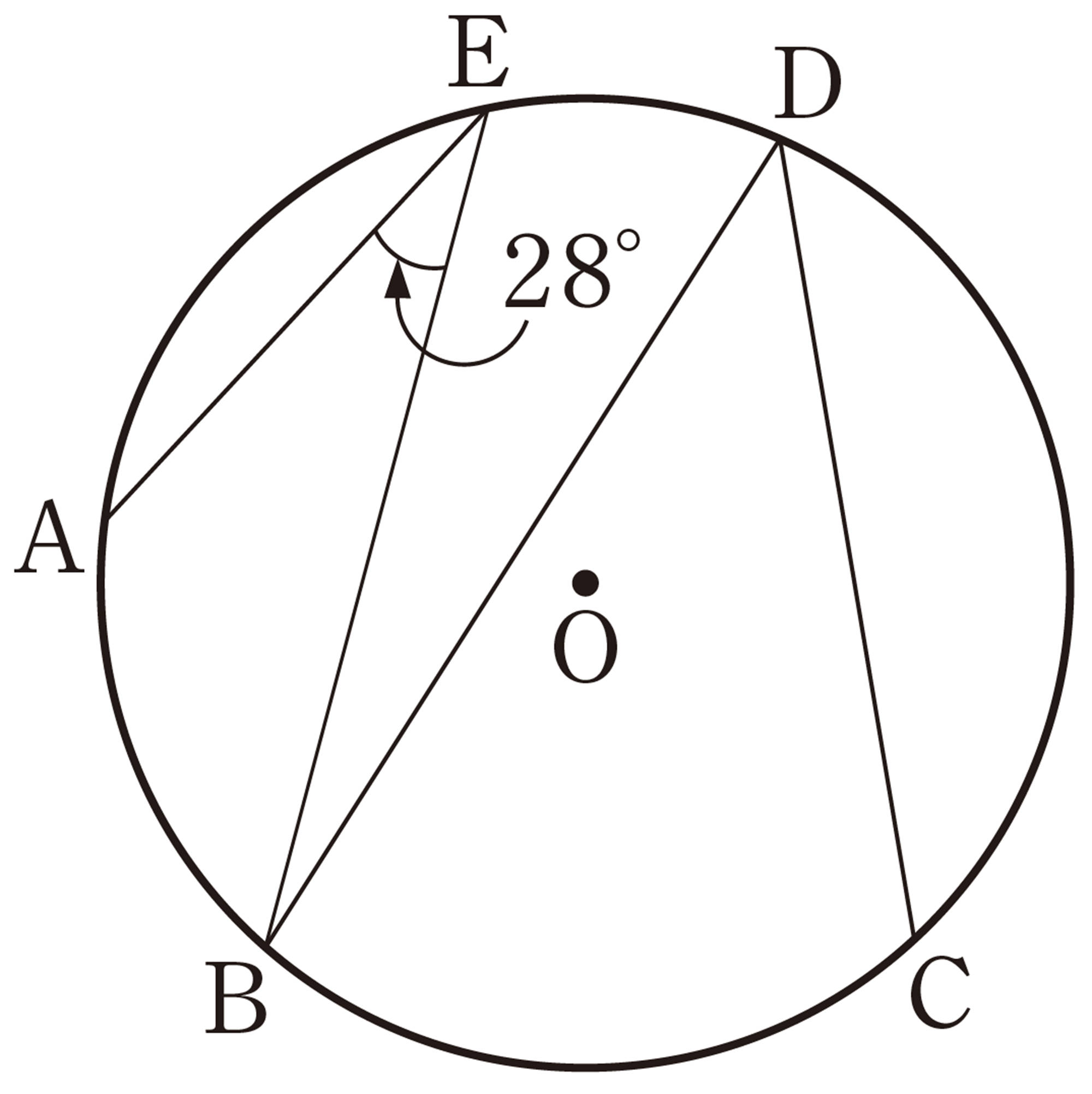
１ 次の図で，[mathjax]\(\angle x\)の大きさを求めなさい。
⑴
⑵
⑶
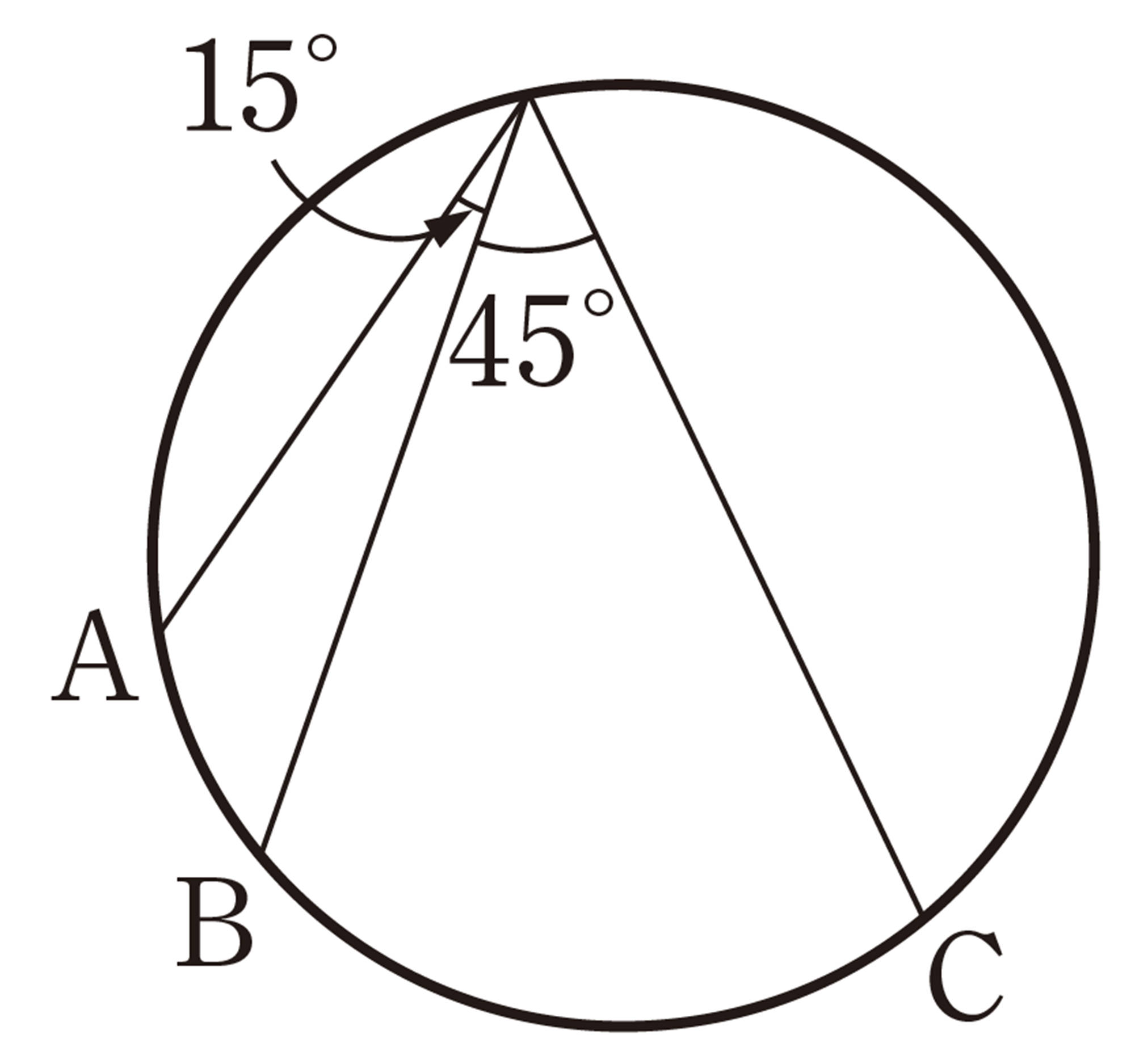
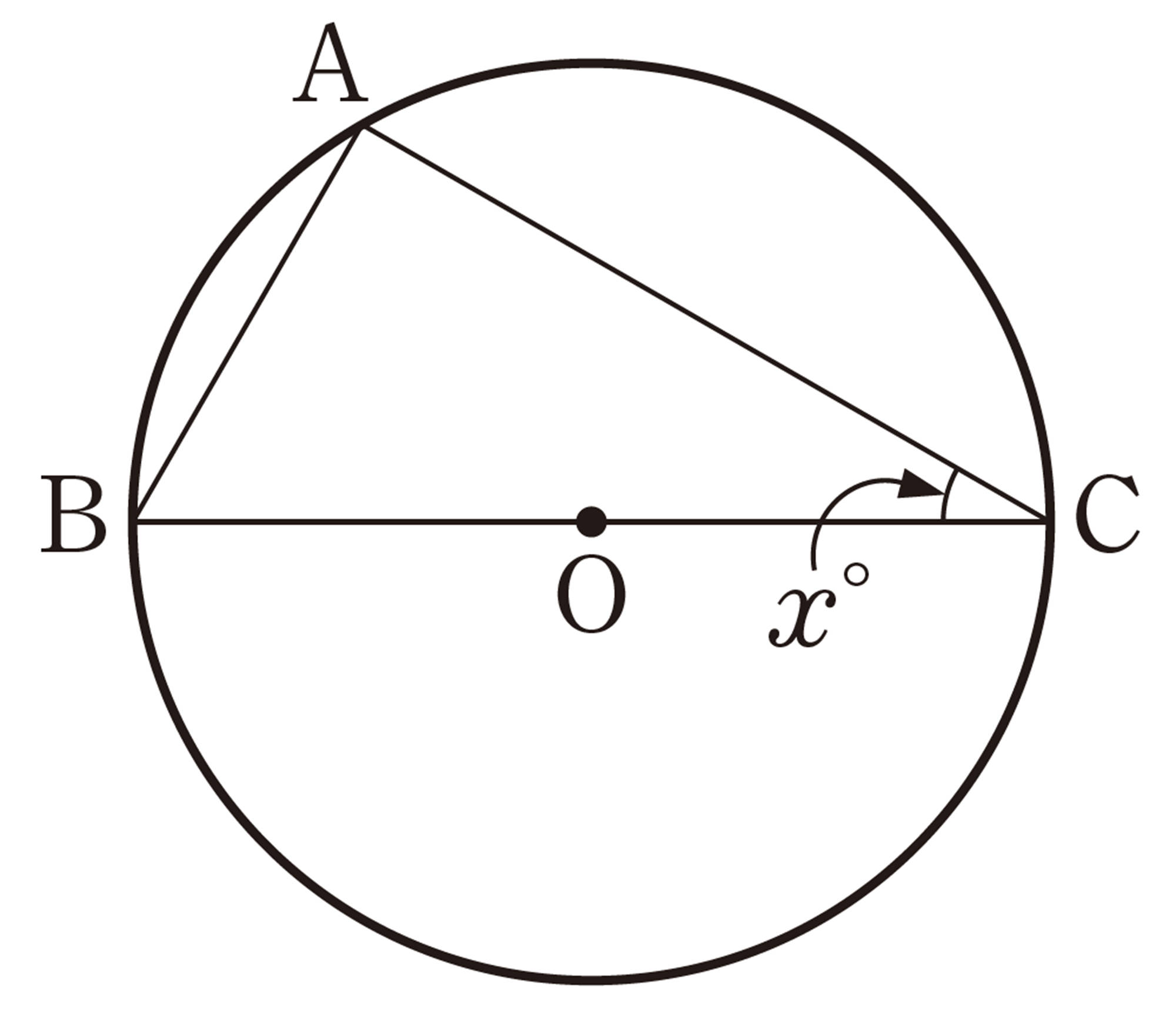
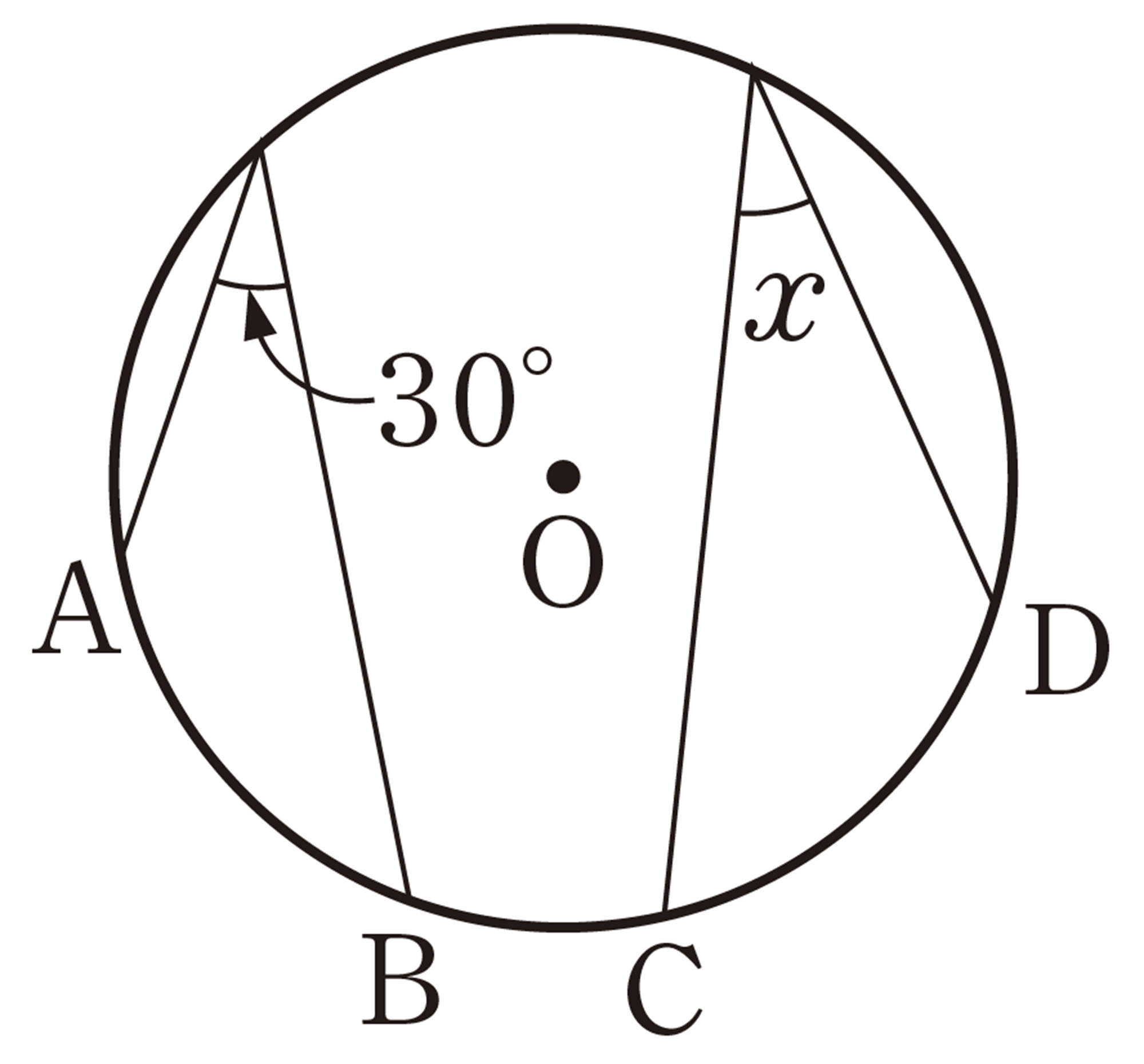
２ 次の図で，[mathjax]\(\angle x\) の大きさを求めなさい。
⑴ [mathjax]\(\stackrel{\huge\frown}{AB} = \stackrel{\huge\frown}{CD}\)
⑵ [mathjax]\(\stackrel{\huge\frown}{CD} = 2 \stackrel{\huge\frown}{AB}\)
４ 右の図のように，[mathjax]\(\triangle ABC\)の頂点B，Cから辺AC，ABに，それぞれ垂線BD，CEを引きます。このとき，点B，Cをふくめて1つの円周上にある4点をいいなさい。
