<3年p.183>
5章のまとめの問題 解答 P.304 基本
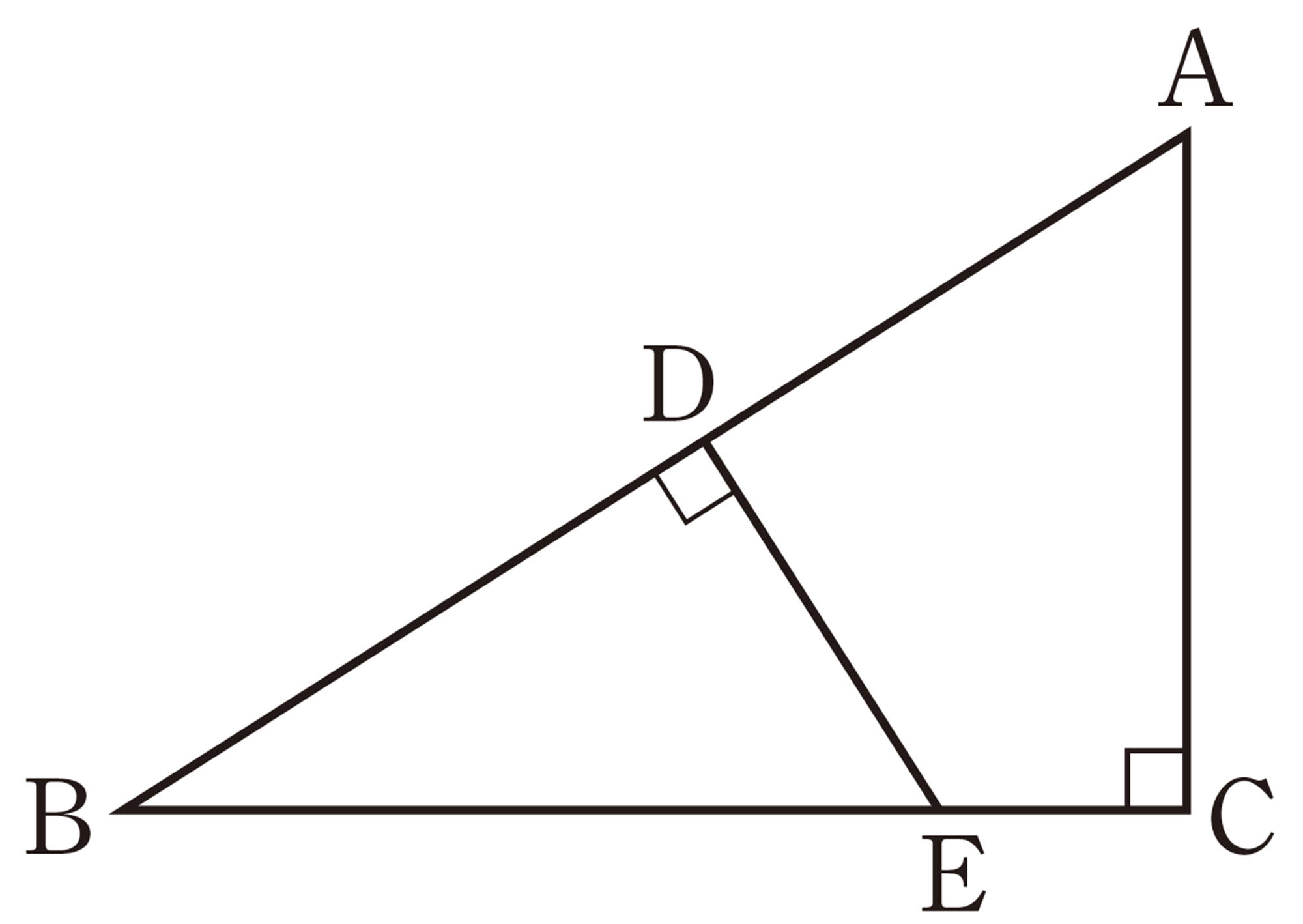
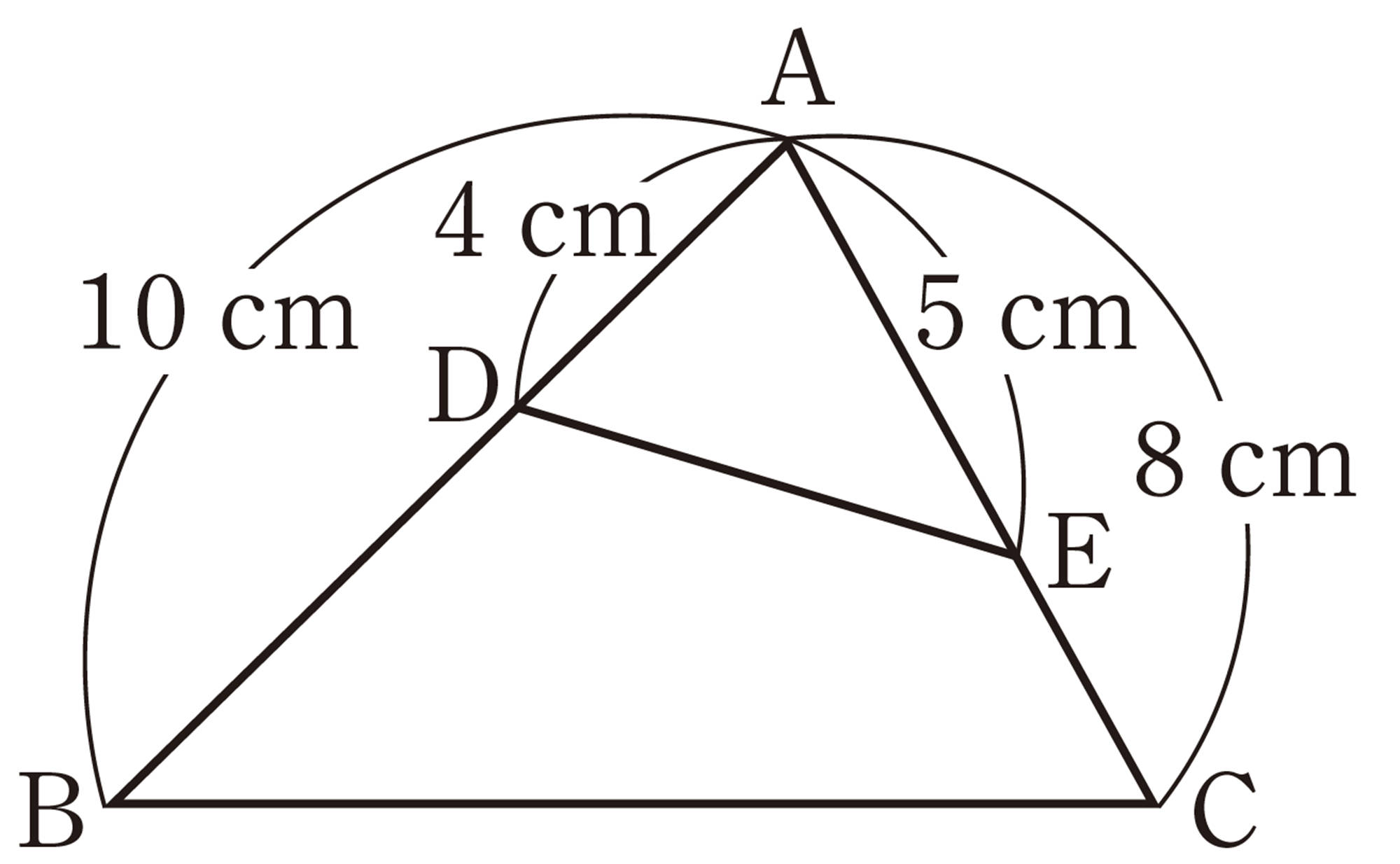
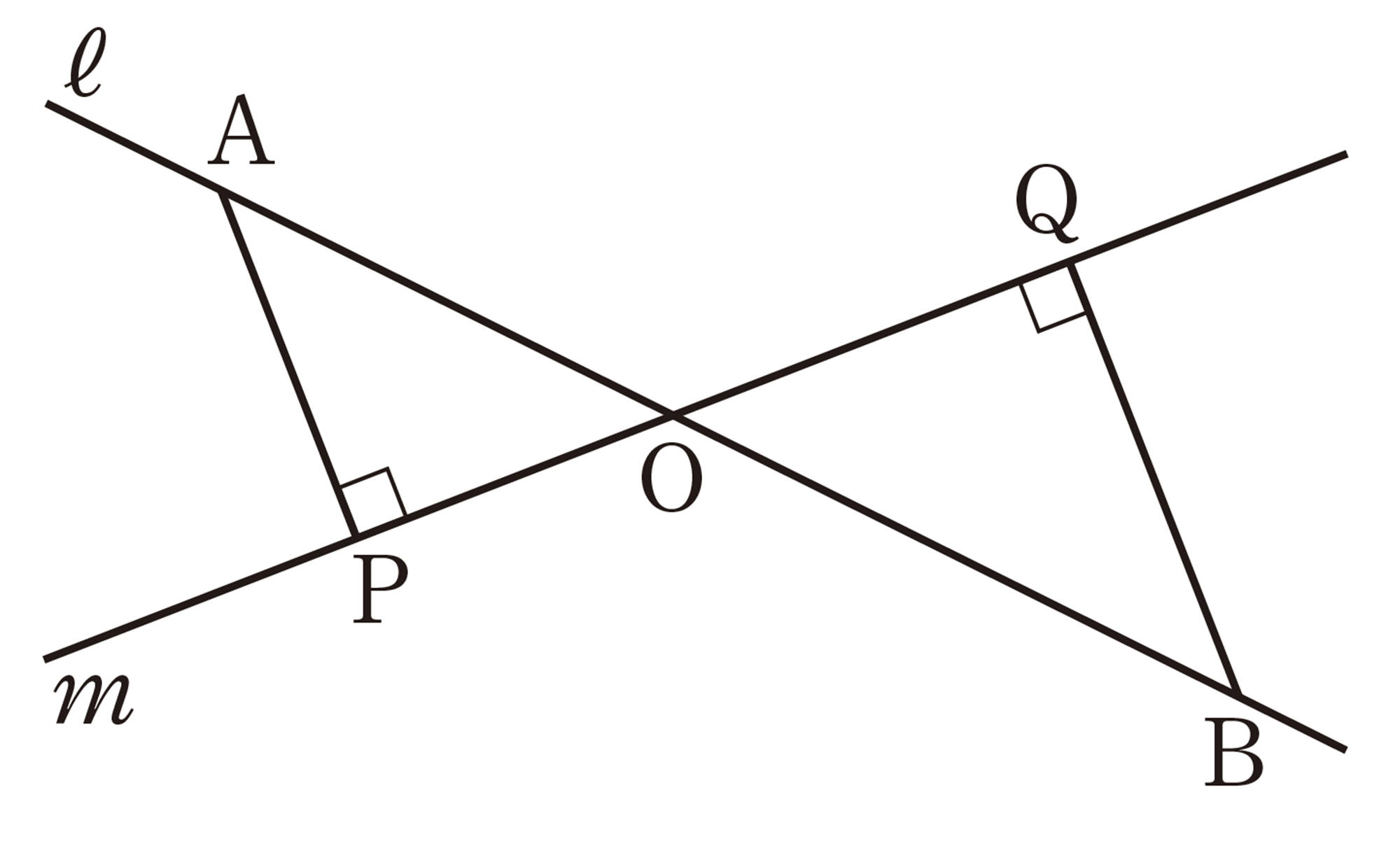
１ 次の図で，相似な三角形を記号[mathjax]\(\backsim\)を使って表しなさい。また，そのときの相似条件をいいなさい。
⑴
⑵
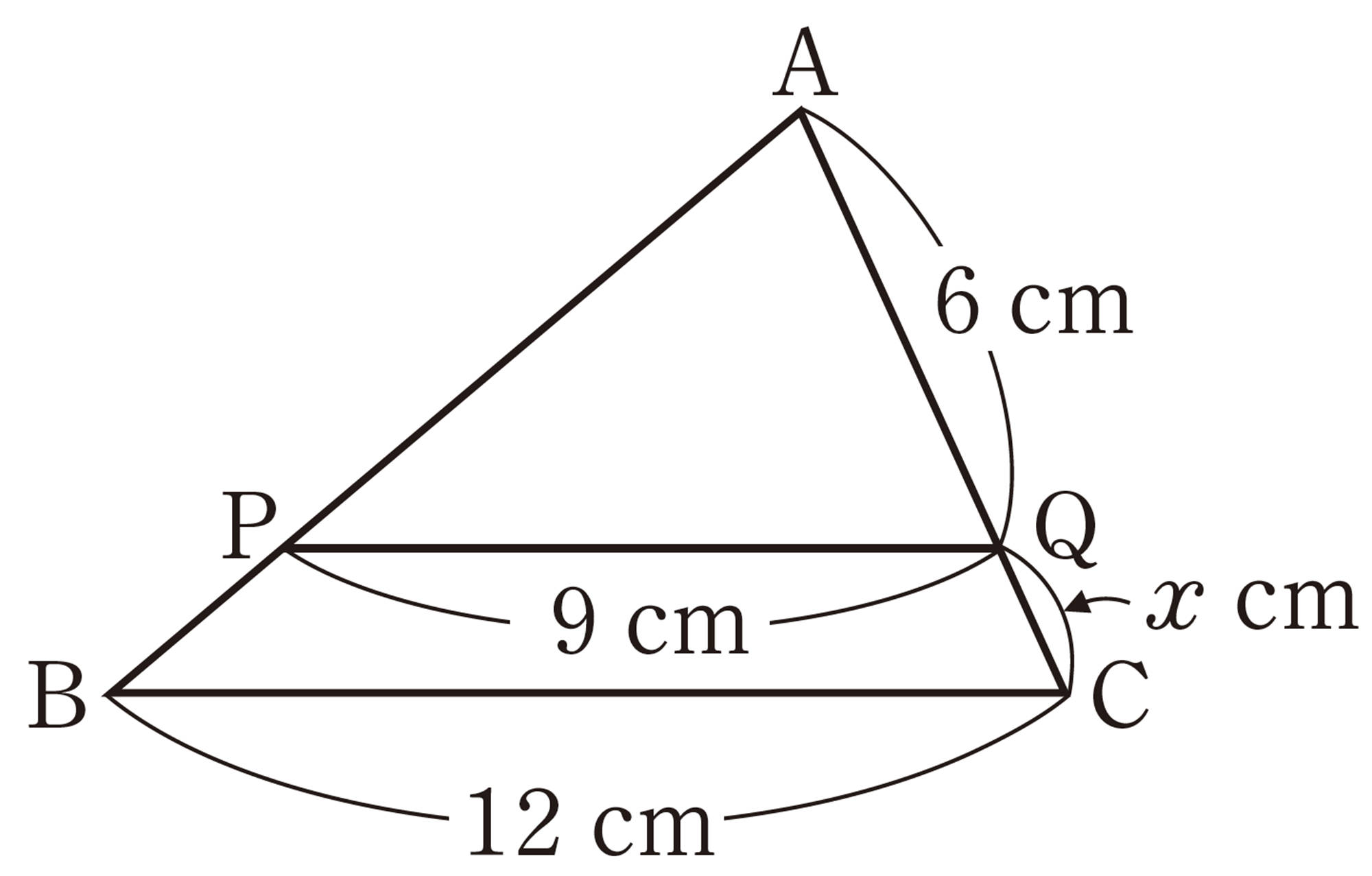
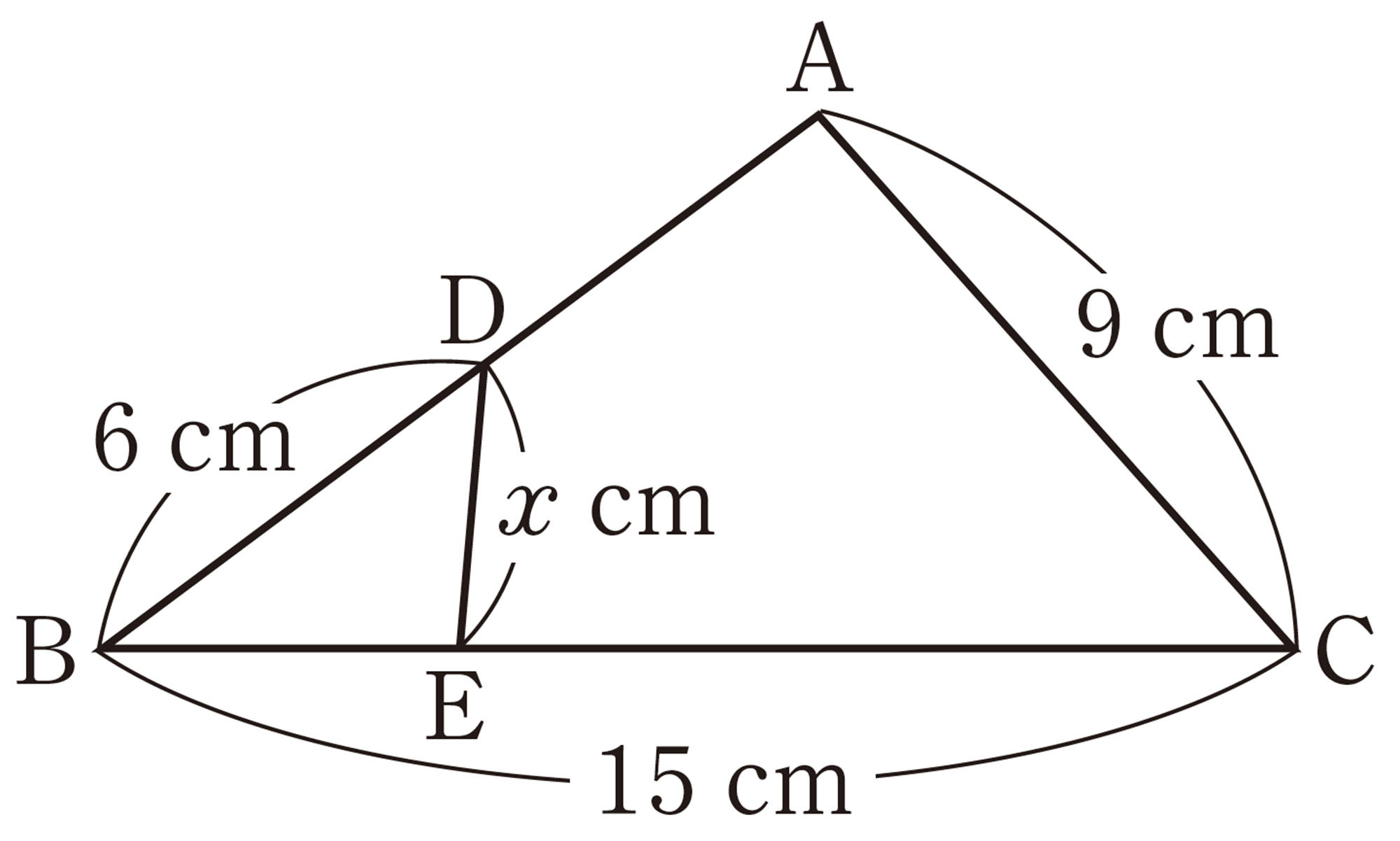
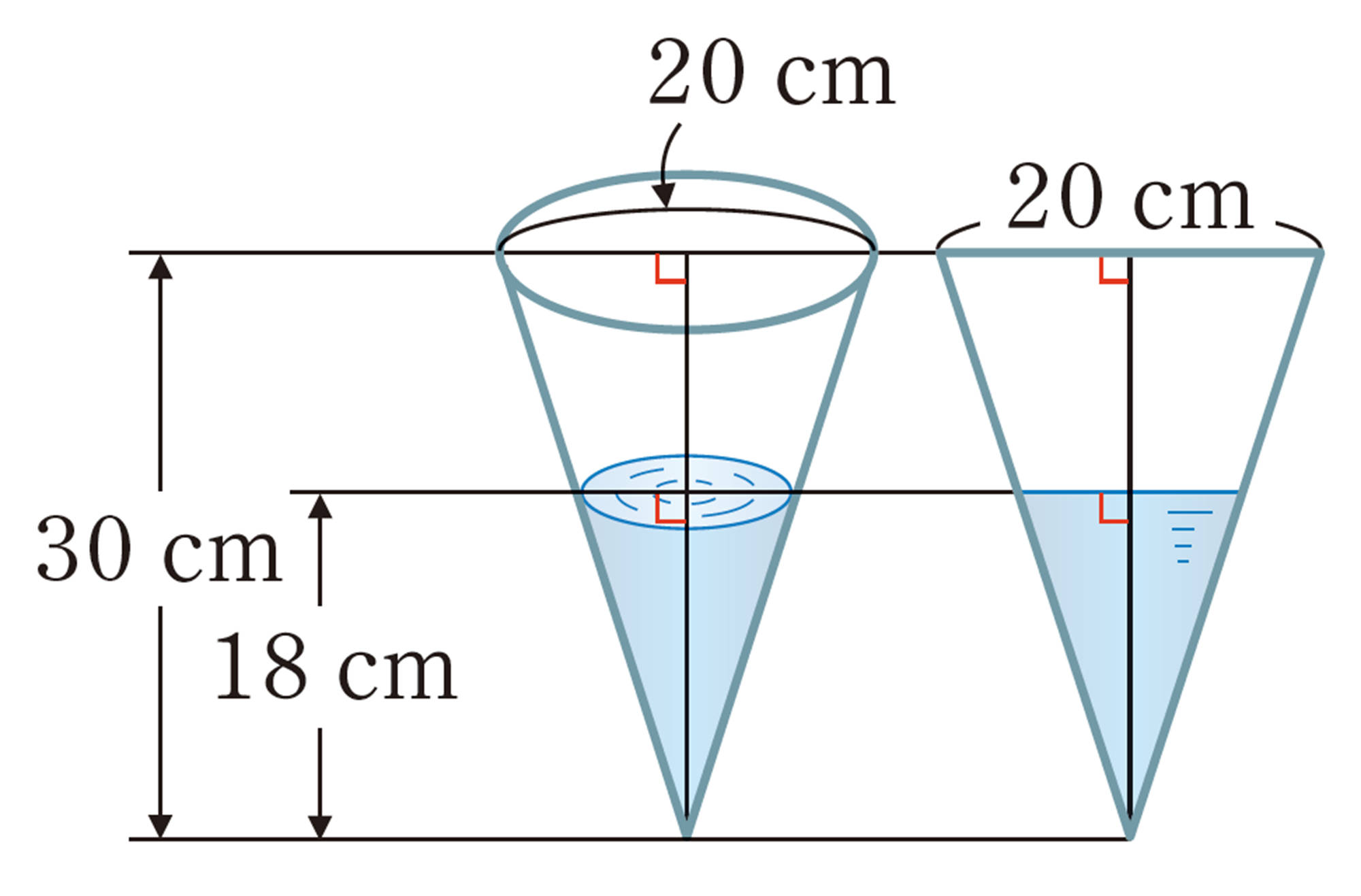
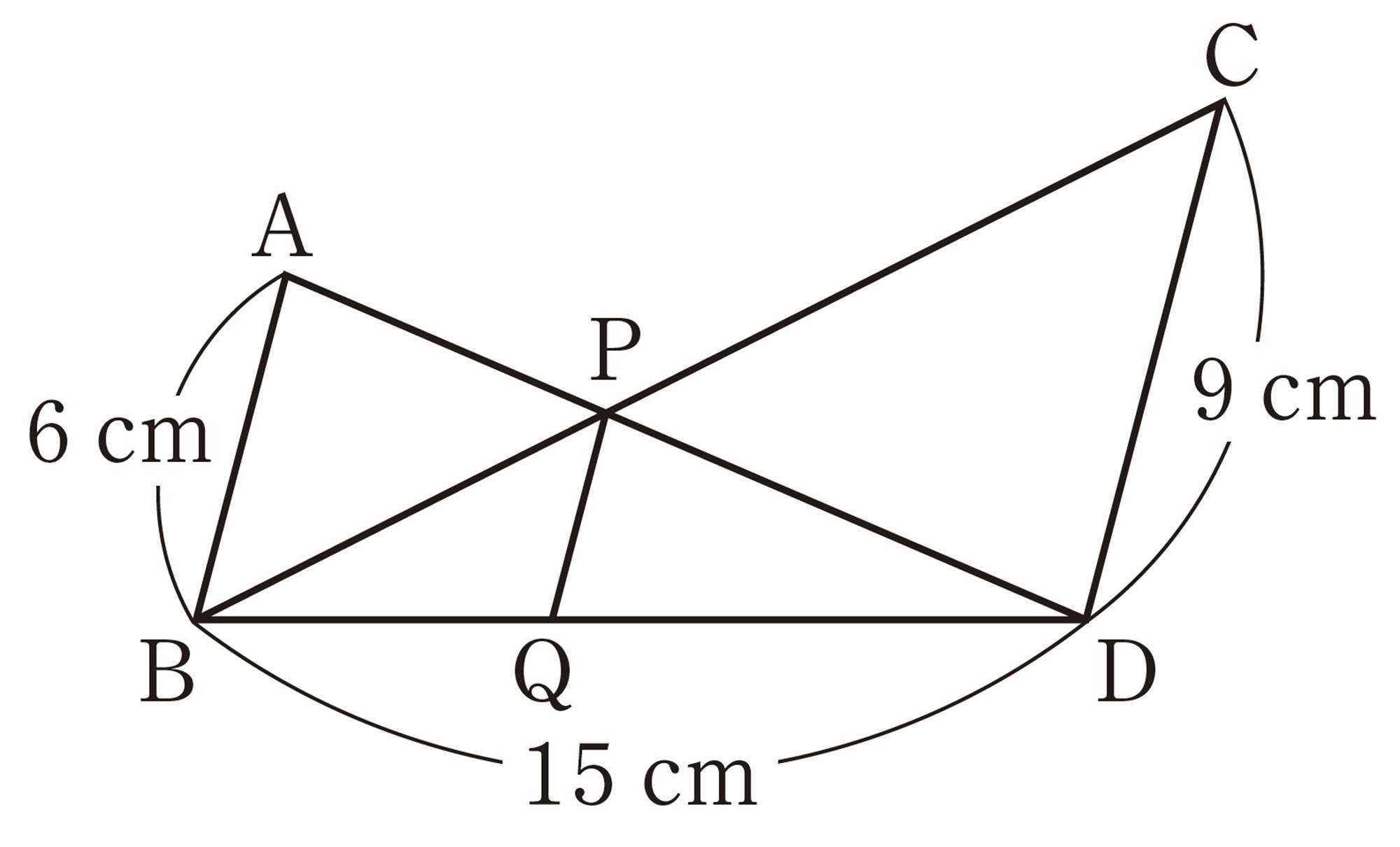
２ 次の図で，xの値を求めなさい。
⑴ [mathjax]\(PQ /\!/ BC\)
⑵ [mathjax]\(\angle BDE = \angle C\)
３ 点Oで交わる2直線ℓ，mがあります。右の図のように，直線ℓ上の2点A，Bから，直線mに垂線AP，BQをそれぞれ引きます。このとき，
[mathjax]\(\triangle APO \backsim \triangle BQO\)
であることを証明しなさい。
４ 底面の直径が20cm，高さが30cmの円錐の形をした容器に，18cmの深さまで水を入れます。次の問いに答えなさい。
⑴ 水面の円の半径を求めなさい。
⑵ 水の体積は，容器の容積の何倍ですか。
<3年p.184>
５章のまとめの問題 応用
１ 右の図で，[mathjax]\(AB /\!/ PQ /\!/ CD\) のとき，線分BQ，PQ の長さを求めなさい。
２ 右の図の四角形 ABCD で，辺 BC，AD，対角線 BD，AC の中点をそれぞれ E，F，G，H とするとき，次の問いに答えなさい。
⑴ 四角形FGEHは平行四辺形であることを証明しなさい。
⑵ [mathjax]\(AB=DC\)のとき，四角形FGEHはどんな四角形になりますか。
３ 右の図のように，長方形の紙ABCDを，点Bが辺CD上にくるように折り返し，その点をQとします。折り目の線分をAPとするとき，[mathjax]\(\triangle ADQ \backsim \triangle QCP\)であることを証明しなさい。
４ 右の図のように，正方形ABCDの辺 BC，CD上に，[mathjax]\(CE=DF\)となる点E，Fをとり，DとE，AとFを結びます。線分DEとAFの交点をHとするとき，[mathjax]\(\triangle ADH \backsim \triangle DFH\)であることを証明しなさい。
<3年p.185>
活用
右の写真は，カップ麺のふつうサイズとビッグサイズの容器です。この2つの容器は相似で，相似比は，約 [mathjax]\(9:10\) になっています。
１ ふつうサイズのカップ麺をつくるために必要な湯の量の目安は300 mLです。ビッグサイズのカップ麺をつくるために必要な湯の量の目安は約何mLですか。
２ 陸さんの妹は，あるスーパーのチラシにあった，ふつうサイズのカップ麺の値段160円，ビッグサイズのカップ麺の値段200円を見て，「容器の高さの比が [mathjax]\(9:10\) で，値段の比が [mathjax]\(4:5\) だから，ふつうサイズの方が割安だ。」と言いました。しかし，陸さんはビッグサイズの方が割安に売られていると考え，その理由を，次の2つの面から説明しました。[mathjax]\(\boxed{\phantom{000}}\)にあてはまる数やことばを入れ，説明を完成させなさい。
①値段
ふつうサイズとビッグサイズの内容量の比は，カップの[mathjax]\(\boxed{\phantom{000}}\)比と考えられるので[mathjax]\(\boxed{\phantom{000}}:\boxed{\phantom{000}}\)である。したがって，ふつうサイズの値段が160円ならば，ビッグサイズの値段は約[mathjax]\(\boxed{\phantom{000}}\)円にするのが適当である。しかし，ビッグサイズの値段は200円である。
したがって，ビッグサイズの方が割安である。
②内容量
ふつうサイズの値段が160円，ビッグサイズの値段が200円であるから，ふつうサイズとビッグサイズの内容量の比は，[mathjax]\(\boxed{\phantom{000}}:\boxed{\phantom{000}}\)にするのが適当である。しかし，ふつうサイズとビッグサイズの内容量の比は，カップの[mathjax]\(\boxed{\phantom{000}}\)比と考えられるので，実際には，[mathjax]\(\boxed{\phantom{000}}:\boxed{\phantom{000}}\)である。
したがって，ビッグサイズの方が割安である。
<3年p.186>
深めよう
問題づくりにチャレンジ！
相似な図形について学んだことを利用して，問題をつくってみましょう。
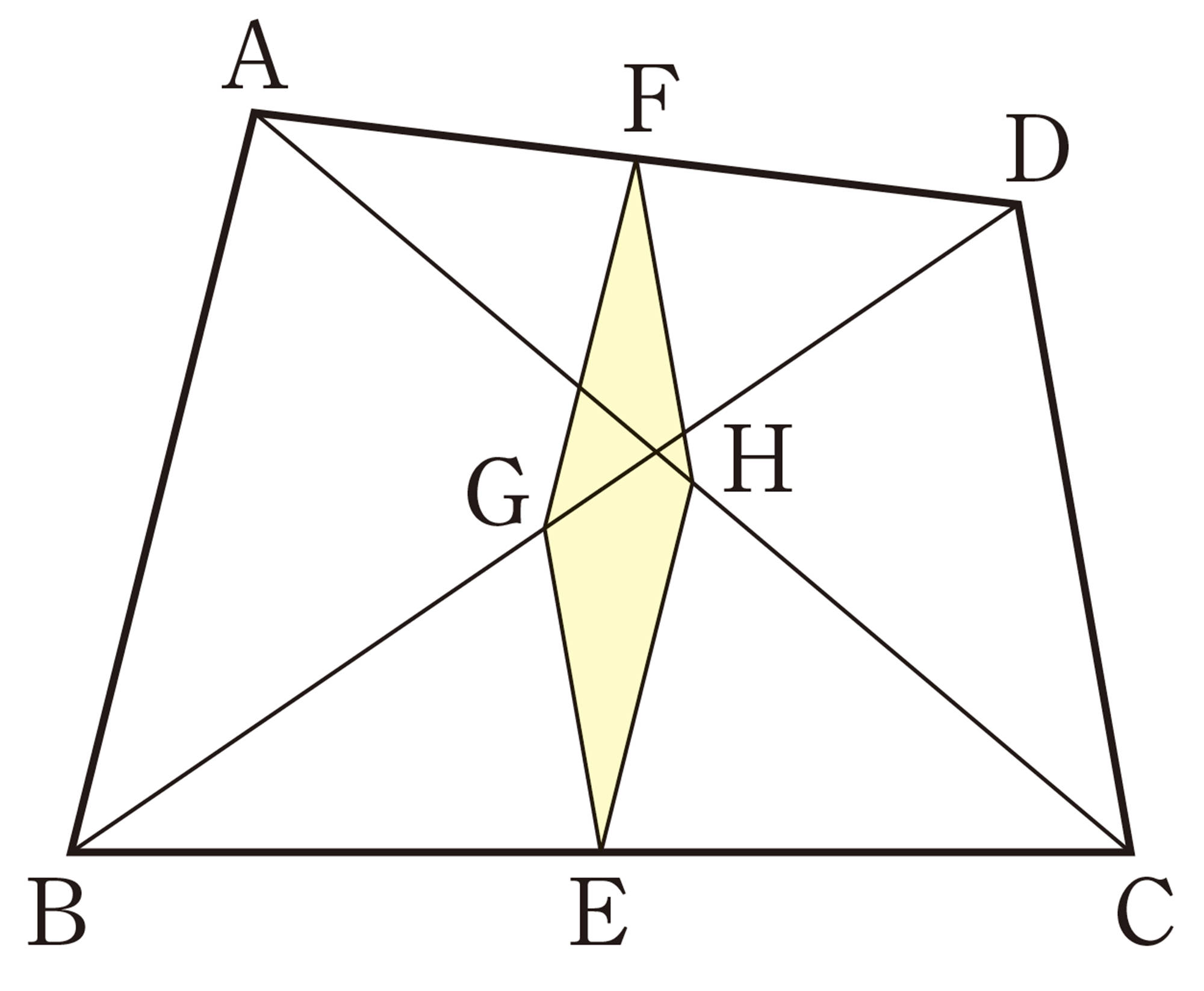
① 次の図のように，▱ABCDの辺BC，CD，DAの中点をそれぞれE，F，Gとし，AとE，GとCを結びます。また，線分BF，辺ADをそれぞれ延長してその交点をHとし，線分BHと線分AE，GCとの交点をそれぞれI，Jとします。この図を使って，相似な図形の性質を利用して解くことのできる問題を，いろいろつくってみましょう。
拓真さんの問題
[mathjax]\(\triangle AIH\)と[mathjax]\(\triangle EIB\)が相似になることを証明しなさい。
美月さんの問題
[mathjax]\(\triangle EIB\)の面積を10cm²とするとき，[mathjax]\(\triangle AIH\)の面積を求めなさい。
② グループの中で，自分がつくった問題やその解き方を説明してみましょう。また，グループごとにつくった問題をまとめ，発表しましょう。
① どんな性質が使えるか ② どんなくふうをしたか についても発表しよう。
