<3年p.167>
２ 線分の比と平行線
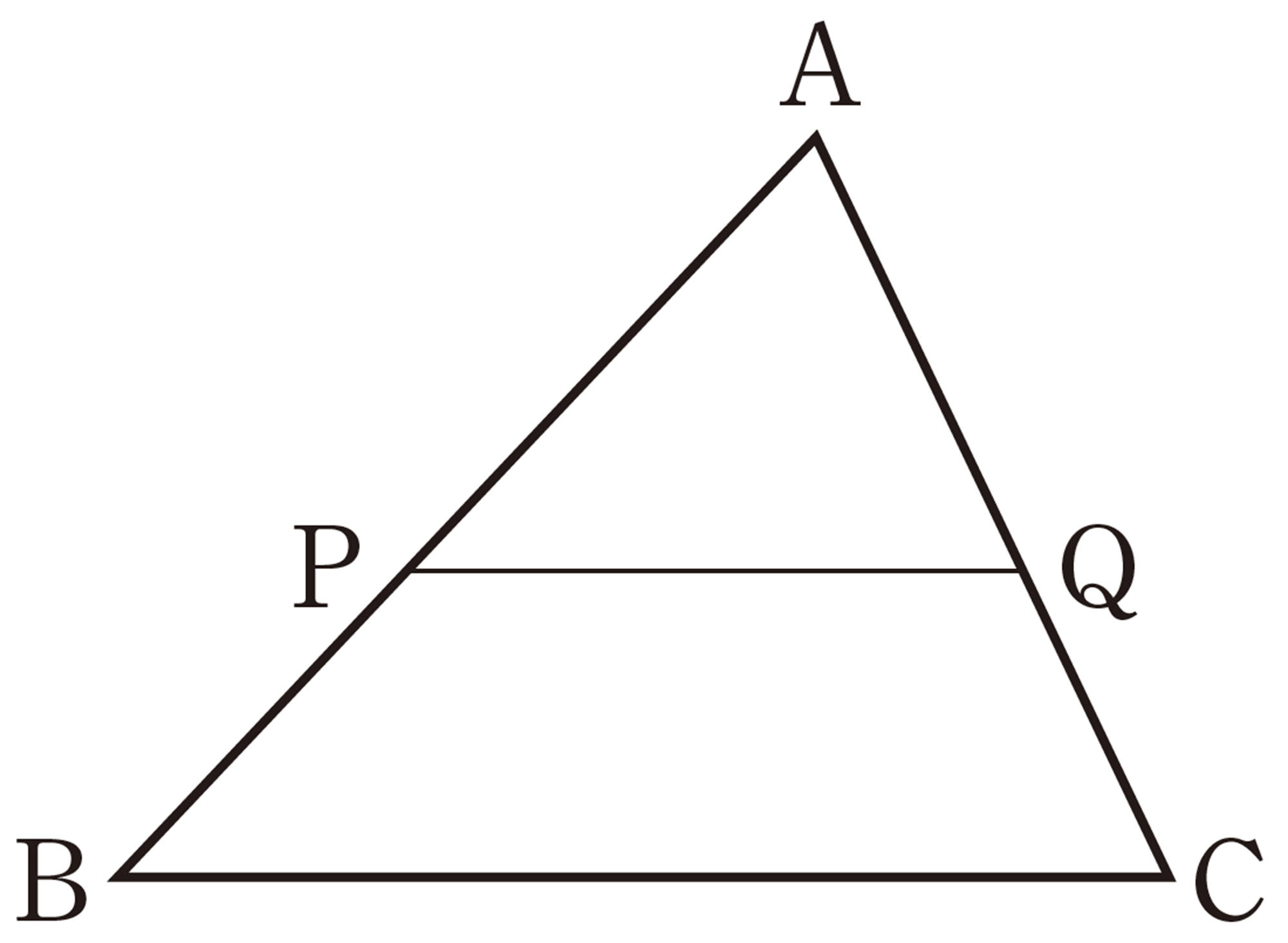
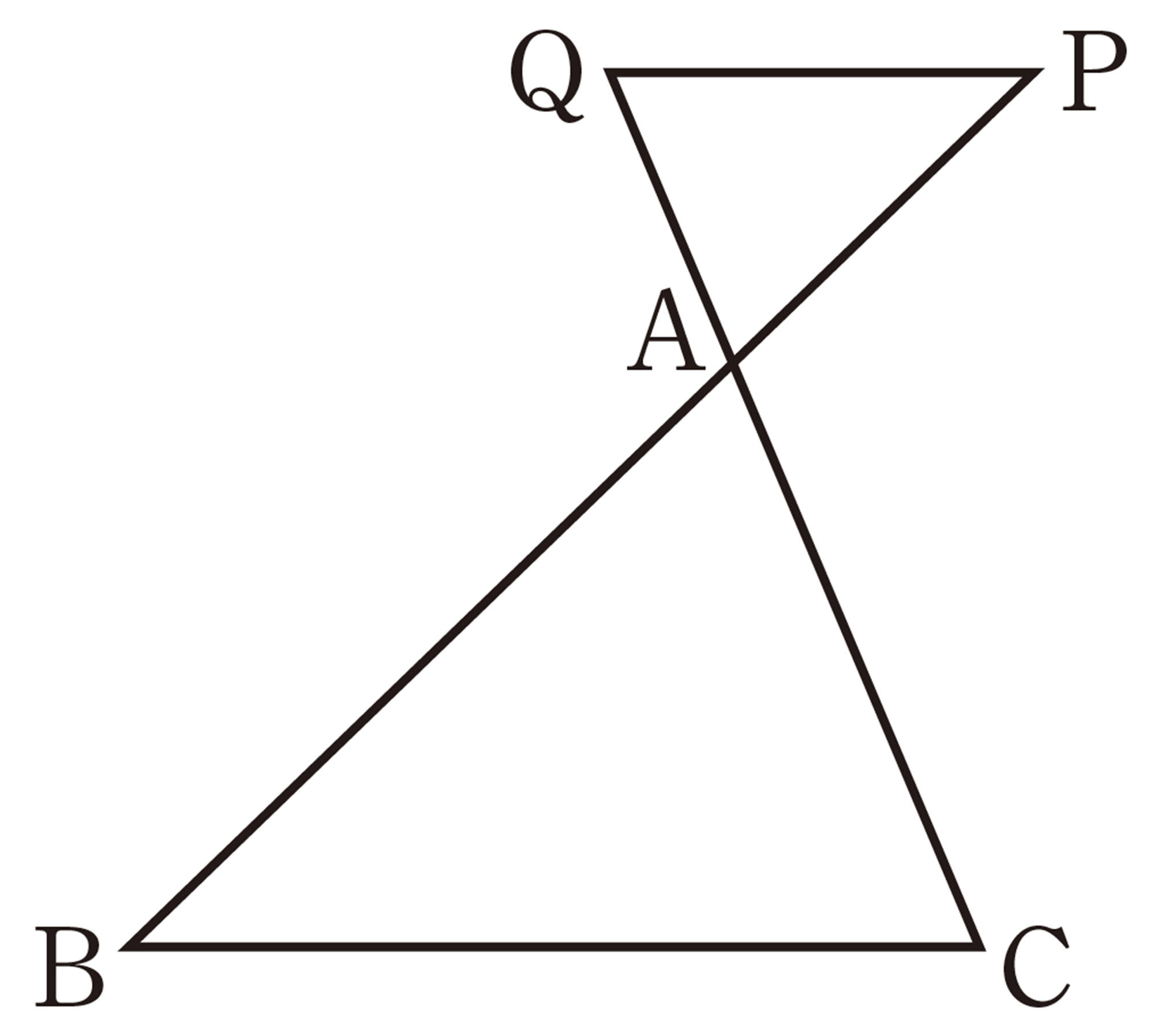
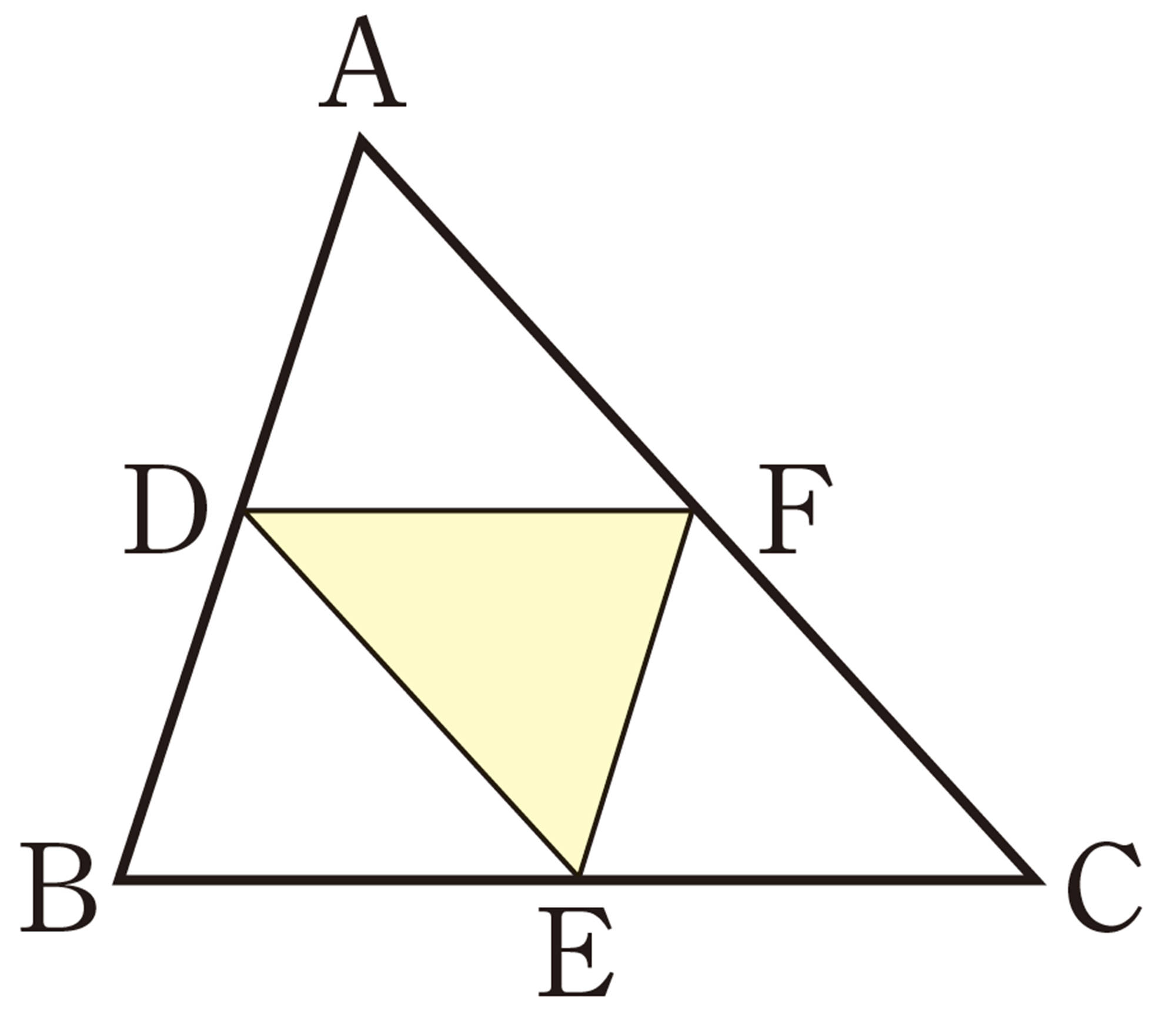
Q Question
右の図のように，[mathjax]\(\triangle ABC\)の辺AB，ACをそれぞれ4等分する点をとりました。
DとG，EとH，FとIを結び，それらの線分と辺BCとの位置関係を調べてみましょう。
「平行線と線分の比」の定理の逆になっているね。
いつでも平行になるといえるのかな。
見方・考え方
根拠を明らかにして証明できるかな。
目標 ▷ 「平行線と線分の比」の定理の逆が成り立つかどうかを考えよう。
例 １ [mathjax]\(\triangle ABC\)の辺AB，AC上に，[mathjax]\(AP:AB=AQ:AC\)となるようにそれぞれ点P，Qをとるとき，[mathjax]\(PQ/\!/BC\)であることを証明しなさい。
証明
[mathjax]\(\triangle APQ\) と[mathjax]\(\triangle ABC\) において，
仮定から，[mathjax]\(AP:AB=AQ:AC \quad \cdots \cdots \mathsf{①}\)
また，[mathjax]\(\hspace{20pt}\angle A\) は共通[mathjax]\(\hspace{57pt} \cdots \cdots \mathsf{②}\)
①， ②より， 2 組の辺の比とその間の角がそれぞれ等しいから，
[mathjax]\(\hspace{67pt}\triangle APQ \backsim \triangle ABC\)
したがって， [mathjax]\(\hspace{18pt}\angle APQ=\angle ABC\)
同位角が等しいから， [mathjax]\(PQ/\!/BC\)
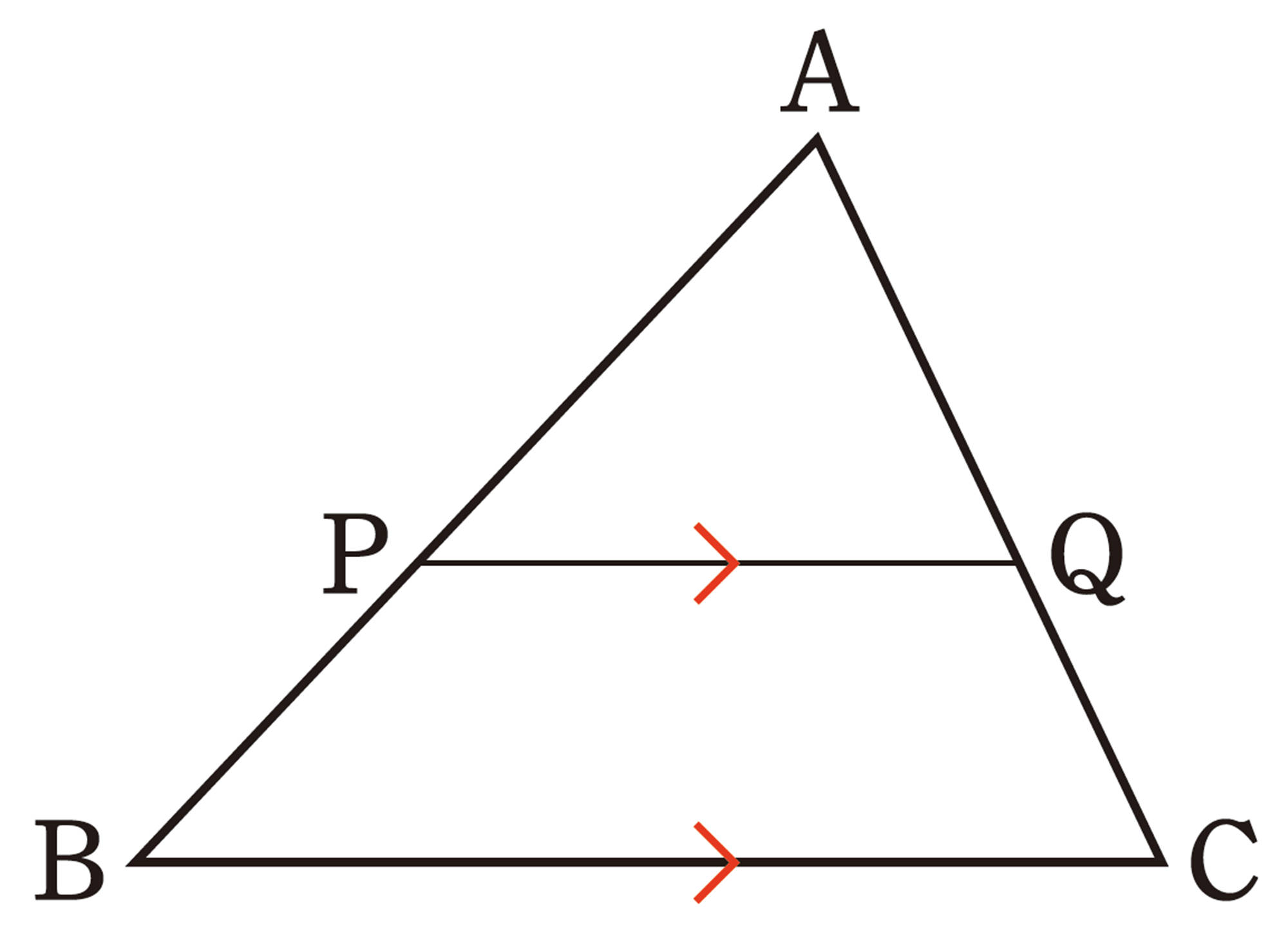
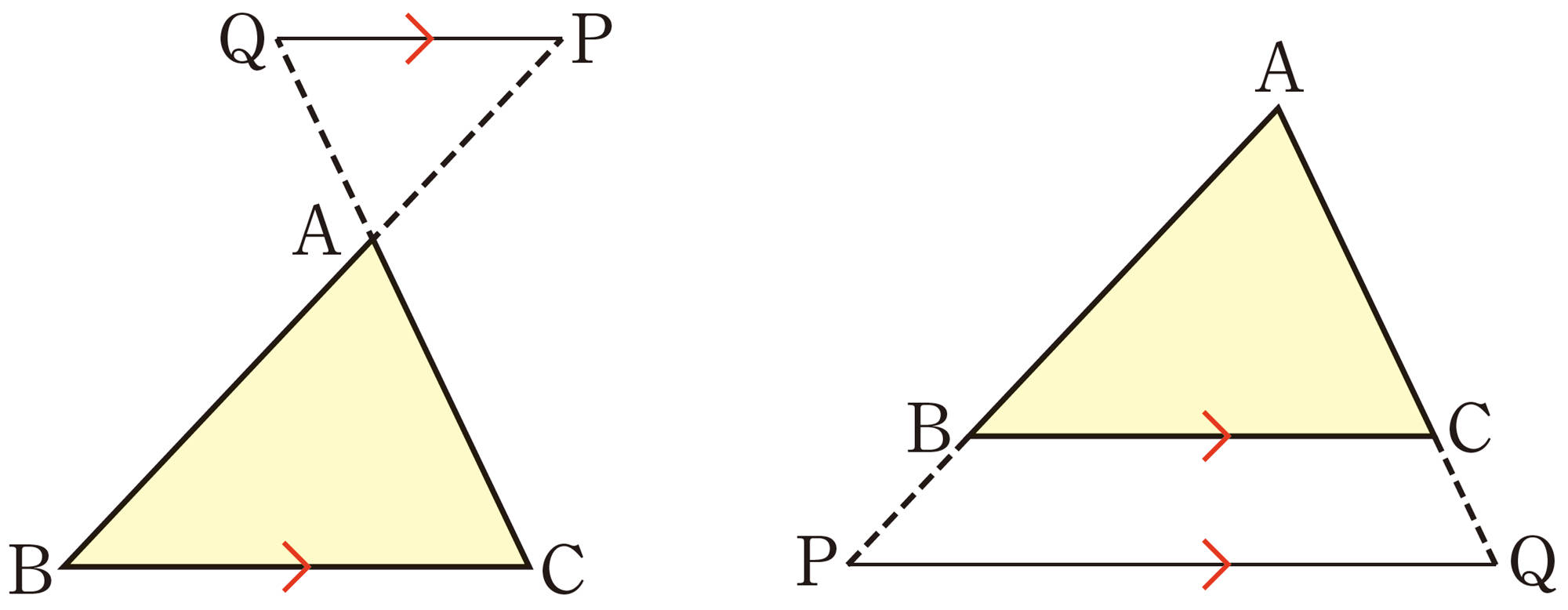
問 １ [mathjax]\(\triangle ABC\)の辺AB，AC上に，[mathjax]\(AP:PB=AQ:QC=3:2\)となるようにそれぞれ点P，Qをとるとき，次の問いに答えなさい。
⑴ [mathjax]\(AP:AB\)，[mathjax]\(AQ:AC\)を求めなさい。
⑵ ⑴で調べたことを使って，[mathjax]\(PQ/\!/BC\)であることを証明しなさい。
<3年p.168>
前ページの例1や問1で調べたことは，次のように，定理としてまとめることができる。
定理
線分の比と平行線
[mathjax]\(\triangle ABC\)の辺AB，AC上の点をそれぞれP，Qとするとき，
❶ [mathjax]\(AP:AB=AQ:AC\) ならば，
[mathjax]\(\hspace{40pt}PQ /\!/ BC\)
❷ [mathjax]\(AP:PB=AQ:QC\)ならば，
[mathjax]\(\hspace{40pt}PQ /\!/ BC\)
問 ２ 右の図で，平行な線分の組をいいなさい。また，その線分が平行といえる理由を説明しなさい。
問 ３ 右の図のように，[mathjax]\(\triangle ABC\)の辺BA，CAの延長上に，
[mathjax]\(AB:AP=AC:AQ=2:1\)
となるように，それぞれ点P，Qをとるとき，[mathjax]\(PQ /\!/BC\)であることを証明しなさい。
上の定理は，点P，Qを辺BA，CAの延長上や，辺AB，ACの延長上にとった場合にも成り立つ。
<3年p.169>
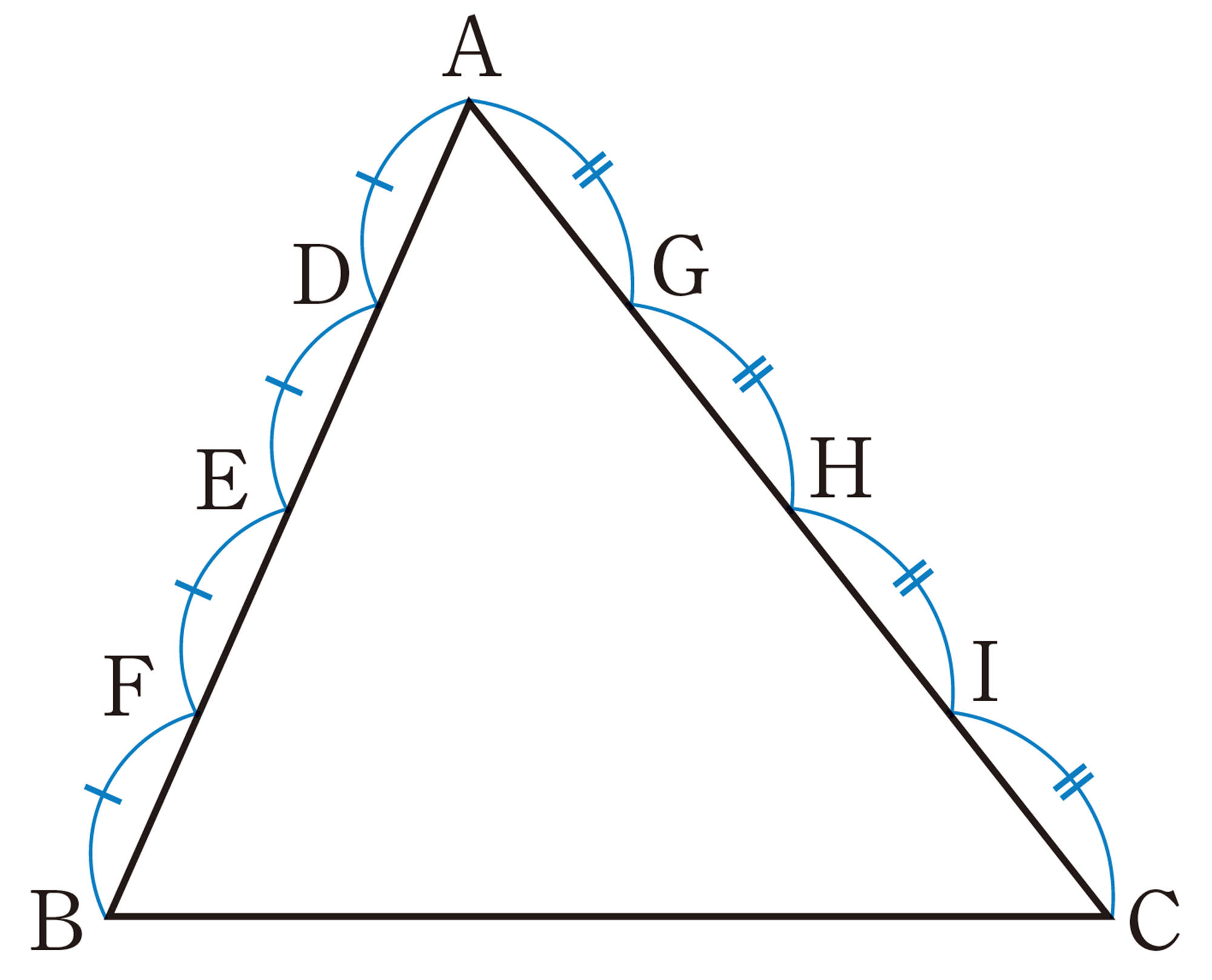
中点連結定理
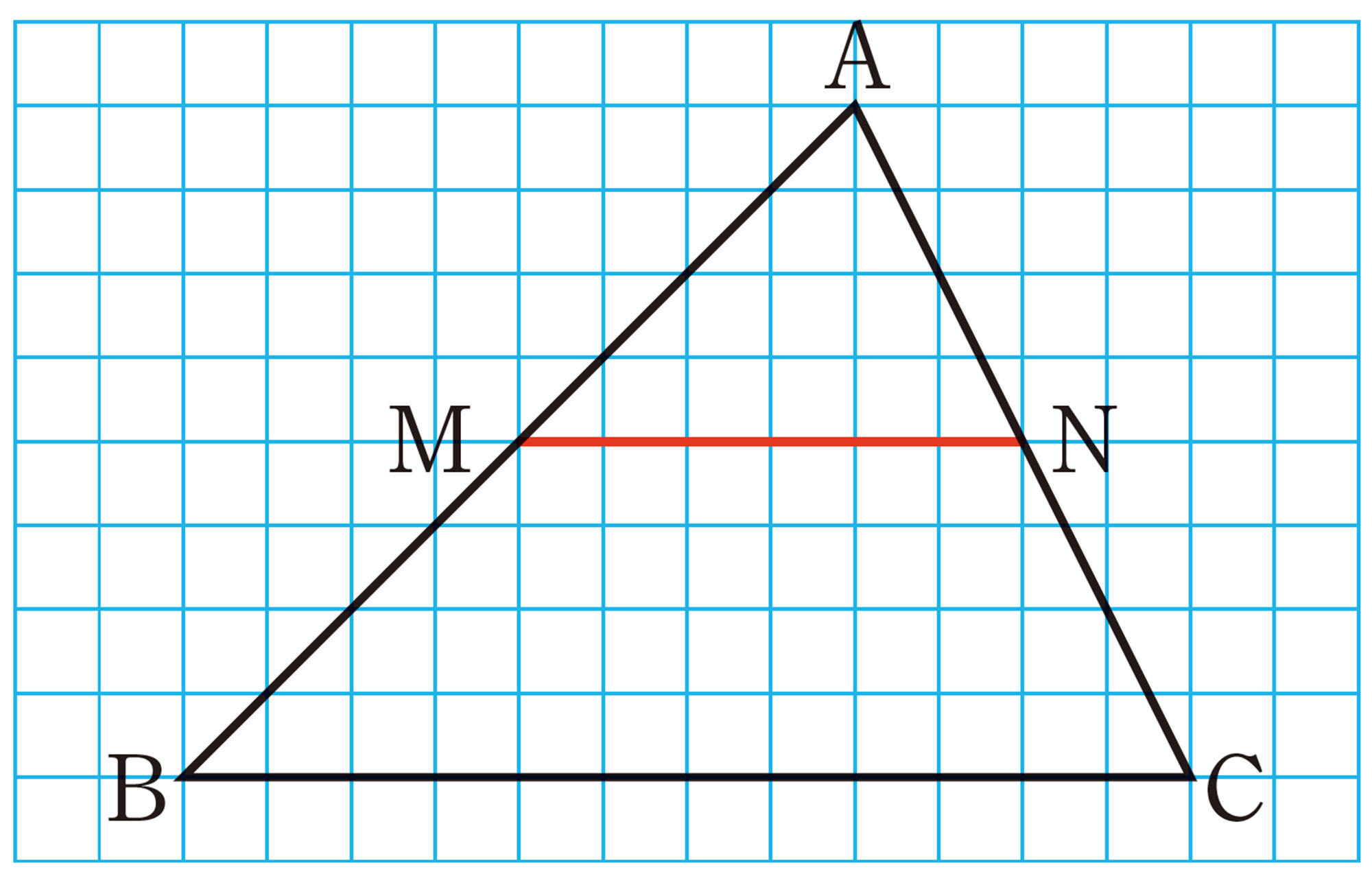
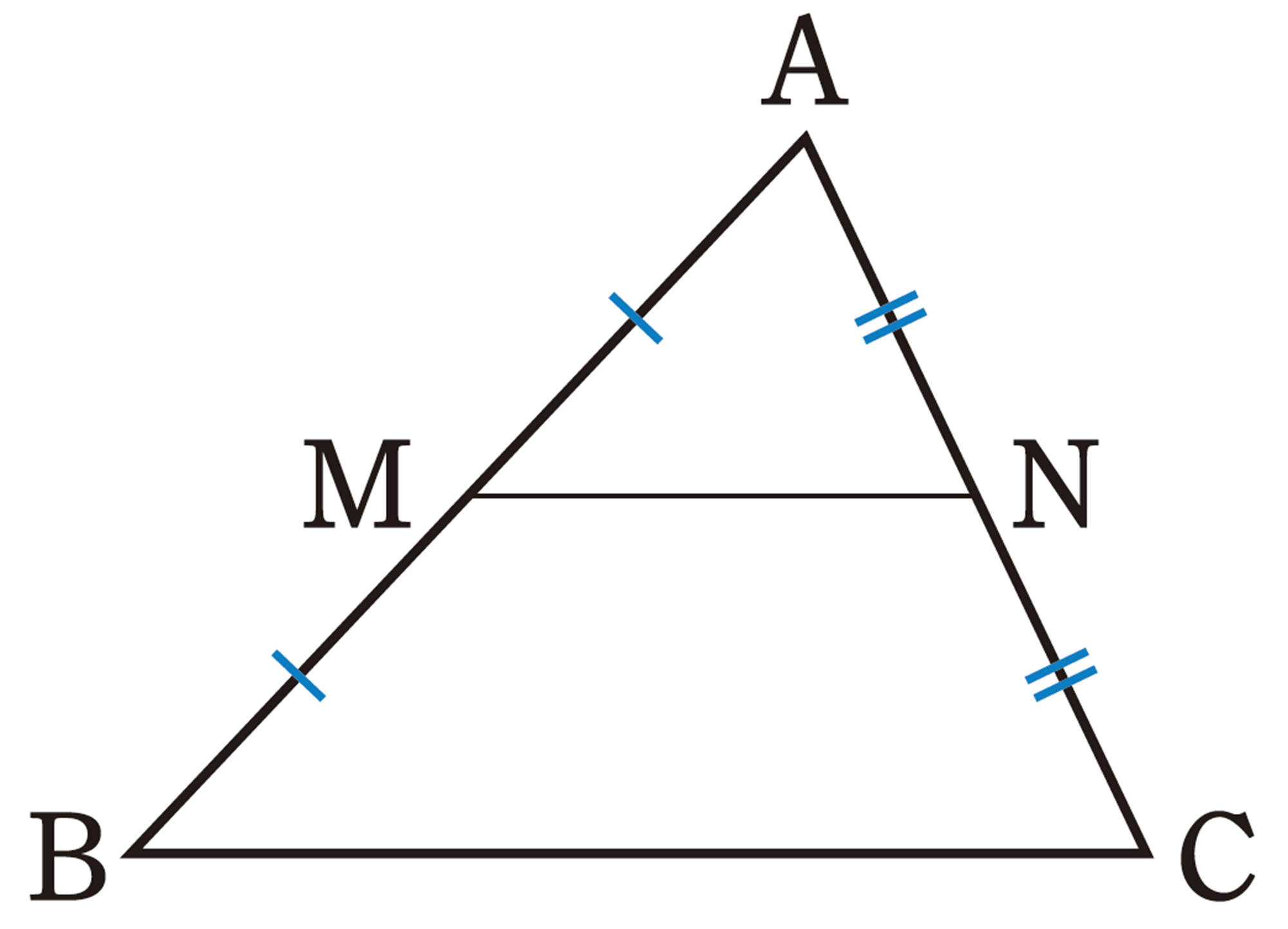
Q Question
[mathjax]\(\triangle ABC\)の辺AB，ACの中点をそれぞれM，Nとすると，線分MNと辺BCの間にはどんな関係があるでしょうか。
線分MNと辺BCは平行になるね。
ほかにもいつでも成り立つ性質はあるのかな。
見方・考え方
いくつかの三角形で調べて，どんなきまりがあるか見つけられるかな。
【Q】の[mathjax]\(\triangle ABC\)で，点M，Nはそれぞれ辺AB，ACの中点であるから，
[mathjax]\(\hspace{116pt}AM:MB=AN:NC=1:1\)
線分の比と平行線の定理から，[mathjax]\(\hspace{27pt}MN/\!/BC\)
平行線と線分の比の定理から，[mathjax]\(MN:BC=AM:AB=1:2\)
したがって，[mathjax]\(\hspace{92pt}MN=\dfrac{1}{2}BC\)
上のことから，次の定理が成り立つことがわかる。
定理
中点連結定理
[mathjax]\(\triangle ABC\)の辺AB，ACの中点をそれぞれM，Nとするとき，
[mathjax]\(MN/\!/BC\)，[mathjax]\(MN=\dfrac{1}{2}BC\)
問 ４ [mathjax]\(\triangle ABC\)の辺AB，BC，CAの中点をそれぞれD，E，Fとするとき，[mathjax]\(\triangle DEF\)と合同な三角形を，すべていいなさい。
問 ５ 右の図の四角形ABCDは，[mathjax]\(AD/\!/BC\) の台形です。辺ABの中点Mから辺BCに平行な直線を引き，対角線AC，辺DCとの交点をそれぞれ O，Nとします。このとき，線分MNの長さを求めなさい。
<3年p.170>
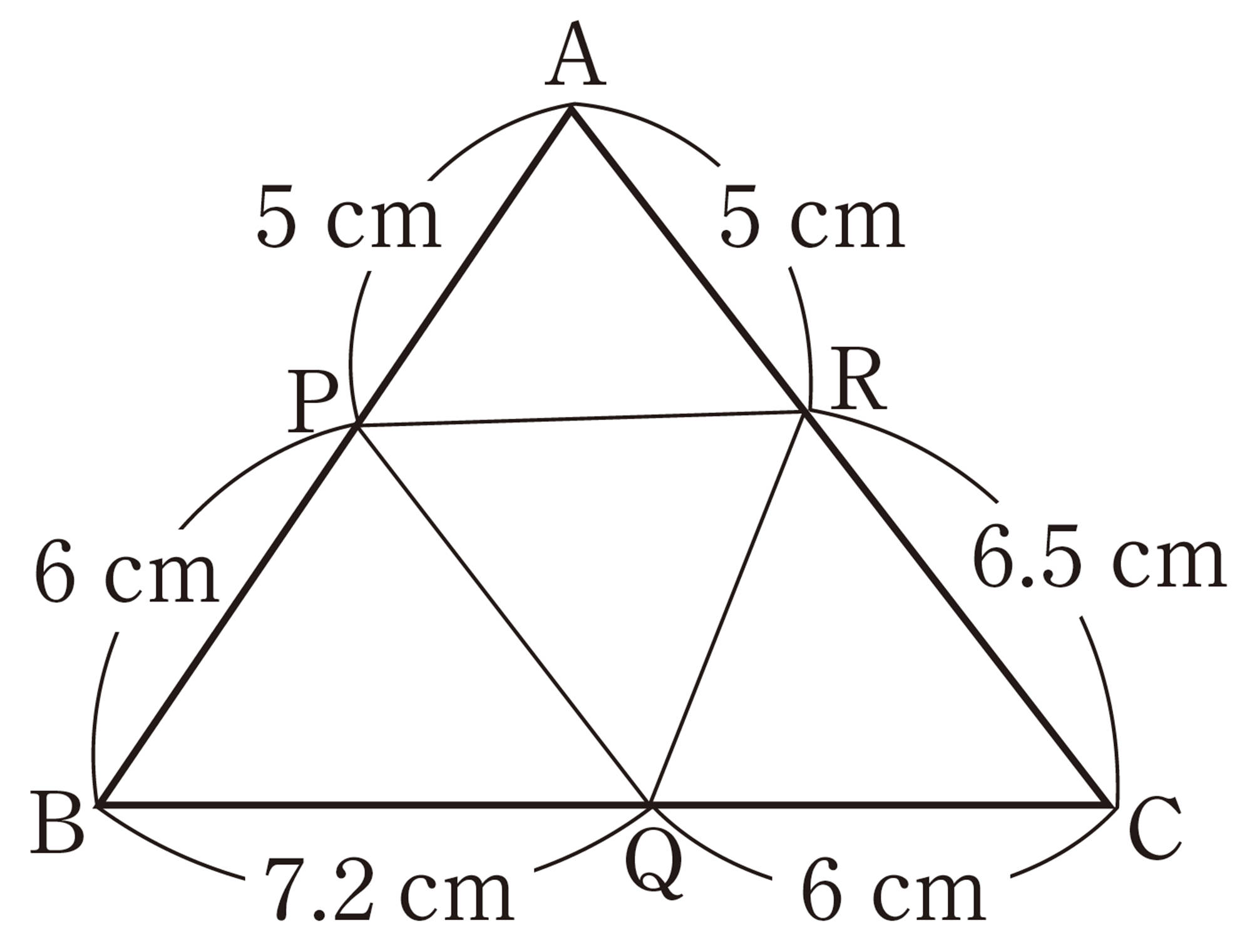
中点連結定理の利用
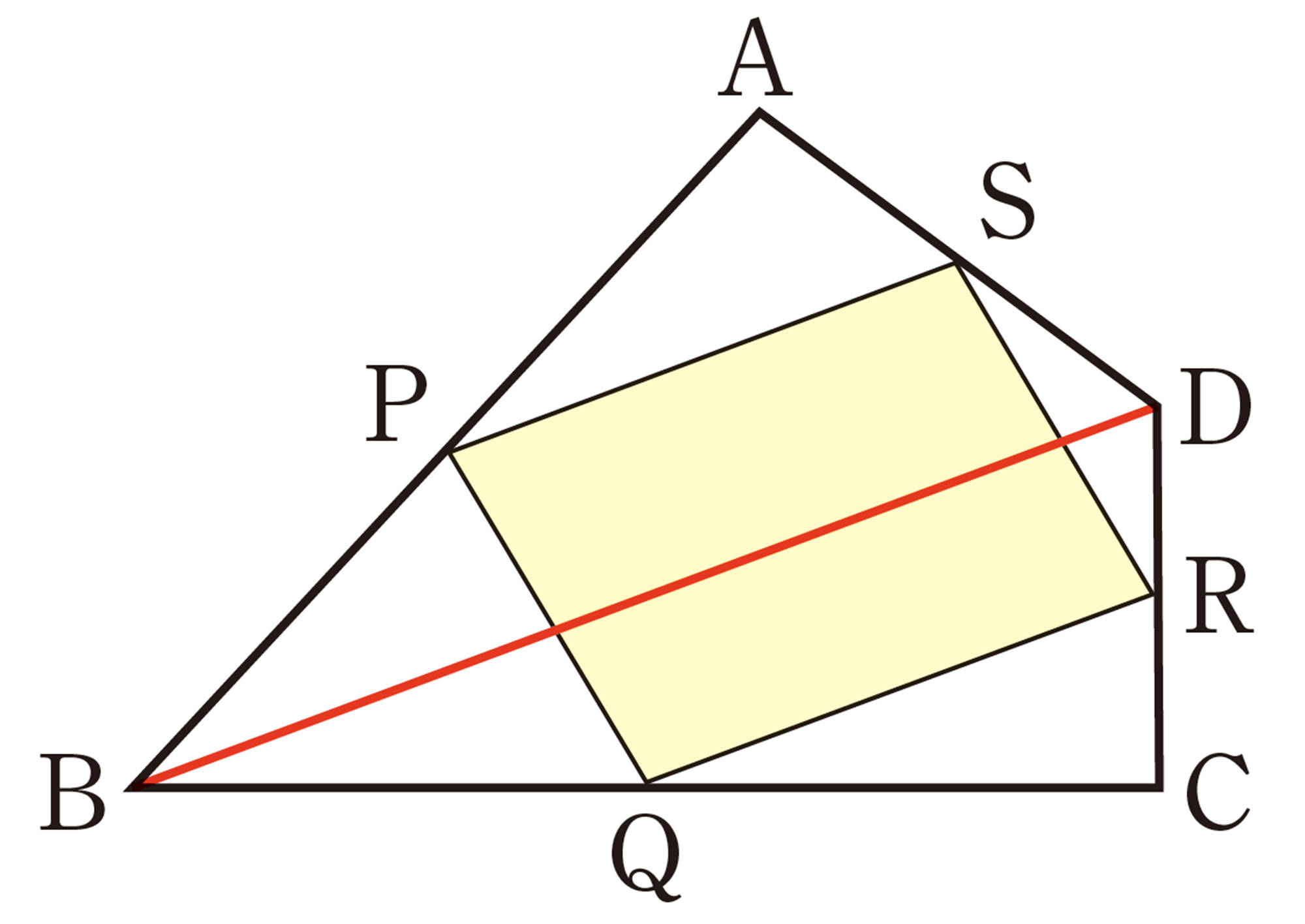
Q Question
右の四角形の4つの辺の中点をとり，順に結んでみましょう。どんな図形ができるでしょうか。また，ほかの四角形についても，同じように調べてみましょう。
いつでも同じ四角形ができるといえるのかな。
見方・考え方
いくつかの四角形で調べて，どんなきまりがあるか見つけられるかな。
１ 四角形ABCDの辺AB，BC，CD，DAの中点をそれぞれ P，Q，R，Sとするとき，四角形PQRSが平行四辺形になる理由を，中点連結定理を使って考えてみましょう。
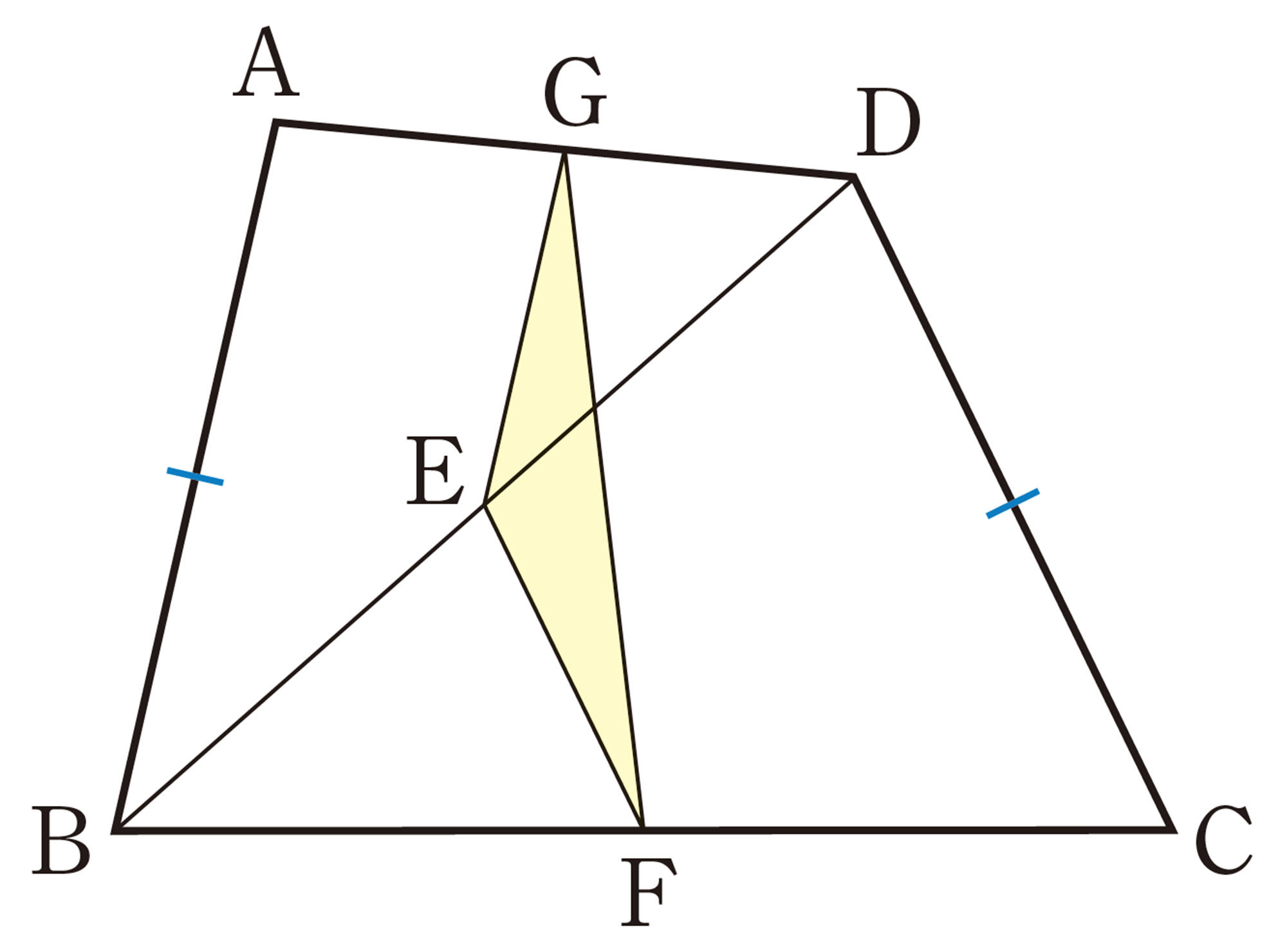
⑴ 対角線BDを引くと，[mathjax]\(\triangle ABD\)の辺BDと線分PSの間には，どんな関係が成り立つでしょうか。
また，[mathjax]\(\triangle CDB\)についてはどうでしょうか。
⑵ ⑴をもとに，四角形 PQRS が平行四辺形になる理由を説明しましょう。
【１】のことがらを証明としてまとめると，次のようになる。
［証明］
対角線BDを引く。
[mathjax]\(\triangle ABD\)において，点P，Sはそれぞれ辺AB，ADの中点であるから，
[mathjax]\(PS/\!/BD，PS=\dfrac{1}{2}BD \quad \cdots \cdots\mathsf{①}\)
[mathjax]\(\triangle CDB\)において，同様にして，
[mathjax]\(QR/\!/BD，QR=\dfrac{1}{2}BD \quad \cdots \cdots\mathsf{②}\)
①，②から，[mathjax]\(PS/\!/QR\)，[mathjax]\(PS=QR\)
1組の対辺が平行で等しいから，四角形PQRSは平行四辺形である。
ほかの「平行四辺形になるための条件」でも証明できるかな。
<3年p.171>
もとの四角形を長方形やひし形にするとどうなるのかな。
２ 前ページの【１】で，四角形ABCDが長方形のとき，四角形PQRSはどんな四角形になるでしょうか。また，四角形ABCDがひし形のときはどうでしょうか。
３ なぜ【２】で調べたことがいえるのかを，説明してみましょう。
長方形やひし形の対角線には，どんな性質があったかな。
４ 四角形ABCDが長方形ではなくても，四角形PQRSがひし形になることがあります。四角形ABCDがどんな条件をもっていれば，四角形PQRSがひし形になるといえるでしょうか。また，四角形ABCDがどんな条件をもっていれば，四角形PQRSが長方形になるといえるでしょうか。
▲トライ 右の図のようなブーメラン形の図形でも，これまで調べたことが成り立つかどうかを調べてみよう。
コンピュータを使うとわかりやすいね。
どんなことがわかったかな
平行線と線分の比の関係を使って，いろいろな図形の性質を証明することができます。
<3年p.172>
確かめよう 2節 平行線と相似
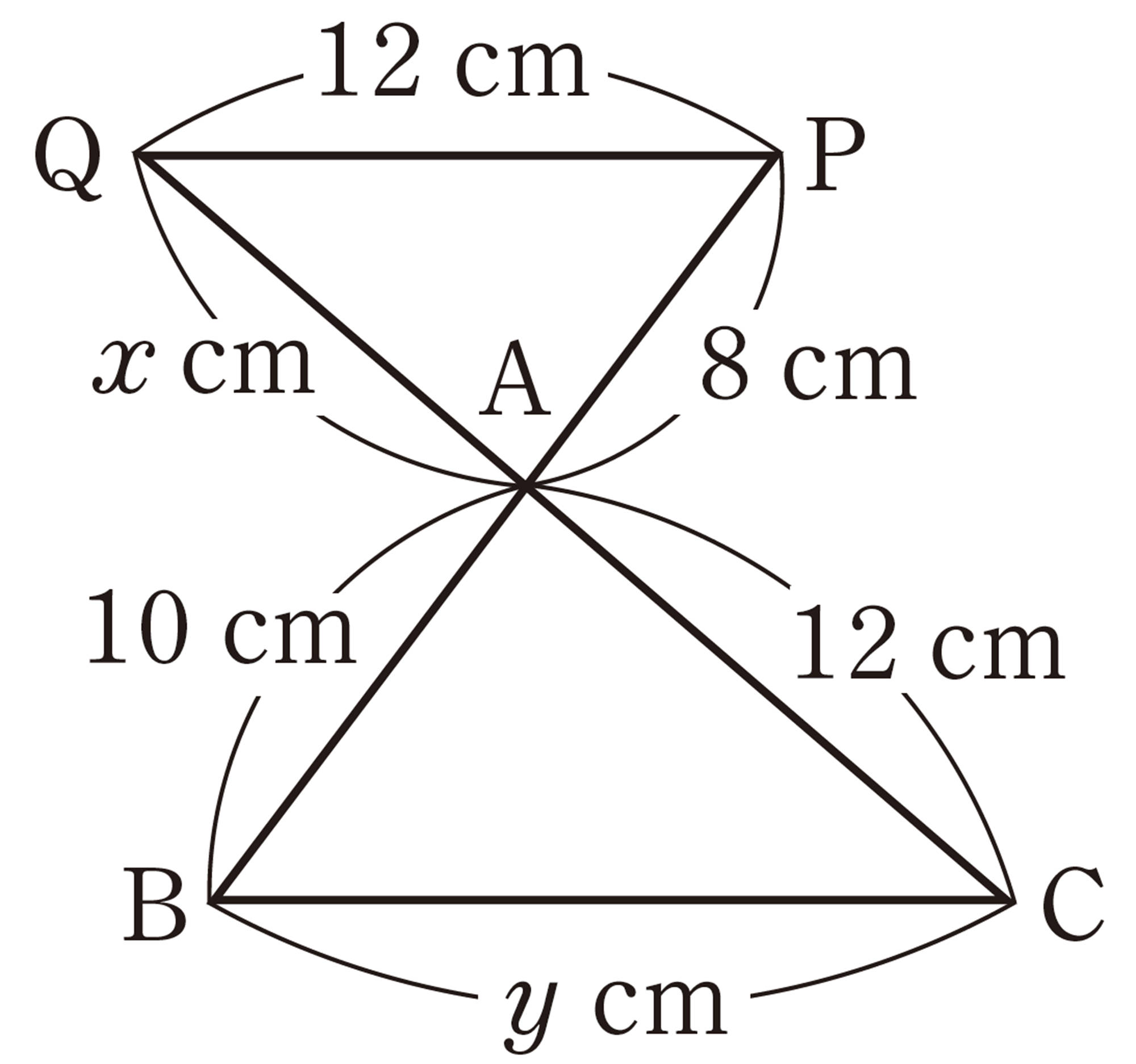
１ 次の図で，[mathjax]\(PQ/\!/BC\)のとき，x，yの値を求めなさい。
⑴
⑵
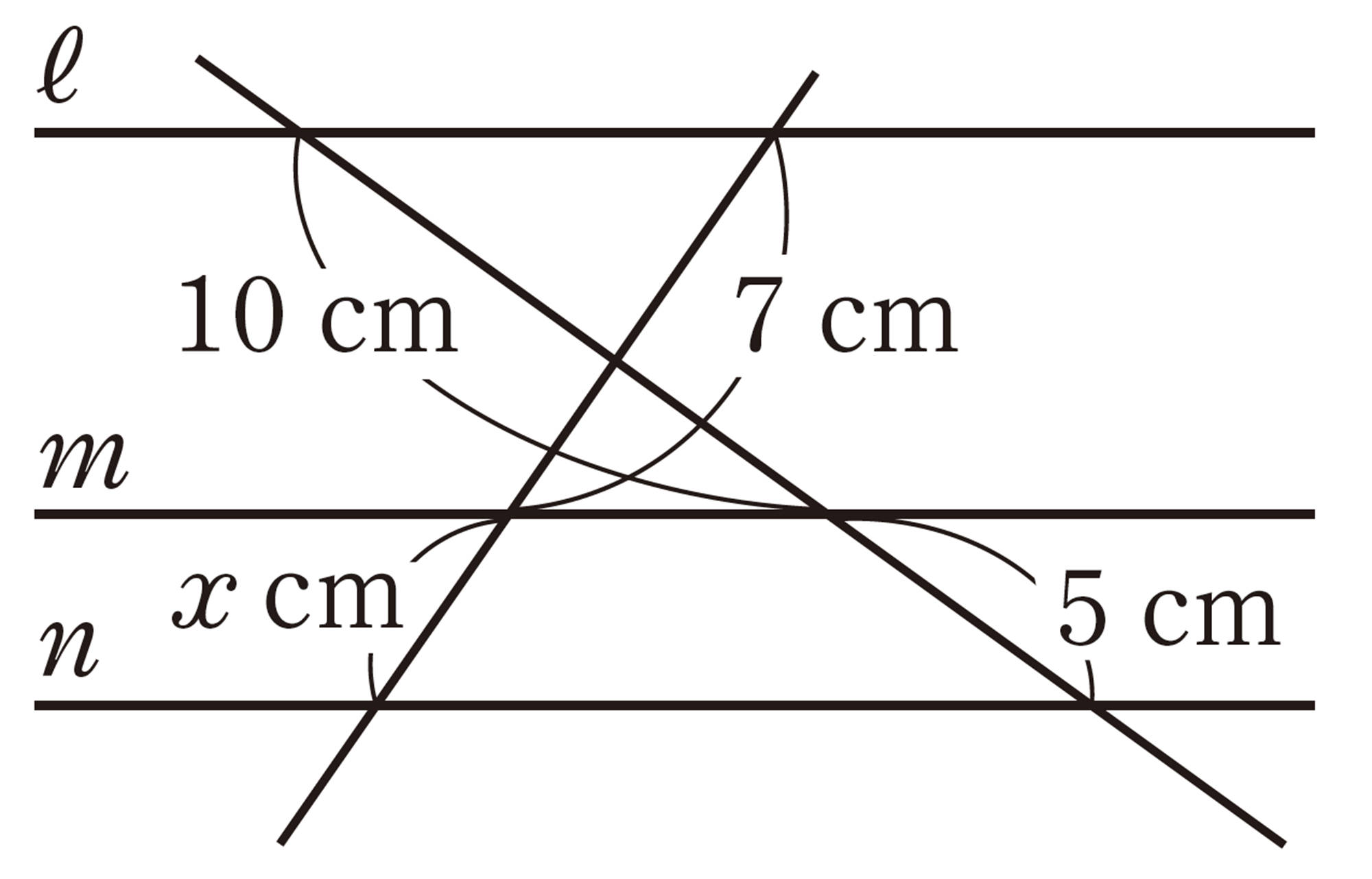
２ 次の図で，[mathjax]\(ℓ/\!/m/\!/n\)のとき，xの値を求めなさい。
⑴
⑵
３ 右の図で，平行な線分の組をいいなさい。また，その理由もいいなさい。
４ 右の図のように，[mathjax]\(AB=DC\)である四角形ABCDで，対角線BDの中点をE，辺BC，ADの中点をそれぞれF，Gとします。次の問いに答えなさい。
⑴ [mathjax]\(\triangle EFG\)はどんな三角形ですか。
⑵ ⑴のことがらを証明しなさい。
