<3年p.160>
2節 平行線と相似
紙を等分できる？
美月さんは，小学校の算数の時間に，ノートの罫線を使って次のようにすると，ひもを5等分できることを学習しました。
【１】 封筒に入れる手紙をきれいに三つ折りにしたいと思います。工作用紙の罫線を使って，手紙を3等分にするには，工作用紙の上に手紙をどのように置けばよいでしょうか。
目盛りは，太い線を使った方がやりやすいね。
次の課題へ！
上のように平行線を使うと，ひもや手紙が等分できるのはなぜかな。
P.161
<3年p.161>
１ 平行線と線分の比
Q Question
右の図のように，等間隔に引かれた平行線上に点A，Bをとり，2点を結びました。線分ABは平行線によって，どのように区切られているでしょうか。また，点Bを同じ直線上で動かした場合はどうでしょうか。
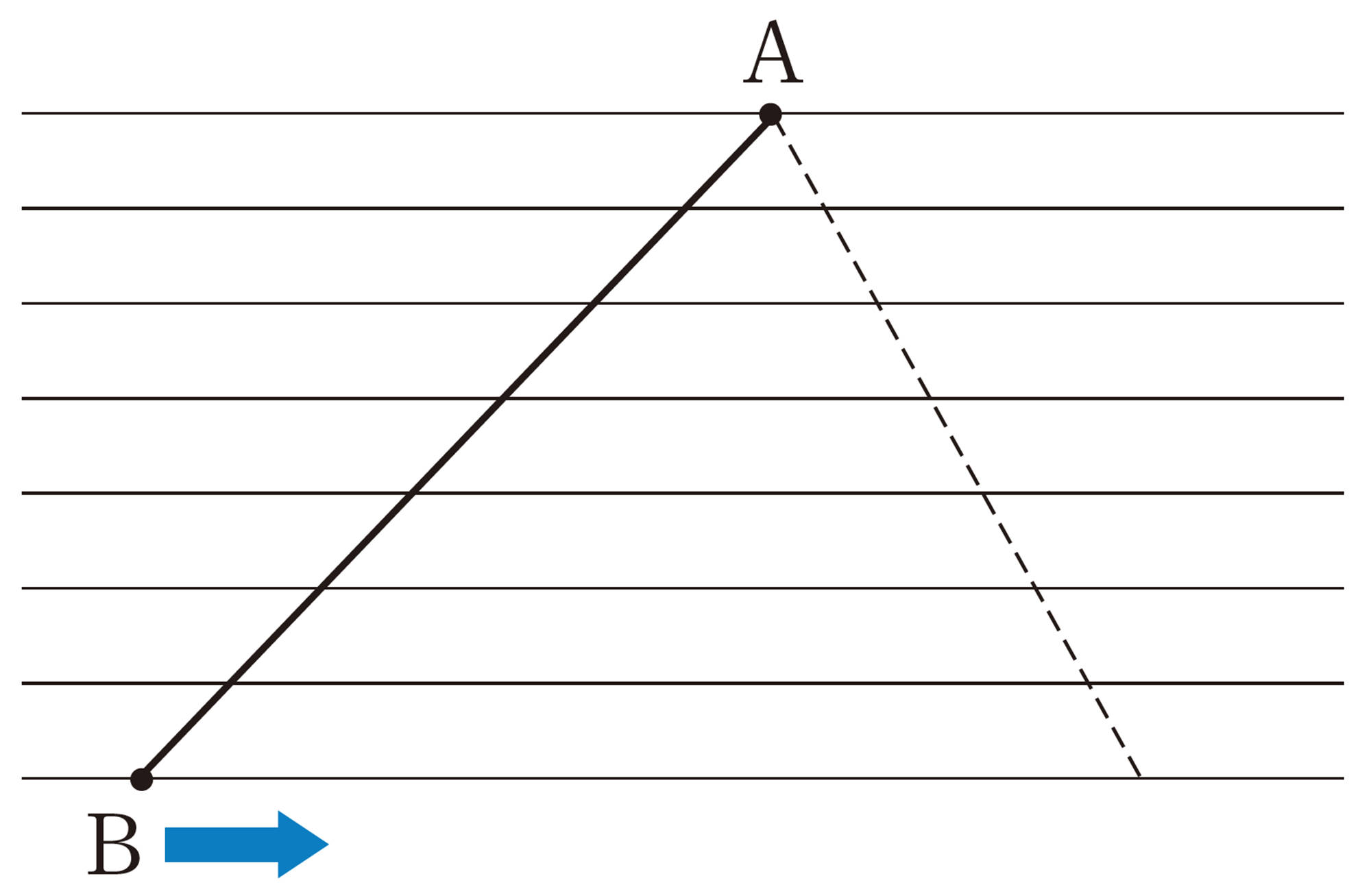
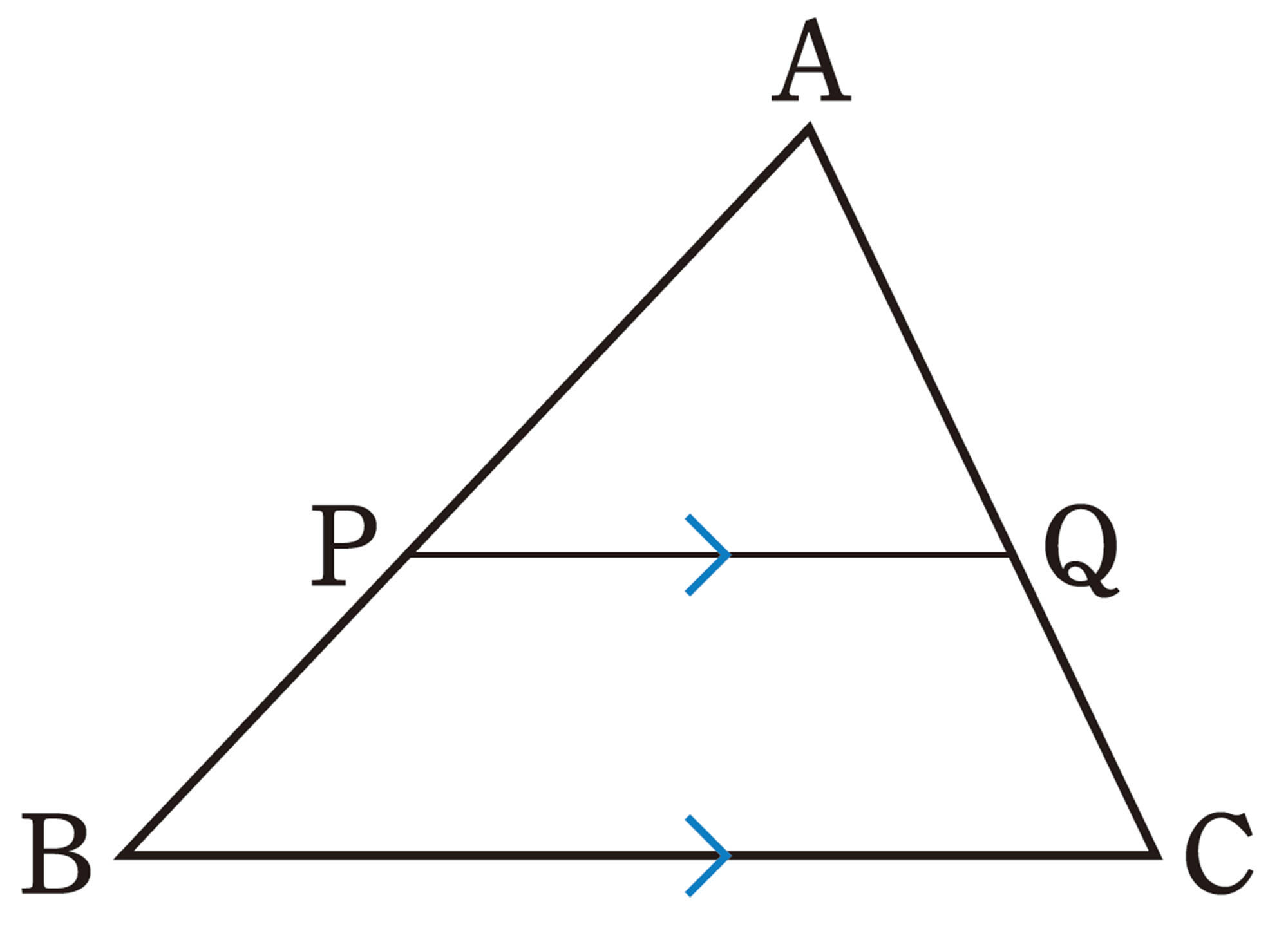
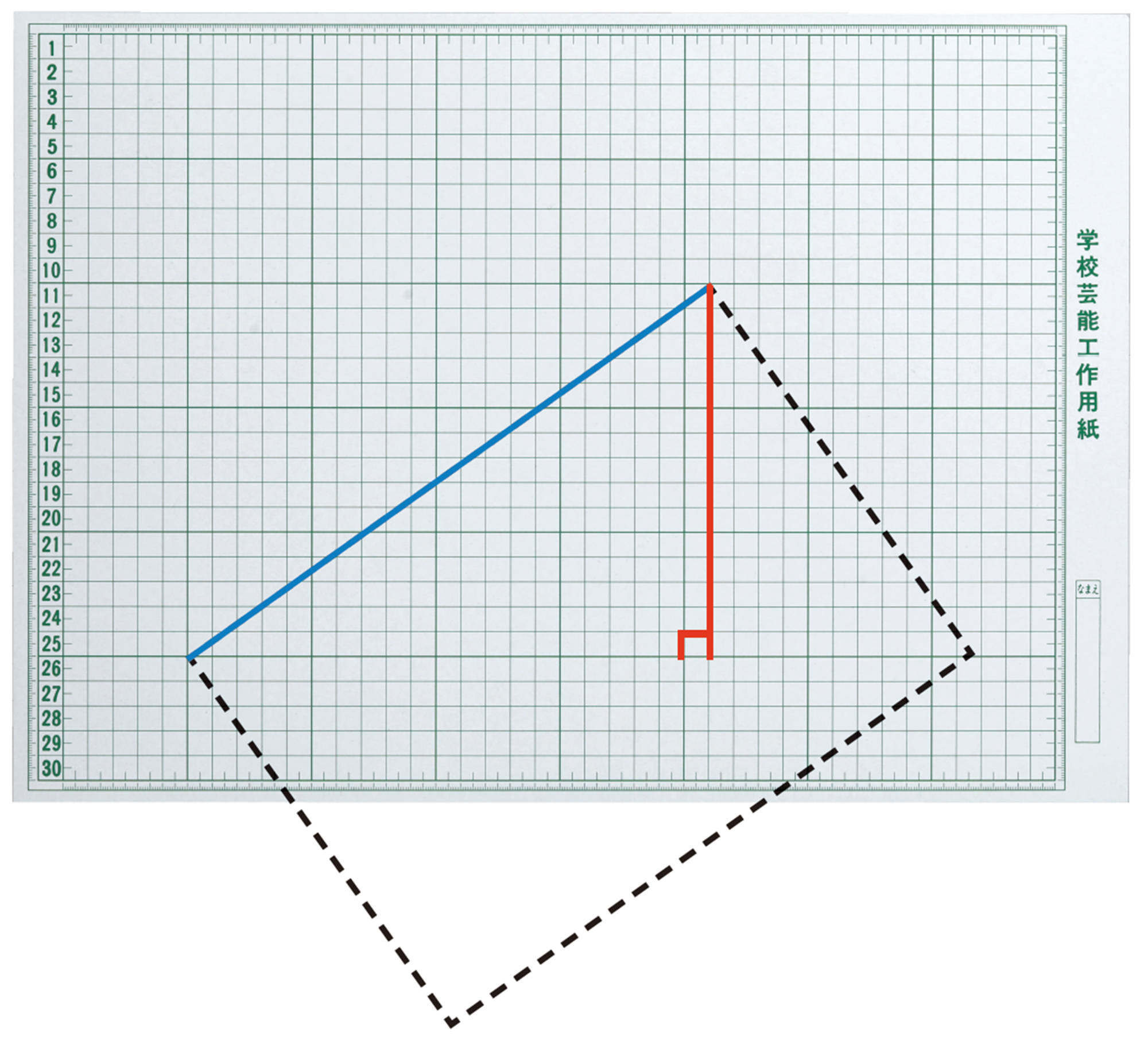
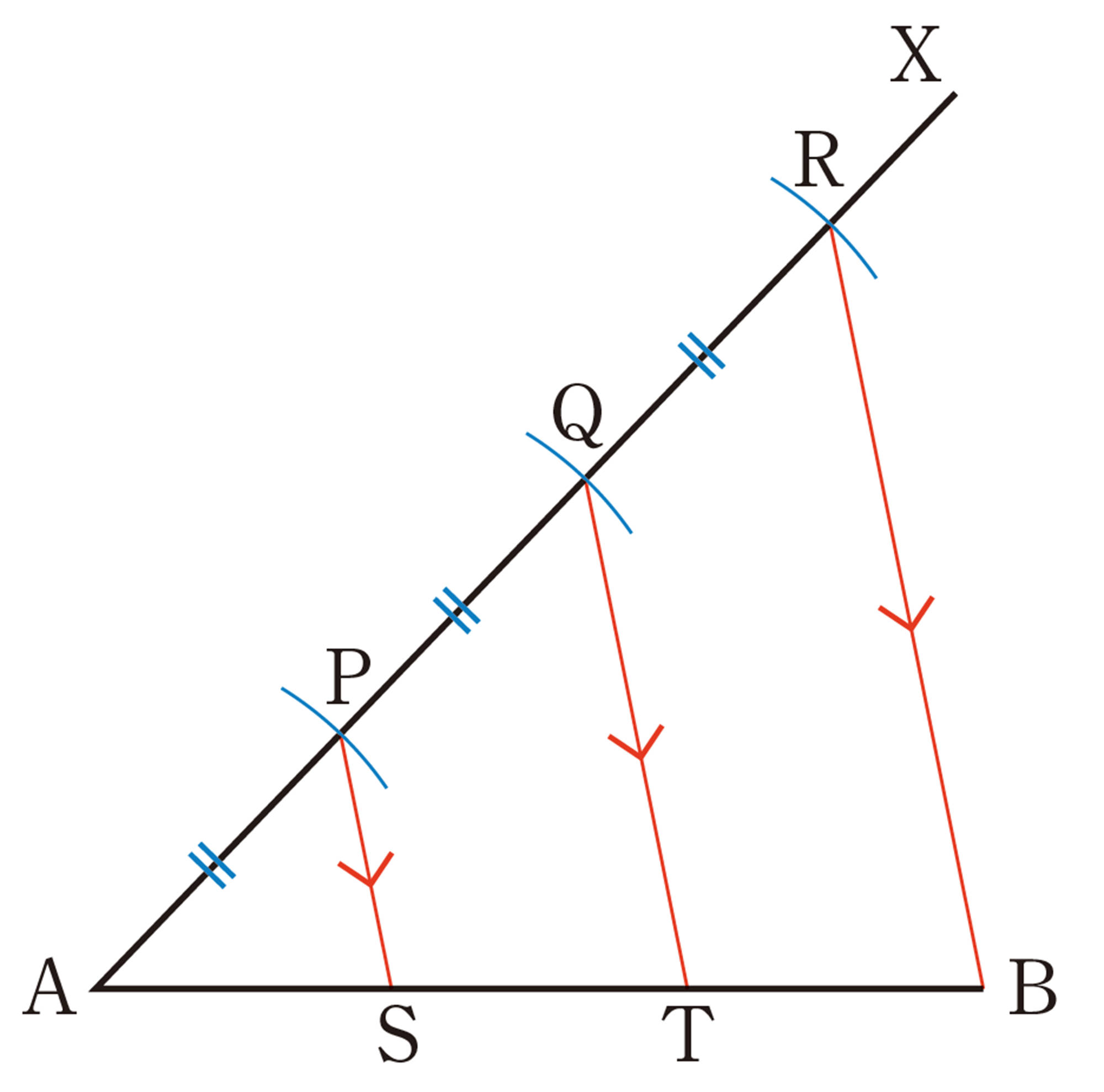
線分 AB は，平行線で等分されているように見えるね
いつでも等分されるといえるのかな。
見方・考え方
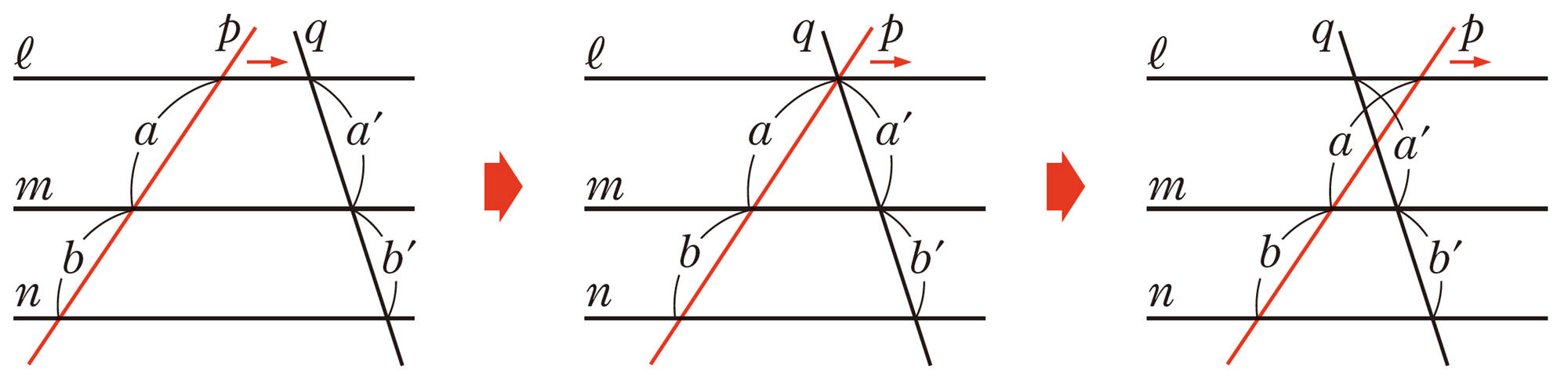
平行線と線分の間にはどんな性質があるか見つけられるかな。
目標 ▷ 平行線によって区切られた線分の長さの比を調べよう。
右の図のように，[mathjax]\(\triangle ABC\)の辺BCに平行な直線ℓを引き，2辺AB，ACとの交点をそれぞれP，Qとするとき，[mathjax]\(\triangle APQ\)と[mathjax]\(\triangle ABC\)の辺の間にどんな関係が成り立つか調べてみよう。
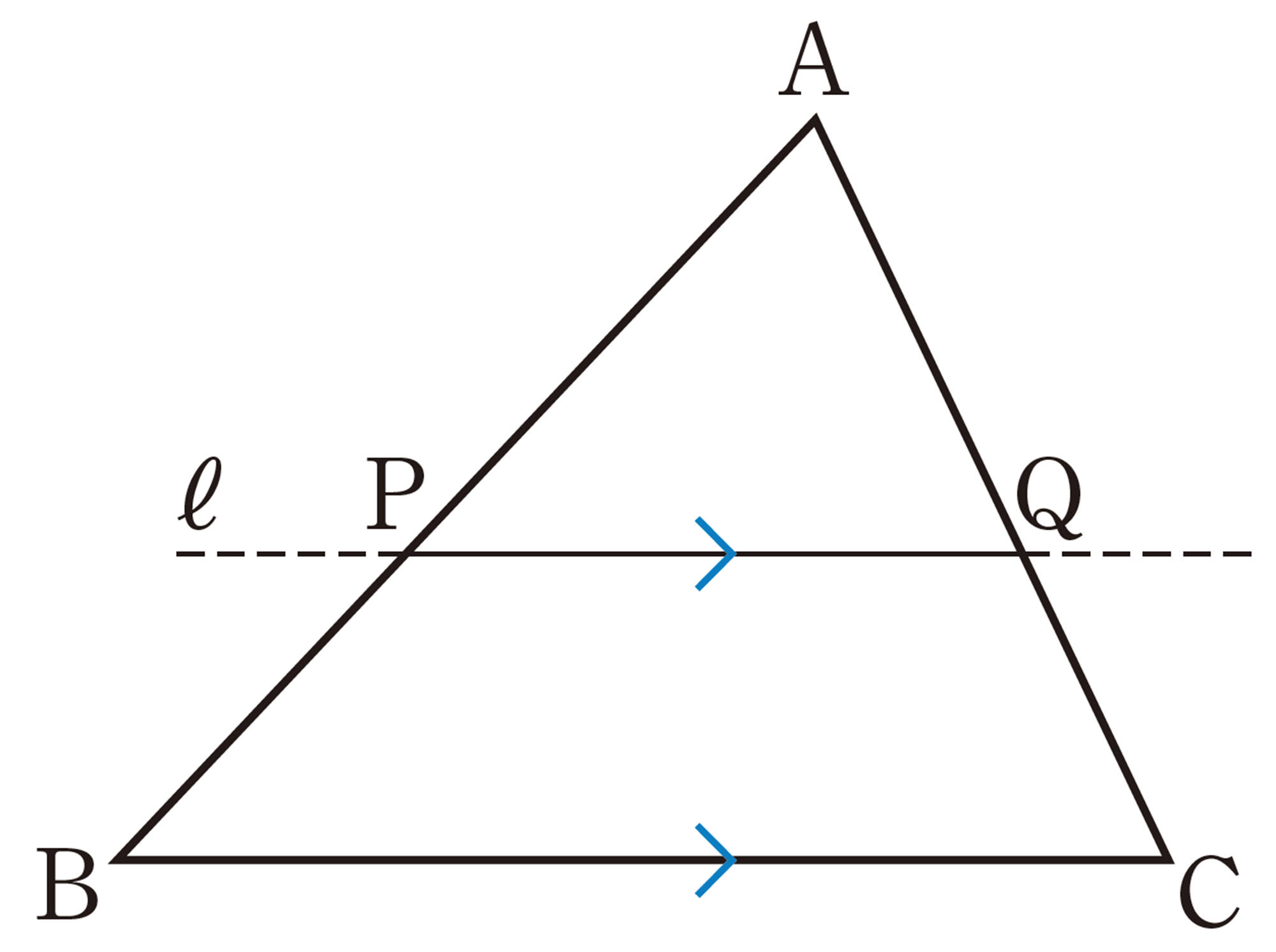
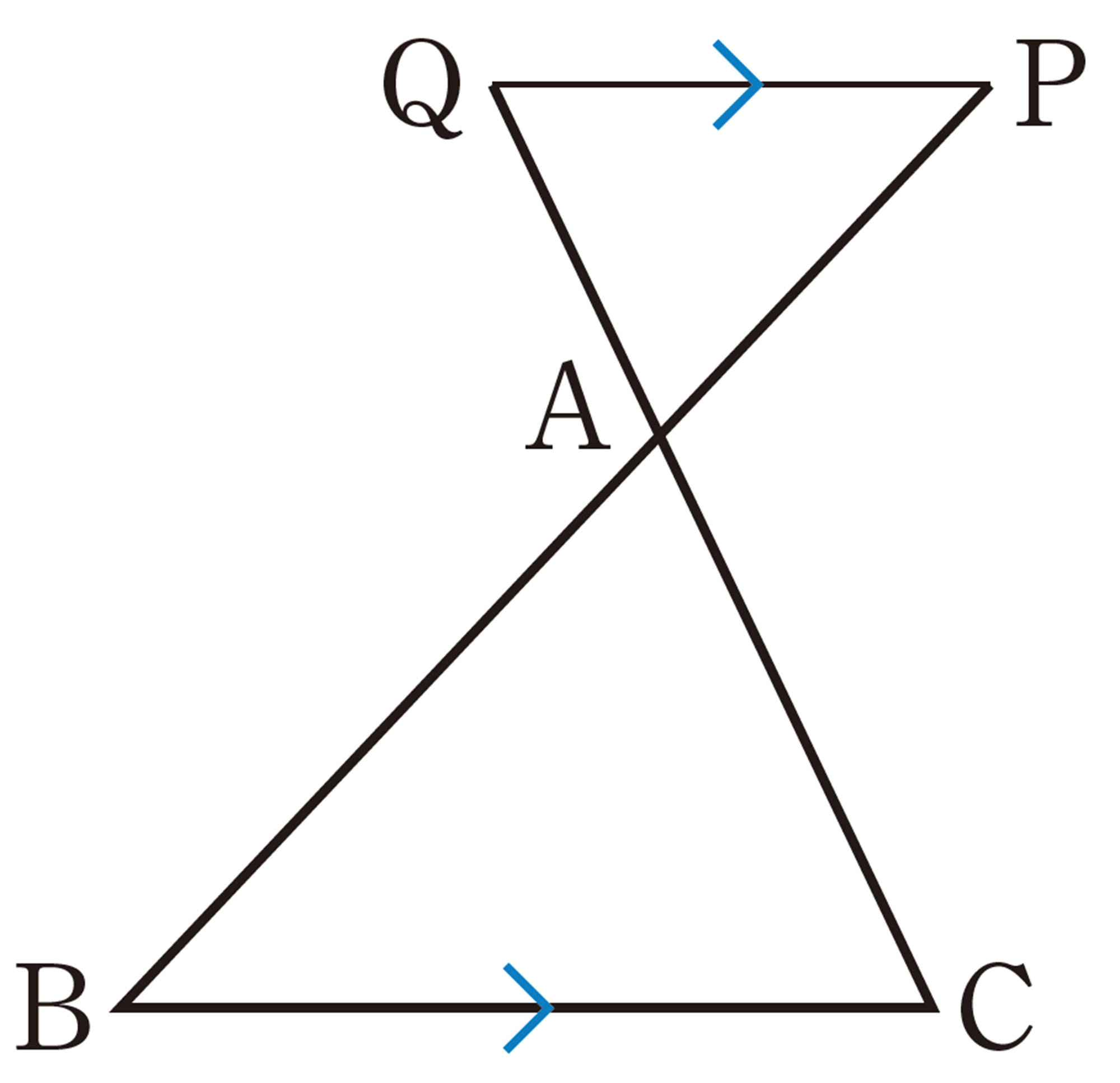
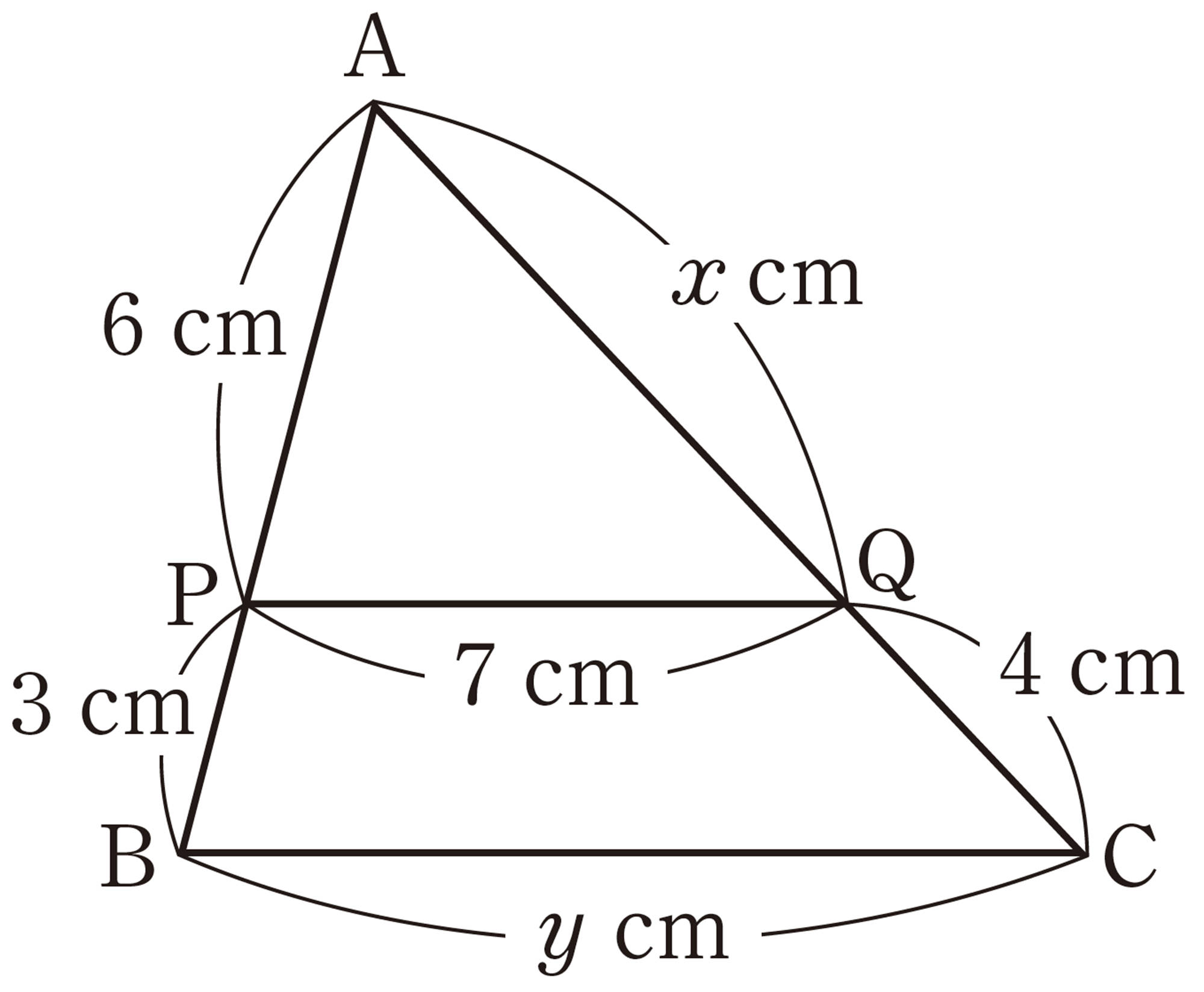
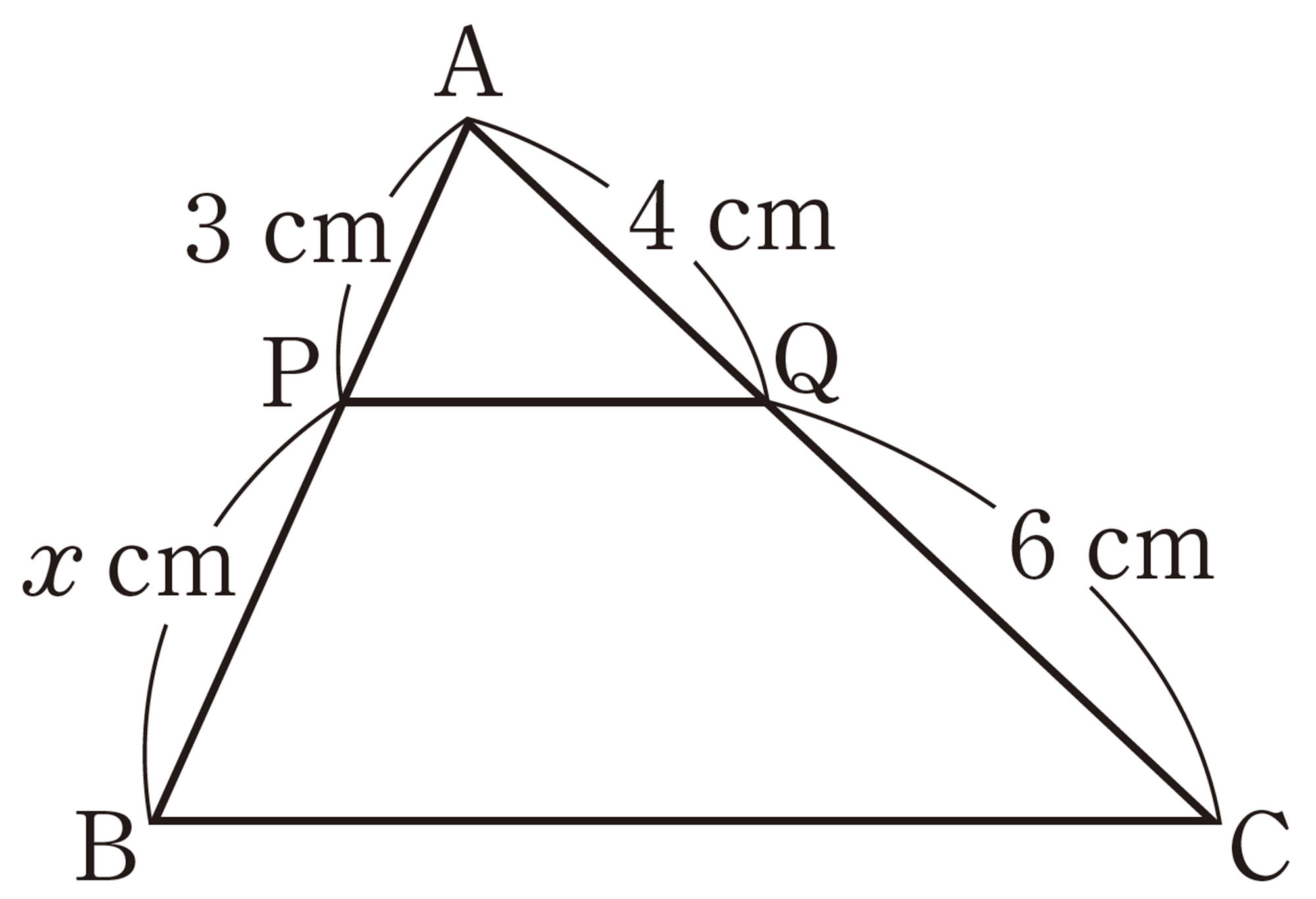
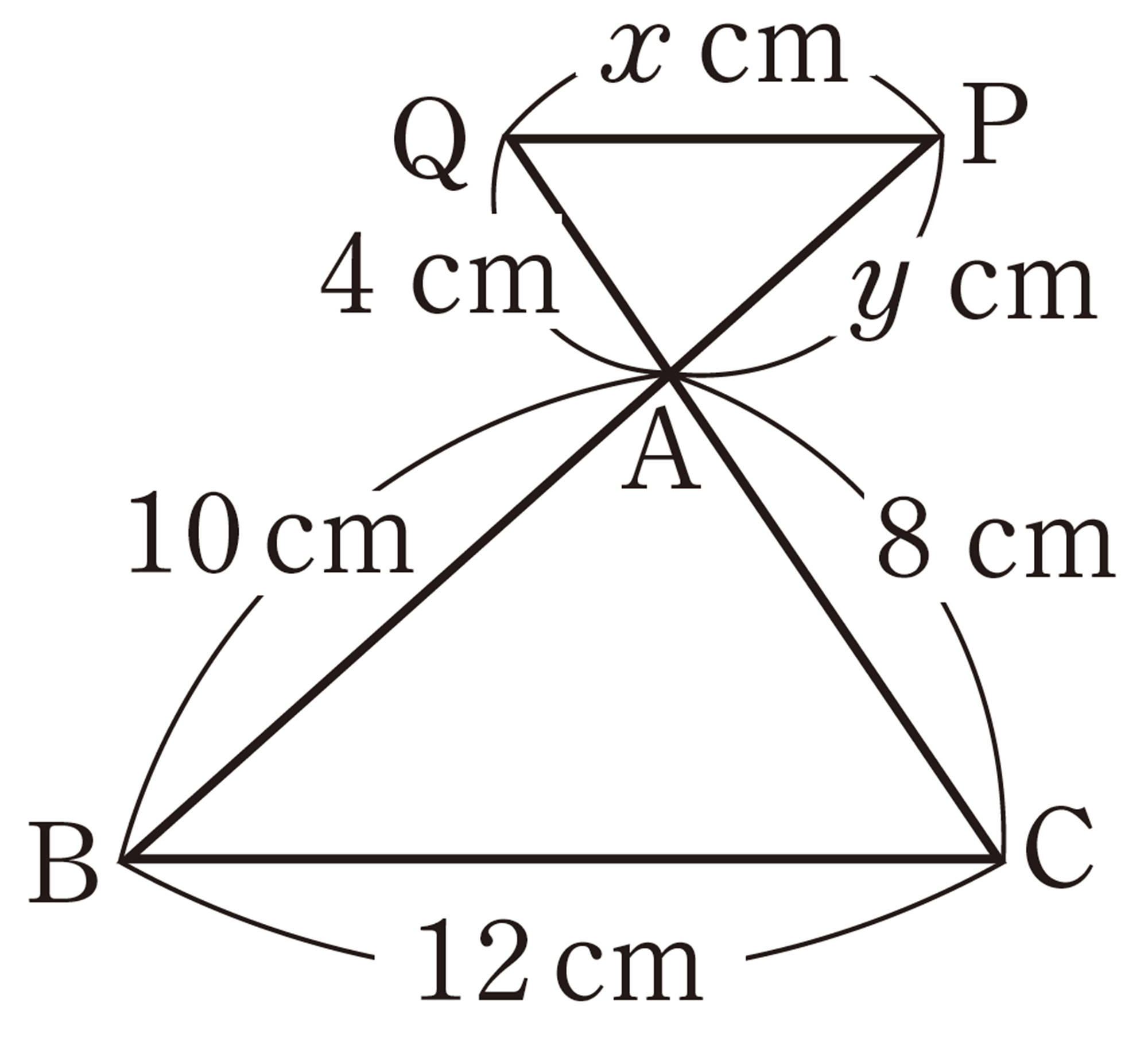
問 １ 右上の図について，次の問いに答えなさい。
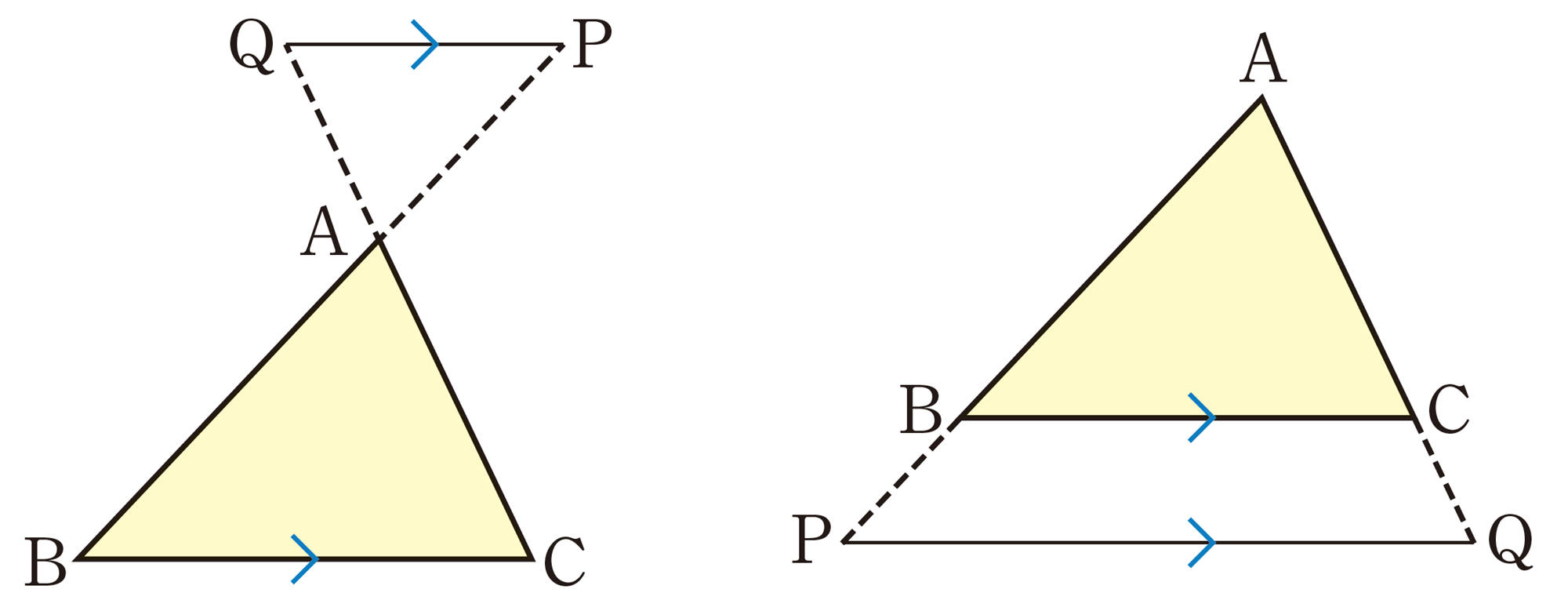
⑴ [mathjax]\(\triangle APQ \backsim \triangle ABC\) であることを証明しなさい。
⑵ [mathjax]\(\triangle APQ\) と[mathjax]\(\triangle ABC\) で，[mathjax]\(AP:AB\)と等しい比になる辺の組をいいなさい。
問 ２ 右の図で，[mathjax]\(PQ /\!/BC\)のとき，[mathjax]\(AP:PB=AQ:QC\)であることを，次の順に証明しなさい。
① 点Pを通り辺ACに平行な直線を引き，辺BCとの交点をRとする。このとき，[mathjax]\(\triangle APQ \backsim \triangle PBR\)を示す。
② 四角形PRCQで，[mathjax]\(PR=QC\)を示す。
③ ①，②から，[mathjax]\(AP:PB=AQ:QC\)を導く。
<3年p.162>
前ページの問1や問2で調べたことは，次のように，定理としてまとめることができる。
定理
平行線と線分の比
[mathjax]\(\triangle ABC\)の辺AB，AC上の点をそれぞれP，Qとするとき，
❶ [mathjax]\(PQ /\!/ BC\) ならば，
[mathjax]\(AP:AB=AQ:AC=PQ:BC\)
❷ [mathjax]\(PQ /\!/ BC\) ならば，
[mathjax]\(AP:PB=AQ:QC\)
問 ３ 160ページの 【1】 のように，等間隔に引かれた平行線を使うと，手紙が3等分できる理由を説明しなさい。
問 ４ [mathjax]\(\triangle ABC\)の辺BA，CAの延長上に，[mathjax]\(PQ/\!/BC\)となるようにそれぞれ点P，Qをとるとき，
[mathjax]\(AP:AB=AQ:AC=PQ:BC\)
であることを証明しなさい。
上の定理は，点 P，Qを辺 BA，CAの延長上や，辺AB，ACの延長上にとった場合にも成り立つ。
<3年p.163>
例 １ 右の図で，[mathjax]\(PQ /\!/ BC\)のとき，xの値を求めなさい。
解答
[mathjax]\(PQ /\!/ BC\)であるから，
答 [mathjax] \( x=8\)
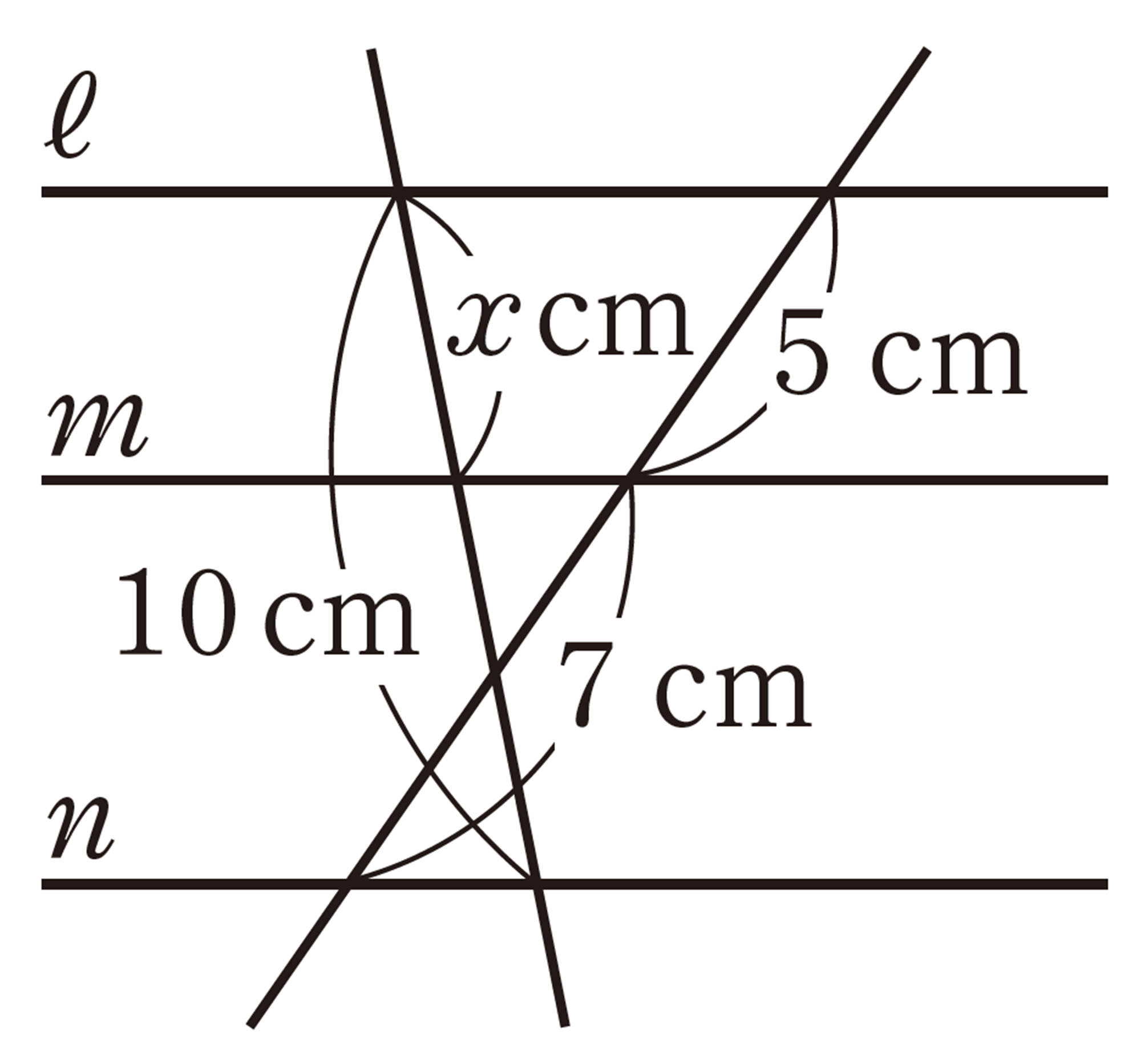
問 ５ 拓真さんは，上の図のyの値を右のように求めました。この求め方は正しいですか。誤りがあれば，正しく直しなさい。
[mathjax]\(PQ /\!/ BC\)であるから，
答 [mathjax]\(y=\dfrac{7}{2}\)
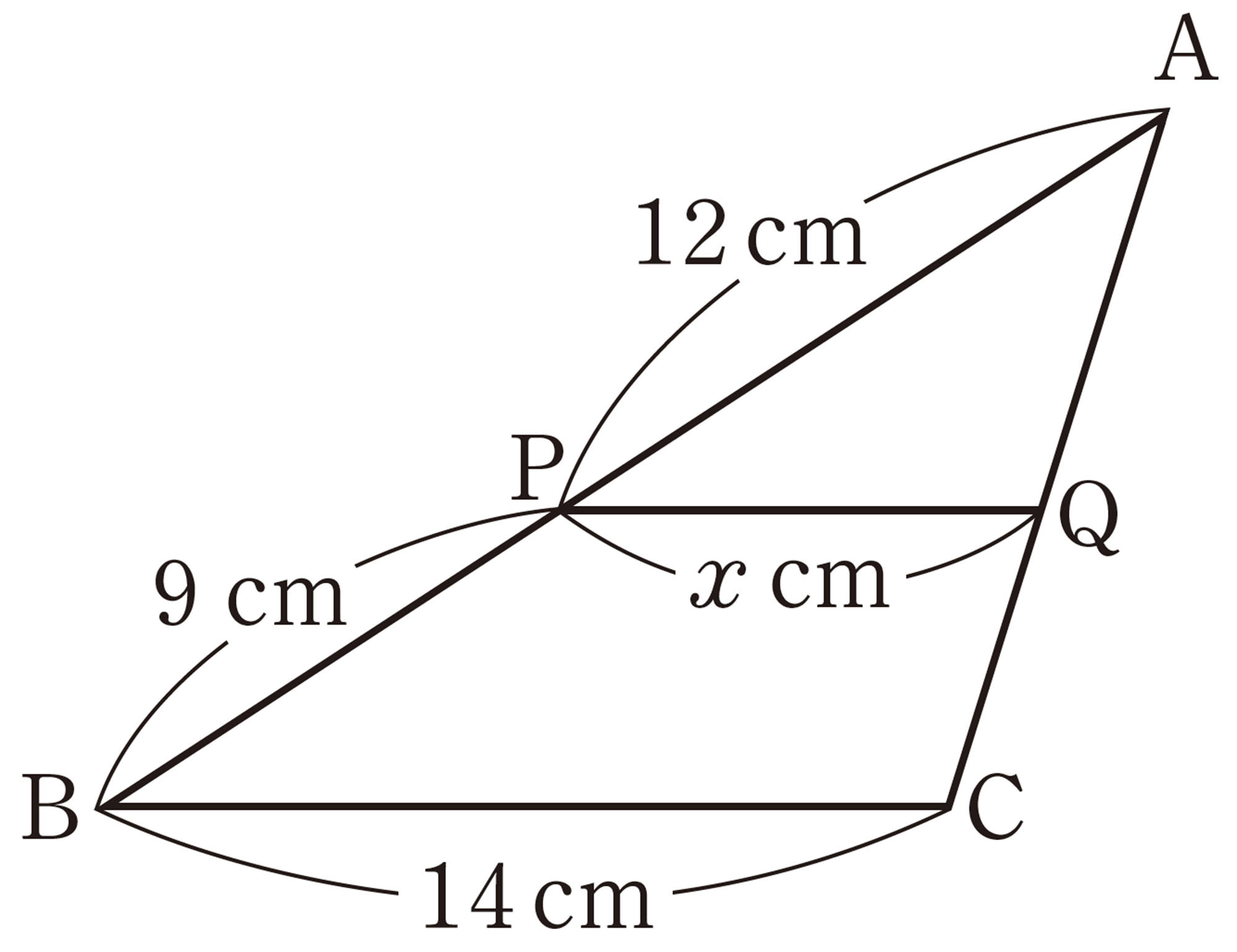
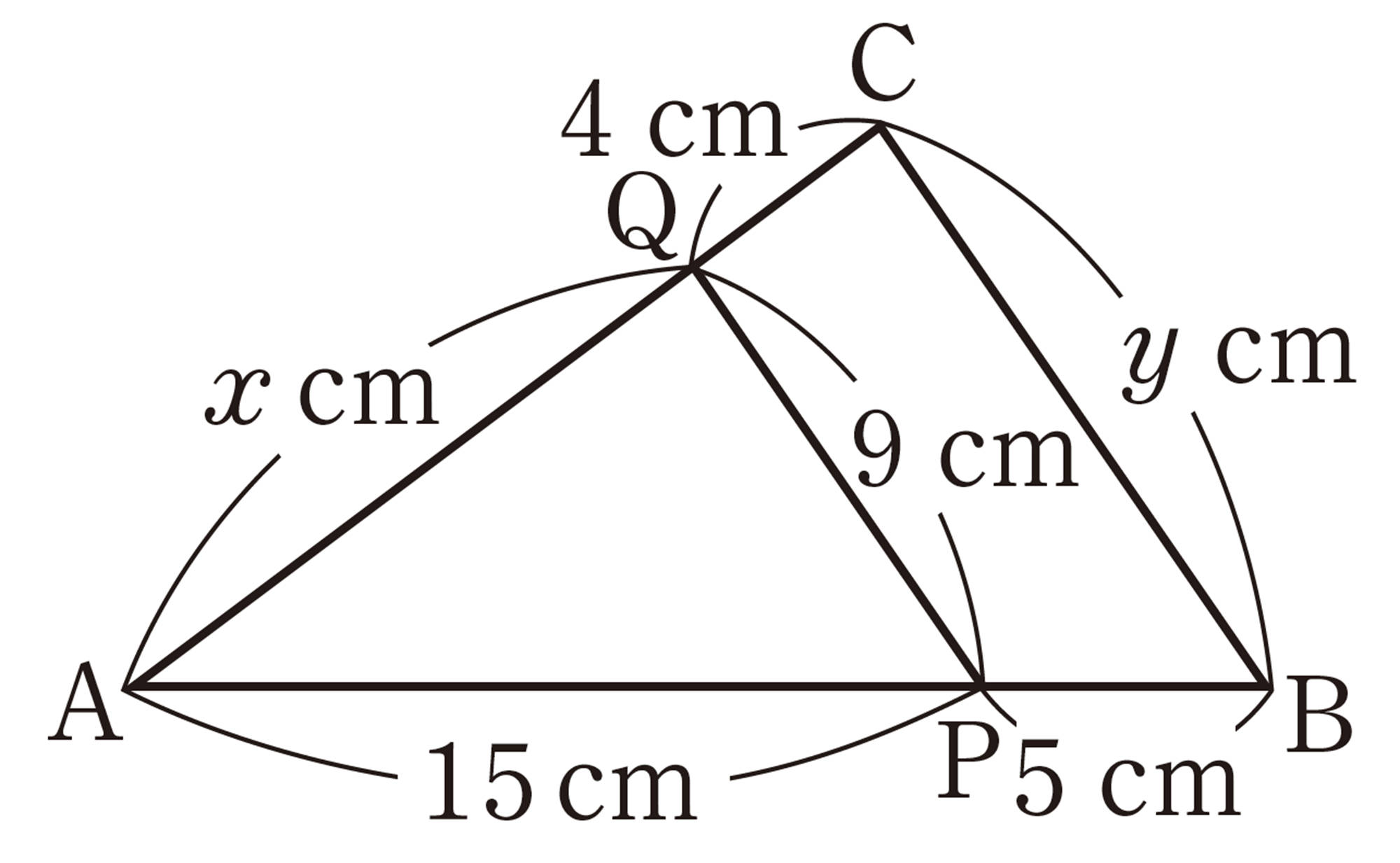
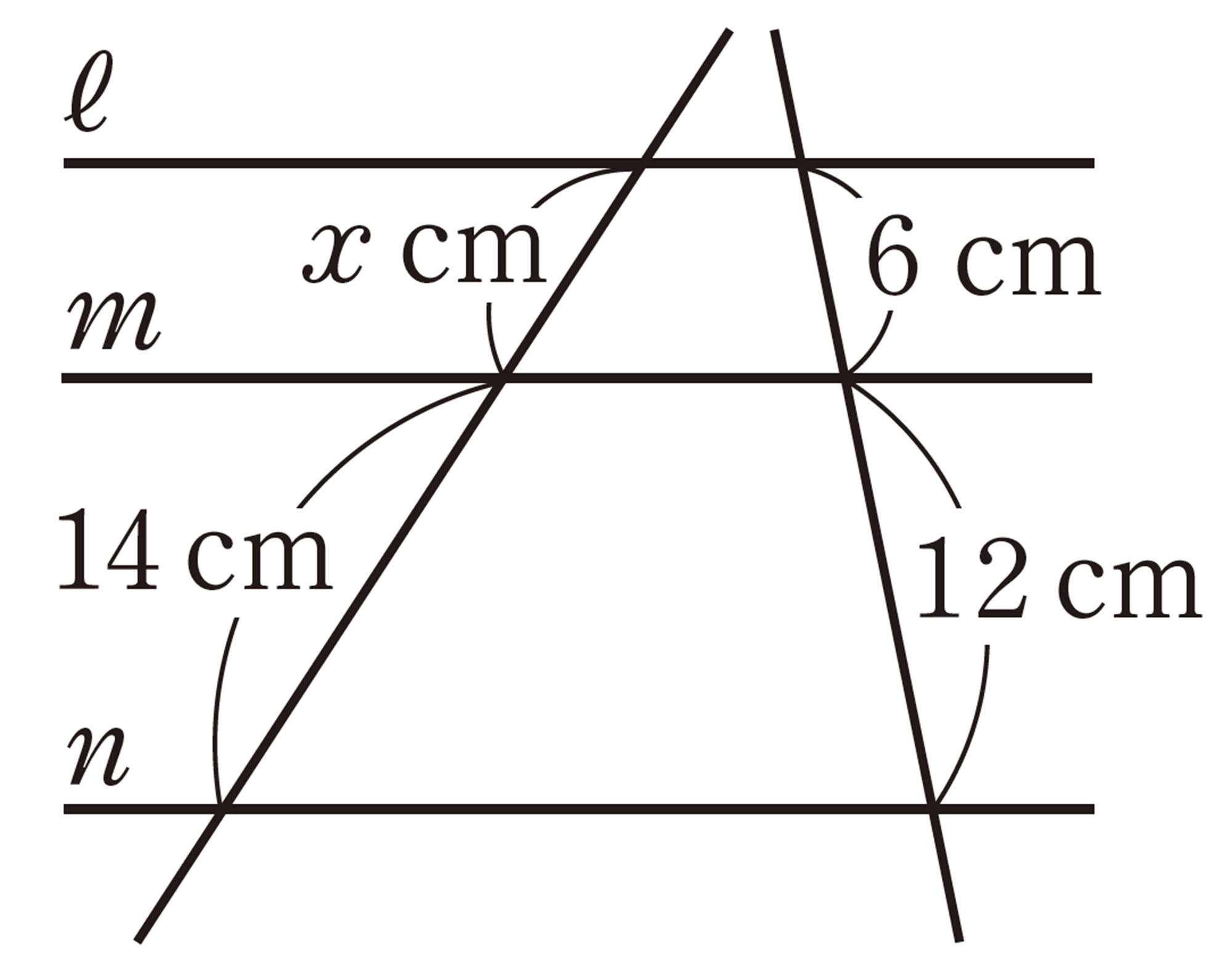
問 ６ 次の図で，[mathjax]\(PQ /\!/ BC\)のとき，x，yの値を求めなさい。
⑴
⑵
⑶
⑷
▲トライ 右の図で，[mathjax]\(PQ /\!/ BC\)のとき，xの長さをaを使って表してみよう。
<3年p.164>
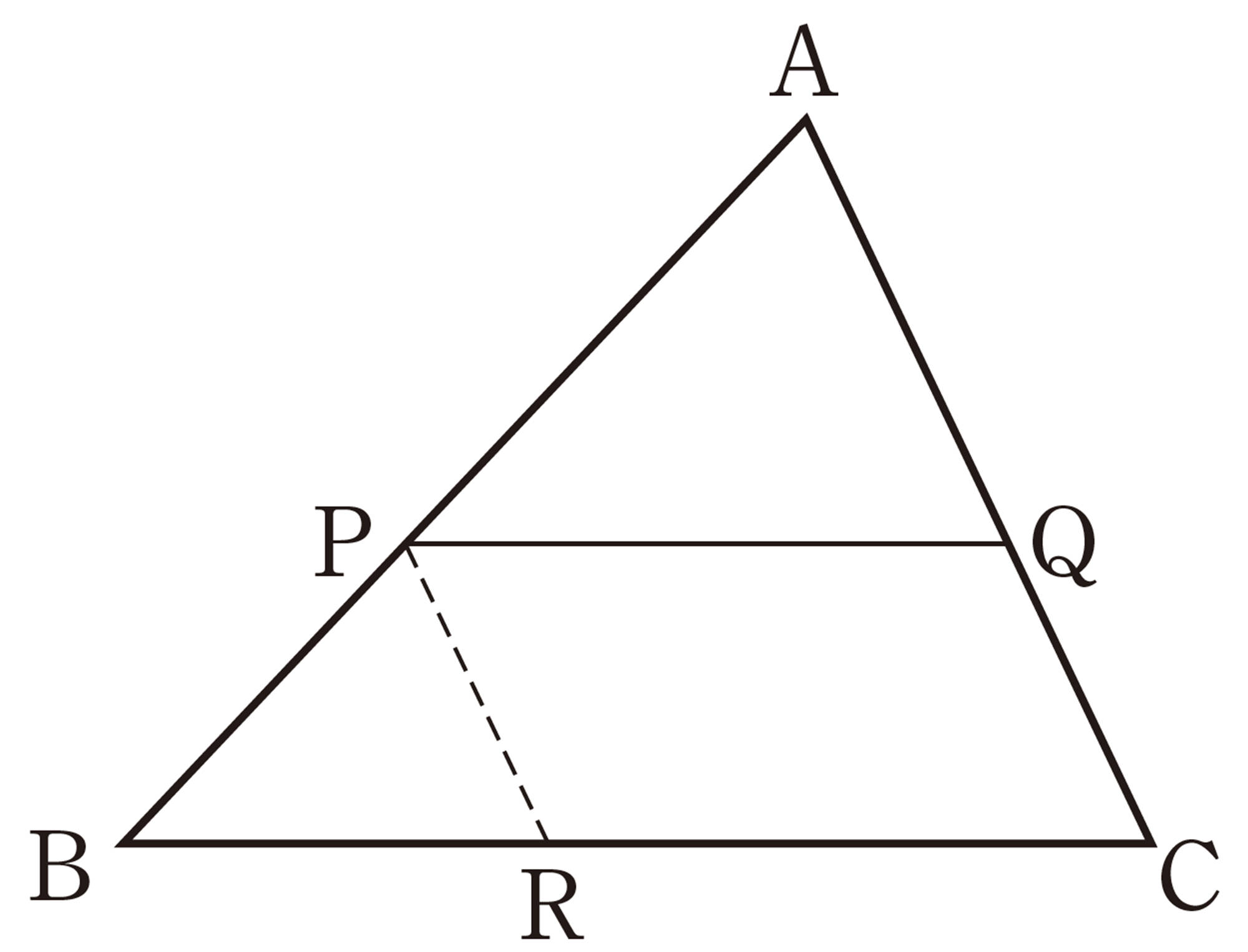
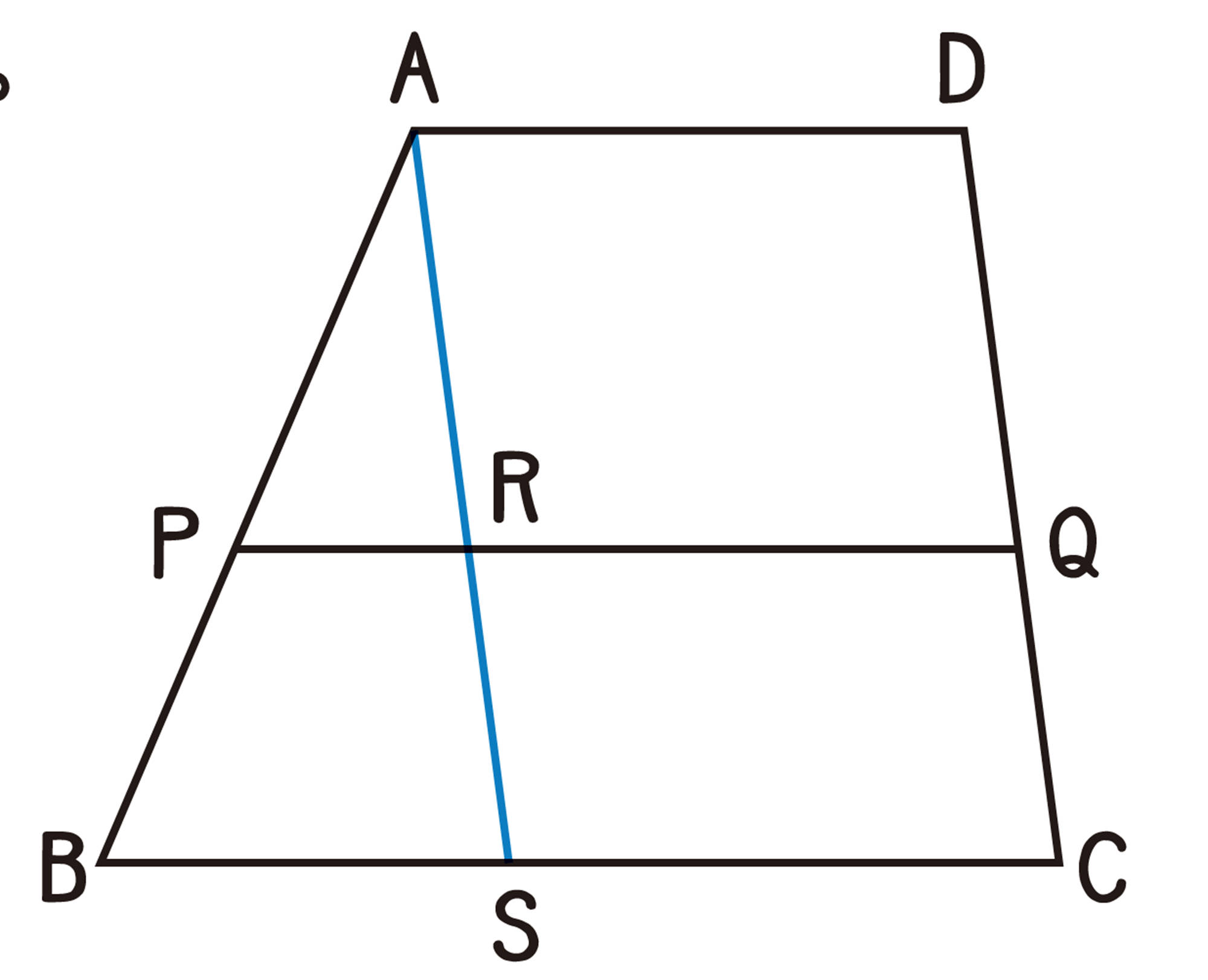
例 ２ [mathjax]\(AD/\!/BC\) である台形ABCDの辺BCに平行な直線を引き，辺AB，DCとの交点をそれぞれP，Qとするとき，[mathjax]\(AP:PB=DQ:QC\)であることを証明しなさい。
証明
点Aを通り辺DCに平行な直線を引き，
PQ，BCとの交点をそれぞれR，Sとする。
[mathjax]\(\triangle ABS\) において，[mathjax]\(PR/\!/BS\) であるから，
[mathjax]\(\hspace{10pt}AP:PB=AR:RS\quad\quad\cdots\cdots \mathsf{①}\)
四角形ARQD， 四角形RSCQ はともに
平行四辺形であるから，
[mathjax]\(\hspace{10pt}AR=DQ，RS=QC \ \quad \cdots\cdots \mathsf{②}\)
①，②から，[mathjax]\(AP:PB=DQ:QC\)
例2で証明したことから，次の定理が成り立つことがわかる。
定理
平行線で区切られた線分の比
平行な3つの直線 ℓ，m，nに，2つの直線p，qが交わっているとき，次のことが成り立つ。
[mathjax]\(a:b=a´:b´\)
上の定理で，直線pを次の図のように移動しても，[mathjax]\(a:b=a´:b´\)が成り立つ。
<3年p.165>
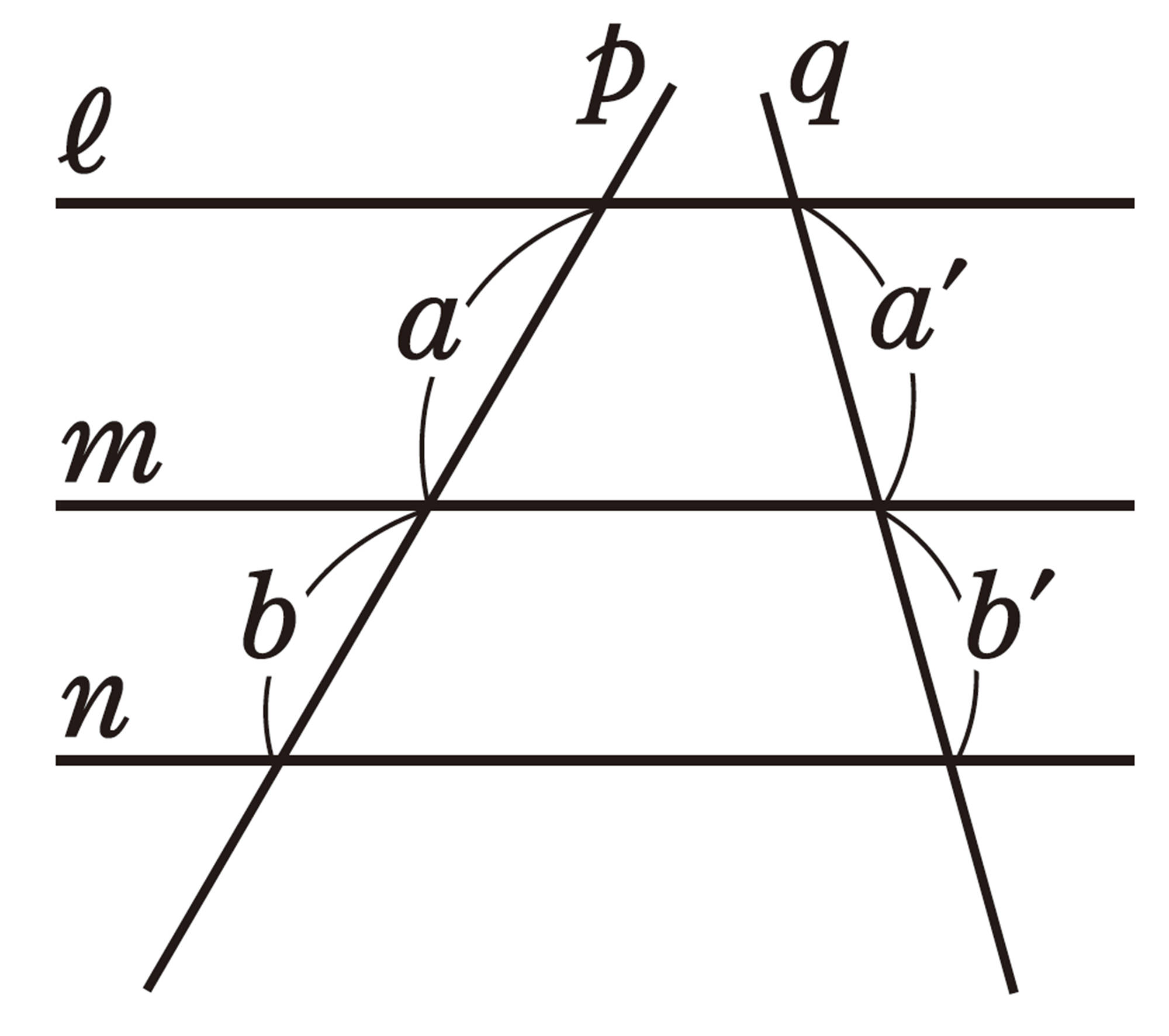
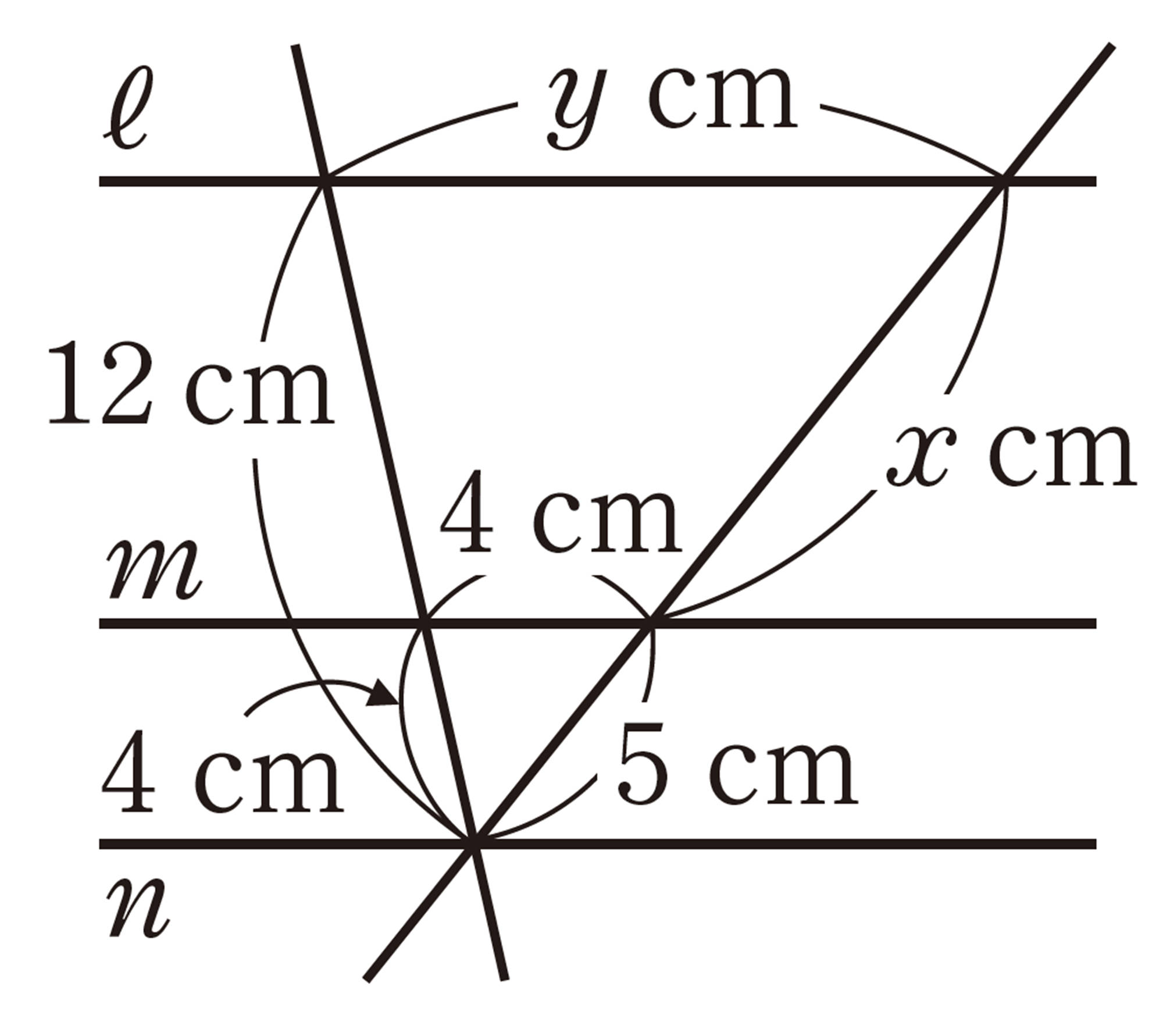
問 ７ 次の図で，[mathjax]\(ℓ/\!/m/\!/n\)のとき，x，yの値を求めなさい。
⑴
⑵
⑶
注意 [mathjax]\(ℓ/\!/m/\!/n\)は，直線ℓ，m，nがたがいに平行であることを表している。
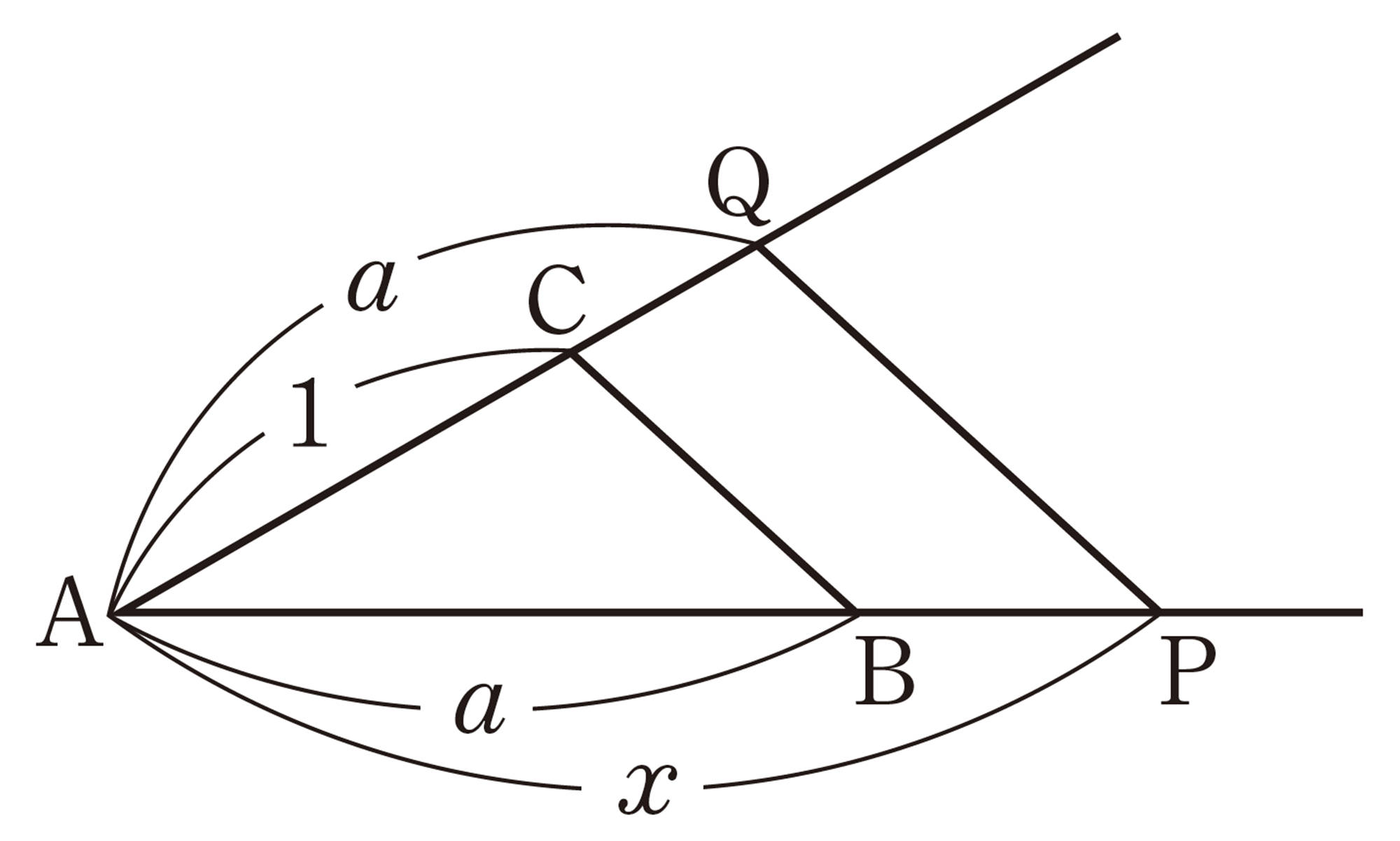
問 ８ 次の①～③は，与えられた線分ABを3等分する手順を示したものです。適当な線分ABをかき，この方法で3等分しなさい。また，この方法で3等分できる理由を説明しなさい。
① 適当な半直線AXを引く。
② 半直線AX上に，点Aから等しい長さで，順に点P，Q，Rをとり，点Rと点Bを結ぶ。
③ 点P，QからRBに平行な直線を引き，ABとの交点を，それぞれS，Tとする。
問 ９ 線分AB上にあり，ABを[mathjax]\(3:2\)の比に分ける点Pを，右の図にかき入れなさい。
線分ABを何等分すればいいのかな。
<3年p.166>
例 ３ [mathjax]\(\triangle ABC\) で，[mathjax]\(\angle A\)の二等分線と辺 BCとの交点をDとするとき，[mathjax]\(AB:AC=BD:DC\)であることを証明しなさい。
考え方 点Cを通りDAに平行な直線と辺BAの延長との交点をEとして，平行線の性質を利用する。
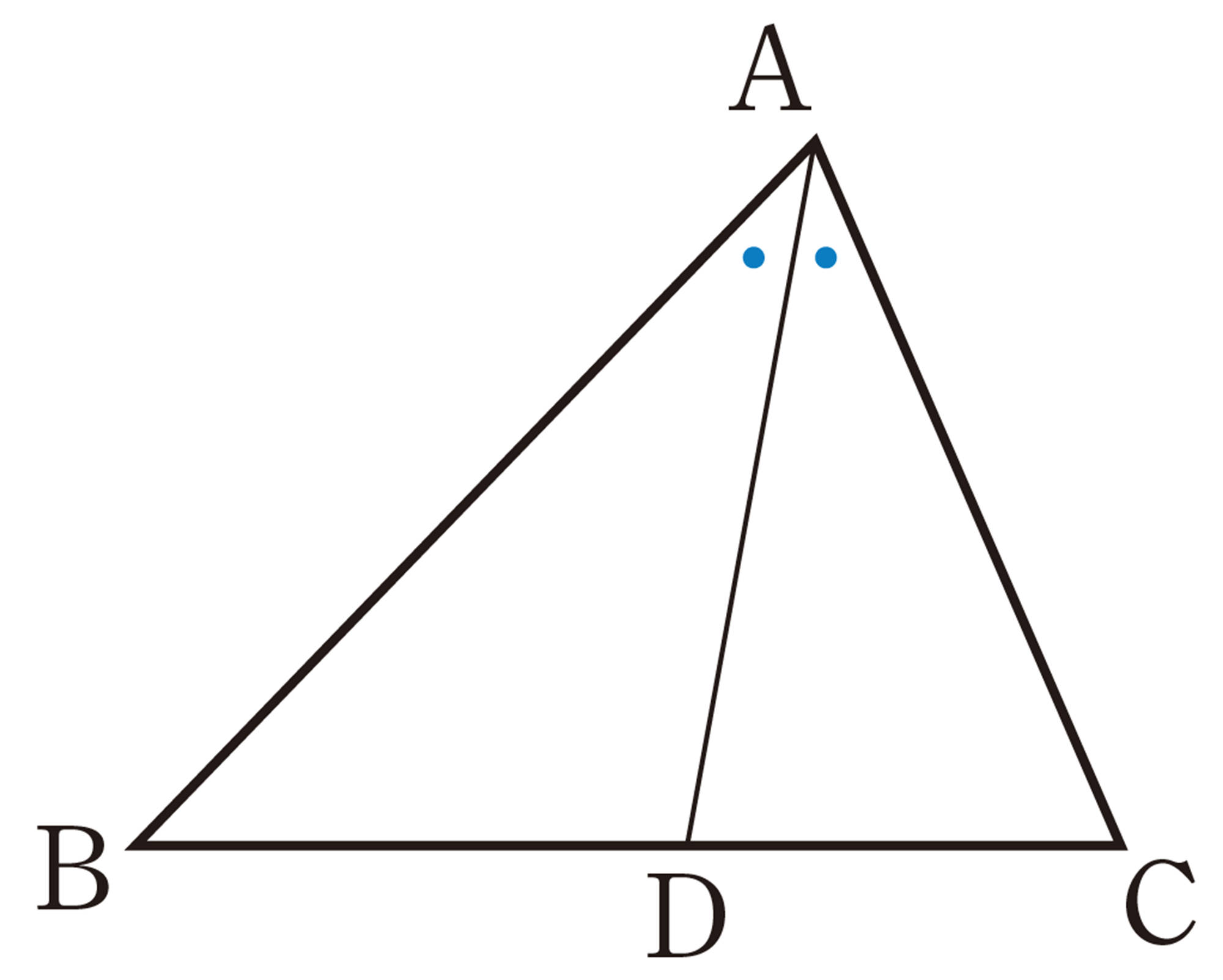
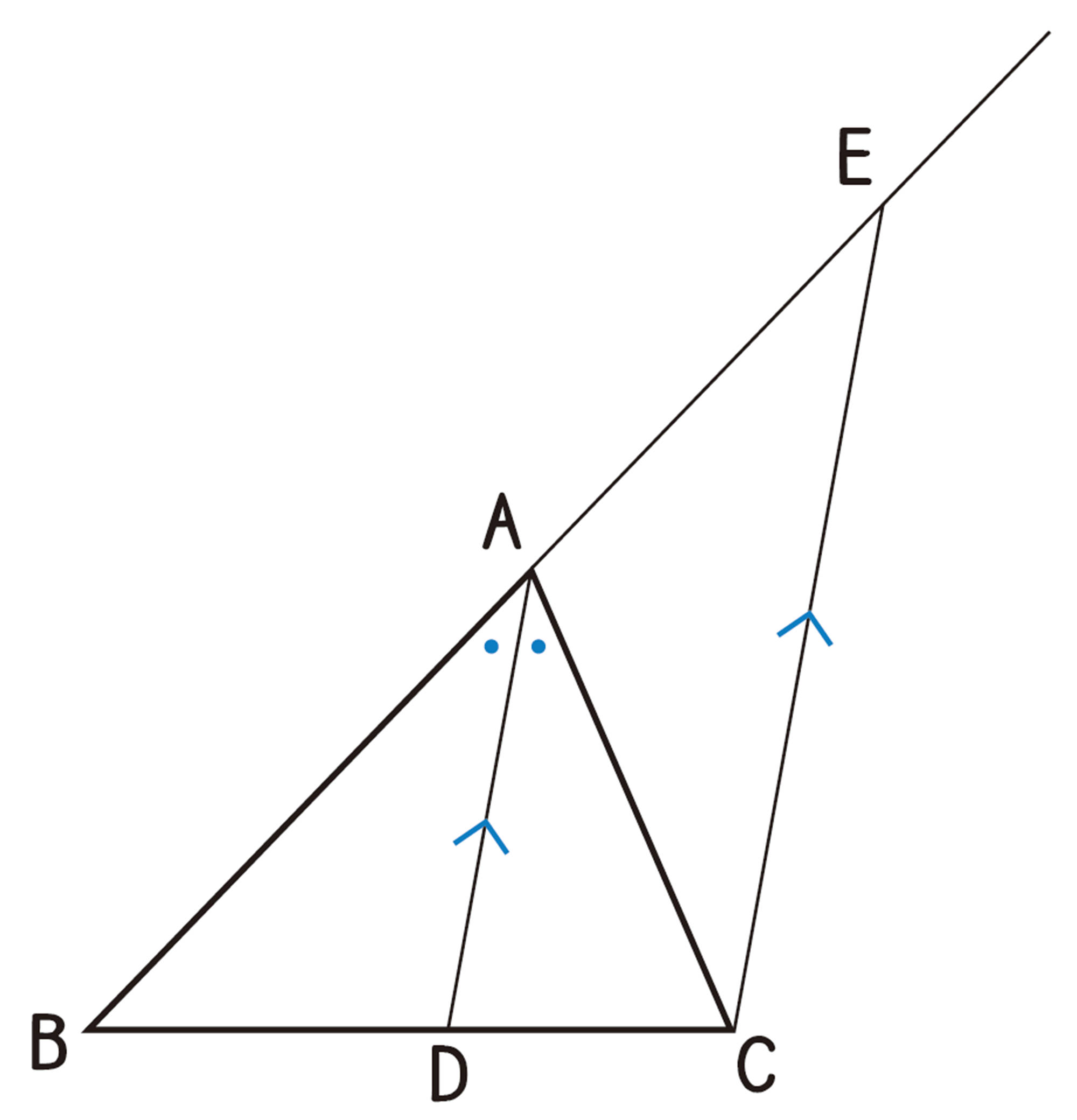
証明
点C を通り線分DA に平行な直線と辺BA の延長との交点をE とする。
[mathjax]\(DA/\!/CE\) から，平行線の同位角は等しいので，
[mathjax]\(\hspace{25pt}\angle BAD=\angle AEC \quad\quad\cdots\cdots \mathsf{①}\)
平行線の錯角は等しいので，
[mathjax]\(\hspace{25pt}\angle CAD=\angle ACE \quad\quad \cdots\cdots \mathsf{②}\)
仮定から，[mathjax]\(\angle BAD=\angle CAD \ \cdots\cdots \mathsf{③}\)
①， ②， ③から，[mathjax]\(\angle AEC=\angle ACE\)
２つの角が等しいから，
[mathjax]\(\triangle ACE\) は二等辺三角形になる。
[mathjax]\(\hspace{25pt}AE=AC \hspace{50pt}\cdots\cdots \mathsf{④}\)
[mathjax]\(\triangle BCE\) において， [mathjax]\(DA/\!/CE\) から，
[mathjax]\(\hspace{25pt}AB:AE=BD:DC \ \cdots\cdots \mathsf{⑤}\)
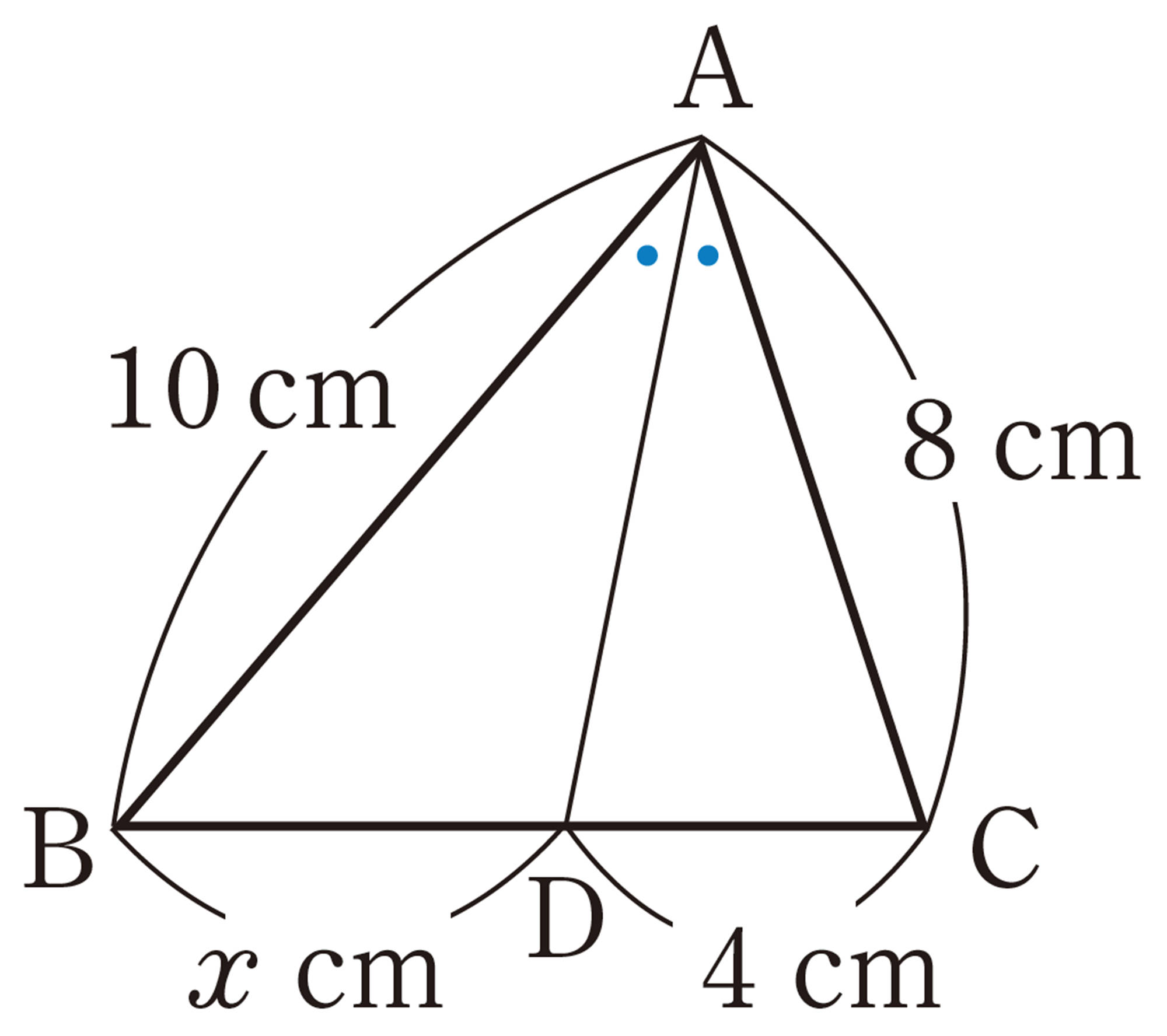
④， ⑤から，[mathjax]\(AB:AC=BD:DC\)
問 10 次の図で，線分ADは[mathjax]\(\angle BAC\)の二等分線です。このとき，xの値を求めなさい。
⑴
⑵
どんなことがわかったかな
「平行線と線分の比」の定理を使って，線分の長さを求めたり，線分の比が等しいことを証明したりすることができます。
次の課題へ！
「平行線と線分の比」の定理の逆は成り立つのかな？
P.167
