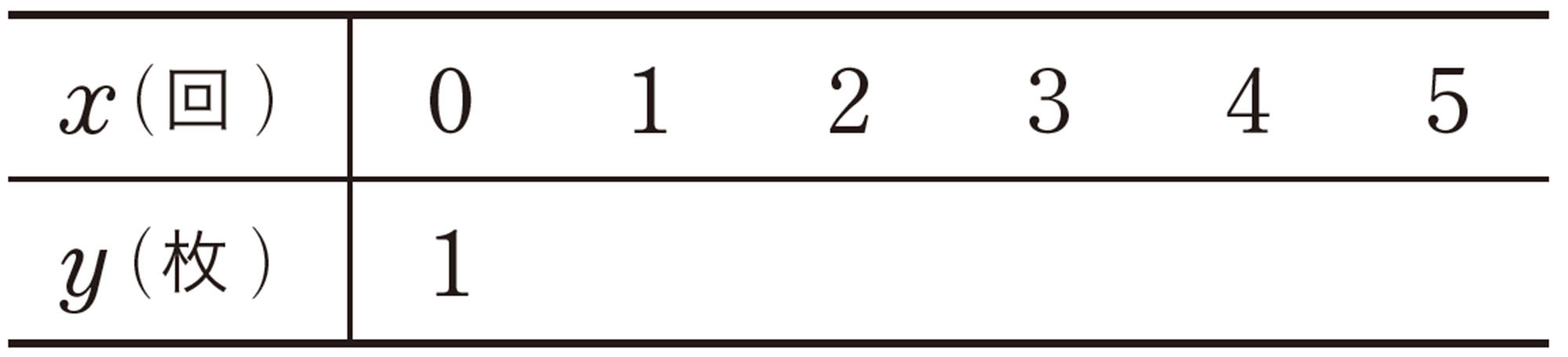<3年p.129>
2節 いろいろな関数
どんな関数があるかな？
身のまわりには，今まで学習した関数のほかにも，いろいろな関数があります。
【１】 ともなって変わる2つの数量を見つけ，どんな関数なのか調べてみましょう。
観覧車に乗ったとき，急に高くなるときがあったよ。
スピードが一定ではなくて，変化しているのかな。
表やグラフに表して，考えてみよう。
時間と高さの2つの数量は，関数の関係にあるのかな。
ほかには，どんな関数があるのかな。
次の課題へ！
どんな関数なのかを調べるには，どうしたらいいのかな？
P.130
<3年p.130>
１ 身のまわりの関数
Q Question
観覧車は，ふつう，一定の速度で回転しています。いま，観覧車の直径を60m，1回転する時間を12分間とします。このとき，ゴンドラがいちばん下の乗降場を出発してからの時間にともなって変わる数量を，見つけてみましょう。
これまでに学んだ関数では表せない関係はあるのかな。
見方・考え方
身のまわりのことがらを関数とみなして考えられるかな。
目標 ▷ 身のまわりからいろいろな関数を見つけ，変化のようすについて調べよう。
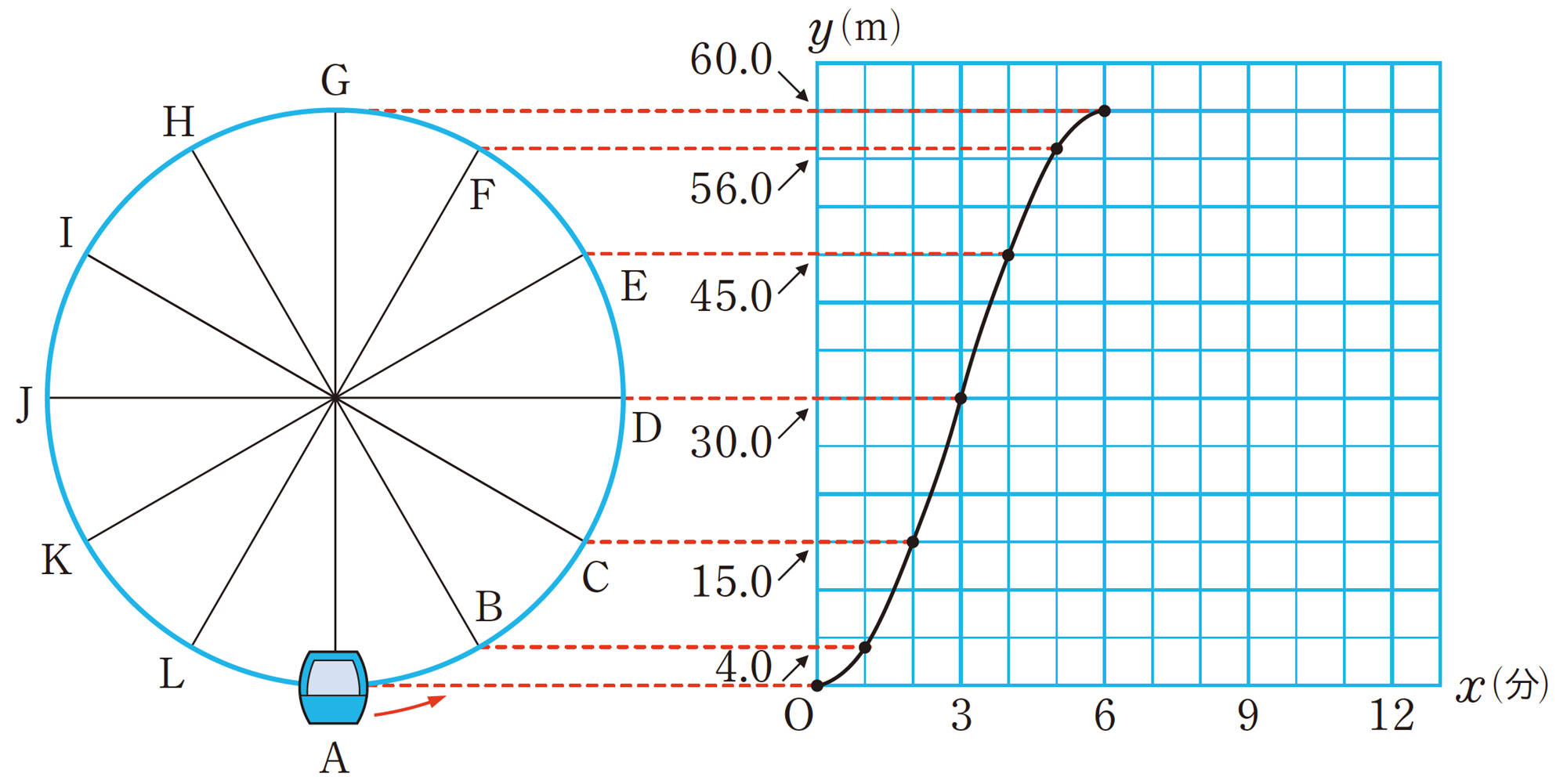
【Q】 で，次の図のように，ゴンドラが A を出発してからx分後の高さを ymとする。このとき，「2分後の高さは[mathjax]\(15.0\)m」のように，xの値を決めると，それに対応するyの値がただ1つ決まるから，yはxの関数である。
[mathjax]\(0 \leqq x \leqq 6\)のとき，この関数のグラフをかくと，次の図のようになる。
問 １ 【Q】で，[mathjax]\(6 \leqq x \leqq 12\)のとき，この関数のグラフを，上の図にかき入れなさい。
問 ２ 【Q】で，観覧車が1回転するとき，ゴンドラの高さの変化についてどんなことがいえますか。グラフをもとに説明しなさい。
<3年p.131>
問 ３ 前ページの【Q】で観覧車が3回転するとき，そのグラフをかいて，気づいたことをいいなさい。
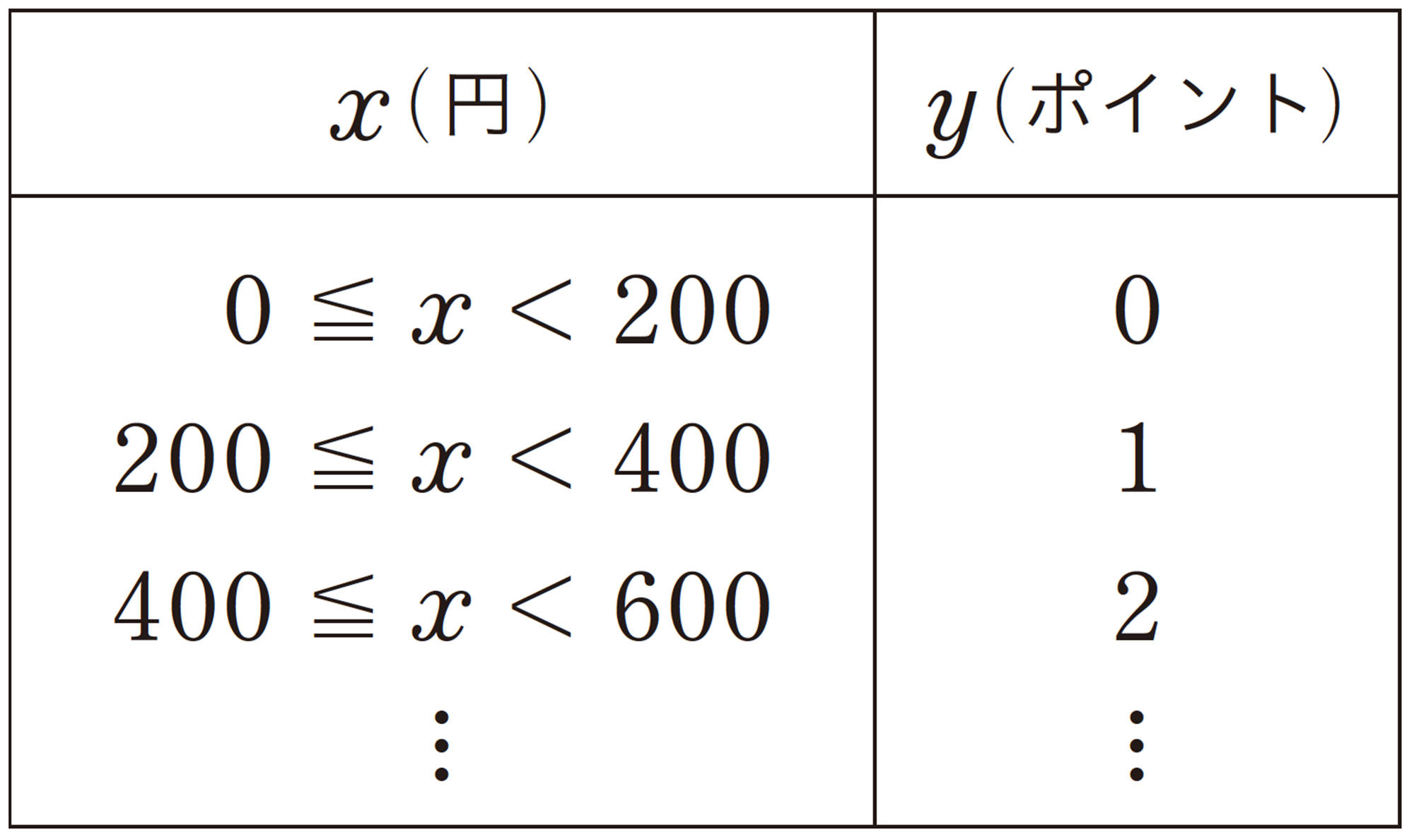
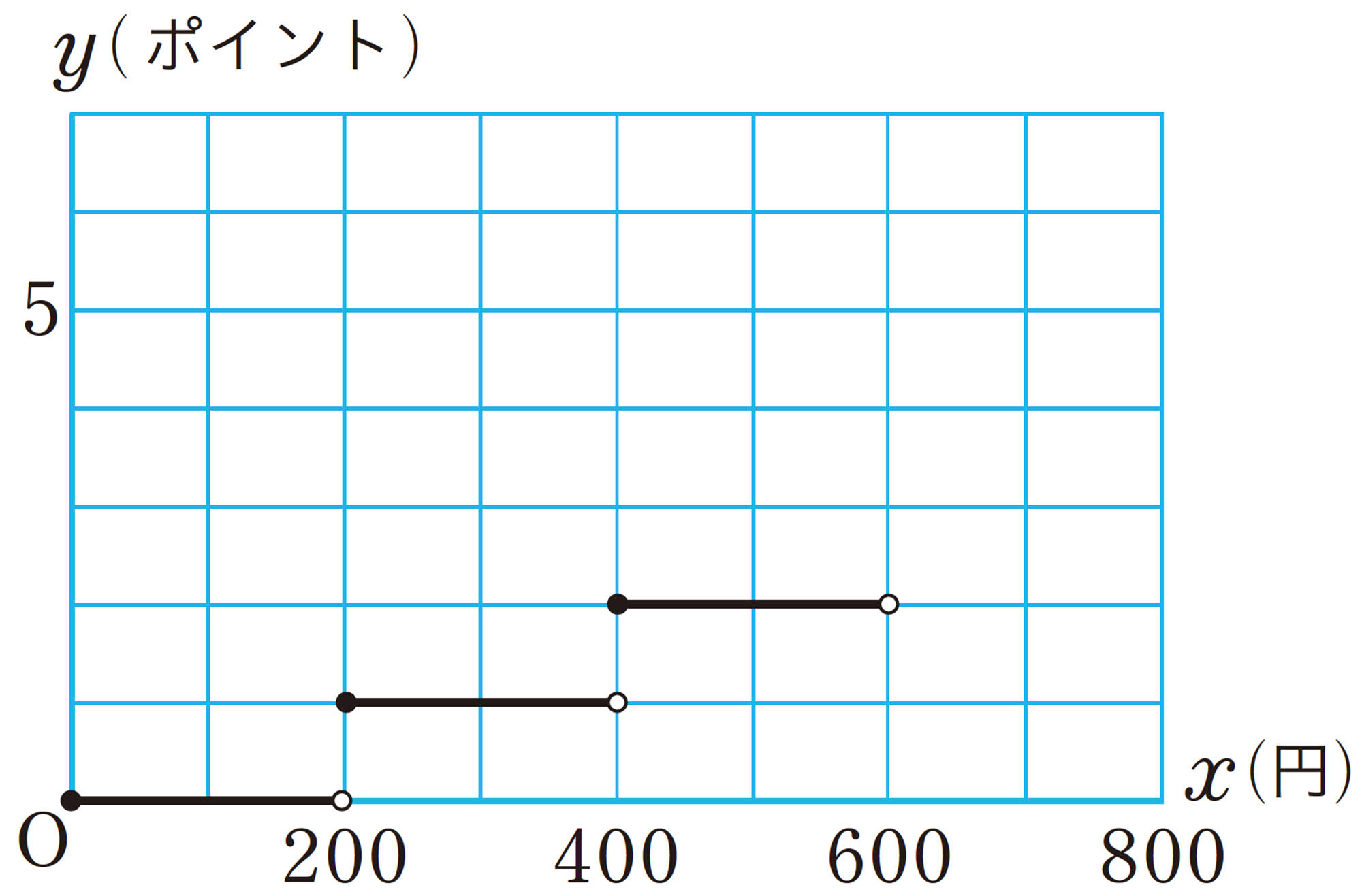
例 １ ある店のポイントカードは，200円買い物をするごとに1ポイントずつ加算される。この店でx円の買い物をしたときのポイントをyポイントとし， xの変域を[mathjax]\(0 \leqq x \lt 600\)としてグラフをかくと，右下の図のようになる。
ふりかえり
▷1年
●はその点をふくむこと，○はその点をふくまないことを表す。
問 ４ 例1について，次の問いに答えなさい。
⑴ 700円の買い物をしたときのポイントを求めなさい。
⑵ 5ポイントをもらうためには最低いくらの買い物が必要ですか。
⑶ yはxの関数といえますか。その理由も説明しなさい。
問 ５ xの変域を[mathjax]\(0 \lt x \leqq 5\)とし，xの値の小数点以下を切り上げた数値をyとします。このとき，次の問いに答えなさい。
⑴ [mathjax]\(x=2.4\)のときのyの値を求めなさい。
⑵ 右の図に，xとyの関係をグラフに表しなさい。
例1や問5のように，yがとびとびの値をとり，グラフが階段状になるものもある。このような場合でもxの値を決めると，それに対応するyの値がただ1つ決まるから，yはxの関数である。
<3年p.132>
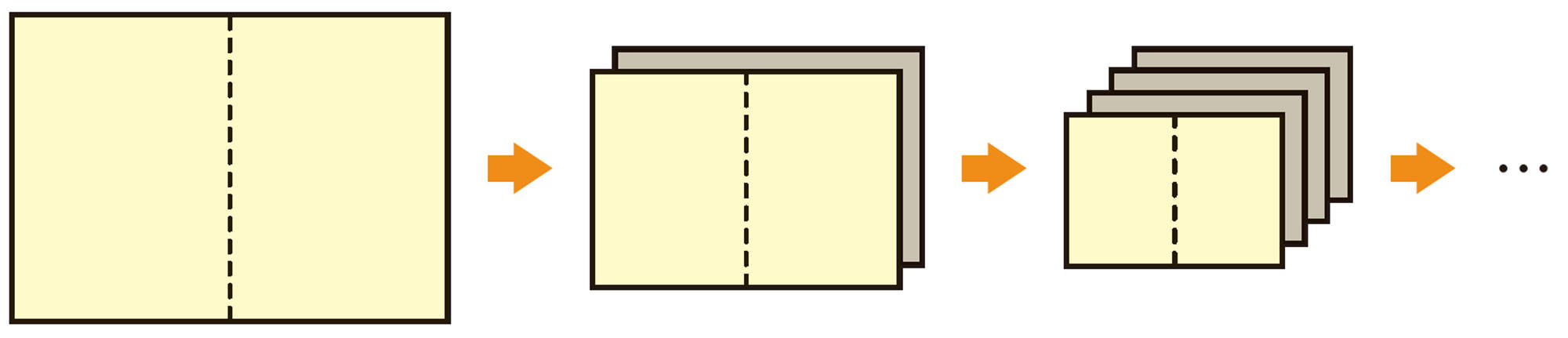
▲トライ 1枚の紙を半分に切ると2枚になります。その2枚を重ねて半分に切ると4枚になります。このような切り方でx回切ったときの紙の枚数をy枚とします。このとき，xの値を決めると，それに対応するyの値がただ1つ決まるので，yはxの関数です。この関数について，次のことを調べてみよう。
⑴ 次の表を完成しなさい。
⑵ ⑴の表の対応するxとyの値の組を座標とする点を，右の図にかき入れてみよう。
⑶ 10回切ったときにできる紙の枚数を求めてみよう。
どんなことがわかったかな
身のまわりから，これまで学んだ関数以外にも，いろいろな形のグラフで表される関数を見つけることができます。
確かめよう 2節 いろいろな関数
１ xの変域を[mathjax]\(0 \leqq x \leqq 5\)とし，xの値の小数第一位を四捨五入した数値をyとします。このとき，次の問いに答えなさい。
⑴ [mathjax]\(x=3.4\)のときのyの値を求めなさい。
⑵ 右の図に，xとyの関係をグラフに表しなさい。
<3年p.133>
4章 「関数 [mathjax]\(y=ax²\)」を学んで
できるようになったこと 身のまわりの課題へ ▷ P.136,137
2つの数量x，yの関係が[mathjax]\(y=ax²\)で表されるとき，yはxの2乗に比例する関数であることが理解できる。
関数[mathjax]\(y=ax²\)のグラフが放物線になることを理解して，グラフをかくことができる。
関数[mathjax]\(y=ax²\)の変化の割合は一定ではないことを理解して，変化の割合を求めることができる。
身のまわりや数学の中から見つけた問題を，2乗に比例する関数とみなして，その特徴を見つけて解決に利用することができる。
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない 数学者 岡潔
日本を代表する数学者の一人に岡潔(1901～1978)という人がいました。近代日本が生んだ最高の数学者といわれることもあります。
岡は，当時世界中の誰も解けなかった関数の未解決の問題を次々と解決していきました。岡の論文は，世界の数学者を驚かせました。数学者の中には，「岡潔」の名を個人名ではなく，数学者の集団だと信じていた人もいたといわれるほどです。
岡は，数学の研究に全精力を捧げた人であり，彼のことばに次のようなものがあります。
「数学は生命の燃焼によってつくるのです。」
「数学は必ず発見の前に一度は行き詰まるのです。行き詰まるから発見するのです。」
<3年p.134>
4章のまとめの問題 解答 P.303 基本
１ 次の㋐〜㋕の中から，下の⑴〜⑶にあてはまる関数を，それぞれ選びなさい。
㋐ [mathjax]\(y=x²\)
㋑ [mathjax]\(y=-x²\)
㋒ [mathjax]\(y=2x+1\)
㋓ [mathjax]\(y=-2x\)
㋔ [mathjax]\(y=2x²\)
㋕ [mathjax]\(y=-2x²\)
⑴ yはxの2乗に比例する。
⑵ [mathjax]\(x \lt 0\)のとき，xの値が増加するとyの値が減少する。
⑶ [mathjax]\(x=0\)のとき，yが最大値0をとる。
２ 右の図のように，同じ大きさの正三角形のタイルを並べて，大きな正三角形をつくっていきます。次の問いに答えなさい。
⑴ x段目のタイルの数をy枚として，yをxの式で表しなさい。
⑵ x段目までのタイルの総数をy枚として，yをxの式で表しなさい。
⑶ 10段目までのタイルの総数を求めなさい。
３ 右の図は，関数[mathjax]\(y=ax²\)のグラフです。次の問いに答えなさい。
⑴ 比例定数aの値を求めなさい。
⑵ xの変域を[mathjax]\(-4 \leqq x \leqq 2\)とするとき， yの最小値と最大値を求めなさい。
⑶ xの値が2から4まで増加するときの変化の割合を求めなさい。
<3年p.135>
応用
１ 関数[mathjax]\(y=ax²\)について，次の場合のaの値を求めなさい。
⑴ [mathjax]\(x=-4\)のとき[mathjax]\(y=4\)
⑵ xの値が1から4まで増加するときの変化の割合が[mathjax] \(-5\)
⑶ xの変域が[mathjax]\(-3 \leqq x \leqq 2\)のとき，yの最大値が3
２ 底面の半径がxcm，高さが30cmの円錐があります。この円錐の体積をycm³として，次の問いに答えなさい。
⑴ yをxの式で表しなさい。
⑵ この円錐の体積が1000cm³のとき，底面の半径は何cm ですか。円周率を[mathjax]\(3.14\)として，小数第二位まで求めなさい。
３ 右の図のように，関数[mathjax]\(y=ax²\)のグラフと関数[mathjax]\(y=x+4\)のグラフの交点を A，Bとします。点A，Bのx座標がそれぞれ-2，4であるとき，次の問いに答えなさい。
⑴ 点Aの座標を求めなさい。
⑵ aの値を求めなさい。
⑶ [mathjax]\(\triangle AOB\)の面積を求めなさい。
４ 右の図のような1辺8cmの正方形ABCDがあります。点Pは，秒速2cm で周上をBからCを通ってDまで動きます。点Qは，点Pと同時に出発して，秒速1cm で周上をBからAまで動きます。点 P，QがBを出発してからx秒後の[mathjax]\(\triangle BPQ\)の面積をycm²とするとき，次の問いに答えなさい。
⑴ [mathjax]\(0 \leqq x \leqq 4\)のとき，yをxの式で表しなさい。
⑵ [mathjax]\(4 \leqq x \leqq 8\)のとき，yをxの式で表しなさい。
<3年p.136>
4章のまとめの問題 活用
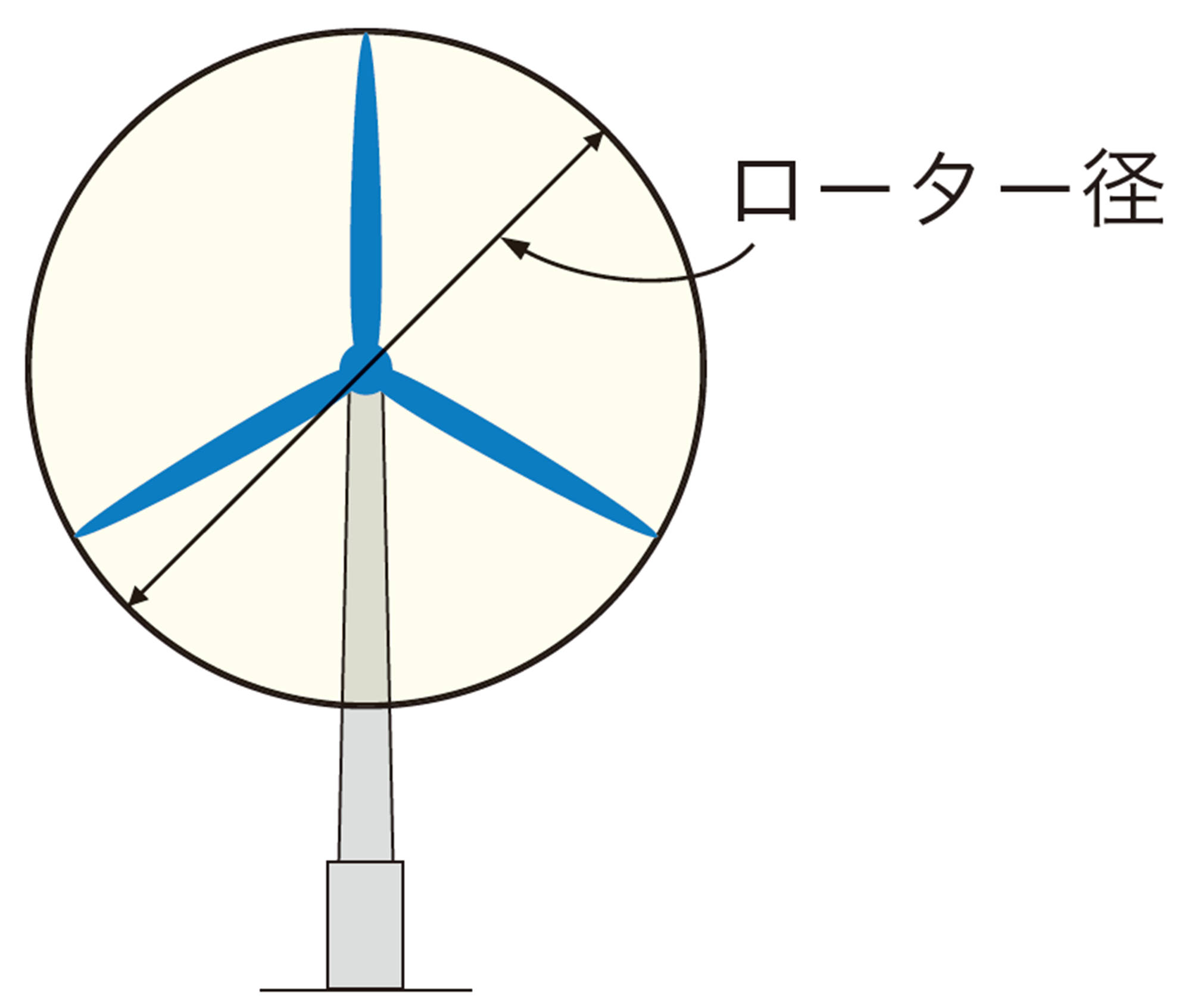
風力発電は，風の力で風車を回して，その力を電気エネルギーに変換しています。風力発電に使われている風車は，ブレード(羽根)が3枚のプロペラ型風車が一般的です。
ブレードが回転してできる円の直径をローター径といい，ローター径が長くなれば，風車から得られるエネルギーは大きくなります。そのため，風車の大型化が進んでいます。
１ 風力発電の風車のローター径の長さをx m，風車の定格出力(安全に出力できる電力)をy kW(キロワット)として，xとyの関係を表すと，次の表のようになります。下の問いに答えなさい。
⑴ ローター径の長さxと風車の定格出力yの間には，どんな関係がありますか。次の①〜③の中から選び，yをxの式で表しなさい。ただし，比例定数は，ローター径の長さが80mの値をもとに，分数で求めなさい。
① yはxに比例する。
② yはxに反比例する。
③ yはxの2乗に比例する。
⑵ 定格出力を4000kW にするときの，ローター径の長さを求める方法を説明しなさい。また，その方法で答えを求めなさい。
＞＞ 関連する職業・仕事 ［エンジニア］
