<3年p.122>
４ 関数[mathjax]\(y=ax²\)の利用
目標 ▷ 関数[mathjax]\(y=ax²\)の関係を利用して，いろいろな問題を解決しよう。
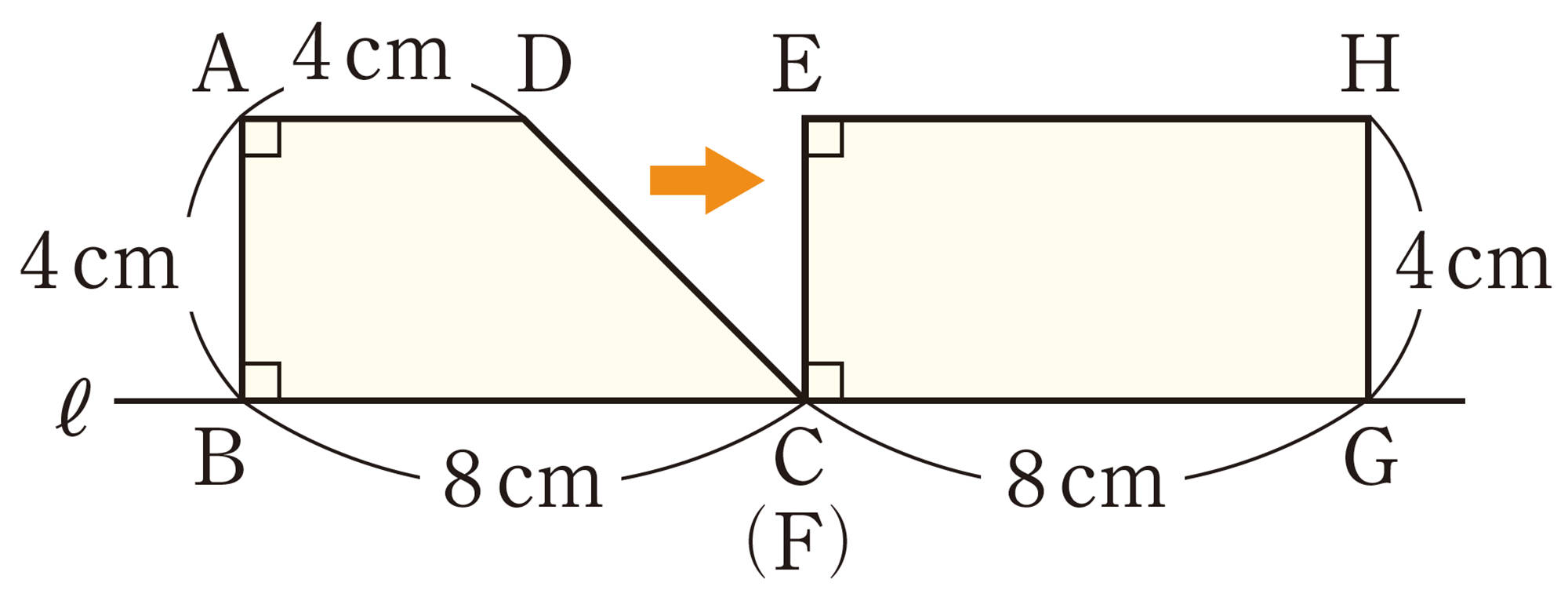
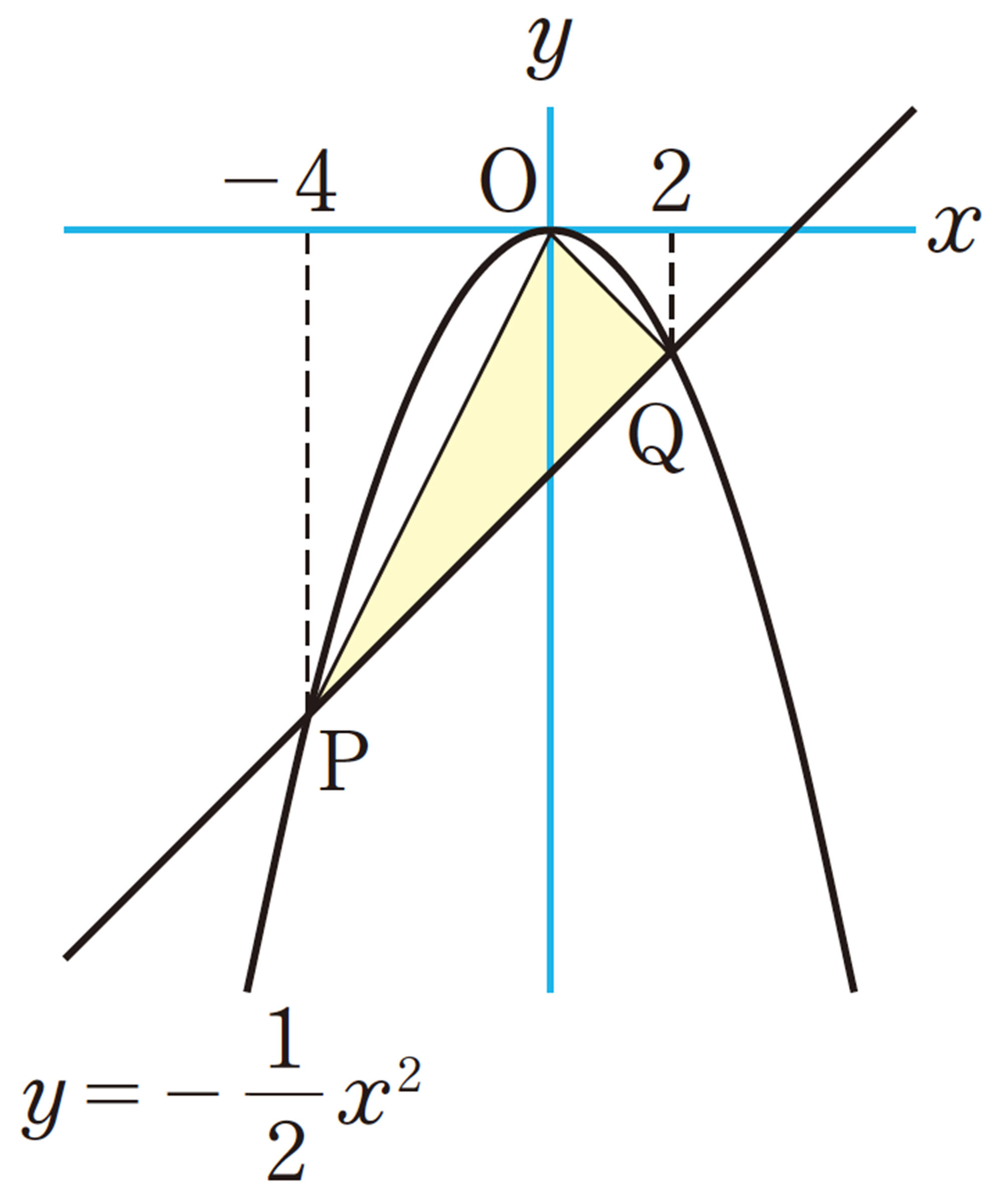
例 １ 次の図㋐のように，台形ABCDと長方形EFGHが直線ℓ上で並んでいます。
㋐
㋑
長方形を固定し，台形を矢印の方向に辺ABと辺EFが重なるまで移動します。[mathjax]\(FC=x\)cmのときの2つの図形が重なる部分の面積をycm²とするとき，xとyの関係を式に表しなさい。
考え方 xの変域を，[mathjax]\(0 \leqq x \leqq 4\)と[mathjax]\(4 \leqq x \leqq 8\)に分けて考える。それぞれの変域のときのyをxの式で表す。
解答
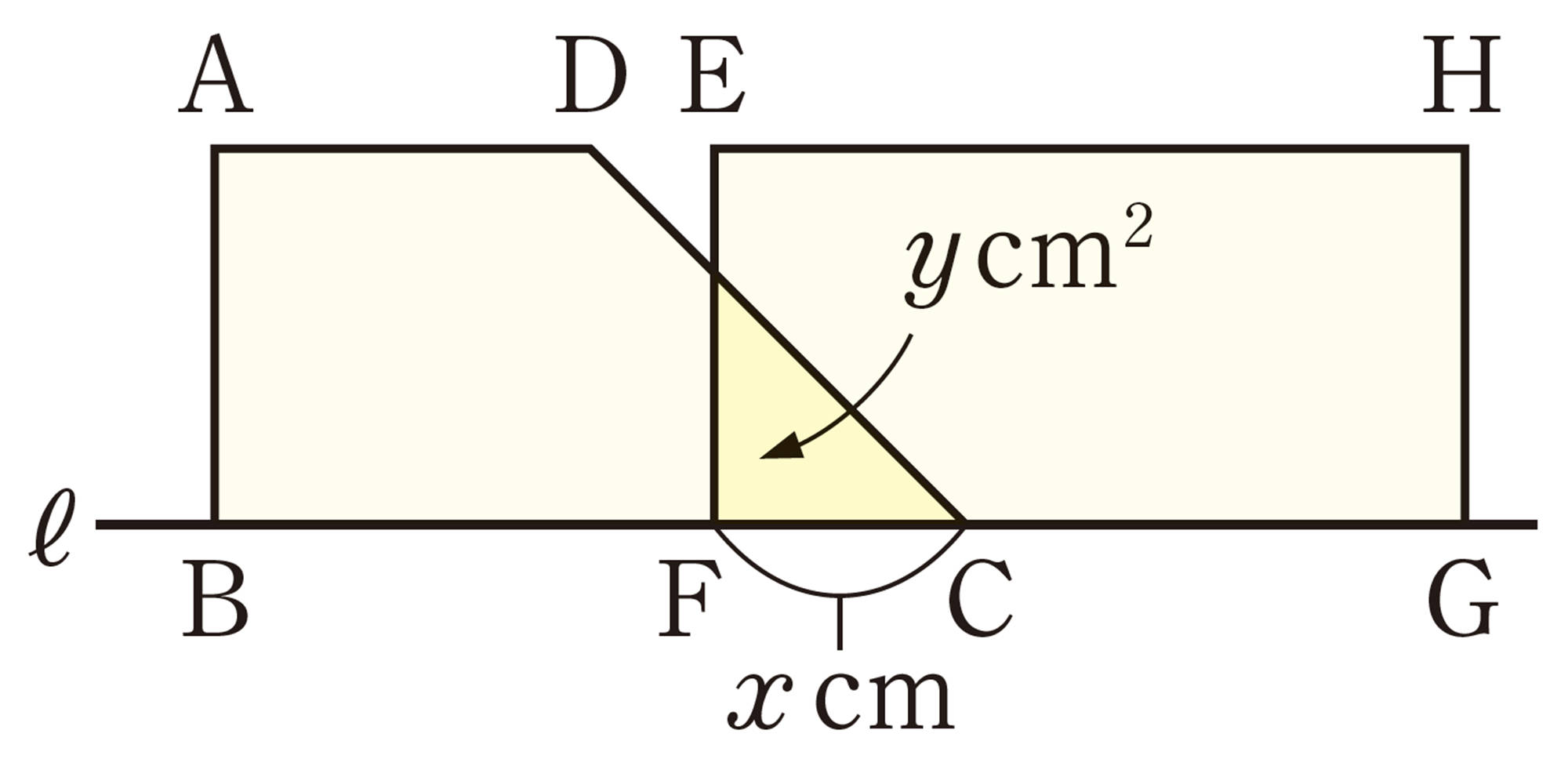
[mathjax]\(0 \leqq x \leqq 4\)のとき，重なる部分は1辺xcmの直角二等辺三角形だから，yをxの式で表すと，次のようになる。
[mathjax]\(\hspace{20pt}y=\dfrac{1}{2}x²\)
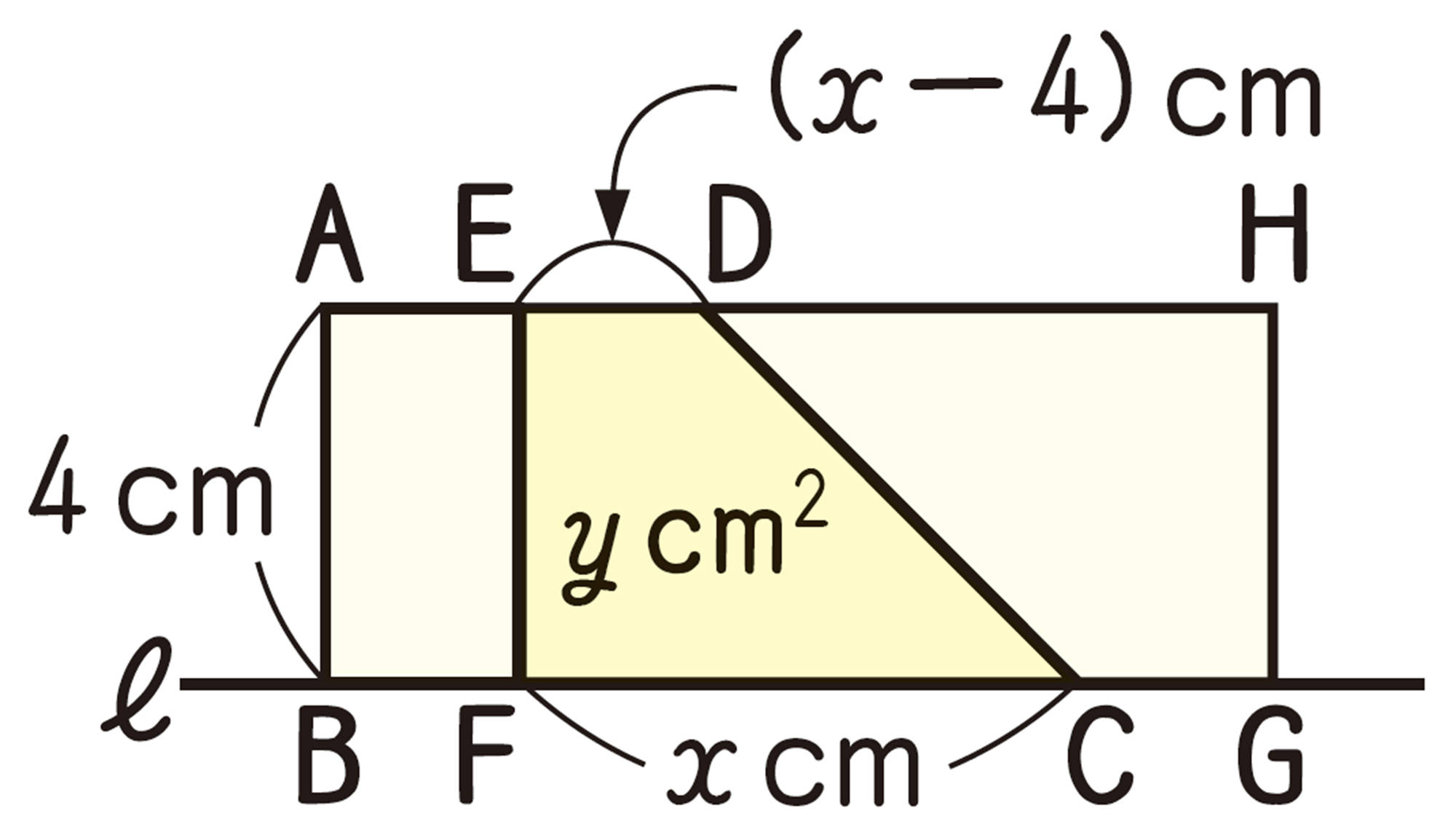
[mathjax]\(4 \leqq x \leqq 8\)のとき，重なる部分は上底[mathjax]\((x-4)\)cm，下底xcm，高さ4cmの台形だから，yをxの式で表すと，次のようになる。
答 [mathjax]\(0 \leqq x \leqq 4\)のとき，[mathjax]\(y= \dfrac{1}{2}x²\)
[mathjax]\(4 \leqq x \leqq 8\)のとき，[mathjax]\(y=4x-8\)
<3年p.123>
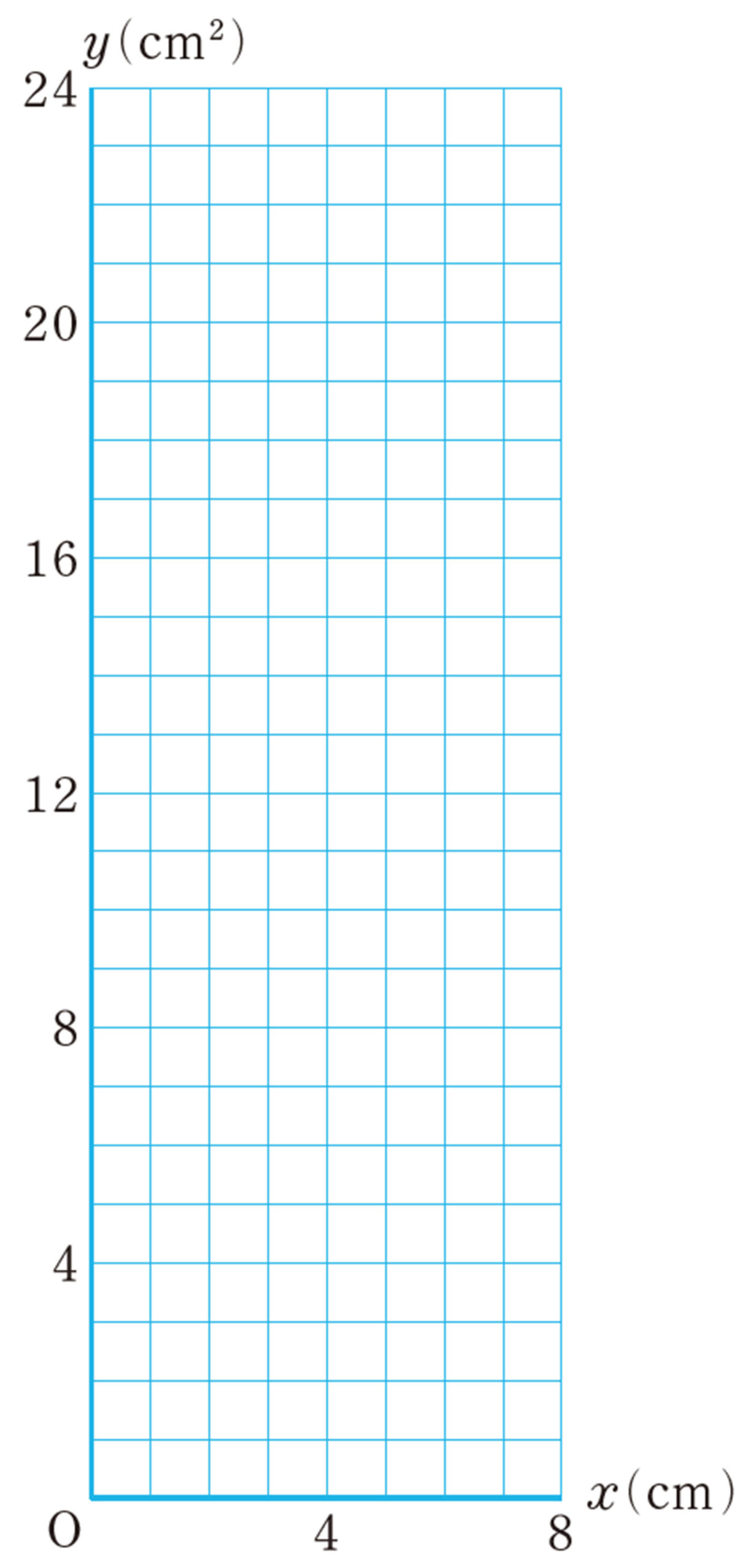
問 １ 前ページの例1について，グラフを前ページの図にかき入れなさい。
問 ２ 前ページの例1について，重なってできる部分の面積が，台形 ABCD の面積の半分になるときのxの値を求めなさい。
例 ２ 右の図のように，関数[mathjax]\(y=ax²\)と関数[mathjax]\(y＝bx+c\)のグラフが点 P，Q で交わっています。点Pの座標が[mathjax]\((-3，9)\)，点Qのx座標が 2のとき，a，b，cの値を求めなさい。
解答
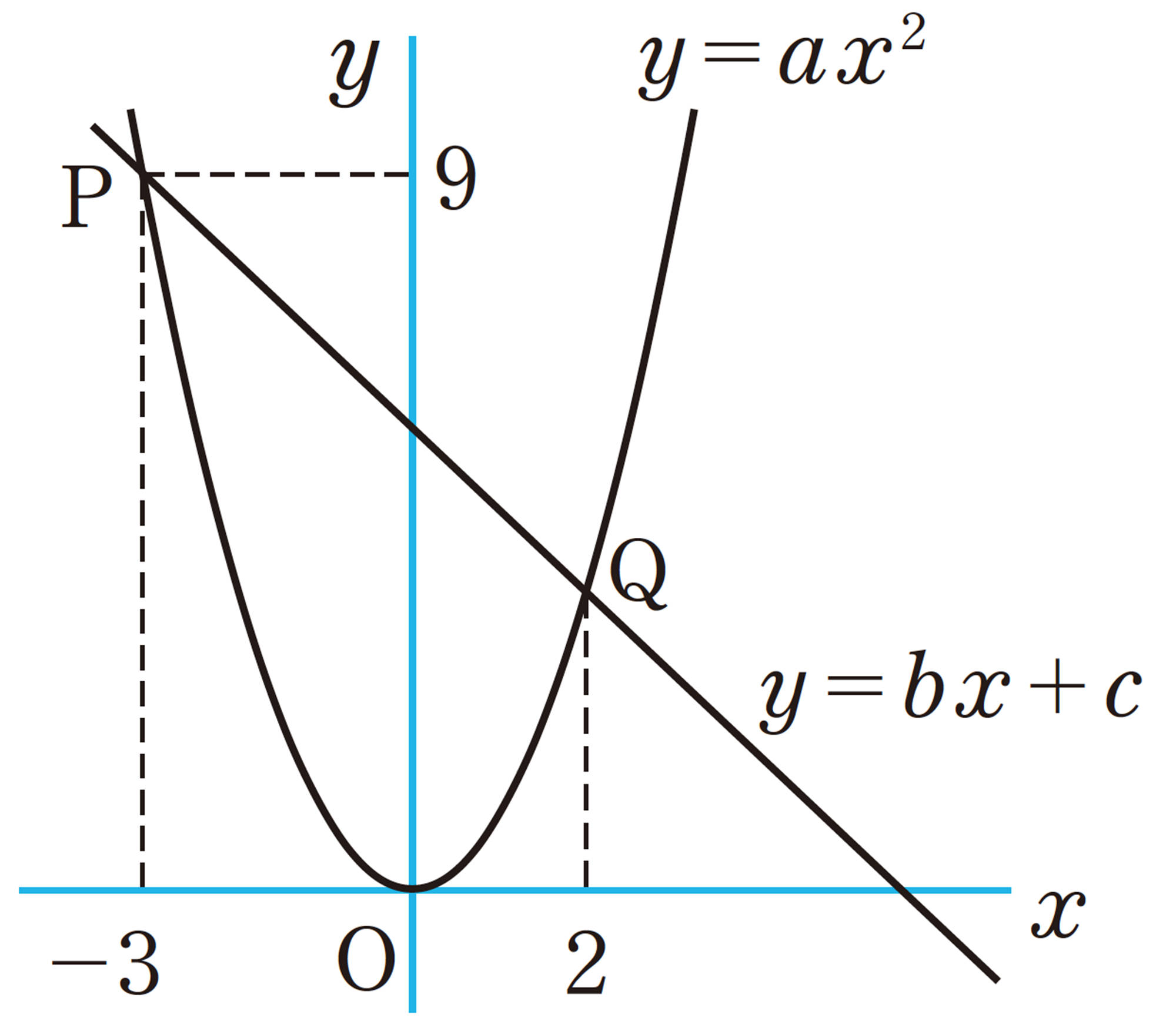
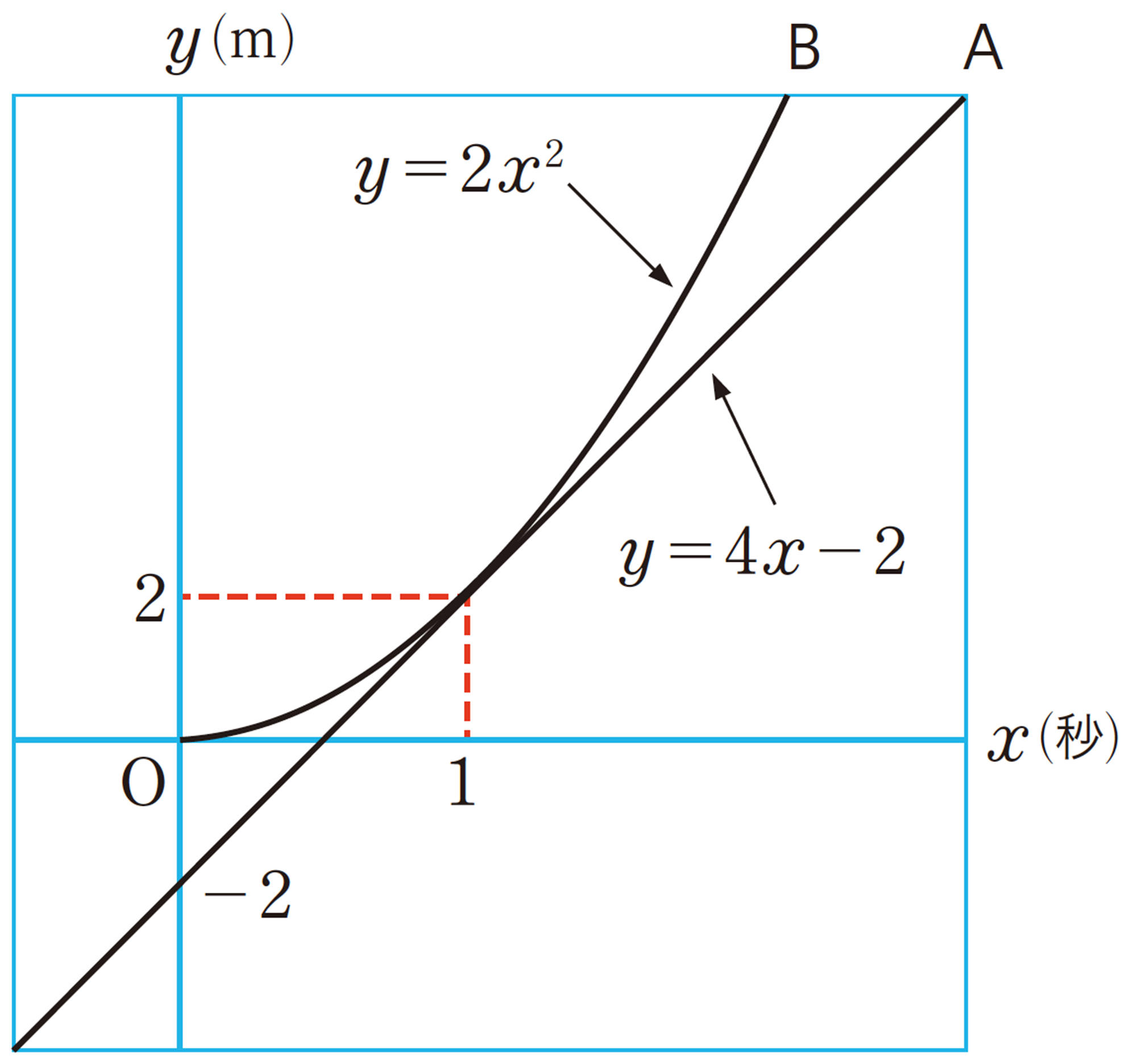
点[mathjax]\(P(-3，9)\)は関数[mathjax]\(y=ax²\)のグラフ上の点だから，[mathjax]\(x=-3\)，[mathjax]\(y=9\)を[mathjax]\(y=ax²\)に代入すると，
点Qのx座標は2だから，[mathjax]\(x=2\)を[mathjax]\(y=x²\)に代入すると，
[mathjax]\(y=bx+c\)が2点[mathjax]\(P(-3，9)\)，[mathjax]\(Q(2，4)\)を通るから，
[mathjax]\(y=-x+c\)に[mathjax]\(x=-3\)，[mathjax]\(y=9\)を代入すると，
答 [mathjax]\(a=1\)，[mathjax]\(b=-1\)，[mathjax]\(c=6\)
問 ３ 右の図のように，関数[mathjax]\(y=-\dfrac{1}{2}x²\)のグラフ上に2点P，Q があります。P，Qのx座標が，それぞれ-4，2であるとき，次の問いに答えなさい。
⑴ 2点 P，Qの座標を求めなさい。
⑵ 2点 P，Qを通る直線の式を求めなさい。
⑶ 座標軸の1目盛りを1cmとして，[mathjax]\(\triangle OPQ\)の面積を求めなさい。
<3年p.124>
Q Question
短距離走で，陸さんがスタートしてから3秒間に進んだ距離を[mathjax]\(0.5\)秒ごとに測定しました。次の表は，陸さんがスタートしてからx秒間にym進んだとして，その結果をまとめたものです。xとyの値の変化について，どんなことが読み取れるでしょうか。
物が落下する速さと同じように，短距離走でも，スタートしてからだんだん速くなっているね。
yはxのどんな関係と考えられるかな。
見方・考え方
時間と距離には，どんな関係があるとみなせるかな。
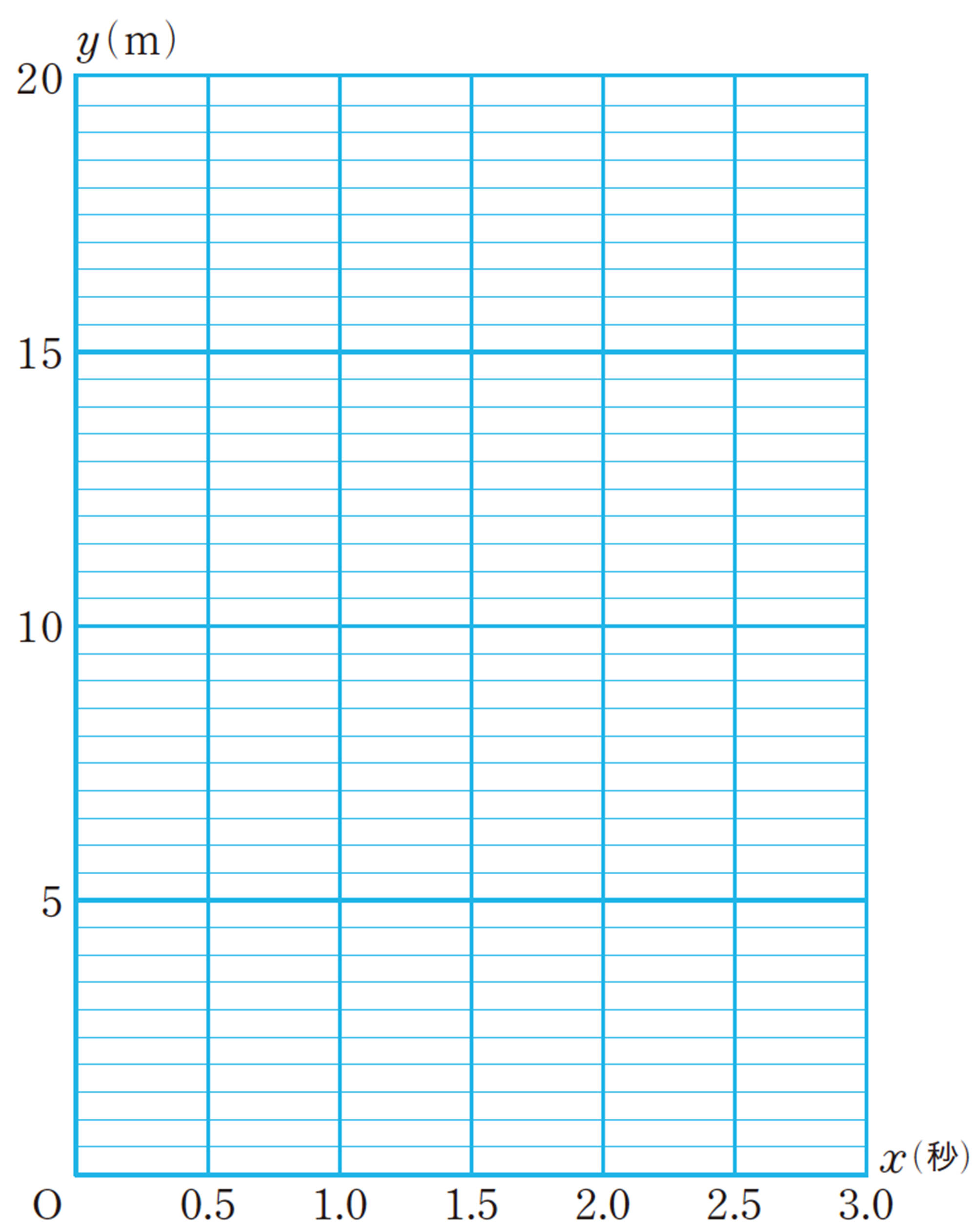
１ yはxの2乗に比例すると考えられるでしょうか。また，それはどんな方法で確かめればよいでしょうか。
２ 上の表の対応するx，yの値の組を座標とする点を，次ページの図にかき入れてみましょう。また，点の並び方から，どんなグラフになるかを予想してみましょう。
３ 【１】 ，【２】 で調べたことから，yは xの2乗に比例すると考えられます。グラフが点[mathjax]\((2.0，8.0)\)を通ると考えて比例定数を求め， yをxの式で表してみましょう。また，そのグラフを次ページの図にかき入れてみましょう。
<3年p.125>
一般に，短距離走では，スタート直後の数秒間は加速し，進む距離は時間の2乗にほぼ比例することが知られています。
４ 大和さんは，秒速4mの一定の速さで走っています。陸さんがスタートするのと同時に，大和さんが同じスタート地点を通過しました。陸さんが大和さんに追いつくのは，スタート地点から何m進んだ地点でしょうか。上の図に，大和さんの進み方を示すグラフをかき入れ，答えを求めてみましょう。
効率よくバトンパスをするためには，次の走者が止まっていたら時間の無駄だね。
関連 ▷ P.126
<3年p.126>
リレーのバトンパス Tea Break
リレーのタイムを短縮するためには，効率のよいバトンの受け渡しをすることが重要です。つまり，「前の走者がどの地点に来たとき，次の走者はスタートをすればよいか」が焦点となります。バトンの受け渡しをする2人の走力や加速のようすをあらかじめ調べておけば，関数のグラフを利用して，適切なスタートのタイミングを求めることができます。
いま，前の走者Aは一定の速さで走り，次の走者Bはスタートして加速しながら走るものとします。
Bがスタートしてからx秒後のスタート地点からの距離をymとし，AとBの走るようすが，それぞれ右のようなグラフになるとき，次のことが読み取れます。
❶ Bがスタートしたとき，Aはスタート地点の2m手前を走っている。
❷ Bはスタートしてから1秒後に，2m進んだ地点でAからバトンを受け取っている。
Bがスタートしたとき，Aがスタート地点の3m手前を走っていたとすると，バトンの受け渡しはできるでしょうか。
実際には，もっと効率よくバトンパスをするために条件を加えていく必要があるね。
<3年p.127>
問 ４ 時速80kmで走っている自動車がブレーキをかけたとき，ブレーキがきき始めてから止まるまでに進む距離はどのくらいですか。
どうやって調べればいいか，ぜんぜんわからないよ。
1年のときの比例や2年のときの1次関数では，どうやって考えたかな。
データから表やグラフをつくって，どんな関数になるかを考えたよ。
グラフから比例や1次関数であるとみなすことができたら，それを式に表して考えたね。
表した式のxやyに数値を代入して，知りたいことを求めることができたね。
時速と止まるまでに進む距離の間に，どんな関係があるかを調べる必要があるね。
時速[mathjax]\(x\)kmで走っている自動車がブレーキをかけたとき，ブレーキが きき始めてから止まるまでに進む距離を[mathjax]\(y\)ｍとすると，[mathjax]\(y\)は[mathjax]\(x\)の2 乗に比例する関数とみなすことができます。
ある自動車が時速40kmで走っているとき，ブレーキがきき始めてから10m進んで止まりました。このとき，次の問いに答えなさい。
⑴ [mathjax]\(y\)を[mathjax]\(x\)の式で表しなさい。
⑵ この自動車が時速80kmで走っているとき，ブレーキがきき始めてから何m進んで止まりますか。求め方を説明しなさい。
⑶ この自動車が，ブレーキがきき始めてから5m 進んで止まるのは，時速何kmのときですか。小数第一位まで求めなさい。また，求め方を説明しなさい。
関連 ▷ P.137
どんなことがわかったかな
身のまわりのことがらを関数[mathjax]\(y=ax²\)とみなすことで，問題を解決できることがあります。
次の課題へ！
身のまわりには，これまで学んできた関数以外の関数もあるのかな？
P.129
<3年p.128>
確かめよう 1節 関数[mathjax]\(y=ax²\)
１ 底辺の1辺がxcm，高さが8cmの正四角柱の体積をycm³とするとき，yをxの式で表しなさい。また，yはxの2乗に比例するといえますか。
□ 関数[mathjax]\(y=ax²\)の式を求めることができる。 ▷関数[mathjax]\(y=ax²\) ・P.106 例2
２ yはxの2乗に比例し，[mathjax]\(x=-3\)のとき[mathjax]\(y=18\) です。yをxの式で表しなさい。また，[mathjax]\(x=-4\)のときのyの値を求めなさい。
３ 次の問いに答えなさい。
⑴ 右の図の①〜③の放物線は，次の㋐〜㋒の関数のグラフです。①〜③は，それぞれどの関数のグラフですか。
㋐[mathjax]\(y=-\dfrac{1}{2}x²\)
㋑[mathjax]\(y=\dfrac{1}{4}x²\)
㋒[mathjax]\(y=2x²\)
⑵ 関数[mathjax]\(y=-\dfrac{1}{4}x²\)のグラフを，上の図にかき入れなさい。
４ 関数[mathjax]\(y=\dfrac{1}{3}x²\)で，xの変域が[mathjax]\(-3 \leqq x \leqq 6\)のときのyの変域を求めなさい。
５ 関数[mathjax]\(y=2x²\)で，xの値が次のように増加するときの変化の割合を求めなさい。
⑴ 1から4まで
⑵ [mathjax] \(-5\)から[mathjax] \(-3\)まで
