<3年p.91>
2節 2次方程式の利用
2次方程式が使えるかな？
美化委員会の活動で，縦8m，横10mの長方形の土地に花だんをつくることになりました。
【１】 この長方形の土地に，幅が一定の道をつくりたいと思います。花だんの面積を48m²にするには，道の幅を何mにすればよいですか。
方程式を作って，それを解けばいいね。
[mathjax] \(1\)，[mathjax] \(2\)年のとき，方程式を利用して問題を解く手順があったね。
次のような手順で，問題を解く。
① 図や表，ことばの式などを使って，数量関係を見つける。
② 文字を使って方程式をつくる。
③ 方程式を解く。
④ 方程式の解が問題に適しているかどうかを確かめ，適していれば問題の答えとする。
1次方程式や連立方程式を利用して問題を解く手順と同じだね。
どんな式をつくることができるかな。
次の課題へ！
身のまわりの問題を2次方程式を使って，解くことができるのかな？
P.92
<3年p.92>
１ 2次方程式の利用
目標 ▷ 2次方程式を利用して，身のまわりの問題を解決しよう。
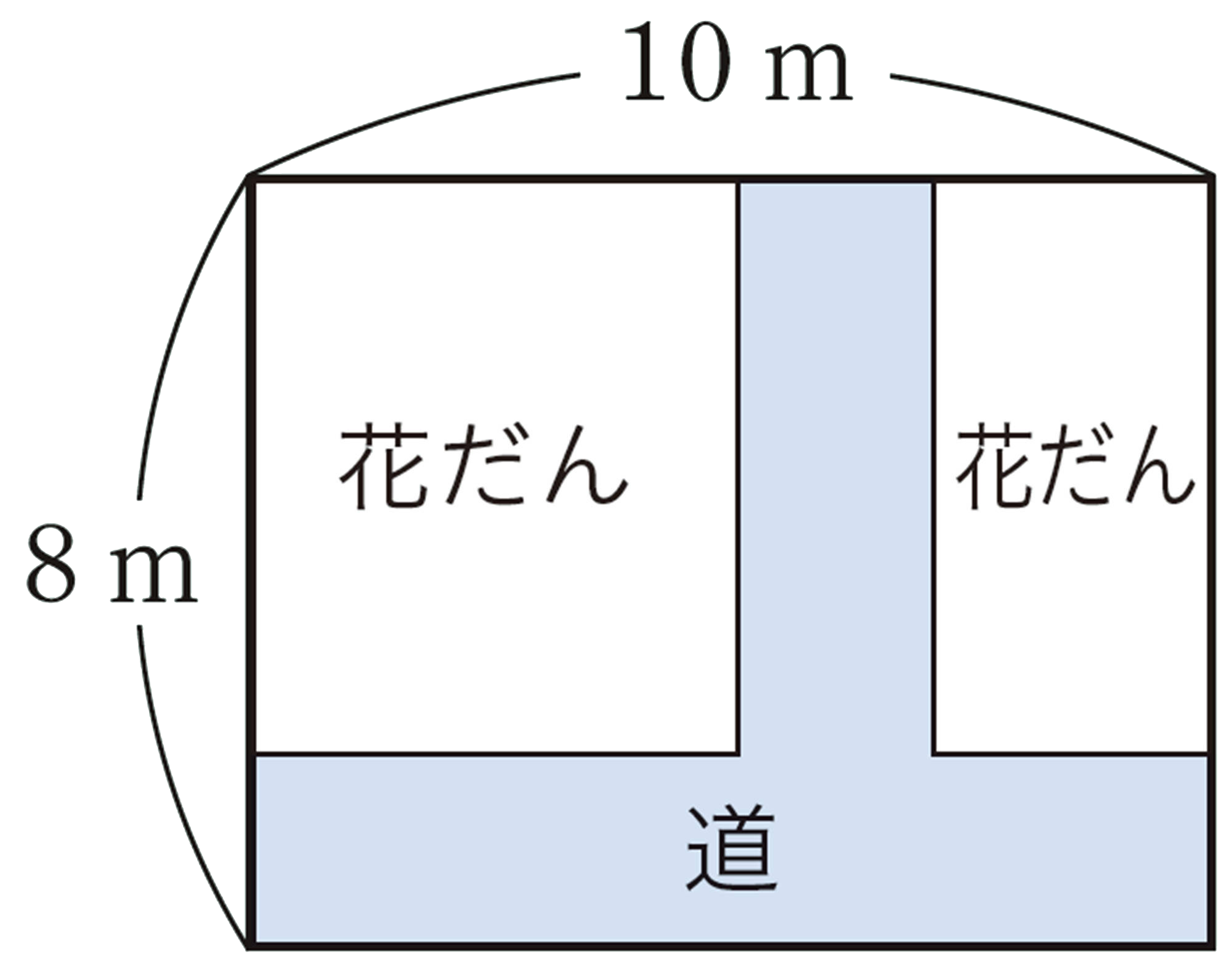
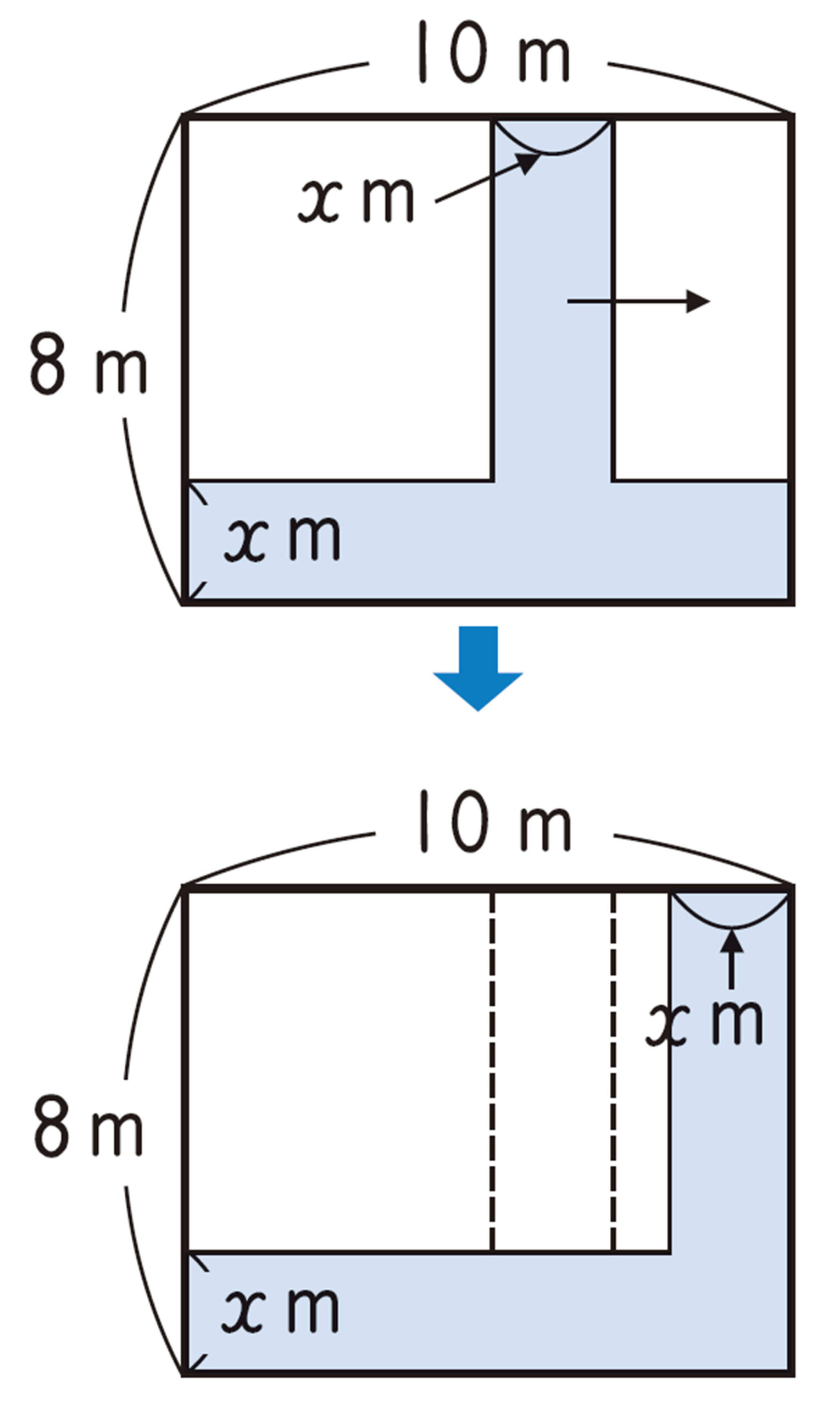
例 １ 前ページの 【１】 の問題を解きなさい。
解答
道の幅をxmとすると，
[mathjax]\(\hspace{48pt}(8-x)(10-x)=48\)
これを解くと，
[mathjax]\(0 \lt x \lt 8\)であるから，
[mathjax]\(x=2\)は問題に適しているが，[mathjax]\(x=16\)は適していない。
答 2m
問 １ 右の図のように，幅20cmの厚紙を左右同じ長さだけ折り曲げ，切り口の長方形の面積を42cm²にします。厚紙を左右何cmずつ折り曲げればよいですか。
例 ２ 連続する2つの整数があります。それぞれを2乗した数の和が85になるとき，この2つの整数を求めなさい。
解答
小さい方の整数をxとすると，大きい方の整数は[mathjax]\(x+1\)と表される。
[mathjax]\(\hspace{59pt}x²+(x+1)²=85\)
これを解くと，
[mathjax]\(x=6\)のとき，2つの整数は，[mathjax] \(6\)，[mathjax] \(7\)
[mathjax]\(x=-7\)のとき，2つの整数は，[mathjax] \(-7\)，[mathjax] \(-6\)
これらは，どちらも問題に適している。
答 [mathjax] \(6\)，[mathjax] \(7\)と[mathjax] \(-7\)，[mathjax] \(-6\)
<3年p.93>
問 ２ 前ページの例2で，大きい方の整数をxとして方程式をつくり，答えを求めなさい。また，「連続する2つの整数」を「連続する2つの自然数」に変えると，答えはどうなりますか。
問 ３ 連続する2つの自然数があります。大きい方の数の2乗から，小さい方の数の2倍をひいた差は26になります。この2つの自然数を求めなさい。
方程式をつくって問題を解くときには，前ページの例1や問2， 問3のように，方程式の解がそのまま問題の答えにならない場合がある。
例 ３ 長さ10 cmの線分ABがあります。点PはAを出発してBまで動きます。このとき，AP，PBをそれぞれ1辺とする2つの正方形の面積の和が52cm²になるのは，点Ｐが何cm動いたときですか。
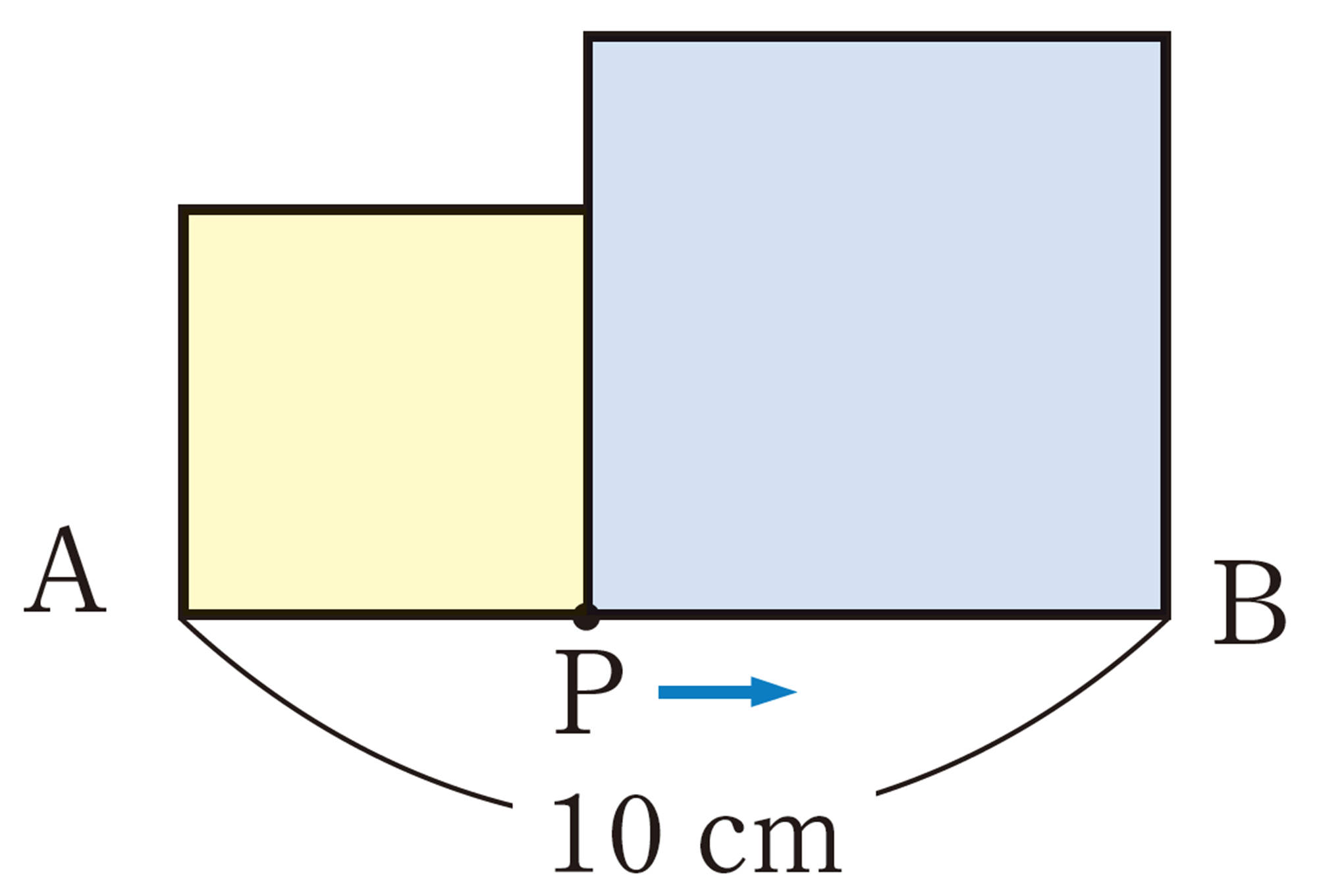
考え方 2つの正方形の面積の和が52cm²であることから，点Ｐが動いた距離をx cmとして，PBをxを使って表し，方程式をつくる。
解答
点Pが動いた距離APをxcmとすると，[mathjax]\(PB=(10-x)\) cm
2つの正方形の面積の和が52cm²であることから，
[mathjax]\(\hspace{58pt}x²+(10-x)²=52\)
これを解くと，
[mathjax]\(0\leqq x \leqq 10\)であるから，どちらも問題に適している。
答 4 cm，6 cm
問 ４ 例3で，2つの正方形の面積の和が70cm²になるのは，点Pが何cm動いたときですか。
どんなことがわかったかな
身のまわりの問題の中には，数量の関係から2次方程式をつくり，2次方程式を利用して解決することができる問題があります。ただし，方程式の解が問題に適しているかどうかを，変域などを考えて確かめる必要があります。
<3年p.94>
確かめよう 2節 2次方程式の利用
１ 右の図のように，正方形の土地の縦を2m短くし，横を3m長くしたところ，その面積が50m²になりました。もとの土地の1辺の長さを求めなさい。
２ ある整数を2乗すると，その整数を6倍して27を加えた数と等しくなります。この整数を求めなさい。
どれが解きやすい？ Tea Break
[mathjax]\((x-3)²=25\)の解き方について考えてみましょう。
拓真さんは，次のように，「因数分解を使った解き方」で解きました。
左辺を展開して整理すると，
[mathjax]\(\hspace{9pt}x²-6x-16=0\)
左辺を因数分解すると，
[mathjax]\((x-8)(x+2)=0\)
[mathjax]\(x-8=0\) または [mathjax]\(x+2=0\)
[mathjax]\(x=8\)，[mathjax]\(x=-2\)
答 [mathjax]\(x=8，x=-2\)
① 「平方根の考えを使った解き方」，「解の公式を使った解き方」でも解いてみましょう。
② 3つの解き方のうち，どの方法が解きやすいと思いますか。自分の考えを説明してみましょう。
因数分解の解き方の方が簡単でいいな。
どんな方程式でも解けるから解の公式がいいな。
<3年p.95>
3章 「2次方程式」を学んで
できるようになったこと 身のまわりの課題へ ▷ P.98
2次方程式を，因数分解や平方根の考えを使って解くことができる。
平方根の考えを使って解の公式を導き，それを使って解を求めることができる。
身のまわりや数学の中から見つけた問題を，2次方程式を使って解決することができる。また，方程式の解が問題に適しているかどうかを確かめることができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない 小学生のガウス
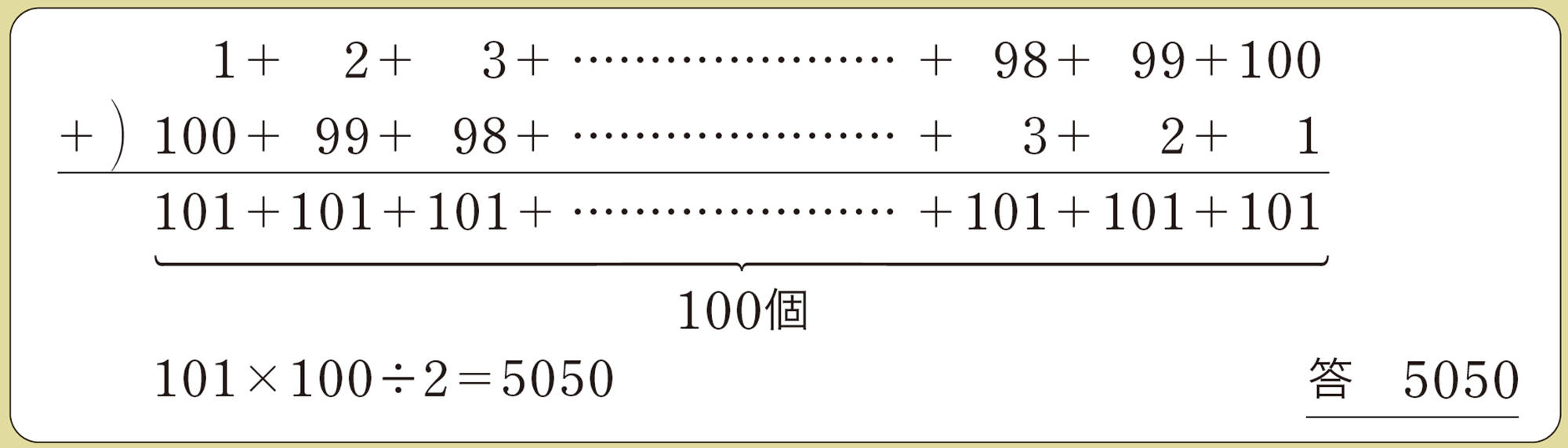
ドイツの数学者ガウスには，小学生のとき，先生から出された「1から100までのすべての自然数の和はいくつか」という問題を，次のような計算ですぐに解いてしまったというエピソードが残っています。
[mathjax]\(101 \times 100 \div 2 = 5050\)
答 5050
⑴ 1からnまでの自然数の和はいくつでしょうか。この計算方法を使って求めてみましょう。
⑵ 1からnまでの自然数の和が78になるのは，nがいくつのときでしょうか。
