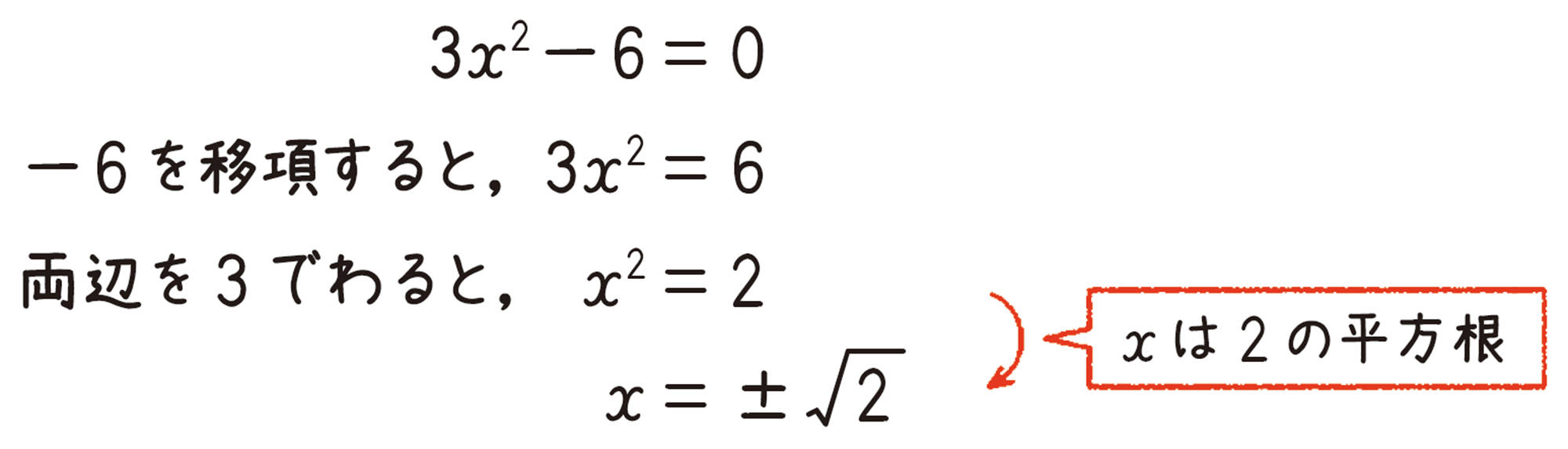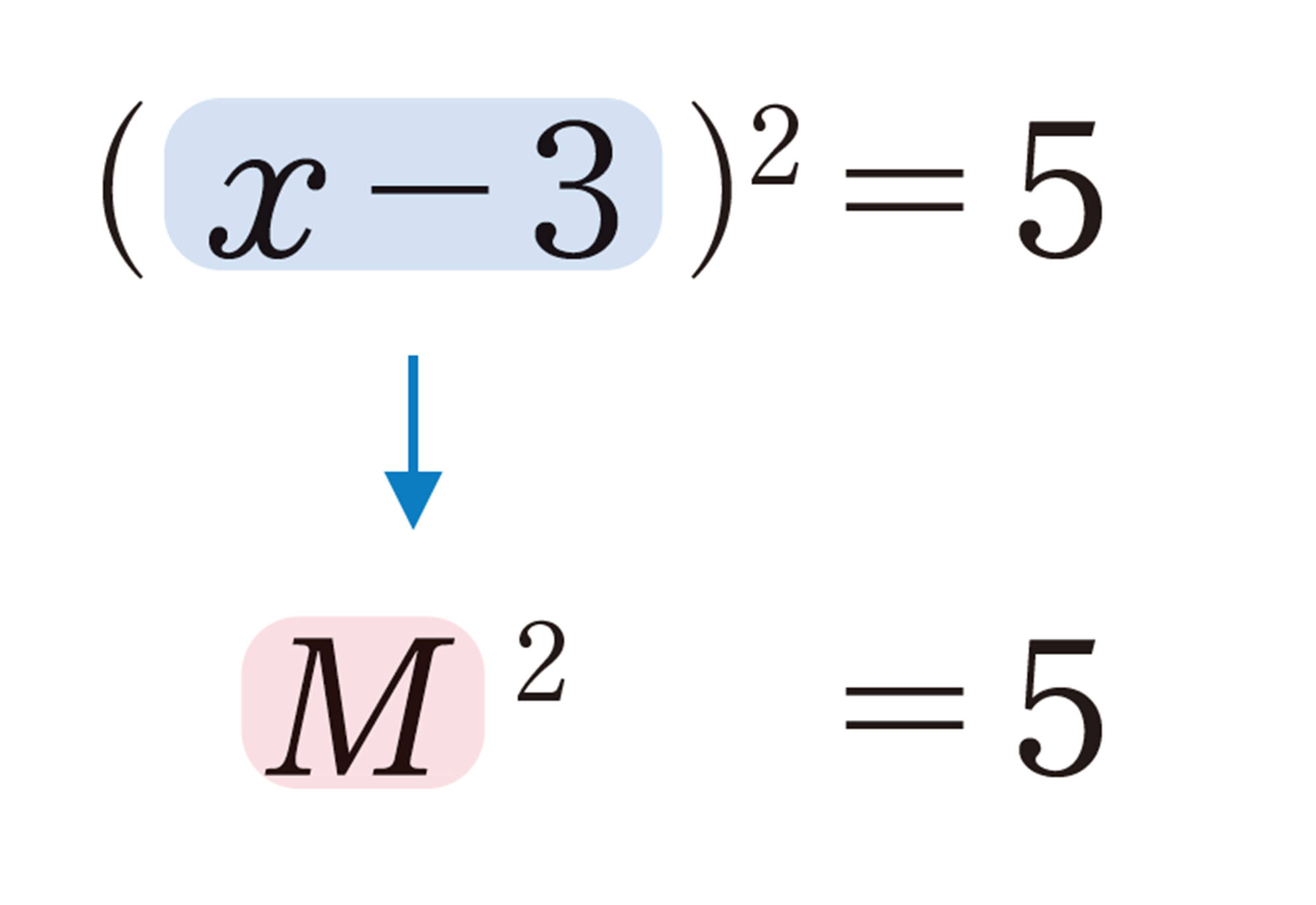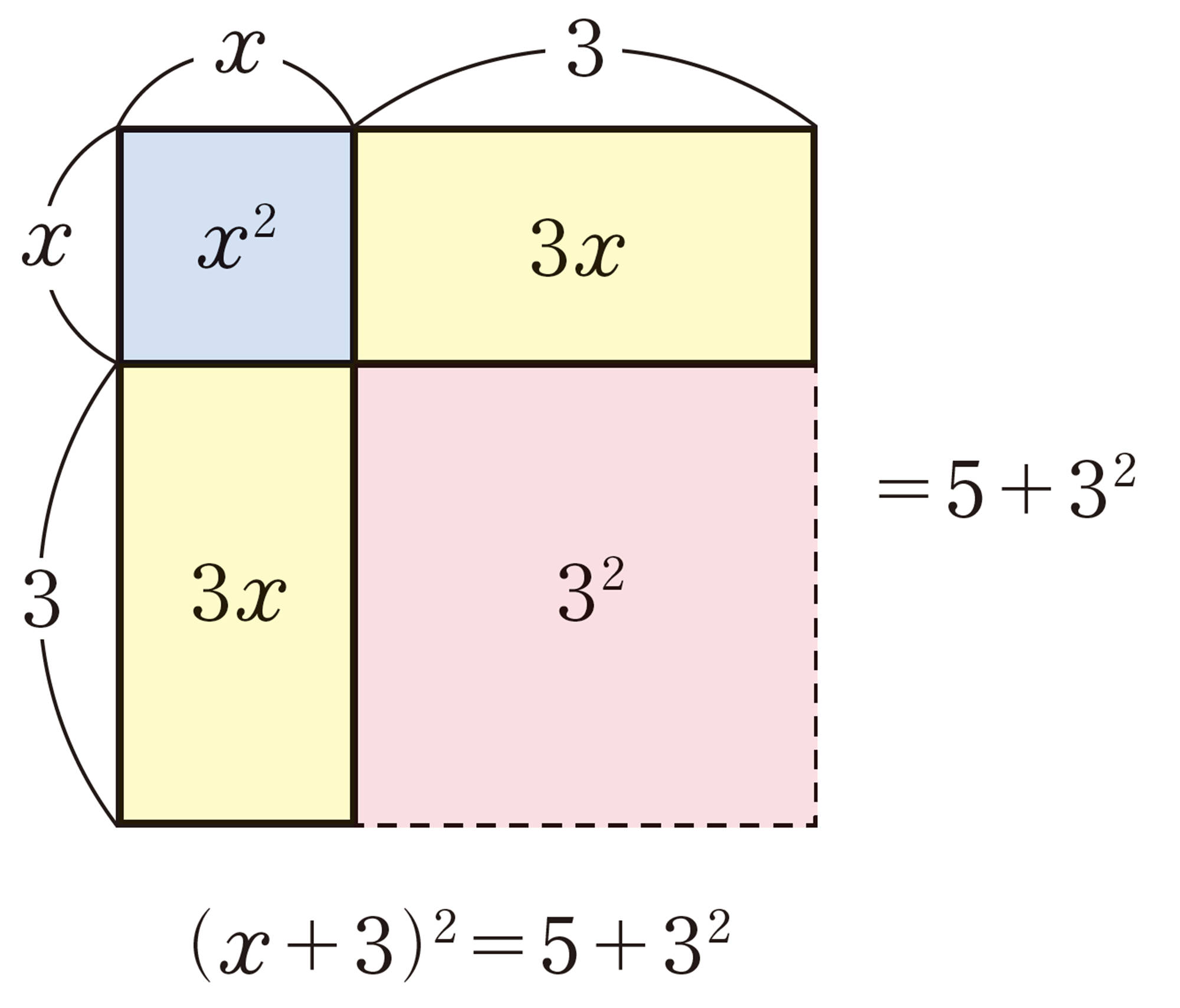<3年p.79>
２ 因数分解を使った解き方
Q Question
76ページの方程式[mathjax]\(x²+2x-24=0\)の左辺を因数分解すると，
[mathjax]\((x-4)(x+6)=0\)
となります。この方程式について，次のことを調べてみましょう。
⑴ [mathjax]\(x=4\)のとき，[mathjax]\((x-4)(x+6)\)の値はいくつでしょうか。
⑵ [mathjax]\(x=-6\)のとき，[mathjax]\((x-4)(x+6)\)の値はいくつでしょうか。
⑶ xが4，-6以外の値をとるとき，[mathjax]\((x-4)(x+6)\)の値が0になることはあるでしょうか。
どんなときに左辺が0になるのかな。
ほかの2次方程式でも，因数分解ができれば同じことがいえるのかな。
見方・考え方
式の形に着目して考えられるかな。
目標 ▷ 因数分解を使って，2次方程式を解く方法を考えよう。
【Q】 からわかるように，方程式[mathjax]\((x-4)(x+6)=0\)を成り立たせるxの値は4と[mathjax] \(-6\)の2つだけで，それ以外にはない。
一般に，数や式について，次のことがいえる。
[mathjax]\(AB=0\)ならば，[mathjax]\(A=0\)または[mathjax]\(B=0\)
この性質を使って，2次方程式を解いてみよう。
例 １ 方程式[mathjax]\((x+2)(x-7)=0\)を解きなさい。
解答
[mathjax] \( (x+2)(x-7)=0 \) であるから，
答 [mathjax] \( x=-2， x=7 \)
<3年p.80>
問 １ 次の方程式を解きなさい。
⑴ [mathjax]\((x-2)(x-6)=0\)
⑵ [mathjax]\((x+1)(x+9)=0\)
⑶ [mathjax]\((x-7)(x+3)=0\)
⑷ [mathjax]\(x(x-15)=0\)
例 ２ 方程式[mathjax]\(x²+2x-15=0\)を解きなさい。
解答
[mathjax]\(x²+2x-15=0\)
左辺を因数分解すると，
[mathjax]\((x+5)(x-3)=0\)
[mathjax]\(x+5=0\) または [mathjax]\(x-3=0\)
[mathjax]\(x=-5\)，[mathjax]\(x=3\)
答 [mathjax]\(x=-5，x=3\)
ふりかえり ▷P.26，27
問 ２ 次の方程式を解きなさい。
⑴ [mathjax]\(x²+5x+6=0\)
⑵ [mathjax]\(x²-7x+10=0\)
⑶ [mathjax]\(x²+x-6=0\)
⑷ [mathjax]\(x²-3x-4=0\)
⑸ [mathjax]\(x²+4x=0\)
⑹ [mathjax]\(x²-16=0\)
例 ３ 方程式[mathjax]\(x²-6x+9=0\)を解きなさい。
解答
見直したときわかりやすいように，「=」をそろえて書いておこう。
[mathjax]\(x²-6x+9=0\)
左辺を因数分解すると，
答 [mathjax]\(x=3\)
ふりかえり ▷P.27
[mathjax]\((x-3)²=0\)は，[mathjax]\((x-3)(x-3)=0\)のことだね。
一般に，2次方程式の解は2つあるが，例3のように，2つの解が一致して解が1つになることがある。
問 ３ 次の方程式を解きなさい。
⑴ [mathjax]\(x²+2x+1=0\)
⑵ [mathjax]\(x²-14x+49=0\)
<3年p.81>
例 ４ 方程式[mathjax]\((x-4)(x+2)=x-8\)を解きなさい。
考え方 左辺を展開し，すべての項を左辺に移項して整理する。
解答
[mathjax]\(\hspace{67pt}(x-4)(x+2)=x-8\)
左辺を展開すると，[mathjax]\(\hspace{4pt}x²-2x-8=x-8\)
移項して整理すると，[mathjax]\(\hspace{13pt}x²-3x=0\)
左辺を因数分解すると，[mathjax]\(x(x-3)=0\)
[mathjax]\(\hspace{80pt}x=0\) または [mathjax]\(x-3=0\)
[mathjax]\(\hspace{80pt}x=0\)，[mathjax]\(x=3\)
答 [mathjax]\(x=0\)，[mathjax]\(x=3\)
問 ４ 次の方程式を解きなさい。
⑴ [mathjax]\(x²-8x=-16\)
⑵ [mathjax]\(x²-8=-x+4\)
⑶ [mathjax]\((x-1)²=3x-5\)
⑷ [mathjax]\(2x²+8=(x-3)(x-6)\)
問 ５ 次の方程式を解きなさい。
⑴ [mathjax]\(2x²+18x+40=0\)
⑵ [mathjax]\(-x²+11x-24=0\)
左辺を因数分解するには，どうすればいいかな。
やってみよう
計算力を高めよう4-1
▷P.90
[mathjax]\(\hspace{68pt}x²=5x\)
両辺を[mathjax]\(x\)でわると，[mathjax]\(x=5\)
答 [mathjax]\(x=5\)
どんなことがわかったかな
2次方程式を[mathjax]\(ax²+bx+c=0\)の形にしたとき，左辺が因数分解できれば，解を求めることができます。
<3年p.82>
３ 平方根の考えを使った解き方
Q Question
方程式[mathjax]\(x²-25=0\)の解き方を考えてみましょう。
左辺は因数分解できそうだね。
移項して，[mathjax]\(x²=25\)の形にして解いてもいいのかな。
見方・考え方
式の形に着目して考えられるかな。
目標 ▷ 平方根の考えを使って，2次方程式を解く方法を考えよう。
[mathjax]\(ax²+c=0\)の形の2次方程式は，[mathjax]\(x²=k\)の形にすると，平方根の考えを使って，次のように解くことができる。
xは25の平方根
注意 [mathjax]\(x=\pm 5\)は，[mathjax]\(x=5\)と[mathjax]\(x=-5\)をまとめて表したものである。
問 １ 平方根の考えを使って，次の方程式を解きなさい。
⑴ [mathjax]\(x²=49\)
⑵ [mathjax]\(x²-36=0\)
⑶ [mathjax]\(x²-17=0\)
例 １ 方程式 [mathjax]\(3x²-6=0\) を解きなさい。
解答
[mathjax]\(\hspace{48pt}3x²-6=0\)
-6を移項すると，[mathjax]\(3x²=6\)
両辺を3でわると，[mathjax]\(x²=2\)
[mathjax]\(\hspace{75pt}x=\pm \sqrt{2}\)
答 [mathjax] \(x=\pm \sqrt{2}\)
xは2の平方根
問 ２ 次の方程式を解きなさい。
⑴ [mathjax]\(2x²=18\)
⑵ [mathjax]\(9x²=4\)
⑶ [mathjax]\(5x²-40=0\)
⑷ [mathjax]\(4x²-3=0\)
<3年p.83>
[mathjax]\((x+p)²=q\) の形の方程式
例 ２ 方程式[mathjax]\((x-3)²=5\)を解きなさい。
考え方 [mathjax]\(x-3=M\)とおくと，[mathjax]\(M²=5\)となり，平方根の考えを使うことができる。
解答
[mathjax]\(\hspace{71pt}(x-3)²=5\)
[mathjax]\(x-3=M\)とおくと，[mathjax]\( \ M²=5\)
[mathjax]\(\hspace{95pt}M=\pm \sqrt{5}\)
Mをもとにもどすと，[mathjax]\(x-3=\pm \sqrt{5}\)
[mathjax]\(\hspace{99pt}x=3 \pm \sqrt{5}\)
答 [mathjax]\(x=3 \pm \sqrt{5}\)
注意 [mathjax]\(x=3 \pm \sqrt{5}\)は，[mathjax]\(x=3+\sqrt{5}\)と[mathjax]\(x=3-\sqrt{5}\)をまとめて表したものである。
例 ３ 方程式[mathjax]\((x+1)²=4\)を解きなさい。
解答
答 [mathjax]\(x=1\)，[mathjax]\(x=-3\)
左辺を展開して整理し，因数分解して解くよりも，楽に解けるね。
問 ３ 次の方程式を解きなさい。
⑴ [mathjax]\((x+2)²=7\)
⑵ [mathjax]\((x-5)²=8\)
⑶ [mathjax]\((x-4)²=9\)
⑷ [mathjax]\((x+3)²=49\)
⑸ [mathjax]\((x-7)²-12=0\)
⑹ [mathjax]\((2x-1)²=4\)
どんなことがわかったかな
2次方程式を[mathjax]\((x+p)²=q\)の形に変形すれば，平方根の考えを使って解を求めることができます。
次の課題へ！
どんな2次方程式でも，[mathjax]\((x+p)²=q\)の形に変形できるのかな？
P.84
<3年p.84>
Q Question
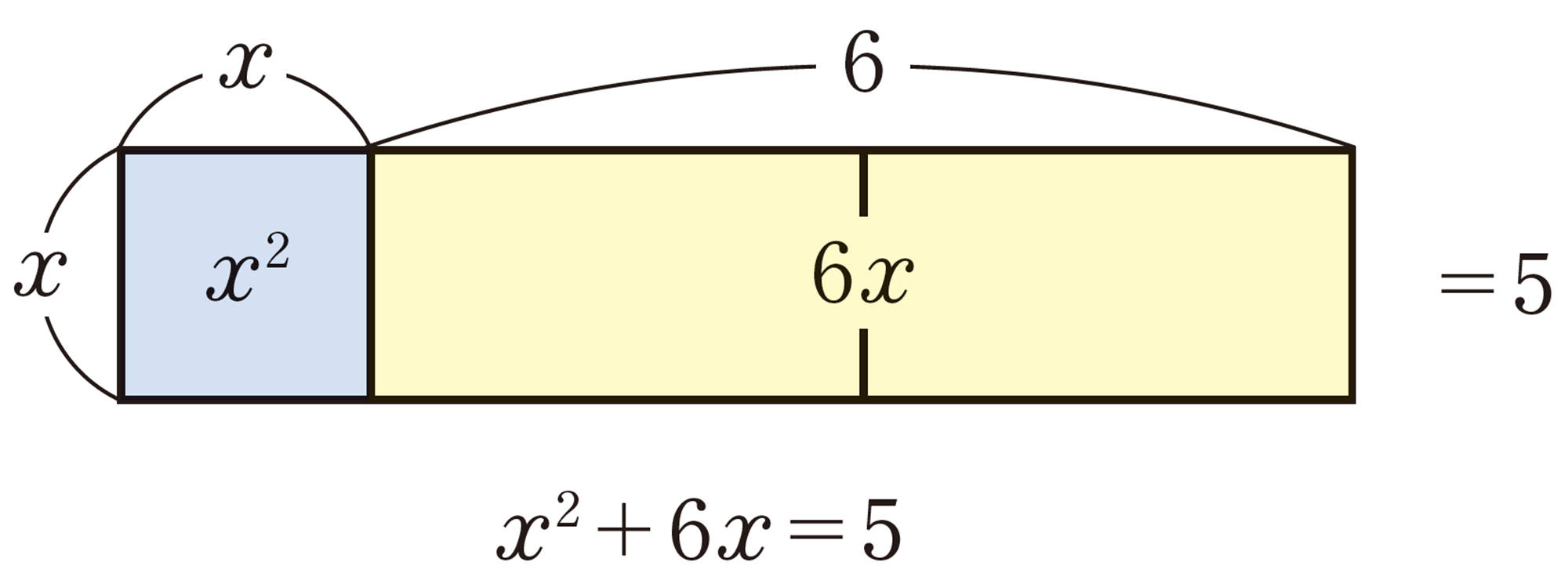
方程式[mathjax]\(x²+6x-5=0\)を[mathjax]\((x+p)²=q\)の形に変形するためにはどうすればよいか話し合ってみましょう。
[mathjax]\(x²+6x-5\)は，このままでは[mathjax]\((x+p)²\)の形にならないね。
左辺が[mathjax]\(x²+6x+9\)になるようにすればいいのかな。
見方・考え方
式のどこに着目して考えればいいかな。
目標 ▷ 2次方程式を，[mathjax]\((x+p)²=q\)の形に変形して解こう。
例 ４ 方程式 [mathjax]\(x²+6x-5=0\) の解は，次のように求めます。
[mathjax]\(\hspace{4pt}x²+6x-5=0\)
-5を移項すると，
[mathjax]\(\hspace{21pt}x²+6x=5\)
ここで，左辺を[mathjax]\((x+p)²\)の形に因数分解するために，
両辺にxの係数6の[mathjax]\(\dfrac{1}{2}\)の2乗を加えると，
[mathjax]\(x²+6x+3²=5+3²\)
左辺を因数分解すると，
問 ４ 次の方程式を解きなさい。
⑴ [mathjax]\(x²-4x=3\)
⑵ [mathjax]\(x²+8x=-14\)
⑶ [mathjax]\(x²+2x-5=0\)
⑷ [mathjax]\(x²-6x-3=0\)
やってみよう
計算力を高めよう4-2
▷P.90
<3年p.85>
前ページの例4と問4では，xの係数が偶数の方程式を解いてきたが，xの係数が奇数の場合も，偶数の場合と同じように考えて解くことができる。たとえば，方程式[mathjax]\(x²+3x+1=0\)は，次のようにして解けばよい。
[mathjax]\(\hspace{85pt}x²+3x+1=0\)
1を右辺に移項すると，[mathjax]\(\hspace{14pt}x²+3x=-1\)
両辺にxの係数3の[mathjax]\(\dfrac{1}{2}\)の2乗，すなわち[mathjax]\(\require{physics}\left(\dfrac{3}{2}\right)^{2}\)を加えると，
[mathjax]\(\hspace{63pt}x²+3x+\require{physics} \left(\dfrac{3}{2}\right)^{2}=-1+ \require{physics} \left(\dfrac{3}{2}\right)^{2}\)
左辺を因数分解すると，
したがって，方程式[mathjax]\(x² + 3x + 1 = 0\)の解は，[mathjax]\(x = \dfrac{-3\pm \sqrt{5}}{2}\)となる。
[mathjax]\(x²+\boxed{\phantom{00}}x+\bigcirc=0\)の形の方程式は，[mathjax]\((x+p)²=q\)の形に変形をすると，解くことができる。
[mathjax]\(2x²+10x-4=0\)のように，[mathjax]\(x²\)の係数が1でない2次方程式は，両辺を[mathjax]\(x²\)の係数でわり，[mathjax]\(x²\)の係数を1にしてから解けばよい。
[mathjax]\(2x²+10x-4=0\)
↓ 両辺を[mathjax]\(x²\)の係数2でわる
[mathjax]\(x²+5x-2=0\)
▲トライ 方程式 [mathjax]\(x²+5x-2=0\)を，[mathjax]\((x+p)²=q\)の形に変形して解いてみよう。
どんなことがわかったかな
どんな2次方程式でも，[mathjax]\((x + p)²=q \)の形に変形して，解を求めることができます。
次の課題へ！
2次方程式は，必ず[mathjax]\((x+p)²=q\)の形に変形しないと解けないのかな？
P.86
