<3年p.73>
３章 Chapter ３ 2次方程式
1節 2次方程式の解き方
2節 2次方程式の利用
文字が2つの連立方程式も解けるようになったね。
加減法や代入法を使って，1次方程式に直して解いたね。
式の中に2次の項があったらどうなるかな。
1次方程式に直せれば解けそうだけど…。
？ 2次の項がある方程式は解けるのかな？
<3年p.74>
1節 2次方程式の解き方
何枚あるの？
太陽光発電は，「太陽電池」と呼ばれる装置を用いて，太陽の光エネルギーを直接電気に変換する発電方式です。
発電時に，地球温暖化の原因とされている二酸化炭素をまったく排出しないので，クリーンであることも大きな特徴です。
<3年p.75>
最近では，学校や公共施設，一般家庭にも太陽電池が設置されるようになりました。
ある建物の屋根に太陽電池が設置されています。この太陽電池1枚で発電できる電力を，200W（ワット）とします。
この太陽電池を屋根全体に長方形にしきつめると，4800Wの電力を出力できるそうです。
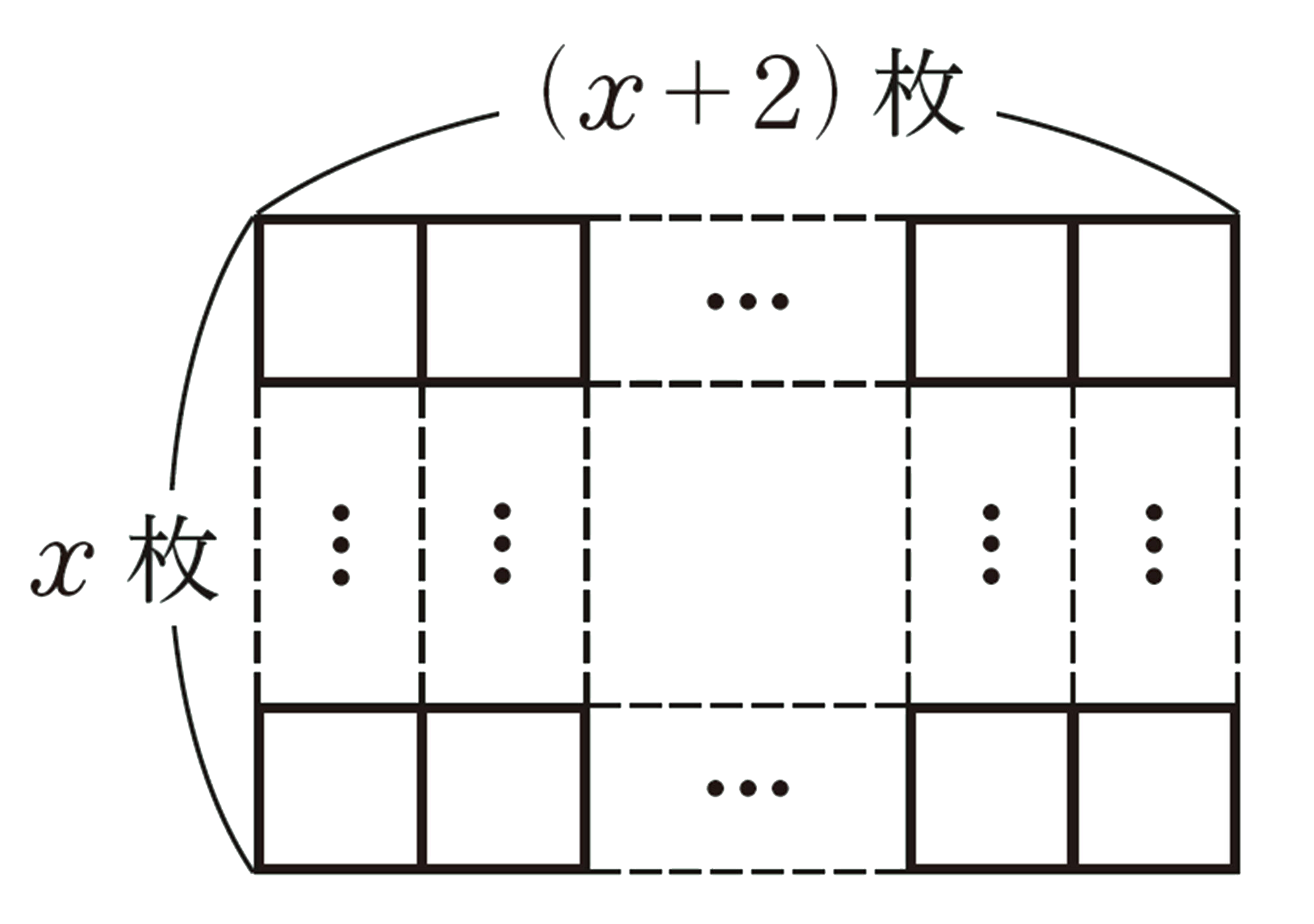
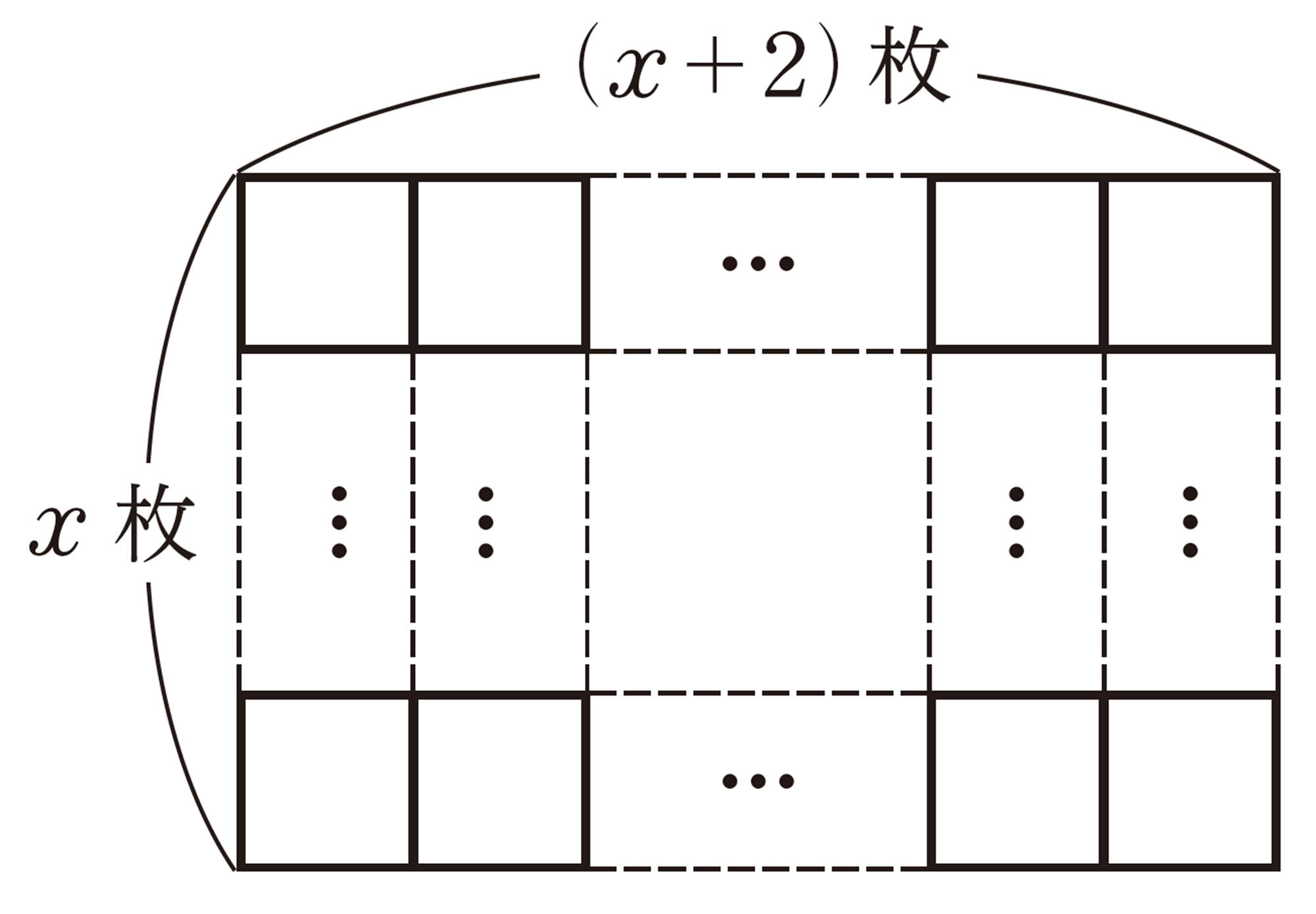
【１】 太陽電池は全部で何枚あるでしょうか。
この建物の屋根に，太陽電池を長方形にしきつめると，横が縦より2枚多くなりました。
【２】 太陽電池は，縦に何枚しきつめてあるでしょうか。太陽電池の枚数に着目して，方程式をつくってみましょう。
縦にx枚しきつめているとして，式をつくろう。
上の問題について，次のような方程式をつくることができます。
[mathjax]\(x(x+2)=24\)
この式の左辺を展開すると，次のようになります。
[mathjax]\(x²+2x=24\)
1次方程式では，xに数を代入したり，等式の性質を使ったりして解を求めたね。
次の課題へ！
2次の項がふくまれている方程式も，1次方程式と同じように考えれば答えが求められるのかな？
P.76
<3年p.76>
１ 2次方程式とその解
Q Question
前ページの2の問題で，縦にx枚しきつめるとすると，
[mathjax]\(x²+2x=24\)
という方程式がつくれました。
xにあてはまる値は，どのようにすれば求められるか，考えてみましょう。
xの2次式になっているね。
1次方程式は，どうやって解いたかな。
見方・考え方
1次方程式と同じように考えられるかな。
目標 ▷ 2次の項がふくまれている方程式について考えよう。
Qの方程式を整理すると，次のようになる。
[mathjax]\(x²+2x-24=0\)
一般に，すべての項を左辺に移項したときに，左辺がxについての2次式，すなわち，aを0でない定数，b，cを定数として，
[mathjax]\(ax²+bx+c=0\)
の形で表される方程式を，xについての2次方程式という。
たとえば，[mathjax]\(x²+2x-24=0\)は，
[mathjax]\(a=1\)，[mathjax]\(b=2\)，[mathjax]\(c=-24\)
の2次方程式である。
問 １ 次の㋐〜㋓の方程式のうち，2次方程式はどれですか。
㋐ [mathjax]\(x²+2x+1=0\)
㋑ [mathjax]\(x²-6x=0\)
㋒ [mathjax]\(4x-8=0\)
㋓ [mathjax]\((x+3)(x-8)=0\)
<3年p.77>
2次方程式の解
Q Question
前ページの方程式[mathjax]\(x²+2x-24=0\)を成り立たせるxの値を調べましょう。
⑴ xに[mathjax] \(-4\)から4までの整数を代入して，方程式が成り立つかどうかを調べてみましょう。
⑵ この方程式を成り立たせるxの値は⑴で見つけた値のほかにあるでしょうか。ある場合には，その値をいいましょう。
左辺の式の値がいくつになったとき，この方程式が成り立つといえるのかな。
見方・考え方
いろいろな数を代入して考えられるかな。
2次方程式を成り立たせるxの値を，その2次方程式の解といい，解をすべて求めることを，その2次方程式を解くという。
Qで調べた結果から，xが[mathjax] \(-6\)と4のとき，方程式[mathjax]\(x²+2x-24=0\)が成り立つ。
したがって，[mathjax] \(-6\)と4は，ともに2次方程式[mathjax]\(x²+2x-24=0\)の解である。
太陽電池の枚数は正の数だから縦が4枚のときが答えだね。
問 ２ [mathjax] \(-2\)，[mathjax] \(-1\)，[mathjax] \(0\)，[mathjax] \(1\)，[mathjax] \(2\)のうち，2次方程式[mathjax]\(x²+2x=0\)の解はどれですか。
問 ３ 次の㋐〜㋓の方程式のうち，[mathjax] \(-1\)と3がともに解である2次方程式はどれですか。
㋐ [mathjax]\(x²+2x-3=0\)
㋑ [mathjax]\(x²-9=0\)
㋒ [mathjax]\(x²+6x+5=0\)
㋓ [mathjax]\(x²-2x-3=0\)
どんなことがわかったかな
2次方程式の解は，文字に数を代入すれば，解かどうか調べることができます。
次の課題へ！
文字に数を代入しないで2次方程式を解く方法はあるのかな？
P.78
<3年p.78>
目標 ▷ 文字に数を代入せずに，2次方程式を解く方法を考えよう。
Q Question
次の㋐〜㋕の2次方程式を解くことができるかどうか考えてみましょう。
見方・考え方
式の形に着目して考えられるかな。
㋐ [mathjax]\((x-2)(x+3)=0\)
㋑ [mathjax]\(x²=4\)
㋒ [mathjax]\(x²-25=0\)
㋓ [mathjax]\(x²+6x−5=0\)
㋔ [mathjax]\(x²+8x=0\)
㋕ [mathjax]\((x-3)²=5\)
拓真さんの考え
㋐は，[mathjax]\((x-2)\times(x+3)=0\)のことだから，数の計算と同じように考えると，[mathjax]\((x-2)\)か[mathjax]\((x+3)\)のどちらかが0であれば，その積も0になる。すなわち，㋐の場合，左辺が，[mathjax]\(x-2=0\)または [mathjax]\(x+3=0\)のとき，方程式は成り立つ。
このことから，右辺を0にして，左辺が因数分解できれば，方程式を解くことができる。
美月さんの考え
㋑は，平方根の考えを使うと，
このことから，左辺が2乗の形になっていれば，方程式を解くことができる。
１ 上の拓真さんの考えで，㋐の方程式の解を求めてみましょう。また，この考え方で解ける2次方程式は，ほかにもあるでしょうか。
２ 上の美月さんの考えで解ける2次方程式は，ほかにもあるでしょうか。
３ 上の2人の考えで解くことができない2次方程式はあるでしょうか。
次の課題へ！
どんな2次方程式なら，因数分解の考えを使って解けるのかな？
P.79
次の課題へ！
どんな2次方程式なら，平方根の考えを使って解けるのかな？
P.82
