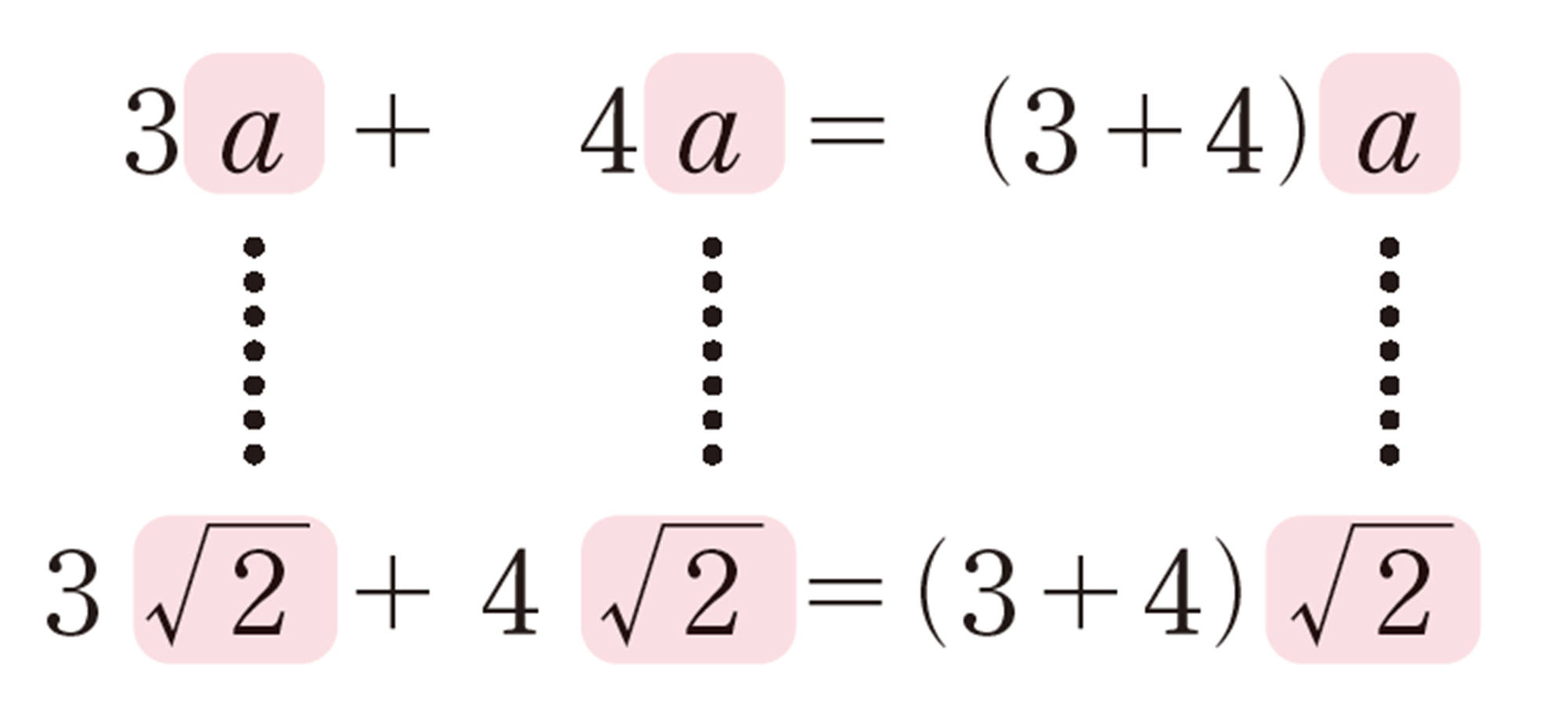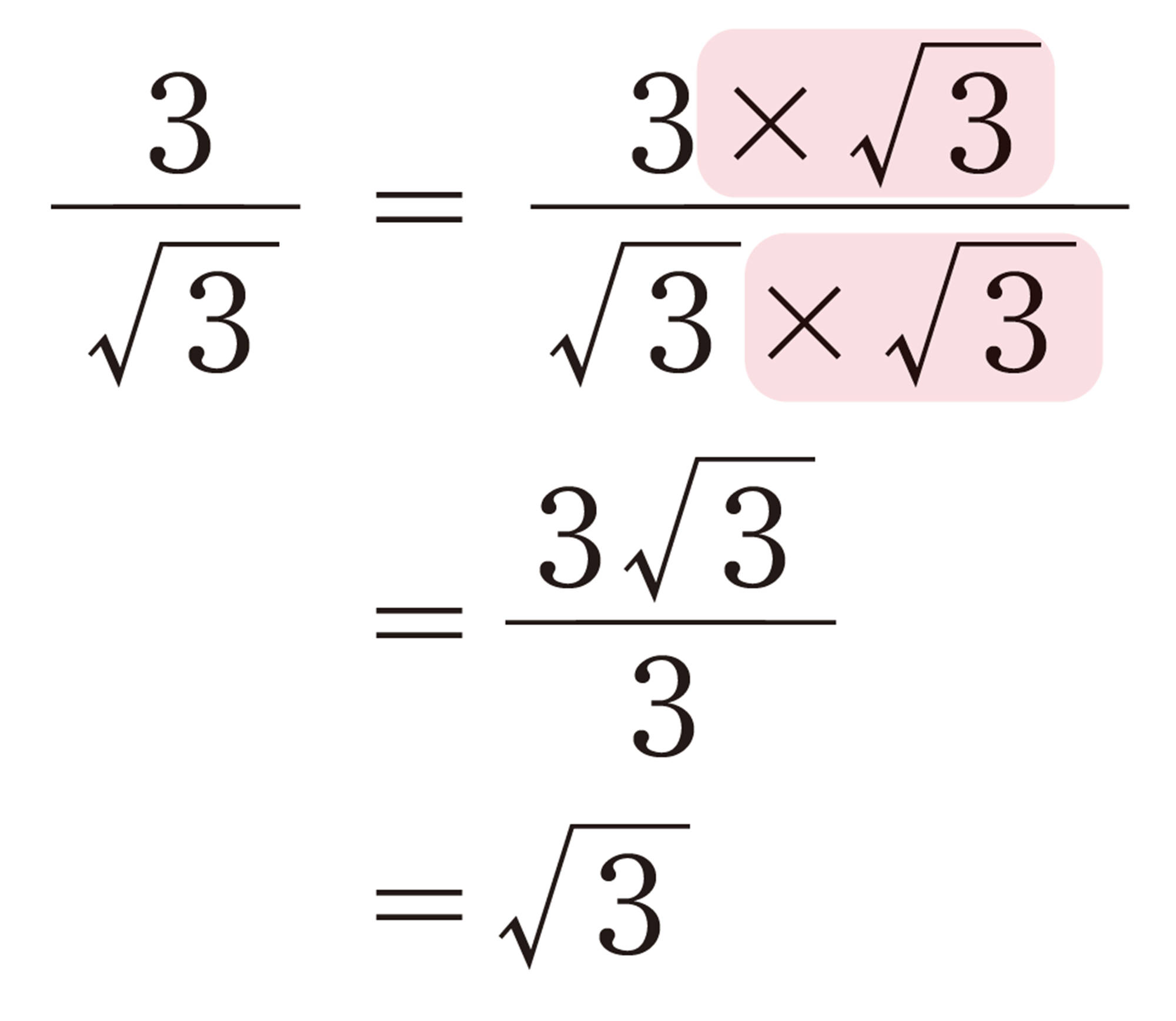<3年p.59>
2 根号をふくむ式の加法・減法
Q Question

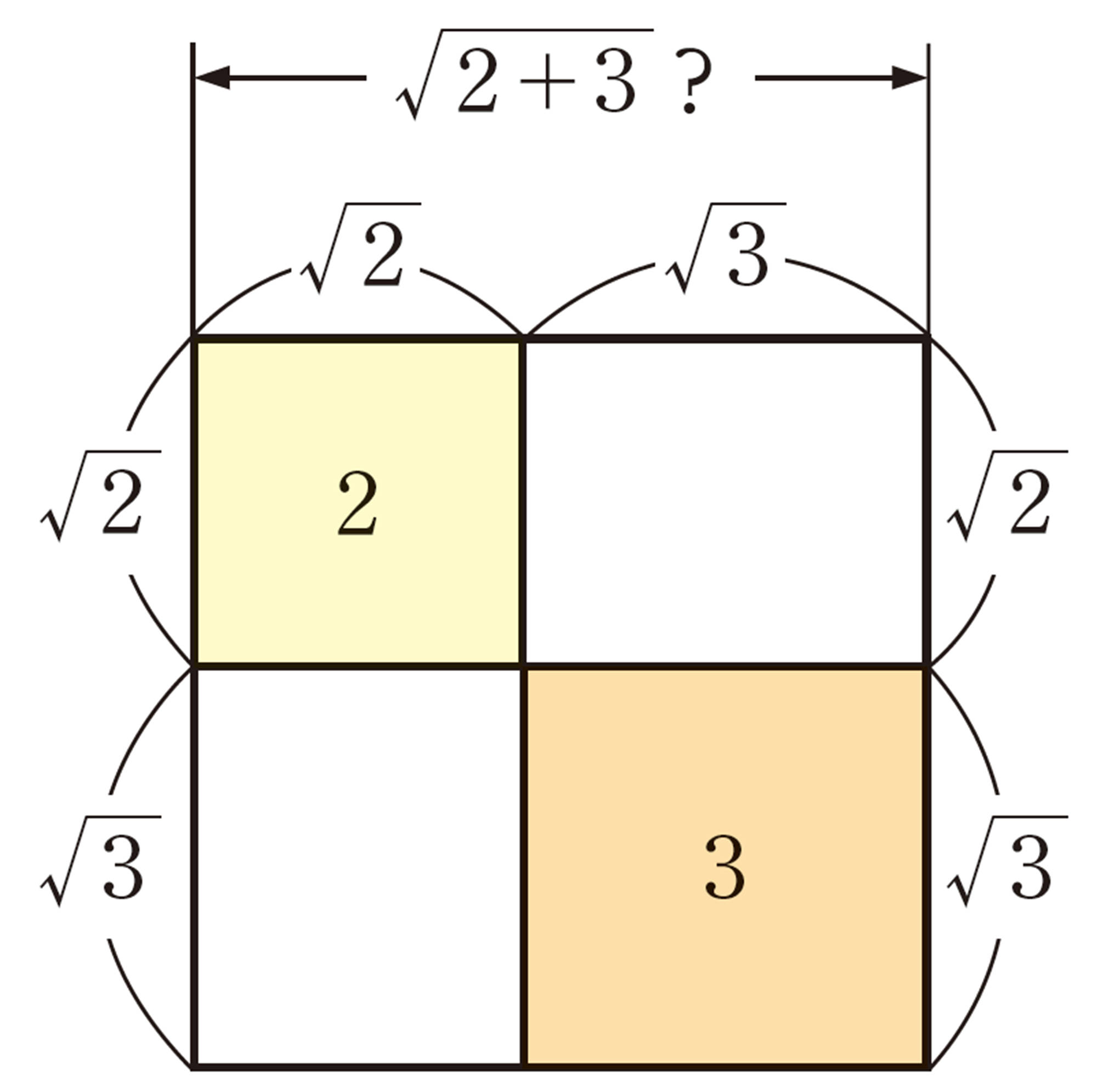
乗法と同じように,[mathjax]\(\sqrt{2}+\sqrt{3}=\sqrt{2+3}\)と考えてもいいのかな。
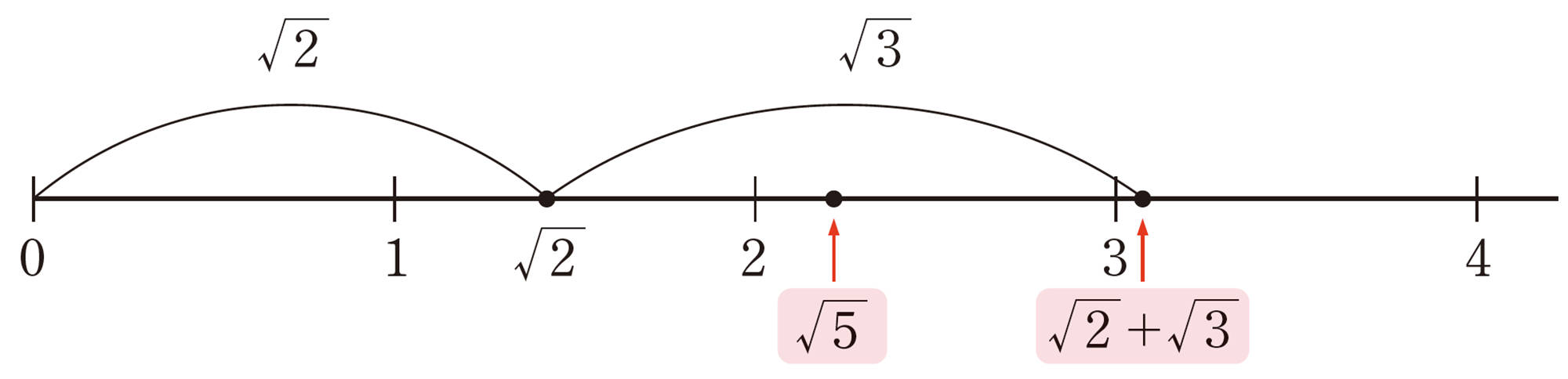
乗法のときと同じように近似値を使って確かめられるかな。

見方・考え方
図をもとにして考えられるかな。
目標 ▷ 根号をふくむ式の加法・減法を考えよう。
[mathjax]\(\sqrt{2}+\sqrt{3}\)は,これ以上簡単にできないが,1つの数を表している。
一方,[mathjax]\(3\sqrt{2}+4\sqrt{2}\)のように,根号の中が同じ数のときは,次のように,分配法則を使って簡単にすることができる。
<3年p.60>
例 1
⑴
⑵
⑴ [mathjax]\(5\sqrt{3} + 2\sqrt{3}\)
⑵ [mathjax]\(6\sqrt{5}-9\sqrt{5}+2\sqrt{5}\)
⑶ [mathjax]\(\sqrt{2}+\sqrt{7}-3\sqrt{2}+\sqrt{7}\)
⑷ [mathjax]\(-2\sqrt{3}+7\sqrt{6}-6\sqrt{6}+4\sqrt{3}\)
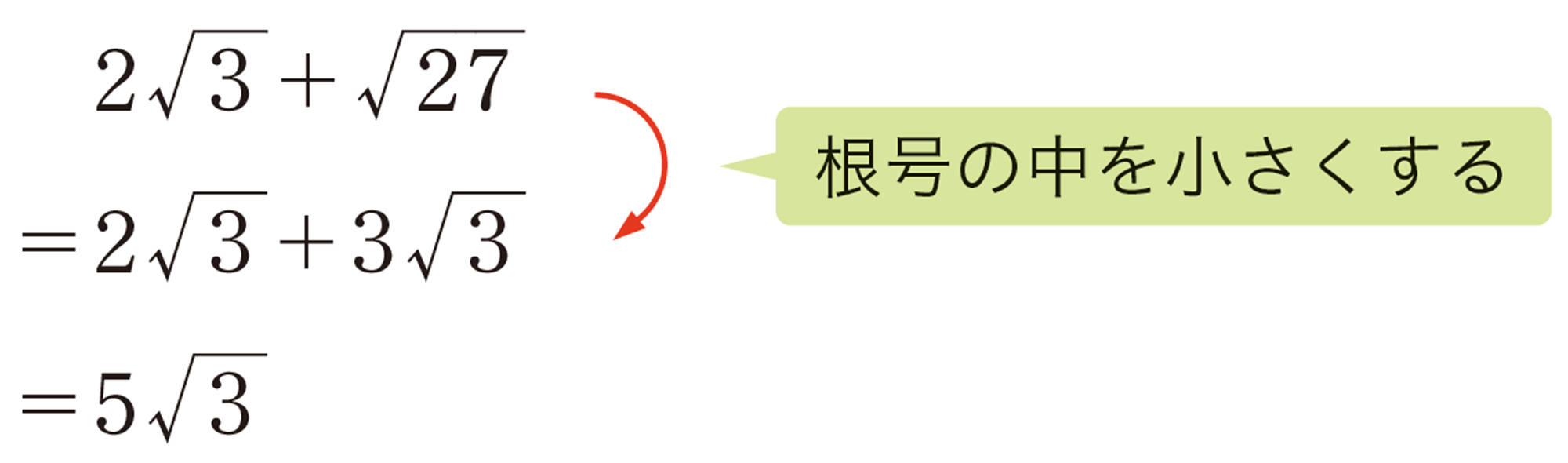
例 2
ふりかえり ▷P.56
問 2 次の計算をしなさい。
⑴ [mathjax]\(\sqrt{7}+\sqrt{28}\)
⑵ [mathjax]\(\sqrt{20}-\sqrt{45}\)
⑶ [mathjax]\(\sqrt{27} -\sqrt{12}+2\sqrt{3}\)
⑷ [mathjax]\(4\sqrt{6}-\sqrt{32}+\sqrt{2}-\sqrt{24}\)
問 3 次の計算をしなさい。
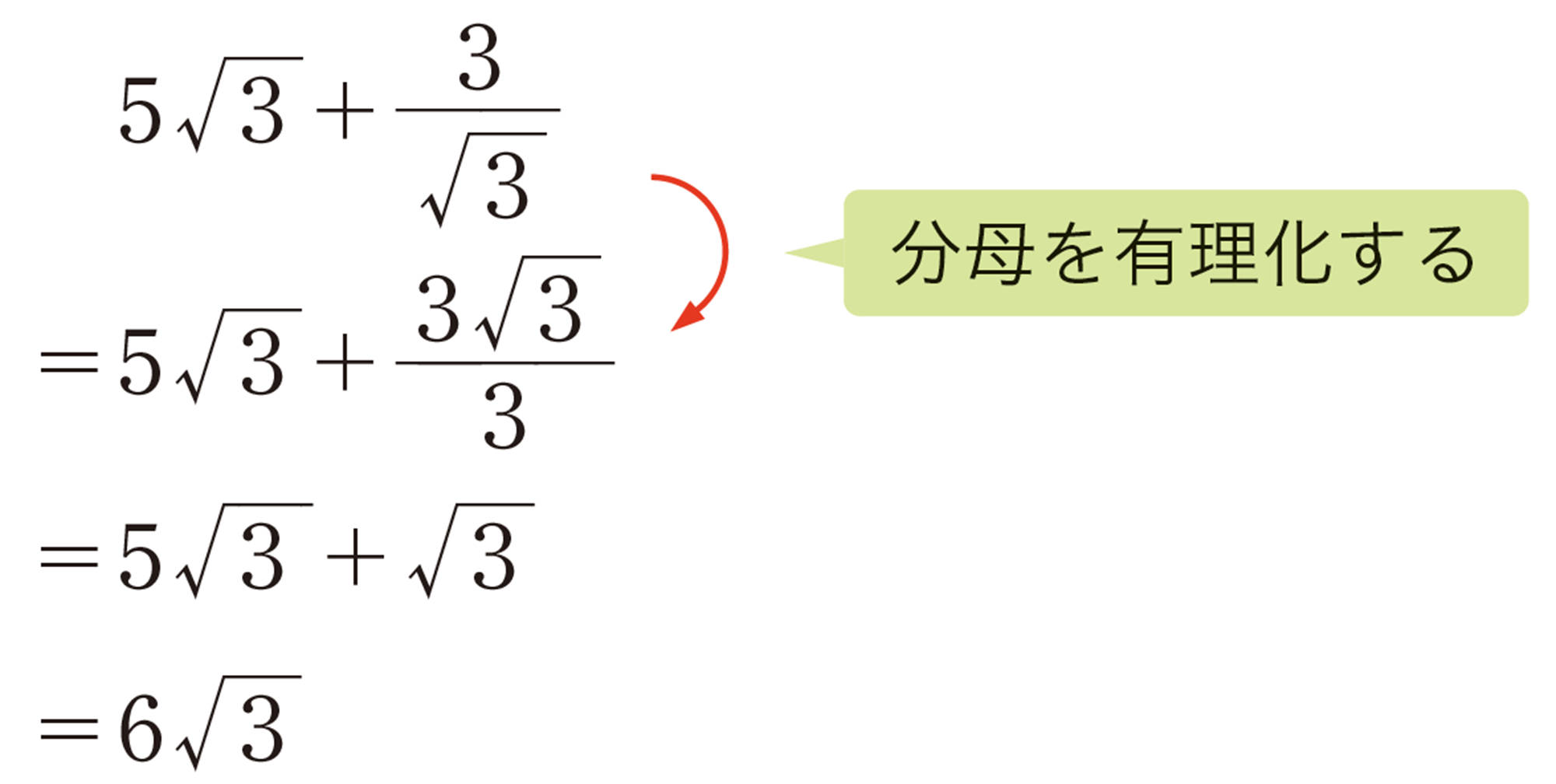
⑴ [mathjax]\(7\sqrt{2}+\dfrac{2}{\sqrt{2}}\)
⑵ [mathjax]\(\sqrt{27}-\dfrac{12}{\sqrt{3}}\)
⑶ [mathjax]\(2\sqrt{5}-\dfrac{5}{\sqrt{5}}+\sqrt{45}\)
⑷ [mathjax]\(\dfrac{4\sqrt{6}}{3}-\dfrac{\sqrt{2}}{3}\)
やってみよう
計算力を高めよう3-2
▷P.67
<3年p.61>
いろいろな計算
例 4
ふりかえり▷1年 分配法則
[mathjax]\(a(b+c)=ab+ac\)
問 4 次の計算をしなさい。
⑴ [mathjax]\(\sqrt{2}(\sqrt{7}-\sqrt{3})\)
⑵ [mathjax]\(\sqrt{5}(3+2\sqrt{5})\)
⑶ [mathjax]\((\sqrt{12}-\sqrt{3})\times\sqrt{3}\)
⑷ [mathjax]\((\sqrt{18}+\sqrt{8})\div\sqrt{2}\)
例 5
乗法公式❶が使えるね。

ふりかえり▷P.16
問 5 次の計算をしなさい。
⑴ [mathjax]\((\sqrt{7}+2)(\sqrt{7}+4)\)
⑵ [mathjax]\((\sqrt{3}+1)²\)
⑶ [mathjax]\((\sqrt{5}-\sqrt{2})²\)
⑷ [mathjax]\((2+\sqrt{3})(2-\sqrt{3})\)
⑸ [mathjax]\((2\sqrt{3}-5)(2\sqrt{3}+4)\)
ふりかえり▷P.17,18
問 6 計算の順序に注意して,次の計算をしなさい。
⑴ [mathjax]\(\sqrt{54}-\sqrt{30}\div\sqrt{5}\)
⑵ [mathjax]\(5\sqrt{7}+\sqrt{7}(\sqrt{14}-1)\)
やってみよう
計算力を高めよう3-3
▷P.67
<3年p.62>
例 6 [mathjax]\(x=\sqrt{7}-2\)のとき,[mathjax]\(x²-4\)の値を求めなさい。
解答
方法①
答 [mathjax]\(7-4\sqrt{7}\)
方法②
答 [mathjax]\(7-4\sqrt{7}\)
問 7 [mathjax]\(x=\sqrt{5}+\sqrt{3}\),[mathjax]\(y=\sqrt{5}-\sqrt{3}\)のとき,次の式の値を求めなさい。
⑴ [mathjax]\(xy\)
⑵ [mathjax]\(x²-y²\)
⑶ [mathjax]\(x²+2xy+y²\)
どんなことがわかったかな
根号をふくむ式の加法や減法は,根号の中が同じ数のとき計算することができます。
次の課題へ!
平方根は,どんなところで使われているのかな?
P.63

乗法公式を使った分母の有理化 発展 高等学校 Tea Break
問7⑴のように,[mathjax]\(\sqrt{5}+\sqrt{3}\)に[mathjax]\(\sqrt{5}-\sqrt{3}\)をかけると,根号をふくまない数になります。この考え方を使うと,次のような数の分母を有理化することができます。
分子と分母に[mathjax]\(\sqrt{5}-\sqrt{3}\)をかけているね。

![]() 次の数の分母を有理化してみましょう。
次の数の分母を有理化してみましょう。
⑴ [mathjax]\(\dfrac{1}{\sqrt{3}-\sqrt{2}}\)
⑵ [mathjax]\(\dfrac{2}{\sqrt{7}+1}\)
<3年p.63>
3 平方根の利用
目標 ▷ 平方根を利用して,身のまわりの問題を解決しよう。
Q Question
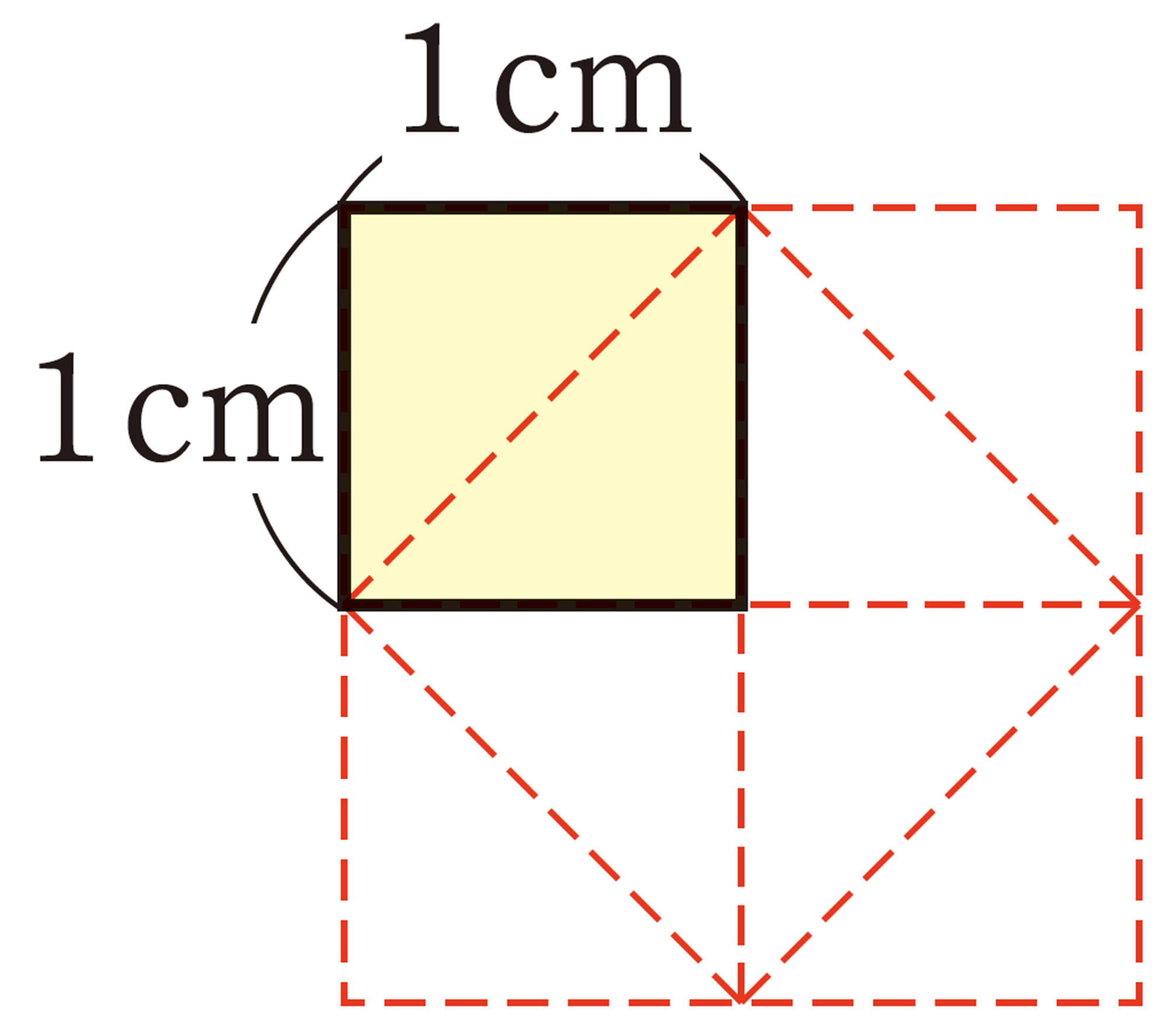
【Q】からわかるように,正方形の1辺と対角線の長さの比は,[mathjax]\(1:\sqrt{2}\)になっている。これをもとに,私たちがふだん使っている紙の寸法の特徴を調べてみよう。
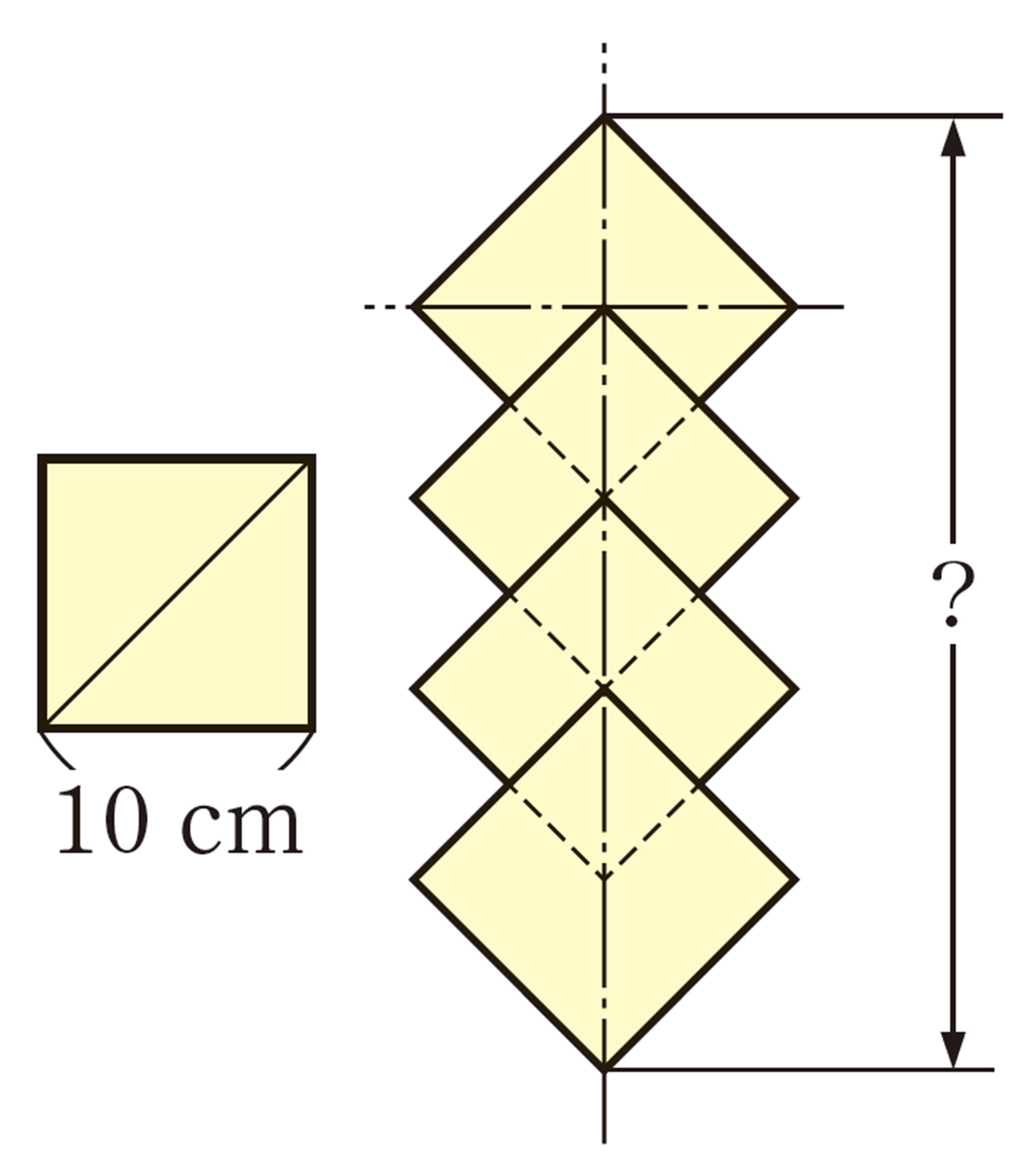
2 この教科書はB5判という規格の紙を使っています。美月さんは,1で調べたことを,次のようにB5判の紙を折って確かめました。実際に紙を折り,この折り方で確かめられる理由を説明してみましょう。
3 私たちがふだん使っている紙には,B5判以外に B4判,A4判,A3判などがあります。これらの2辺の長さの比についても調べてみましょう。
<3年p.65>
確かめよう 2節 根号をふくむ式の計算
1 次の数を[mathjax]\(\sqrt{a}\)の形に表しなさい。
⑴ [mathjax]\(2\sqrt{5}\)
⑵ [mathjax]\(3\sqrt{6}\)
⑶ [mathjax]\(5\sqrt{3}\)
2 次の数を,根号の中ができるだけ小さい自然数になるように,[mathjax]\(a \sqrt{b}\)の形に表しなさい。
⑴ [mathjax]\(\sqrt{12}\)
⑵ [mathjax]\(\sqrt{72}\)
⑶ [mathjax]\(2\sqrt{50}\)
3 次の数の分母を有理化しなさい。
⑴ [mathjax]\(\dfrac{2}{\sqrt{5}}\)
⑵ [mathjax]\(\dfrac{\sqrt{3}}{2\sqrt{2}}\)
⑶ [mathjax]\(\dfrac{3}{\sqrt{6}}\)
4 次の計算をしなさい。
⑴ [mathjax]\(\sqrt{3} \times \sqrt{12}\)
⑵ [mathjax]\(3\sqrt{2} \times (-4\sqrt{5})\)
⑶ [mathjax]\(\sqrt{35} \div \sqrt{7}\)
⑷ [mathjax]\(6\sqrt{18} \div \sqrt{6}\)
5 [mathjax]\(\sqrt{6} = 2.449\),[mathjax]\(\sqrt{60} =7.746\)として,次の数の近似値を求めなさい。
⑴ [mathjax]\(\sqrt{600}\)
⑵ [mathjax]\(\sqrt{0.6}\)
⑶ [mathjax]\(\sqrt{24}\)
6 次の計算をしなさい。
⑴ [mathjax]\(3\sqrt{2} + 5\sqrt{2}\)
⑵ [mathjax]\(2\sqrt{5} – 4\sqrt{3} + 7\sqrt{5} + 3\sqrt{3}\)
⑶ [mathjax]\(\sqrt{50} – \sqrt{8}\)
⑷ [mathjax]\(\sqrt{12} + \sqrt{3} – 3\sqrt{3}\)
7 次の計算をしなさい。
⑴ [mathjax]\(\sqrt{2}(\sqrt{32} – \sqrt{2})\)
⑵ [mathjax]\((4 – \sqrt{7})(4 + \sqrt{7})\)
<3年p.66>
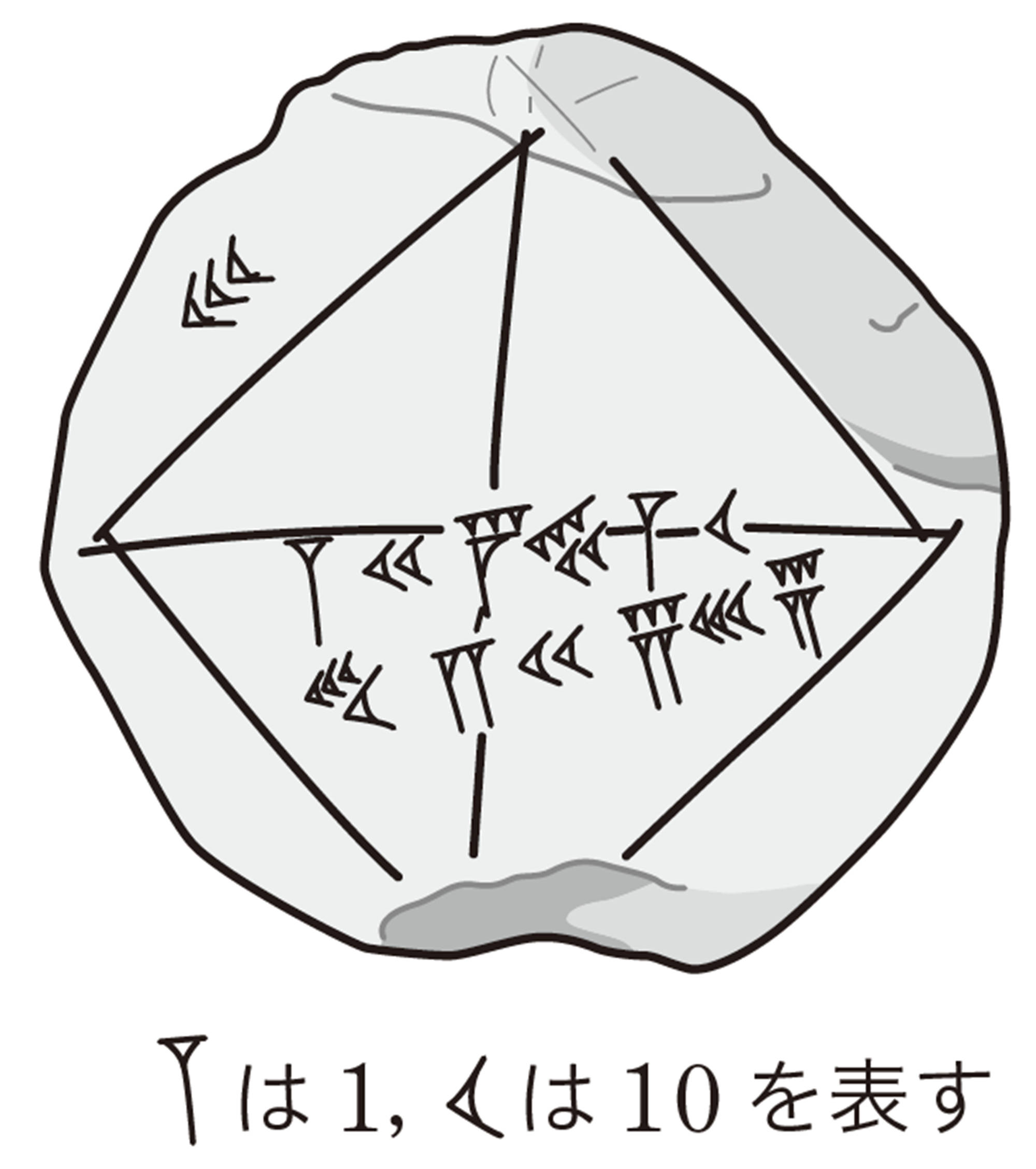
バビロニアの粘土板 Tea Break
メソポタミア文明は紀元前3000年頃,チグリス川とユーフラテス川の間(現在のイラクとその周辺)で発展し,その南部がバビロニアと呼ばれる地域でした。
この地域では数学が発達し,バビロニア人が数の計算や図形についての高い知識をもっていたことが,出土された粘土板からうかがえます。
バビロニアでは60集まると次の位にくり上がる表し方,60進法が使われていました。60進法は,現在でも時間や角度の表し方に受け継がれています。
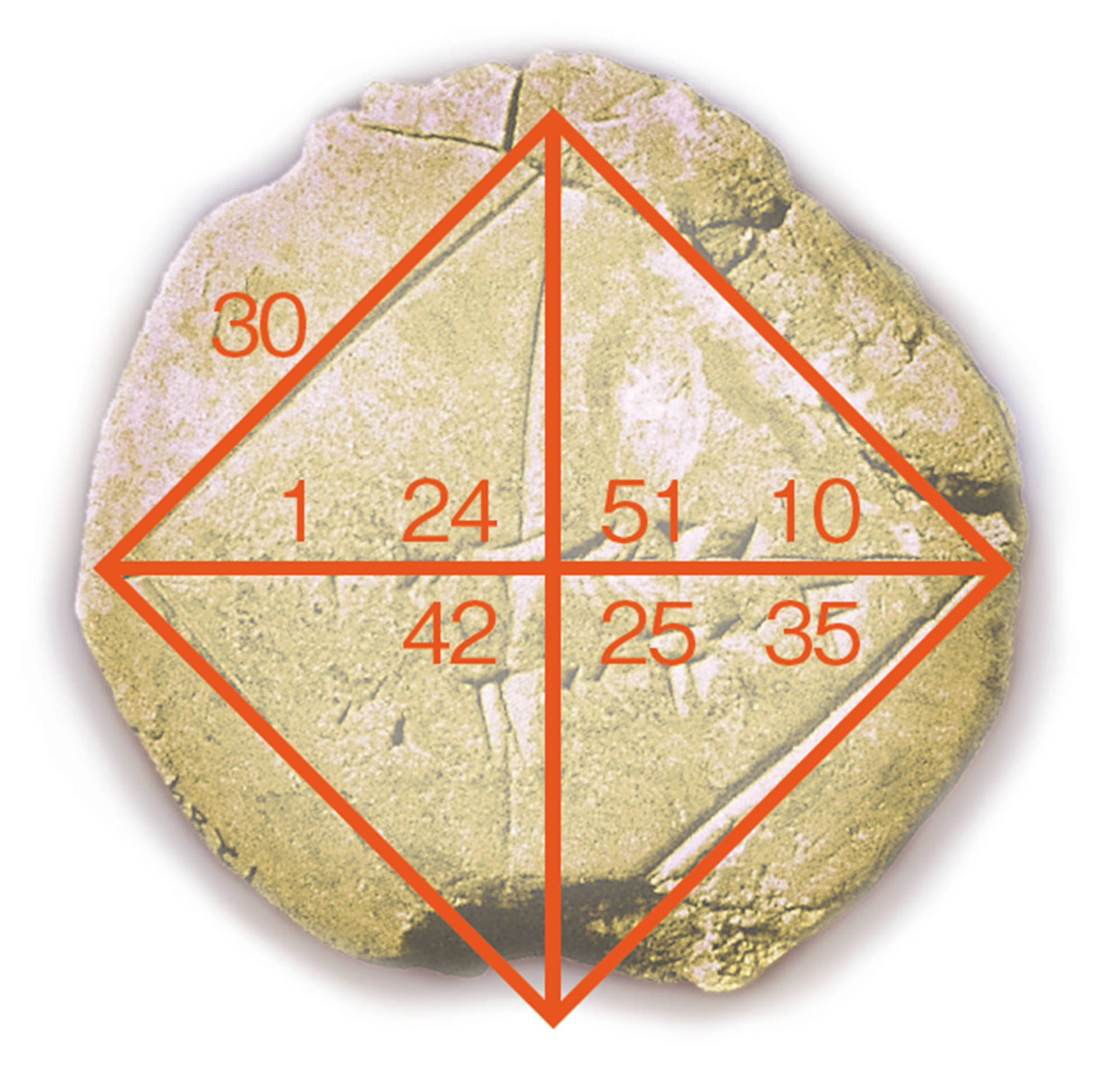
右に示したバビロニアの粘土板に刻まれている楔形文字[mathjax] \(〔1 24 51 10〕\)は,60進法の分数による[mathjax]\( \sqrt{2}\)の近似値です。私たちが使っている10進法に直して計算すると,次のように,小数第五位まで正確な値であることがわかります。
[mathjax]\(1 + \dfrac{24}{60} + \dfrac{51}{60²} + \dfrac{10}{60³} = 1.414212962\dots\)
一方,[mathjax] \(〔42 25 35〕\)は,60進法による1辺30の正方形の対角線の長さの近似値です。
[mathjax]\(42 + \dfrac{25}{60} + \dfrac{35}{60²} = 42.42638888 \dots\)
これらの計算結果から,粘土板に書かれた3 種類の数の間には,
[mathjax]\(30 \times〔1 24 51 10〕=〔42 25 35〕\)
という関係があることがわかります。これは,正方形の対角線の長さが,
(1辺の長さ)[mathjax]\(\times \sqrt{2}\)
で求められることを意味しています。このことから,4000年も昔のバビロニア人が,正方形の1辺と対角線の長さの関係を知っていたと推測できます。