<3年p.39>
1章のまとめの問題 解答 P.300〜301 基本
1 次の計算をしなさい。
⑴ [mathjax]\(6a(a-2)\)
⑵ [mathjax]\((2x-5y) \times (-y)\)
⑶ [mathjax]\((12x²-9xy)÷(-3x)\)
⑷ [mathjax]\((3ab+4a)÷ \dfrac{1}{2}a\)
2 次の式を展開しなさい。
⑴ [mathjax]\((a-b)(x+y)\)
⑵ [mathjax]\((x+1)(3x+2)\)
⑶ [mathjax]\((x+2)(x-3)\)
⑷ [mathjax]\((y-6)²\)
⑸ [mathjax]\((a+3b)(a-3b)\)
⑹ [mathjax]\((2x+3)²\)
3 次の計算をしなさい。
⑴ [mathjax]\(2a(a-2)+(a+1)²\)
⑵ [mathjax]\((x-4)²-(x-8)(x-2)\)
4 次の式を因数分解しなさい。
⑴ [mathjax]\(4a²b-6ab²\)
⑵ [mathjax]\(x²+7x+12\)
⑶ [mathjax]\(x²-6x+9\)
⑷ [mathjax]\(144-x²\)
⑸ [mathjax]\(x²+2x-35\)
⑹ [mathjax]\(4x²+12xy+9y²\)
⑺ [mathjax]\(x²y-9xy+18y\)
⑻ [mathjax]\((x+3)²-2(x+3)\)
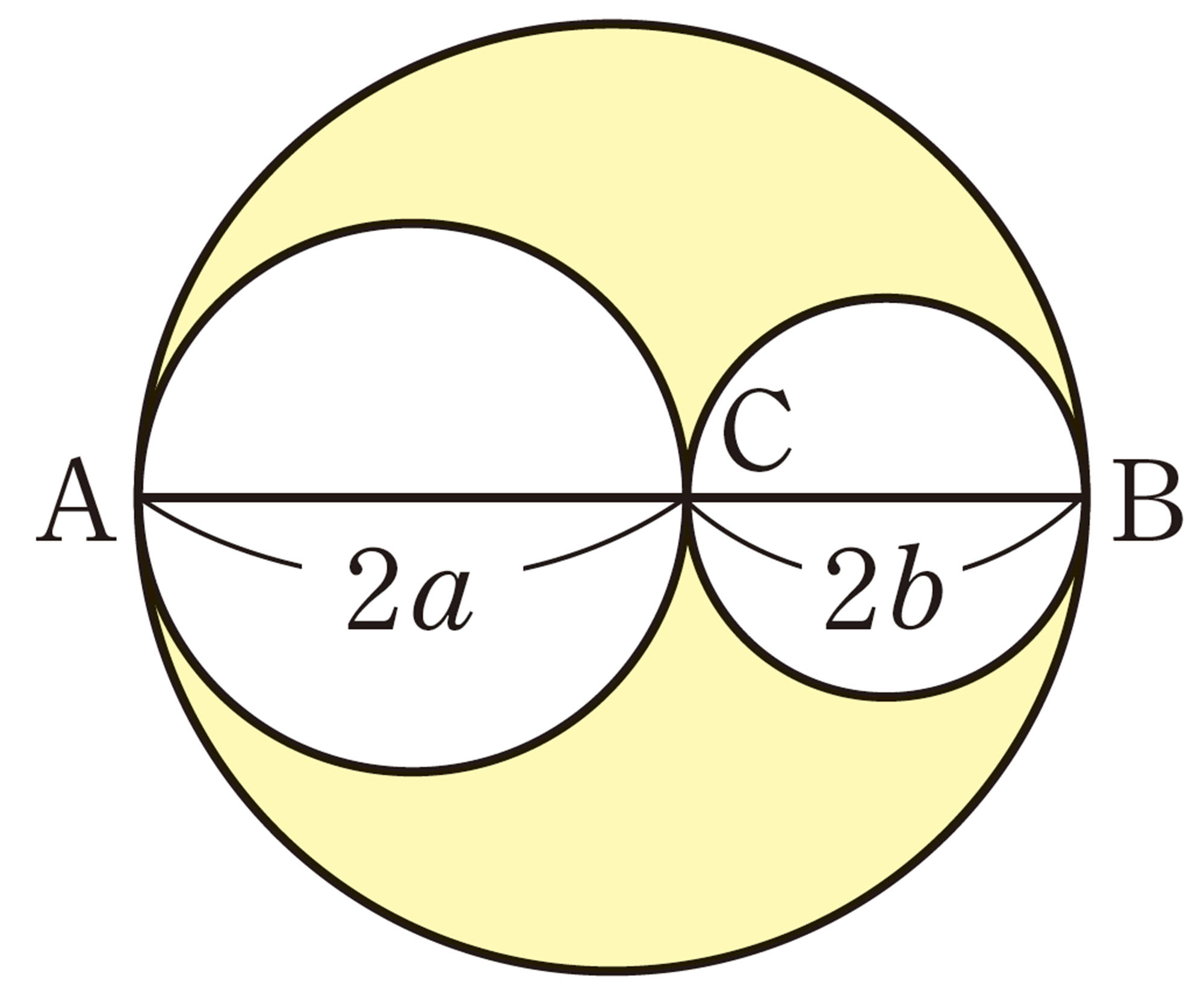
5 連続する3つの整数では,もっとも大きい数の2乗からもっとも小さい数の2乗をひいた差は,中央の数の4倍になることを証明しなさい。
<3年p.40>
1章のまとめの問題 応用
1 次の式を展開しなさい。
⑴ [mathjax]\(\require{physics} \left(x+\dfrac{1}{2}\right)(x-2)\)
⑵ [mathjax]\((7b+a)(a-7b)\)
⑶ [mathjax]\((x+2y-9)²\)
⑷ [mathjax]\((a-b+1)(a+b-1)\)
2 次の式を因数分解しなさい。
⑴ [mathjax]\(x(x+2)-15\)
⑵ [mathjax]\((x+5)²-9(x+5)+20\)
⑶ [mathjax]\(x²-x+ax-a\)
⑷ [mathjax]\(xy-3x-2y+6\)
3 縦am,横2am の長方形の土地があります。この土地の縦を5m長くし,横を3m短くすると,面積はもとの土地よりどれだけ大きくなりますか。また,このとき,面積が55m²大きくなるとすると,もとの土地の縦の長さは何mですか。
4 2つの奇数の積は奇数になることを証明しなさい。
5 [mathjax]\(x=\dfrac{5}{2}\),[mathjax]\(y=\dfrac{3}{2}\)のとき,[mathjax]\(x²-10xy+25y²\)の値を求めなさい。
6 次の式をくふうして計算しなさい。
⑴ [mathjax]\(19²-21²\)
⑵ [mathjax]\(6.9 \times 7.1\)
<3年p.41>
活用
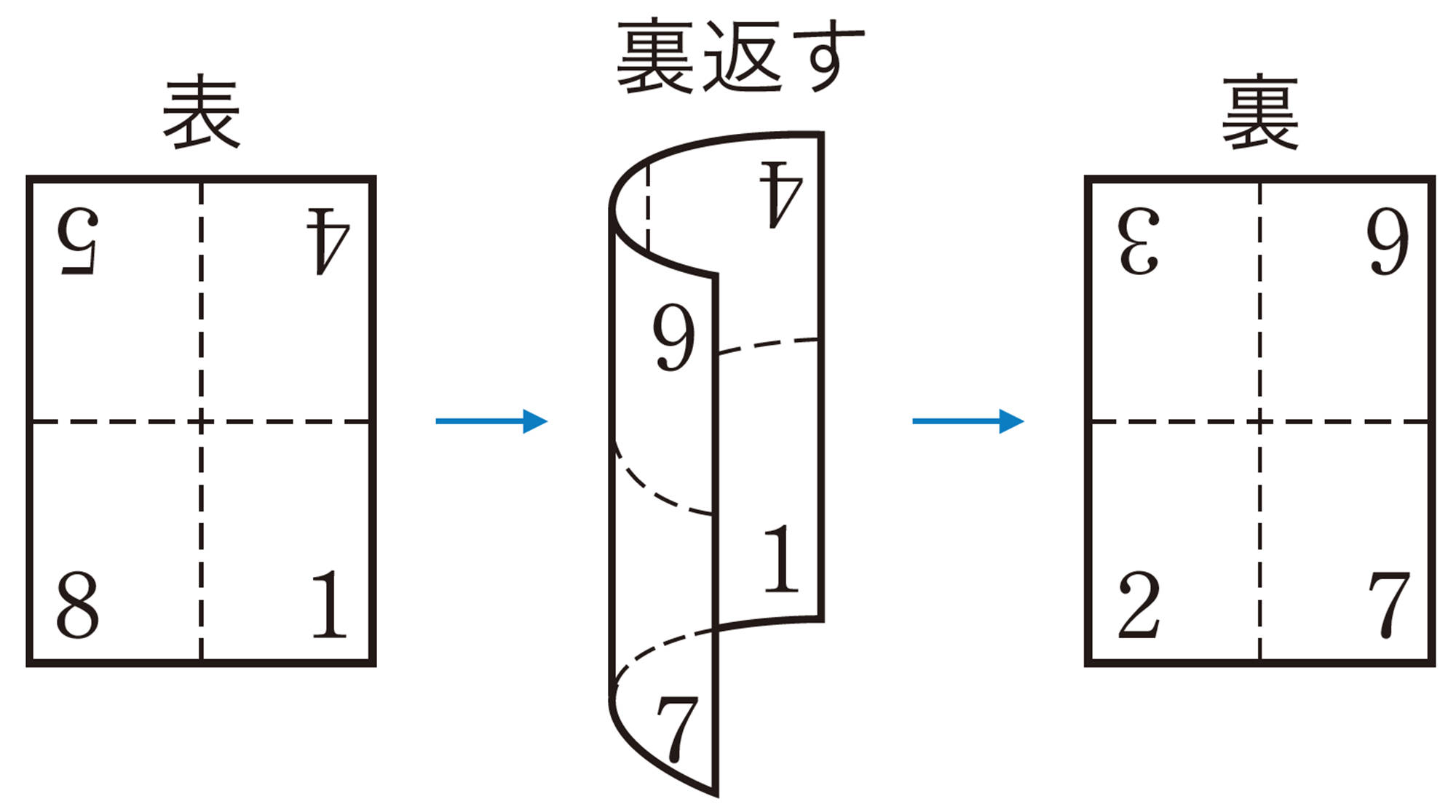
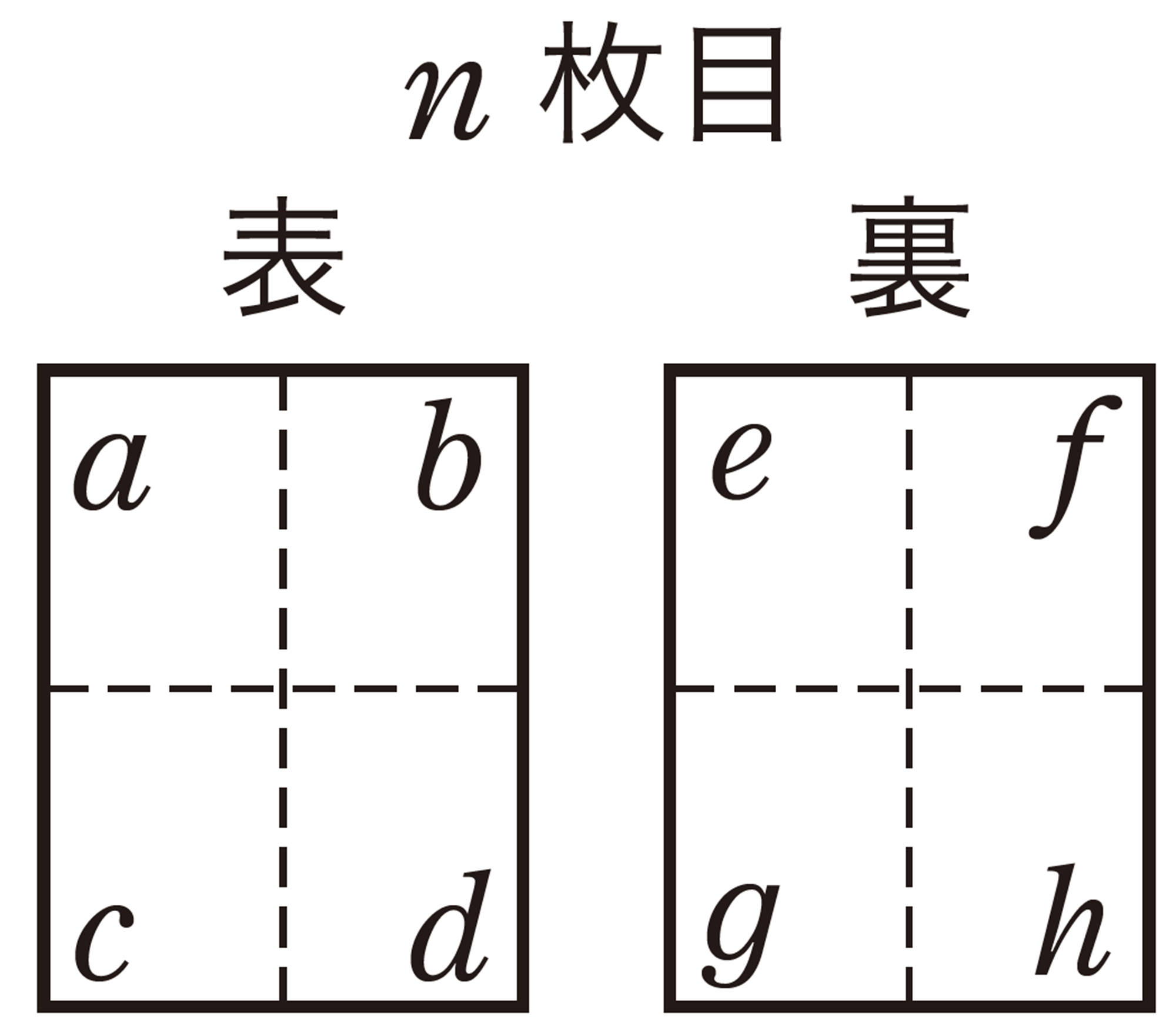
1 ある中学校で,卒業文集をつくることになりました。1枚の大きな紙に8ページ分の印刷をして,それをいくつか束ねて冊子をつくります。このとき,次の問いに答えなさい。ただし,表の右下が最初のページとします。
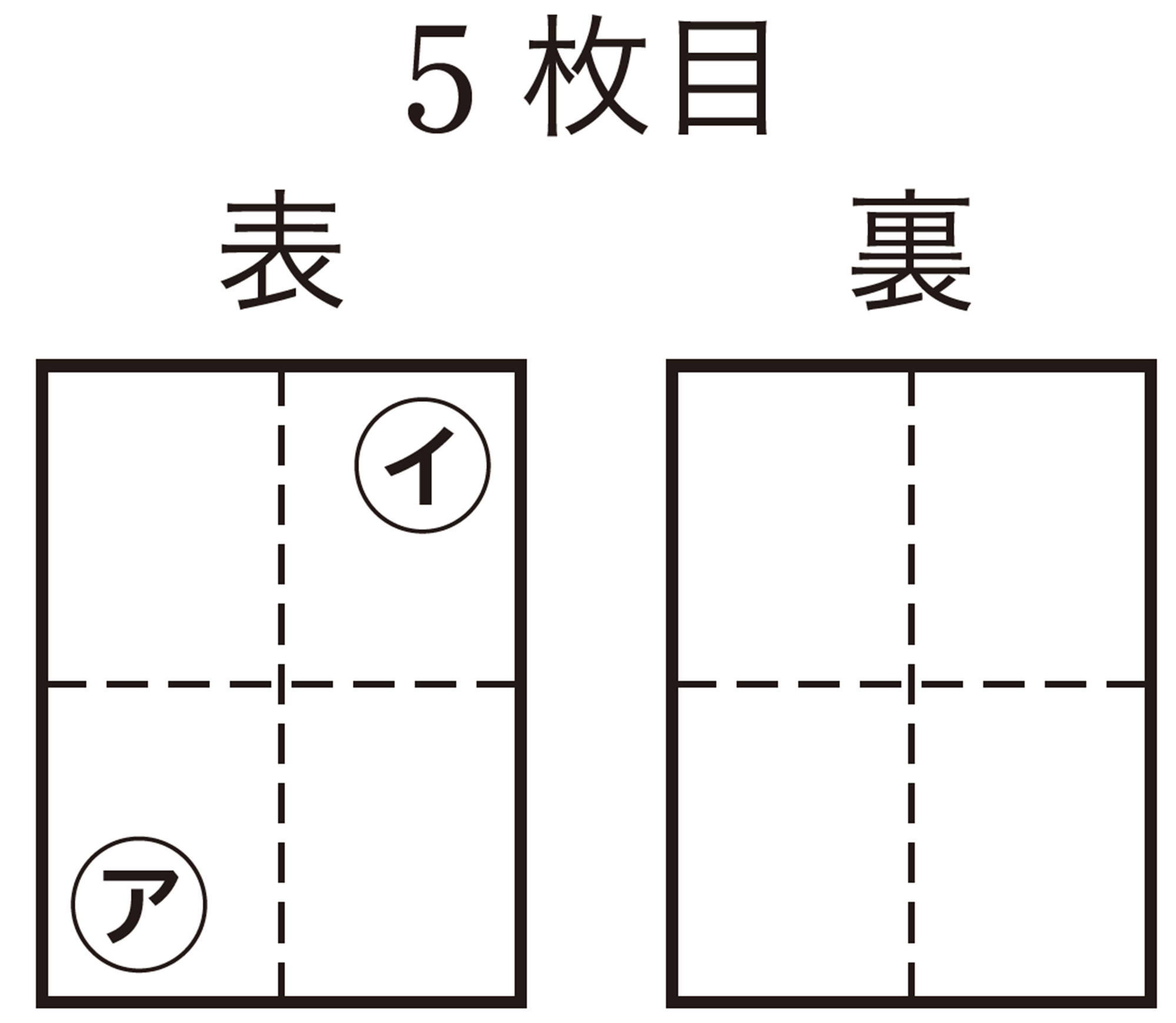
⑴ 図1で,5枚目の大きな紙の㋐,㋑の位置につけられるページ番号を求めなさい。
⑵ 15枚目の大きな紙につけられたページ番号のうち,もっとも小さい数を求めなさい。
⑶ 図2で,[mathjax]\(n\)枚目の大きな紙につけられたページ番号[mathjax]\(c\)を[mathjax]\(n\)を使って表しなさい。
⑷ [mathjax]\(n\)枚目の大きな紙につけられたページ番号で,[mathjax]\(ab-cd=12\)の関係が成り立つことを証明しなさい。
>> 関連する職業・仕事 [出版社,印刷会社]
<3年p.42>
深めよう 簡単に計算する方法
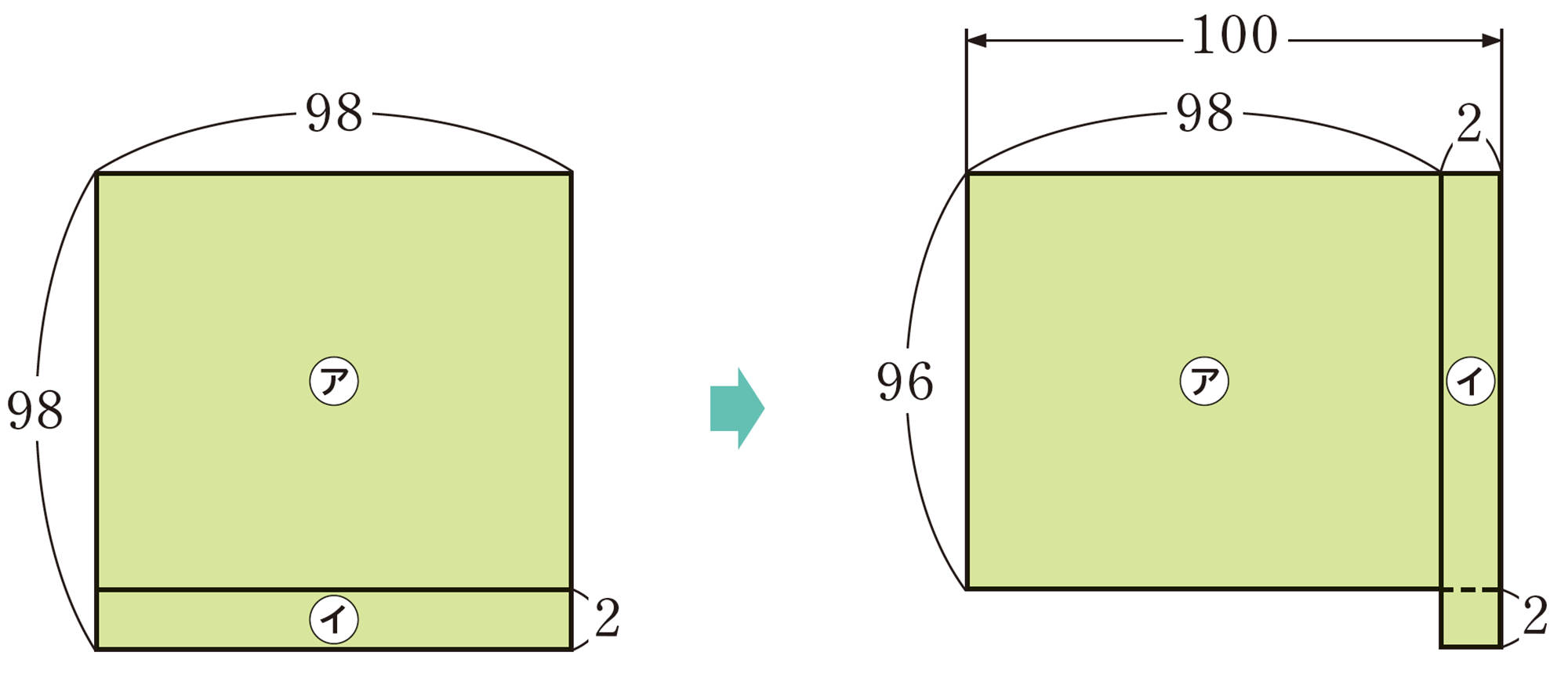
35ページの例3⑵では,[mathjax] \(98²\)の計算をするのに乗法公式を利用して考えました。
ここでは,100に近い数の2乗を簡単に計算するほかの方法を考えてみましょう。
❶ 100と98との差を98からひく [mathjax]\(98-2=96\)
❷ 100と98との差を2乗する [mathjax]\(2²=4\)
❸ ❶を100倍する [mathjax]\(96 \times 100=9600\)
❹ ❸に❷を加える [mathjax]\(9600+4=9604\)
① [mathjax] \(98²\)が上の方法で計算できることを,次の図を使って説明してみましょう。
② この方法で,次の計算をしてみましょう。
⑴ [mathjax] \(99²\)
⑵ [mathjax] \(95²\)
⑶ [mathjax] \(92²\)
③ ①と同じように図を使って,次の計算の方法を考えましょう。 また,その方法で計算してみましょう。
どのような図をかいたら,うまく説明できるかな。

⑴ [mathjax] \(101²\)
⑵ [mathjax] \(103²\)
⑶ [mathjax] \(108²\)