<3年p.21>
確かめよう 1節 多項式の計算
1 次の計算をしなさい。
⑴ [mathjax]\(x(2x + 5y)\)
⑵ [mathjax]\(2x(3x – 4y)\)
⑶ [mathjax]\((6a² – 7a) \div a\)
⑷ [mathjax]\((12a² + 9a) \div 3a\)
2 次の式を展開しなさい。
⑴ [mathjax]\((x + 2)(y + 5)\)
⑵ [mathjax]\((2x + 1)(x – 4)\)
3 次の式を展開しなさい。
⑴ [mathjax]\((a + 5)(a + 9)\)
⑵ [mathjax]\((x – 7)(x + 3)\)
⑶ [mathjax]\((y – 1)(y – 8)\)
⑷ [mathjax]\((a + 8)²\)
⑸ [mathjax]\((x – 3)²\)
⑹ [mathjax]\((y – 4)(y + 4)\)
4 [mathjax]\((x + 1)² + (2 + x)(2 – x)\)を計算しなさい。
筆算の計算と式の展開 Tea Break
小学校のときに学習したかけ算の筆算は,乗法公式を利用しているといえます。筆算では,[mathjax]\(\textsf{2桁} \times \textsf{2桁}\)の計算も,1桁どうしのかけ算をしています。
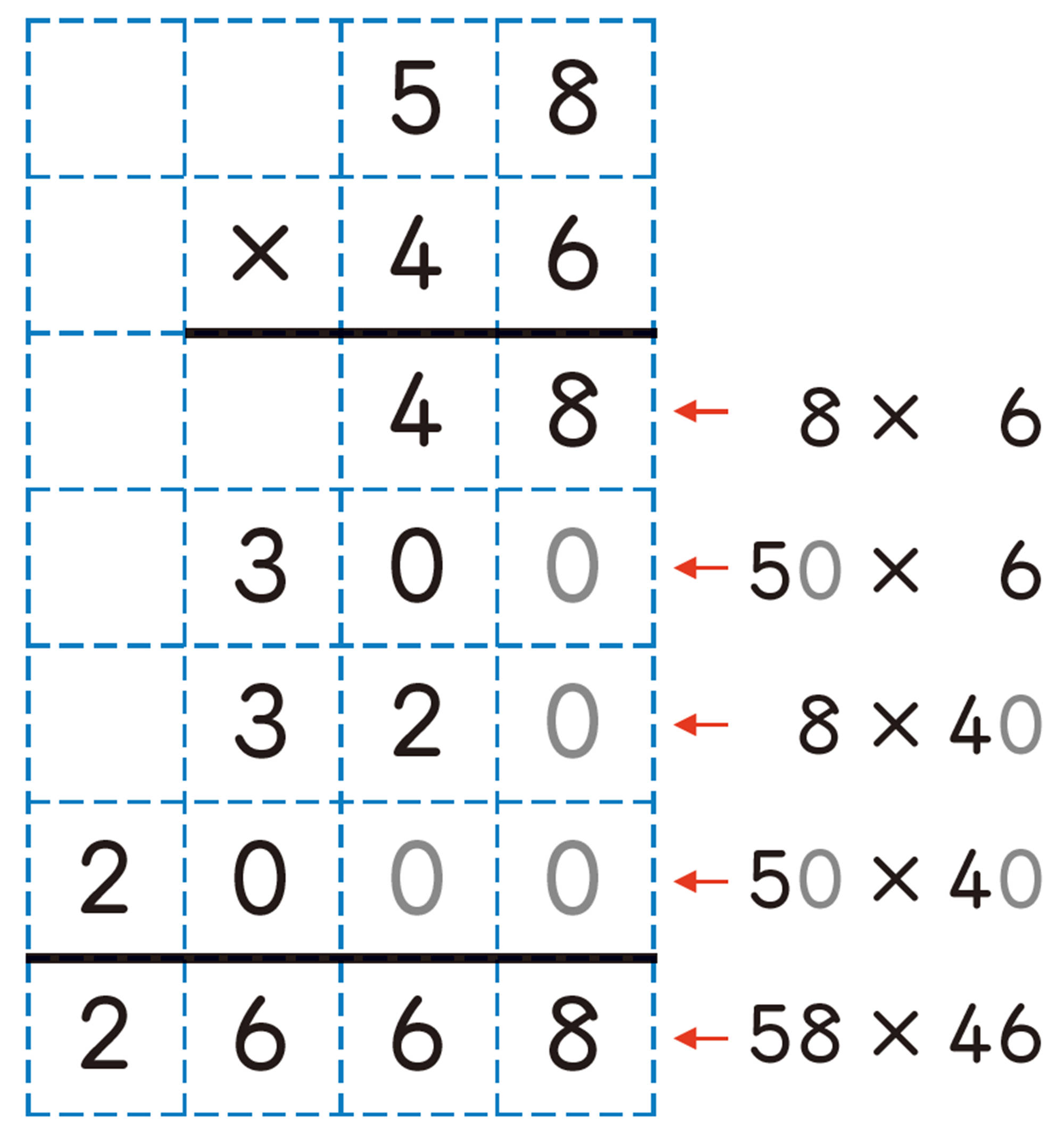
たとえば,[mathjax]\(58 \times 46\)をすると,右のようになります。
順に,[mathjax]\(8 \times 6\),[mathjax]\(50 \times 6\),[mathjax]\(8 \times 40\),[mathjax]\(50 \times 40\)の計算をし,位取りに気をつけて筆算をしています。
これは,
[mathjax]\(58 \times 46=(8+50) \times (6+40)\)
と考えて,式を展開していることになります。