教科書アドバイザー「マスマス！」

2p250 – R7中学校数学QR教材

gkt-horizontal-line

<2年p.250>

　応用　

１
⑴　[mathjax]\(\angle x=105^{\circ}\)
⑵　[mathjax]\(\angle x=68^{\circ}\)
⑶　[mathjax]\(\angle x=90^{\circ}\)

２
[mathjax]\(\angle x=56^{\circ}\)

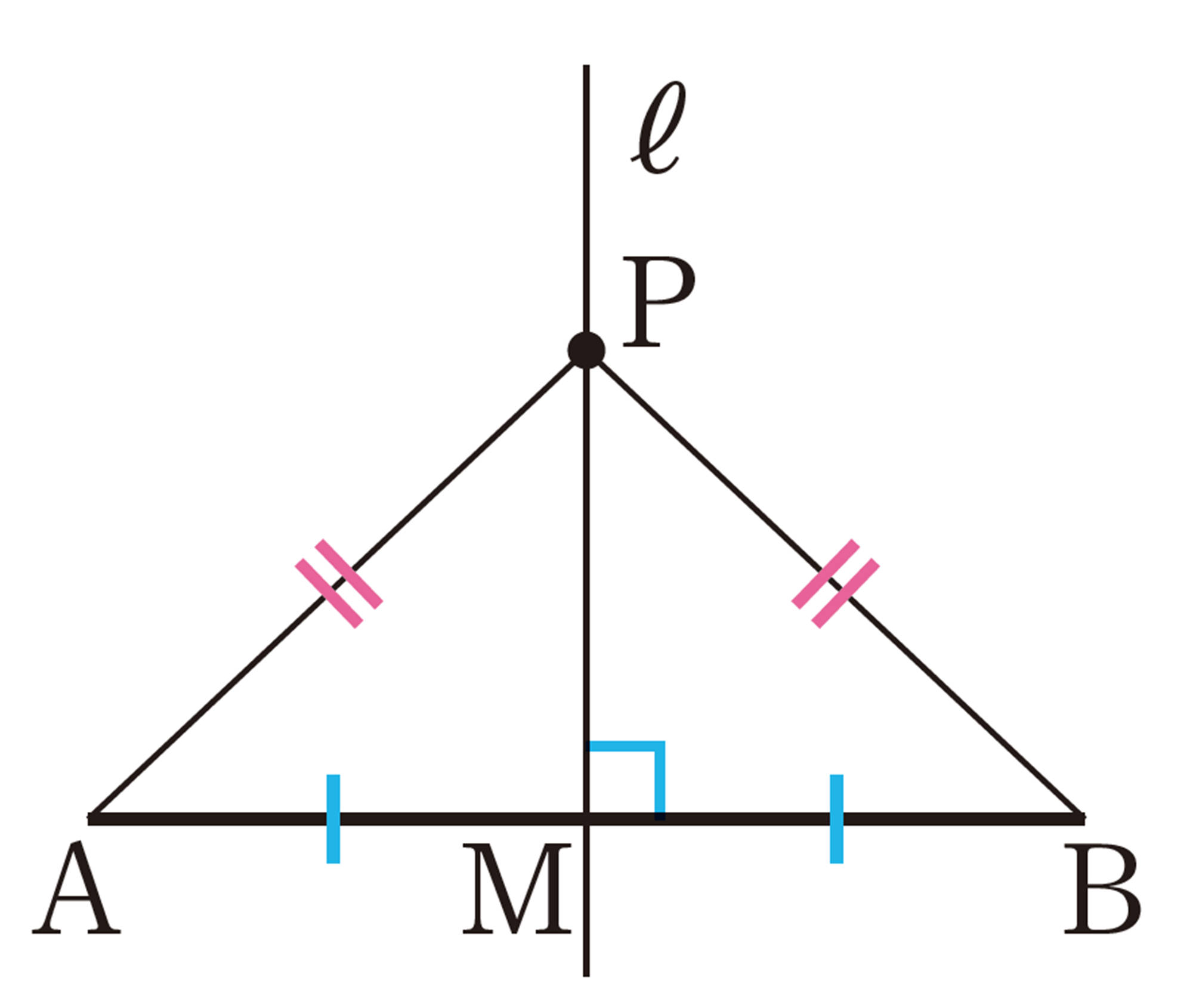
３ ❶　(仮定) [mathjax]\(AM=BM\)，[mathjax]\(PM \bot AB(ℓ \bot AB)\) 　　(結論)[mathjax]\(PA=PB\)

❷　[mathjax]\(PA=PB\)であることをいうためには，PAとPBが対応する辺になる[mathjax]\(\triangle PAM\)と[mathjax]\(\triangle PBM\)が合同であることを証明すればよい。
❸(証明)

　[mathjax]\(\triangle PAM\)と[mathjax]\(\triangle PBM\)において，
　仮定から，

[mathjax]\(\hspace{12pt}\begin{eqnarray}AM&=&BM\quad\cdots\cdots\text{①}\\ \angle PMA=\angle PMB &=&90^{\circ}\hspace{13pt}\cdots\cdots\text{②}\end{eqnarray}\)

共通な辺だから，[mathjax]\(PM=PM\quad\cdots\cdots\text{③}\)
①，②，③より，2組の辺とその間の角がそれぞれ等しいから，
[mathjax]\(\hspace{58pt}\triangle PAM \equiv \triangle PBM\)
　合同な図形の対応する辺は等しいから，
[mathjax]\(\hspace{78pt}PA=PB\)

４

[mathjax]\(\triangle AED\)と[mathjax]\(\triangle FEC\)において，
仮定から，[mathjax]\(\hspace{36pt}DE=CE\hspace{24pt}\cdots\cdots\text{①}\)
平行線の錯角は等しいから，
[mathjax]\(AD/\!/CF\)より，[mathjax]\(\angle ADE=\angle FCE\quad\cdots\cdots\text{②}\)
対頂角は等しいから，
[mathjax]\(\hspace{64pt}\angle AED=\angle FEC\quad\cdots\cdots\text{③}\)
①，②，③より，1組の辺とその両端の角がそれぞれ等しいから，

[mathjax]\(\hspace{62pt}\triangle AED \equiv \triangle FEC\)
合同な図形の対応する辺は等しいから，

[mathjax]\(\hspace{80pt}AE=FE\)

　活用　

１
⑴　[mathjax]\(\triangle ACB\)と[mathjax]\(\triangle DCE\)において，
仮定から，

[mathjax]\(\begin{eqnarray}AC &=& DC & \hspace{22pt}\cdots\cdots\text{①}\\ \angle A=\angle D &=& 90^{\circ}&\quad\cdots\cdots\text{②}\end{eqnarray}\)

対頂角は等しいから，
[mathjax]\(\hspace{12pt}\angle ACB=\angle DCE\quad\cdots\cdots\text{③}\)
①，②，③より，1 組の辺とその両端の角がそれぞれ等しいから，
[mathjax]\(\hspace{10pt}\triangle ACB\equiv \triangle DCE\)
合同な図形の対応する辺は等しいから，
[mathjax]\(\hspace{28pt}AB=DE\)

⑵　㋑

星形n角形　P.145〜146

①　略
②　[mathjax]\(360^{\circ}\)
③　[mathjax]\(540^{\circ}\)
④　表の左から，[mathjax] \(360，540，720，900，1080\)
⑤　略
⑥　略

　5章　　　三角形・四角形　[解答]　

トライ　P.156

略

5章のまとめの問題　P.175〜177

　基本　

１

⑴　頂角
⑵　1つの鋭角，他の1辺
⑶　中点
⑷　4つの角が等しい四角形

２

⑴　[mathjax]\(72^{\circ}\)
⑵　二等辺三角形
　(理由)[mathjax]\(\angle BCD=\angle BDC=72^{\circ}\)であるから。

３

⑴　[mathjax]\(\triangle ABE\)と[mathjax]\(\triangle CDF\)において，
仮定から，[mathjax]\(\angle AEB =\angle CFD=90^{\circ}\quad\cdots\cdots\text{①}\)
平行線の錯角は等しいから，
[mathjax]\(AB/\!/DC\) より，
[mathjax]\(\hspace{40pt}\angle ABE=\angle CDF\hspace{40pt}\cdots\cdots\text{②}\)
平行四辺形の対辺は等しいから，
[mathjax]\(\hspace{56pt}AB=CD\hspace{53pt}\cdots\cdots\text{③}\)
①，②，③より，直角三角形の斜辺と1つの鋭角がそれぞれ等しいから，
[mathjax]\(\hspace{40pt}\triangle ABE\equiv\triangle CDF\)

⑵　CF，錯角，FC，1組の対辺が平行で等しい

４

二等辺三角形

(証明)[mathjax]\(\triangle BMD\)と[mathjax]\(\triangle CME\)において，
仮定から，

[mathjax]\(\hspace{54pt}\begin{eqnarray}BM &=& CM & \hspace{52pt}\cdots\cdots\text{①}\\ MD &=& ME & \cdots\cdots\text{②}\end{eqnarray}\)

MD，MEはそれぞれ辺AB，ACの垂線であるから，
[mathjax]\(\hspace{32pt}\angle MDB=\angle MEC=90^{\circ}\quad\cdots\cdots\text{③}\)
①，②，③より，直角三角形の斜辺と他の1辺がそれぞれ等しいから，

[mathjax]\(\hspace{28pt}\triangle BMD\equiv \triangle CME\)
したがって，[mathjax]\(\angle B=\angle C\)
2つの角が等しいから，[mathjax]\(\triangle ABC\)は二等辺三角形である。

　応用　

１

長方形，正方形

＜ミライ教科書３学年分もくじ＞

＜スグラパ＞

＜ドリルまとめ＞