教科書アドバイザー「マスマス！」

２年９_解答巻末－２（親ページ）246-254

gkt-horizontal-line

<2年p.246>

　1章　　　式の計算　[解答]　

計算力を高めよう１　P.23

１

⑴　[mathjax]\(9x+8y\)
⑵　[mathjax]\(-6a+3b\)
⑶　[mathjax] \(6a²\)
⑷　[mathjax]\(x²-2x+1\)
⑸　[mathjax]\(-2a+9b\)
⑹　[mathjax]\(2x²-5x\)
⑺　[mathjax]\(6x-10y\)
⑻　[mathjax]\(-8x²+14x-2\)
⑼　[mathjax]\(5x-4y-9\)
⑽　[mathjax]\(-9x+15y\)

２

⑴　[mathjax]\(12a-10b+2\)
⑵　[mathjax]\(-27x+12y\)
⑶　[mathjax]\(5a+4b\)
⑷　[mathjax]\(-\dfrac{8}{3}x+4y\)

３

⑴　[mathjax]\(9a\)
⑵　[mathjax]\(7x-3y\)
⑶　[mathjax]\(x+2y\)
⑷　[mathjax]\(5a+7b\)
⑸　[mathjax]\(6x-2y-2\)
⑹　[mathjax]\(\dfrac{-a-3b}{12}\)
⑺　[mathjax]\(\dfrac{11a-b}{24}\)
⑻　[mathjax]\(\dfrac{5x+7y}{6}\)
⑼　[mathjax]\(\dfrac{x-5y}{2}\)

４

⑴　[mathjax]\(-45ab\)
⑵　[mathjax]\(10xy\)
⑶　[mathjax]\(21x³\)
⑷　[mathjax]\(49a²\)
⑸　[mathjax]\(-4a²b\)
⑹　[mathjax]\(-\dfrac{9}{2}x²y\)
⑺　[mathjax]\(2y\)
⑻　[mathjax]\(x²\)
⑼　[mathjax]\(8x\)
⑽　[mathjax]\(-\dfrac{3}{4}a\)
⑾　[mathjax]\(\dfrac{x²}{2y}\)
⑿　[mathjax]\(-5a²\)
⒀　1

1章のまとめの問題　P.34〜37

　基本　

１

⑴　㋑，㋓
⑵　㋑，㋔，㋕

２

⑴　[mathjax]\(9a²+4a\)
⑵　[mathjax]\(-5x-y+5\)
⑶　[mathjax]\(7a-4b\)
⑷　[mathjax]\(-x+6y\)

３

⑴　[mathjax]\(-5x+y\)
⑵　[mathjax]\(2a-2b\)
⑶　[mathjax]\(-3x+19y\)
⑷　[mathjax]\(\dfrac{7x+5y}{12}\)
⑸　[mathjax]\(28xy\)
⑹　[mathjax]\(-6a³\)
⑺　[mathjax]\(81x²\)
⑻　[mathjax]\(-4a\)
⑼　[mathjax]\(14y\)
⑽　[mathjax]\(2x\)

４

⑴

[mathjax]\(\begin{eqnarray} & & 18xy \div 3x \times 2y\\ &=& 18xy \times \dfrac{1}{3x} \times 2y\\ &=& \dfrac{18xy \times 2y}{3x}\\ &=& 12y²\end{eqnarray}\)

⑵

[mathjax]\(\begin{eqnarray} & & 6ab\div\require{physics}\left(-\dfrac{2}{3}a\right)\\ &=& 6ab\times\require{physics}\left(-\dfrac{3}{2a}\right)\\ &=& -9b\end{eqnarray}\)

５

⑴　[mathjax]\(-60\)
⑵　17

６

差が3の3つの整数のうち，もっとも小さい整数を[mathjax]\(n\)とすると，差が3の3つの整数は，[mathjax]\(n\)，[mathjax]\(n+3\)，[mathjax]\(n+6\)と表される。
　それらの和は，

[mathjax]\(\begin{eqnarray} & & n+(n+3)+(n+6)\\ &=& 3n+9\\ &=& 3(n+3)\end{eqnarray}\)

[mathjax]\(n+3\)は整数だから，[mathjax]\(3(n+3)\)は3の倍数である。
したがって，差が3の3つの整数の和は3の倍数である。

７

⑴　[mathjax]\(y=\dfrac{10-3x}{2}\)
⑵　[mathjax]\(c=\dfrac{7a-4b}{3}\)

　応用　

１

⑴　[mathjax]\(-\dfrac{1}{6}x+\dfrac{3}{2}y\)
⑵　[mathjax]\(\dfrac{x-3y}{4}\)
⑶　[mathjax]\(\dfrac{2a³}{b}\)
⑷　[mathjax]\(-\dfrac{15x³}{y²}\)

２

[mathjax]\(3x²-4x-12\)

３

円柱Aの体積は，[mathjax]\(\pi r²h\)

円柱Bの体積は，

[mathjax]\(\begin{eqnarray} & & \pi \times (2r)² \times \dfrac{1}{2}h\\ &=&2 \pi r²h\end{eqnarray}\)

したがって，Bの体積はAの体積の2倍になる。

４

カレンダーの縦に並んだ3つの数のうち，中央の数を[mathjax]\(n\)とすると，縦に並んだ3 つの数は，[mathjax]\(n-7\)，[mathjax]\(n\)，[mathjax]\(n+7\)と表される。
　それらの和は，

[mathjax]\(\begin{eqnarray} & & (n-7)+n+(n+7)\\ &=& 3n\end{eqnarray}\)

[mathjax]\(n\)は中央の数だから，[mathjax]\(3n\) は中央の数の3倍である。したがって，カレンダーの縦に並んだ3つの数の和は，中央の数の3倍である。

　活用　

１

[mathjax]\(100a+10b+c\)，[mathjax]\(100c+10b+a\)，

[mathjax]\(\begin{eqnarray} & & (100a+10b+c)-(100c+10b+a) \\ &=& 99a-99c\\ &=& 99(a-c)\end{eqnarray}\) 　

[mathjax]\(a-c\)は整数だから，[mathjax]\(99(a-c)\) は99の倍数である。

２

㋑，㋔，㋕

３

正しい。
　4桁の自然数の千の位の数をa，百の位の数をb，十の位の数をc，一の位の数をdとすると，
　4桁の自然数は，

　　[mathjax]\(1000a+100b+10c+d\)

　千の位の数と一の位の数を入れかえてできる自然数は，

gkt-horizontal-line

<2年p.247>

[mathjax]\(1000d+100b+10c+a\)
と表される。この2 数の差は，

[mathjax]\(\begin{eqnarray}& &(1000a+100b+10c+d)-(1000d+100b+10c+a)\\ &=& 999a-999d\\ &=& 999(a-d)\end{eqnarray}\)

[mathjax]\(a-d\) は整数だから，[mathjax]\(999(a-d)\)は999の倍数である。
したがって，4 桁の自然数と，その千の位の数と一の位の数を入れかえてできる自然数との差は，999の倍数である。

赤道のまわりにロープを巻くと？　P.38

①　ロープの長さ…([mathjax]\(2\pi r+10\))m，
　　ロープでつくった円の半径…[mathjax]\(\left(r+\dfrac{5}{\pi}\right)\) m
②　[mathjax]\(\dfrac{5}{π}\)m，約[mathjax]\(1.59\)m
▷ [mathjax]\(6.28\) m

　2章　　　連立方程式　[解答]　

計算力を高めよう2　P.53

１

⑴　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=5\\ y=2\end{array} \right. \end{eqnarray}\)

⑵　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3\\ y=-1\end{array} \right. \end{eqnarray}\)

⑶　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=5\\ y=-1\end{array} \right. \end{eqnarray}\)

⑷　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=1\\ y=4\end{array} \right. \end{eqnarray}\)

⑸　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-1\\ y=-2\end{array} \right. \end{eqnarray}\)

⑹　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=0\\ y=-3\end{array} \right. \end{eqnarray}\)

⑺　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-3\\ y=1\end{array} \right. \end{eqnarray}\)

⑻　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-3\\ y=4\end{array} \right. \end{eqnarray}\)

⑼　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-6\\ y=-2\end{array} \right. \end{eqnarray}\)

２

⑴　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3\\ y=5\end{array} \right. \end{eqnarray}\)

⑵　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=\dfrac{3}{2}\\ y=\dfrac{1}{2}\end{array} \right. \end{eqnarray}\)

⑶　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=4\\ y=-1\end{array} \right. \end{eqnarray}\)

⑷　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=\dfrac{1}{3}\\ y=2\end{array} \right. \end{eqnarray}\)

⑸　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3\\ y=5\end{array} \right. \end{eqnarray}\)

⑹　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=4\\ y=3\end{array} \right. \end{eqnarray}\)

３

⑴　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-1\\ y=-2\end{array} \right. \end{eqnarray}\)

⑵　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=2\\ y=-4\end{array} \right. \end{eqnarray}\)

⑶　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=2\\ y=-5\end{array} \right. \end{eqnarray}\)

⑷　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-6\\ y=-5\end{array} \right. \end{eqnarray}\)

⑸　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3\\ y=-4\end{array} \right. \end{eqnarray}\)

⑹　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-\dfrac{4}{9}\\ y=\dfrac{7}{3}\end{array} \right. \end{eqnarray}\)

⑺　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-4\\ y=2\end{array} \right. \end{eqnarray}\)

⑻　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-5\\ y=3\end{array} \right. \end{eqnarray}\)

2章のまとめの問題　P.64〜66

　基本　

１
⑴　いえる

⑵　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=1\\ y=6\end{array} \right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=2\\ y=4\end{array} \right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3\\ y=2\end{array} \right. \end{eqnarray}\)

２

⑴　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-1\\ y=1\end{array} \right. \end{eqnarray}\)

⑵　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=2\\ y=3\end{array} \right. \end{eqnarray}\)

⑶　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=0\\ y=-3\end{array} \right. \end{eqnarray}\)

⑷　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=5\\ y=-5\end{array} \right. \end{eqnarray}\)

⑸　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3\\ y=1\end{array} \right. \end{eqnarray}\)

⑹　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-4\\ y=1\end{array} \right. \end{eqnarray}\)

３

大人1人の入館料をx円，中学生1人の入館料をy円とすると，

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x+3y=1550\\ 2x+5y=2750\end{array} \right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=500\\ y=350\end{array} \right. \end{eqnarray}\)

答　大人1人500円，中学生1人350円

４

長方形の縦をx cm，横をy cmとすると，

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} 2x+2y=28\\ 4x=3y\end{array} \right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=6\\ y=8\end{array} \right. \end{eqnarray}\)

答　縦6 cm，横8 cm

５

略

　応用　

１

⑴　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=10\\ y=2\end{array} \right. \end{eqnarray}\)

⑵　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=5\\ y=-1\end{array} \right. \end{eqnarray}\)

⑶　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=-6\\ y=7\end{array} \right. \end{eqnarray}\)

⑷　[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3\\ y=4\end{array} \right. \end{eqnarray}\)

２
[mathjax]\(a=-1\)，[mathjax]\(b=2\)

３

現在の父親の年齢をx歳，子どもの年齢をy歳とすると，

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=3y\\ x+15=2(y+15)\end{array} \right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{\begin{array}{l} x=45\\ y=15\end{array} \right. \end{eqnarray}\)

答　父親45歳，子ども15歳

gkt-horizontal-line

<2年p.248>

４
この町の昨年の男性の人口をx人，女性の人口をy人とすると，

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} -0.02x+0.04y=48\\ x+y=5373-48 \end{array}\right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=2750\\ y=2575 \end{array}\right. \end{eqnarray}\)

答　男性2750人，女性2575人

５
A町から峠までの道のりをxkm，峠からB町までの道のりをykmとすると，

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} \dfrac{x}{2}+\dfrac{y}{6}=1 \dfrac{40}{60}\\ \dfrac{x}{6}+\dfrac{y}{2}=1\end{array}\right.\end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=3\\ y=1 \end{array}\right. \end{eqnarray}\)

答　4km

６
もとの自然数の十の位の数をx，一の位の数をyとすると，

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x+y=12\\ 10y+x=(10x+y)+18\end{array}\right.\end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=5\\ y=7\end{array}\right.\end{eqnarray}\)

答　57

　活用　

１
⑴

⑵　㋒，㋔

⑶　[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} 2x+y=6\\ x+3y=23\end{array}\right.\end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=-1\\ y=8\end{array}\right.\end{eqnarray}\)

CTスキャンと数学　 P.67

①

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} A+B=6 \hspace{56pt}\cdots\cdots\text{①}\\ C+D=4\hspace{56pt}\cdots\cdots\text{②}\\ A+C=7\hspace{56pt}\cdots\cdots\text{③}\\ B+C=5\hspace{56pt}\cdots\cdots\text{④}\end{array}\right.\end{eqnarray}\)

[mathjax]\(\text{③}-\text{④}\)より，[mathjax]\(A-B=2\quad\cdots\cdots\text{⑤}\)

①と⑤を連立2元1次方程式として解くと，
[mathjax]\(A=4\)，[mathjax]\(B=2\)
[mathjax]\(B=2\)を④に代入すると，
[mathjax]\(2+C=5\)，[mathjax]\(C=3\)
[mathjax]\(C=3\)を②に代入すると，
[mathjax]\(3+D=4\)，[mathjax]\(D=1\)
答　[mathjax]\(A=4\)，[mathjax]\(B=2\)，[mathjax]\(C=3\)，[mathjax]\(D=1\)
② 略

　3章　　　1次関数　[解答]　

3章のまとめの問題　P.102〜104

　基本　

１

㋐，㋑，㋓

２

⑴　[mathjax]\(\dfrac{2}{3}\)
⑵　6
⑶　[mathjax]\(-3 \leqq y \lt 3\)

３

⑴　[mathjax]\(y=4x-3\)
⑵　[mathjax]\(y=2x+5\)
⑶　[mathjax]\(y=-\dfrac{1}{2}x+\dfrac{7}{2}\)

４

⑴　①　[mathjax]\(y=-2x+4\)
　　②　[mathjax]\(y=\dfrac{2}{3}x-3\)

⑵　[mathjax]\(\left (\dfrac{21}{8}\text{，}-\dfrac{5}{4}\right )\)

⑶

５

⑴　12 cm
⑵　24分後

　応用　

１

⑴　24 cm²
⑵　[mathjax]\(y=-\dfrac{1}{2}x+3\)
⑶　[mathjax]\(\dfrac{16}{9}\pi\) cm³

２

⑴　[mathjax]\(0 \leqq x \leqq 4\)のとき，[mathjax]\(y=\dfrac{3}{2}x\)
[mathjax]\(4 \leqq x \leqq 7\)のとき，[mathjax]\(y=-2x+14\)

⑵

gkt-horizontal-line

<2年p.249>

3章のまとめの問題　P.102〜104

　活用　

１

⑴　B印刷とC印刷のグラフの交点の座標，
　　50冊
⑵　25冊
⑶　A印刷…[mathjax]\(y=1000x\)
　　B印刷…[mathjax]\(y=600x+10000\)
　　C印刷…[mathjax]\(0 \lt x \leqq 60\)のとき，[mathjax]\(y=40000\)
⑷　3つのグラフの中から，[mathjax]\(x\)の値が46のときの[mathjax]\(y\)の値がもっとも小さいグラフで表された印刷所を選ぶ。

ダイヤグラム　P.105

❶　[mathjax]\(360 \div 1.5=240\)
　　答　240 km/h
❷　7時50分
❸　F駅で7時15分
❹　①の列車と②の列車がC駅で7時55分にすれちがうこと。
❺　駅で停車していること。

　4章　　　図形の性質の調べ方　[解答]　

トライ　P.123

[mathjax]\(\angle e+\angle c=\angle x\)
[mathjax]\(\angle b+\angle d=\angle y\)
[mathjax]\(\angle a+\angle x+\angle y=180^{\circ}\)より，
[mathjax]\(\angle a+(\angle e+\angle c)+(\angle b+\angle d)=180^{\circ}\)

[mathjax]\(\angle a+\angle c+\angle f+\angle g+\angle d=180^{\circ}\)
[mathjax]\(\angle b+\angle e=\angle f+\angle g\) より，
[mathjax]\(\angle a+\angle c+(\angle b+\angle e)+\angle d=180^{\circ}\)

トライ　P.135

①　直線ℓ上に適当な点Aをとり，Aを中心として，半径APの円をかき，直線ℓとの交点をBとする。
②　点P，Bを中心として，半径APの円をかき，Aと異なる交点をQとする。
③　P，Qを通る直線を引く。

(証明)
[mathjax]\(\triangle ABQ\)と[mathjax]\(\triangle QPA\)において，

[mathjax]\(\hspace{76pt}\begin{eqnarray}AB &=& QP &\hspace{10pt}\cdots\cdots\text{㋐}\\ BQ &=& PA &\cdots\cdots\text{㋑}\end{eqnarray}\)

共通な辺だから，[mathjax]\(\hspace{10pt} AQ=QA \quad\cdots\cdots\text{㋒}\)

㋐，㋑，㋒より，3 組の辺がそれぞれ等しいから，
[mathjax]\(\hspace{60pt}\triangle ABQ \equiv \triangle QPA\)
合同な図形の対応する角は等しいから，

[mathjax]\(\hspace{60pt}\angle QAB=\angle AQP\)
錯角が等しいから，[mathjax]\(AB/\!/PQ\)

トライ　P.139

[mathjax]\(\angle x=130^{\circ}\)

4章のまとめの問題　P.142〜144

　基本　

１
⑴　[mathjax]\(\angle x=50^{\circ}\)，[mathjax]\(\angle y=130^{\circ}\)
⑵　[mathjax]\(\angle x=55^{\circ}\)，[mathjax]\(\angle y=100^{\circ}\)
⑶　[mathjax]\(\angle x=70^{\circ}\)

２
⑴　[mathjax]\(\angle x=55^{\circ}\)
⑵　[mathjax]\(\angle x=45^{\circ}\)
⑶　[mathjax]\(\angle x=55^{\circ}\)

３
⑴　[mathjax]\(120^{\circ}\)
⑵　[mathjax]\(36^{\circ}\)
⑶　七角形

４
⑴　(仮定) [mathjax]\(AB=AD\)，[mathjax]\(\angle ABC=\angle ADE\)
　　(結論) [mathjax]\(BC=DE\)
⑵　[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle ADE\)
⑶　[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle ADE\)において，

仮定から，

[mathjax]\(\hspace{52pt}\begin{eqnarray}AB &=& AD & \quad\cdots\cdots\text{①}\\ \angle ABC &=& \angle ADE & \cdots\cdots\text{②}\end{eqnarray}\)

共通な角だから，[mathjax]\(\angle A=\angle A \hspace{24pt}\cdots\cdots\text{③}\)
①，②，③より，1組の辺とその両端の角がそれぞれ等しいから，
[mathjax]\(\hspace{52pt}\triangle ABC\equiv \triangle ADE\)
合同な図形の対応する辺は等しいから，
[mathjax]\(\hspace{68pt}BC＝DE\)

gkt-horizontal-line

<2年p.250>

　応用　

１
⑴　[mathjax]\(\angle x=105^{\circ}\)
⑵　[mathjax]\(\angle x=68^{\circ}\)
⑶　[mathjax]\(\angle x=90^{\circ}\)

２
[mathjax]\(\angle x=56^{\circ}\)

３ ❶　(仮定) [mathjax]\(AM=BM\)，[mathjax]\(PM \bot AB(ℓ \bot AB)\) 　　(結論)[mathjax]\(PA=PB\)

❷　[mathjax]\(PA=PB\)であることをいうためには，PAとPBが対応する辺になる[mathjax]\(\triangle PAM\)と[mathjax]\(\triangle PBM\)が合同であることを証明すればよい。
❸(証明)

　[mathjax]\(\triangle PAM\)と[mathjax]\(\triangle PBM\)において，
　仮定から，

[mathjax]\(\hspace{12pt}\begin{eqnarray}AM&=&BM\quad\cdots\cdots\text{①}\\ \angle PMA=\angle PMB &=&90^{\circ}\hspace{13pt}\cdots\cdots\text{②}\end{eqnarray}\)

共通な辺だから，[mathjax]\(PM=PM\quad\cdots\cdots\text{③}\)
①，②，③より，2組の辺とその間の角がそれぞれ等しいから，
[mathjax]\(\hspace{58pt}\triangle PAM \equiv \triangle PBM\)
　合同な図形の対応する辺は等しいから，
[mathjax]\(\hspace{78pt}PA=PB\)

４

[mathjax]\(\triangle AED\)と[mathjax]\(\triangle FEC\)において，
仮定から，[mathjax]\(\hspace{36pt}DE=CE\hspace{24pt}\cdots\cdots\text{①}\)
平行線の錯角は等しいから，
[mathjax]\(AD/\!/CF\)より，[mathjax]\(\angle ADE=\angle FCE\quad\cdots\cdots\text{②}\)
対頂角は等しいから，
[mathjax]\(\hspace{64pt}\angle AED=\angle FEC\quad\cdots\cdots\text{③}\)
①，②，③より，1組の辺とその両端の角がそれぞれ等しいから，

[mathjax]\(\hspace{62pt}\triangle AED \equiv \triangle FEC\)
合同な図形の対応する辺は等しいから，

[mathjax]\(\hspace{80pt}AE=FE\)

　活用　

１
⑴　[mathjax]\(\triangle ACB\)と[mathjax]\(\triangle DCE\)において，
仮定から，

[mathjax]\(\begin{eqnarray}AC &=& DC & \hspace{22pt}\cdots\cdots\text{①}\\ \angle A=\angle D &=& 90^{\circ}&\quad\cdots\cdots\text{②}\end{eqnarray}\)

対頂角は等しいから，
[mathjax]\(\hspace{12pt}\angle ACB=\angle DCE\quad\cdots\cdots\text{③}\)
①，②，③より，1 組の辺とその両端の角がそれぞれ等しいから，
[mathjax]\(\hspace{10pt}\triangle ACB\equiv \triangle DCE\)
合同な図形の対応する辺は等しいから，
[mathjax]\(\hspace{28pt}AB=DE\)

⑵　㋑

星形n角形　P.145〜146

①　略
②　[mathjax]\(360^{\circ}\)
③　[mathjax]\(540^{\circ}\)
④　表の左から，[mathjax] \(360，540，720，900，1080\)
⑤　略
⑥　略

　5章　　　三角形・四角形　[解答]　

トライ　P.156

略

5章のまとめの問題　P.175〜177

　基本　

１

⑴　頂角
⑵　1つの鋭角，他の1辺
⑶　中点
⑷　4つの角が等しい四角形

２

⑴　[mathjax]\(72^{\circ}\)
⑵　二等辺三角形
　(理由)[mathjax]\(\angle BCD=\angle BDC=72^{\circ}\)であるから。

３

⑴　[mathjax]\(\triangle ABE\)と[mathjax]\(\triangle CDF\)において，
仮定から，[mathjax]\(\angle AEB =\angle CFD=90^{\circ}\quad\cdots\cdots\text{①}\)
平行線の錯角は等しいから，
[mathjax]\(AB/\!/DC\) より，
[mathjax]\(\hspace{40pt}\angle ABE=\angle CDF\hspace{40pt}\cdots\cdots\text{②}\)
平行四辺形の対辺は等しいから，
[mathjax]\(\hspace{56pt}AB=CD\hspace{53pt}\cdots\cdots\text{③}\)
①，②，③より，直角三角形の斜辺と1つの鋭角がそれぞれ等しいから，
[mathjax]\(\hspace{40pt}\triangle ABE\equiv\triangle CDF\)

⑵　CF，錯角，FC，1組の対辺が平行で等しい

４

二等辺三角形

(証明)[mathjax]\(\triangle BMD\)と[mathjax]\(\triangle CME\)において，
仮定から，

[mathjax]\(\hspace{54pt}\begin{eqnarray}BM &=& CM & \hspace{52pt}\cdots\cdots\text{①}\\ MD &=& ME & \cdots\cdots\text{②}\end{eqnarray}\)

MD，MEはそれぞれ辺AB，ACの垂線であるから，
[mathjax]\(\hspace{32pt}\angle MDB=\angle MEC=90^{\circ}\quad\cdots\cdots\text{③}\)
①，②，③より，直角三角形の斜辺と他の1辺がそれぞれ等しいから，

[mathjax]\(\hspace{28pt}\triangle BMD\equiv \triangle CME\)
したがって，[mathjax]\(\angle B=\angle C\)
2つの角が等しいから，[mathjax]\(\triangle ABC\)は二等辺三角形である。

　応用　

１

長方形，正方形

gkt-horizontal-line

<2年p.251>

２

[mathjax]\(\triangle ABG\)と[mathjax]\(\triangle ECG\)において，
仮定から，[mathjax]\(\hspace{37pt} CD=CE\hspace{25pt}\cdots\cdots\text{①}\)
平行四辺形の対辺は等しいから，

[mathjax]\(\hspace{80pt} AB=CD\hspace{25pt}\cdots\cdots\text{②}\)
①，②より，

[mathjax]\(\hspace{80pt} AB=EC\hspace{25pt}\cdots \cdots\text{③}\)

平行線の錯角は等しいから，[mathjax]\(AB/\!/EF\)より，

[mathjax]\(\hspace{63pt}\angle ABG =\angle ECG\quad\cdots\cdots\text{④}\)
[mathjax]\(\hspace{63pt}\angle BAG=\angle CEG\quad\cdots\cdots\text{⑤}\)
③，④，⑤より，1 組の辺とその両端の角がそれぞれ等しいから，

[mathjax]\(\hspace{60pt}\triangle ABG \equiv \triangle ECG\)
したがって，[mathjax]\(\hspace{27pt} BG=CG\)
[mathjax]\(BC=2AB\)より，[mathjax]\(\ AB=BG\hspace{25pt}\cdots\cdots\text{⑥}\)
同様にして，[mathjax]\(\hspace{10pt}\triangle ABH \equiv \triangle DFH\)
したがって，[mathjax]\(\hspace{30pt}AB=AH\hspace{25pt}\cdots\cdots\text{⑦}\)
⑥，⑦より，[mathjax]\(\hspace{28pt}AH=BG\)
四角形ABGHは，[mathjax]\(AH/\!/BG\)，[mathjax]\(AH=BG\)

であるから，平行四辺形になる。
よって，[mathjax]\(\hspace{45pt}AB=HG\hspace{25pt}\cdots\cdots\text{⑧}\)
⑥，⑦，⑧より，[mathjax]\(AB=BG=GH=HA\)
4つの辺が等しいから，四角形ABGHはひし形である。

３

仮定より，[mathjax]\(AR/\!/QP\)，[mathjax]\(AQ/\!/RP\)だから，四角形ARPQは平行四辺形である。
平行四辺形の対辺は等しいから，
[mathjax]\(\hspace{85pt}PQ=RA\quad\cdots\cdots①\)
平行線の同位角は等しいから，
[mathjax]\(PR/\!/CA\)より，　[mathjax]\( \ \angle BPR=\angle C\quad\cdots\cdots②\)
また，[mathjax]\(\triangle ABC\)は二等辺三角形であるから，
[mathjax]\(\hspace{85pt}\angle B=\angle C \quad\dots\dots\text{③}\)
②，③から，[mathjax]\(\hspace{35pt}\angle B=\angle BPR\)
したがって，[mathjax]\(\hspace{35pt}BR=PR\quad\cdots\cdots\text{④}\)
①，④から，

[mathjax]\(\hspace{65pt}\begin{eqnarray}PQ+PR&=&RA+BR\\ &=&AB\end{eqnarray}\)

　活用　

１

⑴　㋐
⑵　[mathjax]\(\triangle FDC\)において，
仮定から，[mathjax]\(\hspace{20pt}\angle DCB=\angle DCF\quad\dots\dots\text{①}\)
平行線の錯角は等しいから，
[mathjax]\(DF/\!/BC\)より，[mathjax]\(\angle DCB=\angle FDC\quad\cdots\cdots\text{②}\)
①，②から，[mathjax]\(\hspace{15pt}\angle DCF=\angle FDC\)
2つの角が等しいから，[mathjax]\(\triangle FDC\)は二等辺三角形である。
したがって，[mathjax]\(\hspace{30pt}FC=FD\)
⑶　㋓

条件を変えて考えよう　P.178〜179
①　図のどの場合でも，[mathjax]\(AQ=PB\) が成り立つ。
②　略
③　

❶　[mathjax]\(AR=QB\)が成り立つ。
　(証明)[mathjax]\(\triangle ACR\)と[mathjax]\(\triangle QCB\)において，
　仮定から，　

[mathjax]\(\hspace{45pt}\begin{eqnarray}AC&=&QC\hspace{25pt}\cdots\cdots\text{①}\\ CR&=&CB\hspace{25pt}\cdots\cdots\text{②}\\ \angle ACR&=&\angle QCB\quad\cdots\cdots\text{③}\end{eqnarray}\)

①，②，③より，2組の辺とその間の角がそれぞれ等しいから，
[mathjax]\(\hspace{43pt}\triangle ACR\equiv \triangle QCB\)
　したがって，[mathjax]\(AR=QB\)

❷　[mathjax]\(PB=AQ\) が成り立つ。
　(証明)[mathjax]\(\triangle CPB\)と[mathjax]\(\triangle CAQ\)において，
　仮定から，

[mathjax]\(\hspace{56pt}\begin{eqnarray}CP&=&CA\hspace{20pt}\cdots\cdots\text{①}\\ CB&=&CQ\hspace{20pt}\cdots\cdots\text{②}\end{eqnarray}\)

　また，

[mathjax]\(\hspace{40pt}\begin{eqnarray} \angle PCB &=& \angle PCA+\angle ACB\\ &=& 60^{\circ}+\angle ACB\\ \angle ACQ &=& \angle BCQ+\angle ACB\\ &=& 60^{\circ}+\angle ACB\end{eqnarray}\)

よって，[mathjax]\(\angle PCB=\angle ACQ\quad\cdots\cdots\text{③}\)
①，②，③より，2組の辺とその間の角がそれぞれ等しいから，
[mathjax]\(\hspace{40pt}\triangle CPB \equiv \triangle CAQ\)
したがって，[mathjax]\(PB=AQ\)

　6章　　　確率　[解答]　

トライ　P.188

美月さんがグー，チョキ，パーを出すことは同様に確からしいとはいえないため，[mathjax]\(\\dfrac{1}{3}\)の確率でグーを出す考えは正しいとはいえない。

6章のまとめの問題　P.197〜199

　基本　

１

⑴　正しい
⑵　正しくない
⑶　正しくない
⑷　正しくない

２

⑴　[mathjax]\(\dfrac{7}{30}\)
⑵　[mathjax]\(\dfrac{1}{3}\)
⑶　[mathjax]\(\dfrac{2}{3}\)
⑷　[mathjax]\(\dfrac{1}{3}\)

３

⑴　[mathjax]\(\dfrac{1}{5}\)
⑵　[mathjax]\(\dfrac{5}{36}\)
⑶　[mathjax]\(\dfrac{1}{2}\)
⑷　[mathjax]\(\dfrac{1}{8}\)

４

[mathjax]\(\dfrac{3}{5}\)

gkt-horizontal-line

<2年p.252>

　応用　

１

全部で24通り，Aが第3走者になる場合は6通り

２

⑴　[mathjax]\(\dfrac{3}{10}\)
⑵　[mathjax]\(\dfrac{1}{10}\)

３

⑴　27通り
⑵　[mathjax]\(\dfrac{1}{3}\)
⑶　[mathjax]\(\dfrac{1}{9}\)

４

⑴　[mathjax]\(\dfrac{1}{3}\)
⑵　[mathjax]\(\dfrac{7}{36}\)

　活用　

１

⑴　[mathjax]\(\dfrac{1}{3}\)

⑵　(例)残りの2つの箱は当たりとはずれが1つずつで，司会者はそのうちのはずれの箱を開けるから，残った箱は必ず当たりである。

⑶　(例)「箱を変更する」と「箱を変更しない」でそれぞれ100回ずつ行ったときの結果を比較する。

どちらにかける？　P.200

①

目の和が9…[mathjax]\(\{1，2，6\}\)，[mathjax]\(\{1，3，5\}\)，[mathjax]\(\{1，4，4\}\)，[mathjax]\(\{2，2，5\}\)，[mathjax]\(\{2，3，4\}\)，[mathjax]\(\{3，3，3\}\)
目の和が10…[mathjax]\(\{1，3，6\}\)，[mathjax]\(\{1，4，5\}\)，[mathjax]\(\{2，2，6\}\)，[mathjax]\(\{2，3，5\}\)，[mathjax]\(\{2，4，4\}\)，[mathjax]\(\{3，3，4\}\)

②

目の和が9になる場合は25通り，10になる場合は27通りである。したがって，目の和が10になる確率の方が大きい。

　7章　　　データの分布　[解答]　

7章のまとめの問題　P.214〜215

　基本　

１

拓真さん
第1四分位数…6点，第2四分位数…[mathjax]\(6.5\)点，第3四分位数…7点，四分位範囲…1点
美月さん
第1四分位数…[mathjax]\(5.5\)点，第2四分位数…7点，第3四分位数…[mathjax]\(8.5\)点，四分位範囲…3点

箱もひげも美月さんの方が長いので，美月さんの方が広く分布していると考えられる。

　応用　

１

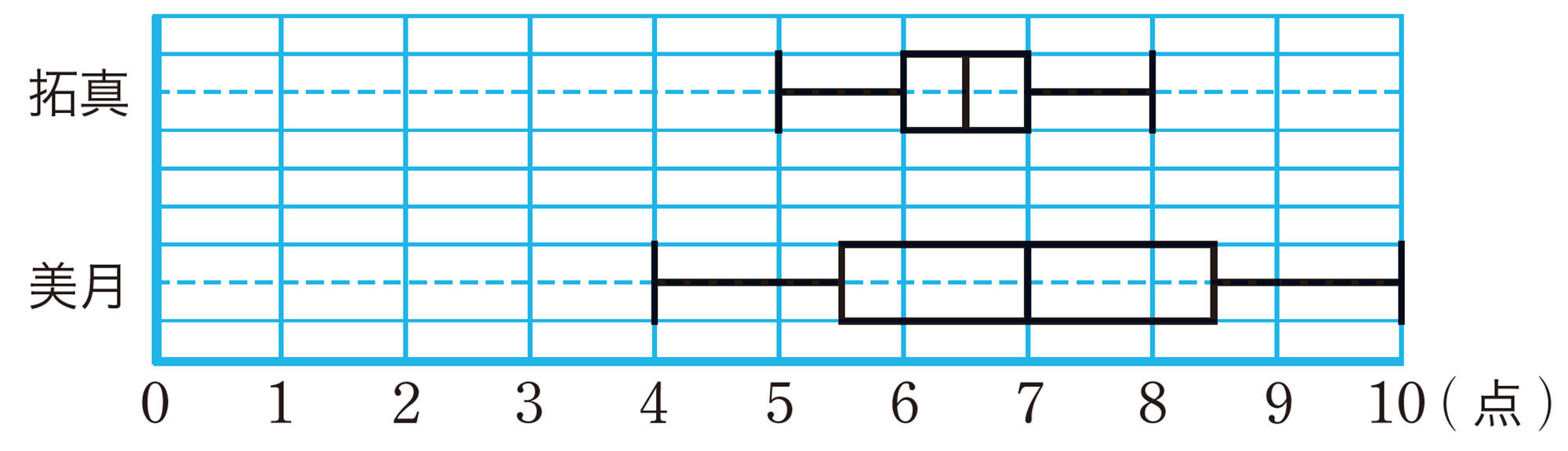
⑴

A組　中央値…22kg

　　　四分位範囲…3kg

　　　範囲…8kg

B組　中央値…22kg

　　　四分位範囲…3kg

　　　範囲…11kg

⑵　いえない。
(理由)値の小さい方から8番目の生徒の22kgが中央値になる。23kg以上の生徒は最大で9番目以降の7人になる。したがって，23kg以上の生徒が半分以上いるとはいえないから。

　活用　

１

(例)㋓
相手投手が昨年投げた球の割合が，ストレート58％，スライダー30％，カーブ6％，フォーク6％であるから，200球で考えると，それぞれ，
ストレート　[mathjax]\(200\times 0.58=116\)（球）
スライダー　[mathjax]\(200 \times 0.3=60\)（球）
カーブ　　　[mathjax]\(200 \times 0.06=12\)（球）
フォーク　　[mathjax]\(200 \times 0.06＝12\)（球）
である。したがって，ストレートは約100球，スライダーは約60球，カーブとフォークは約20球をそれぞれ練習すればよい。

コンピュータを用いた四分位数の求め方　P.216

①　略

　1年の計算・2年の復習　[解答]　

1年の計算　P.238

1
⑴　2
⑵　[mathjax] \(-11\)
⑶　8
⑷　[mathjax] \(-2.5\)
⑸　[mathjax]\(-\dfrac{5}{12}\)
⑹　[mathjax]\(\dfrac{3}{10}\)
⑺　[mathjax] \(-7\)
⑻　4
⑼　[mathjax] \(-1\)
⑽　1
⑾　[mathjax] \(-5\)

2
⑴　[mathjax] \(-21\)
⑵　45
⑶　0
⑷　[mathjax] \(-10\)
⑸　64
⑹　[mathjax] \(-64\)
⑺　7
⑻　0
⑼　[mathjax]\(-\dfrac{1}{10}\)
⑽　[mathjax]\(-\dfrac{2}{3}\)
⑾　15
⑿　[mathjax]\(-\dfrac{3}{4}\)
⒀　4
⒁　33
⒂　3

3
⑴　[mathjax]\(6x\)
⑵　[mathjax]\(-5x\)

gkt-horizontal-line

<2年p.253>

⑶　[mathjax]\(a-9\)
⑷　[mathjax]\(9x-3\)
⑸　[mathjax]\(-2x+7\)
⑹　[mathjax]\(-36x\)
⑺　[mathjax]\(10x\)
⑻　[mathjax]\(-3x\)
⑼　[mathjax]\(8a-16\)
⑽　[mathjax]\(-6x+30\)
⑾　[mathjax]\(3x-5\)
⑿　[mathjax]\(5x-20\)
⒀　[mathjax]\(x+1\)
⒁　[mathjax]\(\dfrac{7}{8}x-6\)

4
⑴ [mathjax]\(x=4\)

⑵ [mathjax]\(x=-9\)

⑶ [mathjax]\(x=9\)

⑷ [mathjax]\(x=-1\)

⑸ [mathjax]\(x=2\)

⑹ [mathjax]\(x=\dfrac{5}{2}\)

⑺ [mathjax]\(x=3\)

⑻ [mathjax]\(x=-2\)

⑼ [mathjax]\(x=-18\)

⑽ [mathjax]\(x=15\)

⑾ [mathjax]\(x=-6\)

⑿ [mathjax]\(x=7\)

⒀ [mathjax]\(x=2\)

⒁ [mathjax]\(x=8\)

　1章　　式の計算　P.239

⑴　[mathjax]\(4a-2b\)
⑵　[mathjax]\(-8x+2y+8\)
⑶　[mathjax]\(-2a+9b\)
⑷　[mathjax]\(-7x²+10x-9\)
⑸　[mathjax]\(x+7y-9\)
⑹　[mathjax]\(-6x²+x-16\)

⑴　[mathjax]\(15x-21y+12\)
⑵　[mathjax]\(-2x+4y\)
⑶　[mathjax]\(-5a+4b\)
⑷　[mathjax]\(14x-16y\)
⑸　[mathjax]\(-\dfrac{5}{6}x-\dfrac{25}{12}y\)
⑹　[mathjax]\(\dfrac{a-14b}{10}\)

⑴　[mathjax]\(-14ab\)
⑵　[mathjax]\(18x³\)
⑶　[mathjax]\(16a³\)
⑷　[mathjax]\(-6x²y\)
⑸　[mathjax]\(-4a\)
⑹　[mathjax]\(12x\)
⑺　[mathjax]\(\dfrac{2a²}{b}\)
⑻　[mathjax]\(-21x²y²\)
⑼　9
⑽　[mathjax]\(-5x³y⁶\)

⑴　[mathjax] \(-10\)
⑵　75
⑶　[mathjax] \(-2\)

連続する3つの偶数は，もっとも小さい数を [mathjax]\(2n\)とすると，[mathjax]\(2n\)，[mathjax]\(2n+2\)，[mathjax]\(2n+4\)と表される。この3つの偶数の和は，　

[mathjax]\(\begin{eqnarray}& & 2n+(2n+2)+(2n+4)\\ &=& 6n+6\\ &=& 6(n+1)\end{eqnarray}\)

[mathjax]\(n+1\) は整数だから，[mathjax]\(6(n+1)\)は6の倍数である。したがって，連続する3つの偶数の和は6の倍数になる。

[mathjax]\(h=\dfrac{3V}{a²}\)

　2章　　連立方程式　P.240

⑴

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=-2\\ y=7\end{array}\right. \end{eqnarray}\)

⑵

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=3\\ y=-2\end{array}\right. \end{eqnarray}\)

⑶

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=-4\\ y=1\end{array}\right. \end{eqnarray}\)

⑷

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=-3\\ y=6\end{array}\right. \end{eqnarray}\)

⑸　

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=5\\ y=3\end{array}\right. \end{eqnarray}\)

⑹

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=7\\ y=-1\end{array}\right. \end{eqnarray}\)

⑴

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=2\\ y=-3\end{array}\right. \end{eqnarray}\)

⑵

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=6\\ y=4\end{array}\right. \end{eqnarray}\)

⑶

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=-8\\ y=6\end{array}\right. \end{eqnarray}\)

⑷

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=-3\\ y=-7\end{array}\right. \end{eqnarray}\)

⑸

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=4\\ y=2\end{array}\right. \end{eqnarray}\)

⑹

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=6\\ y=-3\end{array}\right. \end{eqnarray}\)

3
[mathjax]\(a=-3\)，[mathjax]\(b=4\)

4
A管，B管から1分間に出る水の量を，それぞれxL，yLとすると，

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l}30x+60y=600\\ 60x+20y=600\end{array}\right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=8\\ y=6\end{array}\right . \end{eqnarray}\)

答　A管8L，B管6L

5
8％の食塩水をxg，15％の食塩水をyg混ぜるとすると，

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x+y=700\\ \dfrac{8}{100}x+\dfrac{15}{100}y=\dfrac{12}{100}\times 700\end{array}\right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=300\\ y=400\end{array}\right . \end{eqnarray}\)

答　8％の食塩水300g，15％の食塩水400g

6
A，Bの速さを，それぞれ時速[mathjax]\(x\) km，時速[mathjax]\(y\) kmとすると，

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} 0.5x+0.5y=8\\ x-y=8\end{array}\right. \end{eqnarray}\)

[mathjax]\(\begin{eqnarray} \left\{ \begin{array}{l} x=12\\ y=4\end{array}\right. \end{eqnarray}\)

答　Aの速さ…時速12 km，Bの速さ…時速4 km

　3章　　1次関数　P.241

[mathjax] \(-10\)

gkt-horizontal-line

<2年p.254>

⑴　[mathjax]\(y=-\dfrac{1}{2}x+7\)
⑵　[mathjax]\(y=-x-1\)
⑶　[mathjax]\(y=2x-10\)

⑴　[mathjax]\(ℓ\cdots y=-2x+4\)，[mathjax]\(m\cdots y=\dfrac{2}{3}x-4\)
⑵　[mathjax]\(P(3，-2)\)

⑴　[mathjax]\(y=-6x+54\)
⑵　2秒後と7秒後

⑴　15分後，3000m
⑵　自転車…分速200m，歩き…分速75m

　4章　　図形の性質の調べ方　P.242

1
⑴　[mathjax]\(\angle x=50^{\circ}\)，[mathjax]\(\angle y=70^{\circ}\)
⑵　[mathjax]\(\angle x=36^{\circ}\)
⑶　[mathjax]\(\angle x=44^{\circ}\)，[mathjax]\(\angle y=29^{\circ}\)

2
⑴　[mathjax]\(\angle x=43^{\circ}\)
⑵　[mathjax]\(\angle x=50^{\circ}\)
⑶　[mathjax]\(\angle x=98^{\circ}\)，[mathjax]\(\angle y=141^{\circ}\)

3
⑴　八角形
⑵　[mathjax]\(140^{\circ}\)
⑶　正十五角形

⑴

(仮定) [mathjax]\(AD/\!/BC\)，[mathjax]\(AO=CO\)
(結論) [mathjax]\(AE=CF\)

⑵

[mathjax]\(\triangle AOE\)と[mathjax]\(\triangle COF\)において，
仮定から，[mathjax]\(\hspace{33pt} AO=CO\hspace{25pt}\cdots \cdots①\)
対頂角は等しいから，

[mathjax]\(\hspace{62pt}\angle AOE=\angle COF\quad\cdots \cdots\text{②}\)
平行線の錯角は等しいから，
[mathjax]\(AD/\!/BC\)より，[mathjax]\(\angle EAO=\angle FCO\quad\cdots\cdots\text{③}\)
①，②，③より，1組の辺とその両端の角がそれぞれ等しいから，
[mathjax]\(\hspace{62pt}\triangle AOE\equiv \triangle COF\)
したがって，　[mathjax]\(\hspace{24pt} AE=CF\)

　5章　　三角形・四角形　P.243

⑴　[mathjax]\(\angle x=127^{\circ}\)
⑵　[mathjax]\(\angle x=70^{\circ}\)
⑶　[mathjax]\(\angle x=57^{\circ}\)

[mathjax]\(\triangle DBM\)と[mathjax]\(\triangle ECM\)において，
仮定から，

[mathjax]\( \begin{eqnarray}\angle BDM &=& \angle CEM=90^{\circ}\quad\cdots\cdots\text{①}\\ BM &=& CM\hspace{52pt}\cdots\cdots\text{②}\\ \angle BMD &=& \angle CME\hspace{37pt}\cdots\cdots\text{③}\end{eqnarray}\)

①，②，③より，直角三角形の斜辺と1つの鋭角がそれぞれ等しいから，
[mathjax]\(\hspace{40pt}\triangle DBM \equiv \triangle ECM\)
したがって，[mathjax]\(\hspace{12pt}\angle B=\angle C\)
2つの角が等しいから，[mathjax]\(\triangle ABC\)は二等辺三角形である。

四角形ABCDは平行四辺形であるから，

　[mathjax]\( AB/\!/DC\)，[mathjax]\(AB=DC\quad\dots\dots\text{①}\)
四角形ABEFにおいて，同様にして，

　[mathjax]\(AB/\!/FE\)，[mathjax]\(AB=FE\quad\cdots\cdots\text{②}\)
　①，②から，[mathjax]\(FE/\!/DC\)，[mathjax]\(FE=DC\)
1組の対辺が平行で等しいから，四角形FECDは平行四辺形である。

⑴　[mathjax]\(\triangle ADC\)と[mathjax]\(\triangle ABF\)において，
　四角形ABED，ACGFは正方形であるから，

[mathjax]\(\begin{eqnarray}\hspace{65pt}AD&=&AB\quad\cdots\cdots\text{①}\\ AC&=&AF\quad\cdots\cdots\text{②}\end{eqnarray}\)

また，

[mathjax]\(\hspace{40pt}\begin{eqnarray}\quad\angle DAC &=& 90^{\circ}+\angle BAC\\ \angle BAF &=& 90^{\circ}+ \angle BAC\end{eqnarray}\)

よって，[mathjax]\(\quad\angle DAC=\angle BAF\quad\cdots\cdots\text{③}\)
①，②，③より，2 組の辺とその間の角がそれぞれ等しいから，

[mathjax]\(\hspace{50pt}\triangle ADC \equiv \triangle ABF\)
したがって，[mathjax]\(\hspace{10pt}DC=BF\)

⑵　[mathjax]\(90^{\circ}\)

　6章　　確率　P.244

1
[mathjax]\(0.5\)

2
⑴　[mathjax]\(\dfrac{3}{10}\)

⑵　[mathjax]\(\dfrac{9}{20}\)

3
[mathjax]\(\dfrac{3}{5}\)

4
⑴　[mathjax]\(\dfrac{1}{6}\)

⑵　[mathjax]\(\dfrac{1}{4}\)

⑶　[mathjax]\(\dfrac{7}{18}\)

5
⑴　[mathjax]\(\dfrac{1}{5}\)

⑵　[mathjax]\(\dfrac{11}{15}\)

⑶　[mathjax]\(\dfrac{4}{5}\)

6
[mathjax]\(\dfrac{2}{5}\)

　7章　　データの分布　P.245

⑴　最小値…[mathjax]\(6.5\)秒，最大値…[mathjax]\(9.0\)秒
⑵　第1四分位数…[mathjax]\(7.2\)秒
　　第2四分位数…[mathjax]\(7.6\)秒
　　第3四分位数…[mathjax]\(7.8\)秒
⑶　[mathjax]\(0.6\)秒
⑷

⑴　㋑

⑵　㋒

⑶　㋐

gkt-horizontal-line

<2年p.⑧>

数学の力

数学の発想で見つけた，伝え方の法則

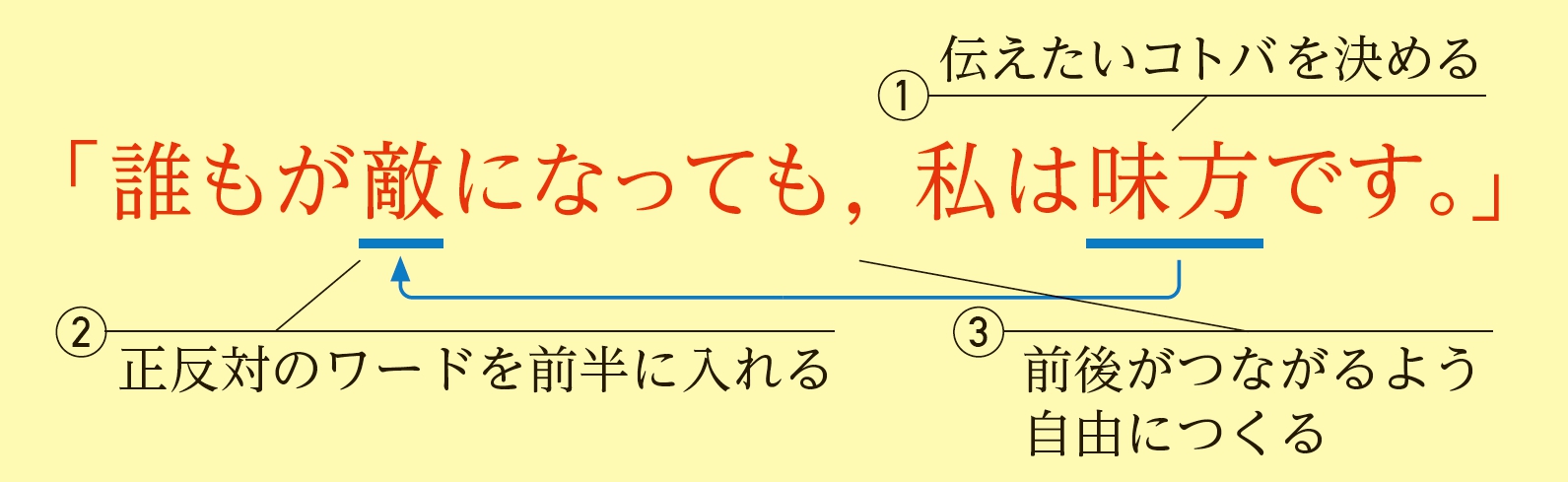
私は中学生の頃，とにかくコミュニケーションが苦手でした。書くことも話すことも，苦手でした。だから国語のテストはいつもダメダメ。一方で，数学は好きでした。
そんな私が，こともあろうについてしまった仕事は，「コピーライター」でした。コピーライターとは，テレビＣＭのコトバや，広告のコトバを書く人で，「人に伝える」ことを仕事にしている人です。もっとも私がついてはいけない仕事だったでしょう。そこからが大変でした。コトバを書いても書いても，ぜんぶボツ。そこで私についたニックネームは「もっともエコでないコピーライター」。つまり，書くだけ紙のムダ。という意味です。
でも，そんな私でも１つだけやっていたことがあります。それは，世の中にある「このコトバいいな」と思うものがあったら，それをノートに書いておくこと。そして，突然その日はやってきました。名言，といわれるコトバを並べて見ていたら「似ている！」と感じたのです。

考えるな，感じろ　［映画　燃えよドラゴン］

美女と野獣［西洋の童話］

天は人の上に人を造らず　人の下に人を造らず　［福沢諭吉］

どれも，正反対のコトバが入っている。「正反対のコトバを入れれば，名言がつくれるんだ！伝え方には法則がある！」そう気づいた瞬間です。まるで，右と左が線せん対たい称しょうな図形をつくるように，コトバをつくればいいのです。

コトバは，センスといわれがちです。そんなコトバから，数学的な発想をもとに，法則を見つけだしたのです。法則があれば，誰でもつくることができます。
コトバと数学は，無関係に見えます。でも，「物ごとの法則を見つける」という数学的な考え方が，コトバの法則発見につながったのです。数学を学ぶと，教科書の問題を解けるようになるだけではありません。毎日の生活で，
あなたの味方になってくれるでしょう。

数学の力

数学の発想で見つけた，伝え方の法則

＜ミライ教科書３学年分もくじ＞

＜スグラパ＞

＜ドリルまとめ＞