<2年p.238>
1年の計算
次の計算をしなさい。
1 次の計算をしなさい。
（正の数，負の数の加法・減法）
⑴ [mathjax]\((-8)+(+10)\)
⑵ [mathjax]\((-4)+(-7)\)
⑶ [mathjax]\((+5)-(-3)\)
⑷ [mathjax]\((-1.7)-(+0.8)\)
⑸ [mathjax]\(\require{physics} \left(-\dfrac{3}{4}\right)+\left(+\dfrac{1}{3}\right)\)
⑹ [mathjax]\(\require{physics} \left(-\dfrac{1}{5}\right)-\left(-\dfrac{1}{2}\right)\)
⑺ [mathjax]\(5-12\)
⑻ [mathjax]\(-4+9-1\)
⑼ [mathjax]\(-\dfrac{5}{7}-\dfrac{2}{7}\)
⑽ [mathjax]\(3-(-7)+(-9)\)
⑾ [mathjax]\(-5+(-2)-6-(-8)\)
2 次の計算をしなさい。
（正の数，負の数の乗法・除法，四則の混じった計算）
⑴ [mathjax]\((-3)\times (+7)\)
⑵ [mathjax]\((-5)\times (-9)\)
⑶ [mathjax]\((-2)\times 0\)
⑷ [mathjax]\(\require{physics} \left(-\dfrac{5}{3}\right)\times 6\)
⑸ [mathjax] \((-8)²\)
⑹ [mathjax] \(-8²\)
⑺ [mathjax]\((-42) \div (-6)\)
⑻ [mathjax]\(0\div (-5)\)
⑼ [mathjax]\(\require{physics} \left(-\dfrac{3}{5}\right)\div 6\)
⑽ [mathjax]\(\dfrac{4}{9}\div \require{physics} \left(-\dfrac{2}{3}\right)\)
⑾ [mathjax]\((-12)\div (-4)\times 5\)
⑿ [mathjax]\(\dfrac{5}{8} \div \require{physics} \left(-\dfrac{1}{4}\right)\times \dfrac{3}{10}\)
⒀ [mathjax]\(8+24 \div (-6)\)
⒁ [mathjax]\(-7 \times (-8-1)-30\)
⒂ [mathjax]\(48 \div (-4)²\)
3 次の計算をしなさい。
（文字式）
⑴ [mathjax]\(5x+x\)
⑵ [mathjax]\(3x-8x\)
⑶ [mathjax]\(-4a-2+5a-7\)
⑷ [mathjax]\((x+1)+(8x-4)\)
⑸ [mathjax]\((6x+5)-(8x-2)\)
⑹ [mathjax]\((-4)\times 9x\)
⑺ [mathjax]\(\dfrac{2}{3}x \times 15\)
⑻ [mathjax]\(18x \div (-6)\)
⑼ [mathjax]\(4(2a-4)\)
⑽ [mathjax]\((x-5)\times (-6)\)
⑾ [mathjax]\((9x-15)\div 3\)
⑿ [mathjax]\((4x-16)\div \dfrac{4}{5}\)
⒀ [mathjax]\(3(2x-3)-5(x-2)\)
⒁ [mathjax]\(\dfrac{1}{4}(-x-6)+\dfrac{3}{8}(3x-12)\)
4 次の方程式や比例式を解きなさい。
（1次方程式）
⑴ [mathjax]\(x-6=-2\)
⑵ [mathjax]\(-6x=54\)
⑶ [mathjax]\(\dfrac{8}{3}x=24\)
⑷ [mathjax]\(9x+5=-4\)
⑸ [mathjax]\(-2x=-14+5x\)
⑹ [mathjax]\(7x-15=x\)
⑺ [mathjax]\(8x-11=5x-2\)
⑻ [mathjax]\(-7x-6=2x+12\)
⑼ [mathjax]\(6(x+4)=4(x-3)\)
⑽ [mathjax]\(0.5x+2=0.7x-1\)
⑾ [mathjax]\(-\dfrac{2}{3}x-7=\dfrac{5}{6}x+2\)
⑿ [mathjax]\(\dfrac{x+3}{2}=\dfrac{4x-3}{5}\)
⒀ [mathjax]\(24:6=8:x\)
⒁ [mathjax]\(2:5=(x-2):(x+7)\)
<2年p.239>
2年の復習
1章 式の計算
1 次の計算をしなさい。
⑴ [mathjax]\(7a-8b-3a+6b\)
⑵ [mathjax]\(-2x+5y+8-6x-3y\)
⑶ [mathjax]\((6a+4b)+(-8a+5b)\)
⑷ [mathjax]\((-5x²+3x-8)-(2x²-7x+1)\)
⑸
⑹
2 次の計算をしなさい。
⑴ [mathjax]\(3(5x-7y+4)\)
⑵ [mathjax]\((8x-16y) \div (-4)\)
⑶ [mathjax]\(7(-3a+2b)+2(8a-5b)\)
⑷ [mathjax]\(4(6x-9y)-5(2x-4y)\)
⑸ [mathjax]\(\dfrac{1}{3}(2x-4y)+\dfrac{3}{4}(-2x-y)\)
⑹ [mathjax]\(\dfrac{3a-4b}{2}-\dfrac{7a-3b}{5}\)
3 次の計算をしなさい。
⑴ [mathjax]\(7a\times(-2b)\)
⑵ [mathjax]\(6x²\times 3x\)
⑶ [mathjax]\((-2a)²\times 4a\)
⑷ [mathjax]\(-\dfrac{3}{4}xy \times 8x\)
⑸ [mathjax]\(12ab \div (-3b)\)
⑹ [mathjax]\(15x² \div \dfrac{5}{4}x\)
⑺ [mathjax]\(3a² \times 4a \div 6ab\)
⑻ [mathjax]\(9xy² \div (-3xy) \times 7x²y\)
⑼ [mathjax]\((-2a)² \div \dfrac{4}{3}a²b³ \times 3b³\)
⑽ [mathjax]\((-8x⁵y⁴)\div \require{physics} \left(-\dfrac{2}{3}x³y\right)\div \require{physics} \left(-\dfrac{12}{5xy³}\right)\)
4 次の問いに答えなさい。
⑴ [mathjax]\(x=2\)，[mathjax]\(y=-3\)のとき，[mathjax]\(-4(x+3y)-2(2x-5y)\)の値を求めなさい。
⑵ [mathjax]\(a=-4\)，[mathjax]\(b=5\)のとき，[mathjax]\(3a²b \times ab \div (-4a²)\)の値を求めなさい。
⑶ [mathjax]\(a=\dfrac{1}{2}\)， [mathjax]\(b=-\dfrac{1}{6}\)のとき，[mathjax]\((-2a)³ \div a⁴b \times (-6a³b²)\)の値を求めなさい。
5 [mathjax] \(2\)，[mathjax] \(4\)，[mathjax] \(6\)のような連続する3つの偶数の和は6の倍数であることを，文字式を使って説明しなさい。
6 正四角錐の体積を求める式
[mathjax]\(V=\dfrac{1}{3}a²h\)
を，[mathjax]\(h\)について解きなさい。
<2年p.240>
2章 連立方程式
1 次の連立方程式を解きなさい。
2 次の連立方程式を解きなさい。
⑸ [mathjax]\(7x-3y=5x+y=22\)
⑹ [mathjax]\(6x+y=5x-y=4x+9\)
3 2組の連立方程式
が同じ解をもつとき，[mathjax]\(a\)，[mathjax]\(b\)の値を求めなさい。
4 容積が600Lの水そうに水を入れるのに，A管とB管を使います。A管で30分入れたあと，B管で60分入れると満水になります。また，A管で60分入れたあと，B管で20分入れても満水になります。A管，B管から1分間に何Lの水が出るかをそれぞれ求めなさい。
5 8％の食塩水と15％の食塩水を混ぜて，12％の食塩水700gをつくります。それぞれ何gずつ混ぜればよいかを求めなさい。
6 周囲が8 kmの池があります。Aは自転車で，Bは歩いて池を回ります。2人が同時に同じ地点を出発し，反対方向に池を回るとき，はじめて出会うまでに30分かかります。また，同じ方向に回るとき，1時間後にAはBにはじめて追いつきます。A，Bの速さを，それぞれ求めなさい。
<2年p.241>
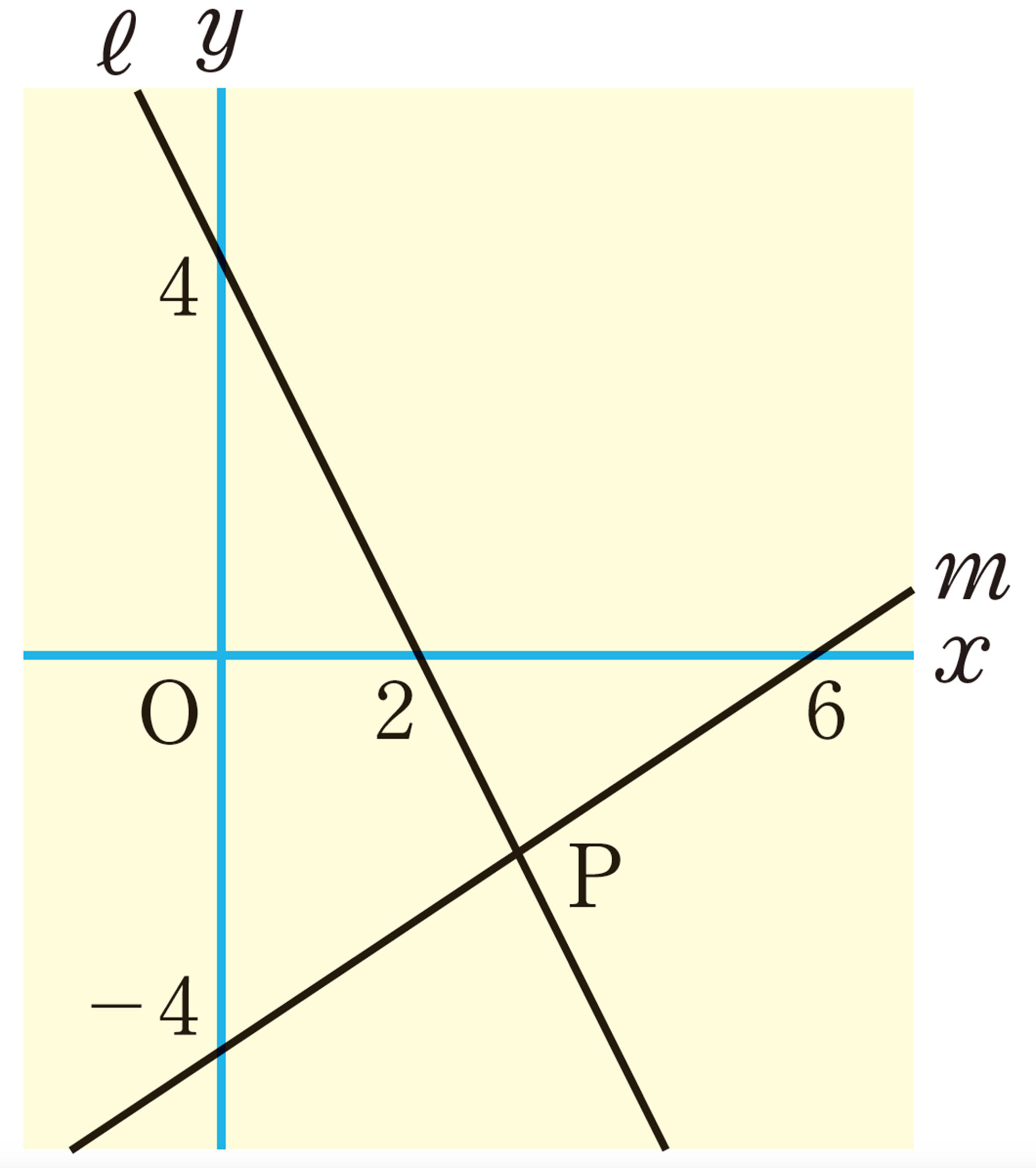
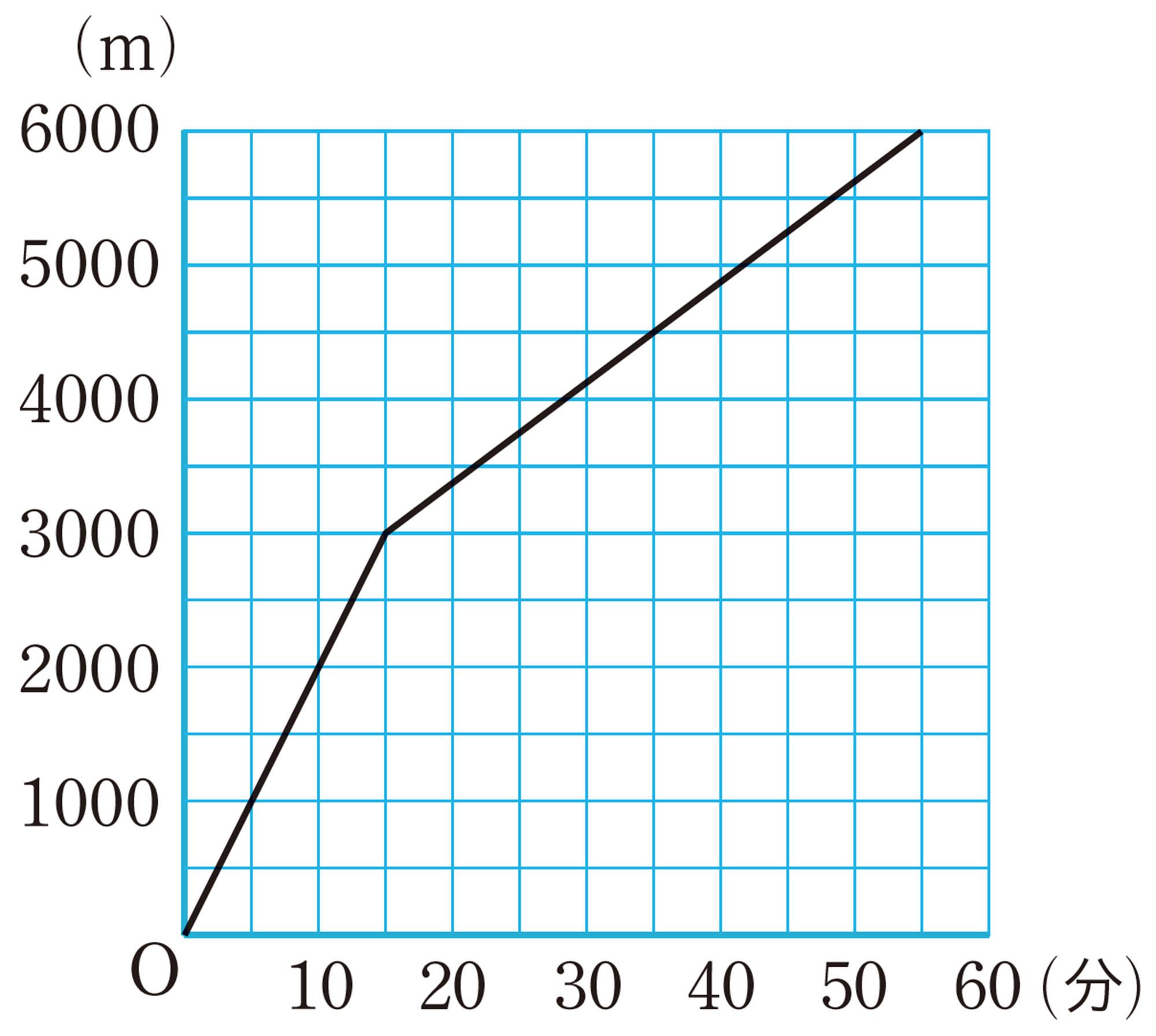
3章 1次関数
2 次の1次関数のグラフを，右の図にかき入れなさい。
⑴ [mathjax]\(y=-3x+4\)
⑵ [mathjax]\(y=\dfrac{3}{4}x-2\)
3 次の直線の式を求めなさい。
⑴ 点[mathjax]\((4，5)\)を通り，傾きが[mathjax]\(-\dfrac{1}{2}\)の直線
⑵ 2点[mathjax]\((-4，3)\)，[mathjax]\((1，-2)\)を通る直線
⑶ 点[mathjax]\((2，-6)\)を通り，直線[mathjax]\(y=2x-9\)に平行な直線
4 右の図について，次の問いに答えなさい。
⑴ 直線ℓ，mの式を求めなさい。
⑵ 直線ℓ，mの交点Pの座標を求めなさい。
5 右の図の正方形ABCDで，点PはAを出発して，秒速2 cmの速さで辺上をB，Cを通ってDまで動きます。点PがAを出発してから[mathjax]\(x\)秒後の[mathjax]\(\triangle PDA\)の面積をy cm²とするとき，次の問いに答えなさい。
⑴ [mathjax]\(6 \leqq x \leqq 9\)のとき，[mathjax]\(y\)を[mathjax]\(x\)の式で表しなさい。
⑵ [mathjax]\(\triangle PDA\)の面積が12 cm²になるのは，点PがAを出発してから何秒後か求めなさい。
6 真央さんは家から6000m離れた公園まで自転車で向かいましたが，途中で友だちに会い，そこから，いっしょに歩いて行きました。右の図は，真央さんが家を出てからの時間と家からの道のりの関係を，グラフに表したものです。次の問いに答えなさい。
⑴ 友だちに会ったのは，家を出てから何分後で，家から何mの地点ですか。
⑵ 真央さんが自転車で走っているときの速さと歩いているときの速さを求めなさい。
<2年p.242>
4章 図形の性質の調べ方
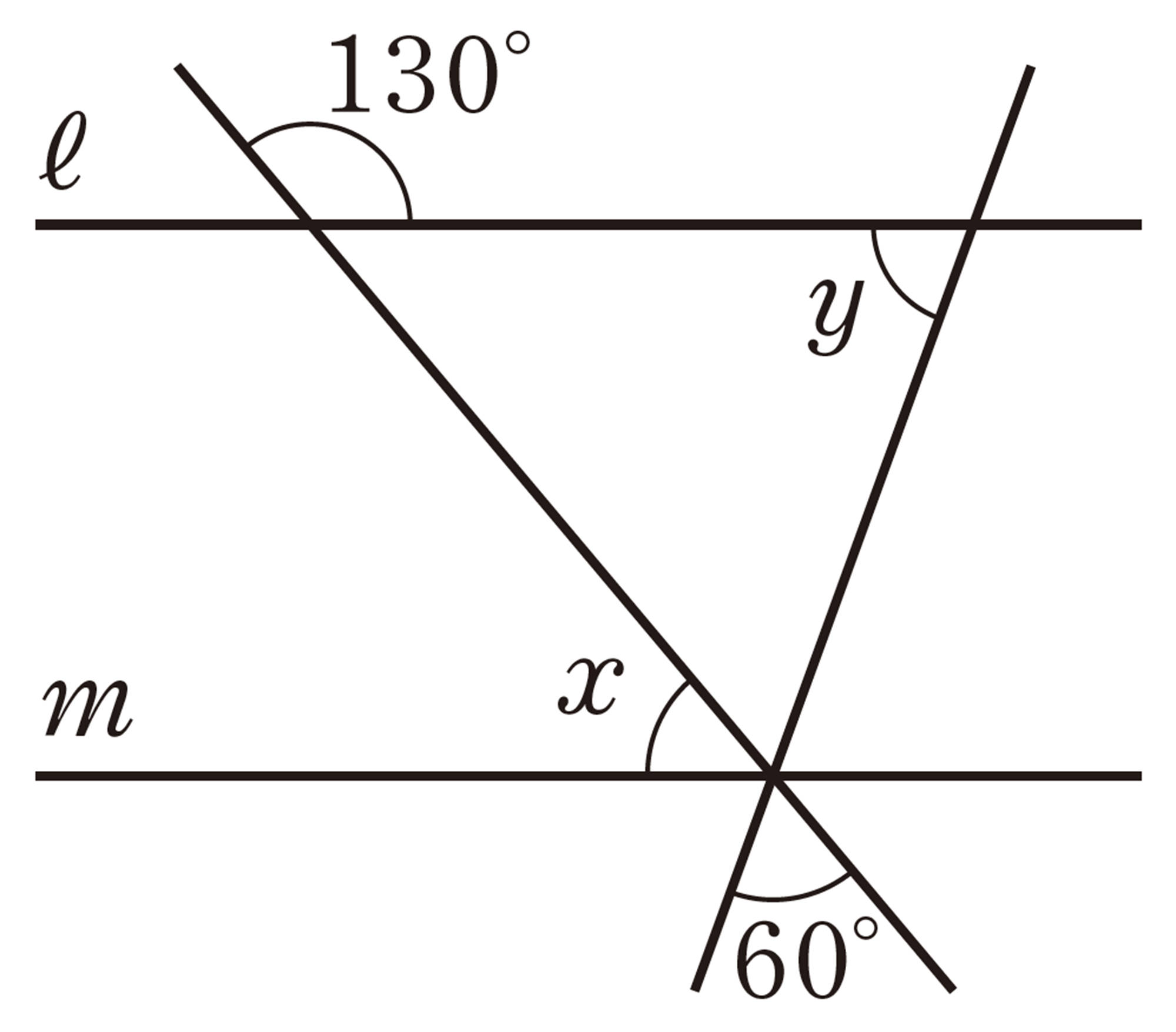
1 次の図で，[mathjax]\(ℓ/\!/m\)のとき，[mathjax]\(\angle x\)，[mathjax]\(\angle y\)の大きさを求めなさい。
⑴
⑵
⑶
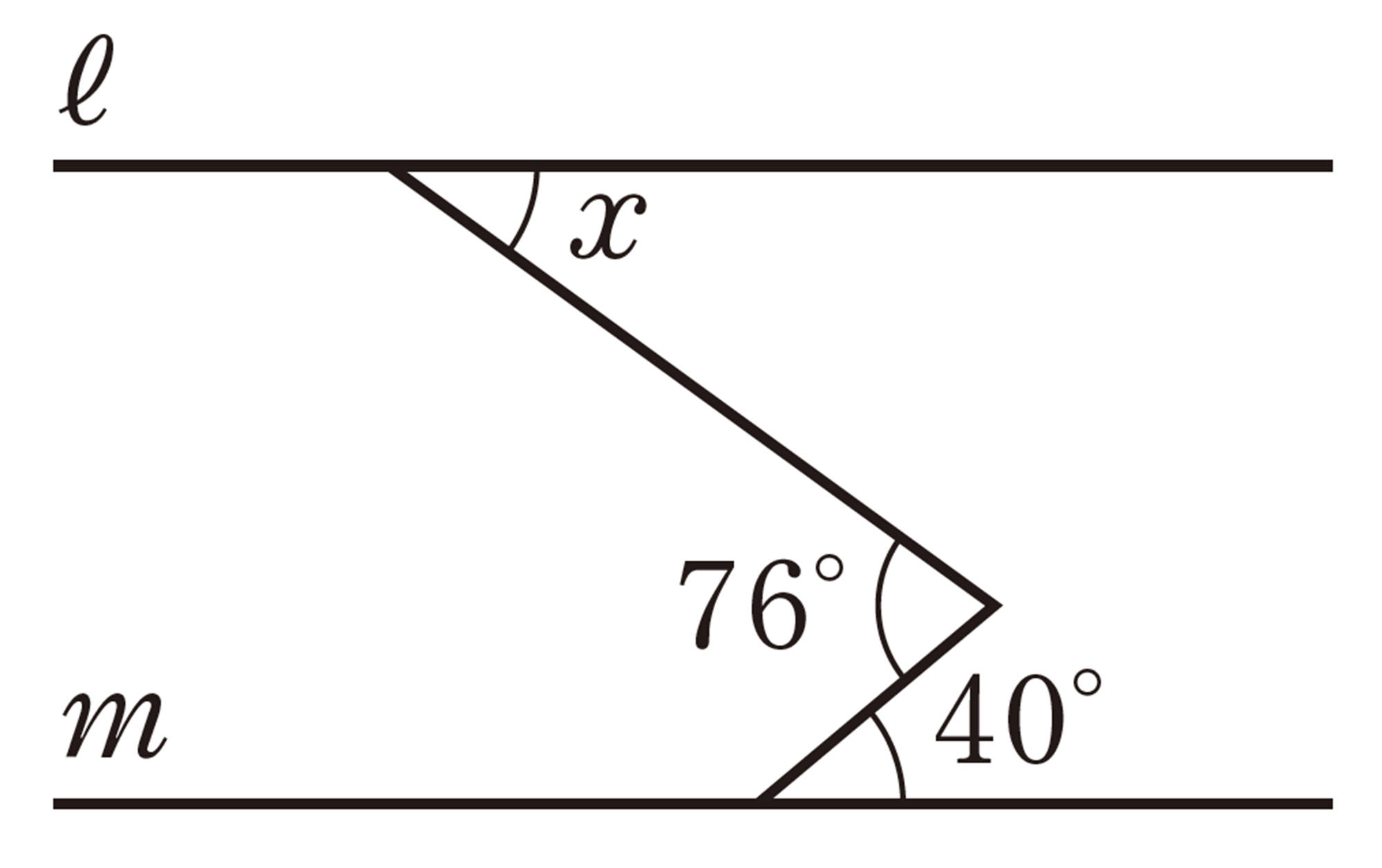
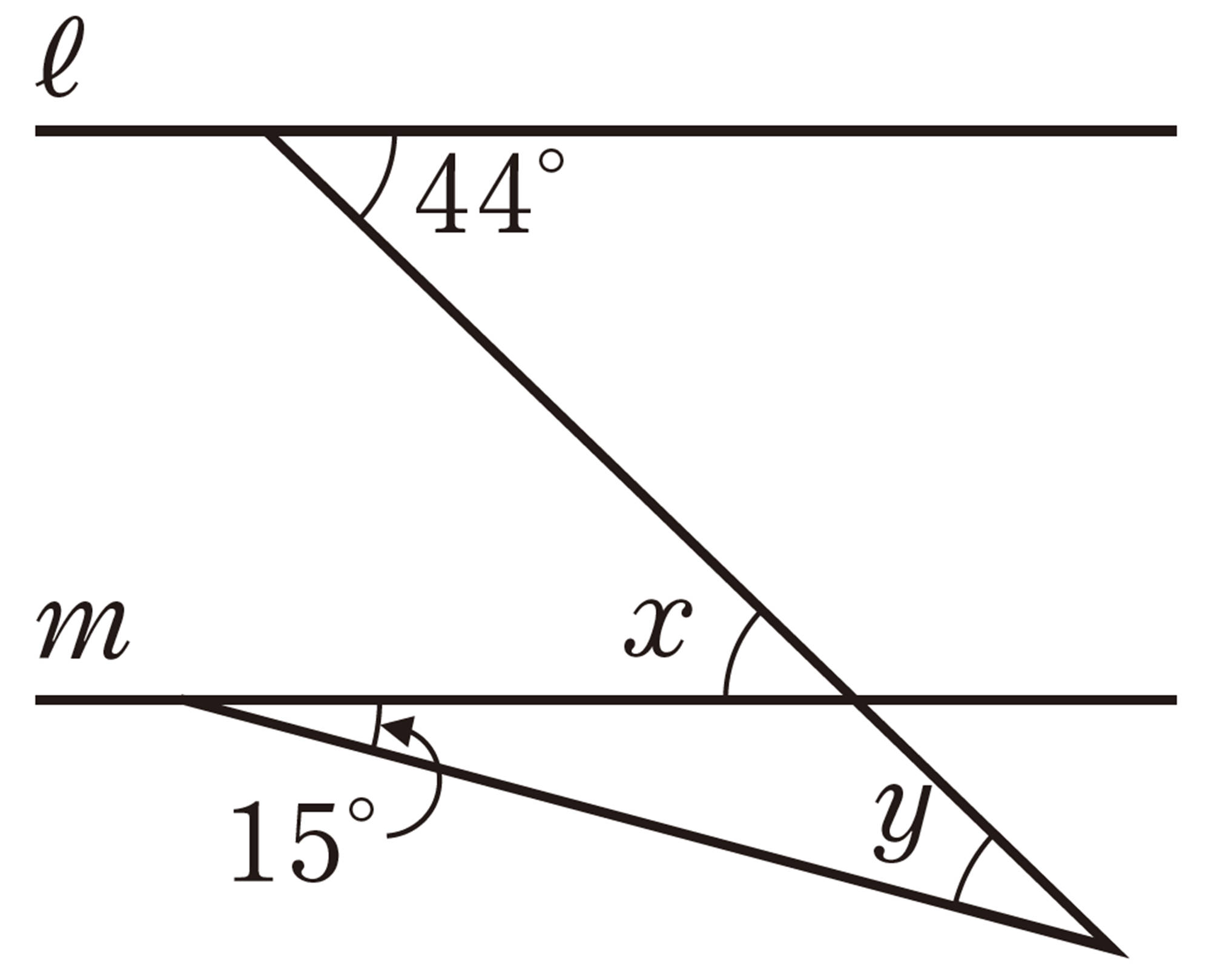
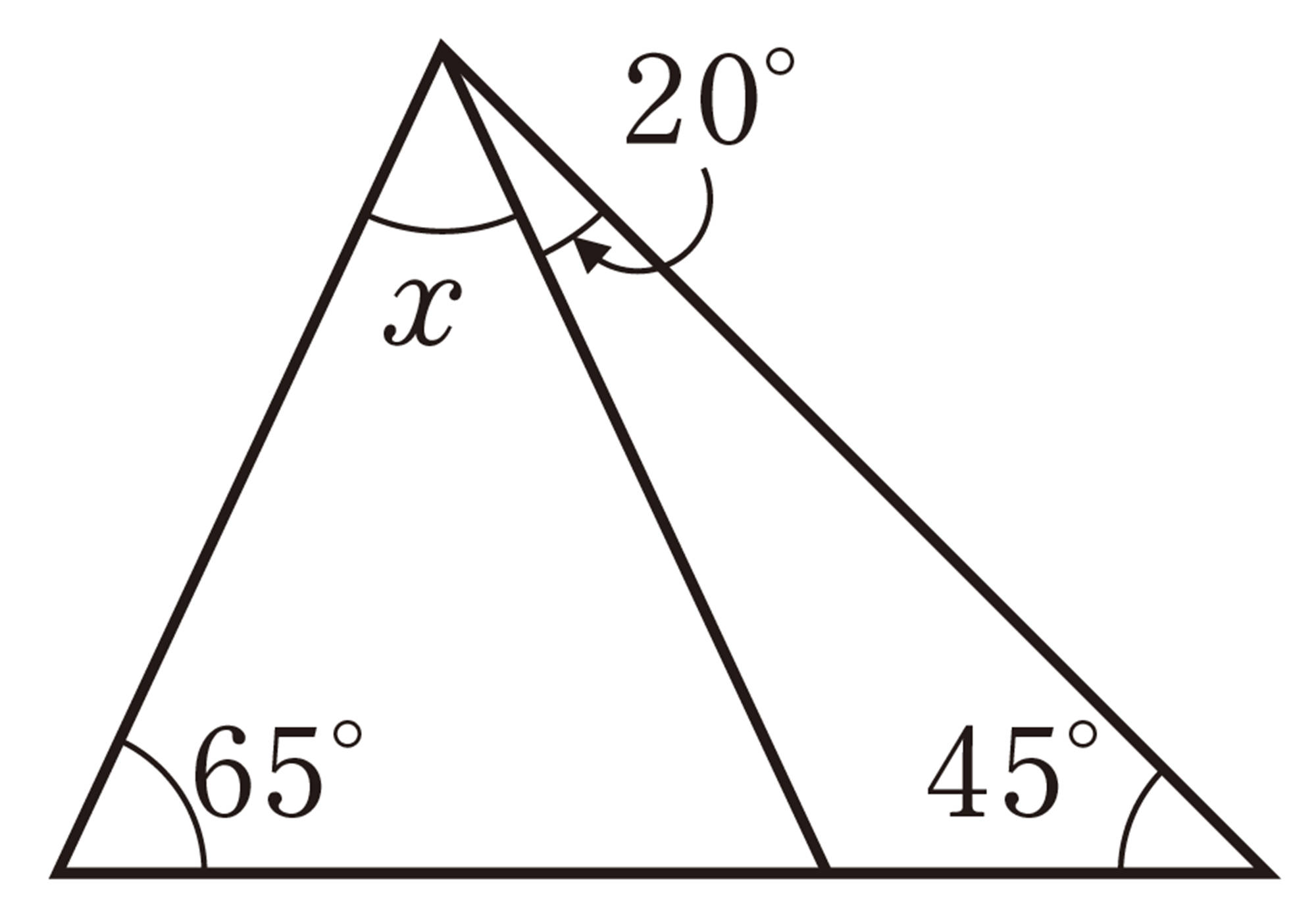
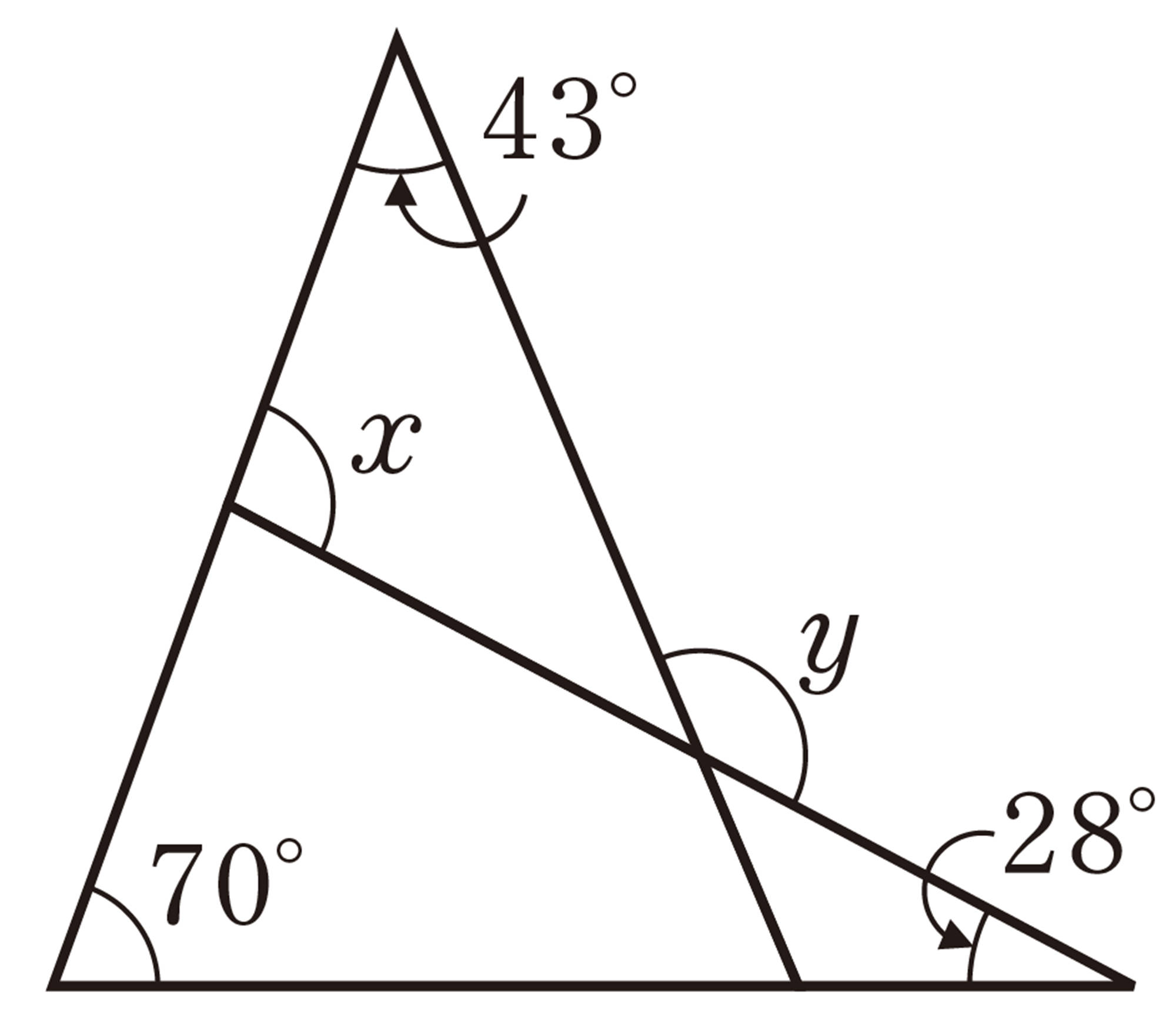
2 次の図で，[mathjax]\(\angle x\)，[mathjax]\(\angle y\)の大きさを求めなさい。
⑴
⑵
⑶
3 次の問いに答えなさい。
⑴ 内角の和が[mathjax]\(1080^{\circ}\)の多角形は何角形ですか。
⑵ 正九角形の1つの内角の大きさを求めなさい。
⑶ 1つの外角の大きさが[mathjax]\(24^{\circ}\)になるのは正何角形ですか。
4 右の図のように，[mathjax]\(AD/\!/BC\)である台形ABCDで，対角線ACの中点Oを通る直線と辺AD，BCとの交点をそれぞれ E，Fとすると，[mathjax]\(AE=CF\)となります。次の問いに答えなさい。
⑴ 仮定と結論をいいなさい。
⑵ このことを証明しなさい。
<2年p.243>
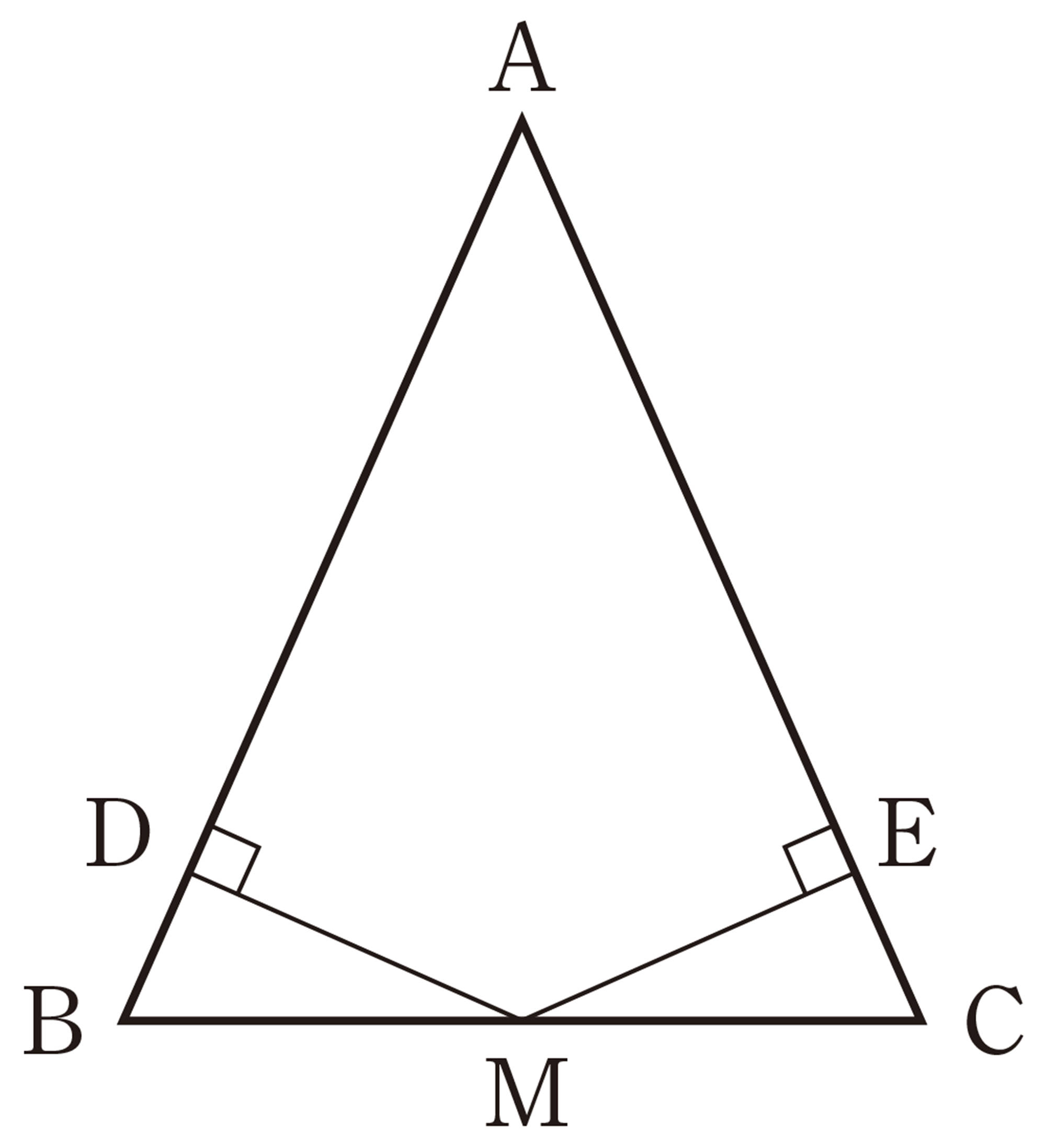
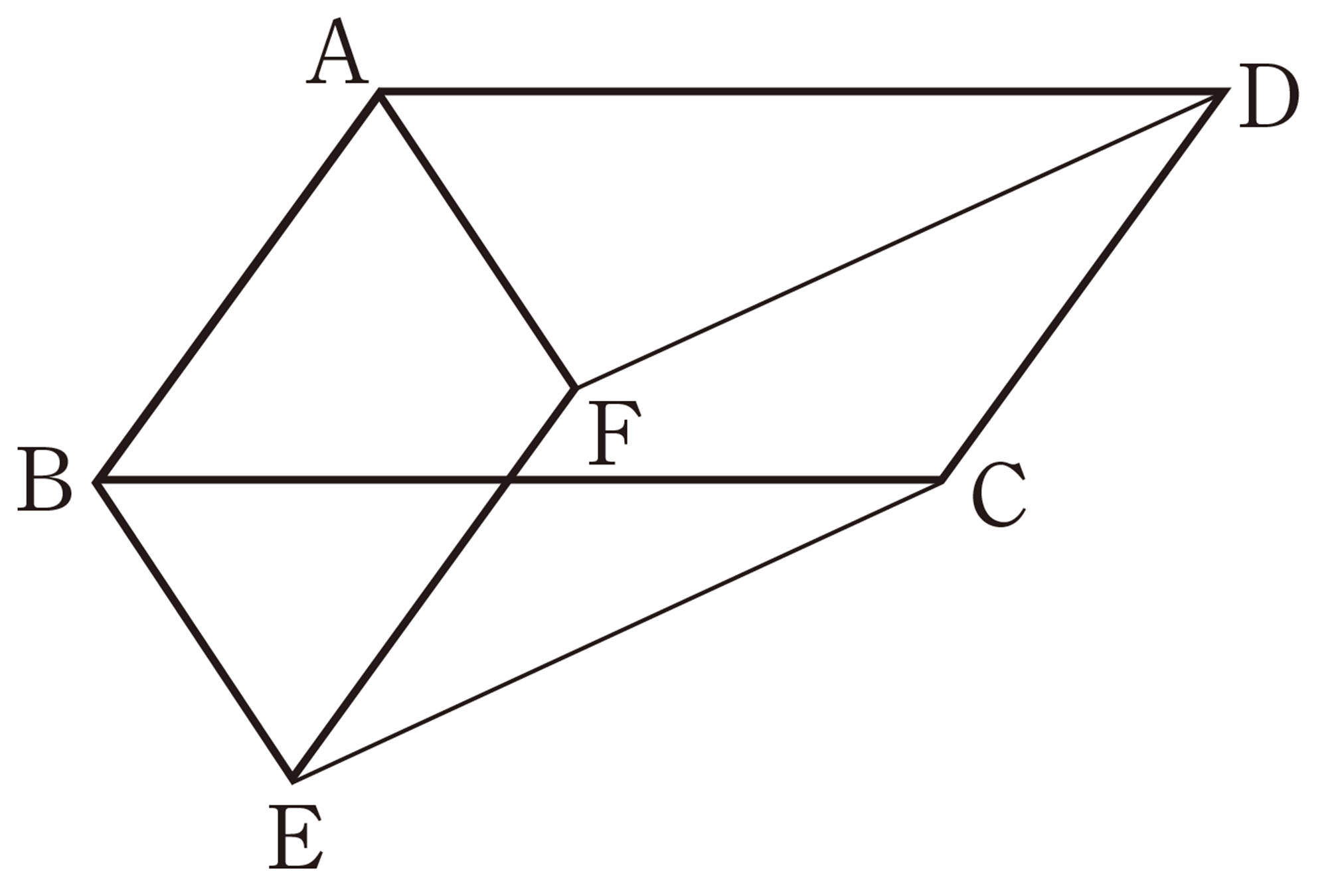
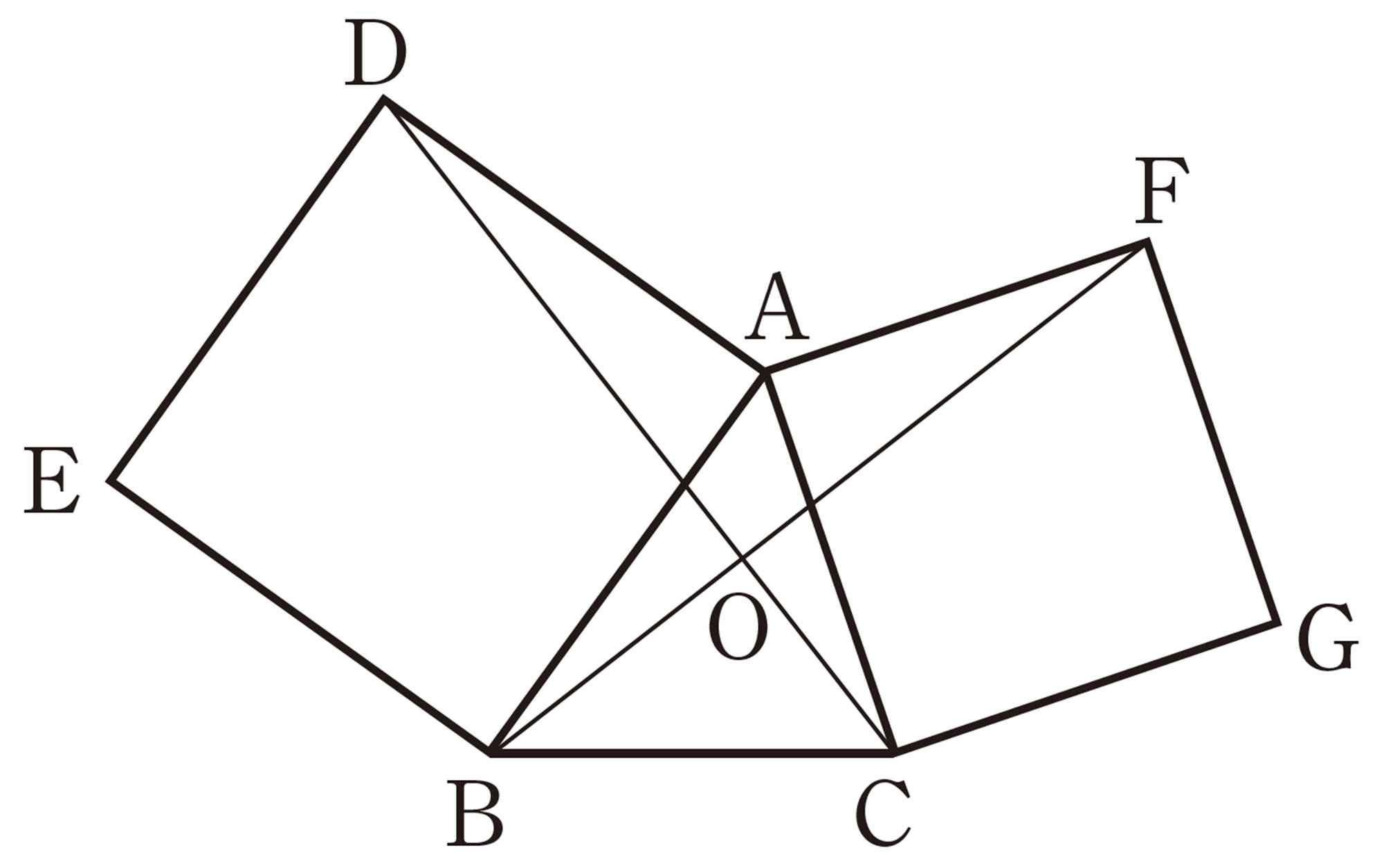
5章 三角形・四角形
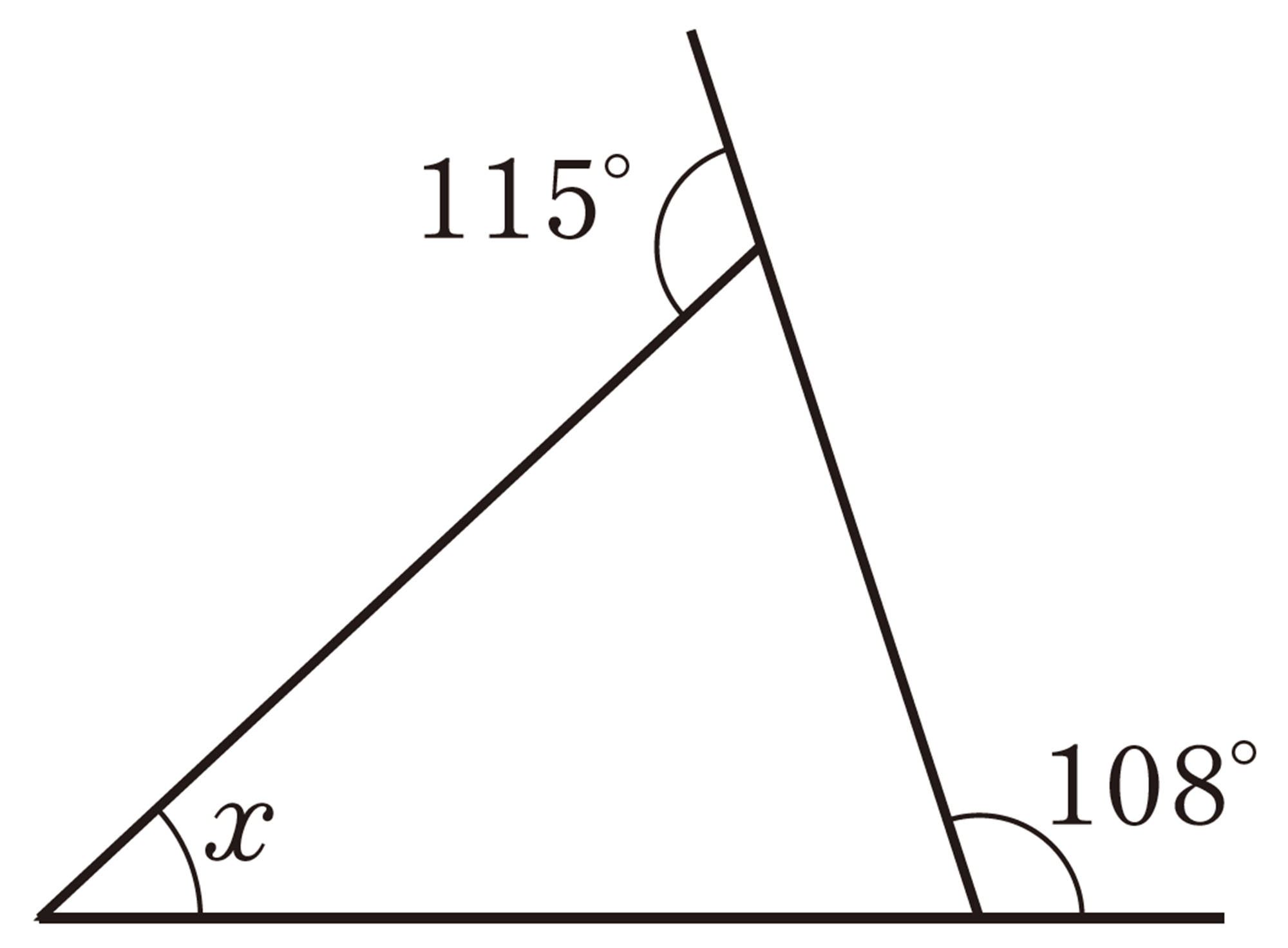
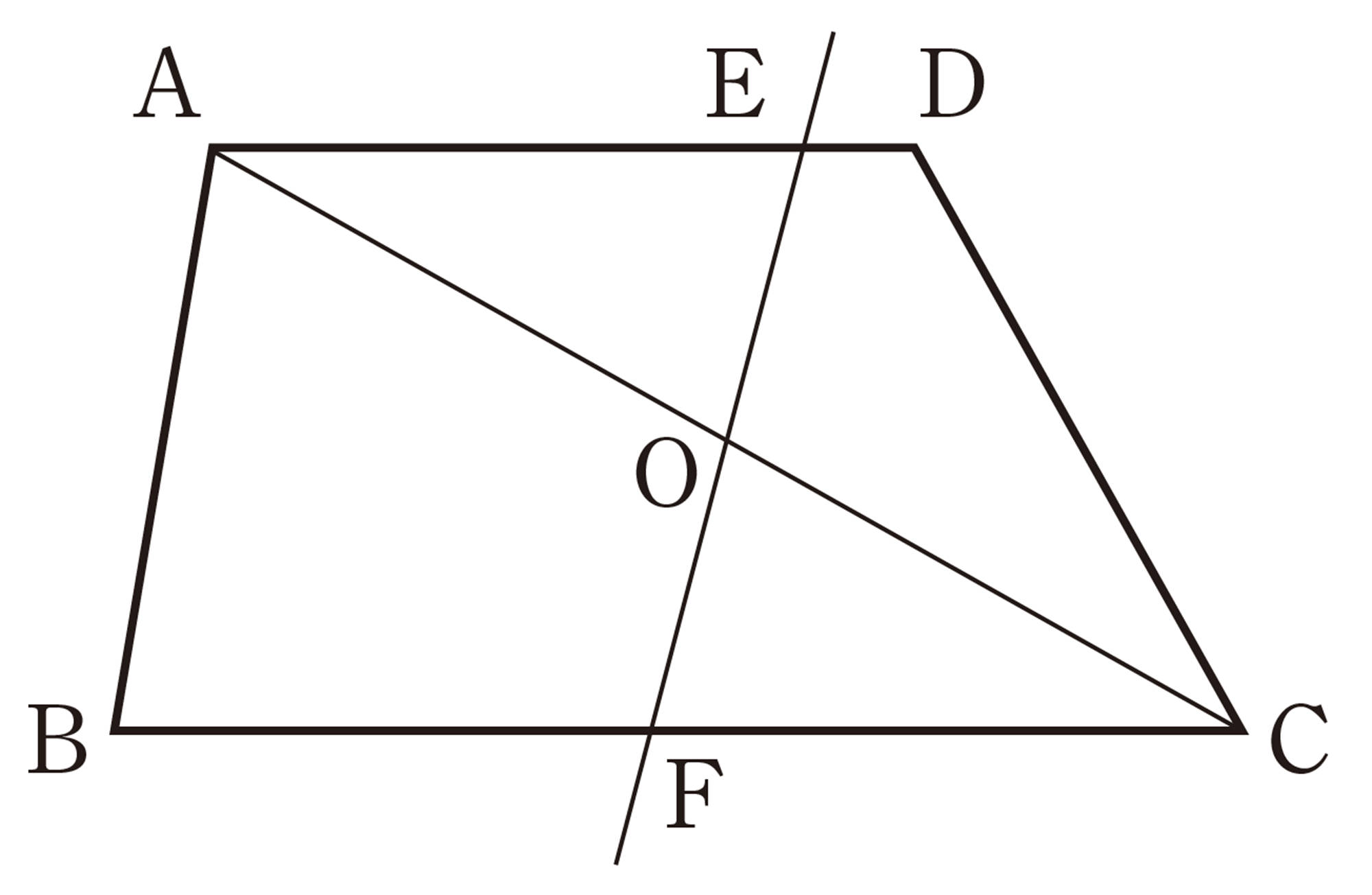
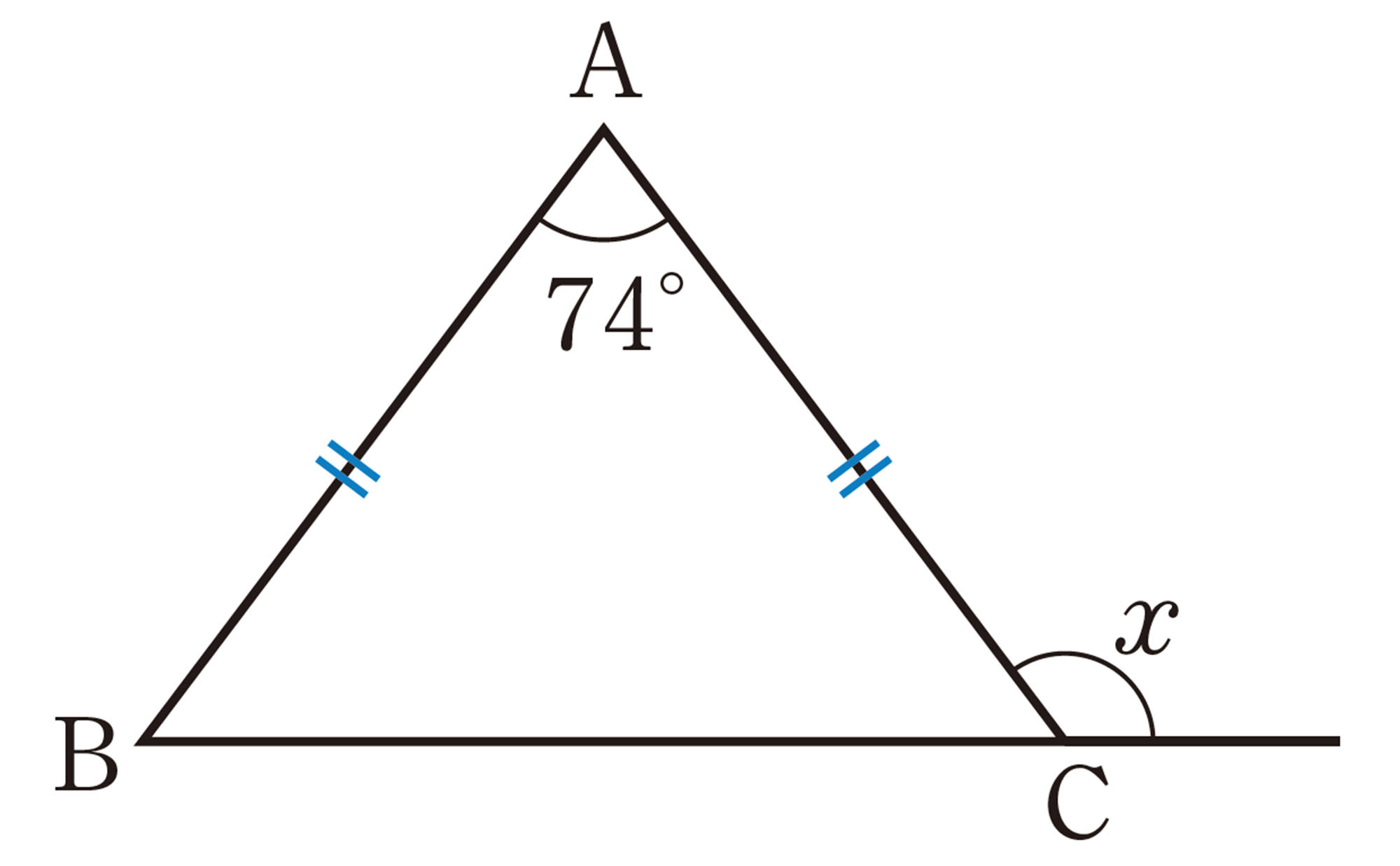
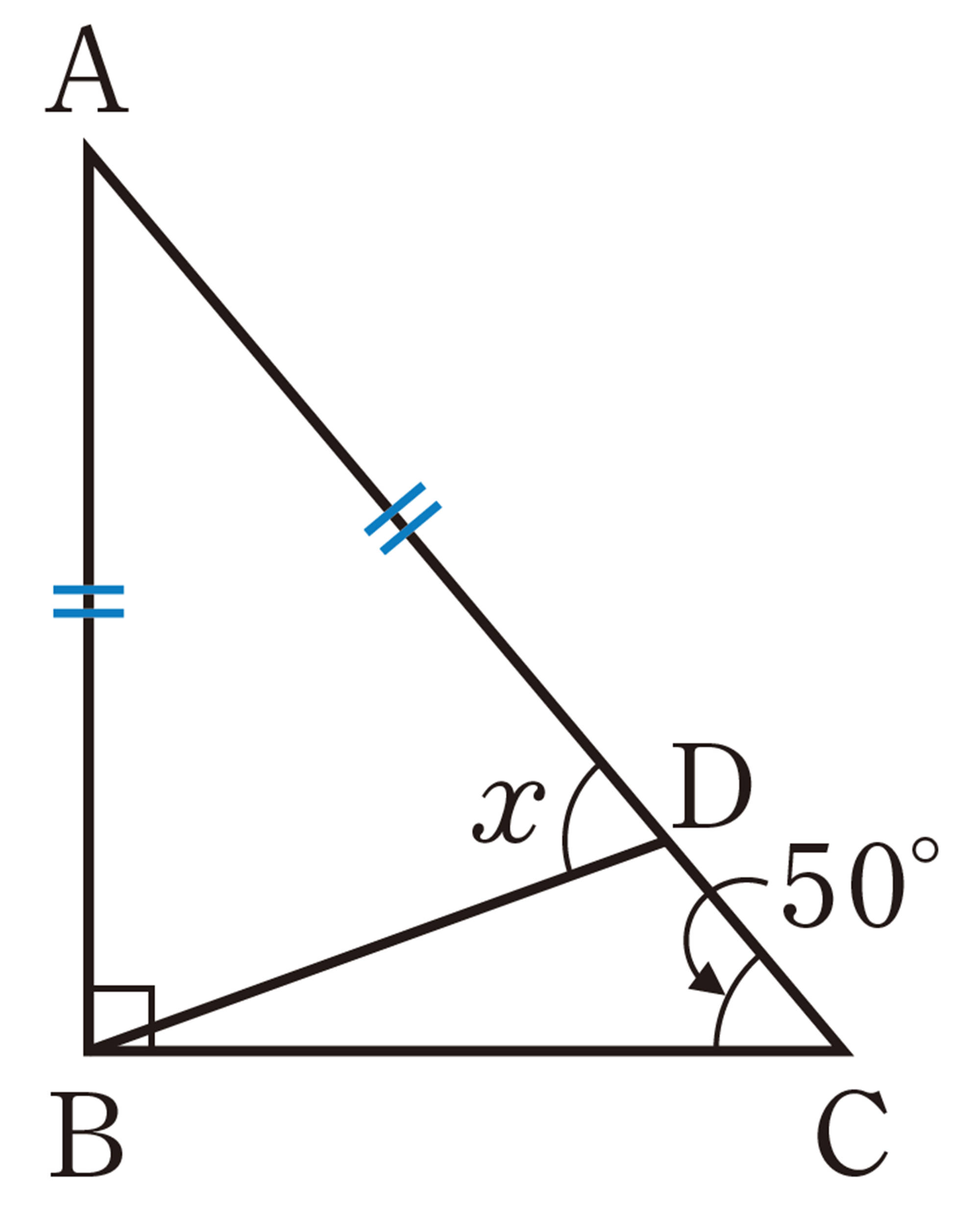
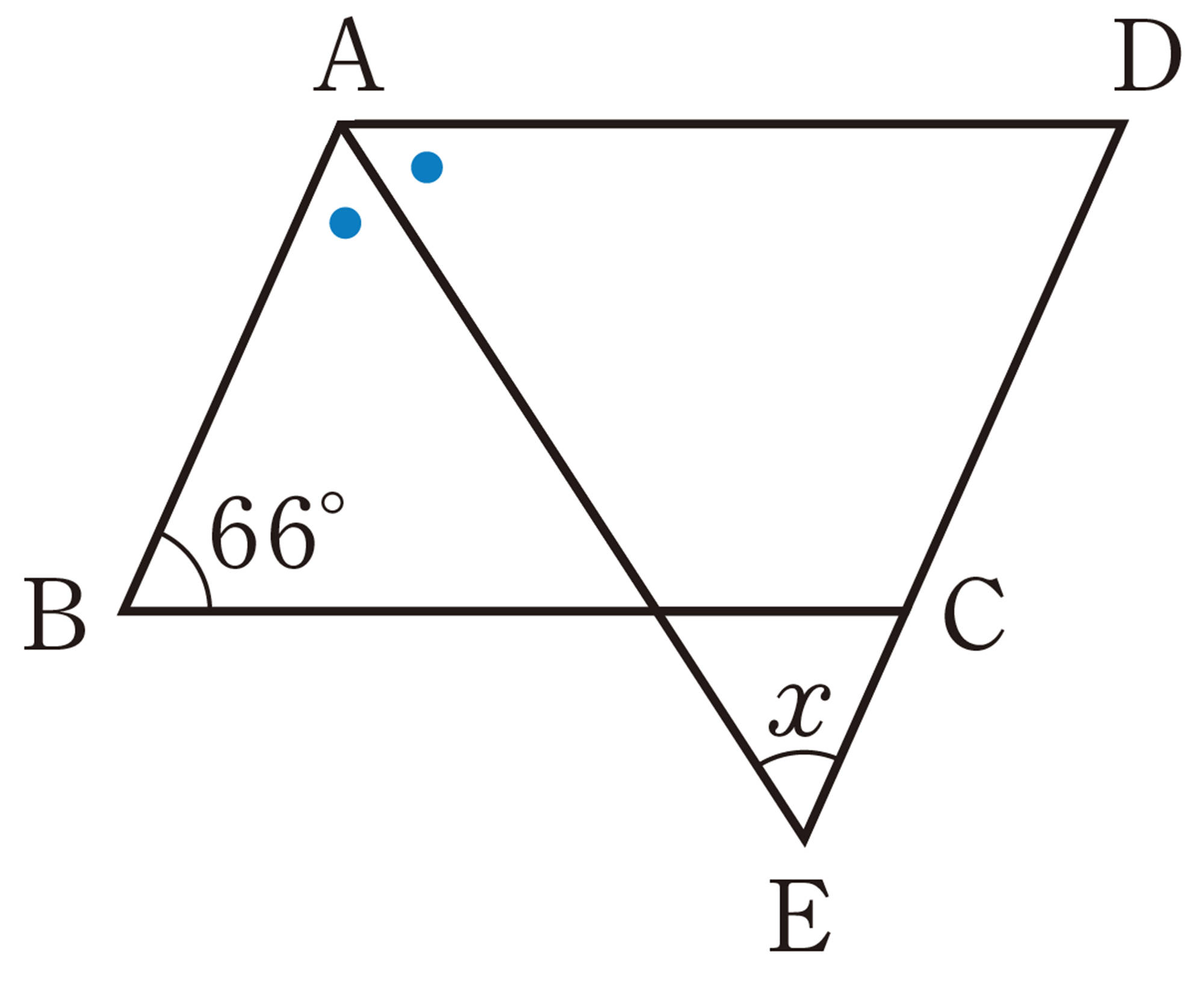
1 次の図で，[mathjax]\(\angle x\)の大きさを求めなさい。
⑴ [mathjax]\(AB=AC\)
⑵ [mathjax]\(AB=AD\)
⑶ 四角形ABCDは平行四辺形AEは[mathjax]\(\angle BAD\)の二等分線
2 右の図のように，[mathjax]\(\triangle ABC\)の辺BCの中点Mから辺AB，ACに垂線を引き，交点をそれぞれD，Eとします。このとき，[mathjax]\(\angle BMD=\angle CME\)ならば，[mathjax]\(\triangle ABC\)は二等辺三角形であることを証明しなさい。
3 右の図で，2つの四角形ABCD，ABEFはともに平行四辺形です。このとき，四角形FECDも平行四辺形であることを証明しなさい。
4 右の図のように，[mathjax]\(\triangle ABC\)の外側に，正方形ABEDと正方形ACGFをつくります。次の問いに答えなさい。
⑴ [mathjax]\(DC=BF\)であることを証明しなさい。
⑵ DCとBFの交点をOとするとき，[mathjax]\(\angle BOC\)の大きさを求めなさい。
<2年p.244>
6章 確率
1 1枚の硬貨を投げて実験を行ったところ，投げる回数が増えるにつれて表向きが出た相対度数が[mathjax]\(0.5\)に近づくようになりました。このとき，裏向きが出る確率を求めなさい。
2 1から20までの数字が1つずつ書かれた20枚のカードがあります。この20枚のカードをよく混ぜて1枚取り出すとき，書かれた数字について，次の確率を求めなさい。
⑴ 3の倍数である確率
⑵ 12以上である確率
3 1から5までの数字が1つずつ書かれた5枚のカードがあります。この5枚のカードをよく混ぜて，1枚ずつ続けて2枚取り出し，取り出した順に左から並べて2桁の整数をつくるとき，それが奇数になる確率を求めなさい。
4 大小2つのさいころを投げるとき，次の確率を求めなさい。
⑴ 出る目が同じ数になる確率
⑵ 出る目の積が奇数になる確率
⑶ 大きいさいころの目をa，小さいさいころの目をbとするとき，[mathjax]\(\dfrac{a}{b}\)が整数になる確率
5 赤玉が3個，白玉が2個，青玉が1個入っている袋の中から同時に2個の玉を取り出すとき，次の確率を求めなさい。
⑴ 2個とも赤玉である確率
⑵ ちがう色の玉が出る確率
⑶ 少なくとも1個は赤玉である確率
6 右の図のように，番号が書かれたいすが一列に並んでいます。いま，1から5までの数字が1つずつ書かれた5枚のカードをよく混ぜて，まず美月さんが1枚引き，続いて拓真さんが1枚引いて，そのカードの数字と同じ番号のいすにすわることにします。このとき，美月さんと拓真さんがとなりどうしになる確率を求めなさい。
<2年p.245>
7章 データの活用
1 男子15人の50m走の記録を調べたところ，次のようになりました。このデータについて，下の問いに答えなさい。
（単位：秒）
⑴ 最小値，最大値を求めなさい。
⑵ 四分位数を求めなさい。
⑶ 四分位範囲を求めなさい。
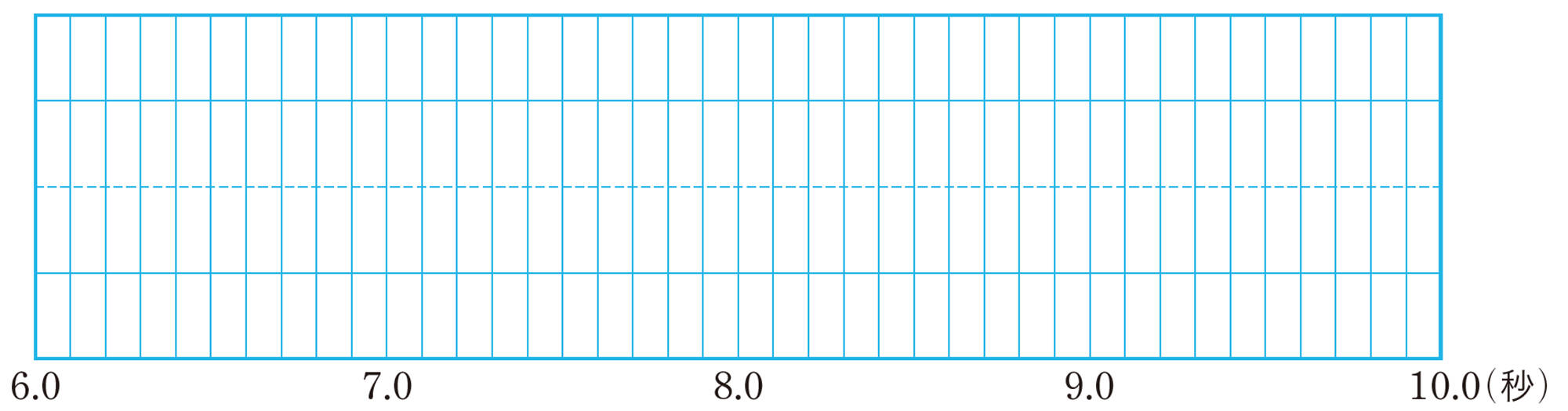
⑷ 次の図に，箱ひげ図で表しなさい。
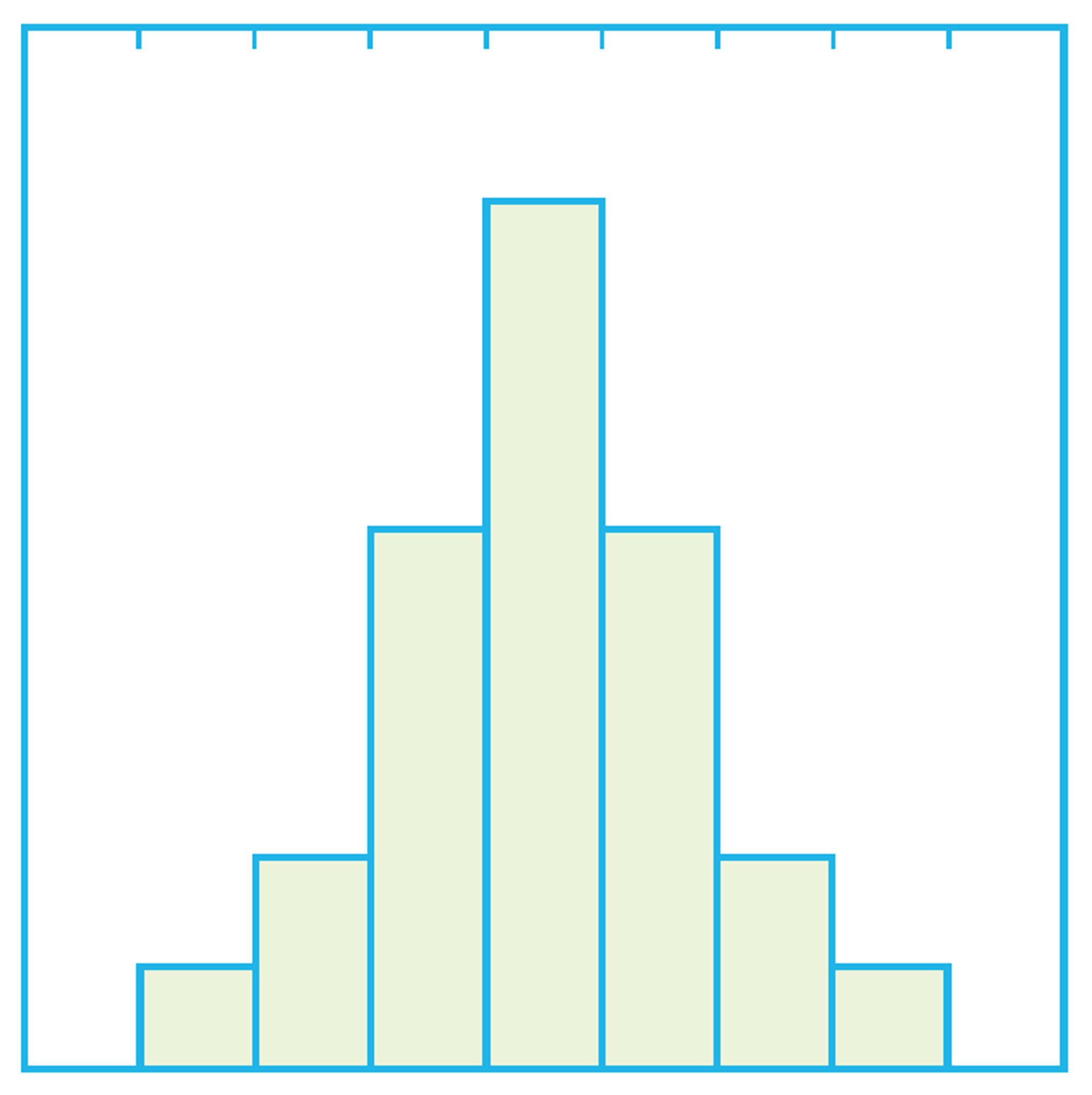
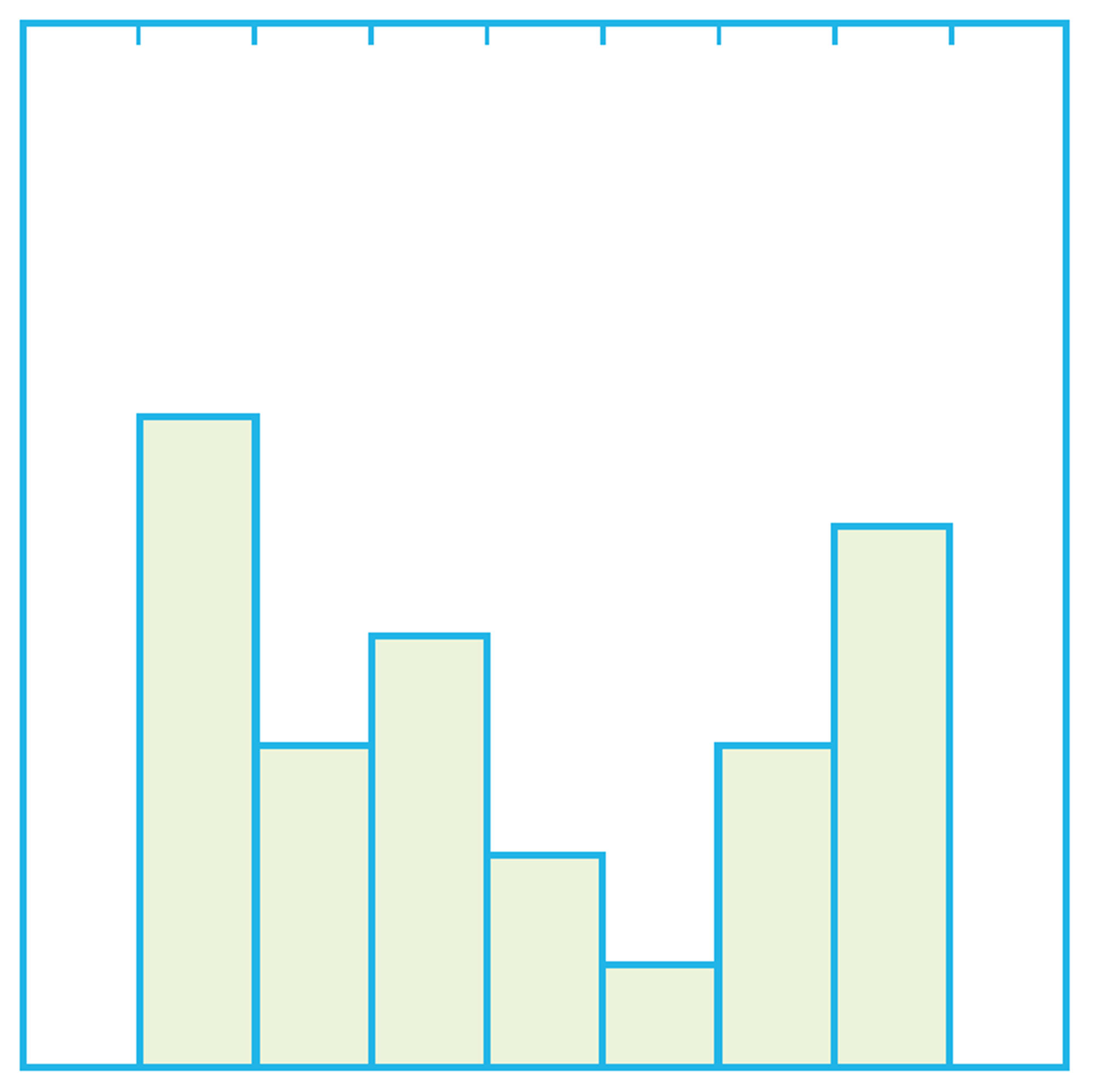
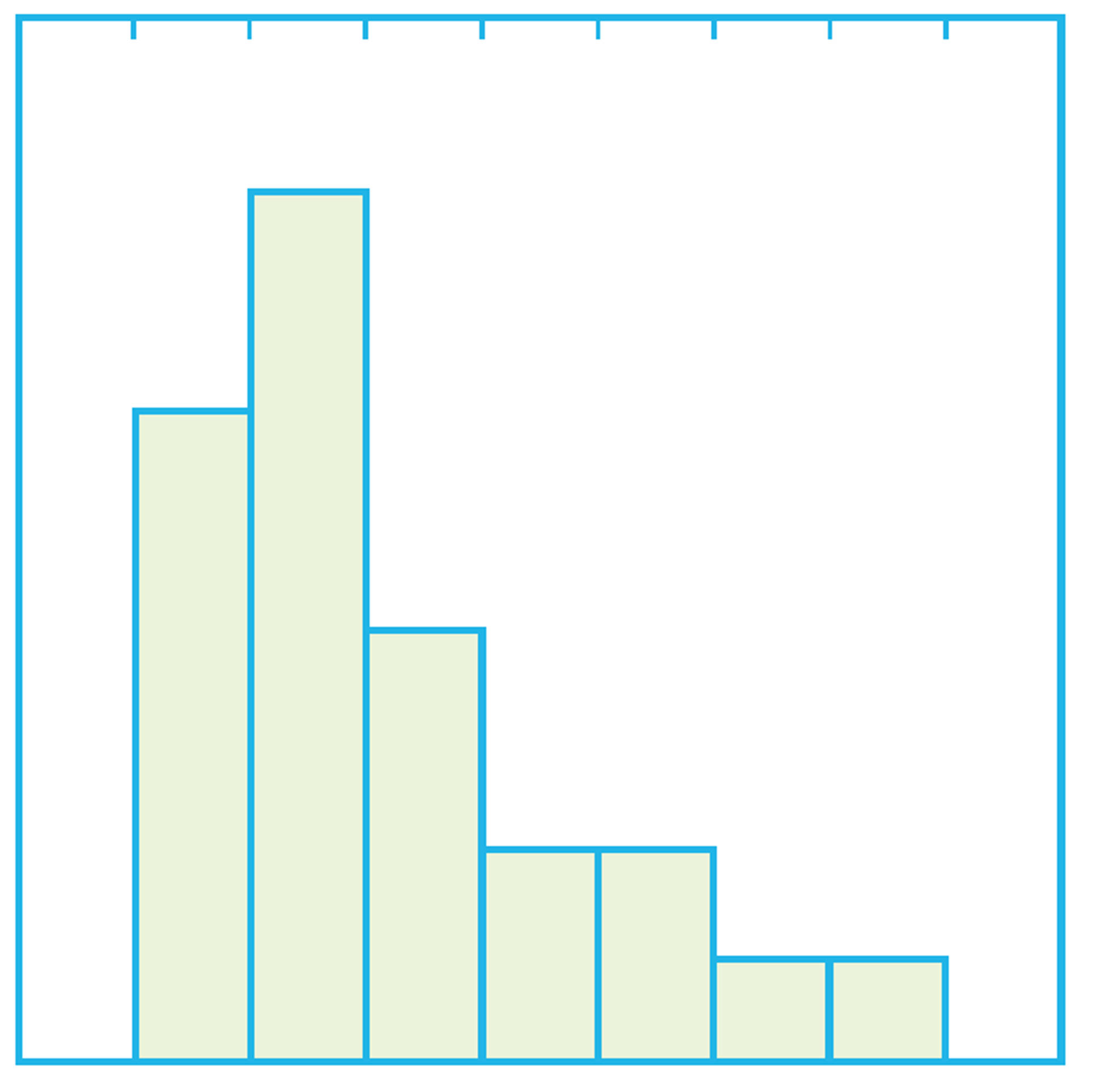
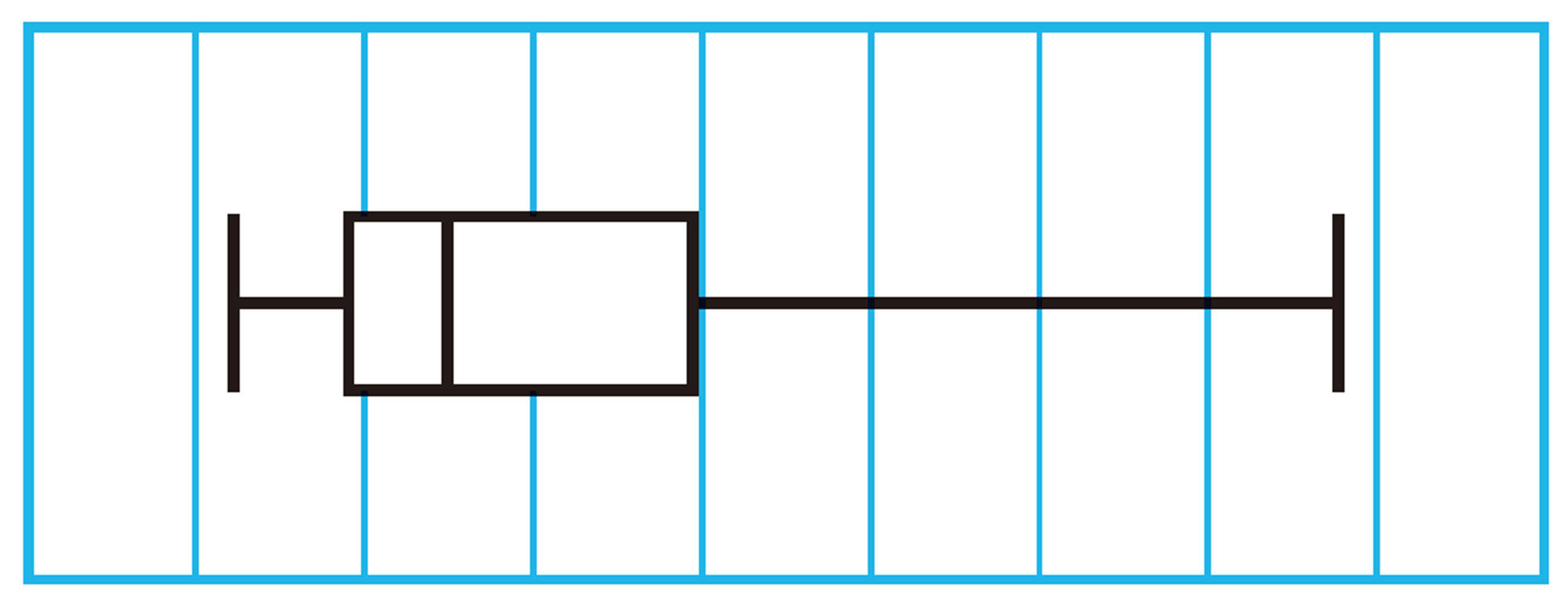
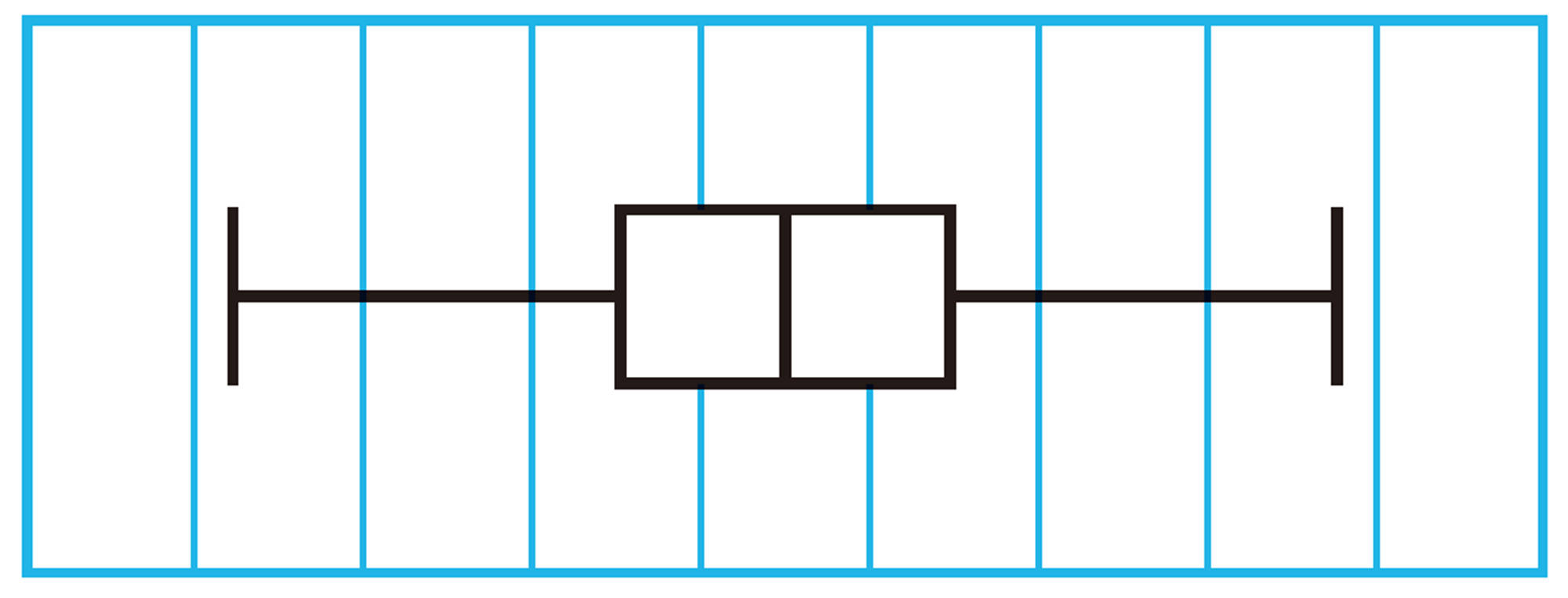
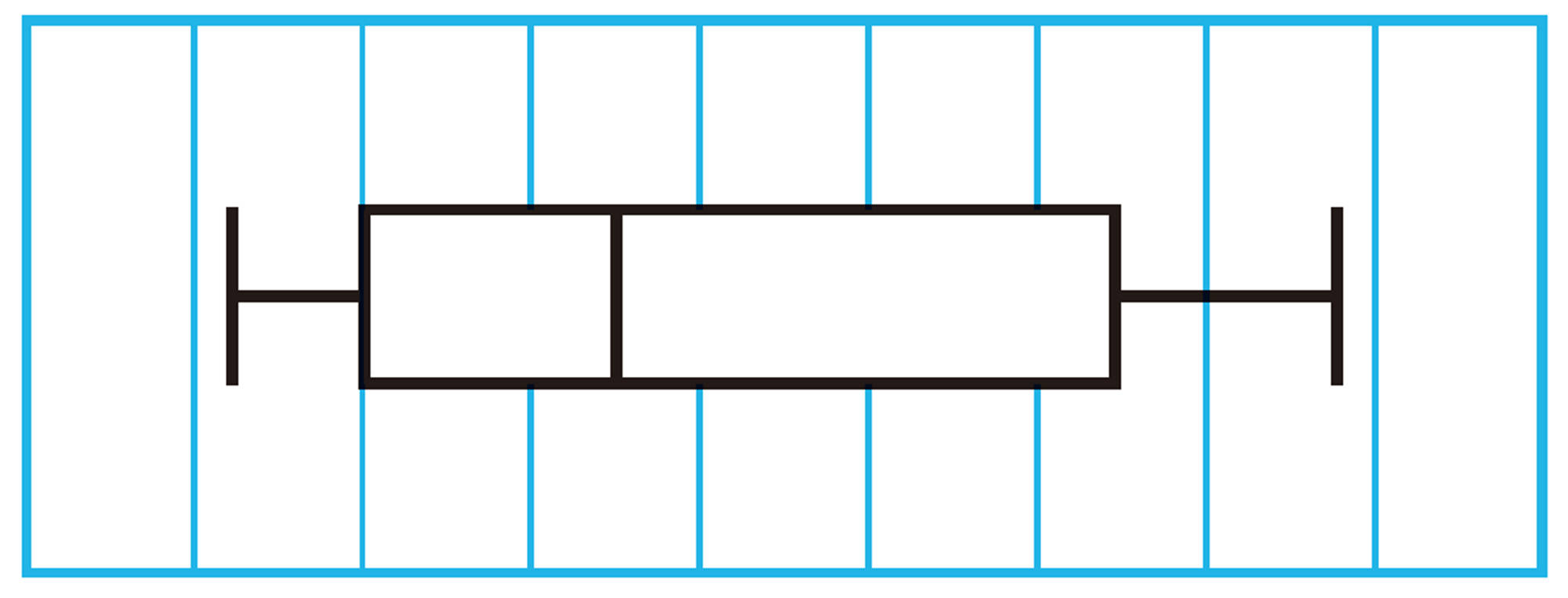
2 次の図は，3つの集団のデータをヒストグラムと箱ひげ図にまとめたものです。⑴～⑶のヒストグラムに対応する箱ひげ図を，下の㋐〜㋒から選びなさい。
⑴
⑵
⑶
㋐
㋑
㋒
