<2年p.228>
Theme 疑問を考えよう
気温は上がっている？
最近は，温暖化が進んでいると聞いたよ。
気温は上がっているといえるかな。
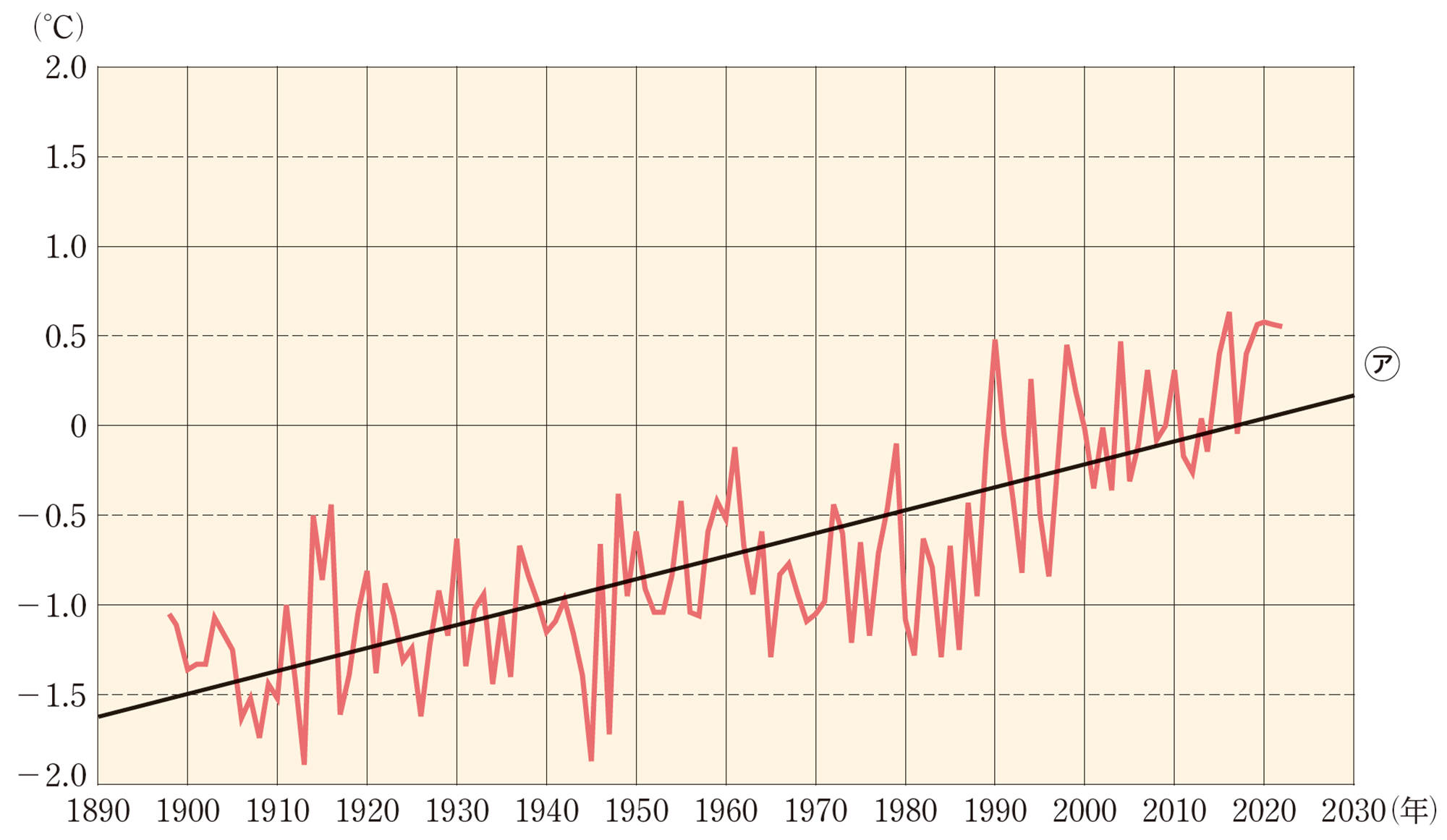
図1は，1898年から2022年までの日本の年平均気温の平年差(平年値との差)の変化を示したグラフです。気温にはさまざまな条件が関連するため，年によって上下動はあるものの，全体としては右上がりの直線㋐にそって変化していること，すなわち，温暖化の傾向にあることがわかります。
注意 日本の年平均気温の平年値との差は，1898年以降観測を継続している全国15地点の観測データをもとに算出される。ここでは，1991年から2020年までの30年間の平均値を，平年値として用いている。
① 図1から，1900年から2000年までの100年間に，日本の年平均気温は約何℃上昇したことが読み取れるでしょうか。
② 図1から，ほかに読み取れることを話し合ってみましょう。
温暖化の原因にはいろいろな説がありますが，一般には，二酸化炭素(CO₂)などの温室効果ガスの急激な増加が大きな原因といわれています。
<2年p.229>
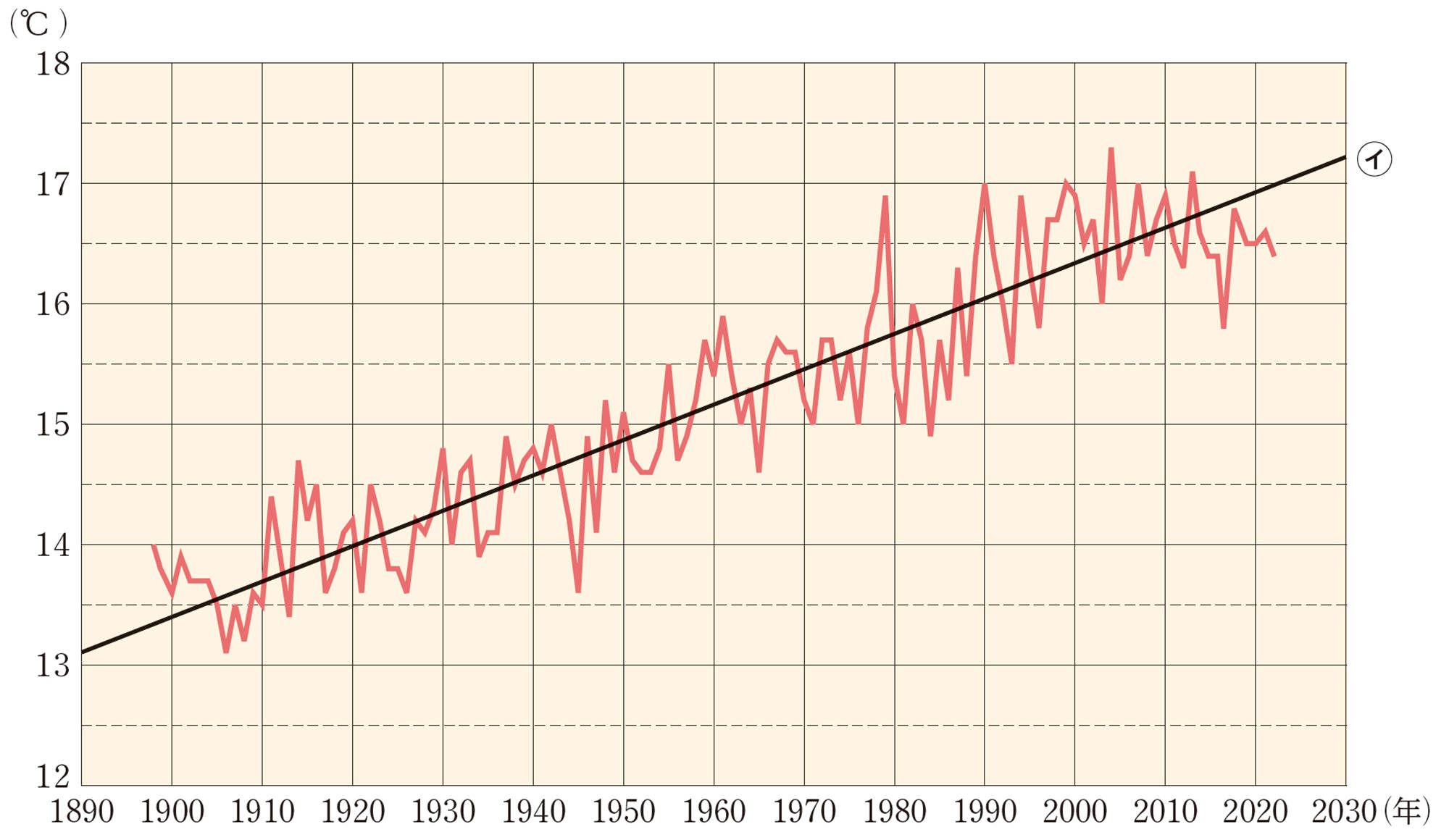
図2は，1898年から2022年までの東京(千代田区大手町)の年平均気温の変化を示したグラフです。東京などの都市部では，気温が周辺地域より高くなるヒートアイランド現象が起きています。その原因として，人口が集中してエネルギー使用量が増加し，熱の排出量が増加していること，コンクリートやアスファルトは熱が蓄積されやすいことなどがあげられます。
③ 図2 をもとに，次のことを調べてみましょう。
① 1900年と2000年の年平均気温を読み取りましょう。
② 年平均気温の変化のグラフを直線㋑とみなすとき，1900年からx年後の年平均気温をy℃として，yをxの式で表してみましょう。
③ 年平均気温の変化を②で考えた1次関数と仮定すると，2050年には，東京の年平均気温は何℃になると予想できるでしょうか。
都市部では，さらに気温が上がっているね。
東京以外にも年平均気温が上がっているところはあるかな。
④ 自分の住んでいる地域の年平均気温の変化のようすを，グラフをつくって調べてみましょう。
<2年p.230>
点字のしくみは？
駅や公共の建物などには，点字で表示されているものがあるね。
点字はどんなしくみでできているのかな。
点字は，右の図のような6つの点に突起(出っぱっているところ)があるかないかの組み合わせによって，1つの文字を構成しています。
① 6つの点の組み合わせで，何通りの文字が表現できるでしょうか。
② 次の図は，0～9の数字を点字で表したものです。数字の表し方について，気づいたことをいいましょう。
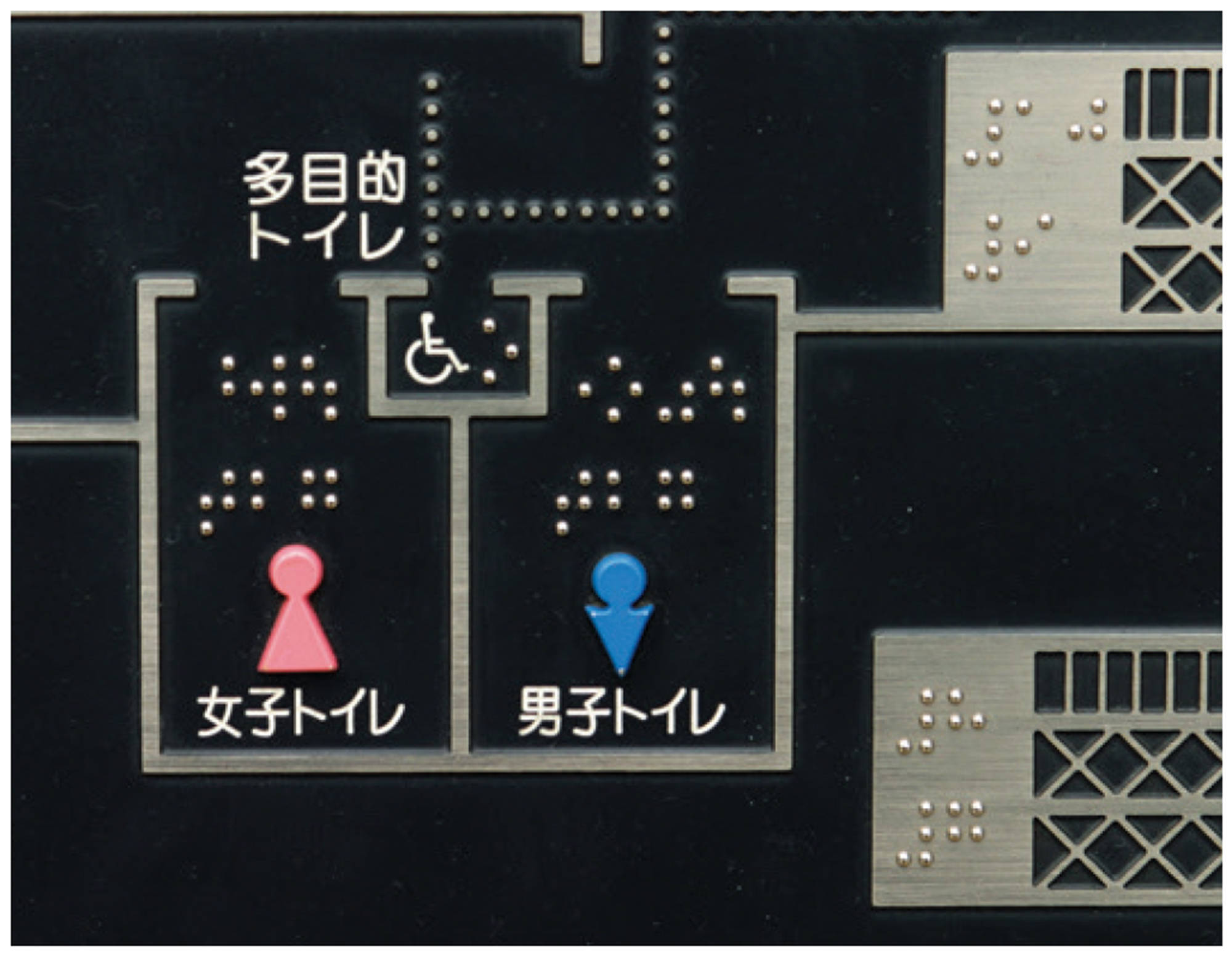
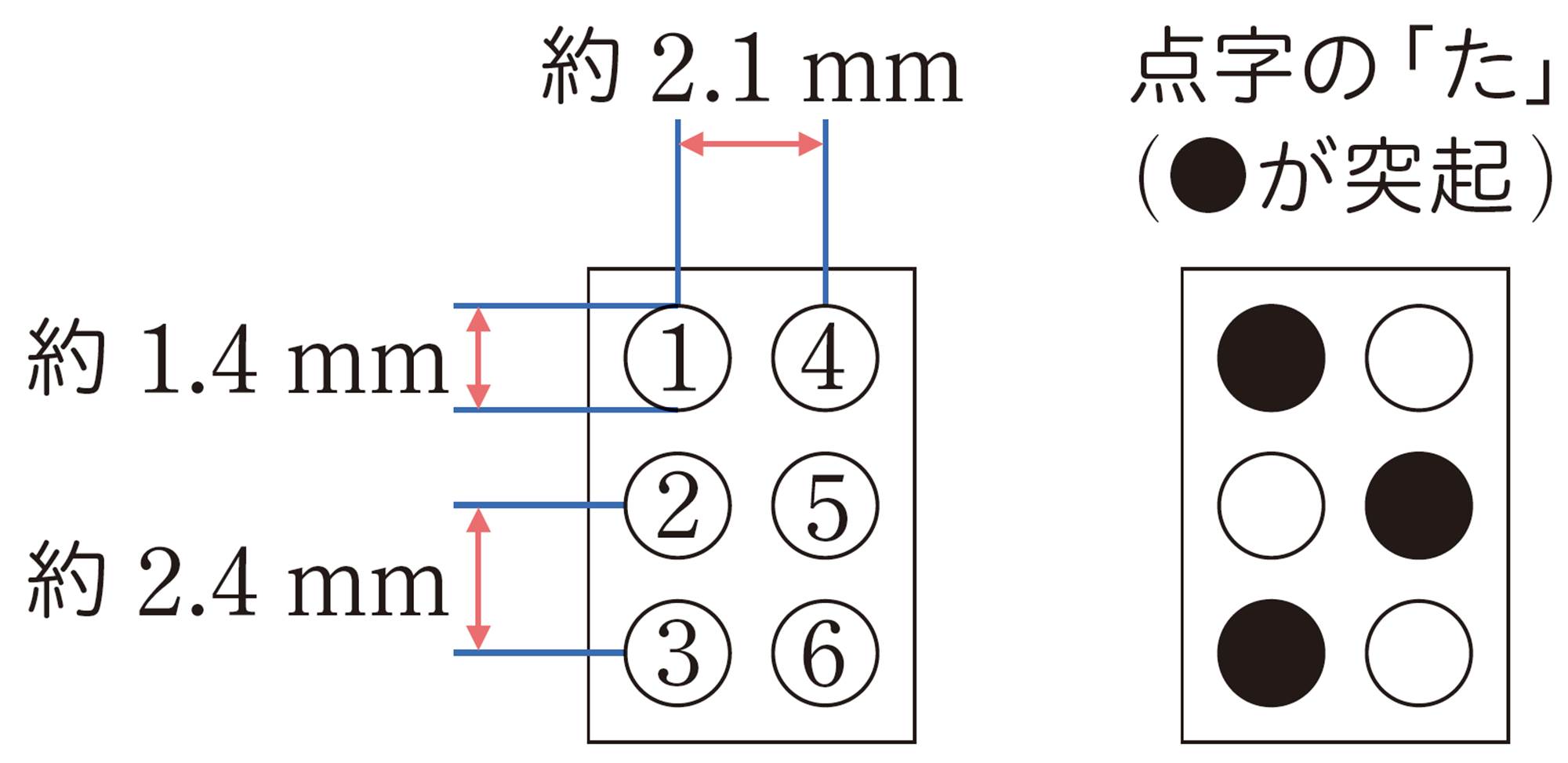
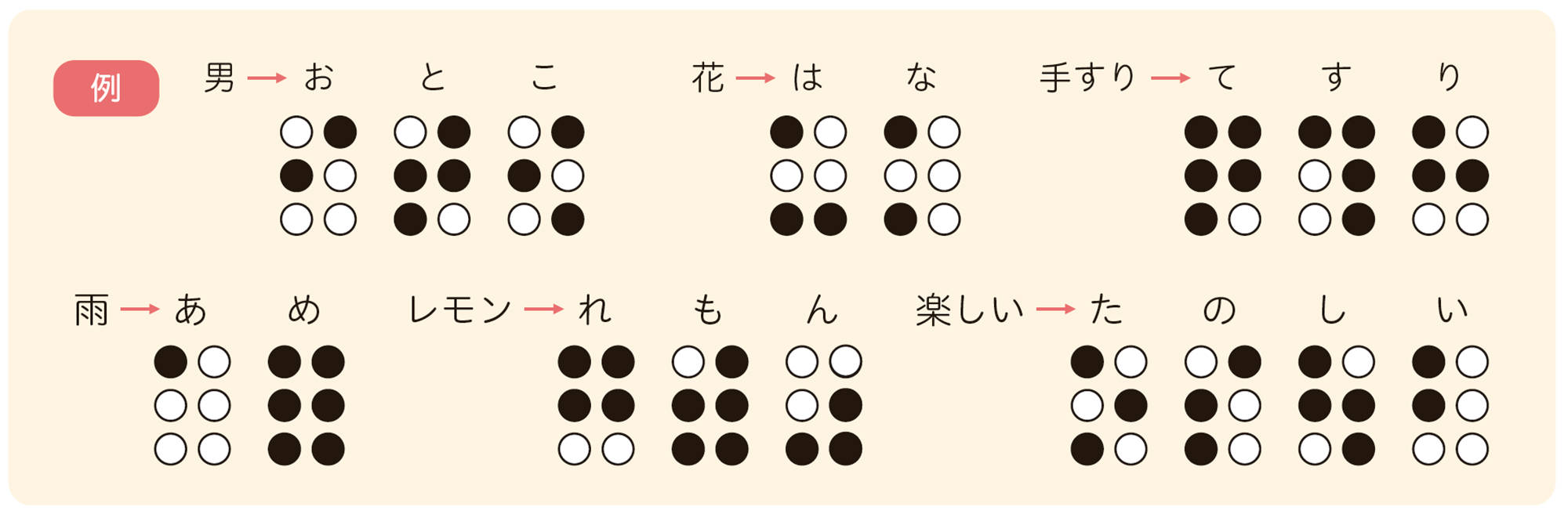
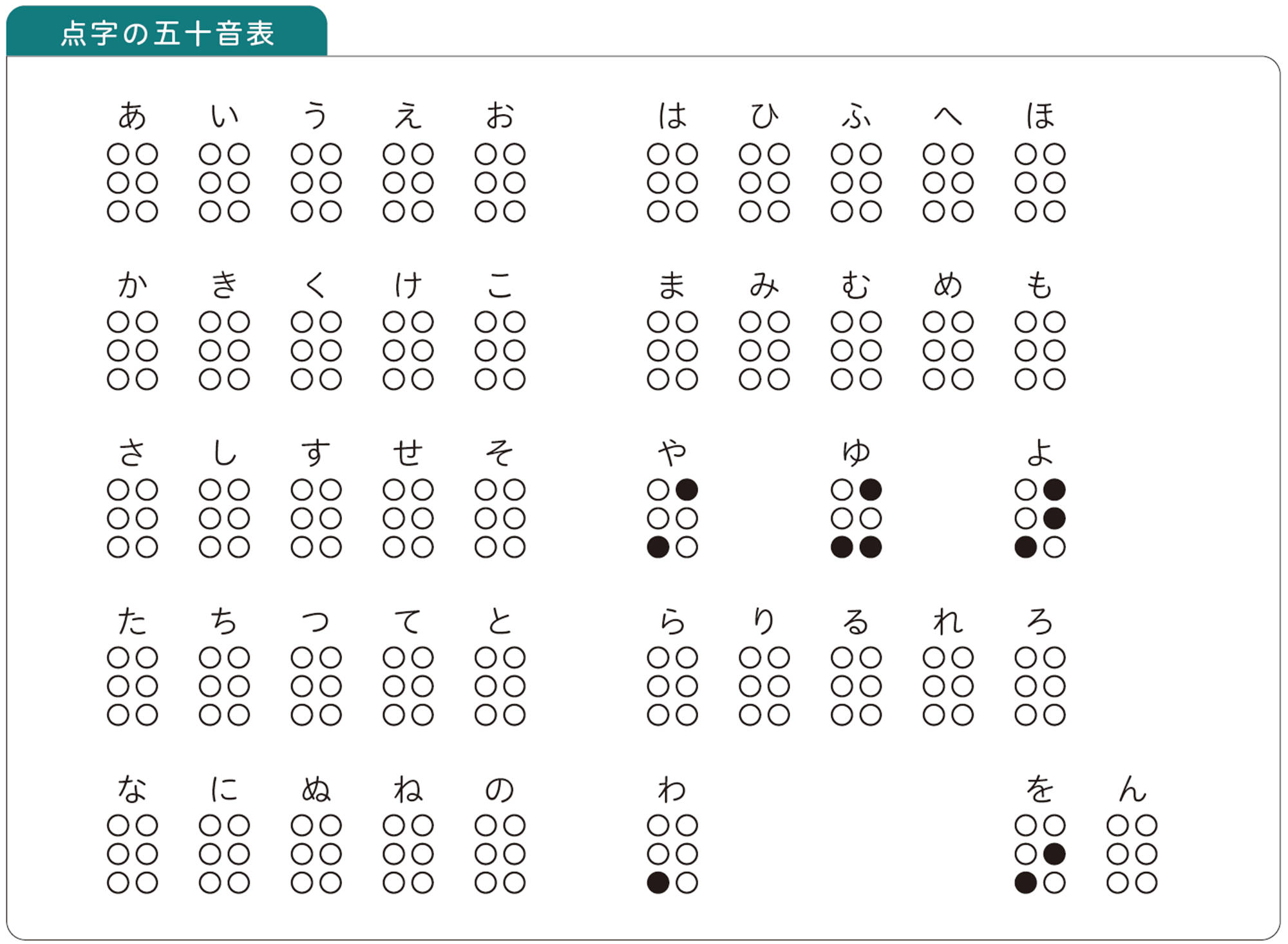
それぞれの数字の最初におかれた
は数符といい，数字であることを示すための記号です。これらの数字を使って，たとえば，613や[mathjax]\(3.14\)は，次のように表します。
<2年p.231>
日本語の点字では，次のような「かな点字」が一般的に使われています。
点字をつくるのに，何かきまりがあるのかな。
五十音表に並べてみるとわかるかな。
③ 点字は，一定の規則のもとにつくられています。上の例を手がかりにして，点字の五十音表を完成させましょう。
④ 点字の規則性について，気づいたことをまとめてみましょう。
<2年p.232>
どちらが有利？ 発展 高等学校
福引きなどの条件はいろいろあるけど，有利か不利かはどうしたら比べられるかな。
総数が多い方が有利なのかな。
ある町の商店Aでは福引き券を500枚，商店Bでは福引き券を1000枚つくり，景品はそれぞれ次の表のようにしました。同じ条件で福引きができるとするとき，どちらの福引き券の方が有利であると考えられるでしょうか。
商店 A
商店 B
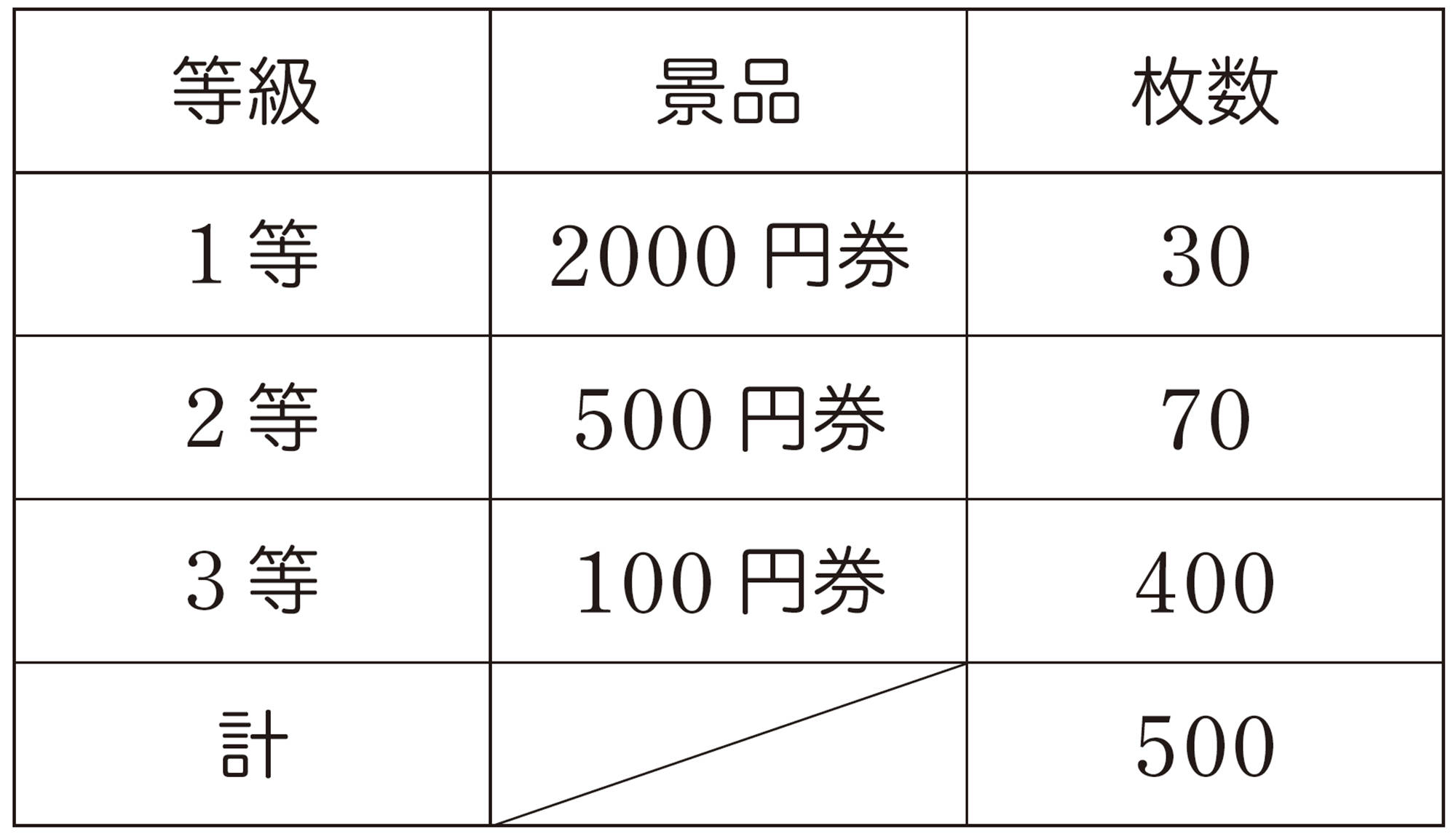
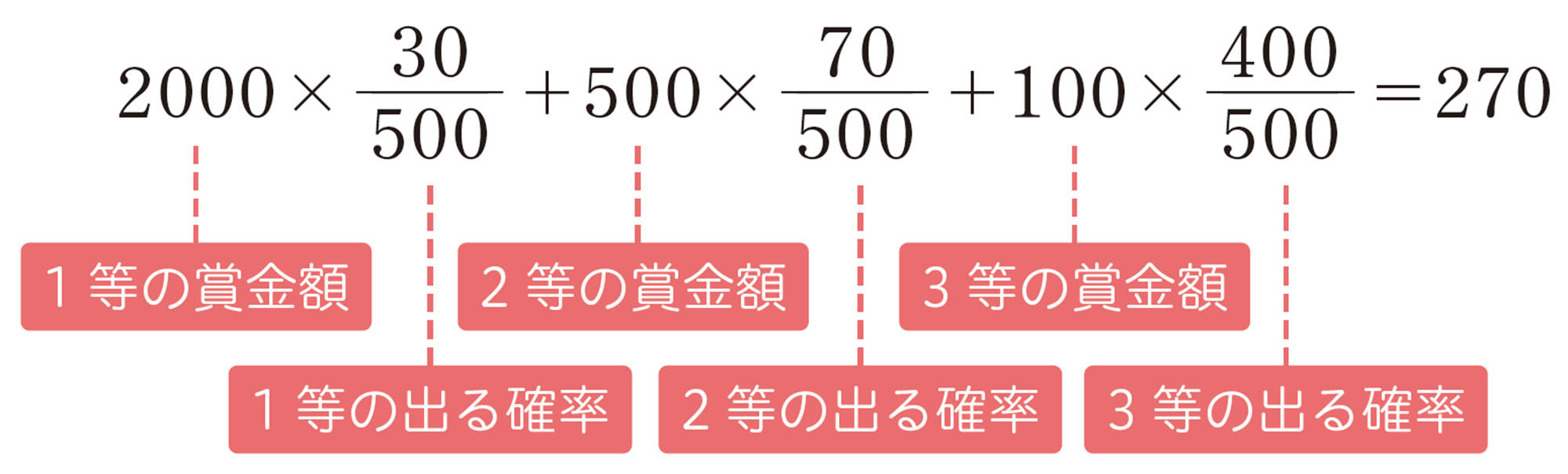
商店Aの福引き券の賞金の総額を求めると，
[mathjax]\(2000\times 30+500\times 70+100\times 400=135000\)より，135000円
福引き券は500枚あるので，1枚当たりの平均の賞金額は，
[mathjax]\(135000\div 500=270\)より，270円
となります。
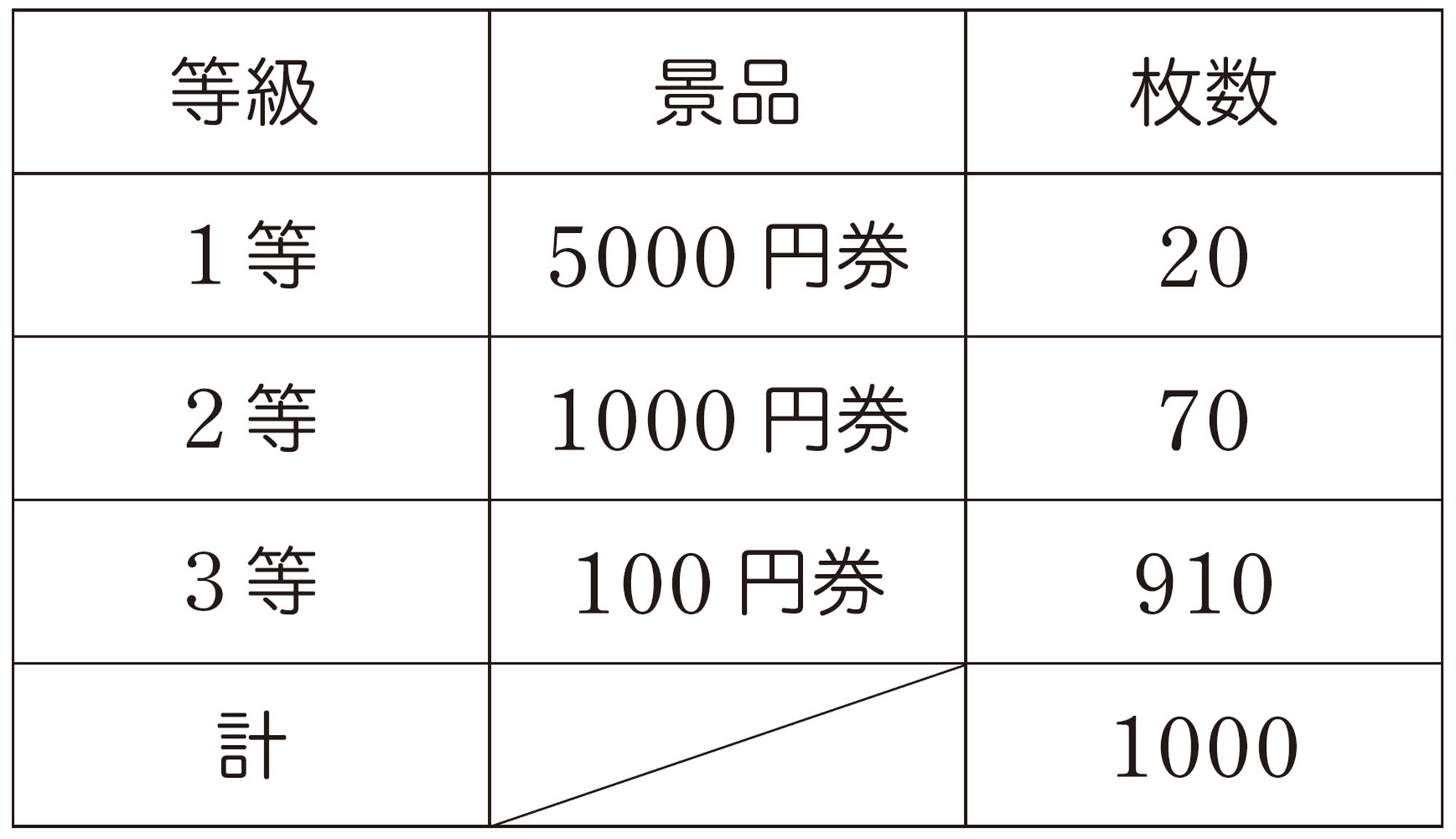
① 商店Bの福引き券の1枚当たりの平均の賞金額を求め，商店Aの福引き券の平均の賞金額270円と比べてみましょう。
1で調べたように，1枚当たりの平均の賞金額で比べると，商店Aの福引き券の方が有利であることがわかります。
これまで調べたような，福引き券1枚当たりの平均の賞金額を，福引き券の賞金の期待値といいます。
<2年p.233>
前ページの商店Aの福引き券の賞金の期待値の計算は，
[mathjax]\(\dfrac{2000\times 30+500\times 70+100\times 400}{500}=270\)
ですが，この式は，次のように書き直すことができます。
[mathjax]\(2000\times\dfrac{30}{500}+500\times\dfrac{70}{500}+100\times\dfrac{400}{500}=270\)
すなわち，この式の左辺は，賞金額とそれが出る確率の積をすべて加えたものになっています。
② 1つのさいころを投げて，出た目の数だけ点数がもらえるとします。このとき，1から6までの目が出る確率はそれぞれ[mathjax]\(\dfrac{1}{6}\)なので，さいころを1回投げるときの得点の期待値は，次の式で求めることができます。
[mathjax]\(1\times\dfrac{1}{6}+2\times \dfrac{1}{6}+3\times\dfrac{1}{6}+4\times \dfrac{1}{6}+5\times\dfrac{1}{6}+6\times\dfrac{1}{6}\)
この式を計算し，得点の期待値を求めてみましょう。
宝くじでは，どのくらいの期待値があるのかな。
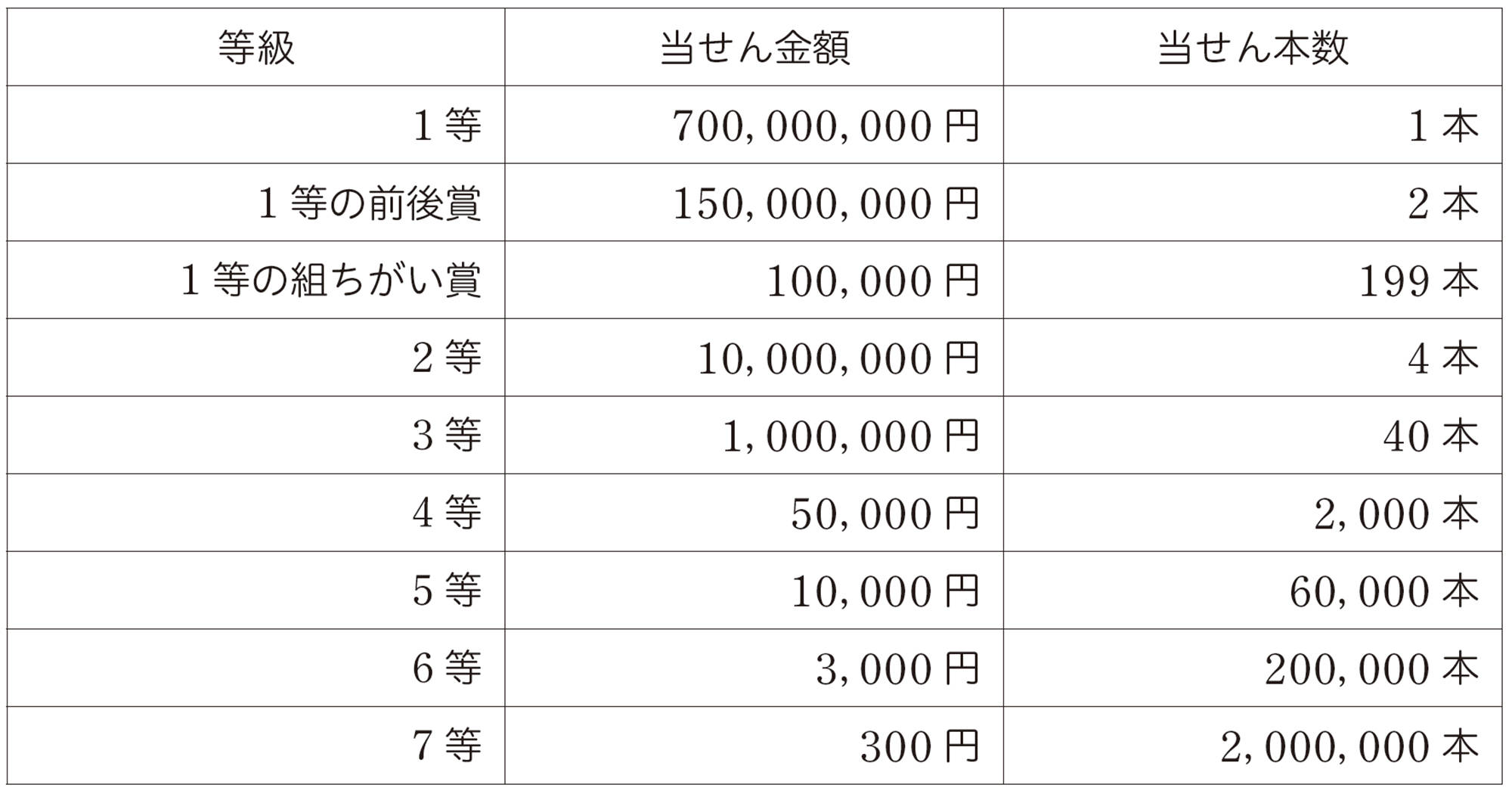
③ ある年の年末ジャンボ宝くじの当せん金額と，2千万本当たりの当せん本数は，次の表のようになっています。この宝くじの当せん金額の期待値を求めてみましょう。
<2年p.234>
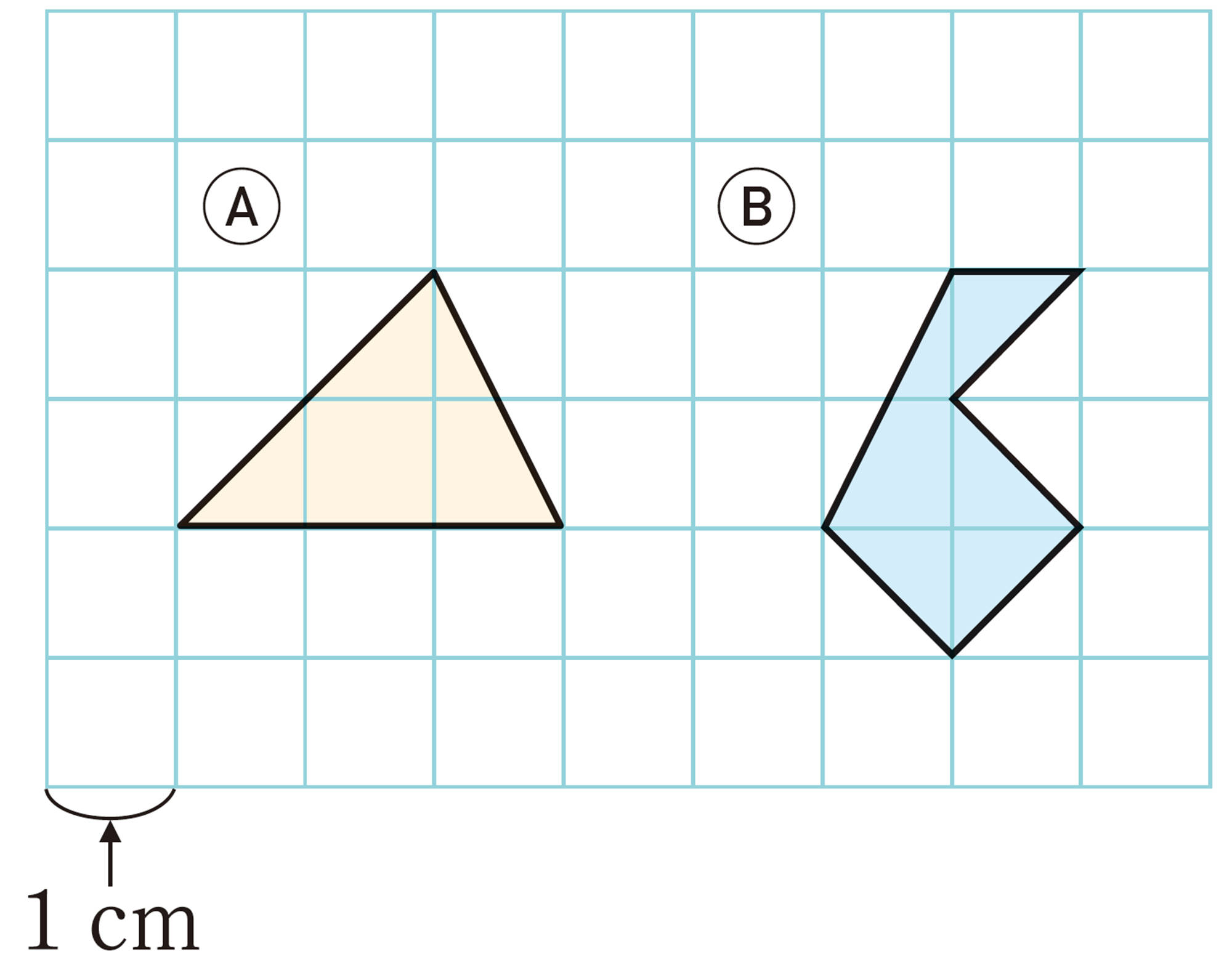
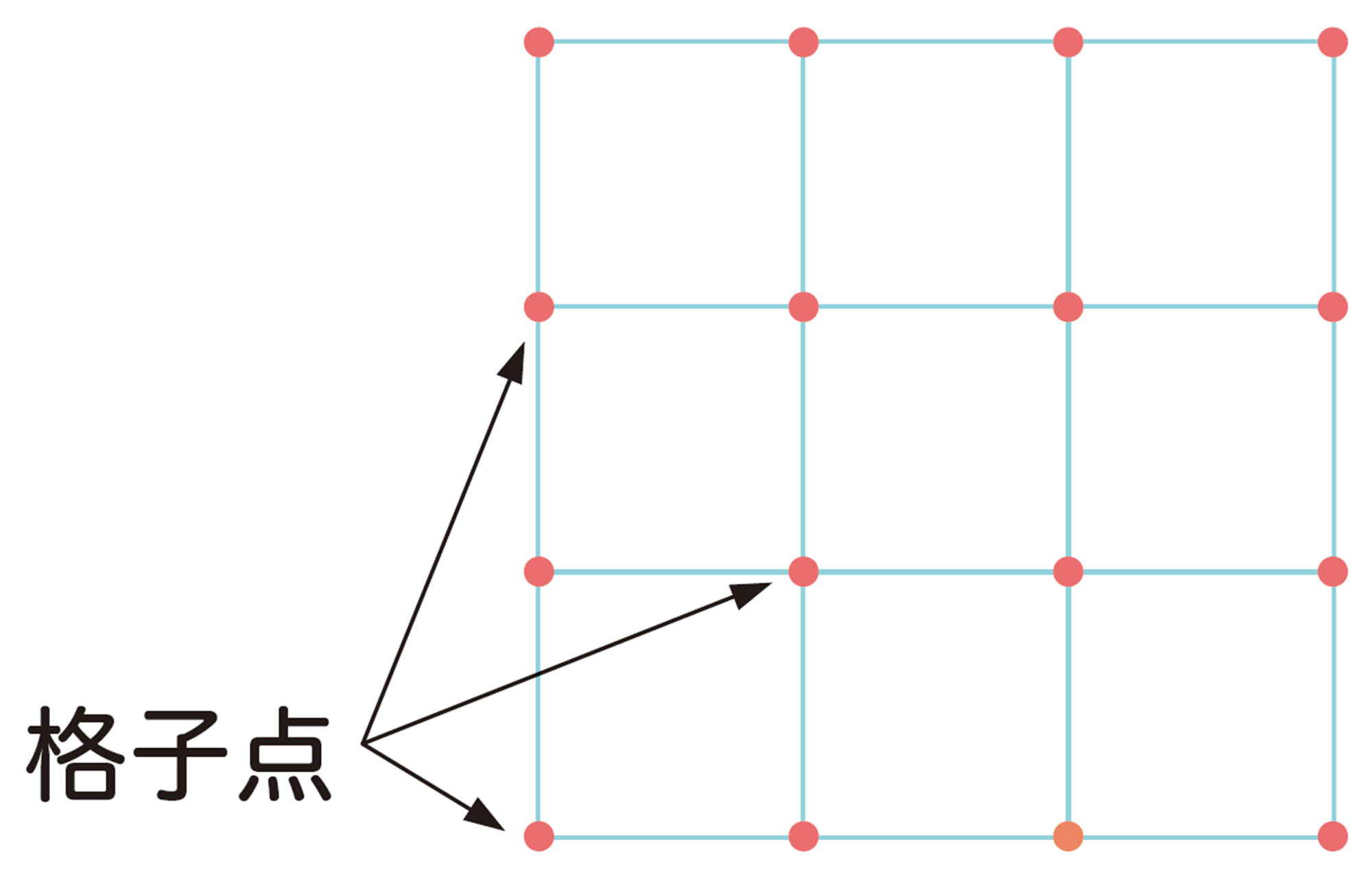
面積は求められる？
① 右の図のような，方眼上にかかれた，Ⓐ，Ⓑの図形の面積はともに3 cm²です。それぞれの図で，共通していることは何でしょうか。
辺が通っている方眼の交点の数が同じだね。
ほかにも，同じことはあるかな。
方眼で，縦線と横線の交点を格子点といいます。
図形の内部や周上にある格子点の数に着目して，図形の面積を調べてみましょう。
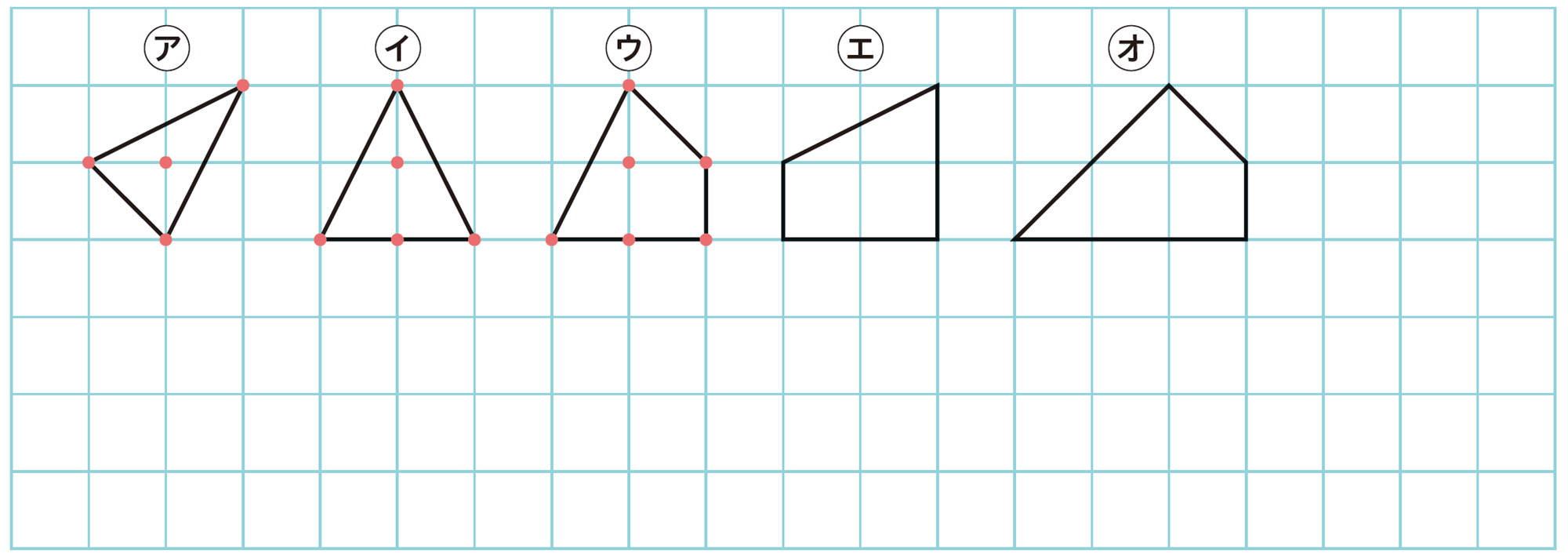
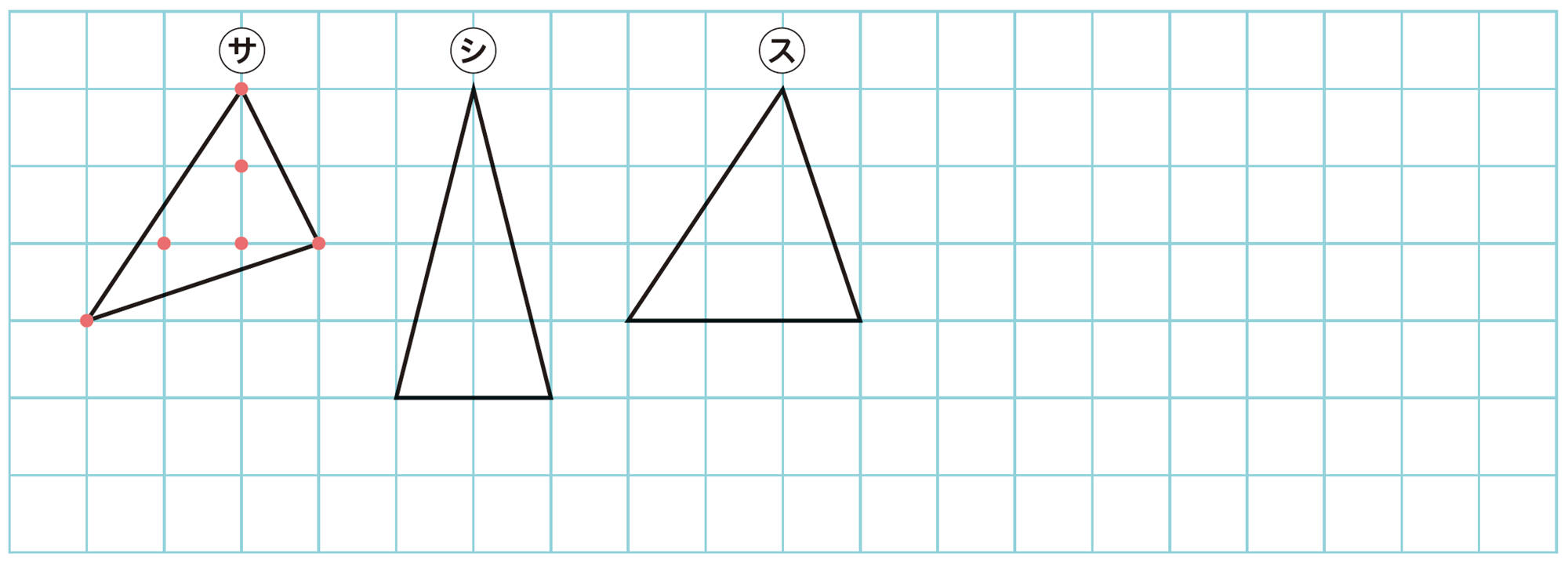
② 内部の格子点が1個の図形
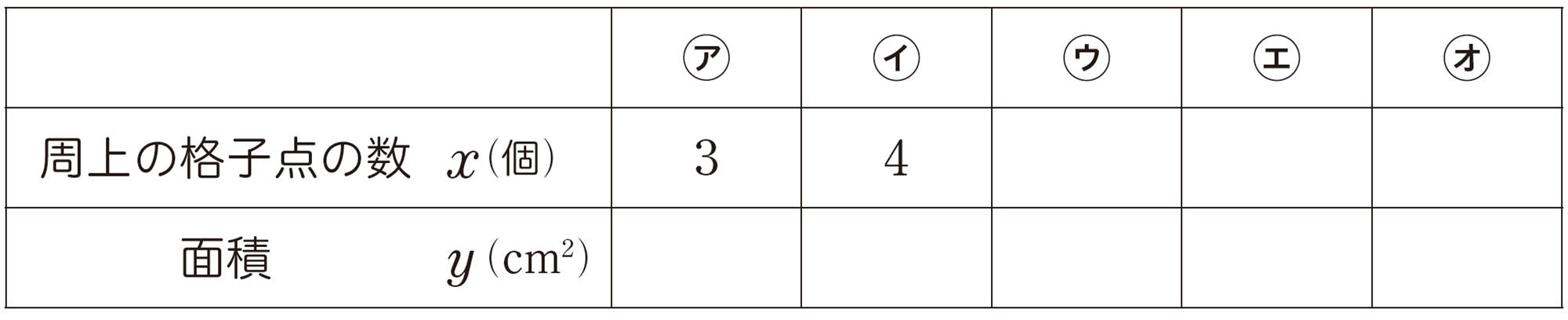
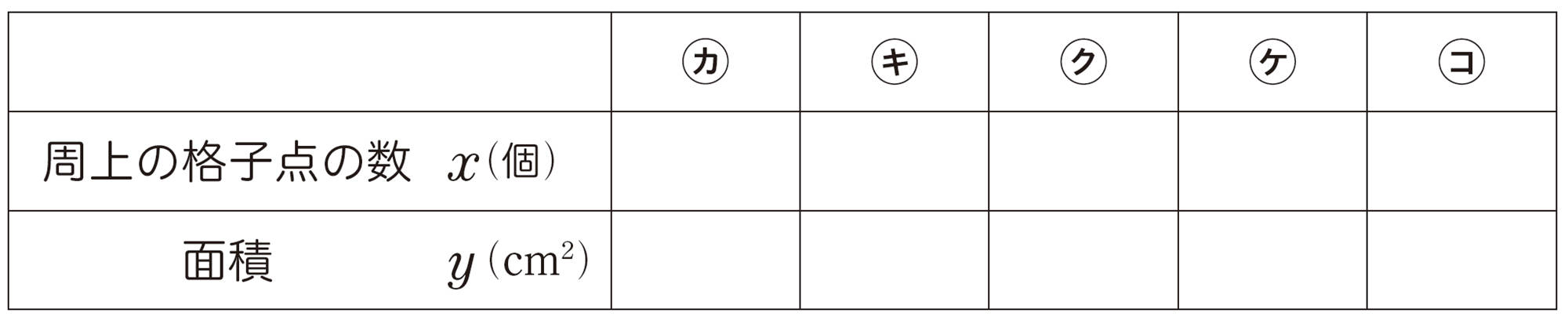
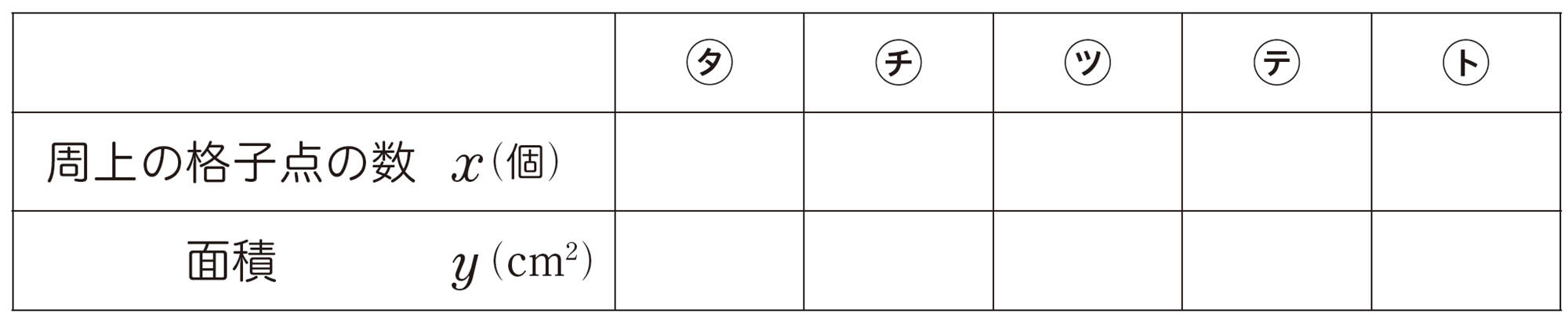
❶ ㋐～㋔の周上の格子点の数と面積をそれぞれ求め，表にまとめてみましょう。
❷ 周上の格子点の数がx個のときの面積をy cm²として，yをxの式で表してみましょう。
<2年p.235>
内部の格子点の数がちがうときはどうなるのかな。
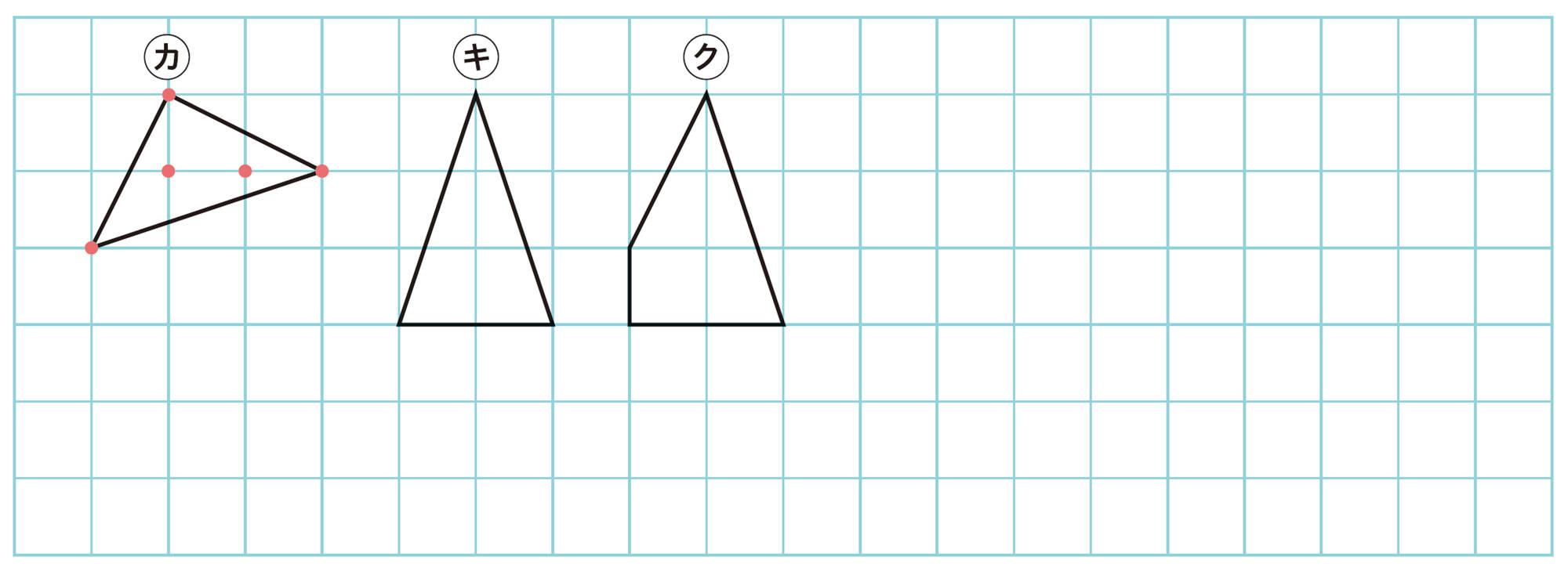
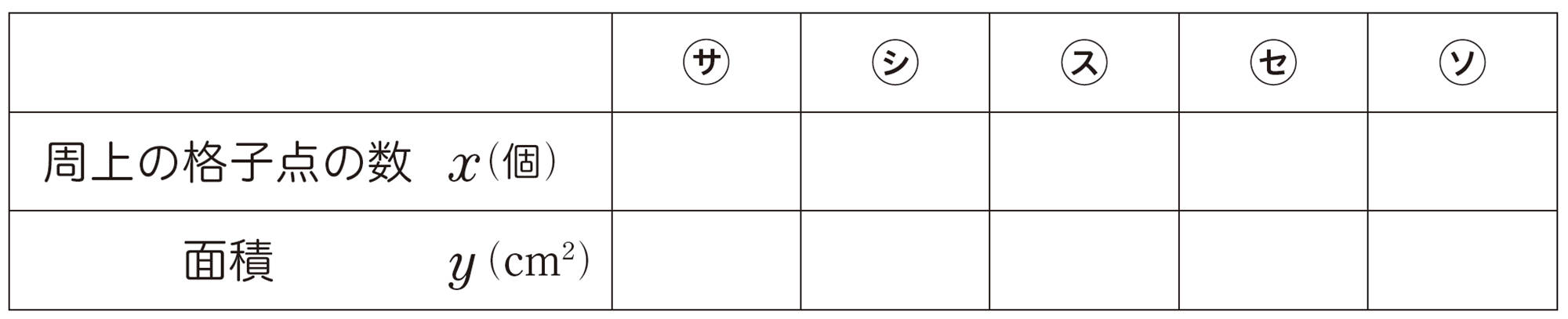
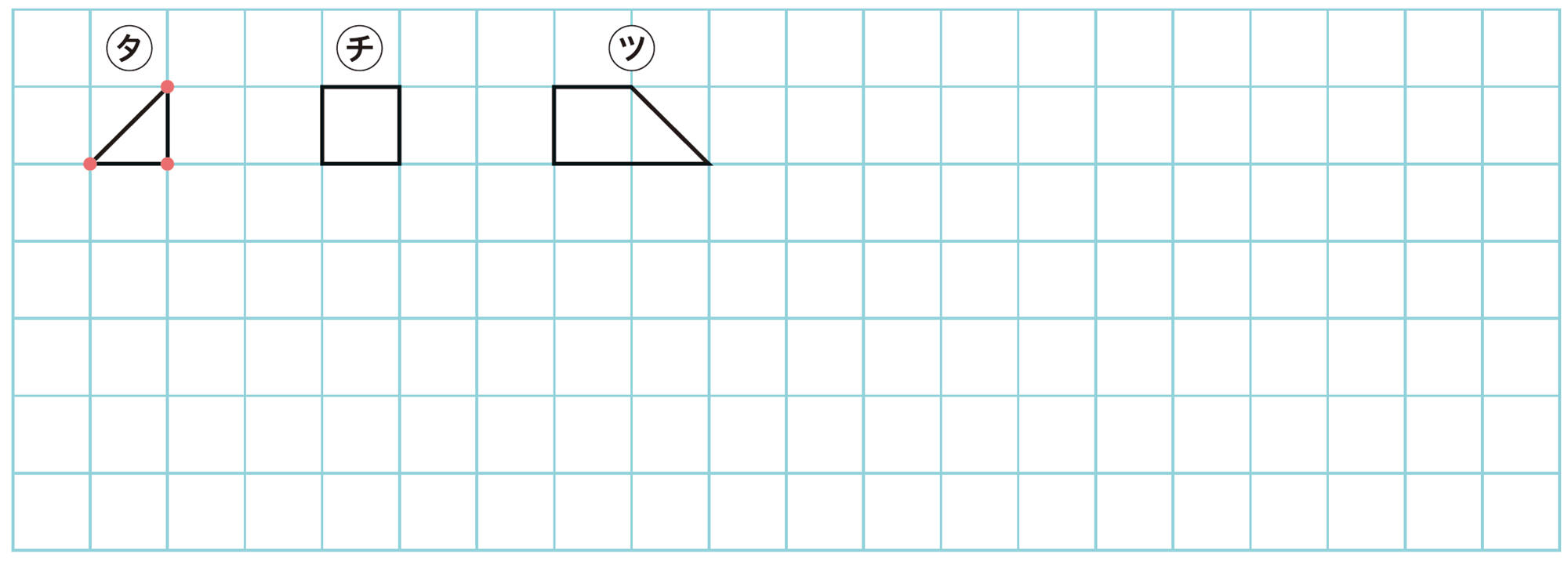
③ 内部の格子点が2個の図形
❶ ㋕～㋗の周上の格子点の数と面積をそれぞれ求め，表にまとめてみましょう。
❷ 内部の格子点が2個の図形㋘，㋙をかき，同じことを調べてみましょう。
❸ yをxの式で表してみましょう。
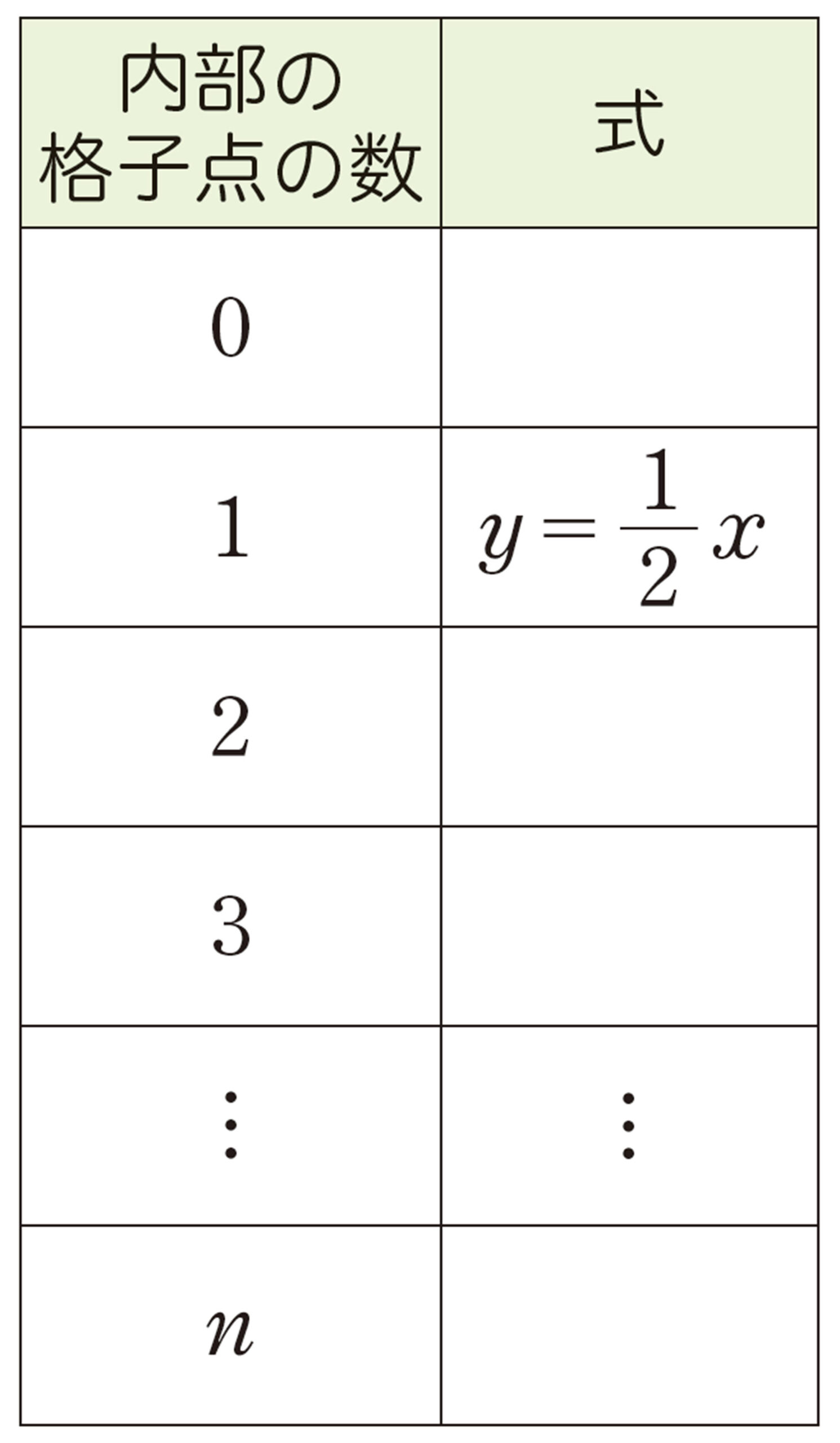
④ 内部の格子点が3個の図形
③と同じことを調べ，yをxの式で表してみましょう。
<2年p.236>
⑤ 内部の格子点がない図形
前ページの③，④と同じことを調べ，yをx の式で表してみましょう。
これまで求めた式を見直してみると，どんなことがわかるかな。
何かきまりがあるかな。
⑥ これまで調べたことを右の表にまとめ，内部の格子点の数を4個，5個，…と増やしたとき，xとyの間にどんな関係が成り立つか予想してみましょう。また，内部の格子点の数をn個として，yをxとnを使った式で表してみましょう。
⑦ ⑥でつくった式が正しいかどうかを，いろいろな図形をかいて確かめてみましょう。
<2年p.237>
Theme 数学の歴史の話
パスカルとフェルマーになってみよう 発展 高等学校
パスカルは貴族のメレから，195ページにあるような質問を投げかけられました。パスカルは，数学者のフェルマーと手紙で意見交換しながら，この質問を解決しました。A，Bのどちらが勝つことも同様に確からしいとするとき，パスカルとフェルマーになったつもりで，この質問を解決していきましょう。
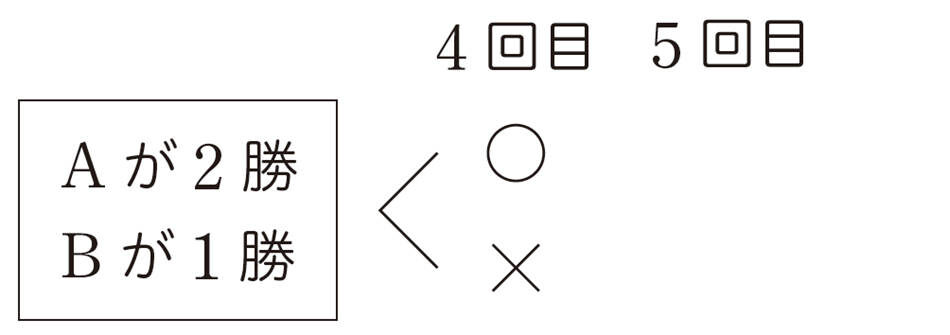
1 パスカルとフェルマーは，手紙のやり取りの中で，A，Bの2人がこのあと勝利する確率をそれぞれ求めて，その確率どおりにかけ金を分配すればよいという結論になりました。勝負は3回まで終わっており，Aが2勝，Bが1勝しています。どちらかの勝利が決まっても，5回目まで勝負を続けるとしたとき，Aが勝利する場合は何通りあるでしょうか。
次の樹形図の続きをかいて，求めてみましょう。
Aの勝ちを○，負けを×とする。
2 1でつくった樹形図をもとにして，A，Bが勝利する確率をそれぞれ求めてみましょう。
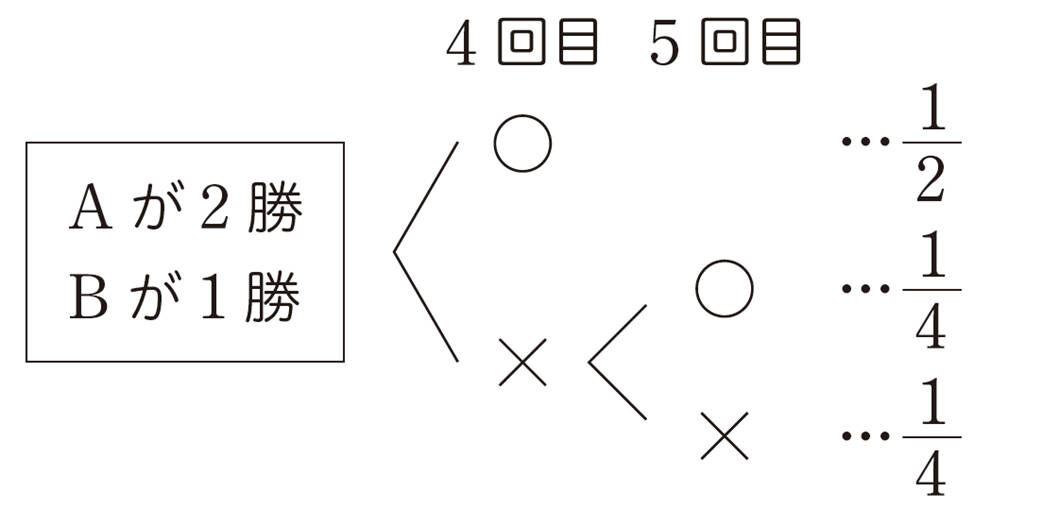
3 真央さんは，メレの質問に対して，次のような樹形図をつくってA，Bが勝利する確率をそれぞれ求めました。真央さんの考え方を説明してみましょう。
Aの勝ちを○ ，負けを×とする。
4 メレの質問と同じように，先に3回勝った方が勝ちとするとき，Aが2回勝った時点で勝負を中止したら，かけ金はAとBの間でどのように分けると公平になるでしょうか。
