<2年p.201>
７章 Chapter ７ データの分布
1節 データの分布
いろいろな都市で1月の日ごとの最高気温を調べて，ヒストグラムにしてみたよ。
似ているところやちがうところがあるね。
こんなにたくさんあると比べにくいね。
だいたいの傾向がわかればいいんだけど…。
？ 複数のデータの傾向がわかりやすいグラフは？
<2年p.202>
1節 データの分布
降水量は多くなったのか？
各地で，雨による土砂災害が起きています。
最近では，短時間に集中的に雨が降ることも増えています。
各地域の過去と現在の降水量がどのように変わっているのかを調べ，
比べてみることにしました。
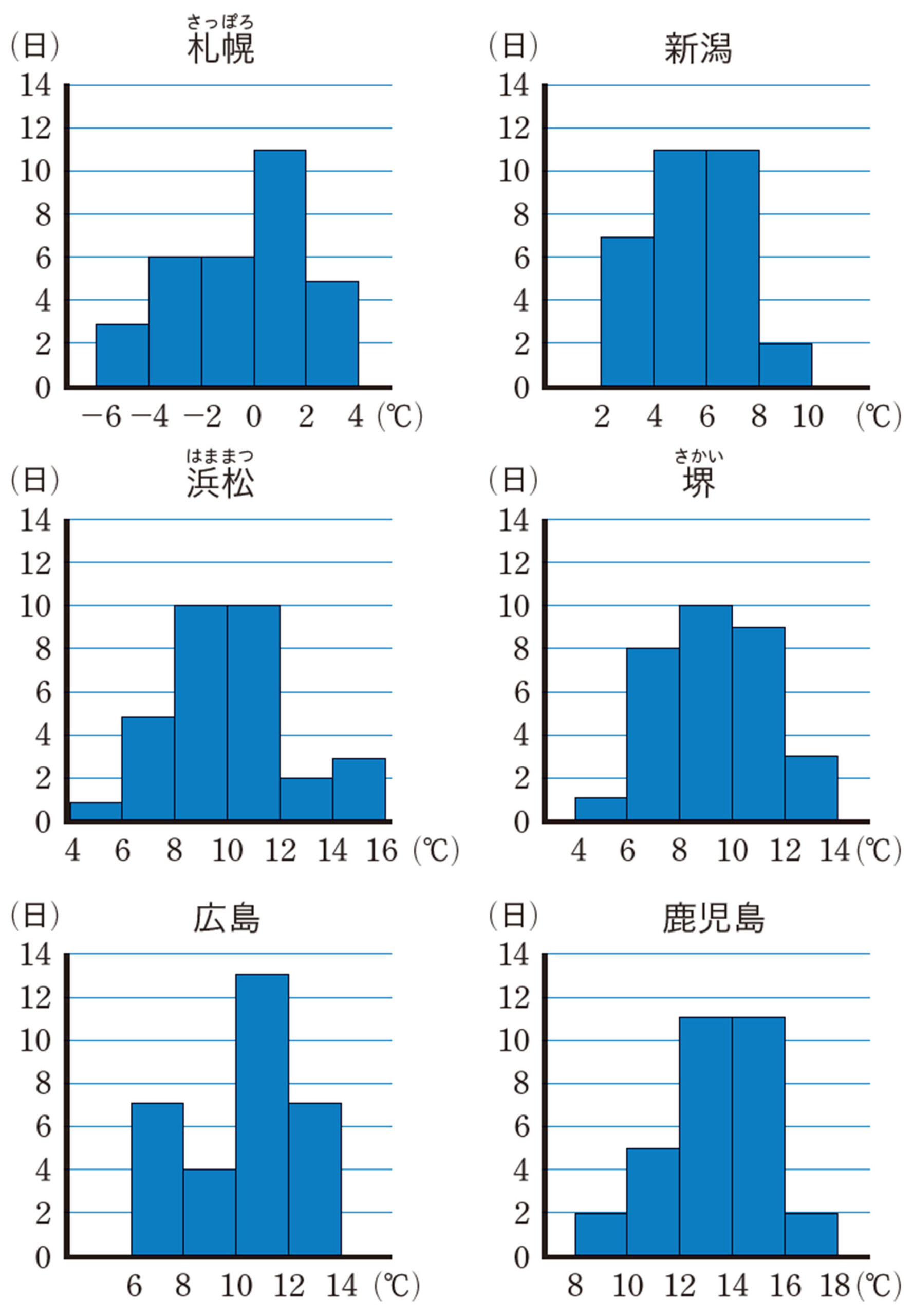
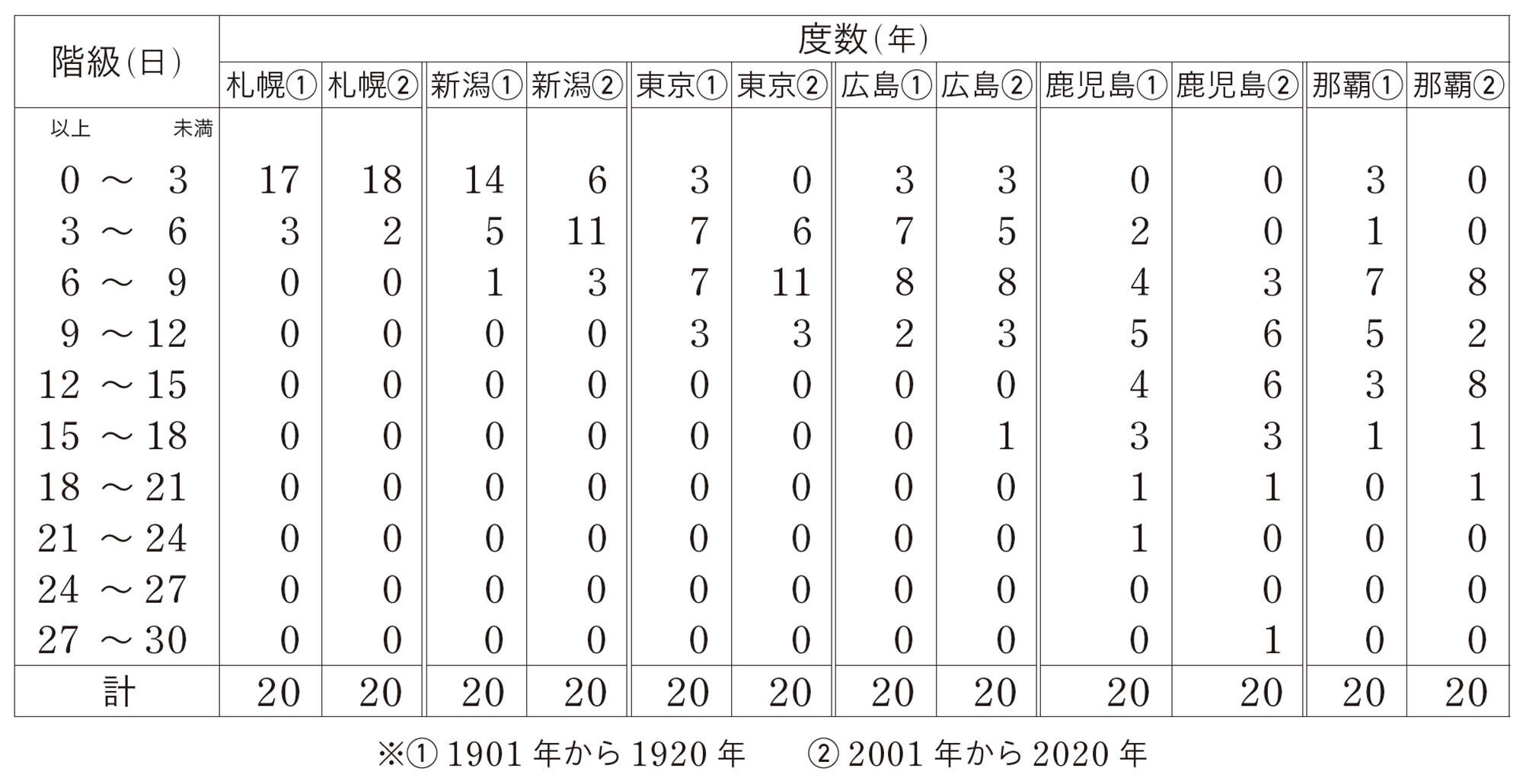
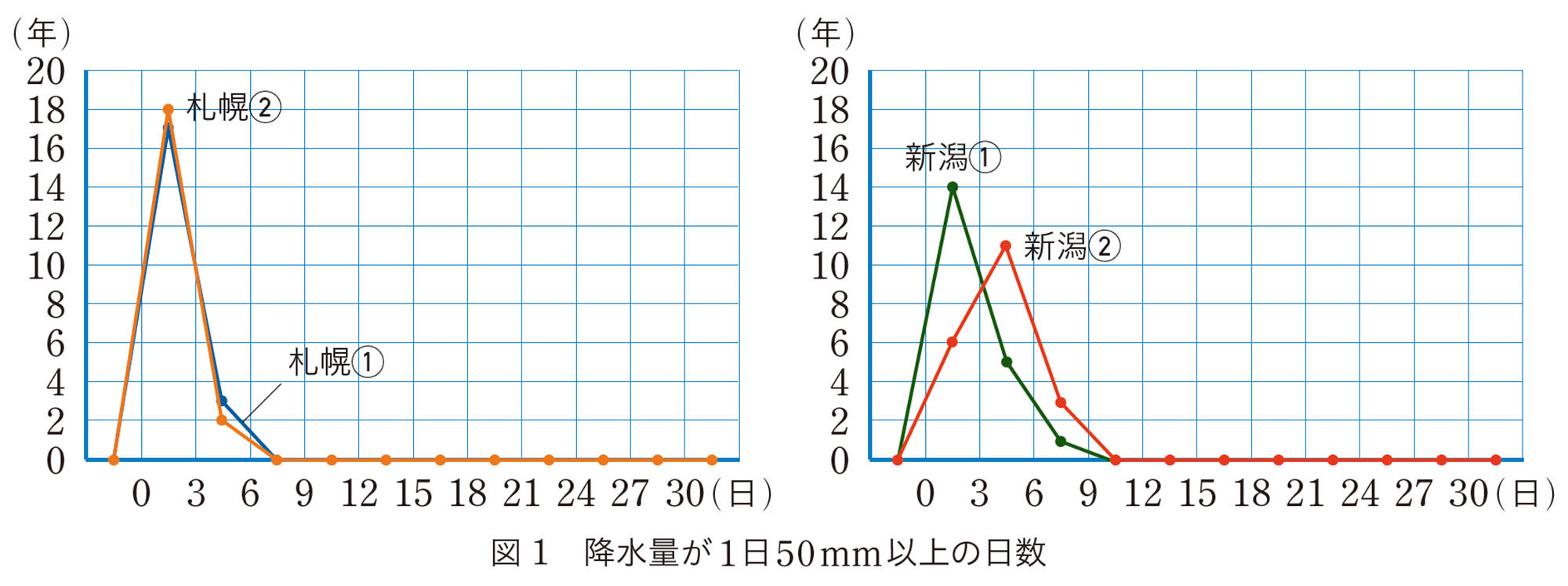
そこで，札幌市，新潟市，東京（大手町），広島市，鹿児島市，那覇市のそれぞれの場所について，1901年から1920年と2001年から2020年の間で，1日の降水量が50mmを超えた日が，各年で何日あったかを調べてみました。
次の度数分布表から，どんなことがわかるか話し合ってみましょう。
それぞれの場所で，①と②を比べればいいね。
度数分布表だけでは，よくわからないね。
<2年p.203>
【１】 前ページの表をもとに，札幌市と新潟市のデータを度数折れ線に表してみました。
ほかの場所についても，度数折れ線で表してみましょう。どんなことがわかるでしょうか。
新潟は，山の位置がちがっているね。
【２】 降水量が1日50mm 以上の日数について，先生が次のような図を見せてくれました。この図が，どのように表されているかについて，話し合ってみましょう。
はじめて見る図だね。どのようにつくっているのかな。
次の課題へ！
四角形や線分の部分には，どんな意味があるのかな？
P.204
<2年p.204>
１ 箱ひげ図
Q Question
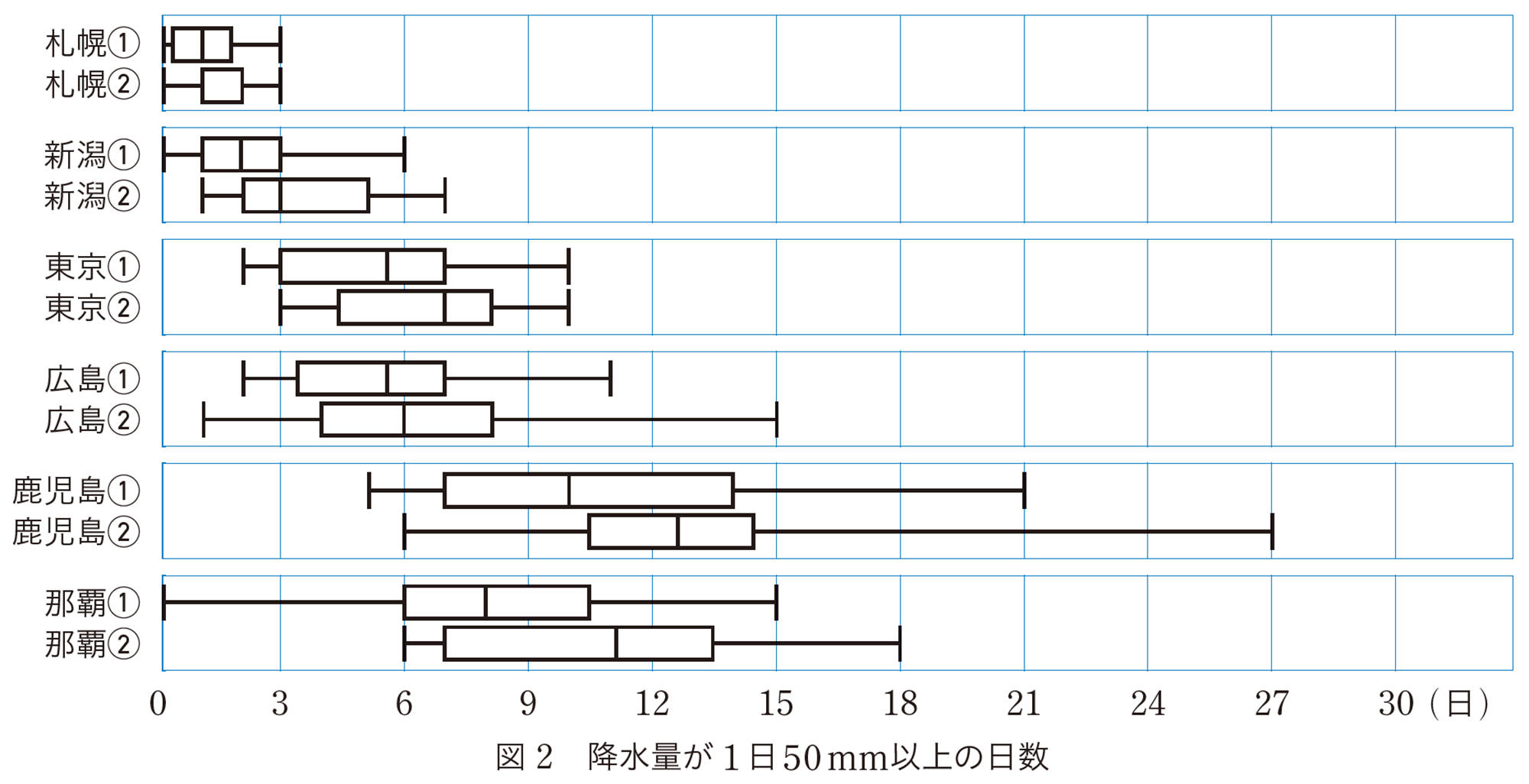
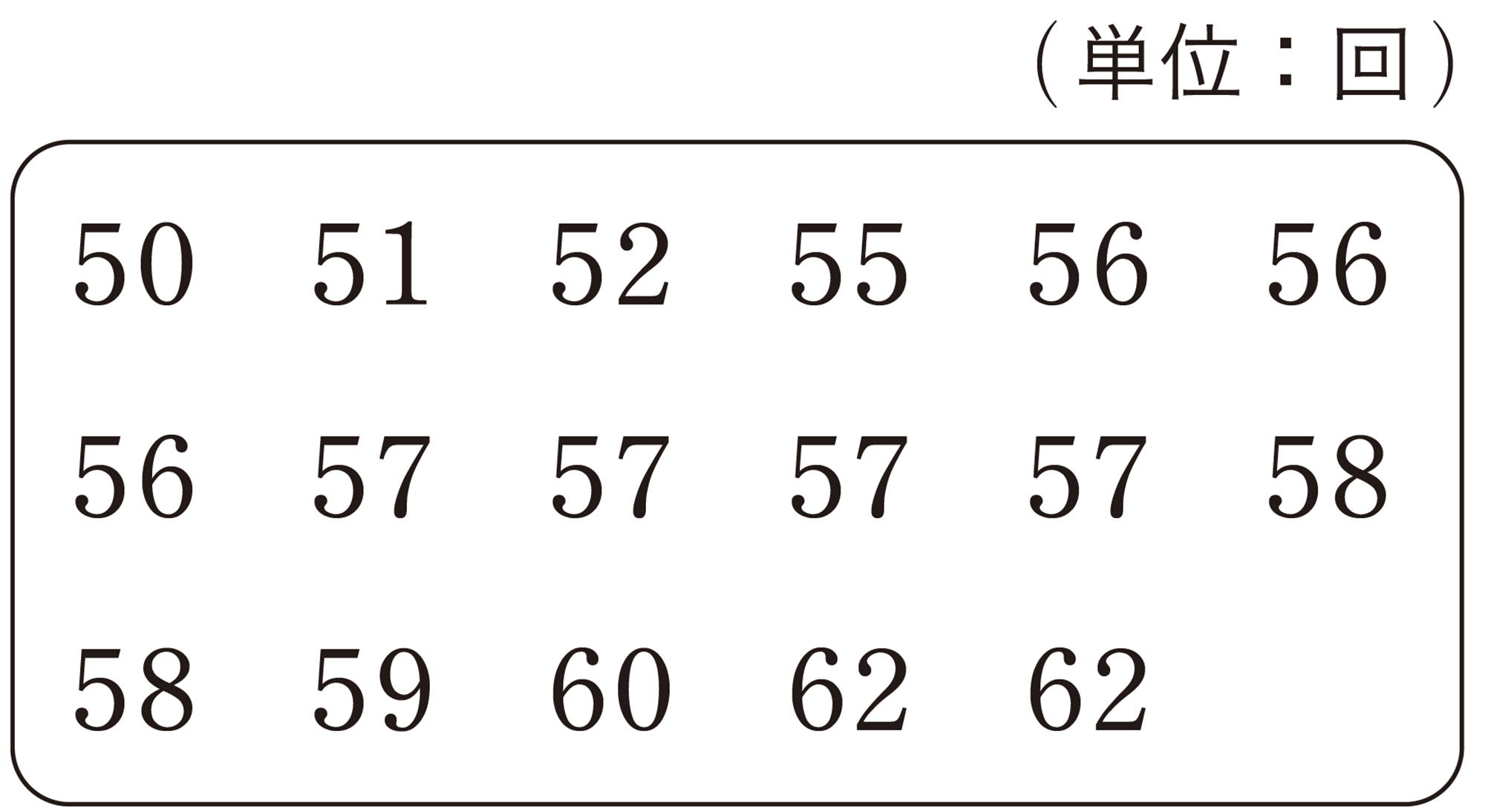
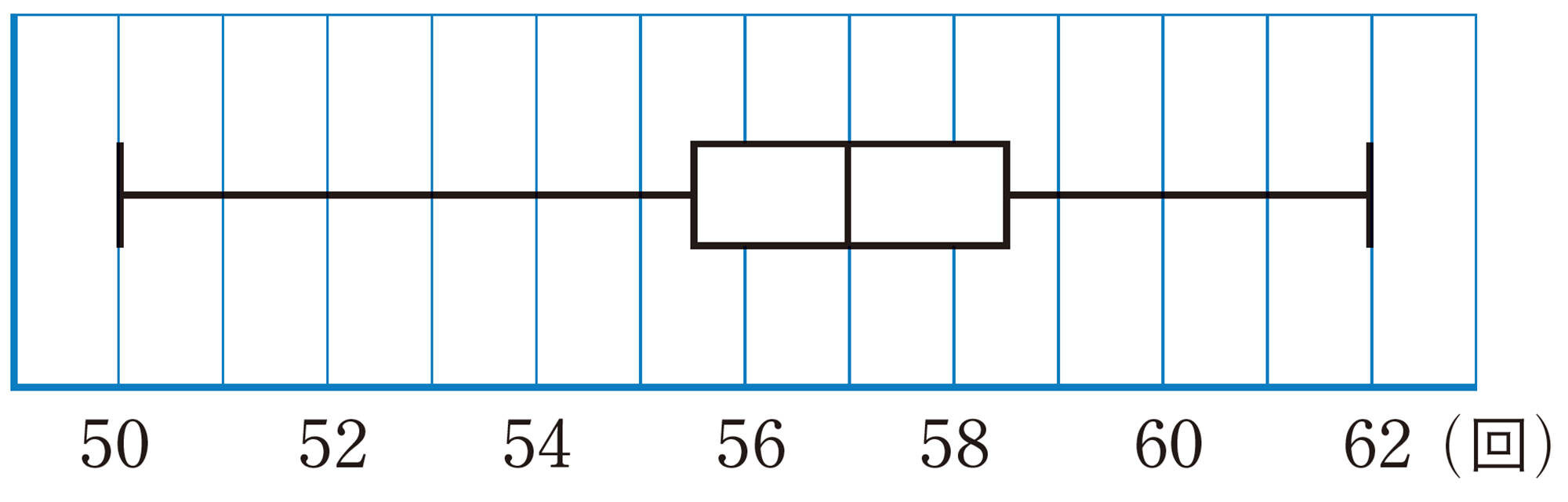
あるクラスの17人の反復横とびのデータを少ない順に並べると，次のようになりました。また，このデータを前ページの図2のように表すと，図3になります。四角形や線分は，何を表しているでしょうか。
このことから，どんなことがわかるか話し合ってみましょう。
前ページの図2や上の図3は，どのように見ればいいのかな。
どのようにかいたのかな。
見方・考え方
どこに着目して考えればいいかな。
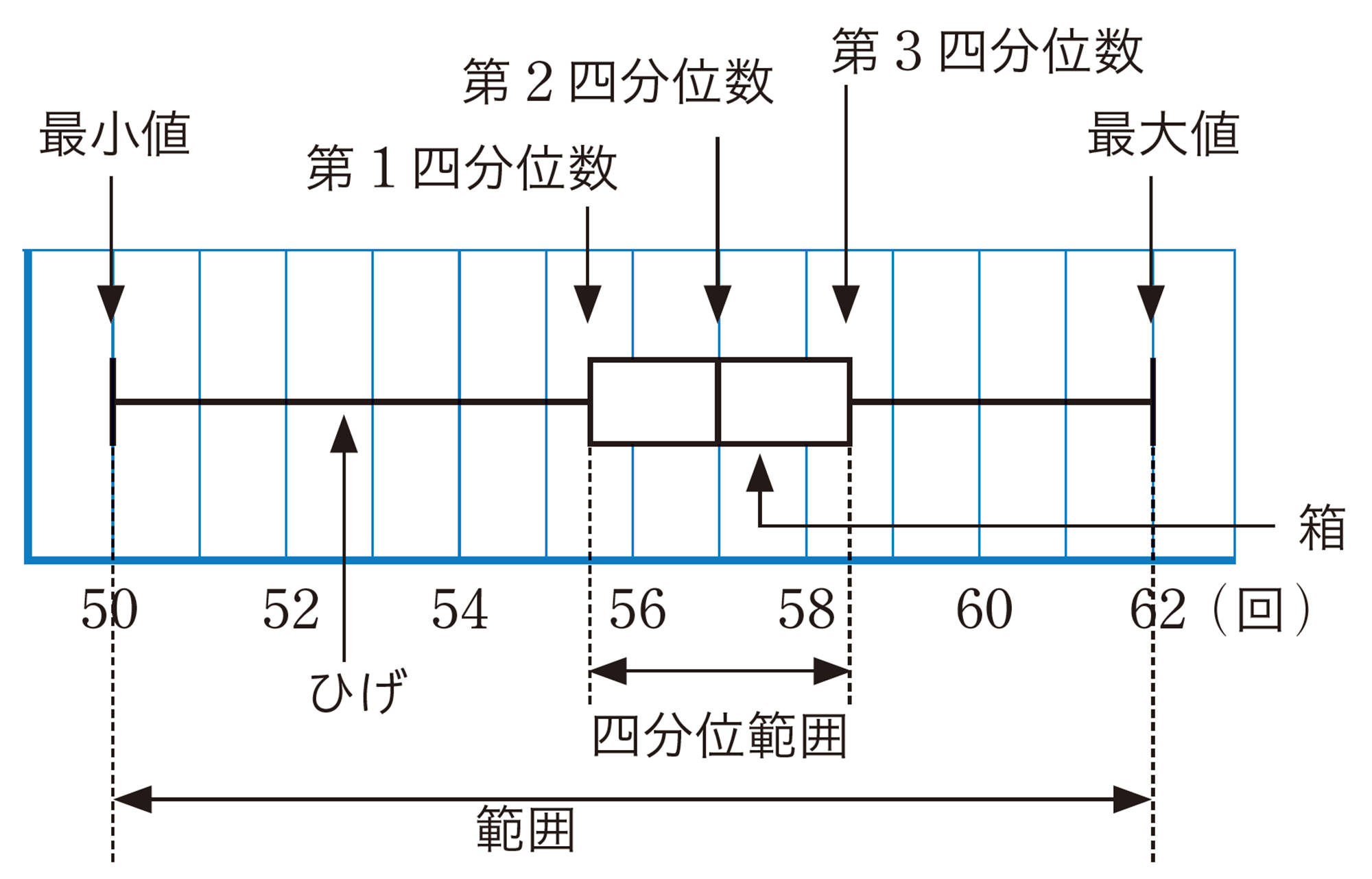
前ページの図2や，Qの図3のようなグラフを箱ひげ図という。
目標 ▷ 箱ひげ図について調べよう。
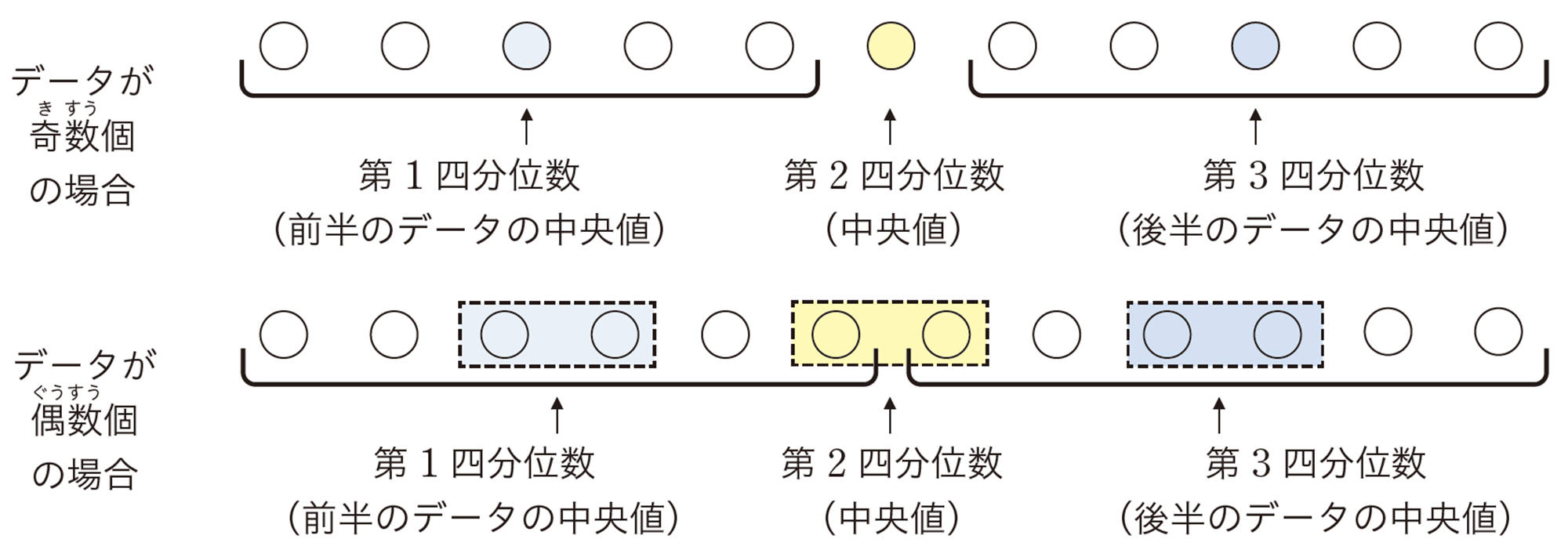
あるデータを小さい順に並べたとき，そのデータを4等分したときの3つの区切りの値を小さい方から順に，第1四分位数 ，第2四分位数（中央値），第3四分位数といい，これらをまとめて四分位数という。
<2年p.205>
例 １ 前ページのQの反復横とびのデータでは，第2四分位数（中央値）は，9番目の57回となる。この9番目の値の前後で2つに分けたときの1番目から8番目の値の中央値[mathjax]\(55.5\)回が第1四分位数となり，10番目から17番目の値の中央値[mathjax]\(58.5\)回が第3四分位数となる。
第3四分位数と第1四分位数の差を，四分位範囲という。前ページのQの反復横とびのデータの四分位範囲は，次のようになる。
[mathjax]\(58.5-55.5=3\)（回）
箱ひげ図は，右の図のように，最小値，第1四分位数，第2四分位数，第3四分位数，最大値を使って表されている。
また，ひげの端から端までの長さは範囲，箱の幅は四分位範囲を表している。
注意 箱ひげ図は，縦，横どちらで表してもよい。
問 １ 10人でルーラーキャッチを行ったデータを調べたところ，右のようになりました。このデータについて，次の図に箱ひげ図で表しなさい。
（単位：cm）
どんなことがわかったかな
データの分布を，四分位数や箱ひげ図で表すことができます。
次の課題へ！
箱ひげ図からは，どんなことが読み取れるのかな？
P.206
