<2年p.189>
2 いろいろな確率
Q Question
目標 ▷ 起こり得るすべての場合が同様に確からしいときの確率を求めよう。
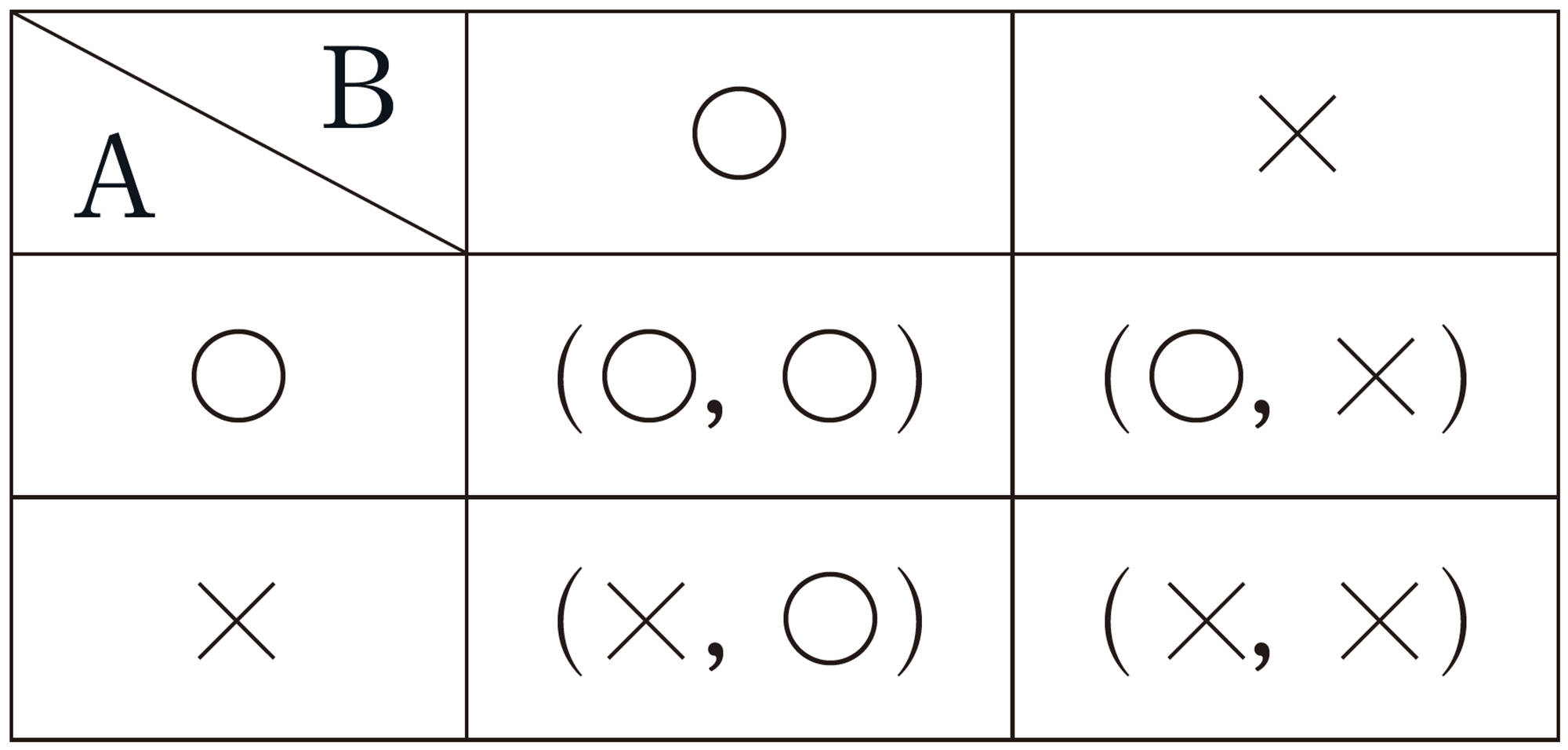
2枚の硬貨の表や裏の出方は,次のように考えることができる。
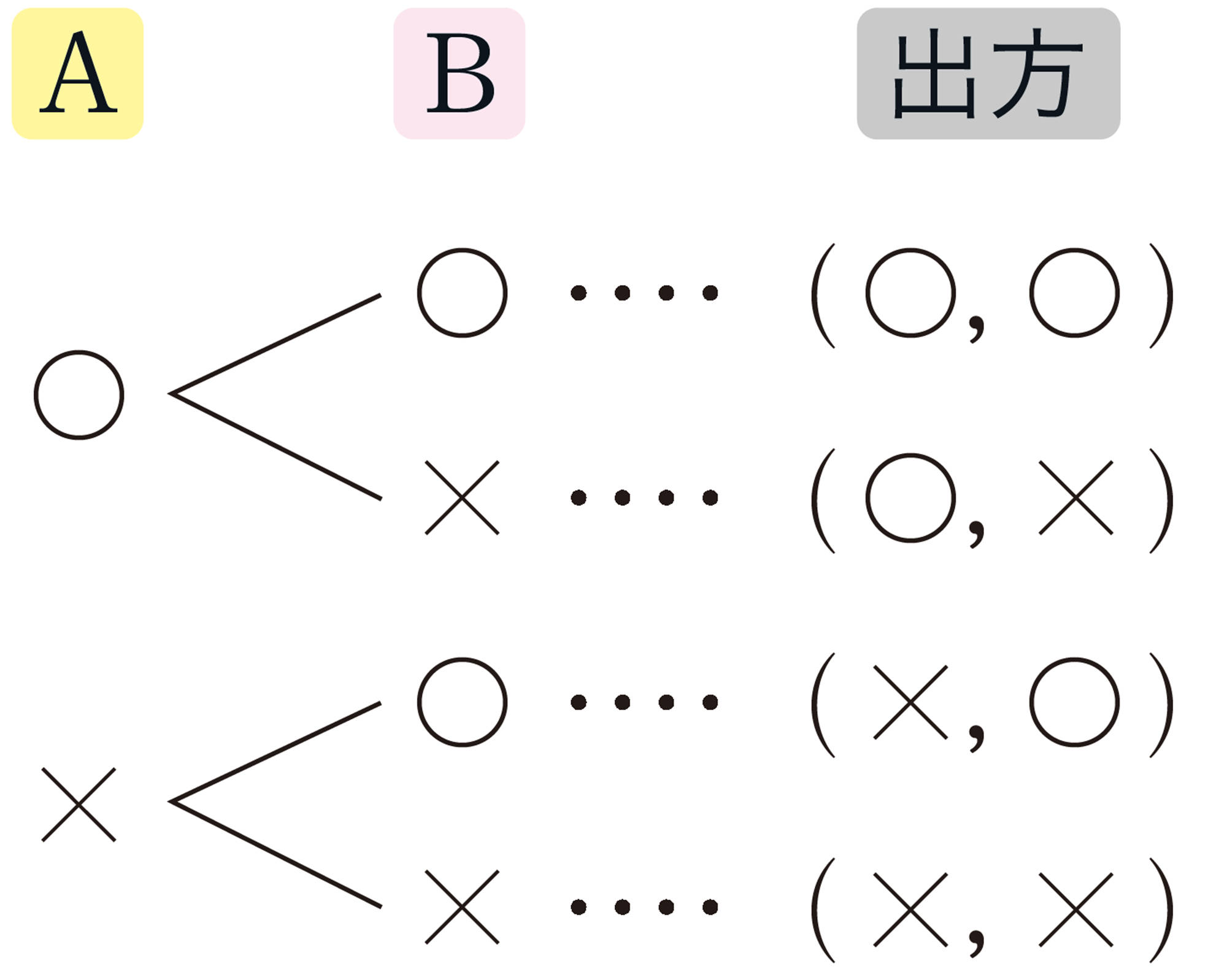
硬貨Aには,表と裏の2通りの出方があり,それぞれについて,硬貨Bにも表と裏の2通りの出方がある。したがって,次の表や図からわかるように,全体では [mathjax]\((2\times 2)\) 通りの場合がある。
㋑のような図を,樹形図 という。
この場合,(○ , ○),(○ ,×),(× , ○),(× ,×)の4通りは,どれも同様に確からしい。このうち,1枚が表でもう1枚が裏になる場合は,(○,×),(× , ○)の2通りあるから,その確率は次のようになる。
[mathjax]\(\dfrac{2}{4}=\dfrac{1}{2}\)
問 1 2枚の硬貨A,Bを同時に投げるとき,次の確率を求めなさい。
⑴ 2枚とも表になる確率
⑵ 2枚とも裏になる確率
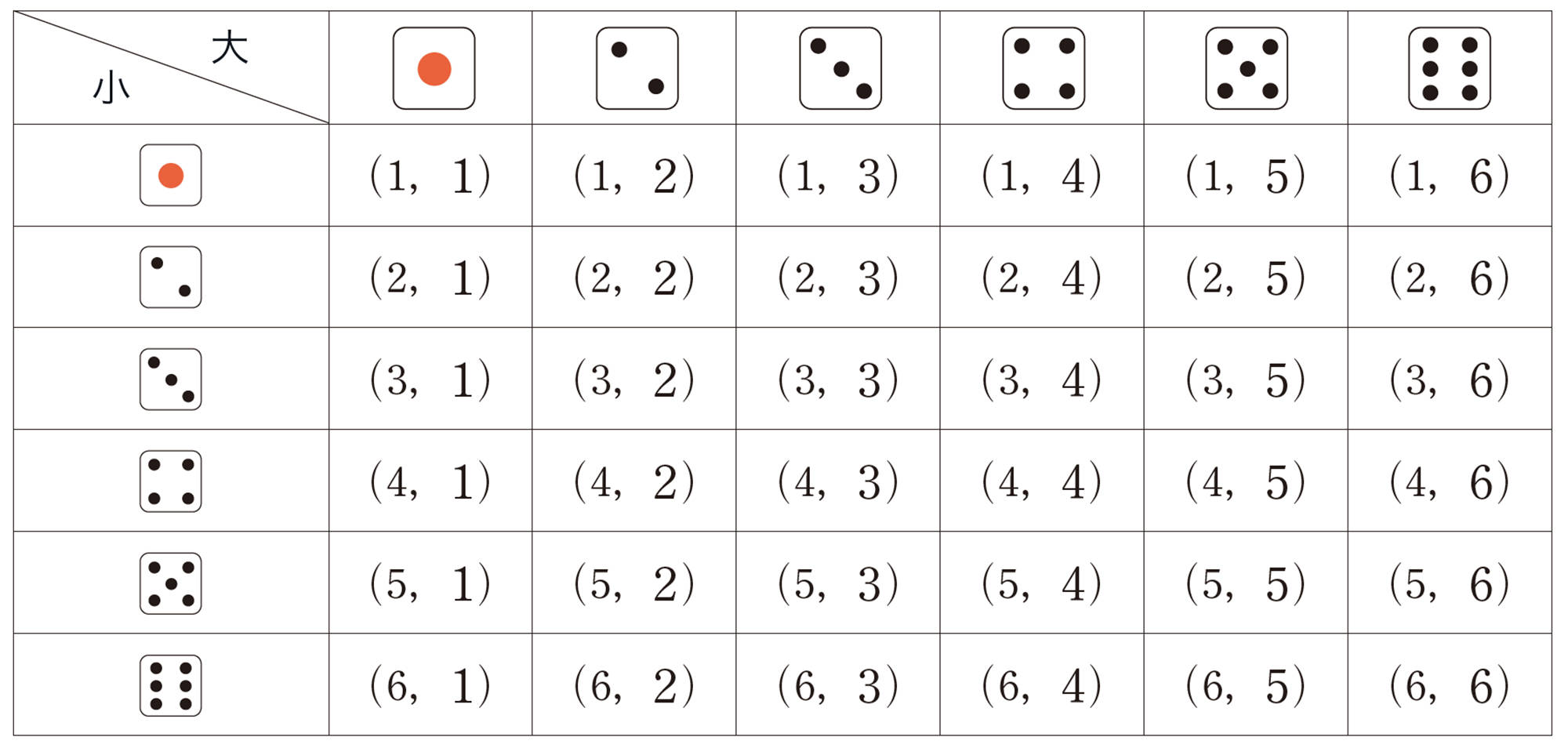
考え方 2つのさいころを投げるときに起こり得るすべての場合を,次のような表をつくって,出る目の和が9になる場合が何通りあるかを調べる。
解答
起こり得る場合が全部で36通りあり,どの目の組み合わせが出ることも同様に確からしい。このうち, 目の和が9になる場合は,
[mathjax]\((3, 6)\),[mathjax]\((4, 5)\),[mathjax]\((5, 4)\),[mathjax]\((6, 3)\)
の4通りあるから,求める確率は,
[mathjax]\(\dfrac{4}{36}=\dfrac{1}{9}\)
答 [mathjax] \( \dfrac{1}{9} \)
<2年p.191>
問 4 大小2つのさいころを同時に投げるとき,次の問いに答えなさい。
⑴ 出る目の和が4になる確率を求めなさい。
⑵ 出る目の和が10以上になる確率を求めなさい。
⑶ 出る目の和がいくらのとき,確率がもっとも大きくなりますか。
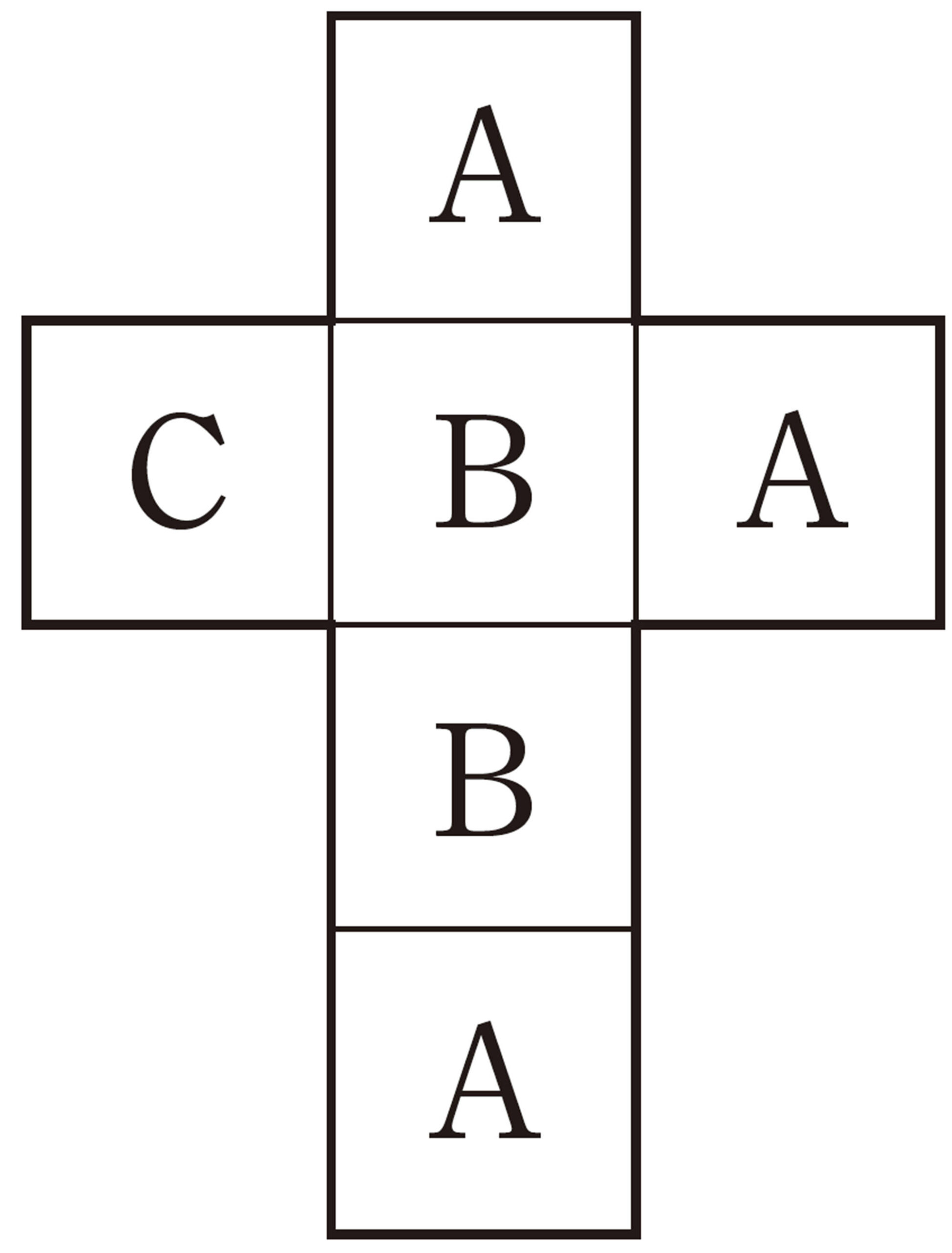
問 5 182,183ページの問題で,㋐~㋕の確率をそれぞれ求め,「1 等」と「はずれ」を決めなさい。
㋐ [mathjax]\(\large{\boxed{A} \ \boxed{A}}\)
㋑ [mathjax]\(\large{\boxed{A} \ \boxed{B}}\)
㋒ [mathjax]\(\large{\boxed{A} \ \boxed{C}}\)
㋓ [mathjax]\(\large{\boxed{B} \ \boxed{B}}\)
㋔ [mathjax]\(\large{\boxed{B} \ \boxed{C}}\)
㋕ [mathjax]\(\large{\boxed{C} \ \boxed{C}}\)
<2年p.192>
Q Question
2人でくじ引きをするとき,先に引くかあとに引くか,どちらを選んだ方が当たりやすいでしょうか。

早いもの勝ちだから,先の方がいいんじゃないかな。
でも,残り物には福があるともいうよね。

見方・考え方
具体的な場面で考えられるかな。

Aの当たる確率が[mathjax]\(\dfrac{1}{3}\)なのはわかるね。だけど,Bの当たる確率はAの結果によるからわからないね。
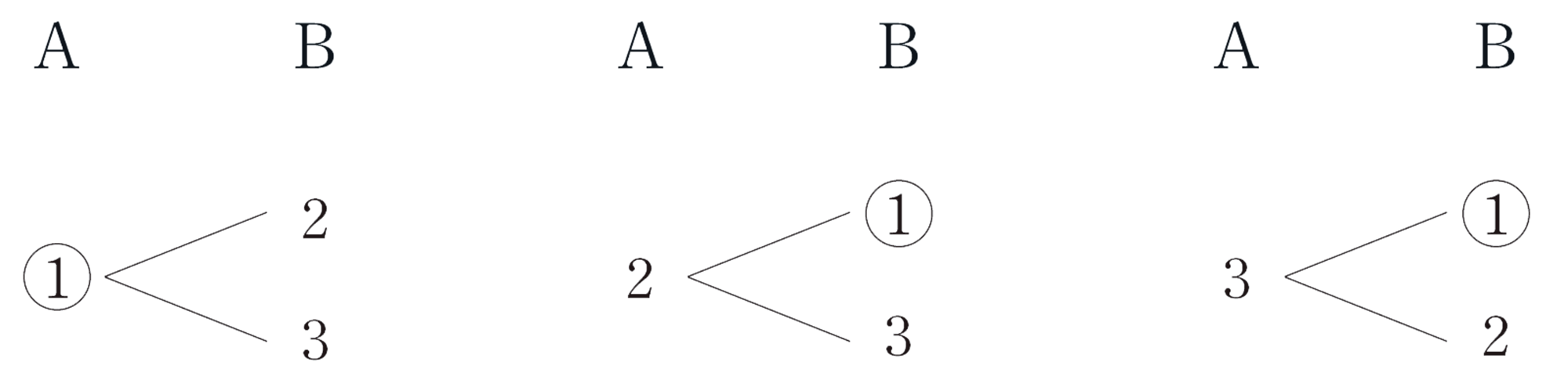
かりに,Aが①を引いたら,Bは2か3。2を引いたら,①か3。このように,仮定して考えればいいよ。


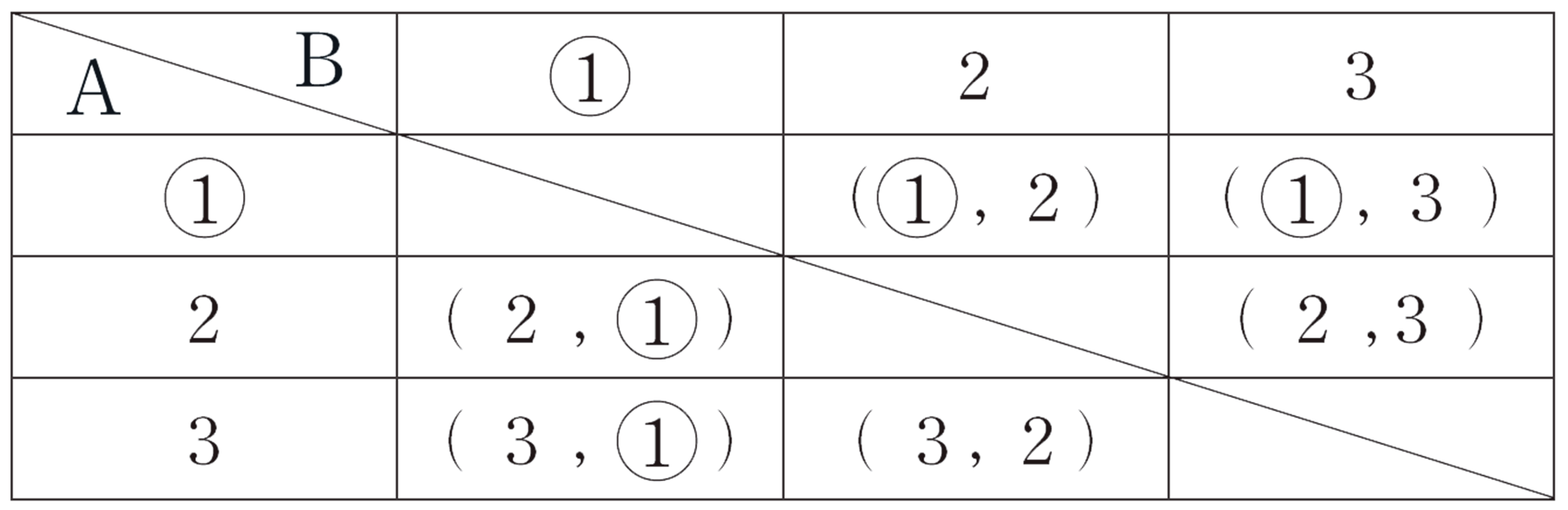
そうだね。そのことをわかりやすく表すにはどうしたらいいかな。
図や表を使って表せば,よさそうだよ。

⑵ 次の2人の考えを説明しましょう。また,拓真さん,美月さんの考えで,それぞれのA,Bが当たる確率を求めましょう。
<2年p.193>
⑶ これまでのことから,このくじを引くとき,先に引くかあとに引くか,どちらを選んだ方がよいと考えられるでしょうか。
本数などの条件を変えると,当たる確率はどうなるのかな。

3 当たりの本数やはずれの本数をいろいろと変えて,くじを引く順番と当たる確率について調べてみましょう。
当たりを3本,はずれを2本にして,2人でくじを引くとどうなるかな。


当たりを1本,はずれを3本にして,2人でくじを引いたときはどうなるかな
4 自分で求めた結果や,友だちが求めた結果をもとにして,くじ引きでは,引く順番と当たる確率にどんな関係があるか話し合ってみましょう。
2人でくじ引きをしたときは,先に引いてもあとに引いても,当たる確率は変わらなそうだね。


くじを引く人数が変わっても,同じことがいえるのかな。
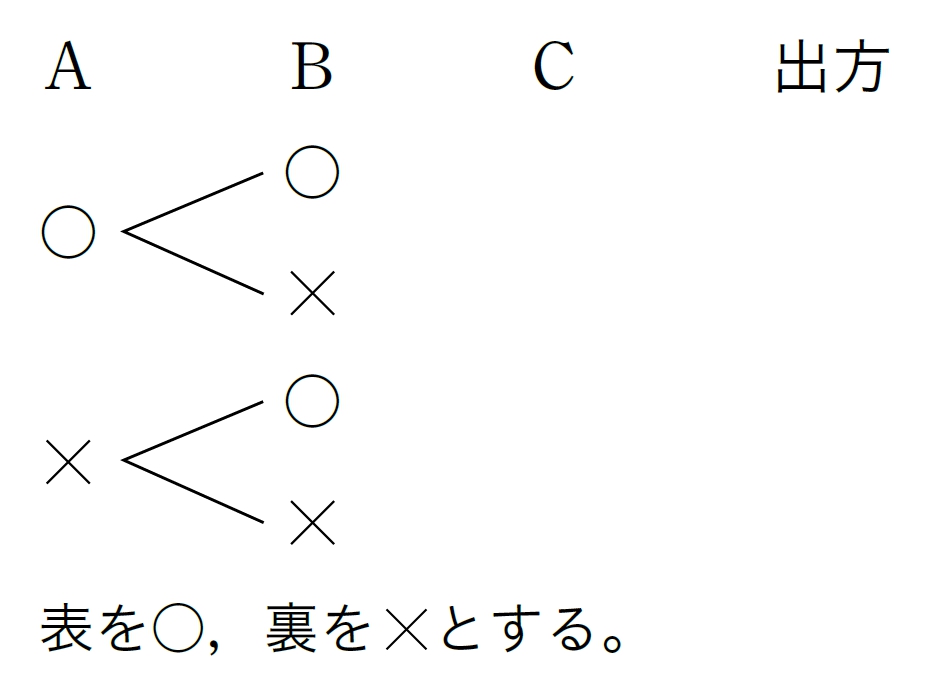
問 6 3枚のカードの中に1枚だけ当たりのカードがあります。この3枚のカードを,A,B,Cの3人が順に1枚ずつ引くとき,カードを引く順番と当たりやすさには関係があるか,確率をもとに説明しなさい。ただし,引いたカードは,もとにもどさないものとします。
3人で引くとき,表で考えることはできるかな。

<2年p.194>
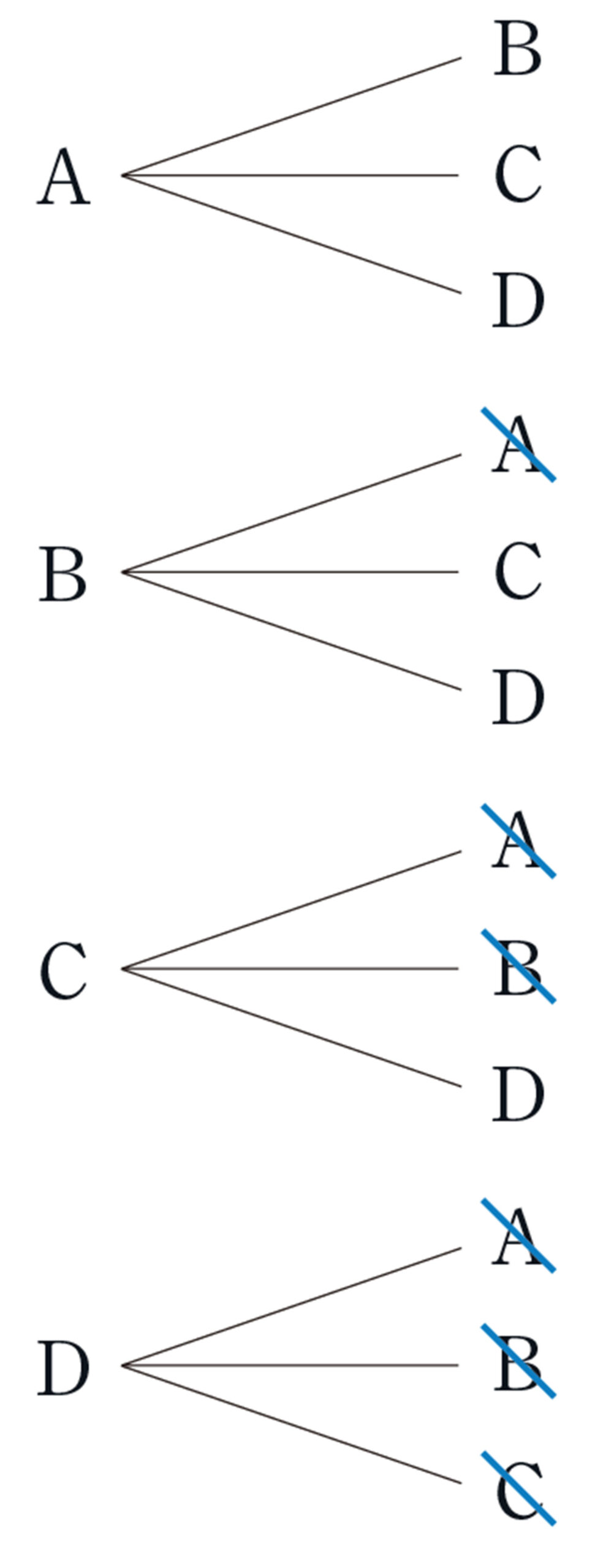
考え方 この場合,選ばれる順番は関係しない。たとえば,AとBが選ばれることと,BとAが選ばれることは同じと考えてよい。この選び方を,[mathjax]\(\{A,B\}\) と書くことにして,場合の数を求める。
解答
これまでと同じように考えることもできるけど,[mathjax]\(B-A\)と[mathjax]\(A-B\) が同じと考えると,簡単になるね。


表を使っても考えられそうだね。
問 7 例2で,生徒Dが選ばれる確率を求めなさい。
問 8 A,B,C,D,Eの5つのサッカーチームの中から,2つのチームをくじで選ぶとき,次の確率を求めなさい。
⑴ AとEの2 チームが選ばれる確率
⑵ Cが選ばれる確率
どんなことがわかったかな
起こり得るすべての場合が同様に確からしいとき,すべての場合を樹形図や表を使って数え上げることで,その確率を求めることができます。