<2年p.170>
３ 特別な平行四辺形
Q Question
次の表の四角形で，左側にあげた性質をつねにもつものには〇，そうでないものには×を書き入れてみましょう。また，この表から，気づいたことを話し合ってみましょう。
平行四辺形になるための条件を満たすのは，どんな四角形かな。
ほかの図形でも，共通することがあるのかな。
見方・考え方
まとめて見ると，どんなことがわかるかな。
目標 ▷ 平行四辺形になるための条件を満たす四角形について調べよう。
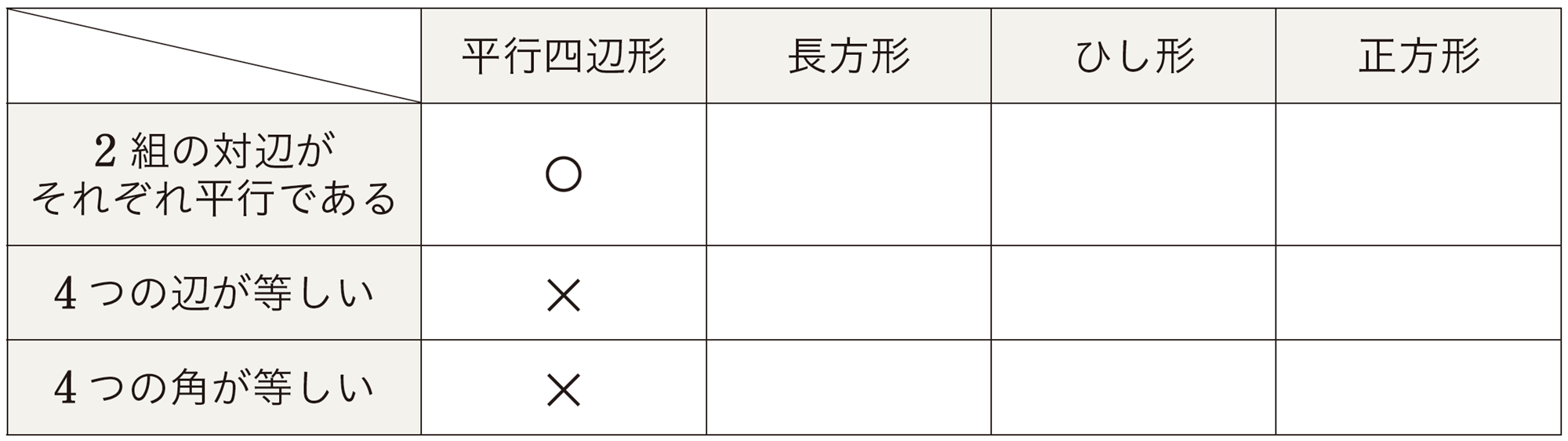
長方形，ひし形，正方形は，次のように定義される。
定義
4つの角が等しい四角形を長方形という。
4つの辺が等しい四角形をひし形という。
4つの角が等しく，4つの辺が等しい四角形を正方形という。
長方形の定義「4つの角が等しい四角形」は，平行四辺形になるための条件「2組の対角がそれぞれ等しい」を満たしている。
したがって，長方形は平行四辺形であるといえる。
問 １ ひし形は平行四辺形といえますか。また，その理由を説明しなさい。
<2年p.171>
長方形やひし形，正方形は，平行四辺形の特別な場合である。したがって，これらの四角形は，平行四辺形の性質をすべてもっている。
また，正方形は，長方形の特別な場合であり，ひし形の特別な場合でもある。したがって，正方形は，長方形とひし形の両方の性質をもっている。
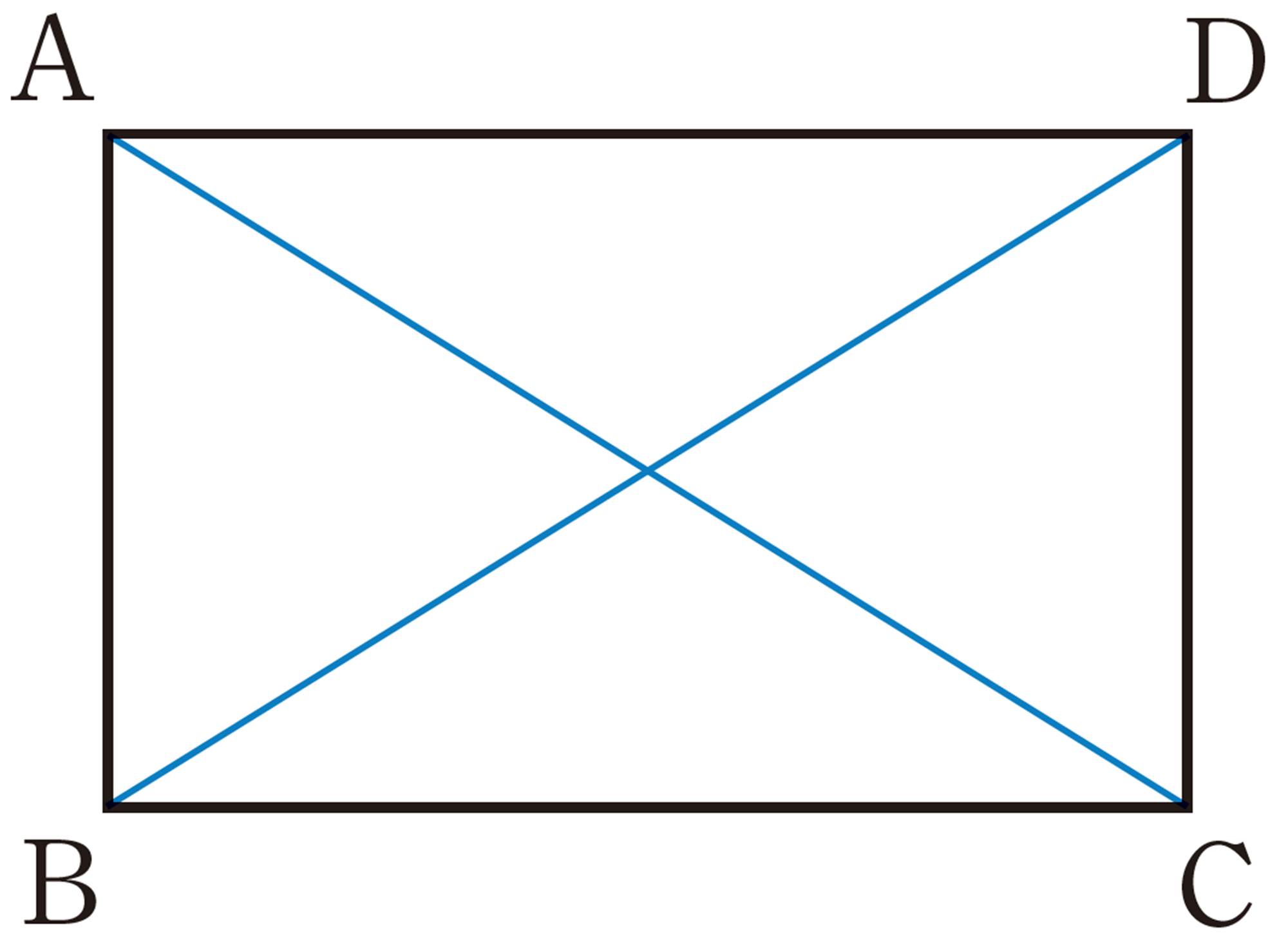
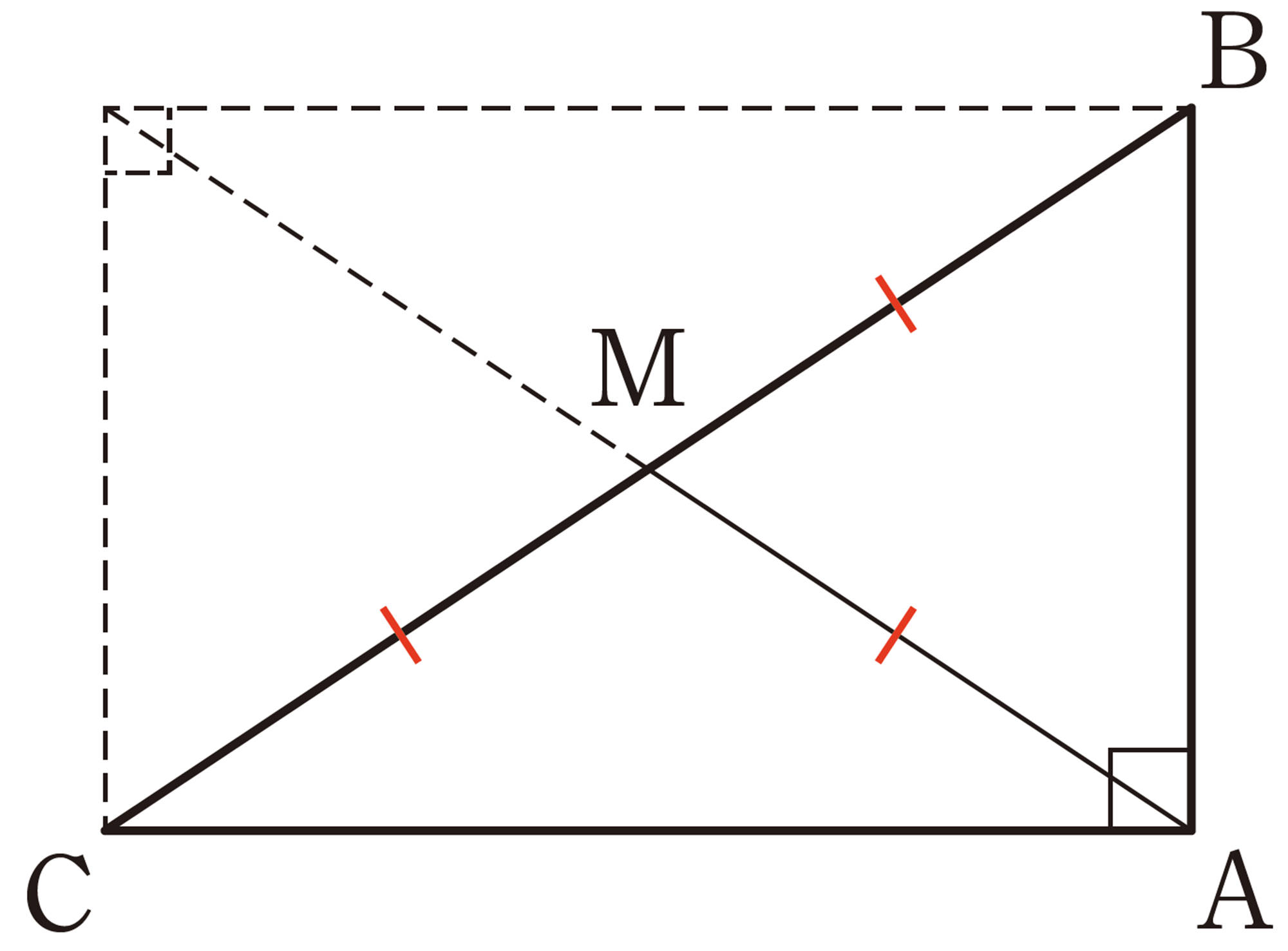
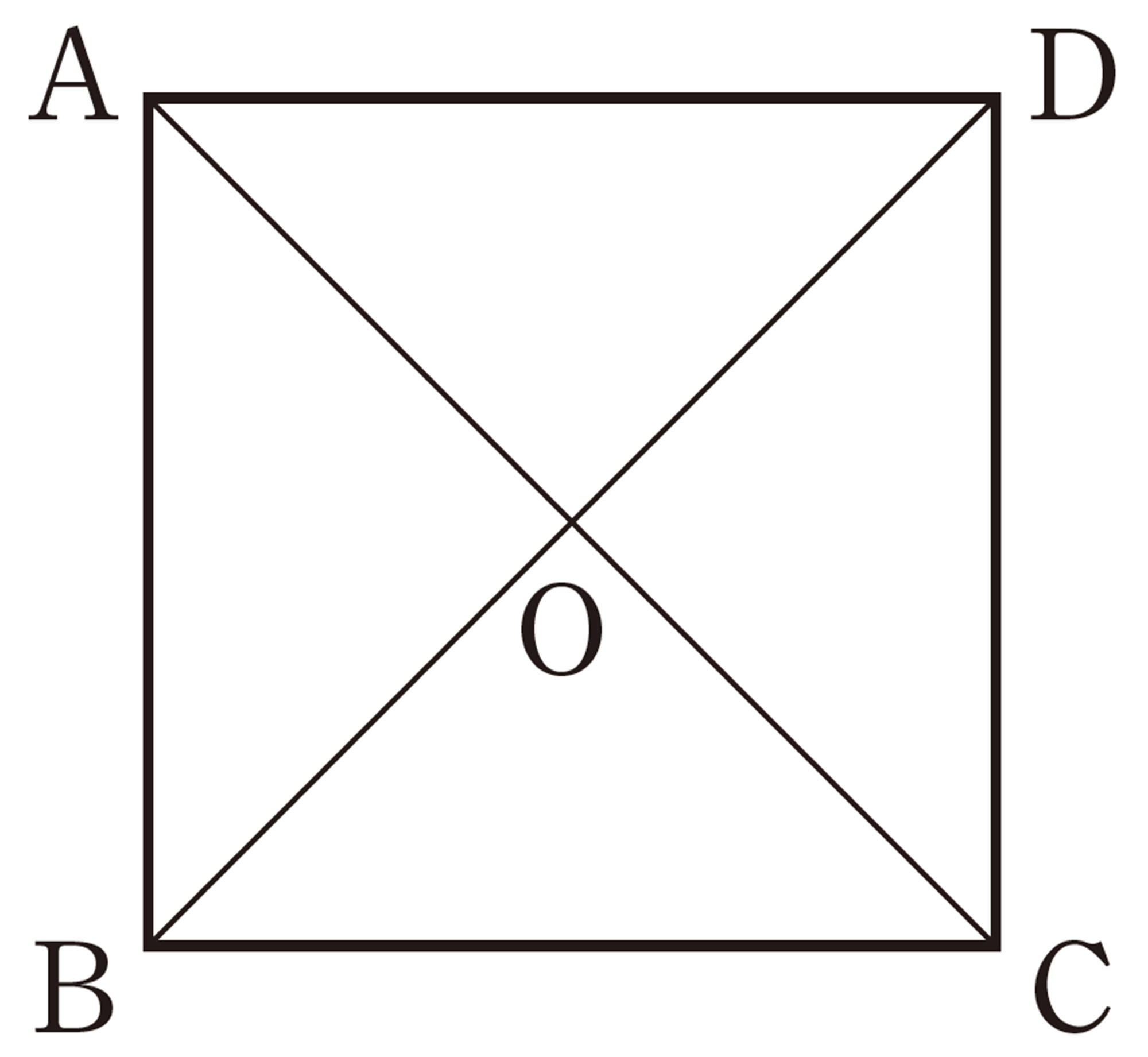
例 １ 長方形ABCDで，2つの対角線ACとDBの長さは等しいことを証明しなさい。
証明
[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle DCB\) において，
仮定から，
[mathjax]\(\angle ABC=\angle DCB\quad\cdots\cdots\text{①}\)
長方形の対辺は等しいから，
[mathjax]\(AB=DC\qquad\cdots\cdots\text{②}\)
また，BC は共通[mathjax]\(\cdots\cdots\text{③}\)
①， ②， ③より， 2 組の辺とその間の角がそれぞれ等しいから，
[mathjax] \(\hspace{40pt}\triangle ABC\equiv \triangle DCB\)
したがって，[mathjax]\(\hspace{7pt}AC=DB\)
平行四辺形の性質が使えるね。
問 ２ ひし形ABCDで，2つの対角線ACとBDは垂直に交わることを証明しなさい。ただし，ACとBDの交点をOとします。
長方形，ひし形，正方形の対角線には，次のような性質がある。
⑴ 長方形の対角線は長さが等しい。
⑵ ひし形の対角線は垂直に交わる。
⑶ 正方形の対角線は長さが等しく，垂直に交わる。
長方形の対角線の性質から，右の図のように，直角三角形ABCの斜辺BCの中点をMとするとき，[mathjax]\(AM=BM=CM\) であることがわかる。
<2年p.172>
Q Question
平行四辺形にどんな条件を加えれば，長方形，ひし形，正方形になるかを考えてみましょう。
辺の長さや角の大きさが等しいとき，どうなるかな。
見方・考え方
どこに着目して考えればいいかな。
１ ▱ABCDに，次の㋐や㋑の条件を加えると，それぞれどんな四角形になるでしょうか。
㋐ [mathjax]\(AB=BC\)
㋑ [mathjax]\(\angle A=90^{\circ}\)
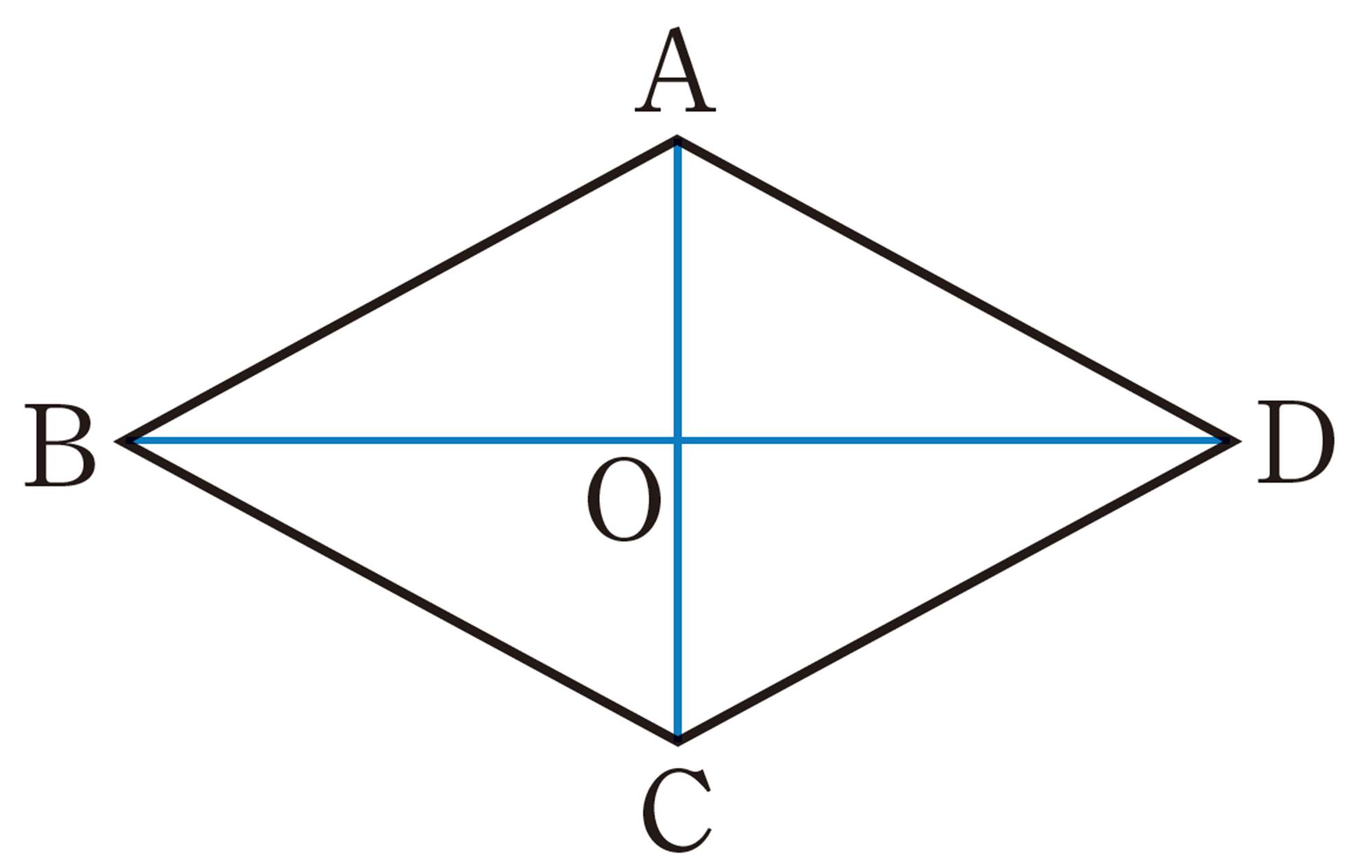
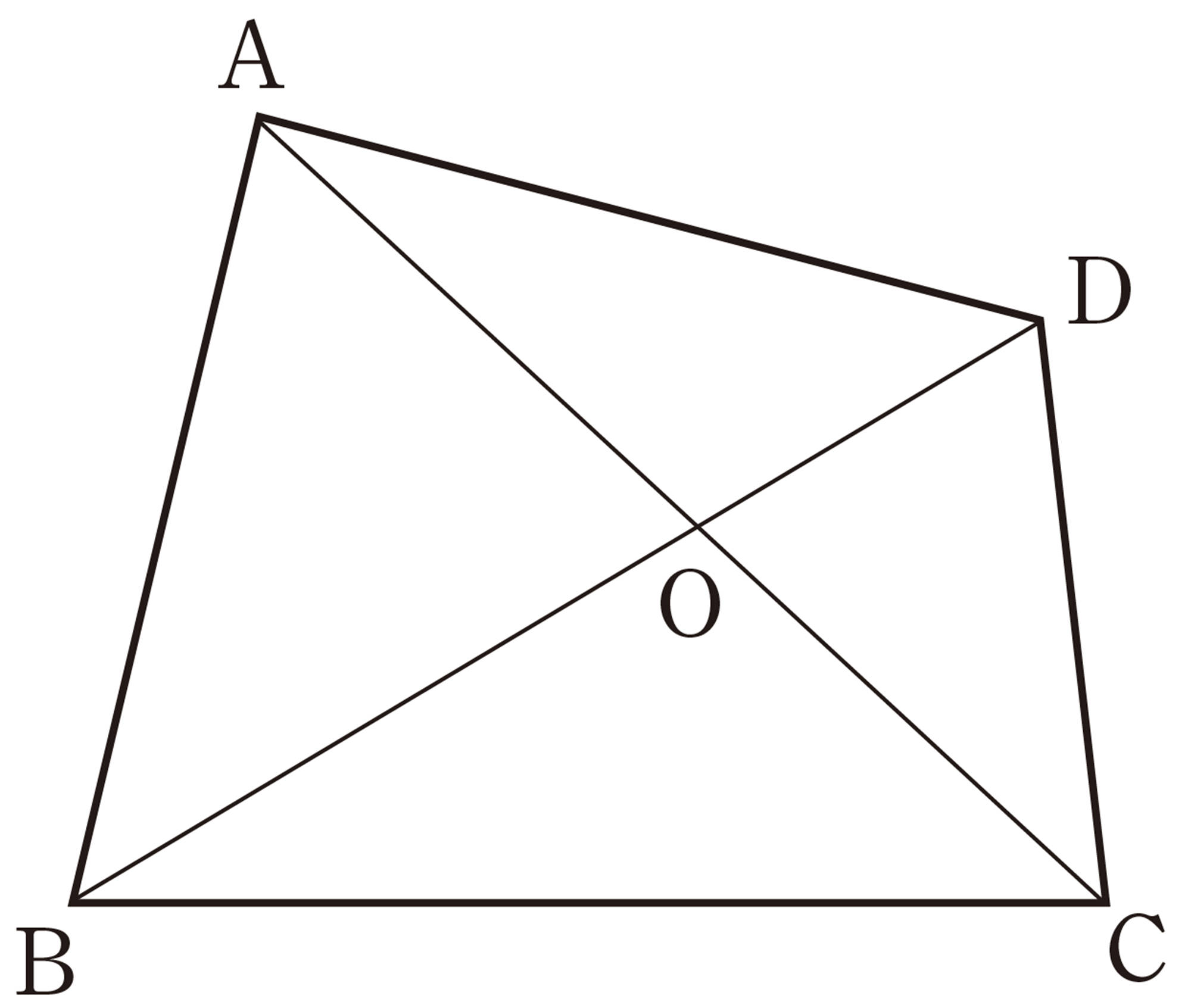
２ 美月さんは，【１】 ㋐について，この四角形はひし形になると考え，次のように説明しました。
美月さんの考え
平行四辺形の対辺は等しいから，[mathjax]\(AB=DC\)，[mathjax]\(AD=BC\)である。これに，[mathjax]\(AB=BC\)，つまり，となり合う辺が等しいという条件を加えると，4つの辺がすべて等しくなる。
したがって，▱ABCDはひし形になる。
【１】 ㋑について，この四角形が長方形になることを説明してみましょう。
３ 平行四辺形が長方形やひし形になるためには，ほかにどんな条件があるでしょうか。また，正方形になるためには，さらにどんな条件を加えればよいでしょうか。条件を考え，その理由を説明してみましょう。
対角線を使って考えられるかな。
どんなことがわかったかな
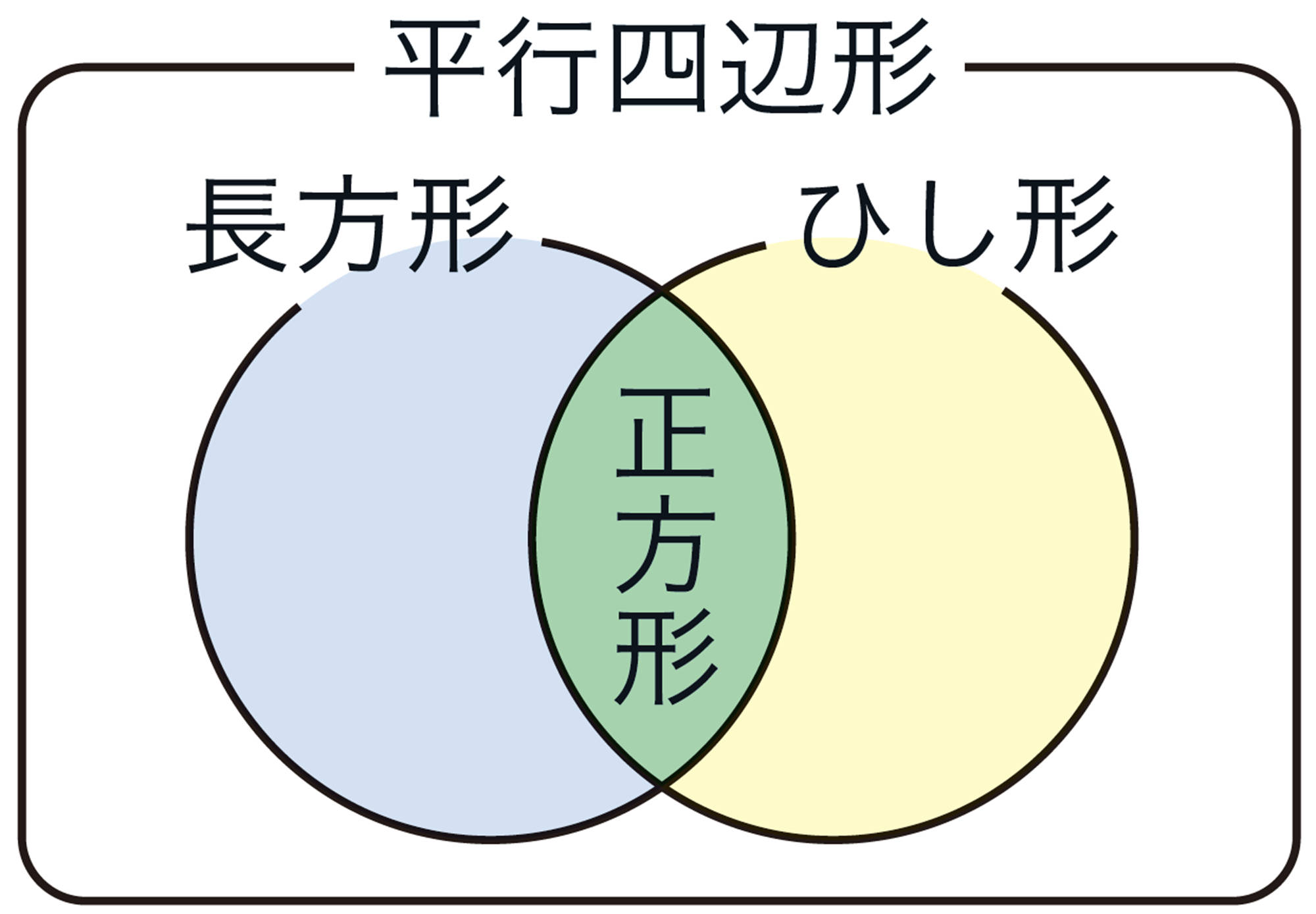
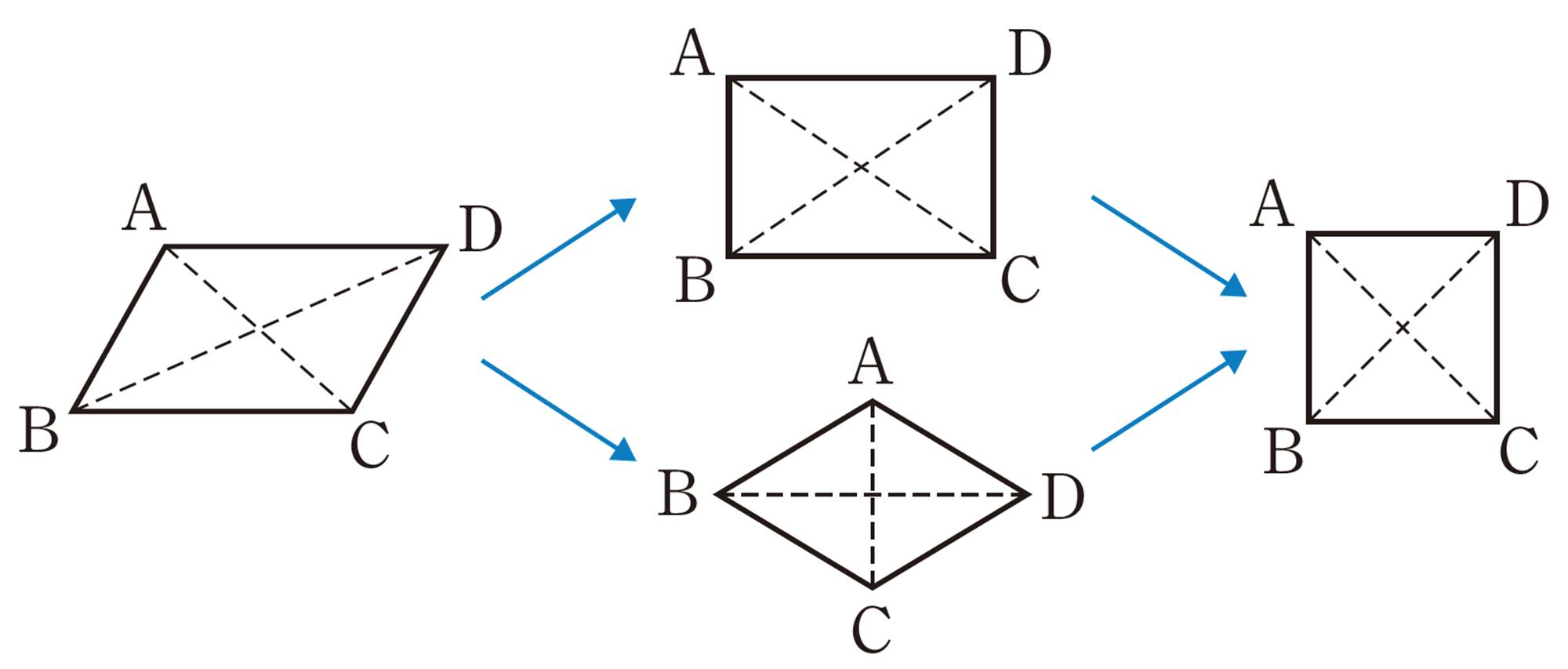
長方形やひし形，正方形は，平行四辺形になるための条件を満たしているため，平行四辺形であるとまとめることができます。
<2年p.173>
確かめよう ２節 四角形
１ 平行四辺形の定義をいいなさい。
２ ▱ABCDの辺AD，BC上に，[mathjax]\(AE=CF\)となるようにそれぞれ点E，Fをとるとき，[mathjax]\(BE=DF\)であることを証明しなさい。
３ 次の㋐〜㋓のうち，四角形ABCD が必ず平行四辺形になるのはどの場合ですか。
㋐ [mathjax]\(AD/\!/BC\)，[mathjax]\(AB=DC\)
㋑ [mathjax]\(AB/\!/DC\)，[mathjax]\(AB=DC\)
㋒ [mathjax]\(AO=CO\)，[mathjax]\(BO=DO\)
㋓ [mathjax]\(AO=BO\)，[mathjax]\(CO=DO\)
４ [mathjax]\(\triangle ABC\)の辺AB，ACの中点をそれぞれD，Eとし，DEの延長上に[mathjax]\(DE=EF\)となるように点Fをとります。
このとき，次の問いに答えなさい。
⑴ 四角形ADCFは平行四辺形であることを証明しなさい。
⑵ [mathjax]\(DF=BC\)であることを証明しなさい。
５ 正方形の対角線にはどんな性質がありますか。右の図の正方形ABCDを使って表しなさい。
<2年p.174>
5章 「三角形・四角形」を学んで
できるようになったこと
二等辺三角形の性質や，二等辺三角形になるための条件を理解し，それらを使って図形の新たな性質が成り立つことを証明することができる。
平行四辺形の性質や，平行四辺形になるための条件を理解し，それらを使って図形の新たな性質が成り立つことを証明することができる。
正三角形が二等辺三角形の特別な場合であることや，長方形やひし形，正方形は平行四辺形の特別な場合であることを理解することができる。
身のまわりや数学の中から見つけた問題を，学んできた図形の性質を使って解決することができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない ワイパーの形
右の写真のように，車の窓ガラスには，窓についた水滴や汚れをふき取るためのワイパーがついています。このワイパーを図で表すと，右の図のようになります。このとき，ワイパーを支える部分は，[mathjax]\(AB=DC\)，[mathjax]\(AD=BC\)となっていて，つねに平行四辺形になるようになっています。
ほかにも，図形の性質を利用したものがないか，探してみましょう。
<2年p.175>
5章のまとめの問題 解答 P.250〜251 基本
１ 次の[mathjax]\(\boxed{\phantom{000}}\)にあてはまることばをいいなさい。
⑴ 二等辺三角形の[mathjax]\(\boxed{\phantom{000}}\)の二等分線は，底辺を垂直に2等分する。
⑵ 2つの直角三角形は，斜辺と[mathjax]\(\boxed{\phantom{00000}}\)，または，斜辺と[mathjax]\(\boxed{\phantom{00000}}\)がそれぞれ等しければ，合同である。
⑶ 平行四辺形の2つの対角線は，それぞれの[mathjax]\(\boxed{\phantom{000}}\)で交わる。
⑷ 長方形は，[mathjax]\(\boxed{\phantom{00000000}}\)と定義される。
２ 頂角[mathjax]\(\angle A=36^{\circ}\)の二等辺三角形ABCで，[mathjax]\(\angle B\)の二等分線を引き，辺ACとの交点をDとするとき，次の問いに答えなさい。
⑴ [mathjax]\(\angle BDC\)の大きさを求めなさい。
⑵ [mathjax]\(\triangle BCD\)はどんな三角形ですか。また，その理由を説明しなさい。
３ ▱ABCDの頂点A ，Cから対角線BDに垂線AE，CFをそれぞれ引くとき，次の問いに答えなさい。
⑴ [mathjax]\(\triangle ABE \equiv \triangle CDF\)であることを証明しなさい。
⑵ 四角形AECFは平行四辺形であることを次のように証明しました。[mathjax]\(\boxed{\phantom{000}}\)をうめて，証明を完成させなさい。
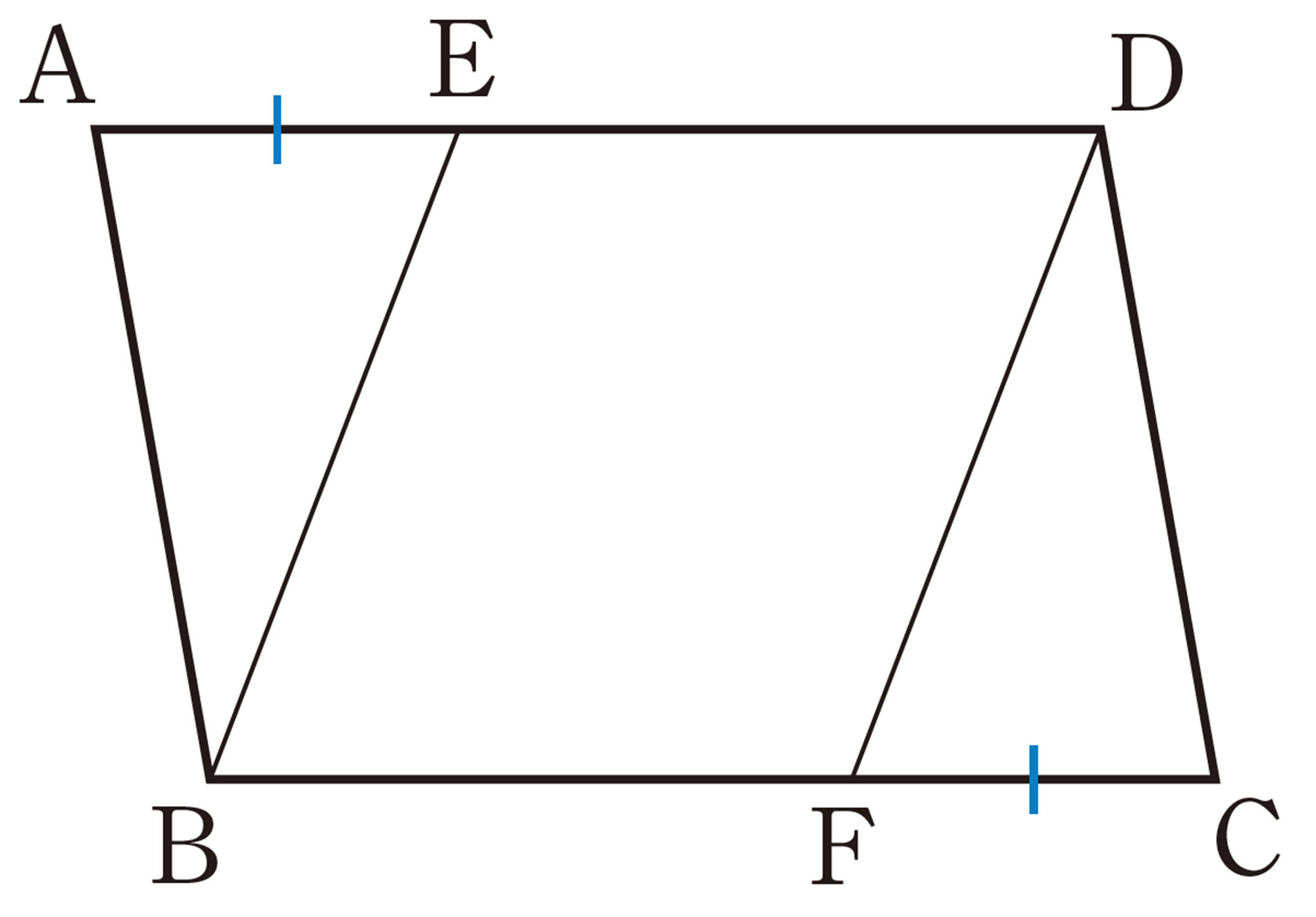
［証明］
[mathjax]\(\triangle ABE\equiv \triangle CDF\)から，[mathjax]\(AE=\boxed{\phantom{000}}\quad\cdots\cdots\text{①}\)
仮定から，[mathjax]\(\hspace{46pt}\angle AEF=\angle CFE\)
[mathjax]\(\boxed{\phantom{000}}\)が等しいから， [mathjax]\(\hspace{20pt}AE /\!/ \ \boxed{\phantom{000}}\quad\cdots\cdots\text{②}\)
①，②より，[mathjax]\(\boxed{\phantom{00000000}}\)から，四角形 AECF は平行四辺形である。
<2年p.176>
４ 右の図のように，[mathjax]\(\triangle ABC\)の辺BCの中点Mから，辺AB，ACへそれぞれ垂線MD，MEを引きます。このとき，[mathjax]\(MD=ME\)ならば，[mathjax]\(\triangle ABC\)はどんな三角形ですか。また，そのことを証明しなさい。
５章のまとめの問題 応用
１ 右の図のように，▱ABCDの4つの角[mathjax]\(\angle A\)，[mathjax]\(\angle B\) ，[mathjax]\(\angle C\) ，[mathjax]\(\angle D\)の二等分線でできる四角形EFGHはどんな四角形ですか。また，▱ABCDが長方形のとき，四角形EFGHはどんな四角形ですか。
２ ▱ABCDで[mathjax]\(BC=2AB\)のとき，CDを延長し，[mathjax]\(CD=CE=DF\)となるように点E，Fをとります。AEとBCの交点をG，BFとADの交点をHとすると，四角形ABGHはひし形であることを証明しなさい。
３ 二等辺三角形ABCの底辺BC上の点Pから，辺 AB，ACに平行な直線を引き，辺AC，ABとの交点をそれぞれQ，Rとします。このとき，[mathjax]\(PQ+PR=AB\)であることを証明しなさい。
<2年p.177>
活用
１ 次の問題は，下のように証明できます。
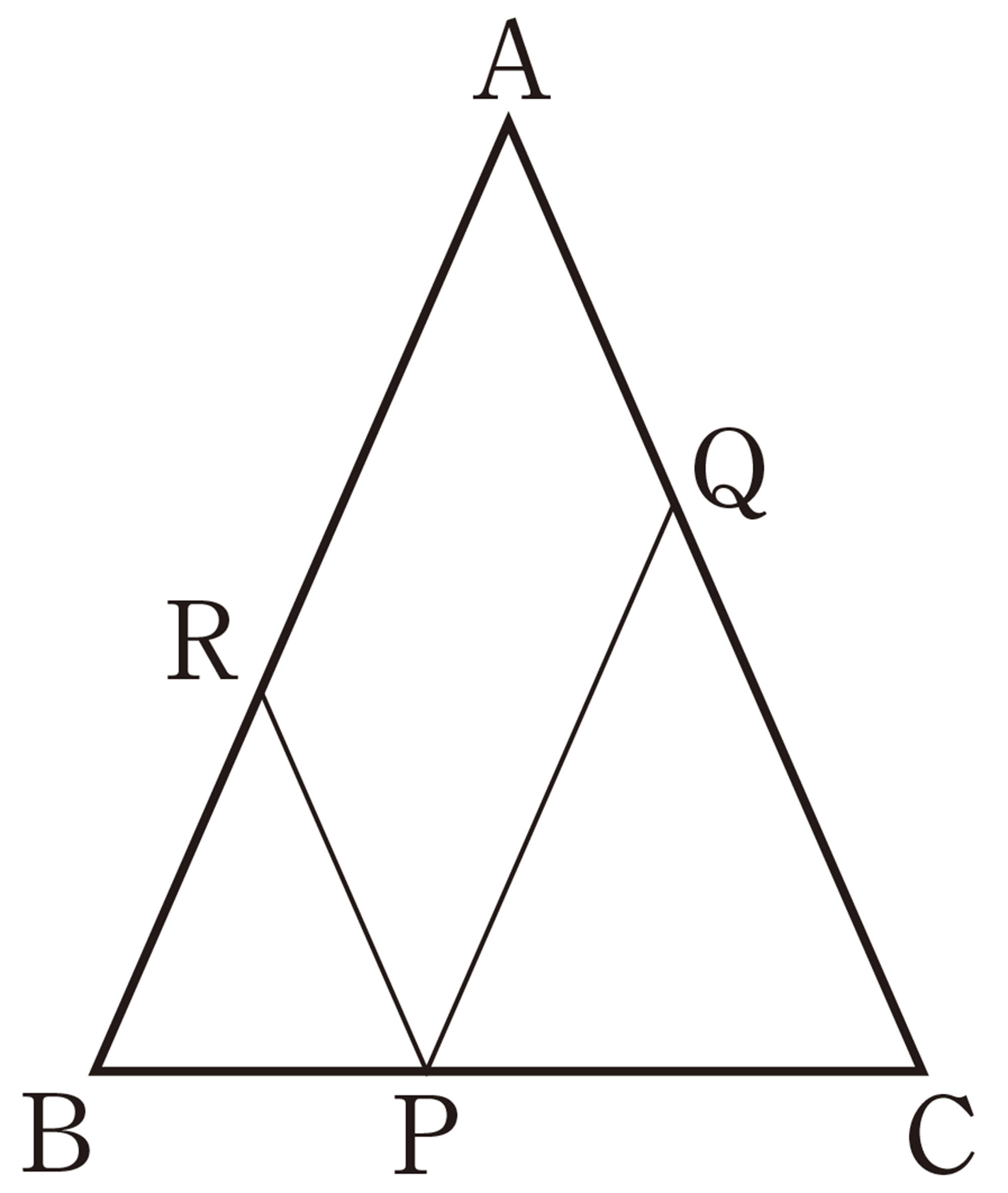
［問題］
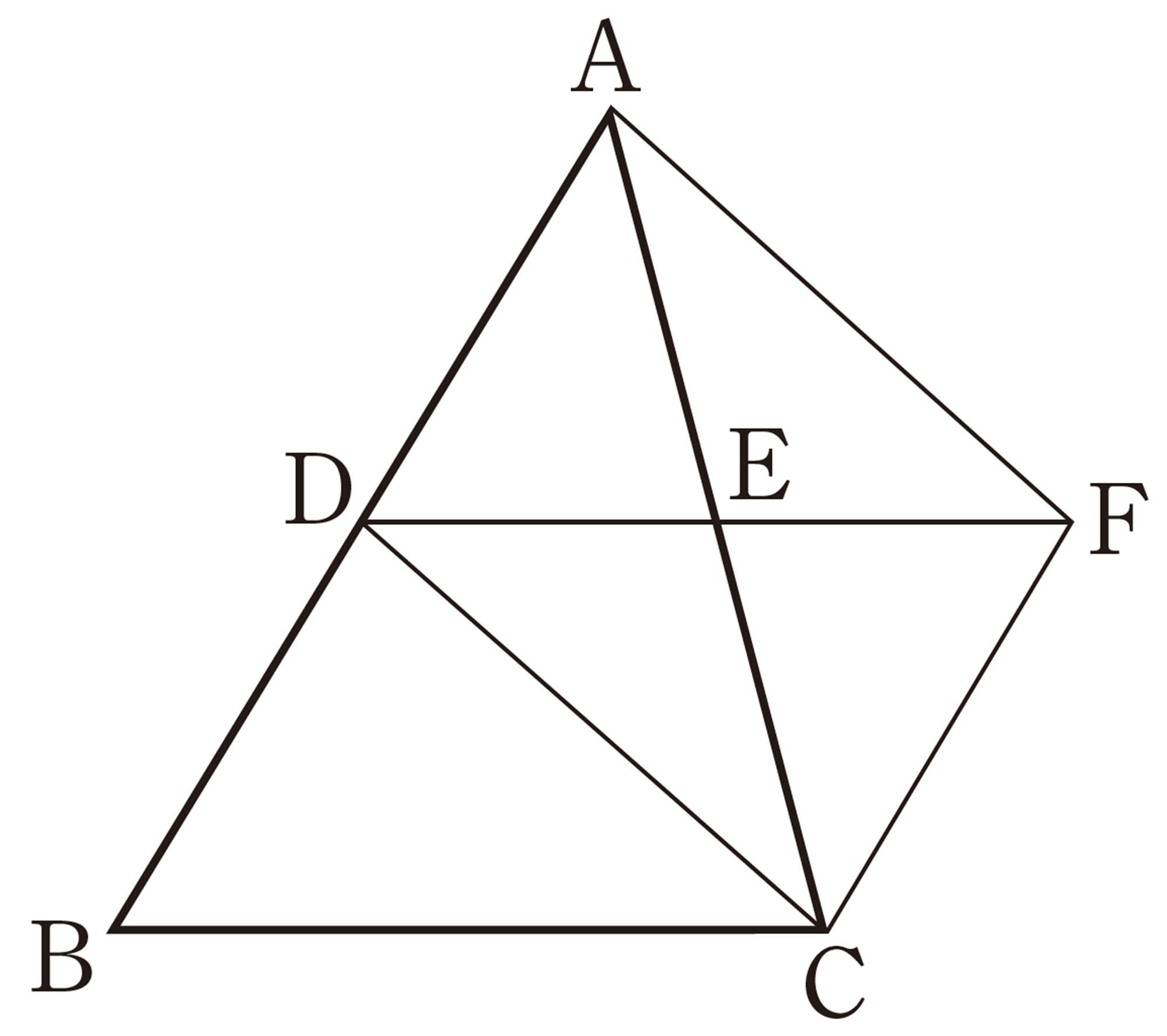
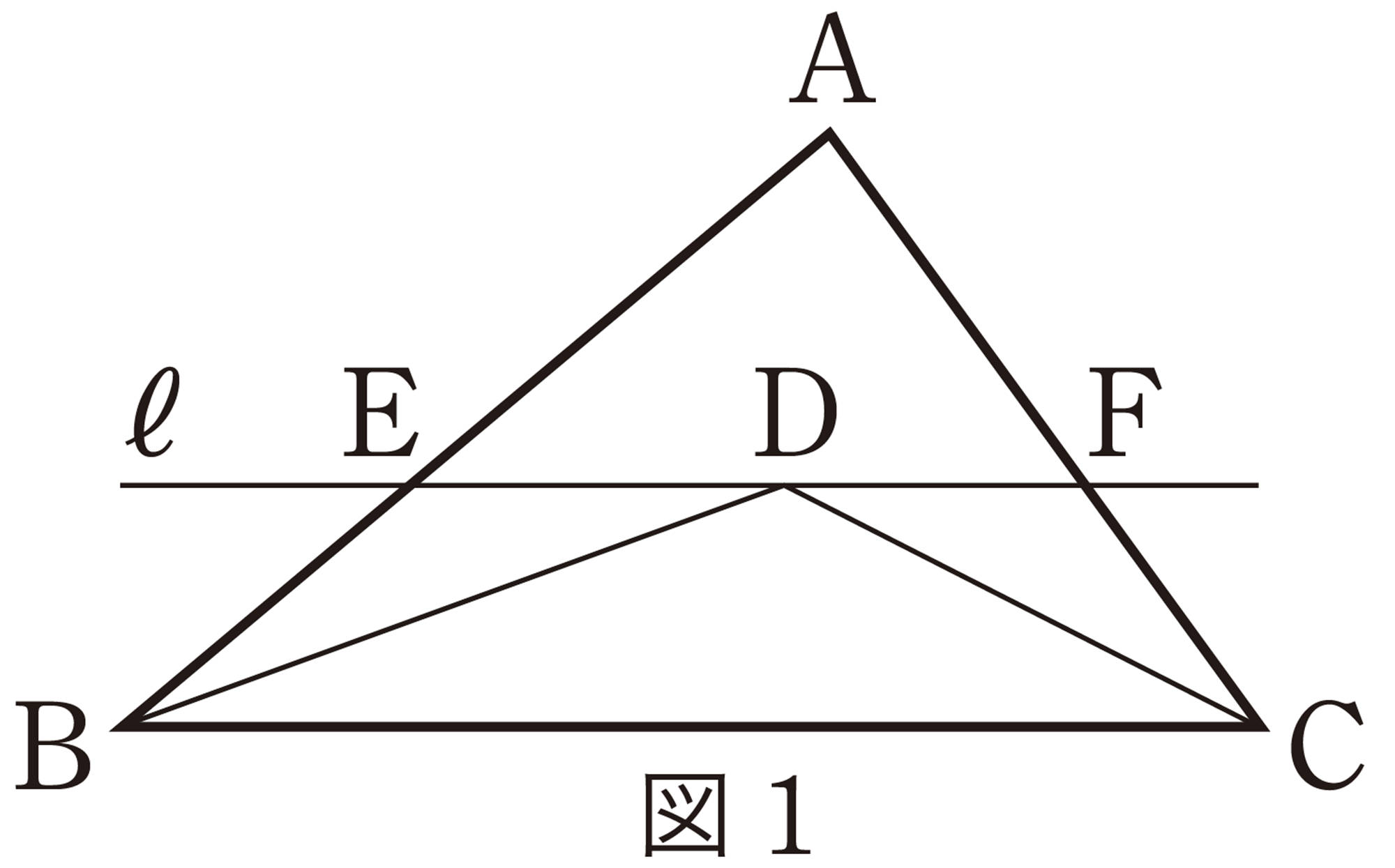
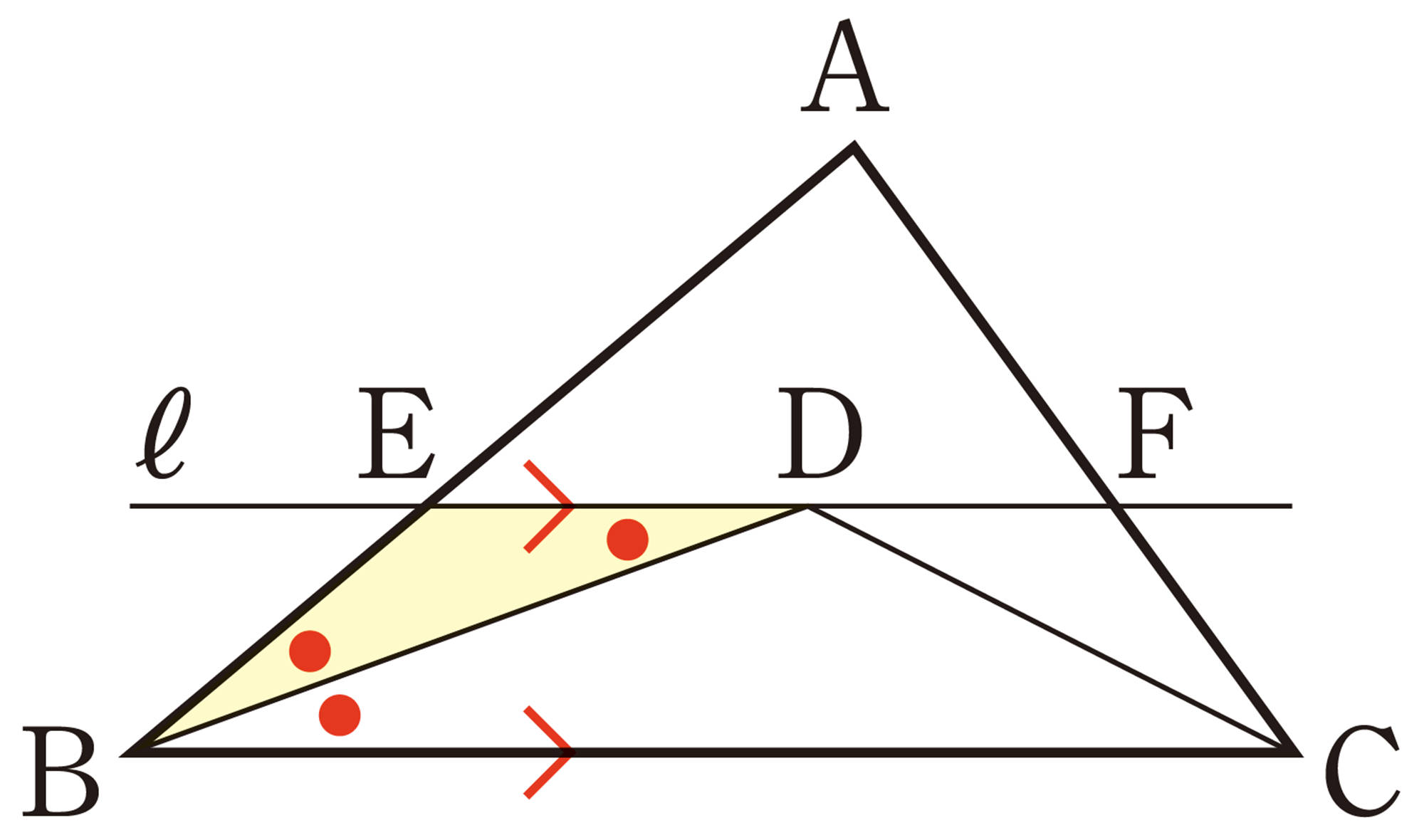
図1のように，[mathjax]\(\triangle ABC\)において，[mathjax]\(\angle ABC\)の二等分線と[mathjax]\(\angle ACB\)の二等分線を引き，それらの交点をDとします。Dを通り，辺BCに平行な直線ℓを引き，ℓと辺AB，ACとの交点をそれぞれE，Fとします。このとき，[mathjax]\(EB=ED\)となることを証明しなさい。
［証明］
[mathjax]\(\triangle EBD\)において，
仮定から，[mathjax]\(\hspace{24pt}\angle DBC=\angle EBD\quad\cdots\cdots\text{①}\)
平行線の錯角は等しいから，
[mathjax]\(ED/\!/BC\)より，[mathjax]\(\angle DBC =\angle EDB\quad\cdots\cdots\text{②}\)
①，②から，[mathjax]\(\hspace{14pt}\angle EBD = \angle EDB\)
2つの角が等しいから，[mathjax]\(\triangle EBD\)は二等辺三角形である。
したがって，[mathjax]\(\hspace{28pt}EB=ED\)
次の⑴〜⑶の問いに答えなさい。
⑴ 上の証明の下線部「仮定から」の仮定を，次の㋐〜㋓の中から1つ選びなさい。
㋐ BDは[mathjax]\(\angle ABC\)の二等分線である。
㋑ CDは[mathjax]\(\angle ACB\) の二等分線である。
㋒ 直線ℓは点Dを通り，辺BCに平行な直線である。
㋓ [mathjax]\(EB=ED\)である。
⑵ 図1で，[mathjax]\(FC=FD\)であることを証明しなさい。
⑶ [mathjax]\(\triangle EBD\)と[mathjax]\(\triangle FCD\)が二等辺三角形であることから，図1において，[mathjax]\(\triangle AEF\)のまわりの長さと等しいものがあることがわかります。次の㋐〜㋔の中から1つ選びなさい。
㋐ [mathjax]\(AE+AF\)
㋑ [mathjax]\(AE+AC\)
㋒ [mathjax]\(AB+AF\)
㋓ [mathjax]\(AB+AC\)
㋔ [mathjax]\(DB+DC\)
<2年p.178>
深めよう 条件を変えて考えよう
157ページの問10で，次のことを証明しました。
線分AB上に点Cをとり，AC，BCをそれぞれ1辺とする正三角形ACP，CBQをつくると，[mathjax]\(AQ=PB\)である。
① [mathjax]\(\triangle CBQ\)を点Cを回転の中心として回転移動したとき，[mathjax]\(AQ=PB\)が成り立つかどうかを調べてみましょう。
2つの正三角形の位置関係に着目しよう。
<2年p.179>
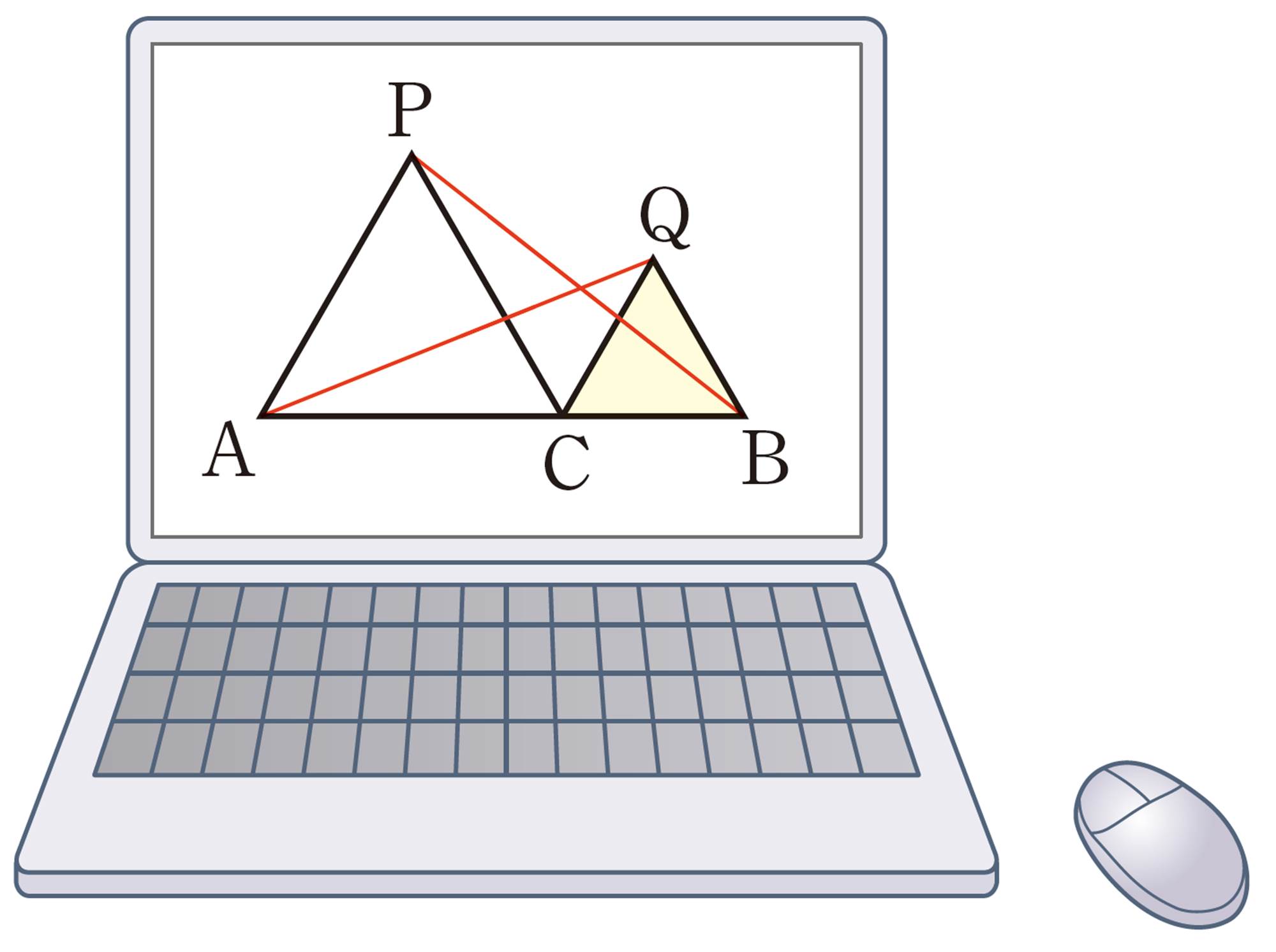
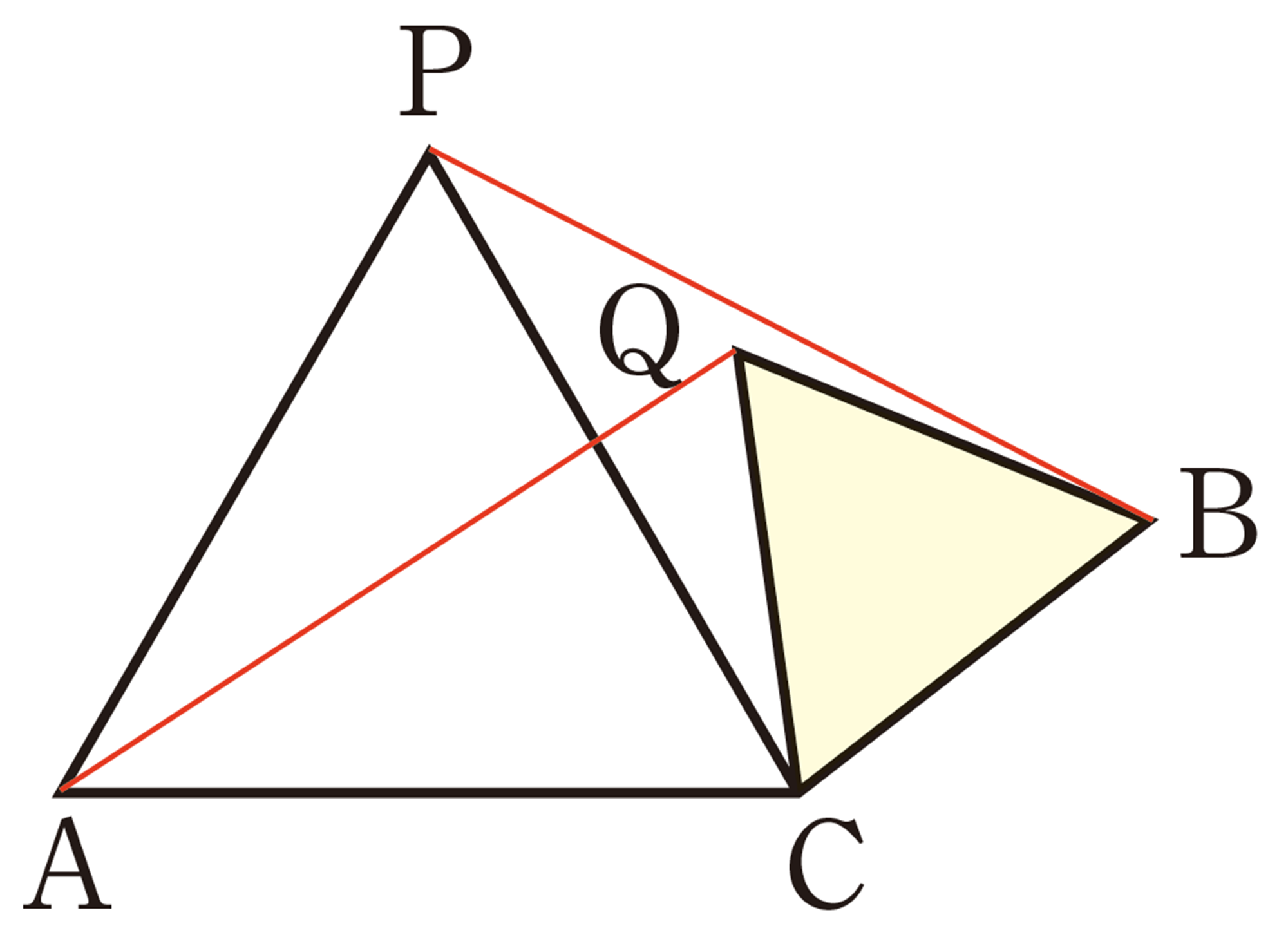
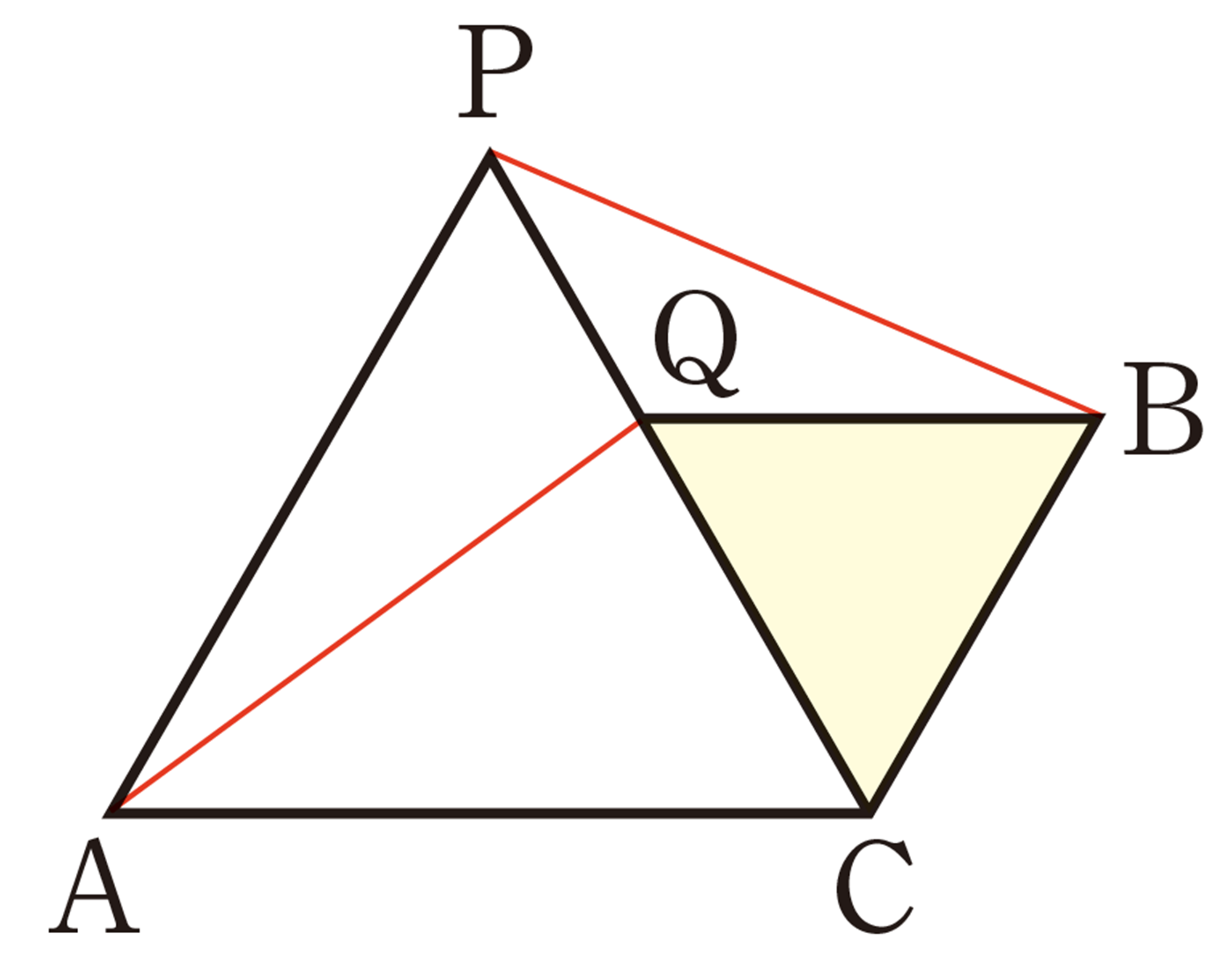
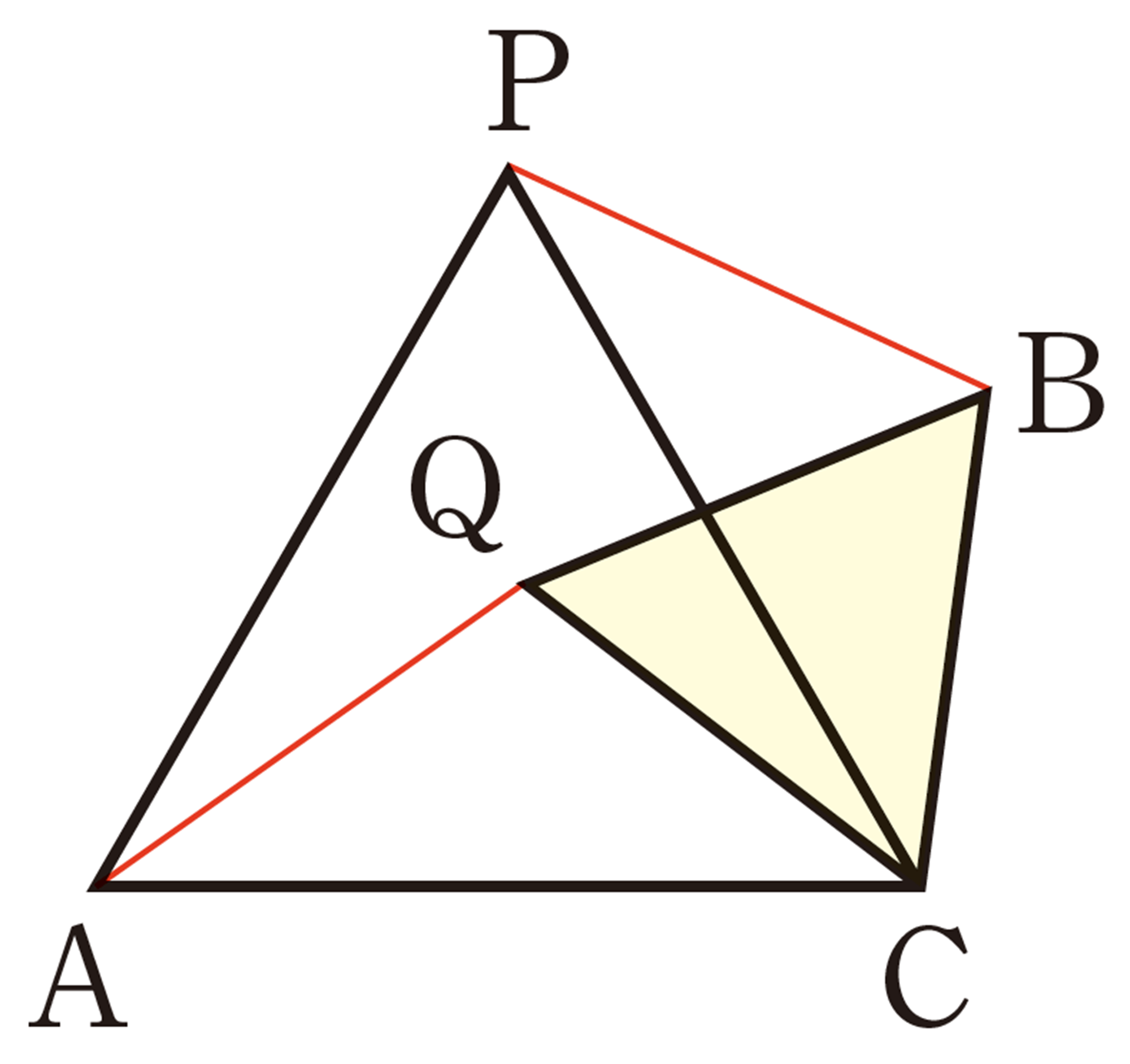
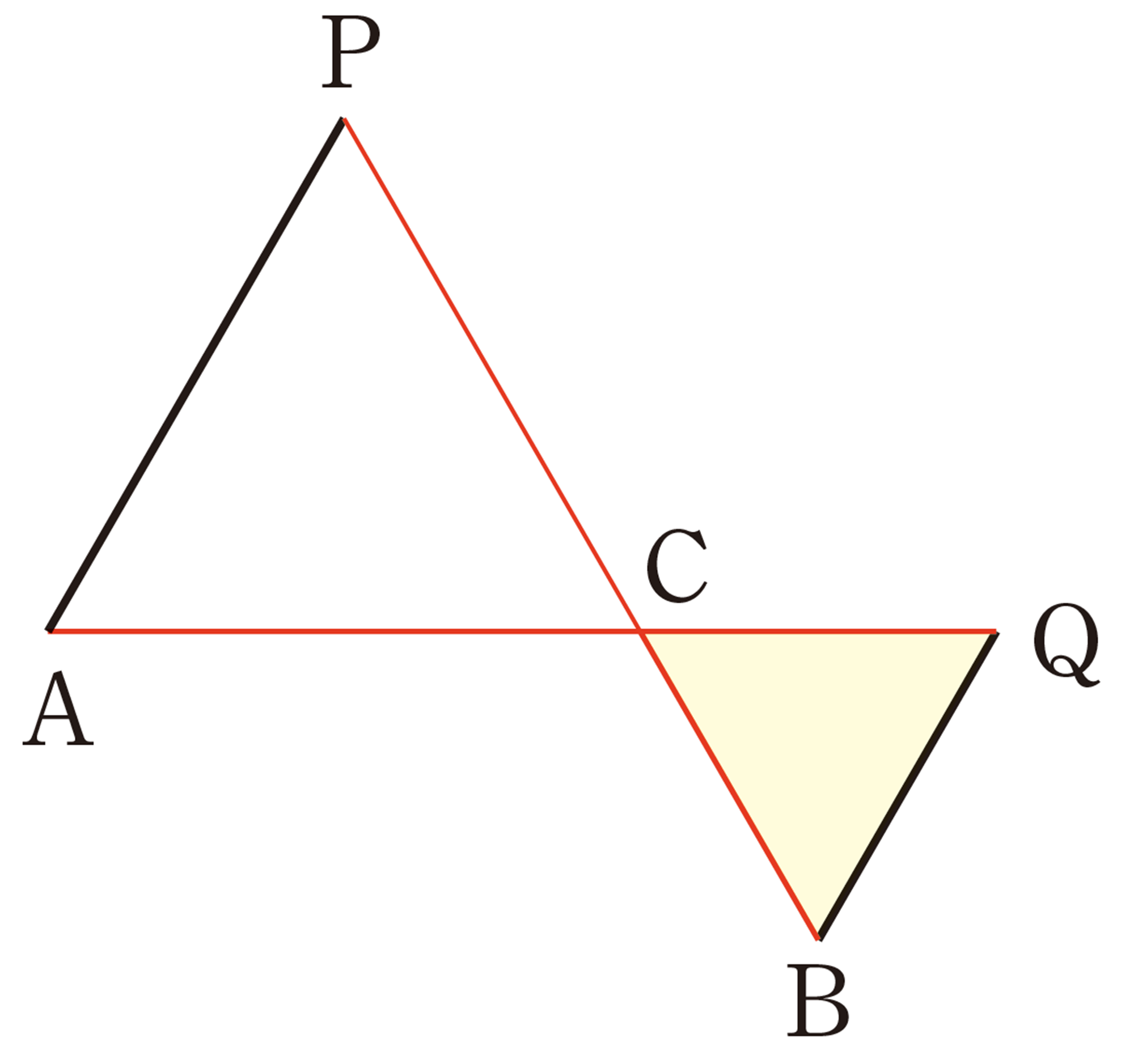
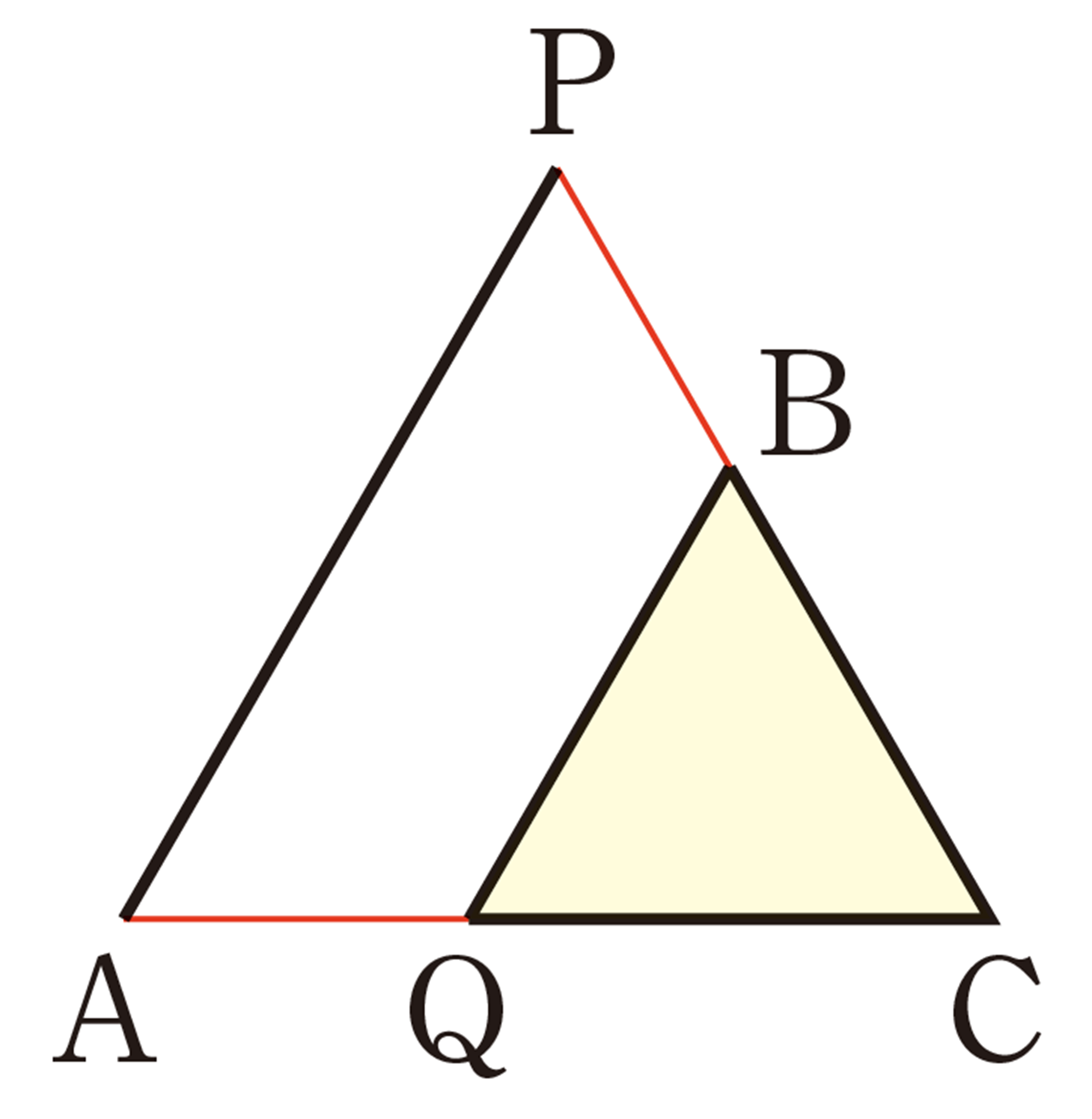
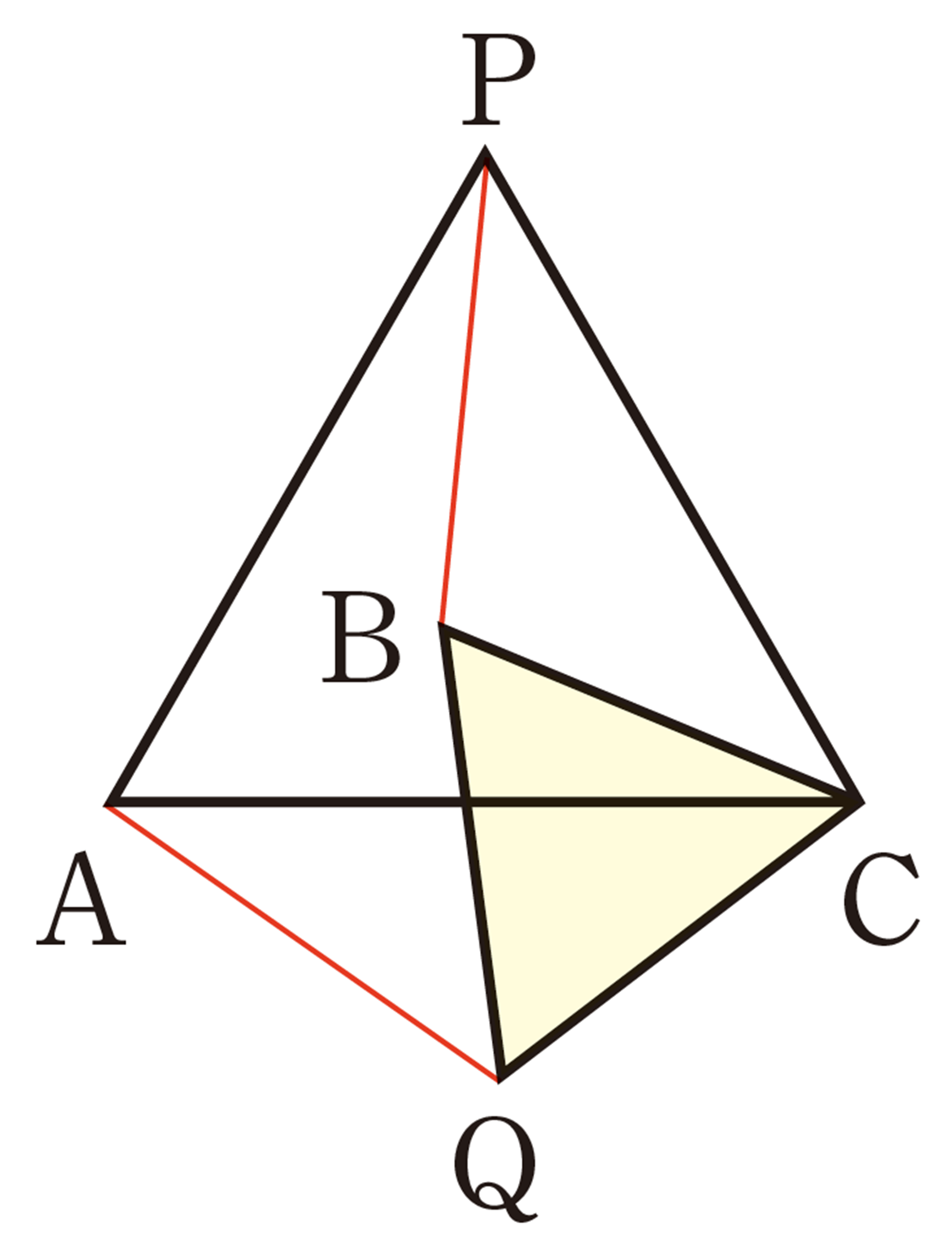
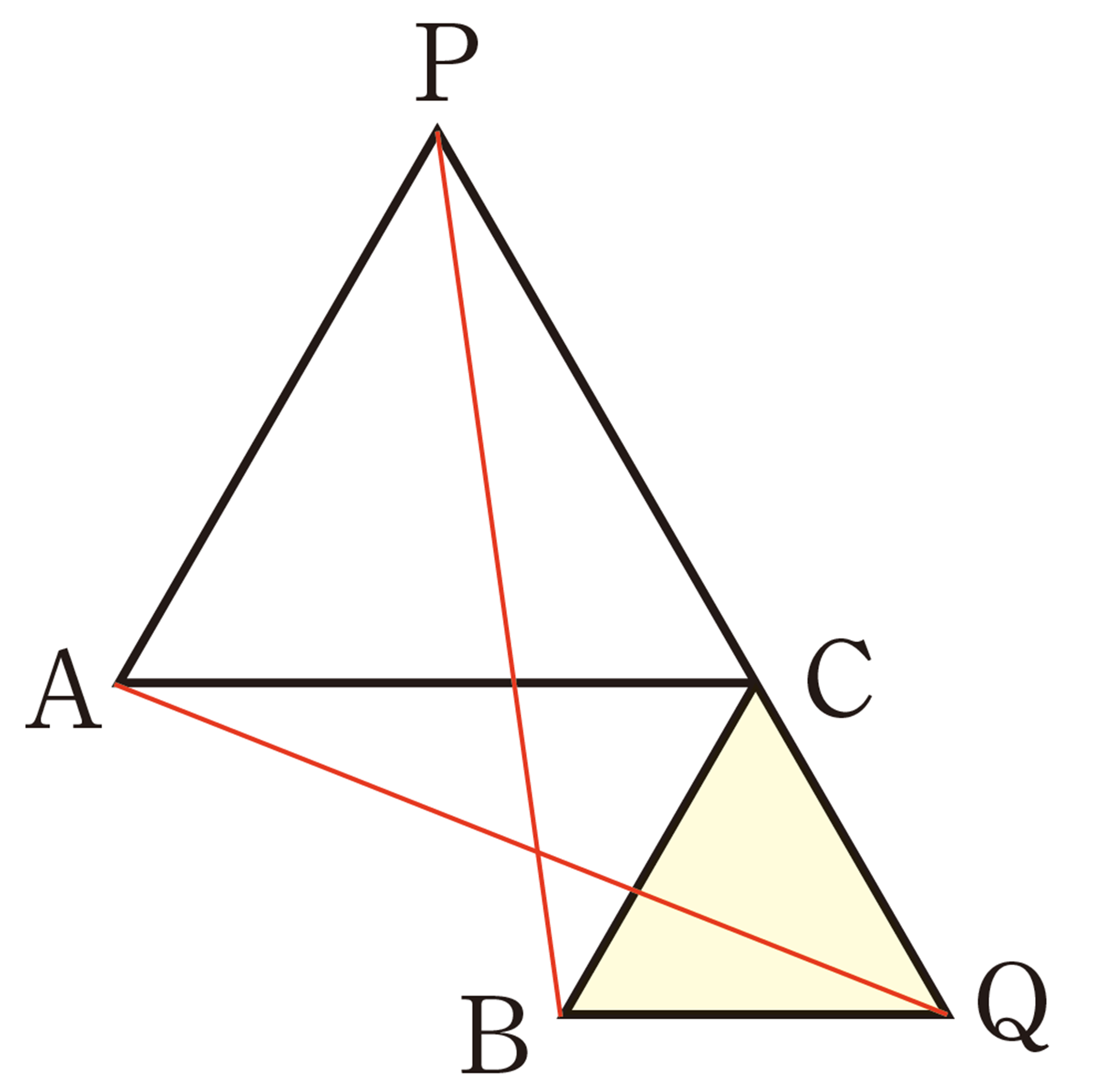
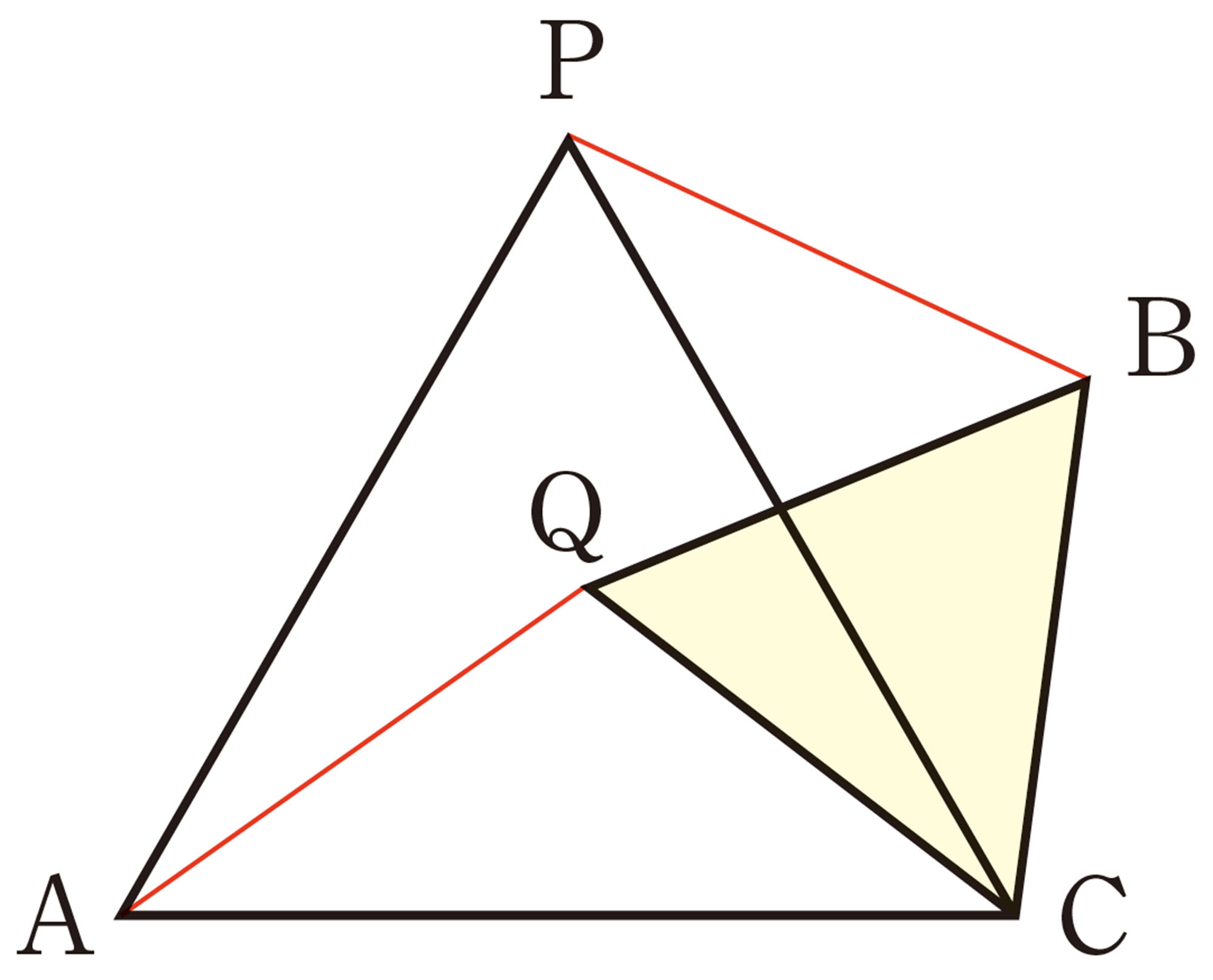
② 前ページの①で調べたことを証明してみましょう。
たとえば，㋒の場合に[mathjax]\(AQ=PB\)が成り立つことは，次のように証明することができます。
［証明］
[mathjax]\(\triangle QAC\)と[mathjax]\(\triangle BPC\)において，
仮定から，[mathjax]\(\hspace{8pt}AC=PC\quad\quad\cdots\cdots\text{①}\)
[mathjax]\(\hspace{50pt}QC=BC\quad\quad\cdots\cdots\text{②}\)
また，
よって，[mathjax]\(\angle ACQ = \angle PCB\quad\cdots\cdots\text{③}\)
①，②，③より，2組の辺とその間の角がそれぞれ等しいから，
[mathjax]\(\hspace{32pt}\triangle QAC \equiv \triangle BPC\)
したがって，[mathjax]\(AQ=PB\)
はじめの問題と，証明のどの部分が変わっているかな。
このほかの場合についても，[mathjax]\(AQ=PB\)が成り立つことを証明してみましょう。
③ 次のように，条件の一部分を変えたとき，どんなことが成り立つかを調べてみましょう。また，そのことを証明してみましょう。
❶ 正三角形を正方形に変える。
❷ 点Cを線分AB外にとる。
