gkt-horizontal-line
<2年p.168>
問 ３ 四角形ABCDの2つの対角線の交点をOとするとき，[mathjax]\(AO=CO\)，[mathjax]\(BO=DO\)ならば，[mathjax]\(AB/\!/DC\)，[mathjax]\(AD/\!/BC\)であることを証明しなさい。
問 ４ 四角形ABCDで，[mathjax]\(AD/\!/BC\)，[mathjax]\(AD=BC\)ならば，四角形ABCDは平行四辺形であることを証明しなさい。
これまで調べたことは，次のようにまとめることができる。
平行四辺形になるための条件
四角形は，次のどれか1つが成り立てば，平行四辺形である。
[mathjax]\(❶ \text{2組の対辺がそれぞれ平行である。}\hspace{40pt}\cdots\text{(定義)}\)
[mathjax]\(\begin{eqnarray}
\left.\begin{array}{l}
❷ \text{2組の対辺がそれぞれ等しい。}\\
❸ \text{2組の対角がそれぞれ等しい。}\\
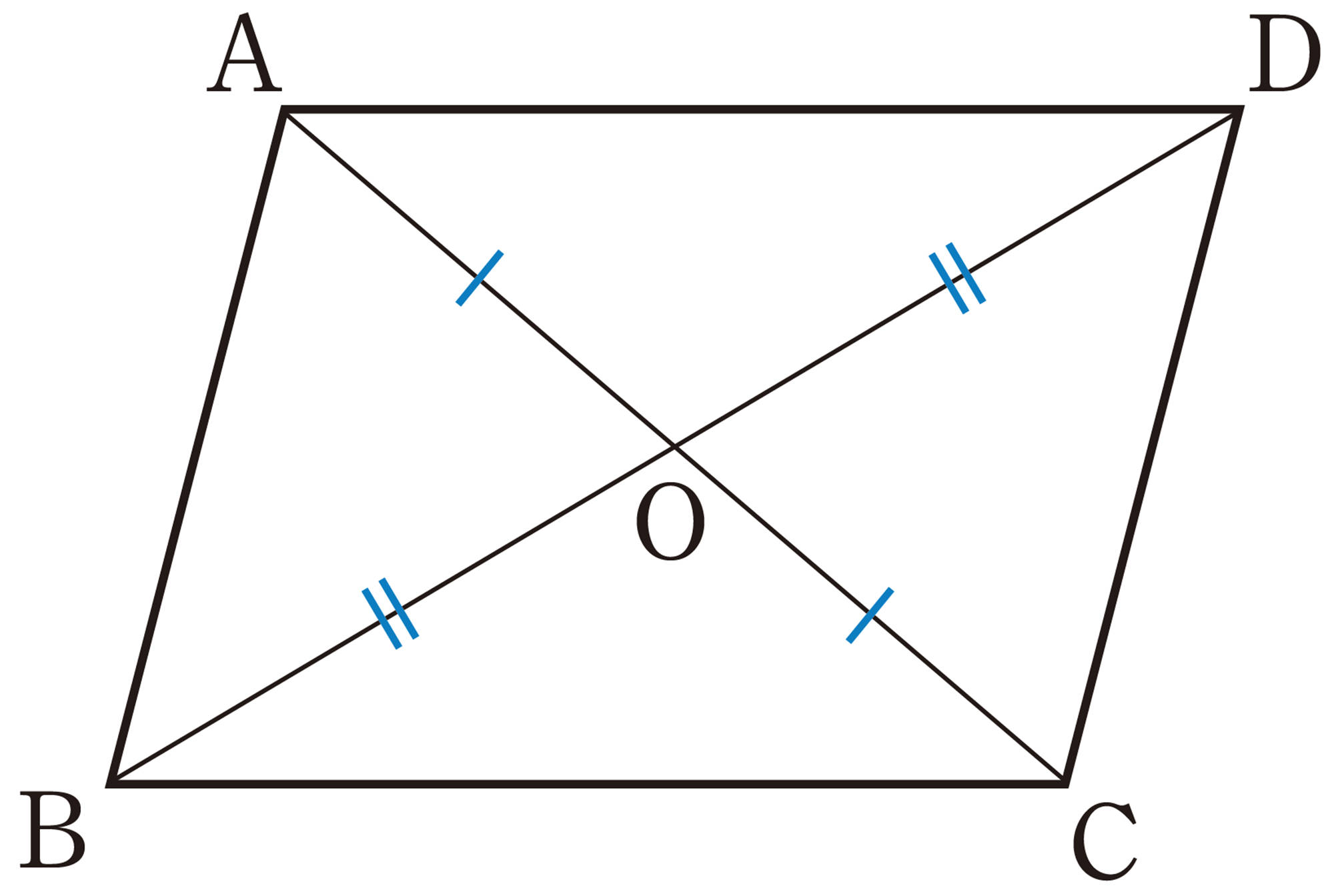
❹ \text{2つの対角線がそれぞれの中点で交わる。}\\
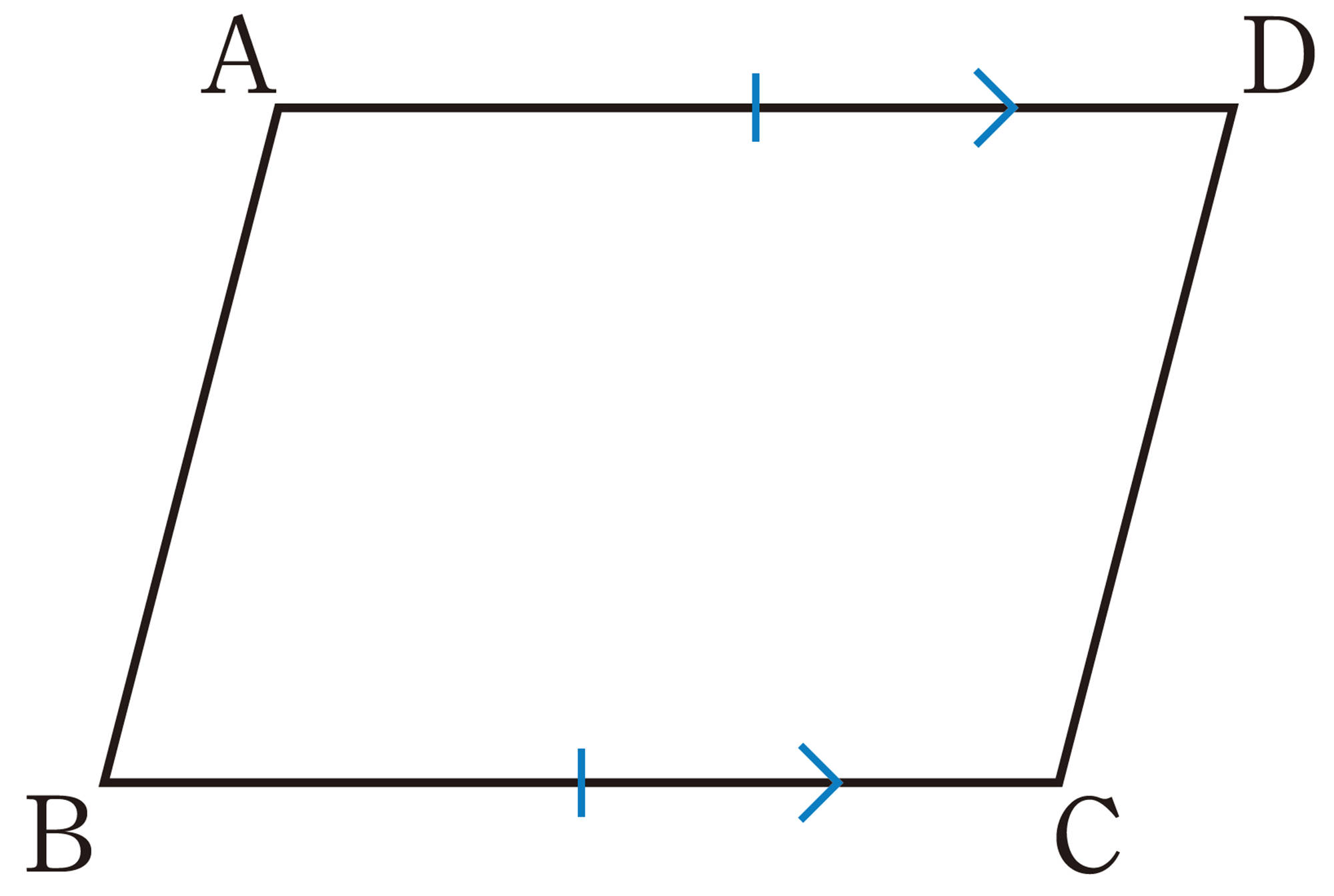
❺ \text{1組の対辺が平行で等しい。}
\end{array} \right\}
\end{eqnarray}\quad\cdots\text{(定理)}\)
問 ５ 四角形ABCDの2つの対角線の交点をOとするとき，次のような条件の場合，四角形ABCDは平行四辺形であるといえますか。
⑴ [mathjax]\(AB/\!/DC\) ，[mathjax]\(AD=BC\)
⑵ [mathjax]\(AB/\!/DC\)，[mathjax]\(\angle A=\angle C\)
⑶ [mathjax]\(AB/\!/DC\) ，[mathjax]\(OA=OC\)
⑷ [mathjax]\(\angle A=\angle C\)，[mathjax]\(OA=OC\)
問 ６ 162ページの【１】で，2枚のふせんを右のように重ねたとき，重なった部分の四角形はどんな四角形になりますか。また，その理由を説明しなさい。
