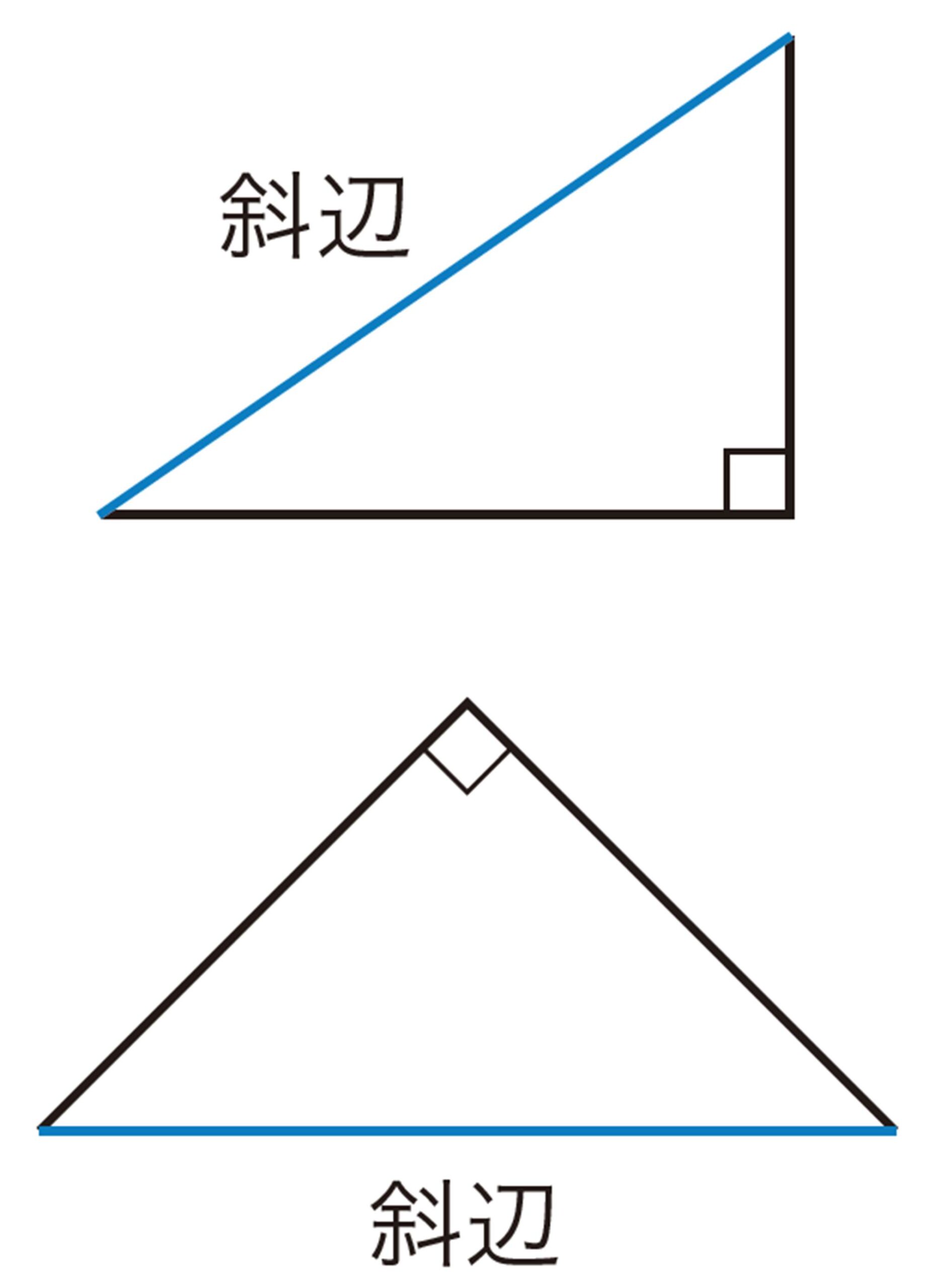
<2年p.153>
2つの角が等しい三角形
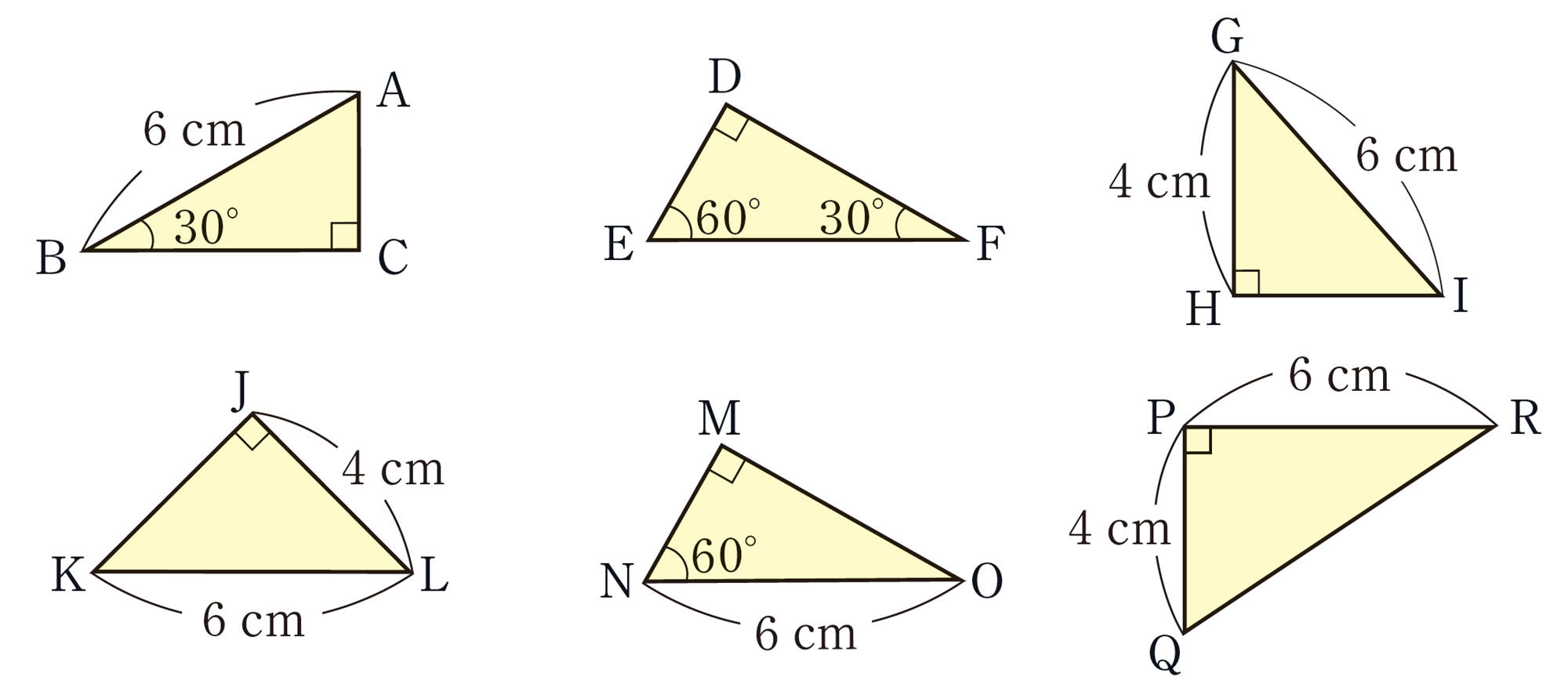
Q Question
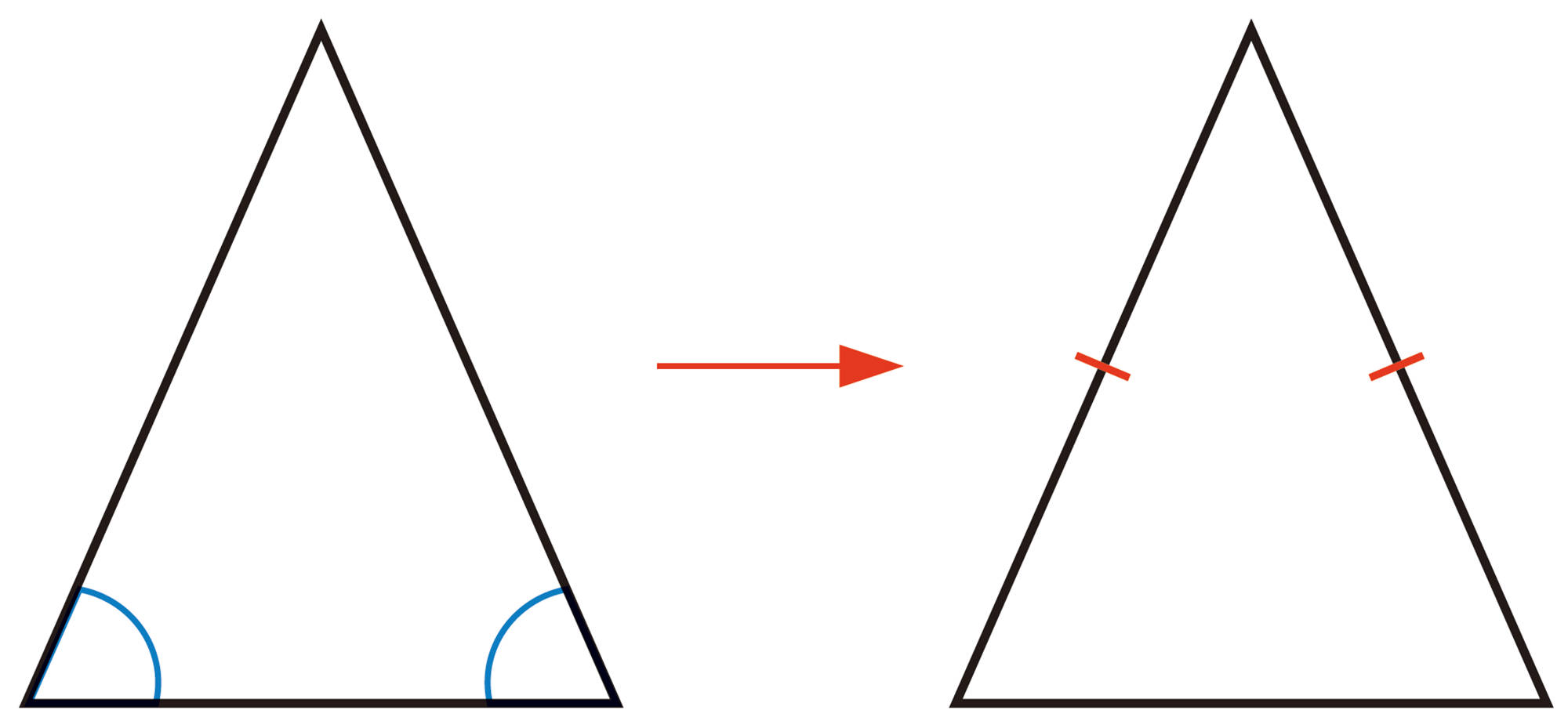
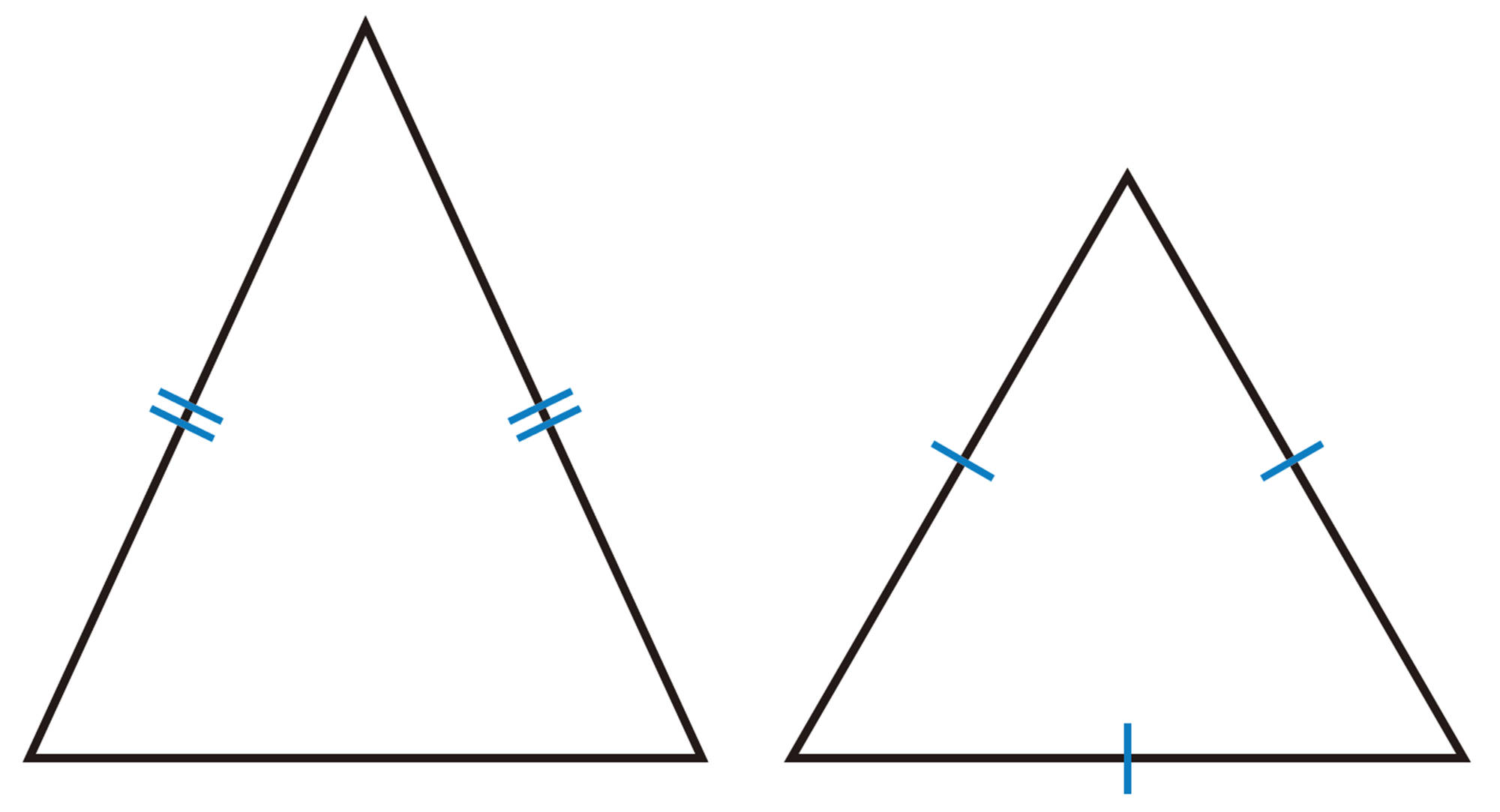
2つの角が等しい三角形をいくつかかいて,二等辺三角形になるかどうか確かめましょう。 また, 反例が見つかるかどうか話し合ってみましょう。

「2つの角が等しい三角形ならば,二等辺三角形である」は,「二等辺三角形ならば,2つの底角は等しい」の逆だね。
この逆は,いつでも正しいといえるのかな。

見方・考え方
根拠を明らかにして,説明できるかな。
2つの角が同じになる三角形をかこう。

目標 ▷ 二等辺三角形の性質の逆が成り立つかどうかを考えよう。
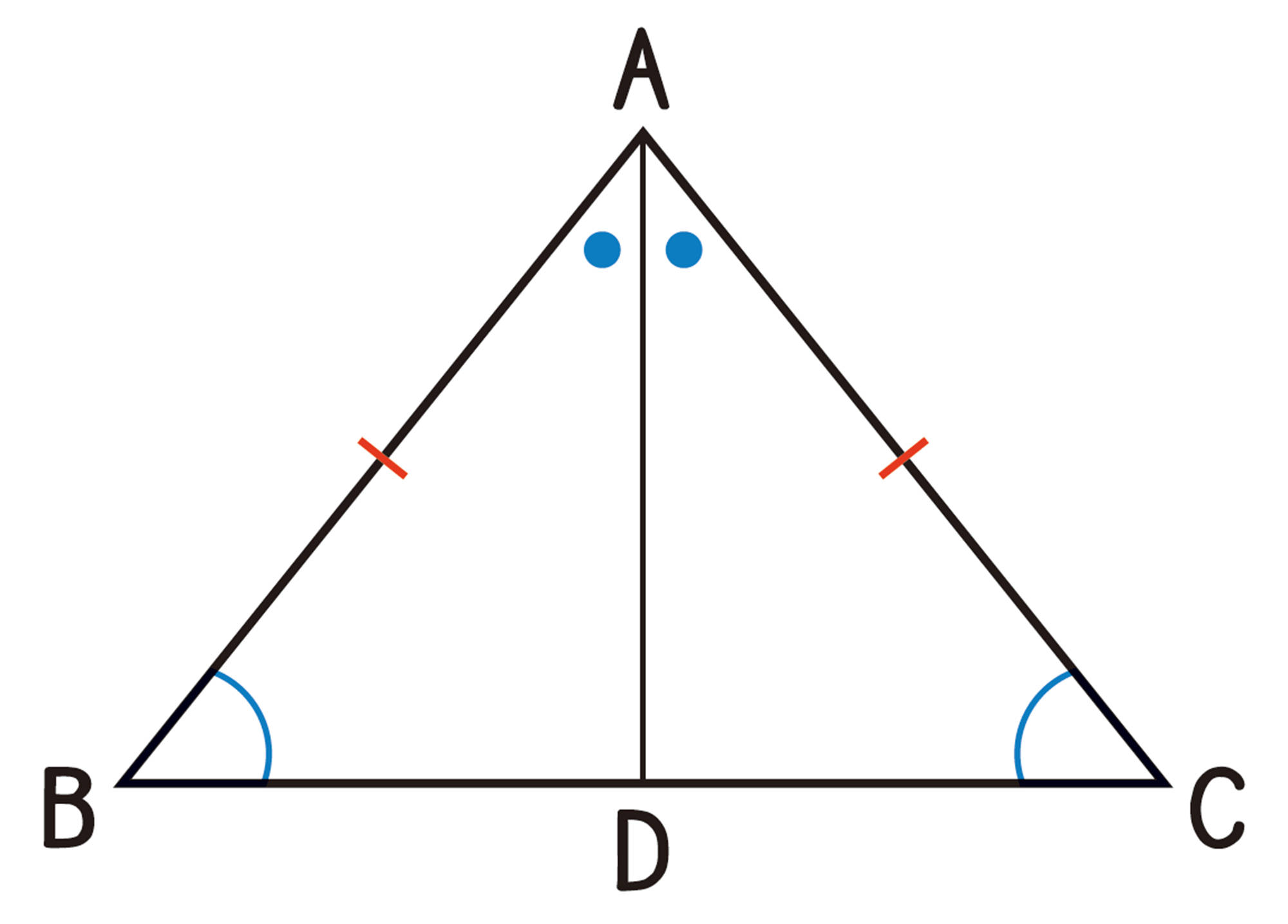
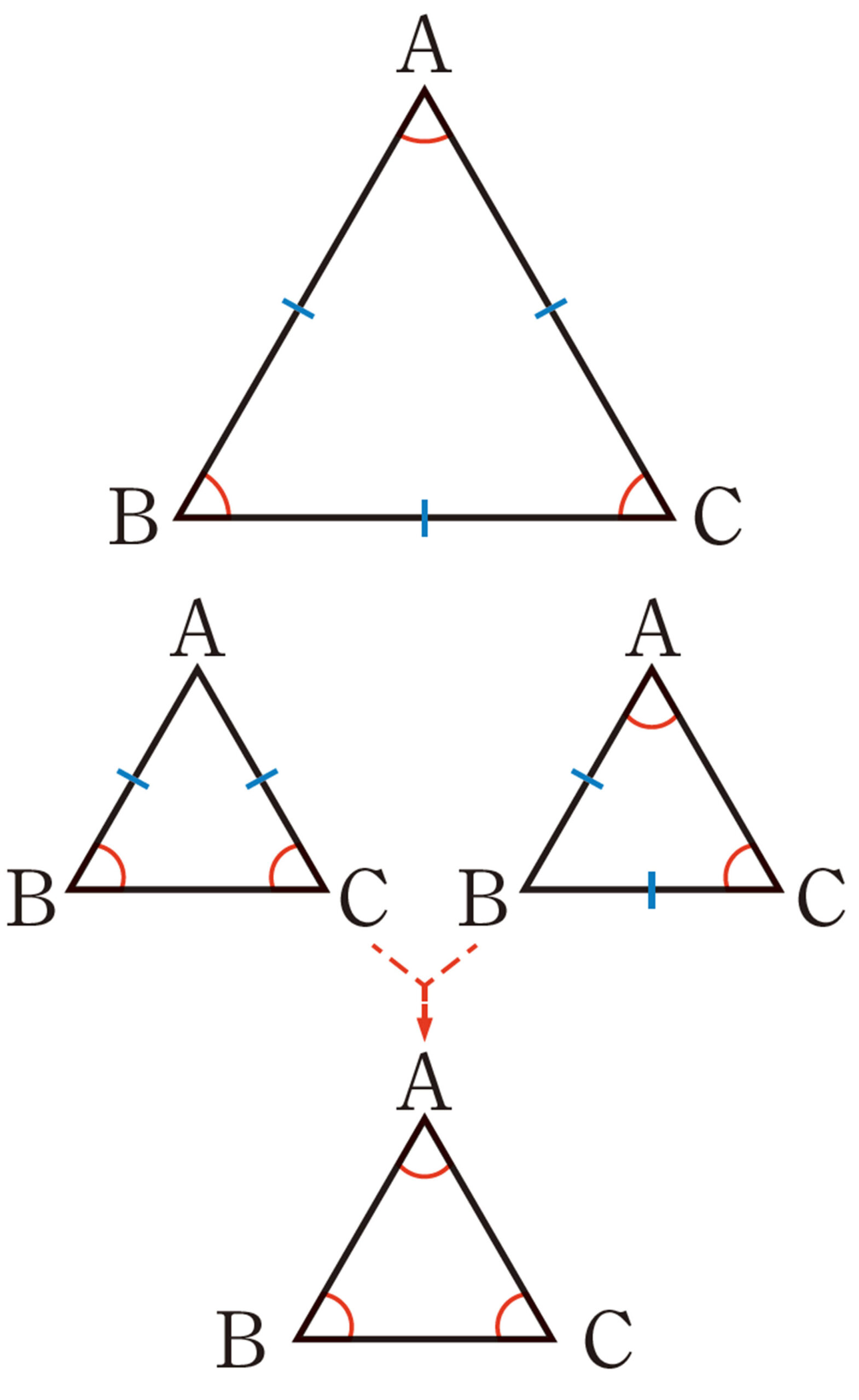
例 2 [mathjax]\(\triangle ABC\) において,[mathjax]\(\angle B=\angle C\) ならば,[mathjax]\(AB=AC\) であることを証明しなさい。
考え方 [mathjax]\( AB=AC\) を導くために,2つの線分が対応する辺となるような合同な三角形を見つければよい。そのために,[mathjax]\(\angle A\) の二等分線を引いて,2つの三角形に分けて考える。
証明
[mathjax]\(\angle A\)の二等分線を引き,辺BCとの交点をDとする。
[mathjax]\(\triangle ABD\) と [mathjax]\(\triangle ACD\) において,
三角形の内角の和は [mathjax]\( 180^{ \circ }\) であるから,
②,③,④より,1 組の辺とその両端の角がそれぞれ等しいから,
[mathjax]\(\triangle ABD \equiv \triangle ACD\)
したがって, [mathjax]\(AB=AC\)
<2年p.154>
前ページの例2で証明したことは,次のように,定理としてまとめることができる。
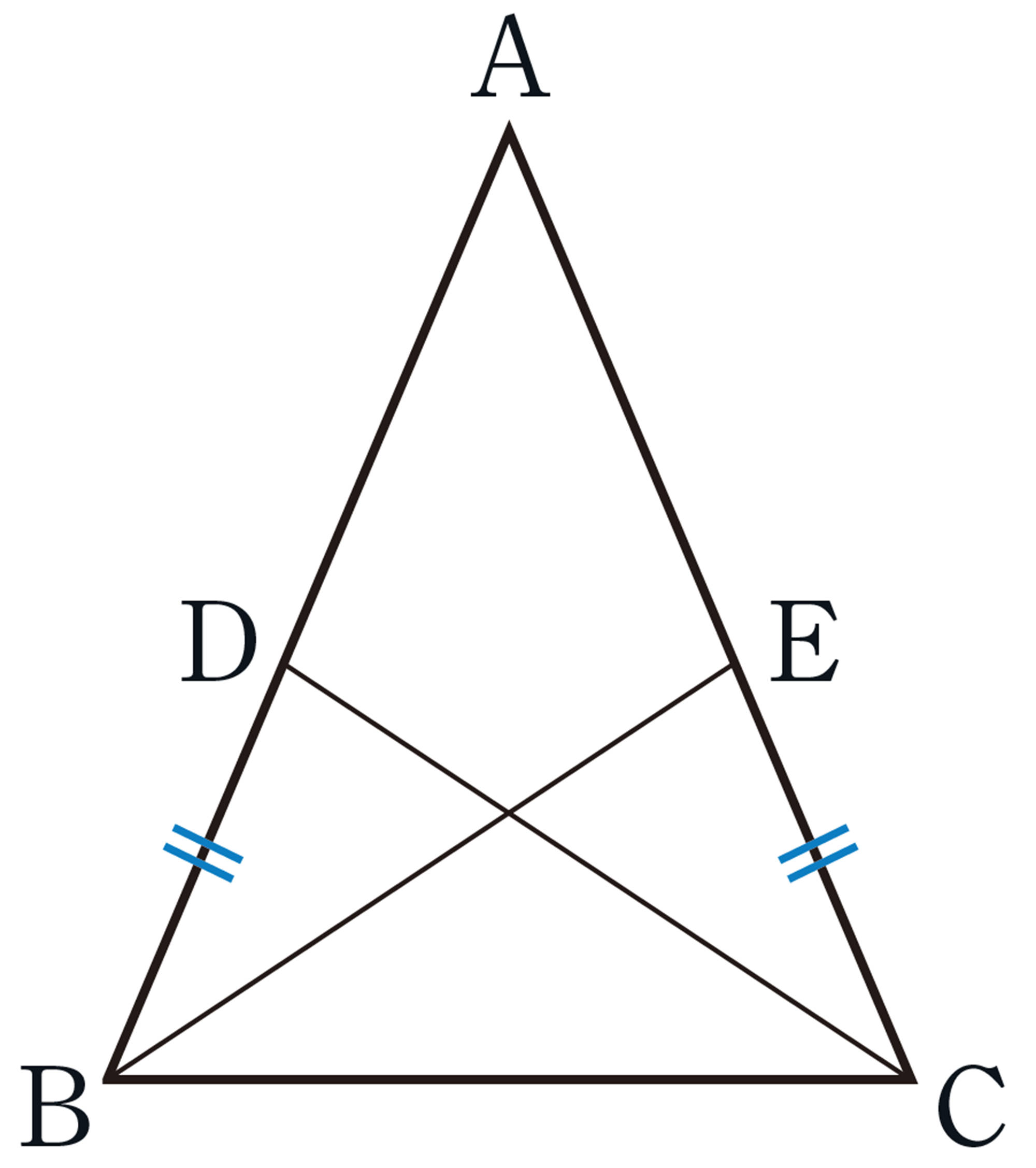
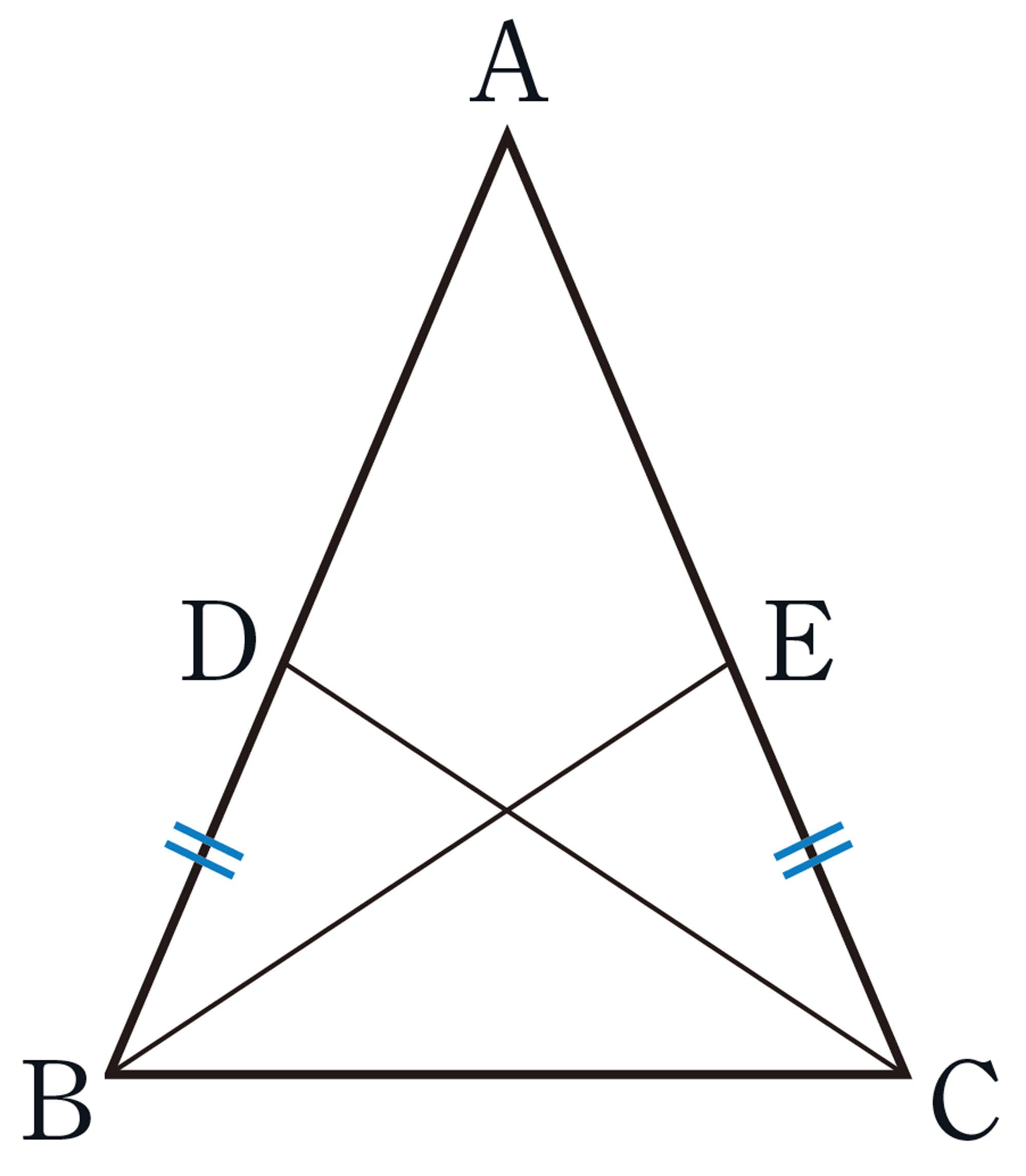
Q Question
<2年p.155>
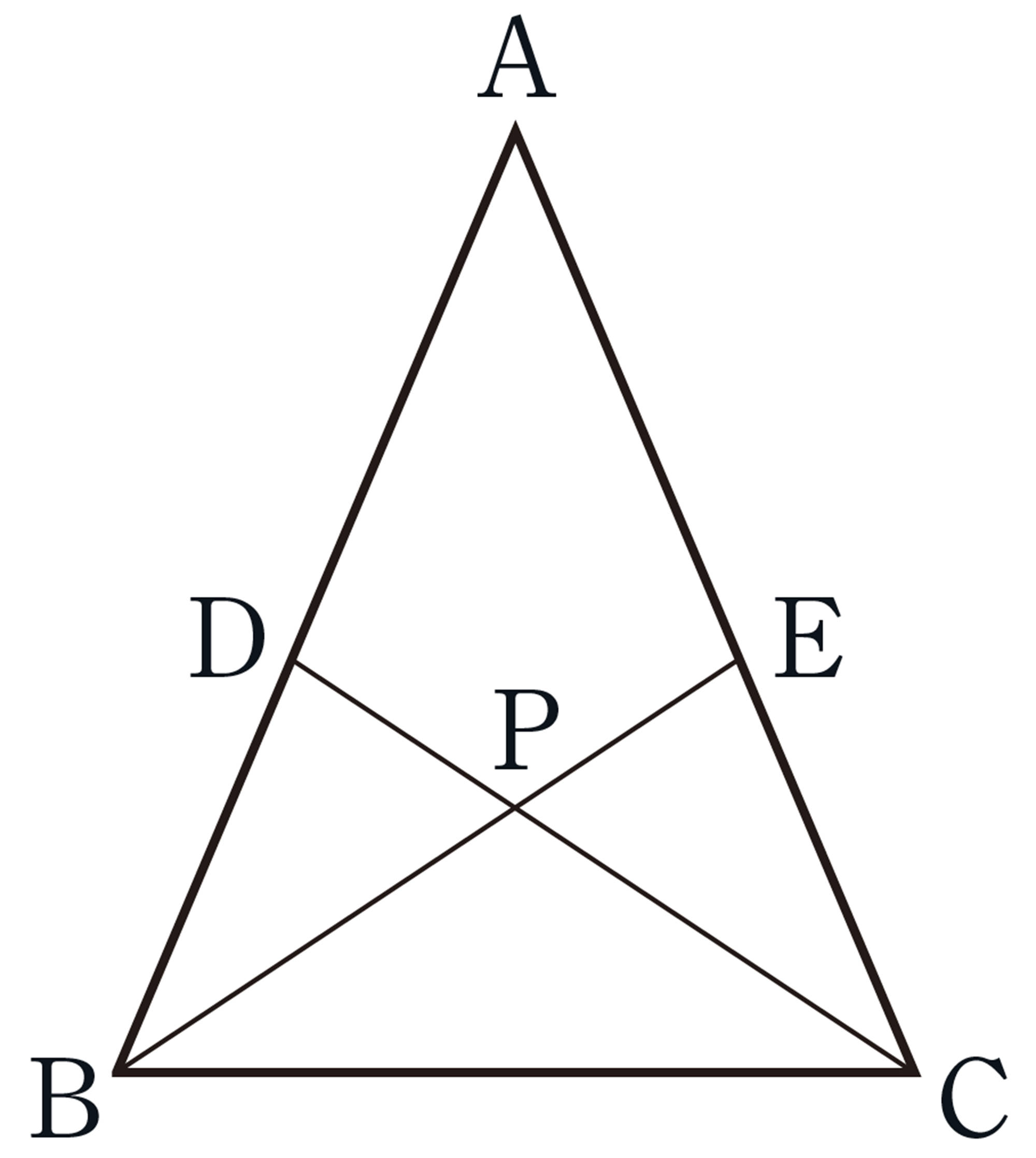
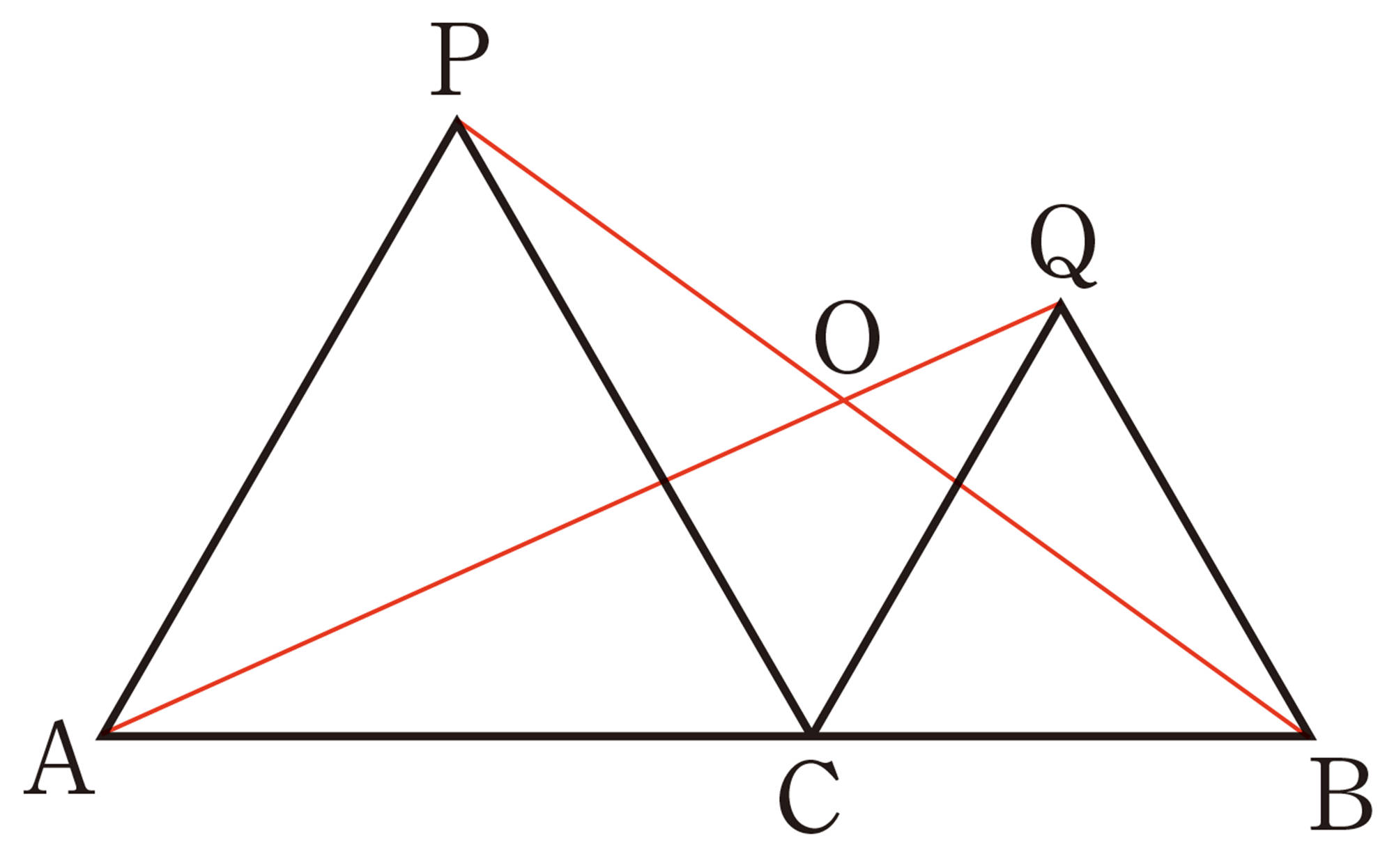
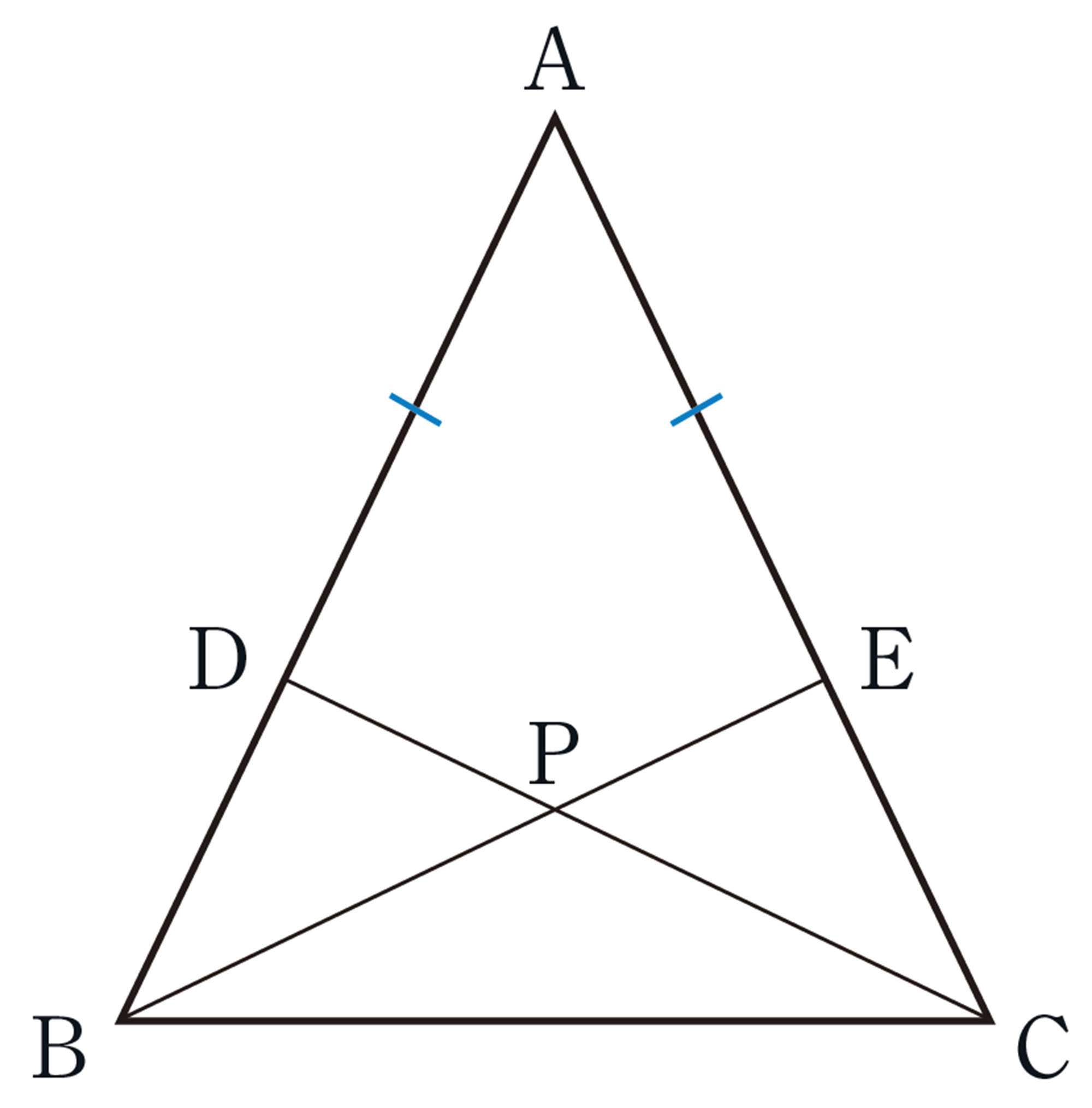
問 7 前ページの【Q】の問題で,[mathjax]\(BE=CD\) となることを証明しなさい。
⑴ どのように証明したらよいか,話し合いなさい。

[mathjax]\(BE=CD\) を証明するには,BE,CDが対応する辺になるような合同な三角形を見つければいいね。
結論から逆に考えたんだね。[mathjax]\(\triangle ABE\)と[mathjax]\(\triangle ACD\),または[mathjax]\(\triangle CBE\)と[mathjax]\(\triangle BCD\)を使ってできないかな。


たとえば,[mathjax]\(\triangle ABE\)と[mathjax]\(\triangle ACD\)の合同を示すには,三角形の合同条件のどれが使えそうかな。
使えそうな合同条件を予想しながら,[mathjax]\(\triangle ABE\)と[mathjax]\(\triangle ACD\)の合同を示して,[mathjax]\(BE=CD\) を証明してみよう。

⑵ 真央さんは,[mathjax]\(BE=CD\) を,次のように証明しました。この証明について,話し合いなさい。
これでいいのかな?
[mathjax]\(\triangle ABE\) と [mathjax]\(\triangle ACD\) において,
[mathjax]\(AE=AC-CE\) ,[mathjax]\(AD=AB-BD\) であるから,
よって,①,③,④より,[mathjax]\(\triangle ABE \equiv \triangle ACD\)
どの三角形の合同条件を使ったのかが書いてあると,ほかの人にもわかりやすいと思います。 また,最後の結論も書いておいた方がいいです。

⑶ [mathjax]\(BE=CD \) となることの証明を,友だちにわかりやすいように書きなさい。
<2年p.156>

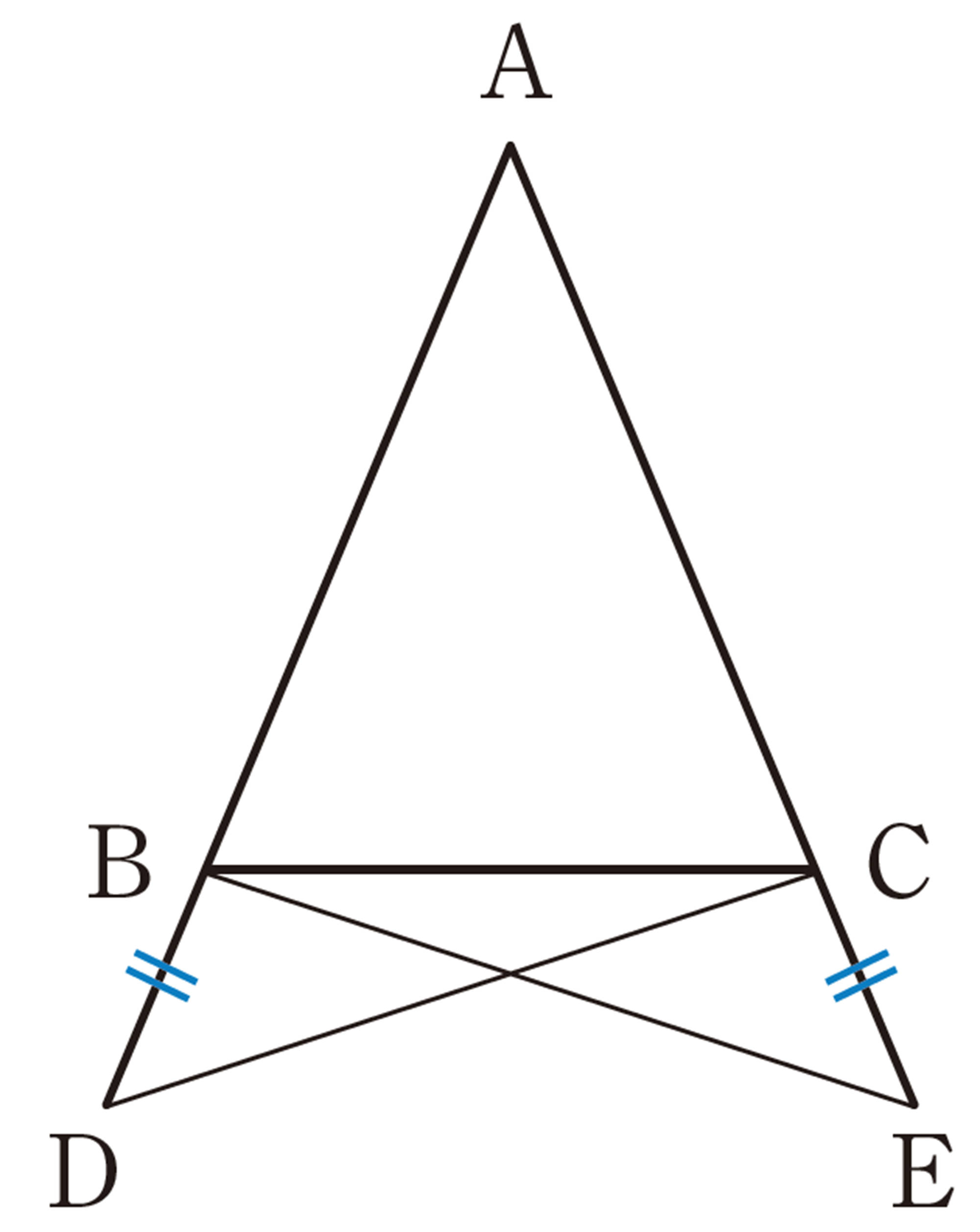
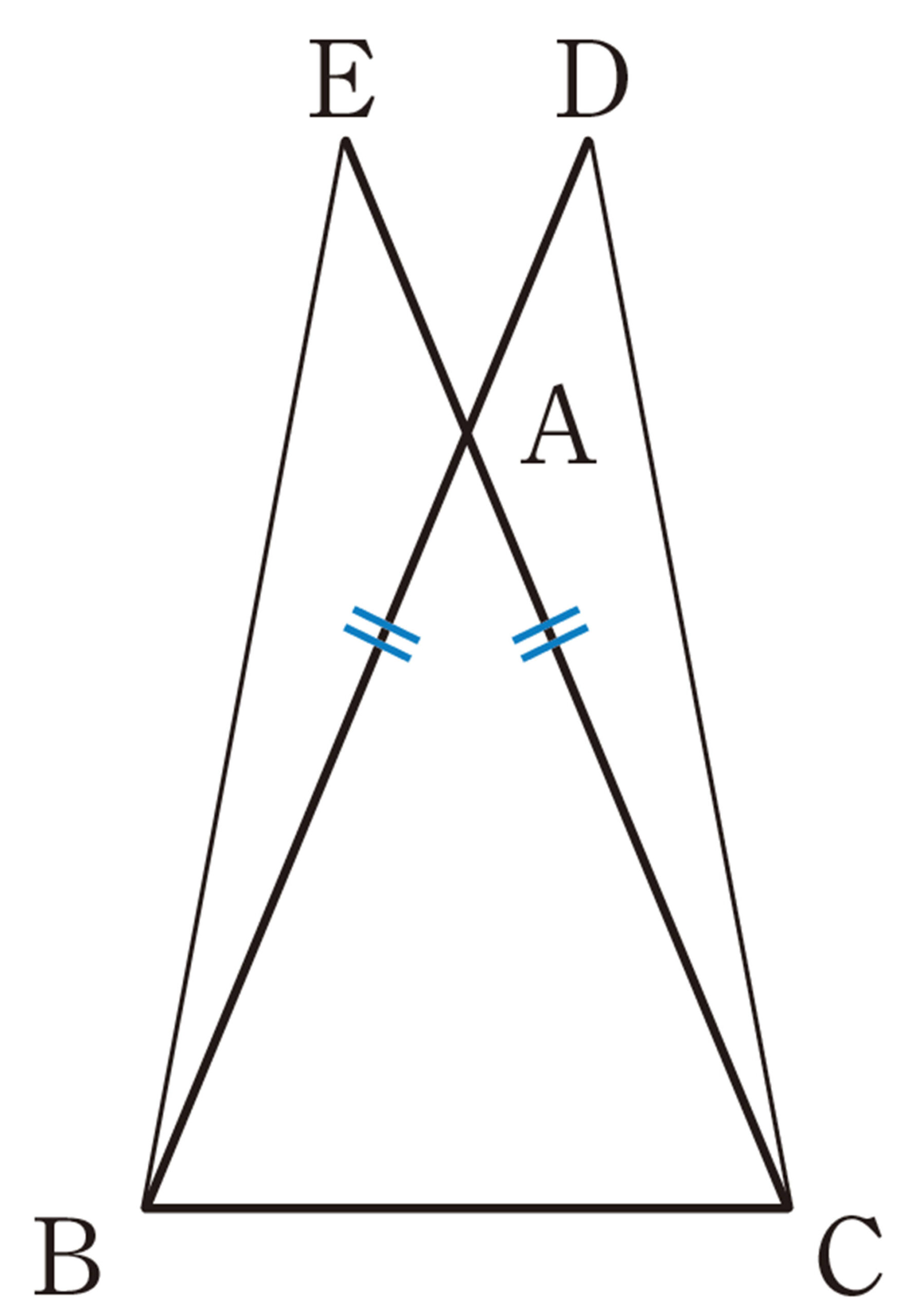
[mathjax]\(BE=CD\) を証明するのに,[mathjax]\(\triangle CBE\) と [mathjax]\(\triangle BCD\) の合同を示すとしたら,どの三角形の合同条件を使えばいいのかな。
点D,Eが辺AB,ACの延長線上にある場合も,同じように [mathjax]\(BE=CD\) がいえるのかな。

正三角形の性質
正三角形は,次のように定義される。
定義 3つの辺が等しい三角形を正三角形という。
Q Question
<2年p.157>
前ページの【Q】からわかるように,正三角形は二等辺三角形の特別な場合とみることができる。
問 8 [mathjax]\(\triangle ABC\) において,[mathjax]\(AB=BC=CA\) ならば,[mathjax]\(\angle A=\angle B=\angle C\) であることを証明します。次の [mathjax]\(\boxed{\phantom{00}}\) をうめて,証明を完成させなさい。
[証明]
[mathjax]\(\triangle ABC\) を [mathjax]\(AB=AC\) の二等辺三角形と考えると,
[mathjax]\(\angle B=\angle \boxed{\phantom{00}}\) ・・・・・・①
[mathjax]\(\triangle ABC\) を [mathjax]\(BA=\boxed{\phantom{0000}}\) の二等辺三角形と考えると,
[mathjax]\(\angle A=\angle \boxed{\phantom{00}}\) ・・・・・・②
①,②から,[mathjax]\(\angle A=\angle B=\angle C\)
問 9 [mathjax]\(\triangle ABC\) において,[mathjax]\(\angle A=\angle B=\angle C\) ならば,[mathjax]\(AB=BC=CA\) であることを証明しなさい。
どんなことがわかったかな
2つの角が等しい三角形は,二等辺三角形になります。正三角形は特別な二等辺三角形といえます。
また,三角形の合同を示すことにより,対応する辺や角が等しいことを証明することができます。
次の課題へ!
直角三角形も特別な三角形だけど,どんな性質があるのかな?
P.158

<2年p.158>
2 直角三角形の合同
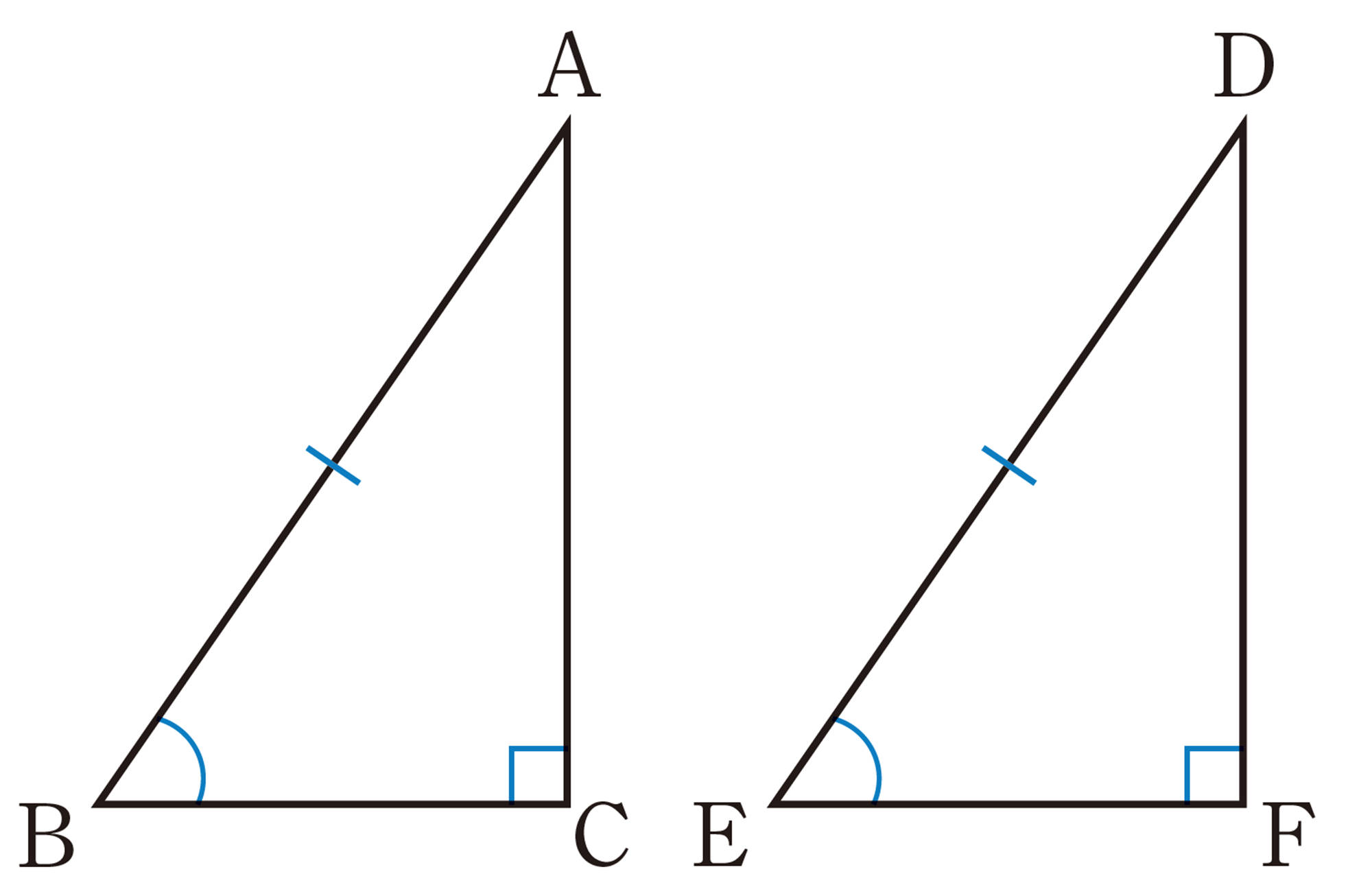
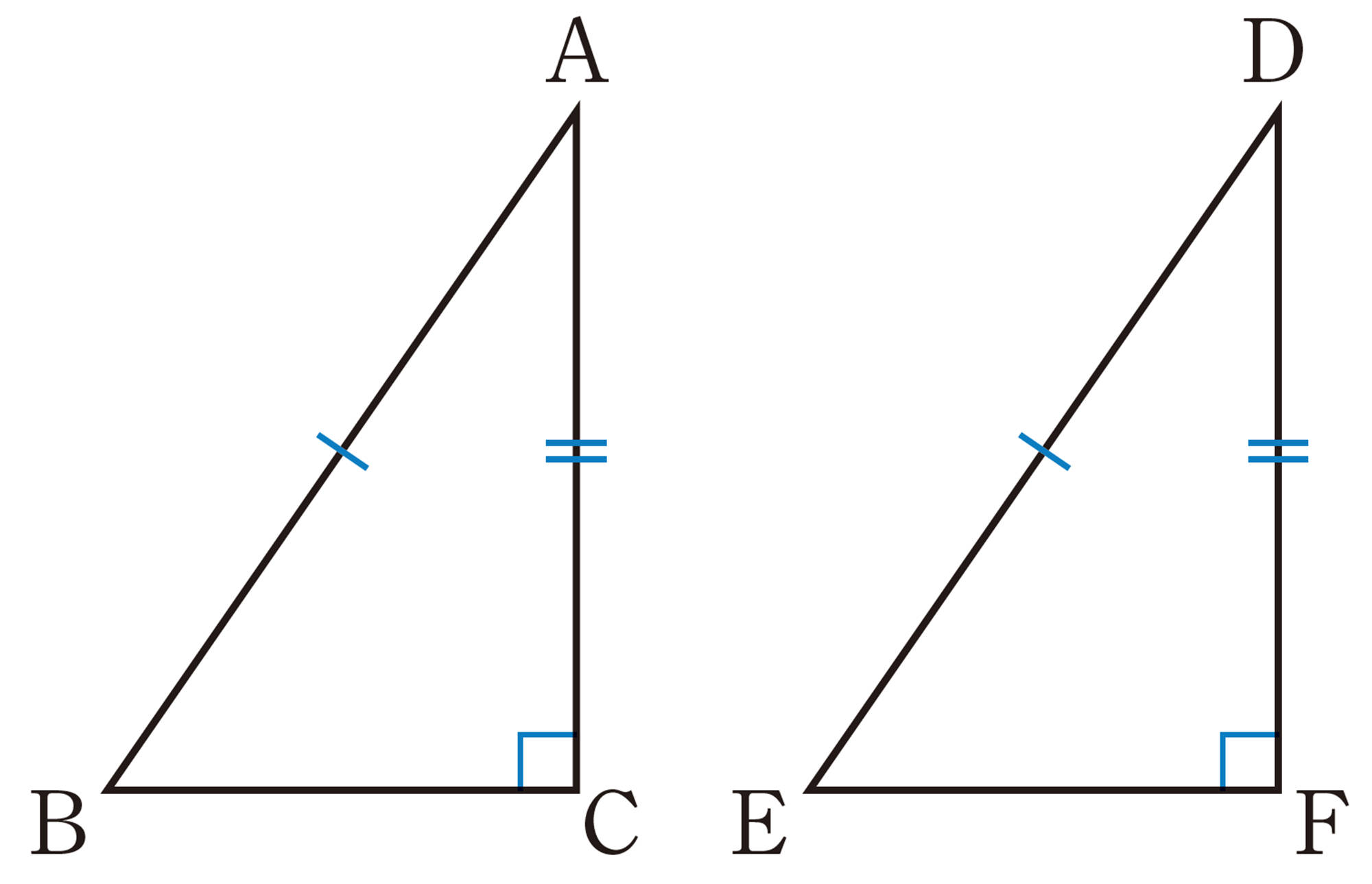
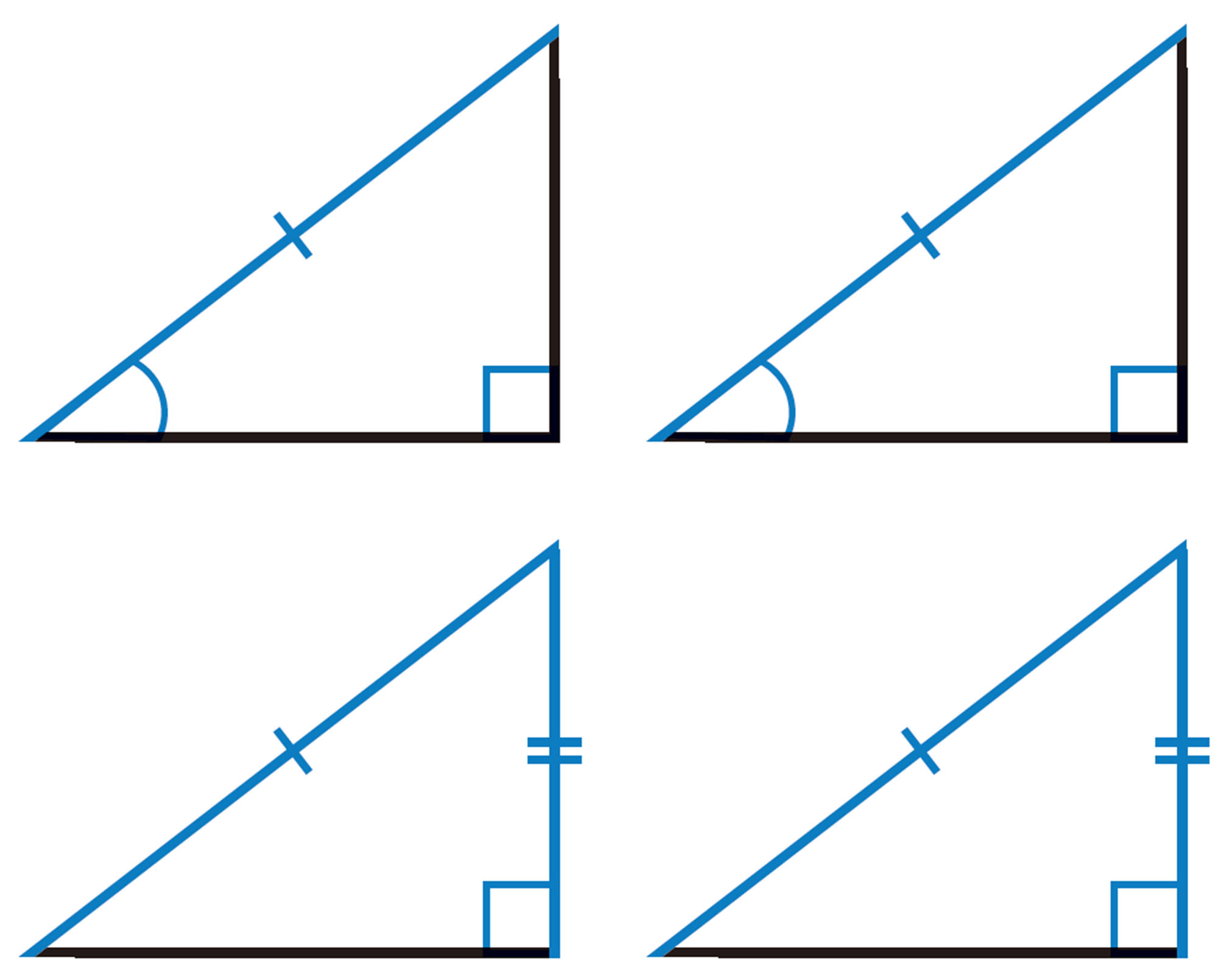
Q Question

1辺と2つの角が等しいね。
合同条件をそのまま使えないから,どうすればいいのかな。

見方・考え方
根拠を明らかにして,説明できるかな。
目標 ▷ 二等辺三角形の性質を使って,直角三角形が合同になる条件について調べよう。
<2年p.159>
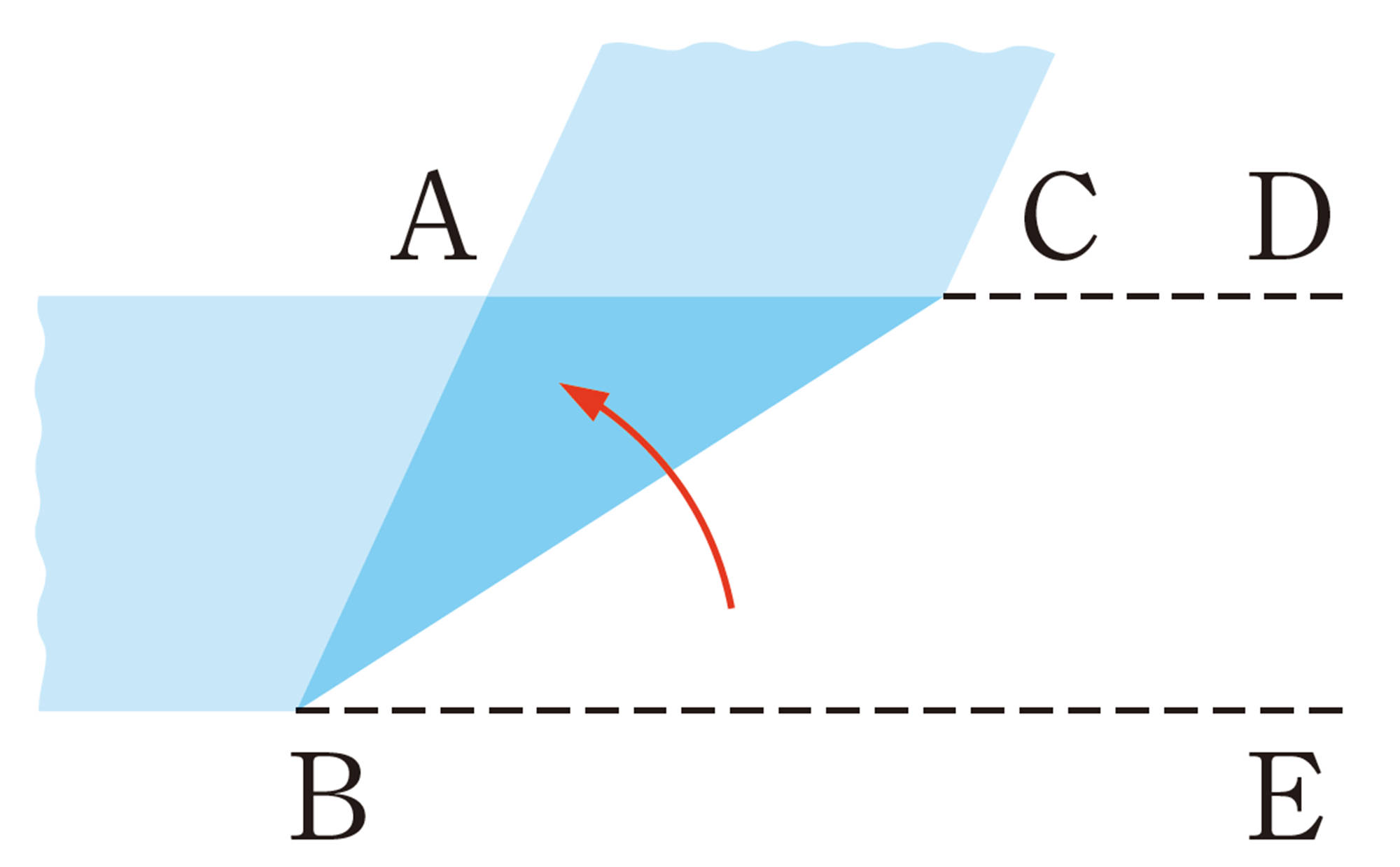
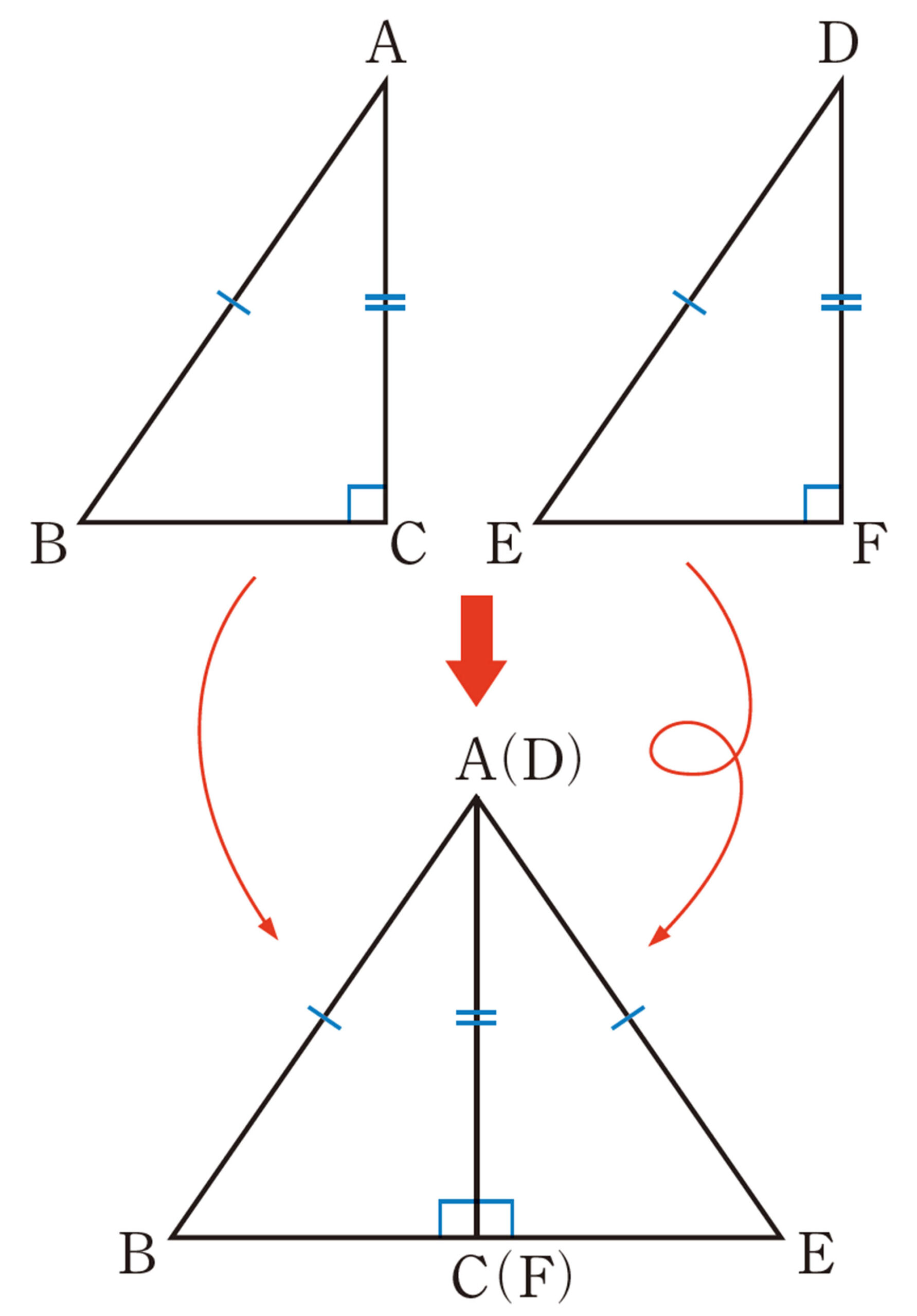
問 1 前ページの図で,右のように,[mathjax]\(\triangle DEF\) を裏返して,等しい辺ACとDFを重ね合わせると,[mathjax]\(\angle C=\angle F=90^{\circ}\) であるから,3点[mathjax]\(B,C(F),E\)は一直線上に並び,[mathjax]\(\triangle ABE\) ができる。この図について,次の問いに答えなさい。
⑴ [mathjax]\(\triangle ABE\) で,[mathjax]\(\angle B=\angle E\) となる理由をいいなさい。
⑵ ⑴を使って,[mathjax]\(\triangle ABC \equiv \triangle AEC\) を証明しなさい。
これまで調べたことは,次のように,定理としてまとめることができる。直角三角形では,三角形の合同条件のほかに,次の合同条件も使える。
<2年p.160>
直角三角形の合同条件を使って,図形の性質を証明してみよう。
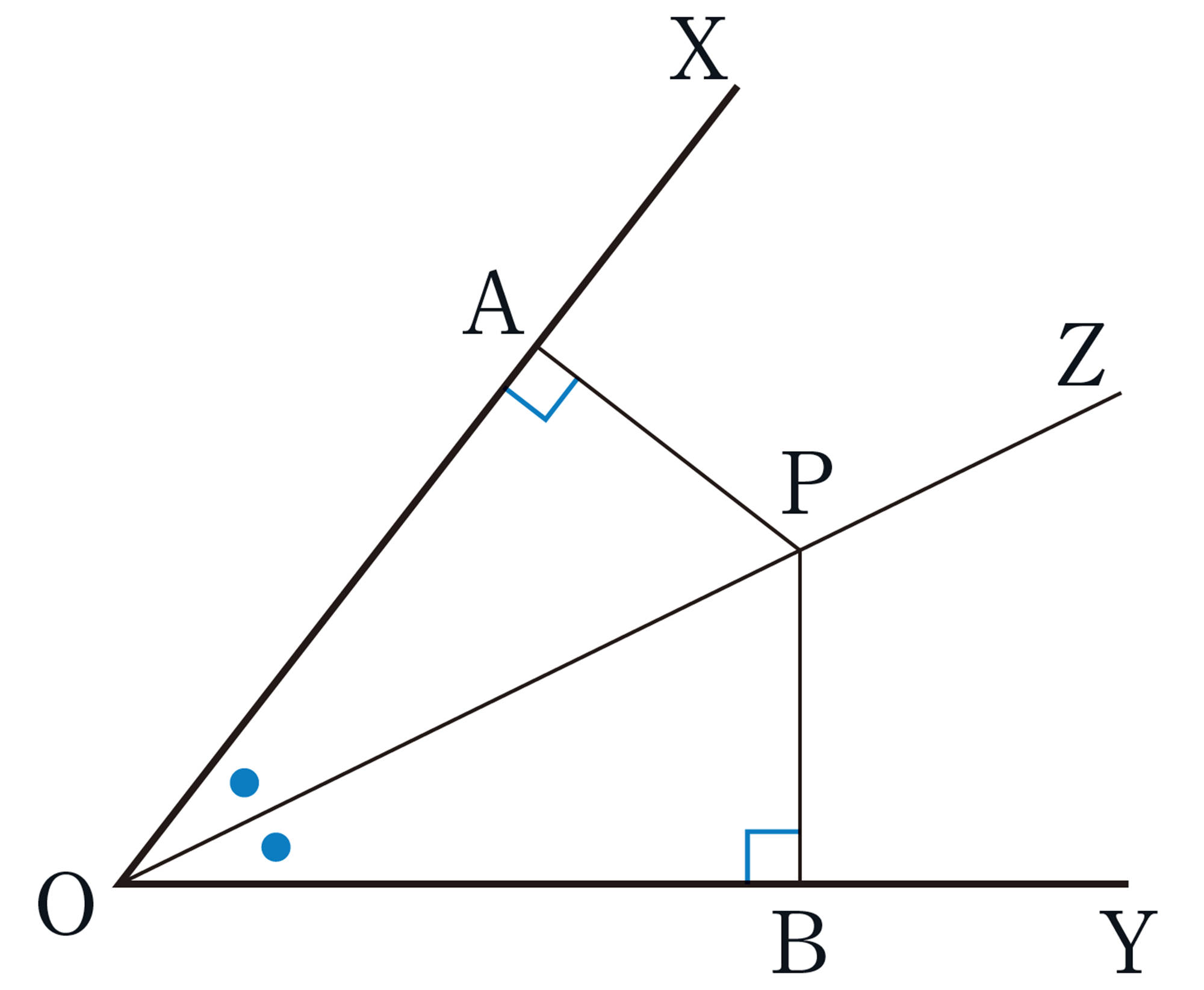
考え方 [mathjax]\(PA=PB\)を導くために,2つの線分が対応する辺となるような合同な三角形を見つけ,それらが合同であることを示せばよい。
証明
[mathjax]\(\triangle AOP\)と[mathjax]\(\triangle BOP\)において,
仮定から,[mathjax]\(\angle PAO=\angle PBO=90^{\circ}\cdots\cdots\text{①}\)
[mathjax]\(\hspace{42pt}\angle AOP=\angle BOP\hspace{28pt}\cdots\cdots\text{②}\)
また,[mathjax]\(\hspace{17pt}OP\)は共通[mathjax]\(\hspace{62pt}\cdots\cdots\text{③}\)
①, ②, ③より, 直角三角形の斜辺と1 つの鋭角がそれぞれ等しいから,
[mathjax] \(\hspace{40pt}\triangle AOP\equiv \triangle BOP\)
したがって,[mathjax]\(\hspace{8pt}PA=PB\)
<2年p.161>
確かめよう 1節 三角形
1 二等辺三角形と正三角形の定義を,それぞれいいなさい。
3 直角三角形の合同条件について,次の□にあてはまることばを書き入れなさい。
① 斜辺と1つの[mathjax]\(\boxed{\phantom{000}}\)がそれぞれ等しい。
② 斜辺と他の[mathjax]\(\boxed{\phantom{000}}\)がそれぞれ等しい。