<2年p.138>
図形の性質のまとめ
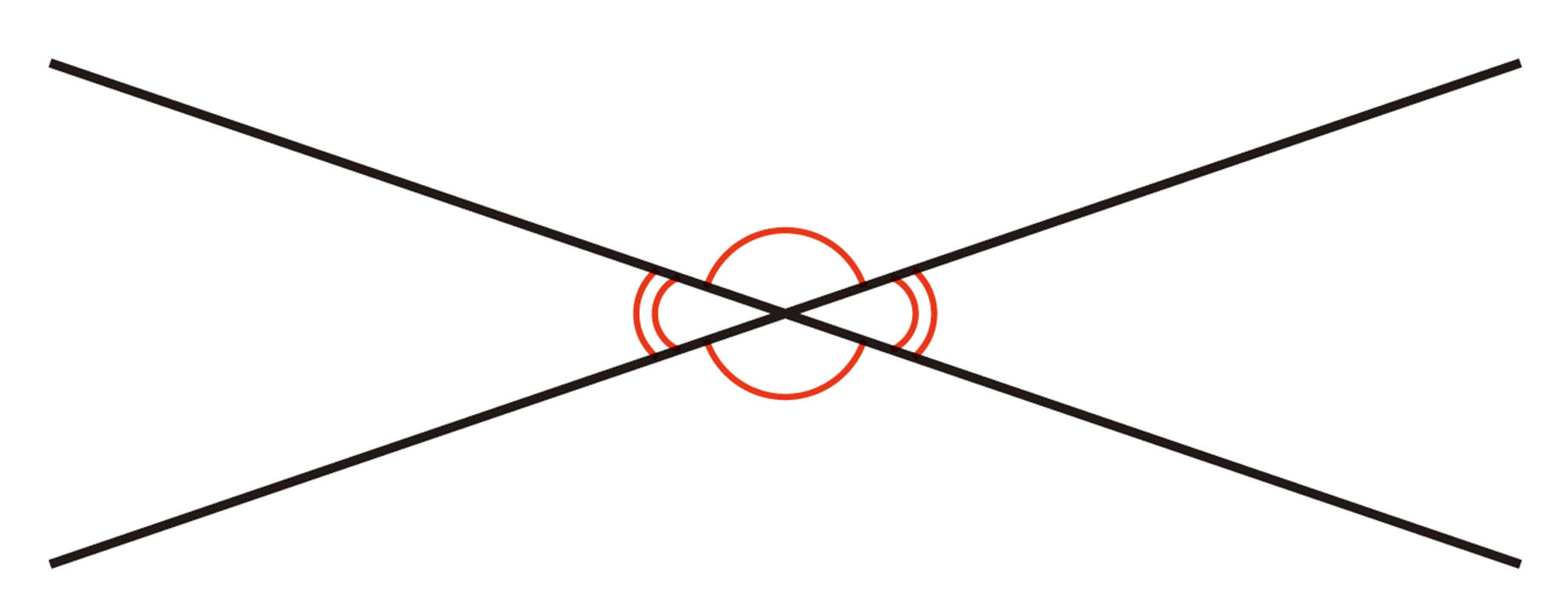
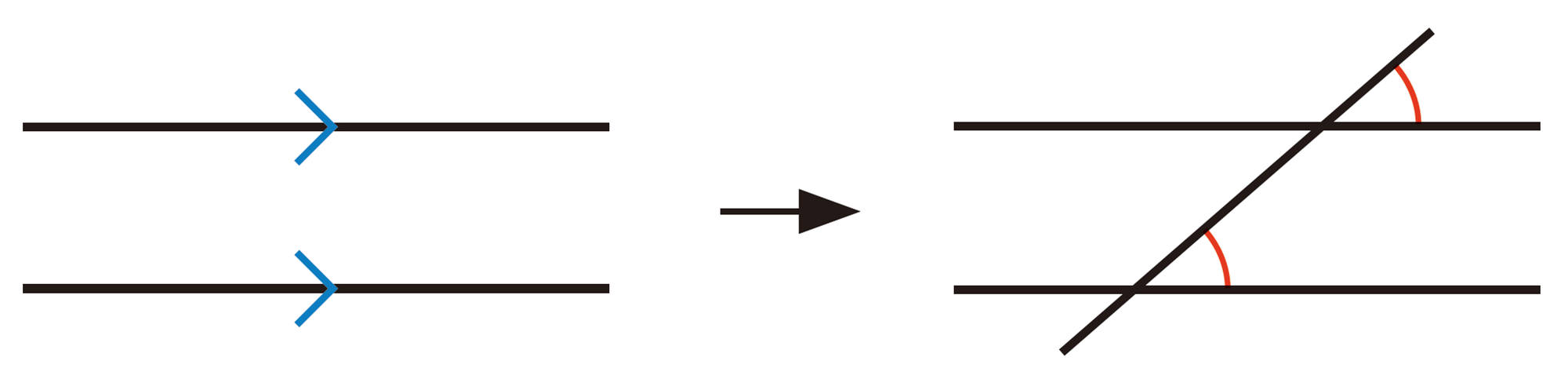
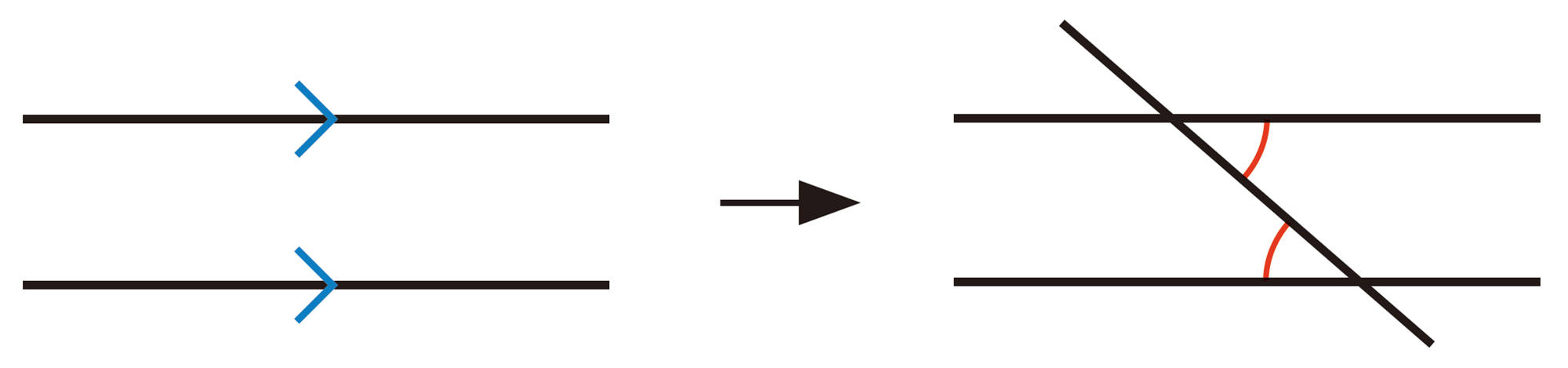
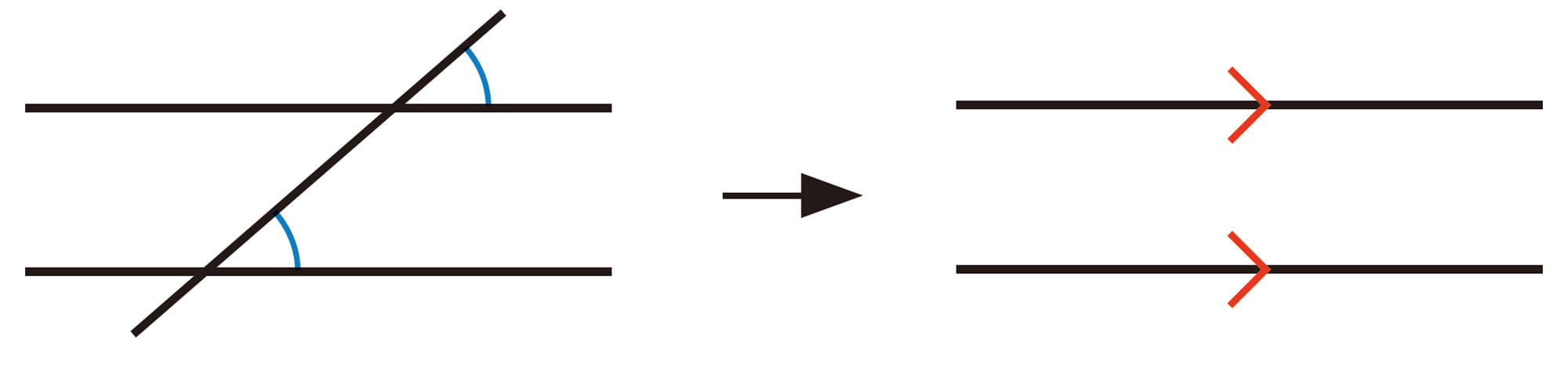
これまで学んだことのうち，証明の根拠としてよく用いられる図形の性質をまとめておこう。
対頂角の性質
対頂角は等しい。
平行線の性質
2直線に1つの直線が交わるとき，次のことが成り立つ。
① 2直線が平行ならば，同位角は等しい。
② 2直線が平行ならば，錯角は等しい。
平行線になるための条件
2直線に1つの直線が交わるとき，次のことが成り立つ。
① 同位角が等しいならば，2直線は平行である。
② 錯角が等しいならば，2直線は平行である。
三角形の角の性質
① 三角形の内角の和は，[mathjax]\( 180^{ \circ }\) である。
② 三角形の外角は，これととなり合わない2つの内角の和に等しい。
<2年p.139>
合同な図形の性質
① 合同な図形では，対応する線分の長さはそれぞれ等しい。
② 合同な図形では，対応する角の大きさはそれぞれ等しい。
三角形の合同条件
2つの三角形は，次のどれか1つが成り立てば合同である。
① 3組の辺がそれぞれ等しい。
② 2組の辺とその間の角がそれぞれ等しい。
③ 1組の辺とその両端の角がそれぞれ等しい。
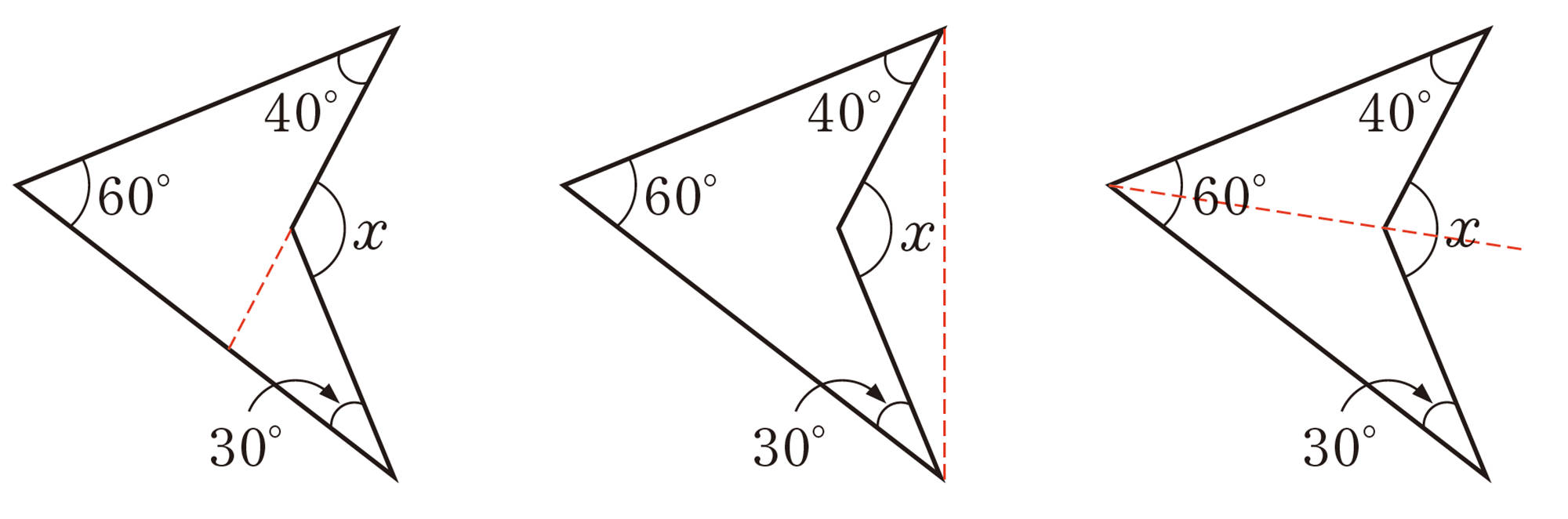
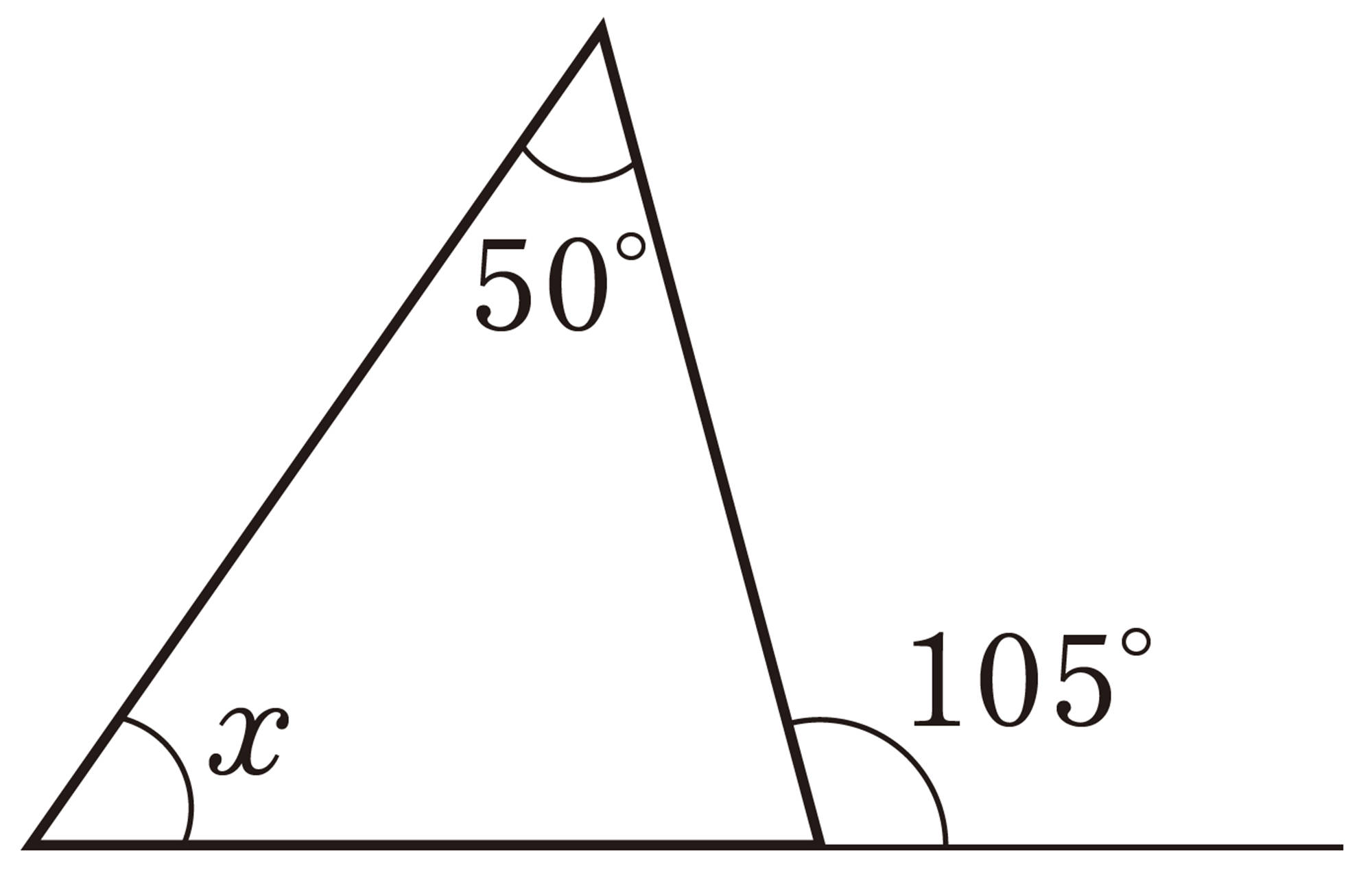
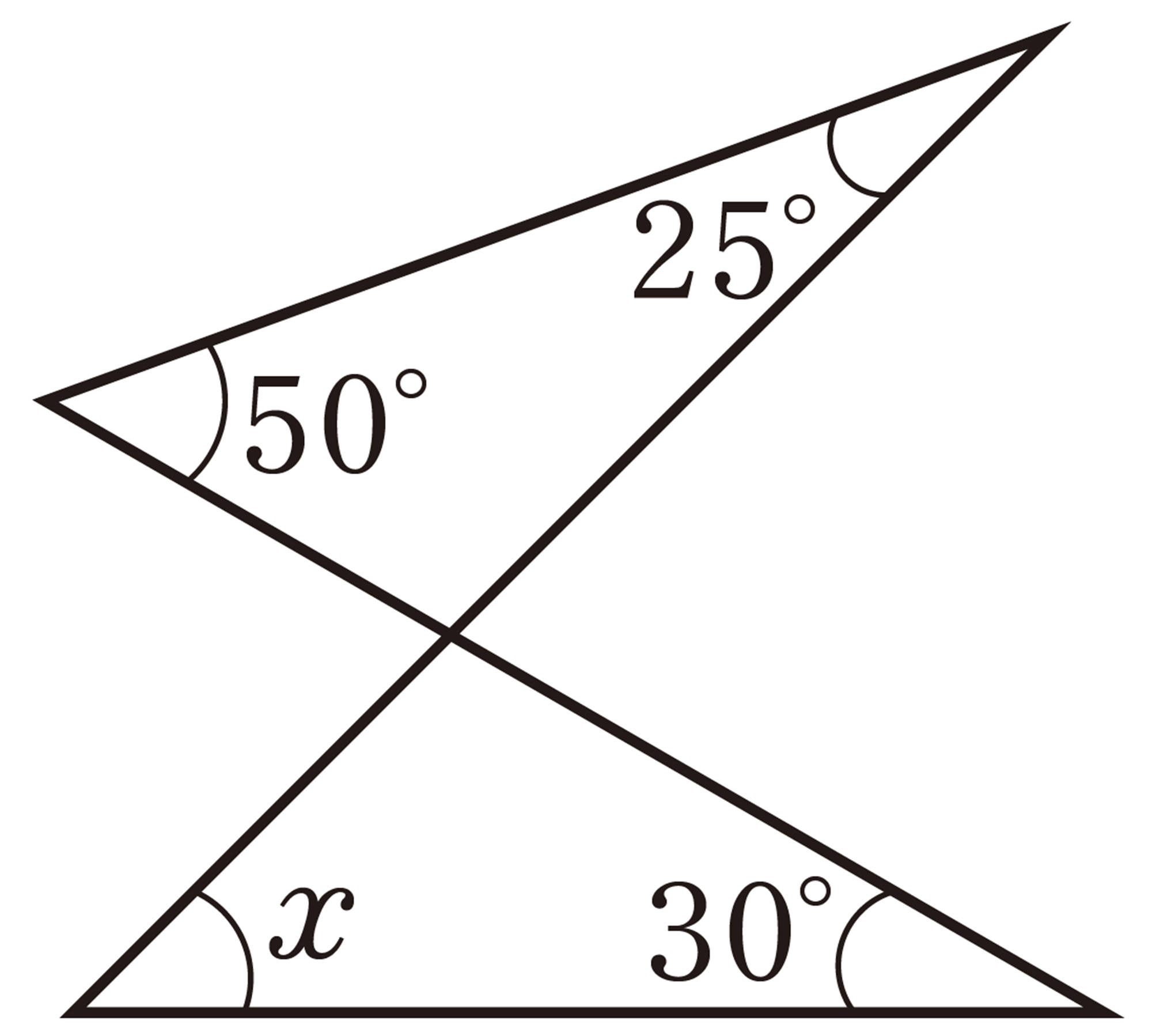
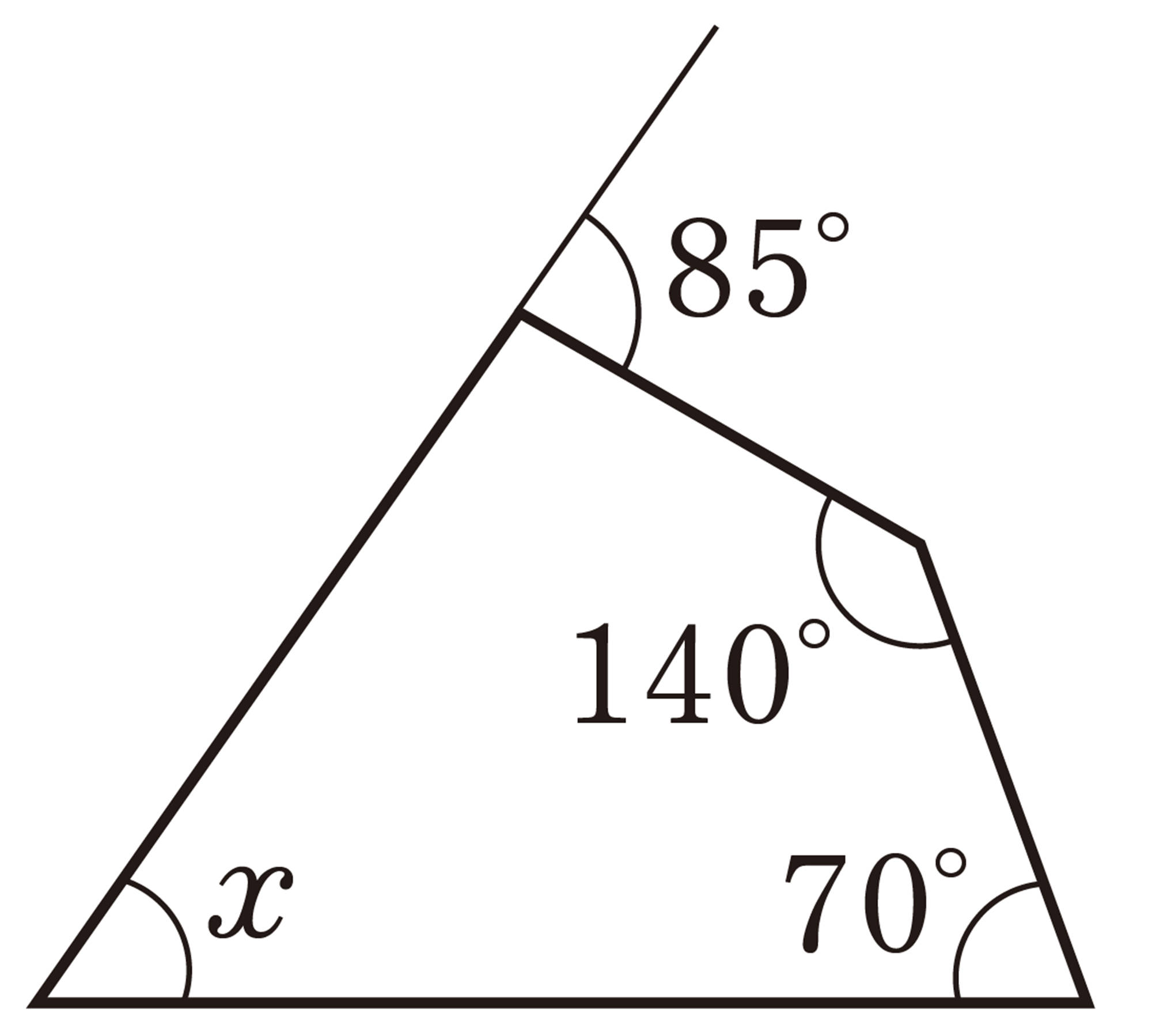
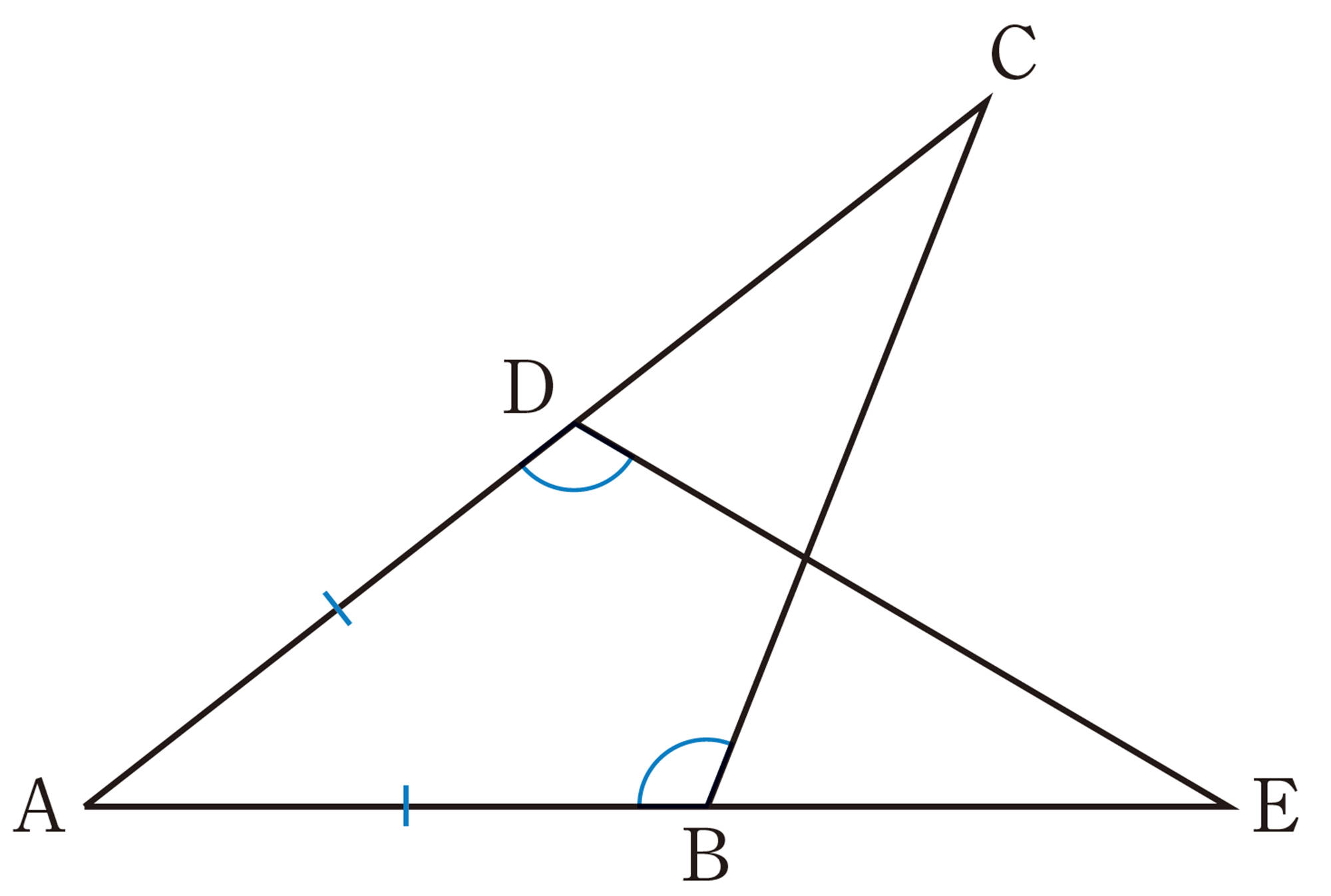
▲トライ 次の図のようなブーメラン形の図形で，[mathjax]\(\angle x\) の大きさをいろいろな方法で求めてみよう。
どんなことがわかったかな
これまでに学んだり，証明したりしてきた図形の性質を使えば，そのほかの図形の性質が成り立つことや作図の根拠などを証明することができます。
<2年p.140>
確かめよう 2節 図形の合同
１ 次の⑴〜⑶に，それぞれどんな条件を1つ加えれば，[mathjax]\(\triangle ABC\) と [mathjax]\(\triangle DEF\) は合同になりますか。それぞれ1つ答えなさい。
⑴ [mathjax]\(BC=EF\)，[mathjax]\(CA=FD\)
⑵ [mathjax]\(BC=EF\)，[mathjax]\(\angle B=\angle E\)
⑶ [mathjax]\(\angle A=\angle D\) ，[mathjax]\(\angle B=\angle E\)
２ 平行で長さの等しい線分ABと線分CDがあります。点Aと点D，点Bと点Cをそれぞれ結び，その交点をOとすると，[mathjax]\(AO=DO\) です。次の問いに答えなさい。
⑴ 上の図を完成させ，仮定と結論をいいなさい。
⑵ このことの証明を，次のような手順ですすめようとするとき，①〜⑤の根拠となることがらをいいなさい。
[mathjax]\(\triangle AOB\) と [mathjax]\(\triangle DOC\) において，
３ 「正方形の2つの対角線の長さは等しい」の逆をいいなさい。また，それが正しいかどうかを調べなさい。
<2年p.141>
4章 「図形の性質の調べ方」を学んで
できるようになったこと 身のまわりの課題へ ▷ P.144
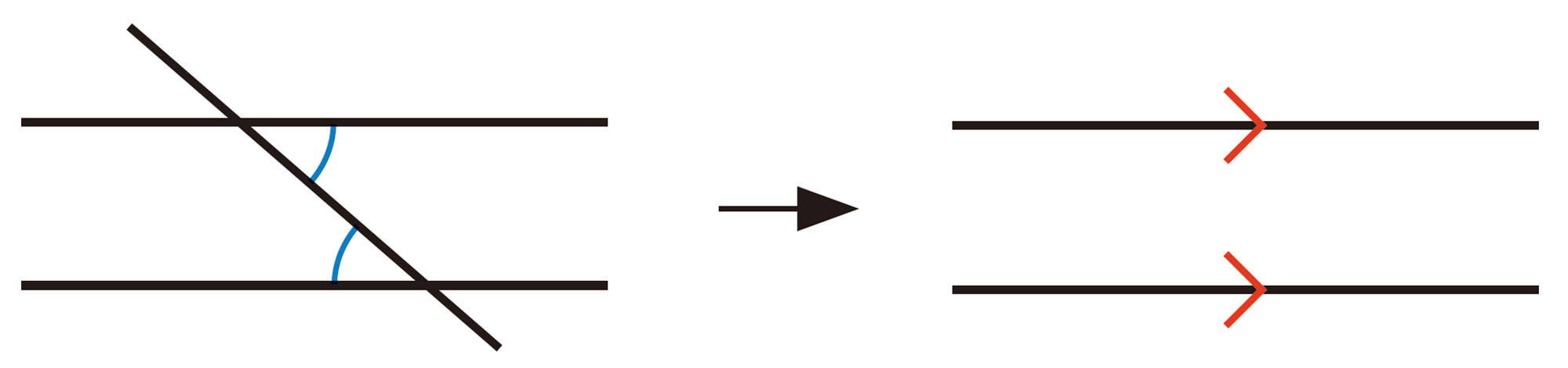
対頂角や，平行線と同位角，錯角の性質を理解し，それを利用することができる。
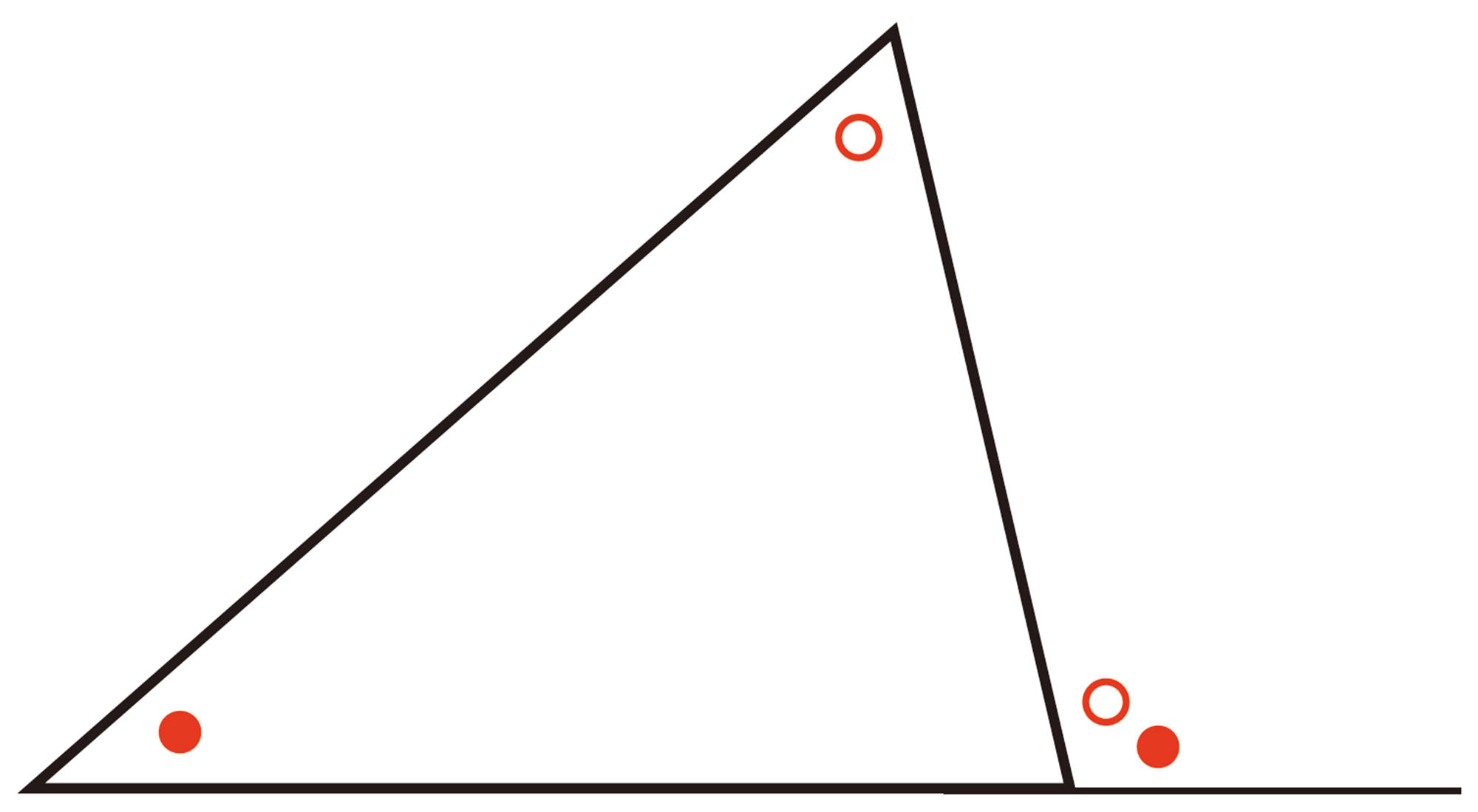
多角形の内角や外角の性質を見つけ，それを利用することができる。
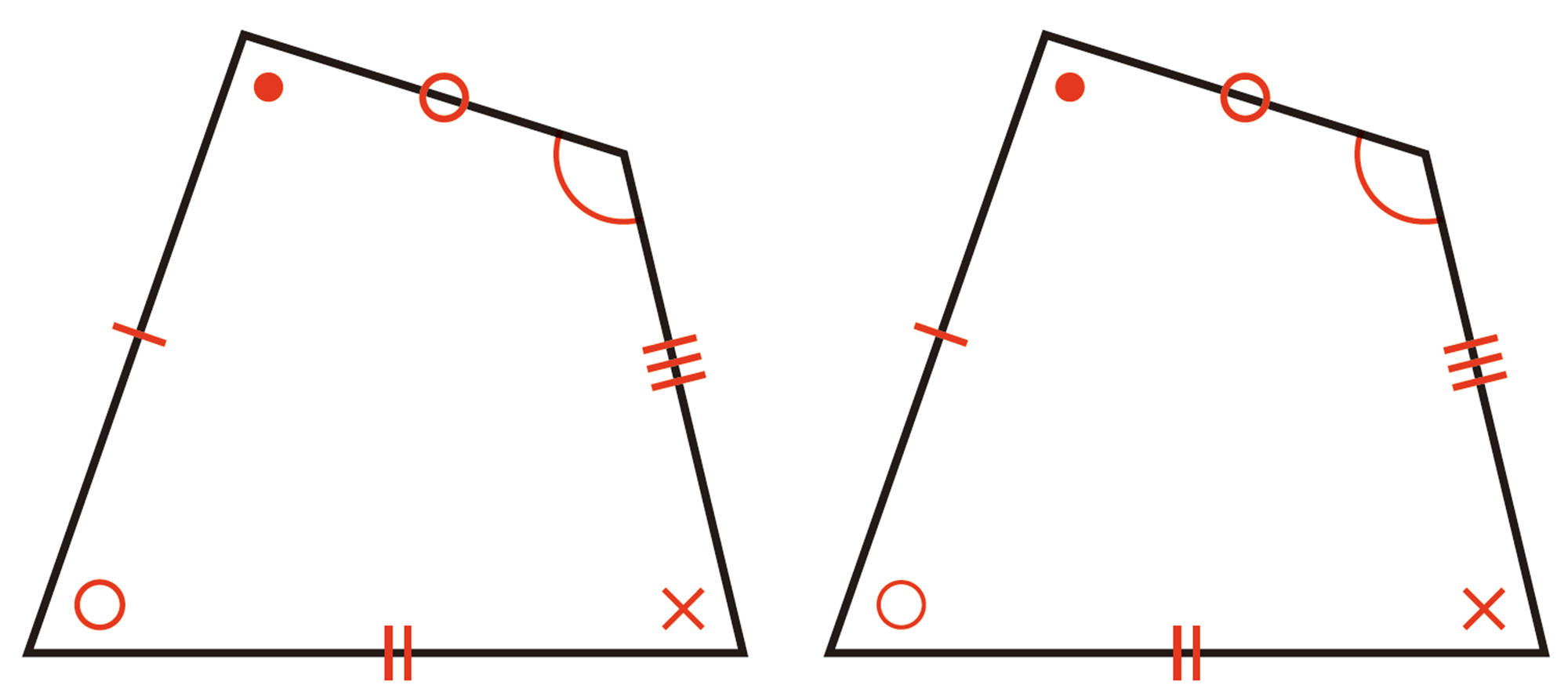
2つの図形が合同のとき，その性質から辺の長さや角の大きさを求めることができる。
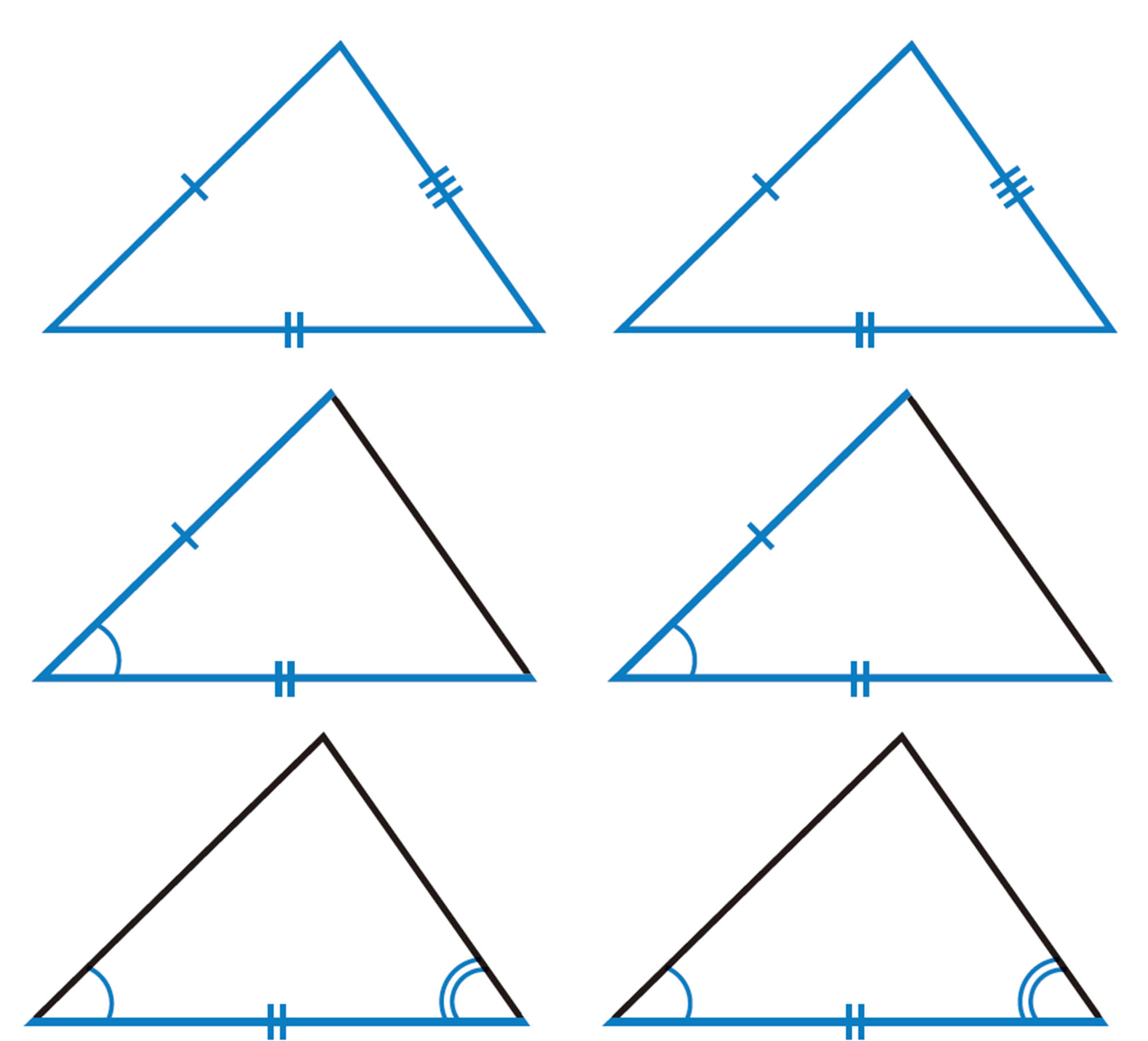
合同な図形の性質や，三角形の合同条件を理解し，いろいろな図形の性質を証明することができる。
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない トラス構造
建物の屋根や橋などで，よく三角形を組み合わせて造られているものを見かけます。これはトラス構造と呼ばれる形式です。
三角形は3つの辺の長さが決まれば，1つに決まりますが，四角形は4つの辺の長さが決まっても，1つに決まりません。したがって，次の図のように，横から押すと，三角形は変形しませんが，四角形は変形します。
このような三角形の性質を利用して，強度が強くなるように，身のまわりの建造物は造られています。
<2年p.142>
４章のまとめの問題 解答 P.249〜250 基本
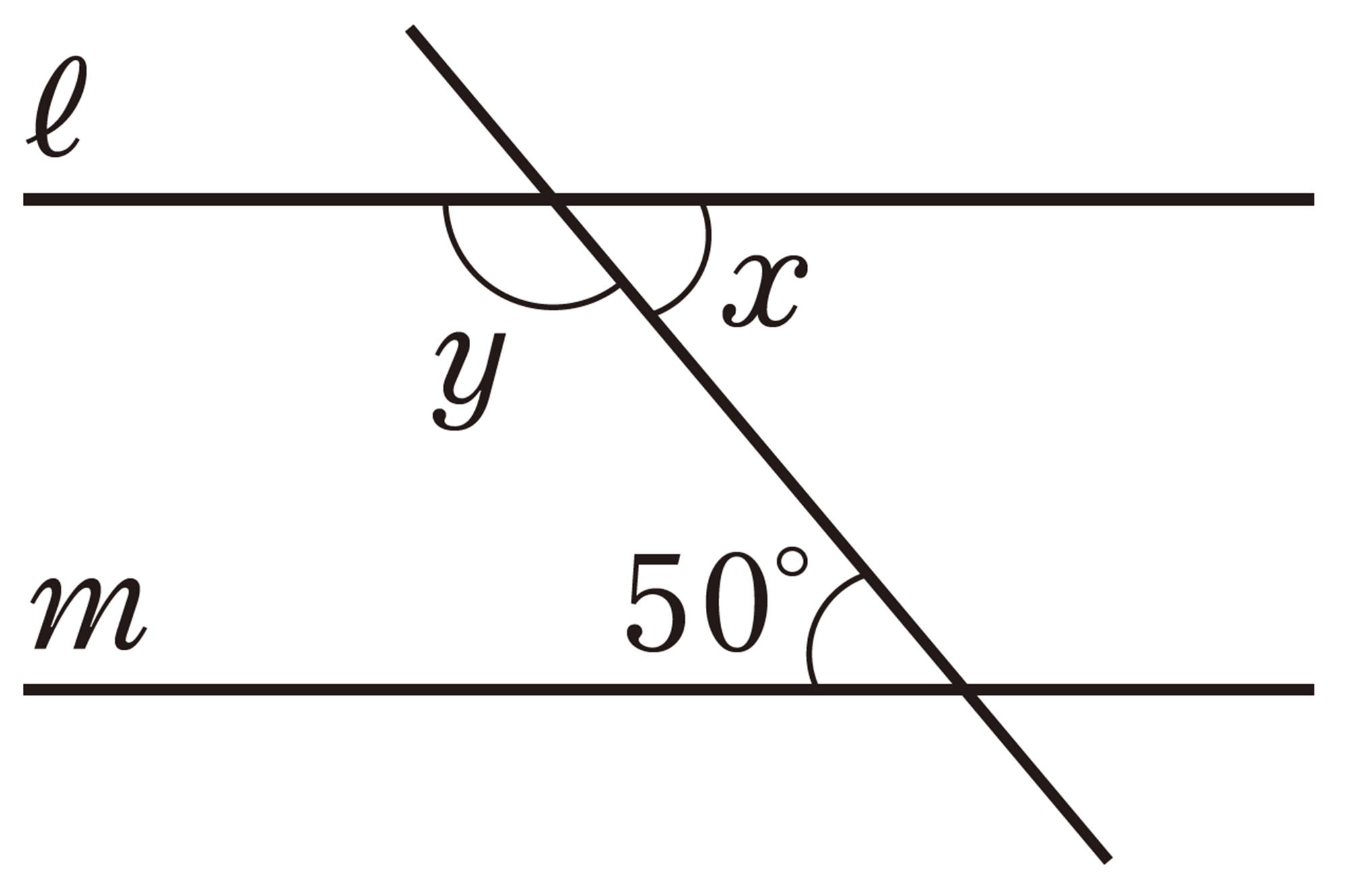
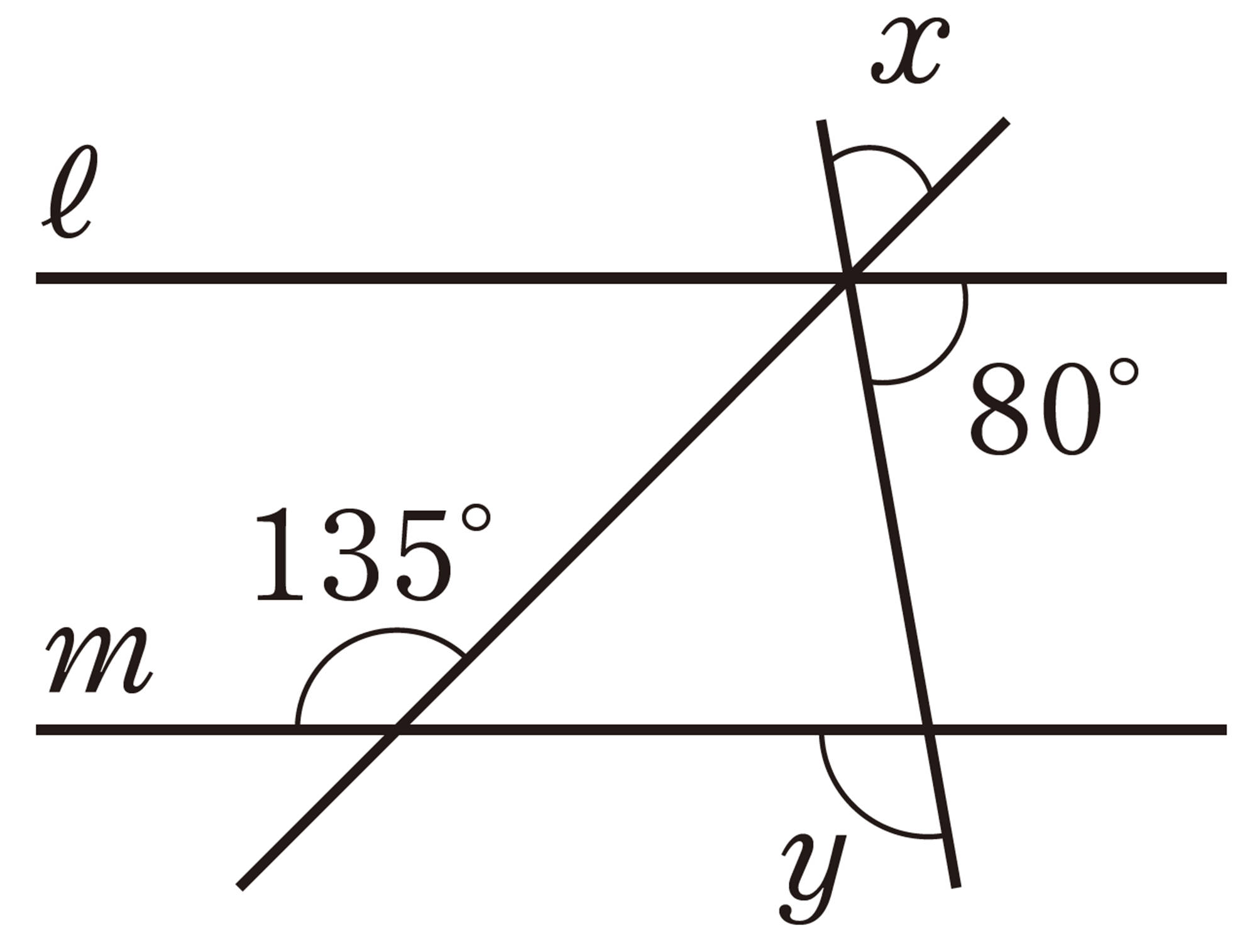
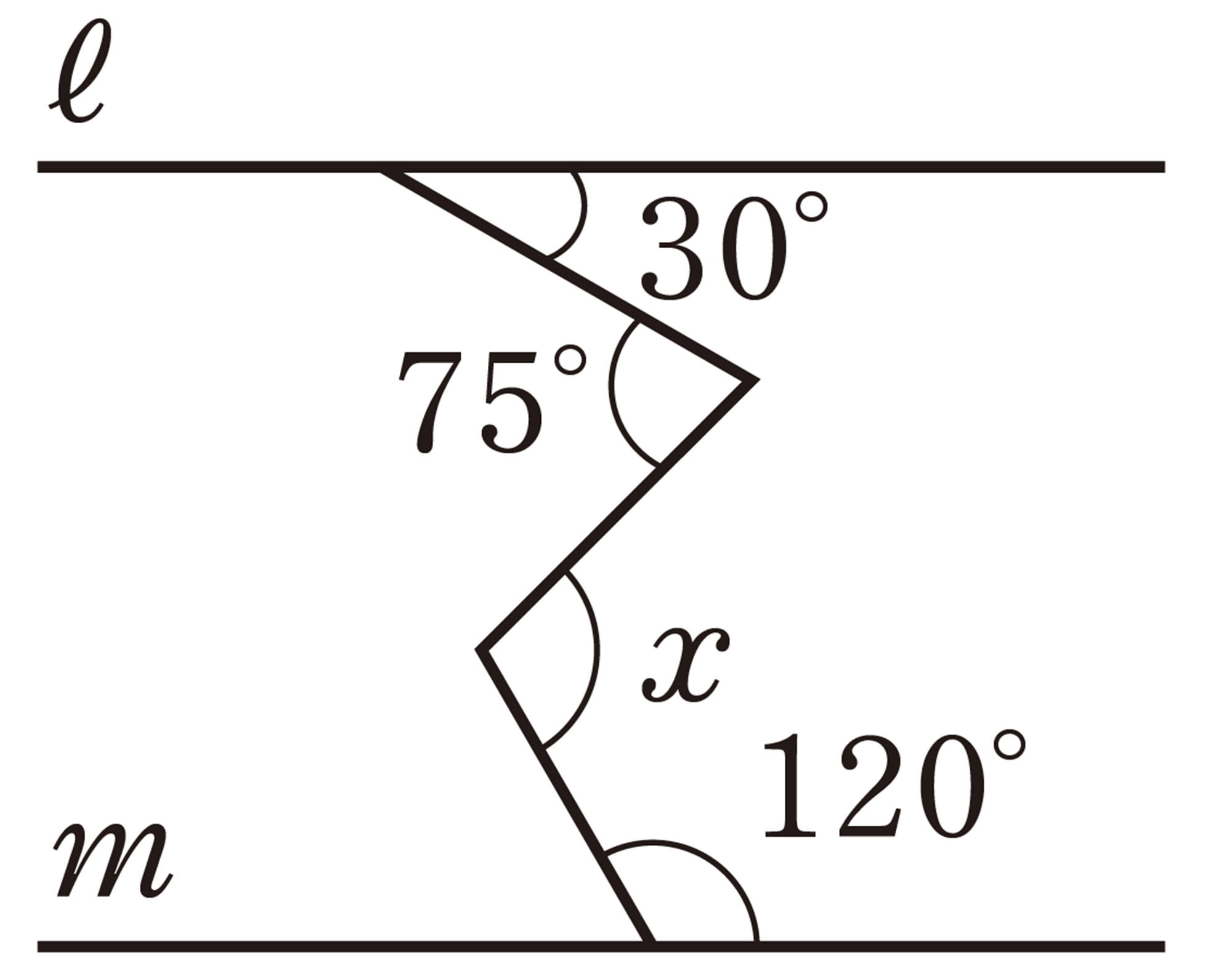
１ 次の図で，[mathjax]\(ℓ/\!/m\) のとき，[mathjax]\(\angle x\)，[mathjax]\(\angle y\) の大きさを求めなさい。
⑴
⑵
⑶
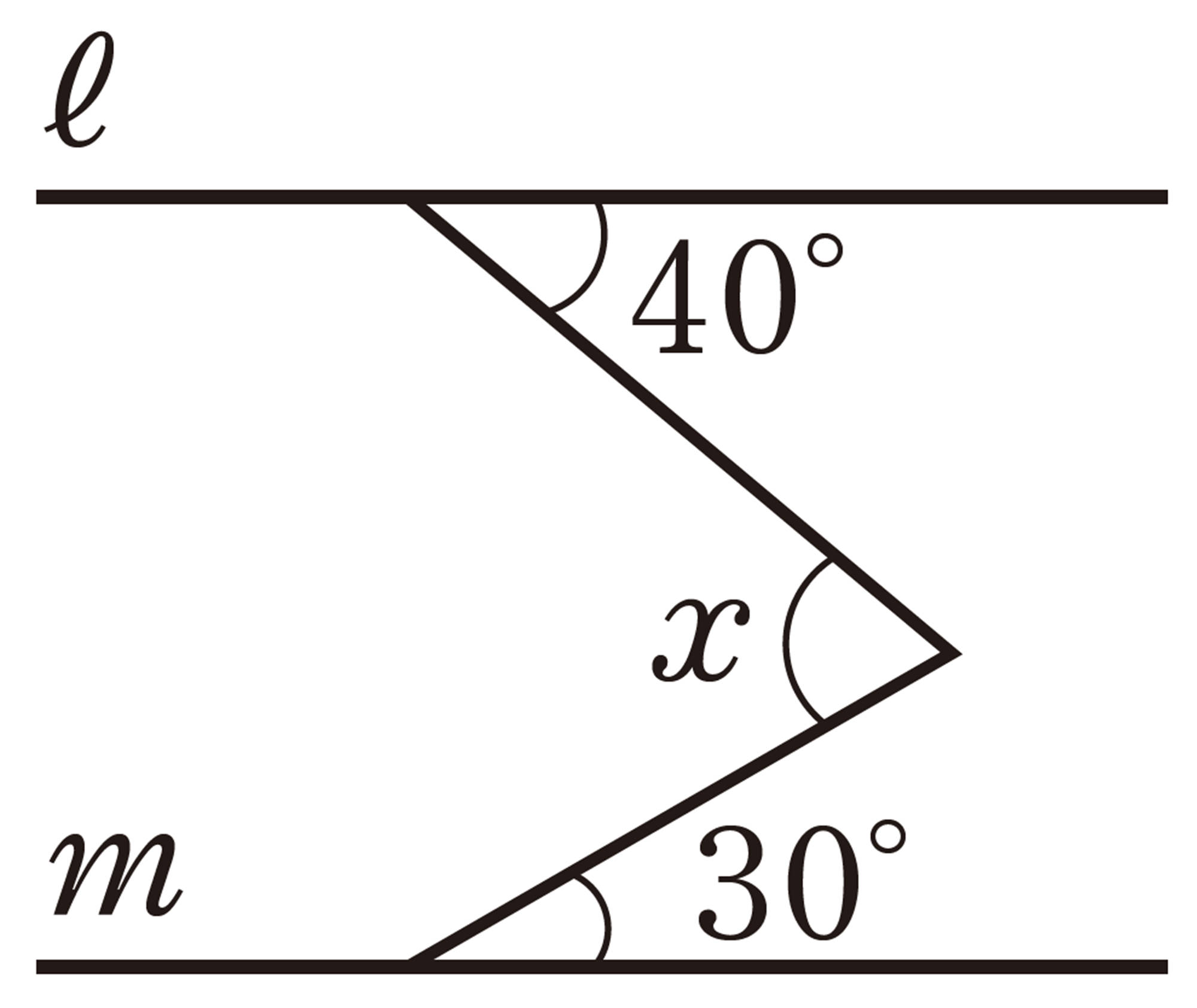
２ 次の図で，[mathjax]\(\angle x\) の大きさを求めなさい。
⑴
⑵
⑶
３ 次の問いに答えなさい。
⑴ 正六角形の1つの内角の大きさを求めなさい。
⑵ 正十角形の1つの外角の大きさを求めなさい。
⑶ 内角の和が [mathjax]\( 900^{ \circ }\) の多角形は何角形ですか。
４ 右の図で，[mathjax]\(AB=AD\) ，[mathjax]\(\angle ABC=\angle ADE\) ならば，[mathjax]\(BC=DE\) です。次の問いに答えなさい。
⑴ 仮定と結論をいいなさい。
⑵ 仮定から結論を導くには，どの三角形とどの三角形の合同をいえばよいですか。
⑶ このことを証明しなさい。
<2年p.143>
応用
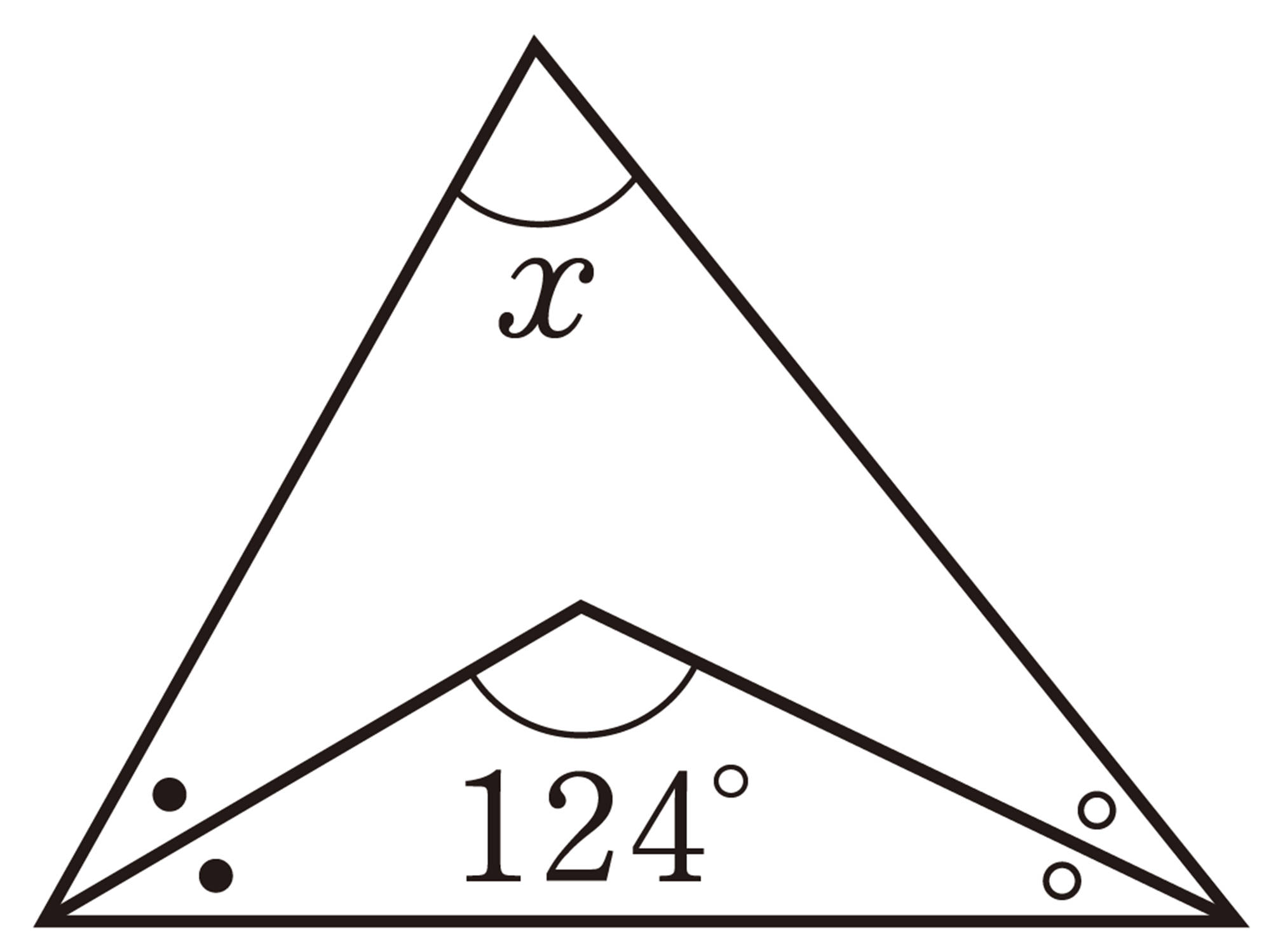
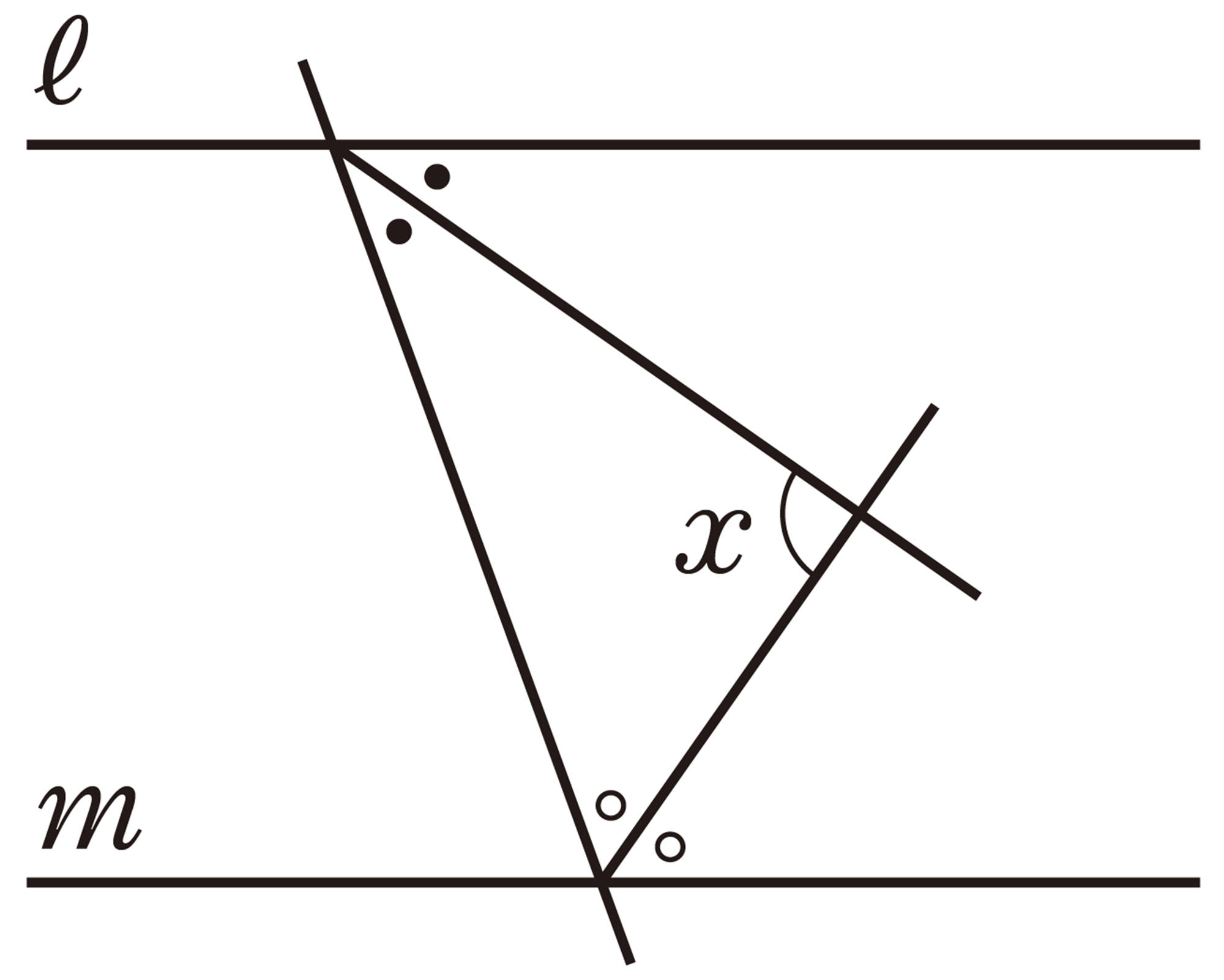
１ 次の図で，[mathjax]\(\angle x\) の大きさを求めなさい。ただし，[mathjax]\(ℓ/\!/m\) で，同じ印をつけた角は等しいとします。
⑴
⑵
⑶
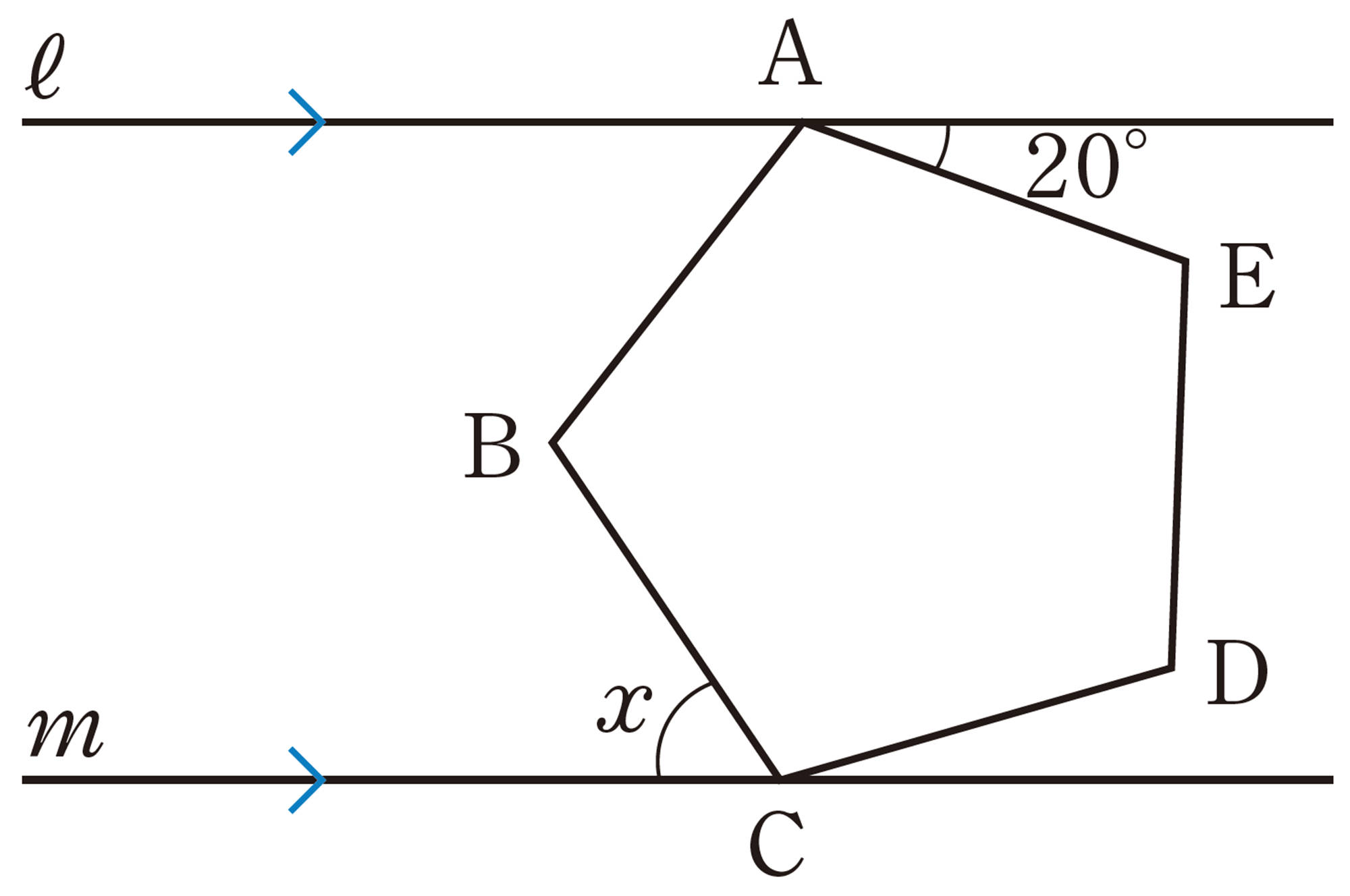
２ 次の図で，正五角形 ABCDEの頂点A，Cは，それぞれ平行な2直線 [mathjax]\(ℓ\)，[mathjax]\(m\) 上にあります。このとき，[mathjax]\(\angle x\) の大きさを求めなさい。
３ 次のことがらを，132ページの手順①〜③にしたがって，証明しなさい。
線分ABの垂直二等分線 [mathjax]\(ℓ\) を引き，ABと [mathjax]\(ℓ\) との交点をMとする。
このとき，[mathjax]\(ℓ\) 上に点Pをとると，[mathjax]\(PA=PB\) である。
４ [mathjax]\(AD/\!/BC\) の台形ABCDで，辺CDの中点をEとし，AとEを結びます。AEの延長とBCの延長との交点をFとするとき，[mathjax]\(AE=FE\) であることを証明しなさい。
<2年p.144>
4章のまとめの問題 活用
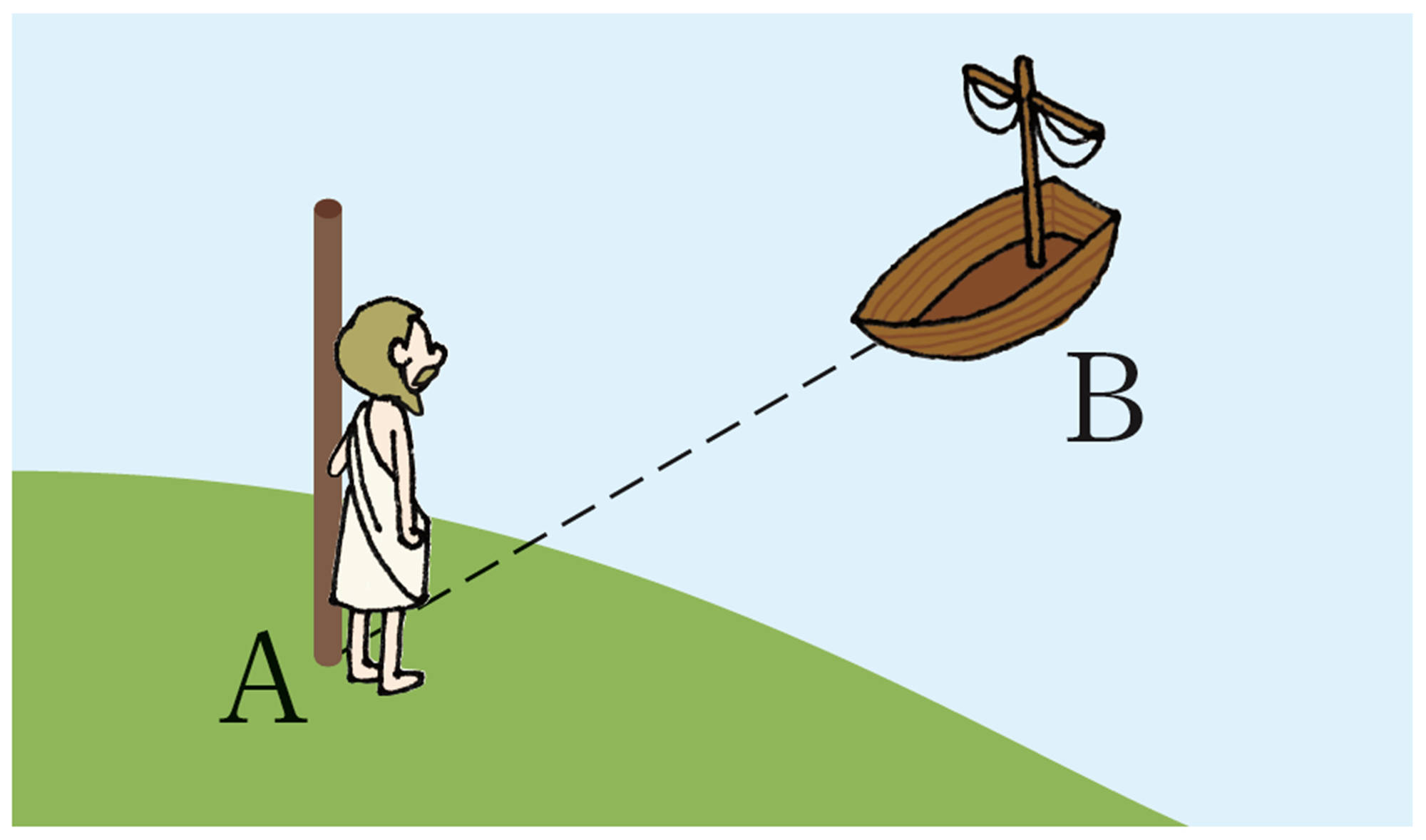
紀元前6世紀頃の古代ギリシャの数学者ターレスは，次のように，陸上から直接測ることができない船までの距離を求めたといわれています。
ターレスの方法
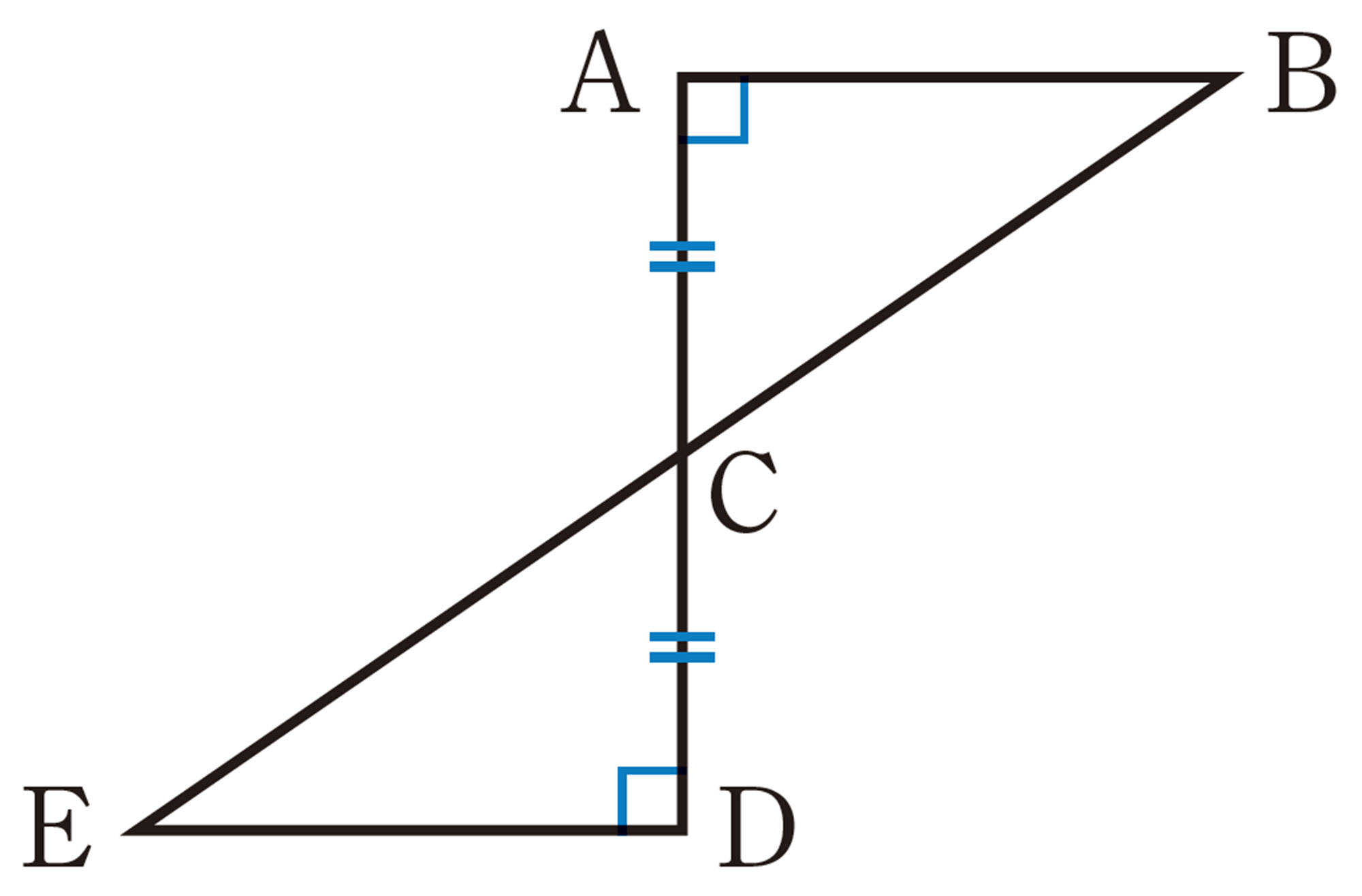
① 陸上の点Aから船Bを見る。
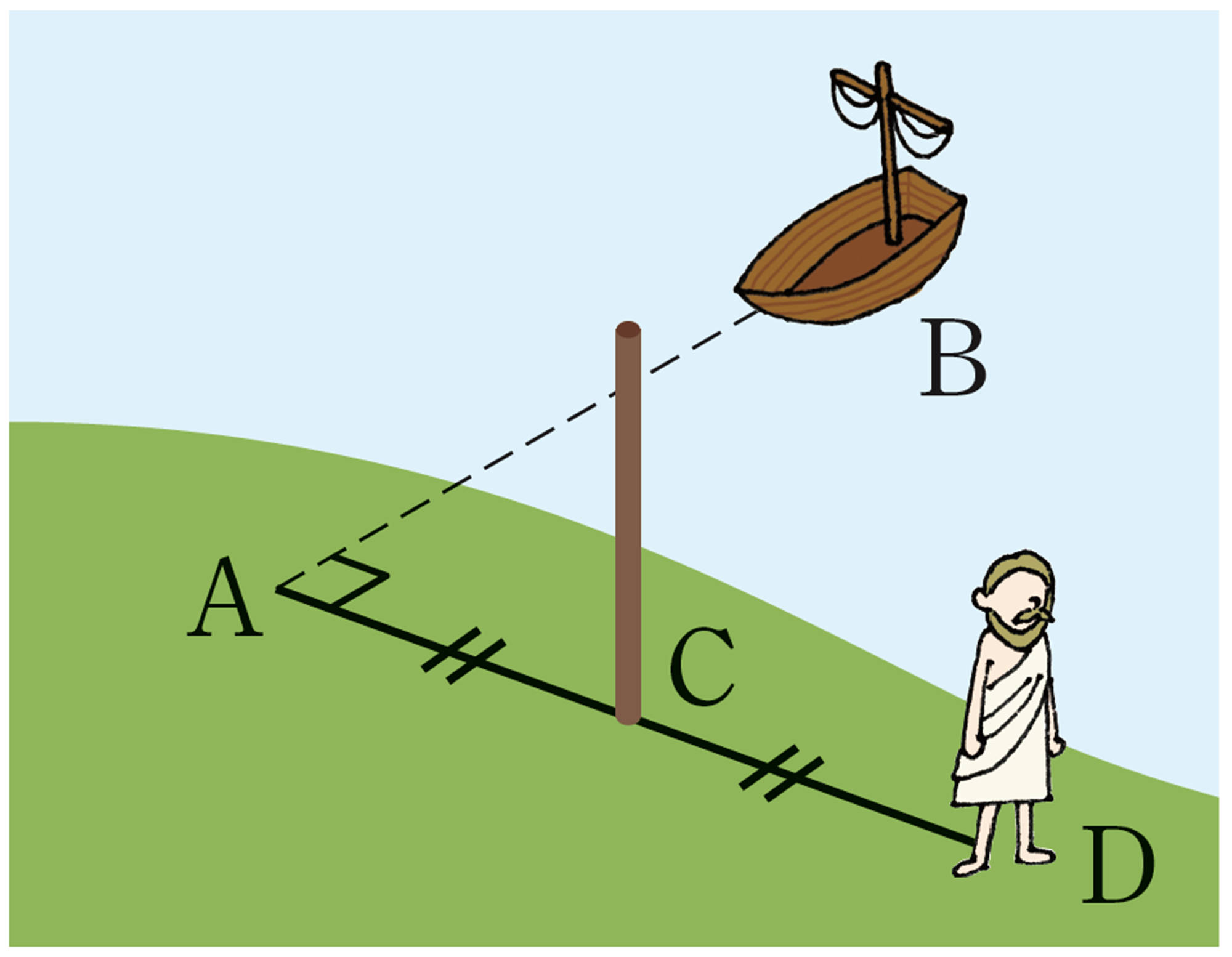
② 点Aで体の向きを [mathjax]\( 90^{ \circ }\) 変え，距離を決めてまっすぐ歩いて棒を立て，その点をCとする。さらに同じ方向に点Aから点Cまでの距離と同じだけまっすぐ歩いて立ち止まり，その点をDとする。
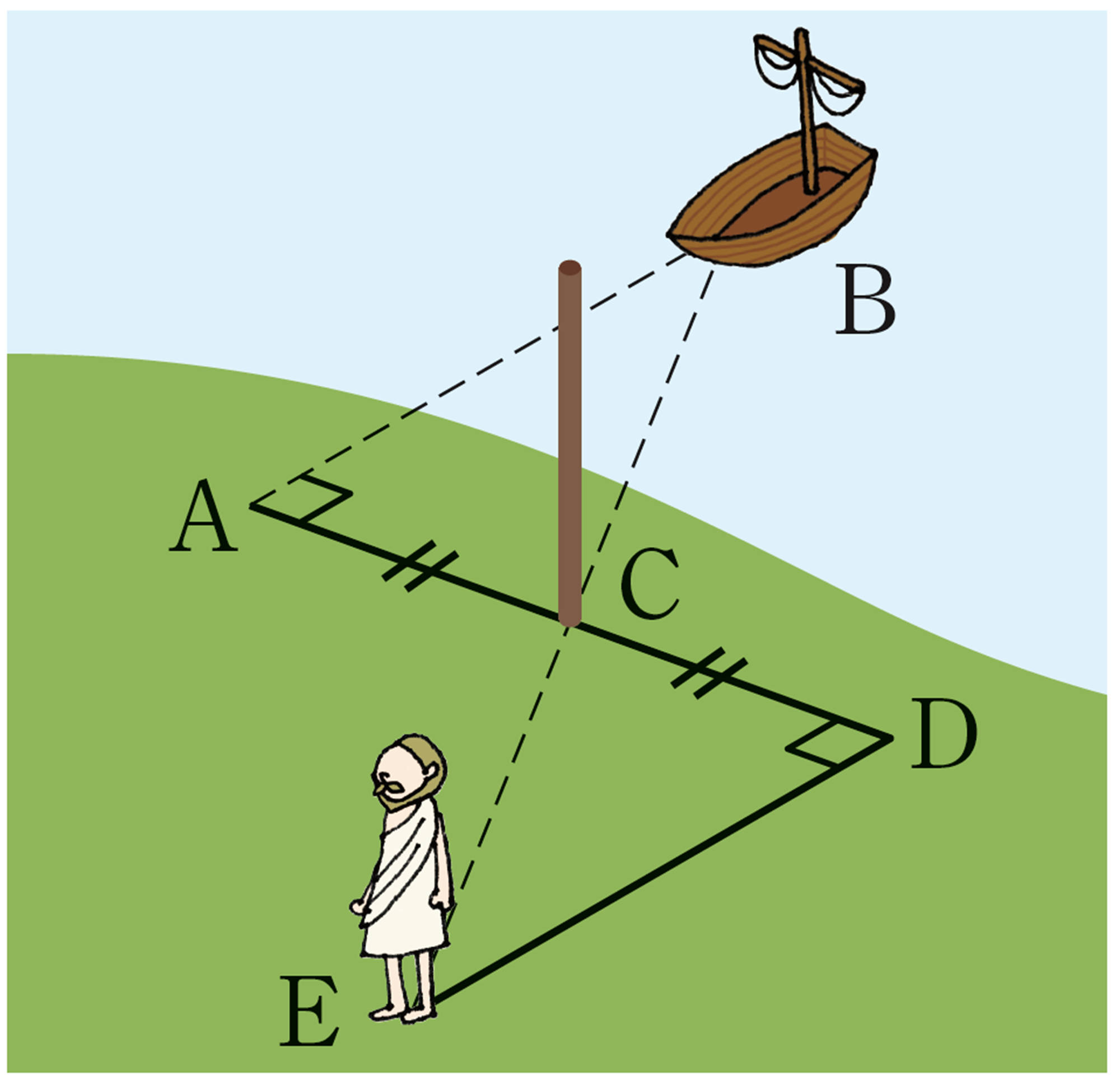
③ 点Dで点Cの方を向き，船Bとは反対側に体の向きを [mathjax]\( 90^{ \circ }\) 変える。そこからまっすぐ歩き，点Cに立てた棒と船Bが重なって見える点をEとする。
④ 点Dから点Eまでの距離を測る。
１ 次の問いに答えなさい。
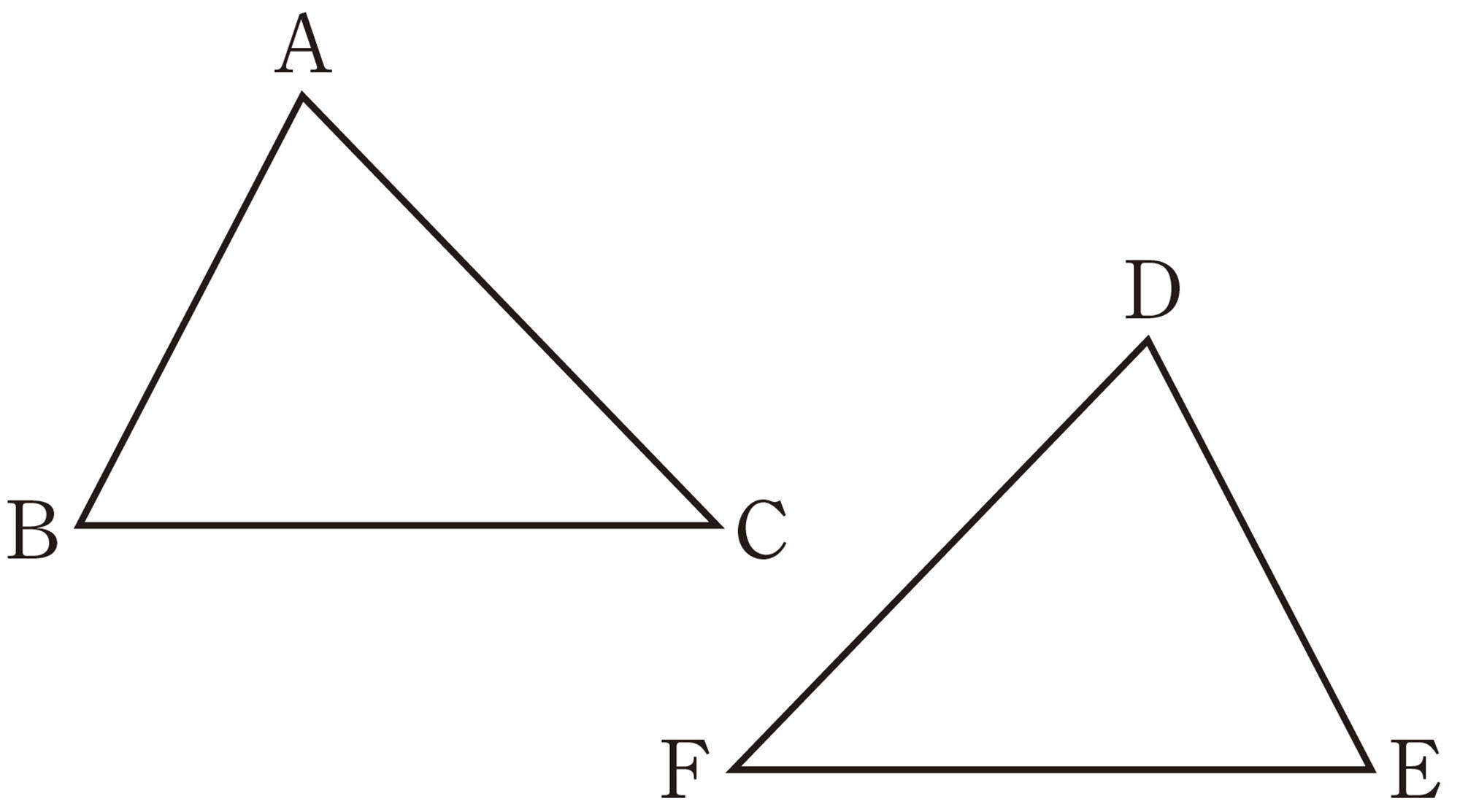
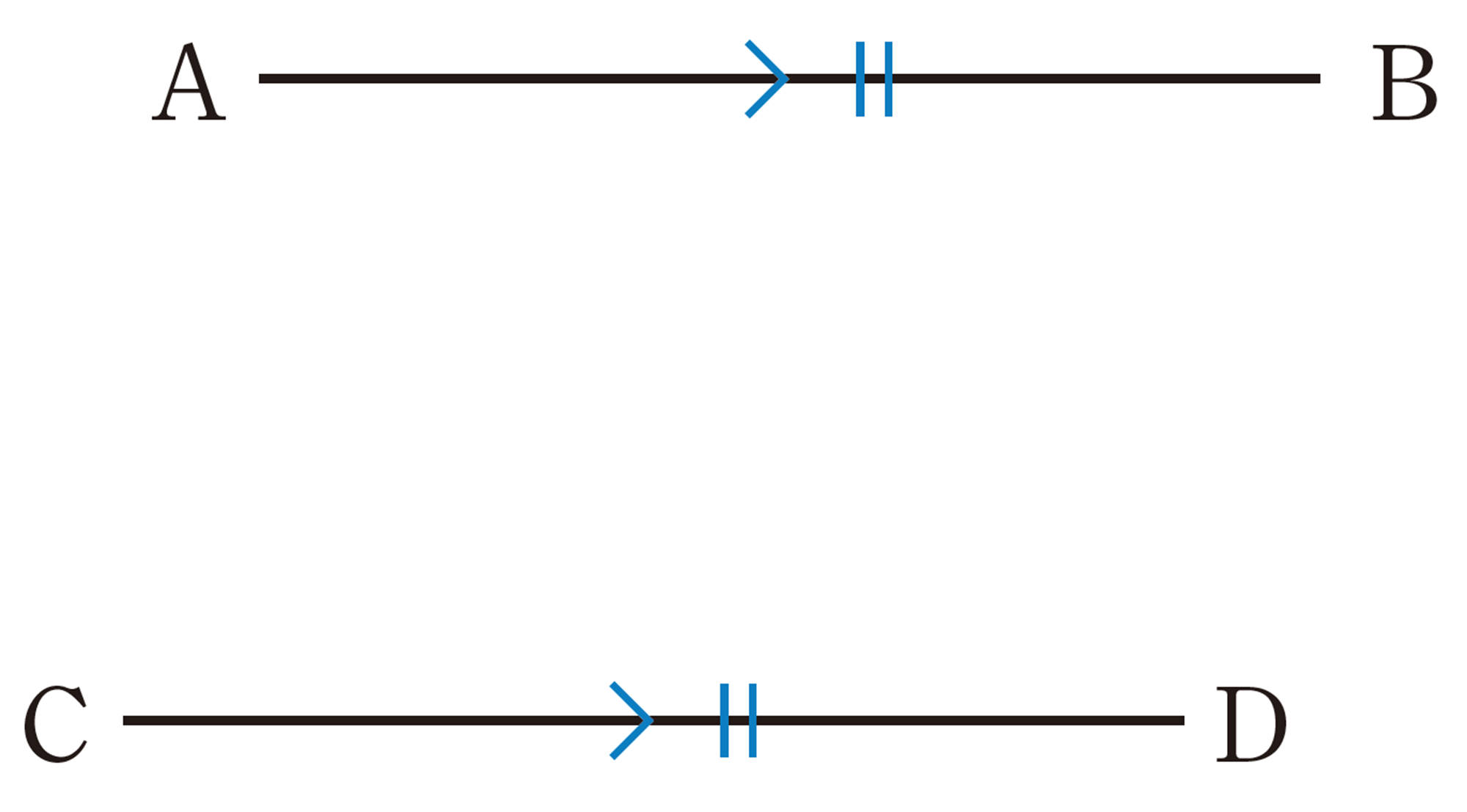
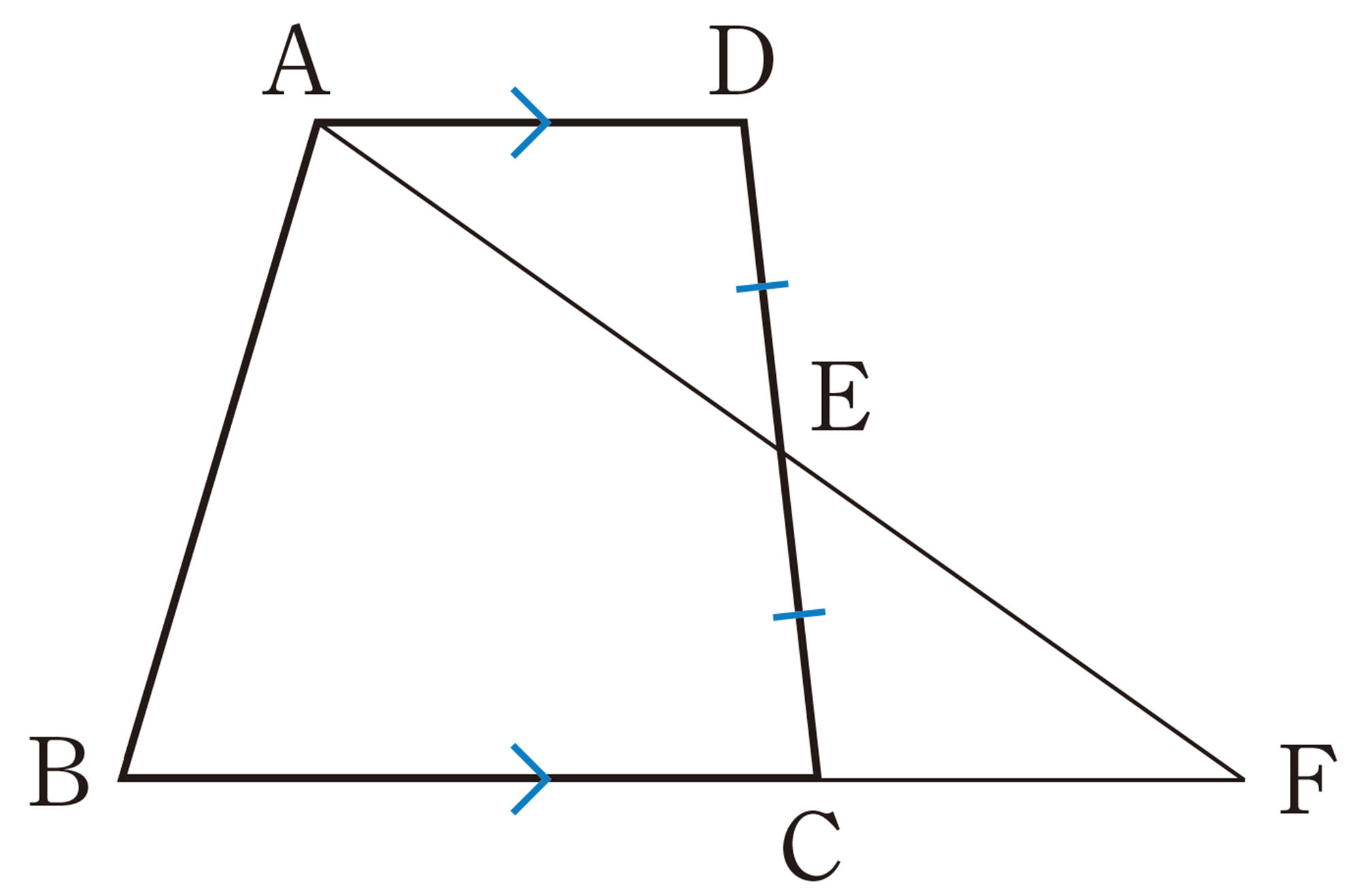
⑴ ターレスの方法では，右の図で， [mathjax]\(AB=DE\) となることを使って船までの距離を求めました。 [mathjax]\(AB=DE\) となることを証明しなさい。
⑵ ターレスの方法では，[mathjax]\(\angle BAC\) と [mathjax]\(\angle EDC\) の大きさを [mathjax]\( 90^{ \circ }\) にしています。次の㋐〜㋓は，この [mathjax]\(\angle BAC\) と [mathjax]\(\angle EDC\) の大きさについて述べたものです。正しいものを1つ選びなさい。
㋐ [mathjax]\(\angle BAC\) と [mathjax]\(\angle EDC\) がどちらも [mathjax]\( 90^{ \circ }\) のときだけ，[mathjax]\(\triangle ABC \equiv \triangle DEC\) を利用して船までの距離を求めることができる。
㋑ [mathjax]\(\angle BAC=\angle EDC\) であれば，[mathjax]\( 90^{ \circ }\) にしなくても，[mathjax]\(\triangle ABC \equiv \triangle DEC\) を利用して船までの距離を求めることができる。
㋒ [mathjax]\(\angle BAC\) を [mathjax]\( 90^{ \circ }\) にすれば，[mathjax]\(\angle EDC\) を何度にしても，[mathjax]\(\triangle ABC \equiv \triangle DEC\) を利用して船までの距離を求めることができる。
㋓ [mathjax]\(\angle BAC\) と [mathjax]\(\angle EDC\) の大きさを等しくしなくても，[mathjax]\(\triangle ABC \equiv \triangle DEC\) を利用して船までの距離を求めることができる。
<2年p.145>
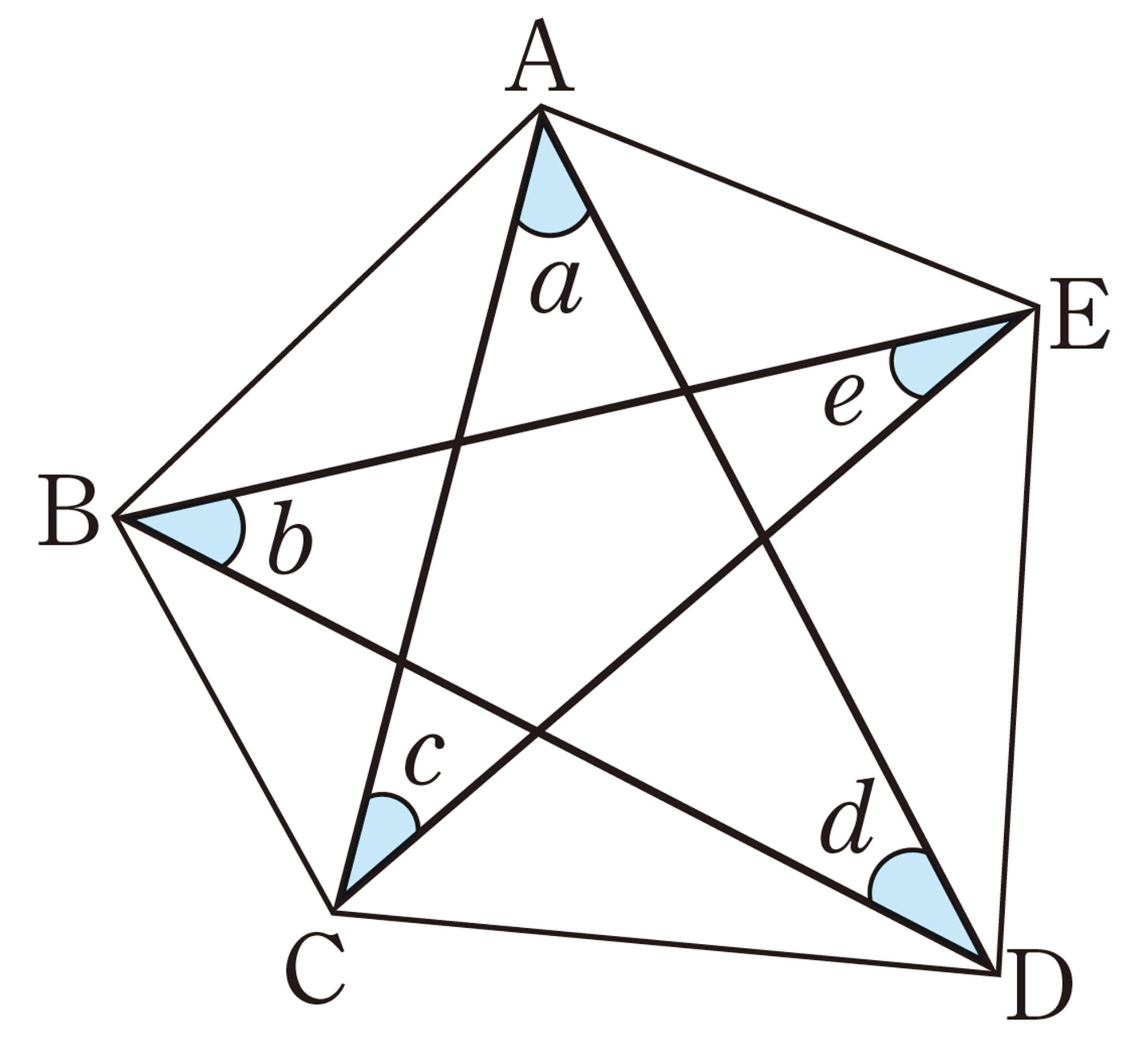
深めよう 星形 [mathjax]\( n \) 角形
123ページで，星形五角形の先端部分の5つの角の和が [mathjax]\( 180^{ \circ }\) になることを説明しました。星形五角形は，右の図のように，五角形の頂点を1つ飛ばして結んでいくと，かくことができます。
同じように， [mathjax]\( n \) 角形を使って星形 [mathjax]\( n \) 角形をかいたとき，先端部分の [mathjax]\( n \) 個の和が，どうなるか考えてみましょう。
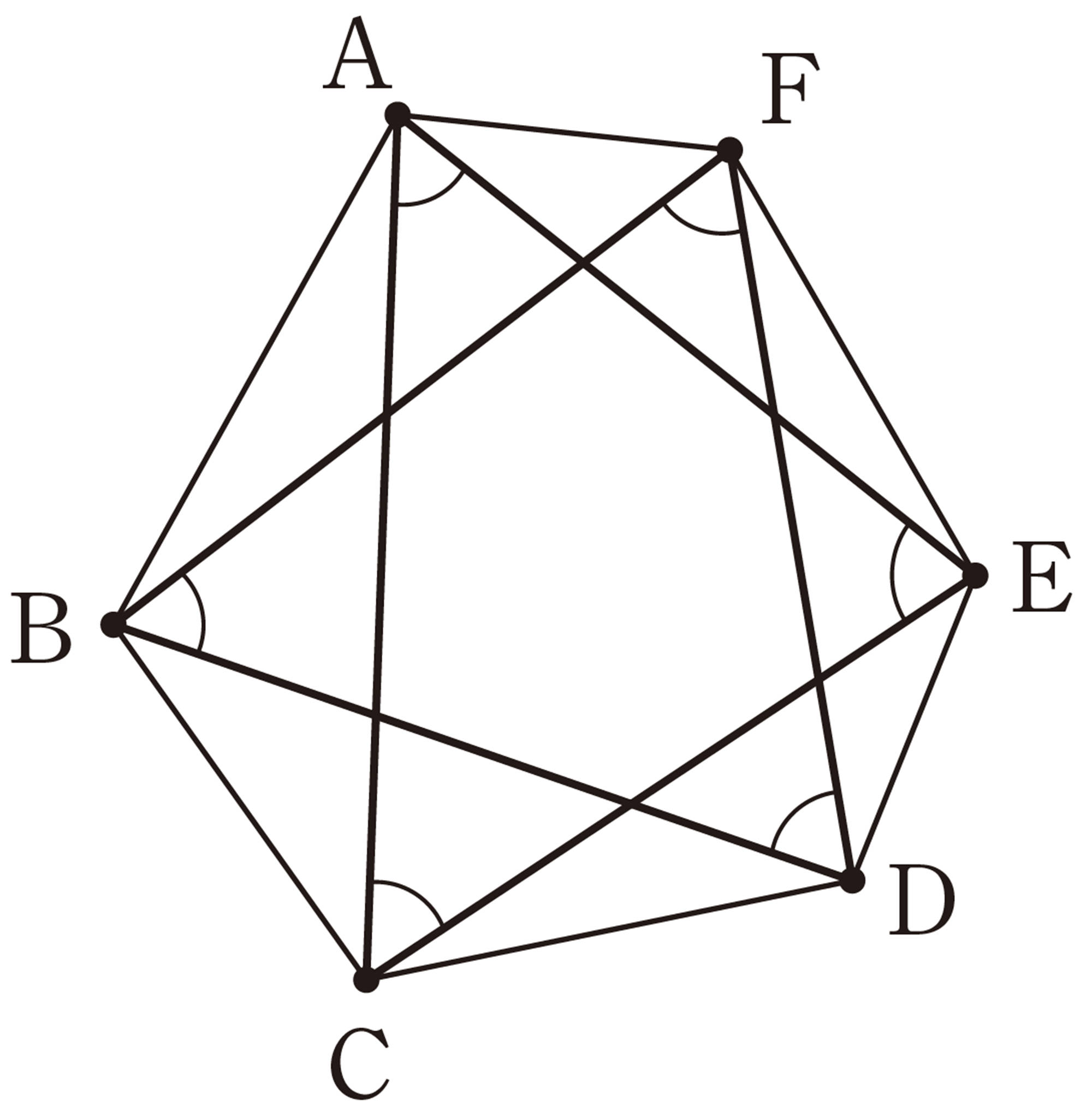
① 星形六角形について，調べてみましょう。
六角形の頂点を1つ飛ばして結び，星形六角形をかいてみましょう。
頂点を1つ飛ばして結ぶと，三角形になるよ。
三角形を2つ重ねた図でいいのかな。
② 六角形の頂点を1つ飛ばして結ぶ星形六角形は，右の図のような図形になります。
この星形六角形の先端部分の6つの角の和を求めてみましょう。
③ 次に，星形七角形について，調べてみましょう。
七角形の頂点を1つ飛ばして結ぶ星形七角形は，右の図のような図形になります。
この星形七角形の先端部分の7つの角の和を求めてみましょう。
<2年p.146>
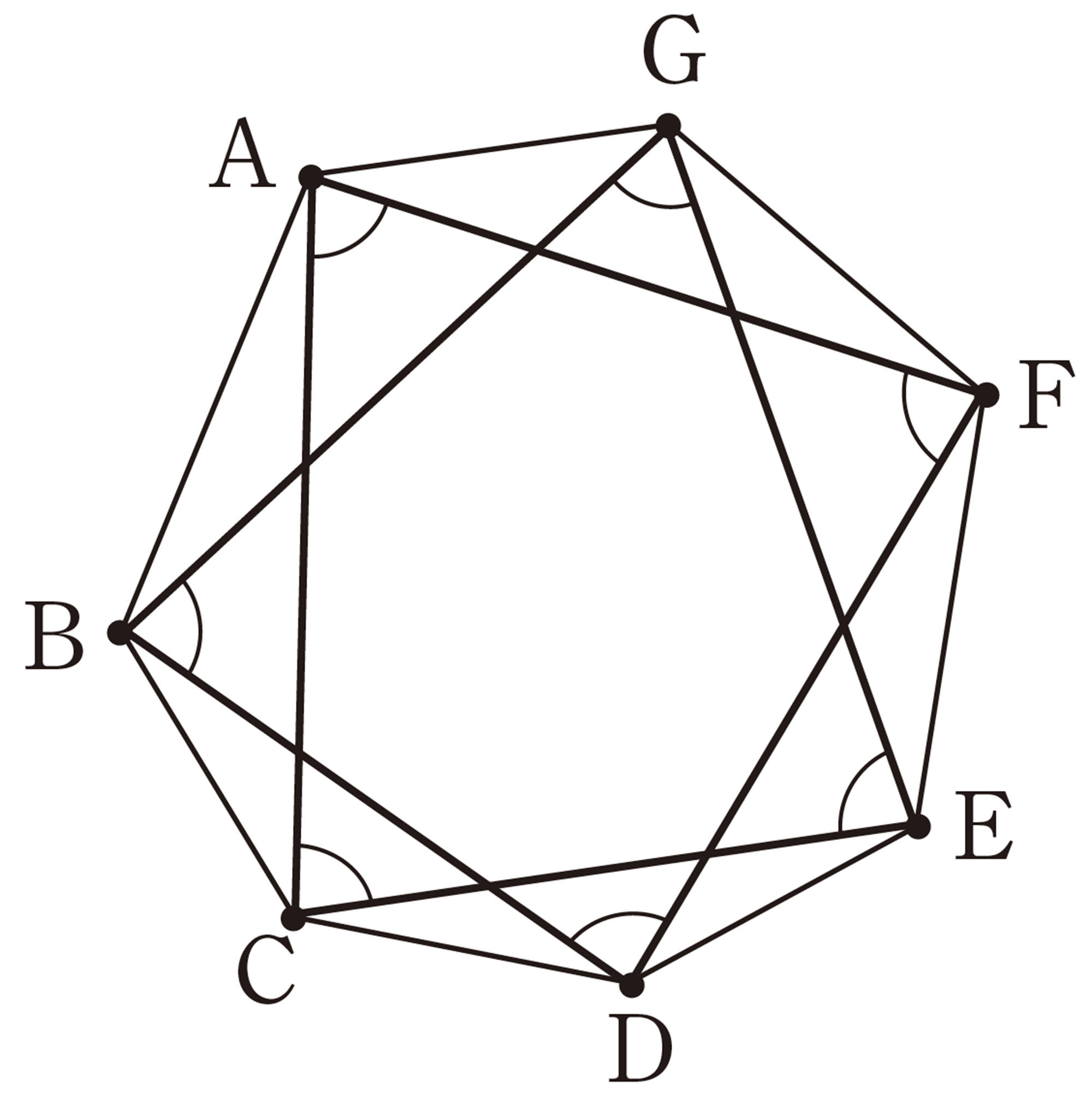
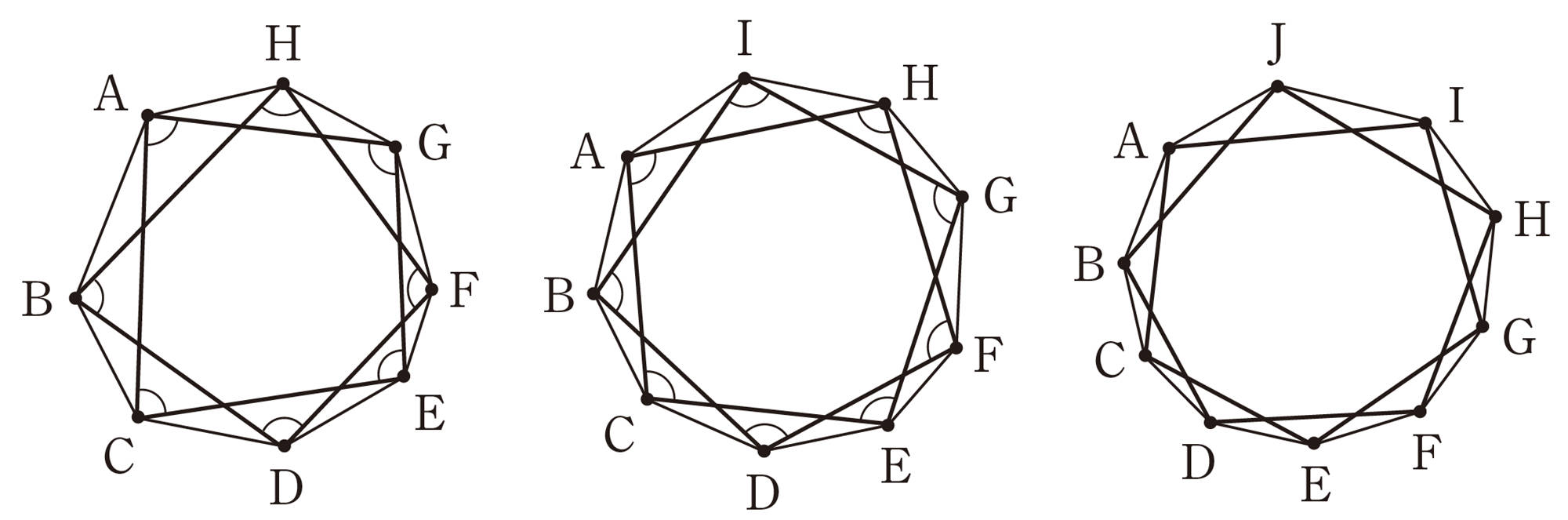
④ ここまでの結果を表にしてみましょう。この結果から，星形八角形，星形九角形，星形十角形の先端部分の角の和を予想してみましょう。
八角形の頂点を1つ飛ばして結ぶ星形八角形は，四角形を2つ重ねた図形になるね
そうすると，星形十角形は，五角形を2つ重ねた図形になりそうだね。
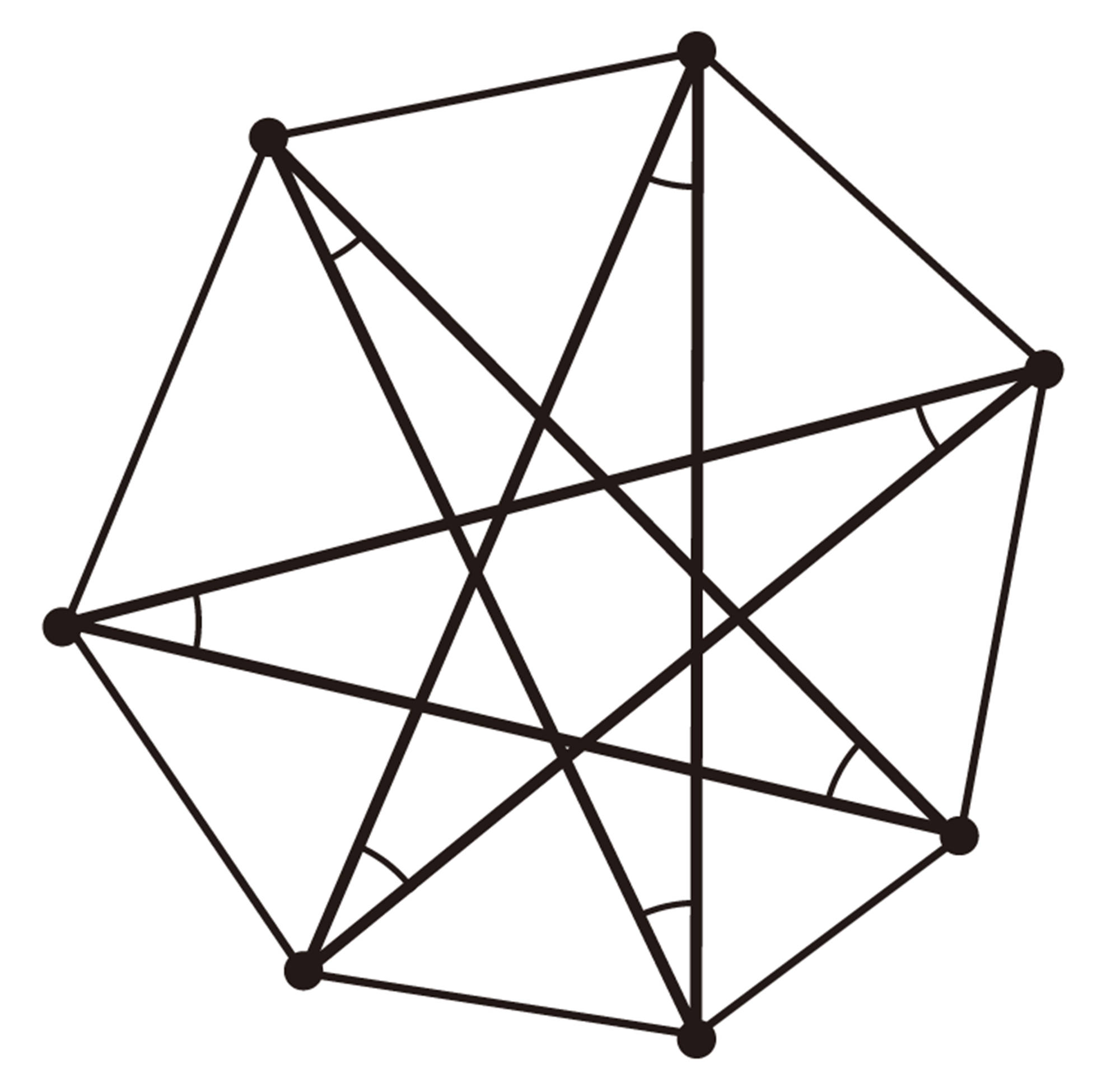
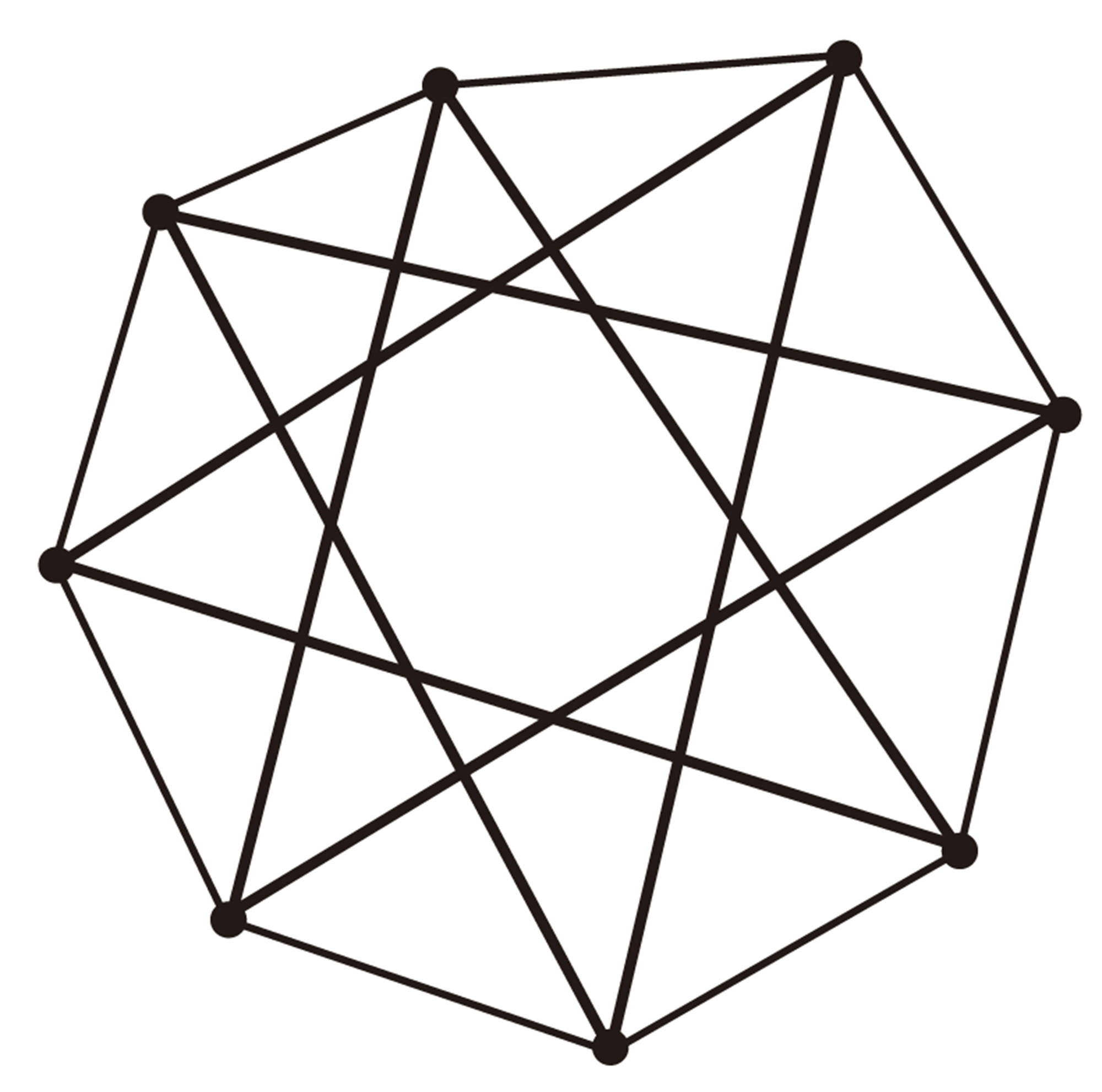
⑤ 星形八角形，星形九角形，星形十角形は，次のような図になります。 ④で予想したことが正しいかどうかを，星形八角形，星形九角形，星形十角形の先端部分の角の和を求めて確かめてみましょう。
⑥ ここまで，星形 [mathjax]\( n \) 角形の先端部分の角の数を変えて，先端部分の [mathjax]\( n \) 個の角の和のきまりについて調べました。もっと調べてみたいと思ったことや疑問があれば書きましょう。 また，224～227ページを参考にして，調べてみたいことをレポートにまとめる活動にもチャレンジしてみましょう。
多角形の頂点を1つ飛ばして結んだ図形について考えたね。
頂点を2つ飛ばして結んだ図形の先端部分の角の和は，どうなるのかな。
