<2年p.125>
2節 図形の合同
図形の合同をいうためには，何が必要？
小学校で，2つの図形がぴったり重なるとき，2つの図形が合同であることを学習しました。
【１】 次の図で，[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle DEF\) は合同な三角形といえるでしょうか。また，どのように確かめることができるでしょうか。
ぴったり重ね合わせることができるとき，2つの図形は合同だね。
移動すれば，ぴったり重ね合わせることができるかどうか確かめられそうだね。
次の課題へ！
どうすれば2つの三角形が合同であることを確かめられるかな？
P.125
１ 合同な図形
目標 ▷ 合同な図形の性質について調べよう。
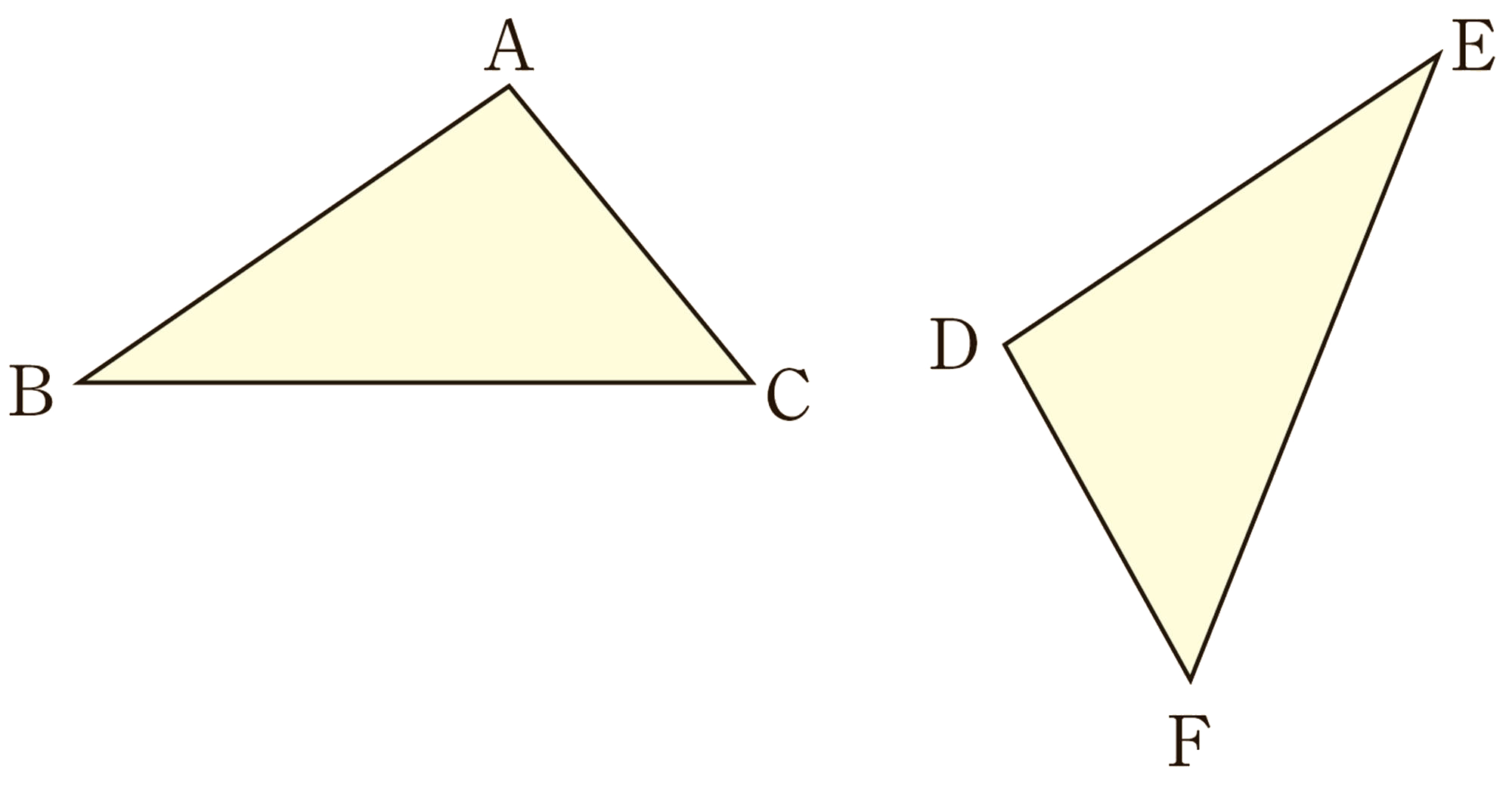
問 １ 巻末②の図を使って，1の[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle DEF\) が合同であることを確かめなさい。 また，対応する点，対応する辺，対応する角をいいなさい。
[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle DEF\) が合同であることを，記号[mathjax]\(\equiv\)を使って
[mathjax]\(\triangle ABC \equiv \triangle DEF\)
と表し，「三角形ABC合同三角形DEF」と読む。
注意 合同の記号[mathjax]\(\equiv\)を使うときは，対応する点が同じ順序になるように表す。
<2年p.126>
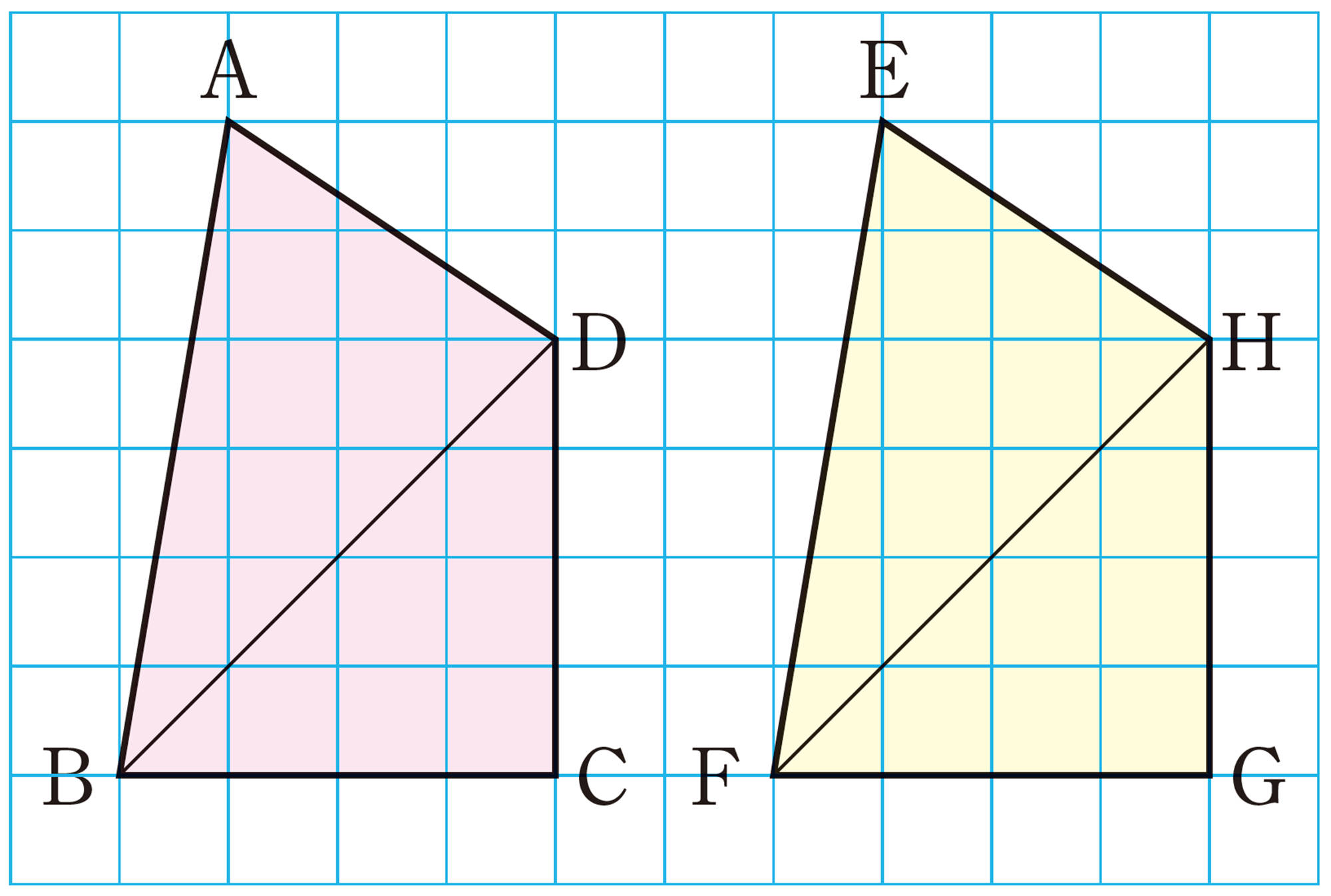
問 ２ 次の図で，[mathjax]\(\mathsf{四角形}ABCD \equiv \mathsf{四角形}EFGH\) であるとき，次の問いに答えなさい。
⑴ 対応する辺をすべていいなさい。
⑵ 対応する角をすべていいなさい。
⑶ 線分BDと線分FHの長さを比べなさい。
⑷ [mathjax]\(\angle ABD\) と [mathjax]\(\angle EFH\) の大きさを比べなさい。
問2の図で，[mathjax]\(\mathsf{四角形}ABCD \equiv \mathsf{四角形}EFGH\) であることから，対応する辺や対応する角について，次のことがいえる。
[mathjax]\(AB=EF\)，[mathjax]\(BC=FG\)，[mathjax]\(CD=GH\)，[mathjax]\(DA=HE\)
[mathjax]\(\angle A = \angle E\)，[mathjax]\(\angle B = \angle F\) ，[mathjax]\(\angle C = \angle G\) ，[mathjax]\(\angle D = \angle H\)
一般に，合同な図形には次の性質がある。
合同な図形の性質
① 合同な図形では，対応する線分の長さはそれぞれ等しい。
② 合同な図形では，対応する角の大きさはそれぞれ等しい。
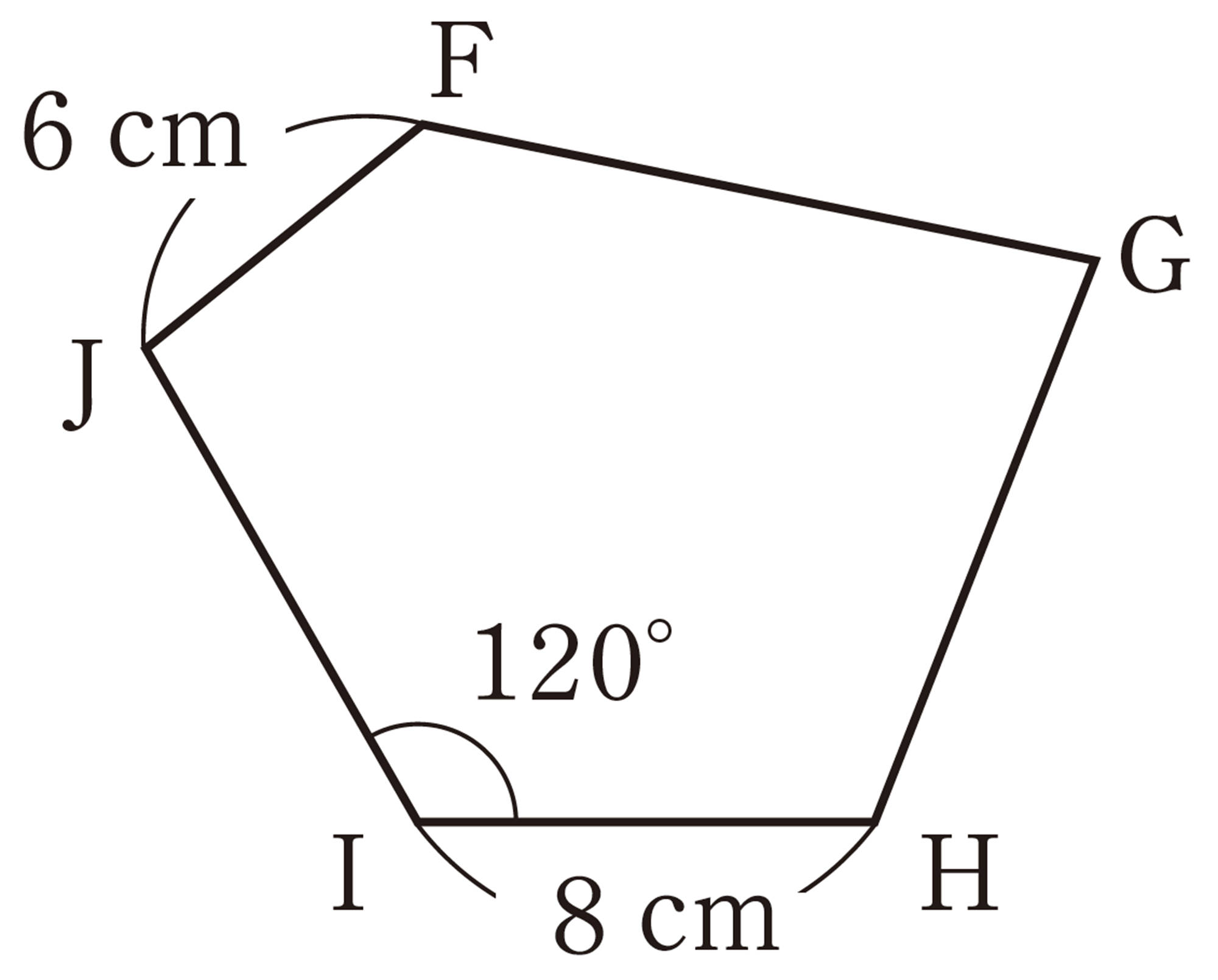
問 ３ 次の図で，[mathjax]\(\mathsf{五角形}ABCDE \equiv \mathsf{五角形}FGHIJ\) です。長さのわかる辺や大きさのわかる角を見つけ，その長さや角度を図に書き入れなさい。
どんなことがわかったかな
合同な図形は，ぴったり重ね合わせることができるから，対応する線分の長さや角の大きさが等しくなります。
次の課題へ！
ぴったり重ね合わせられなくても，線分の長さや角の大きさを使って，合同かどうか確かめられるのかな？
P.127
<2年p.127>
２ 三角形の合同条件
Q Question
次の[mathjax]\(\triangle ABC\) をかいてみましょう。[mathjax]\(\triangle ABC\) は1つに決まるといえるでしょうか。
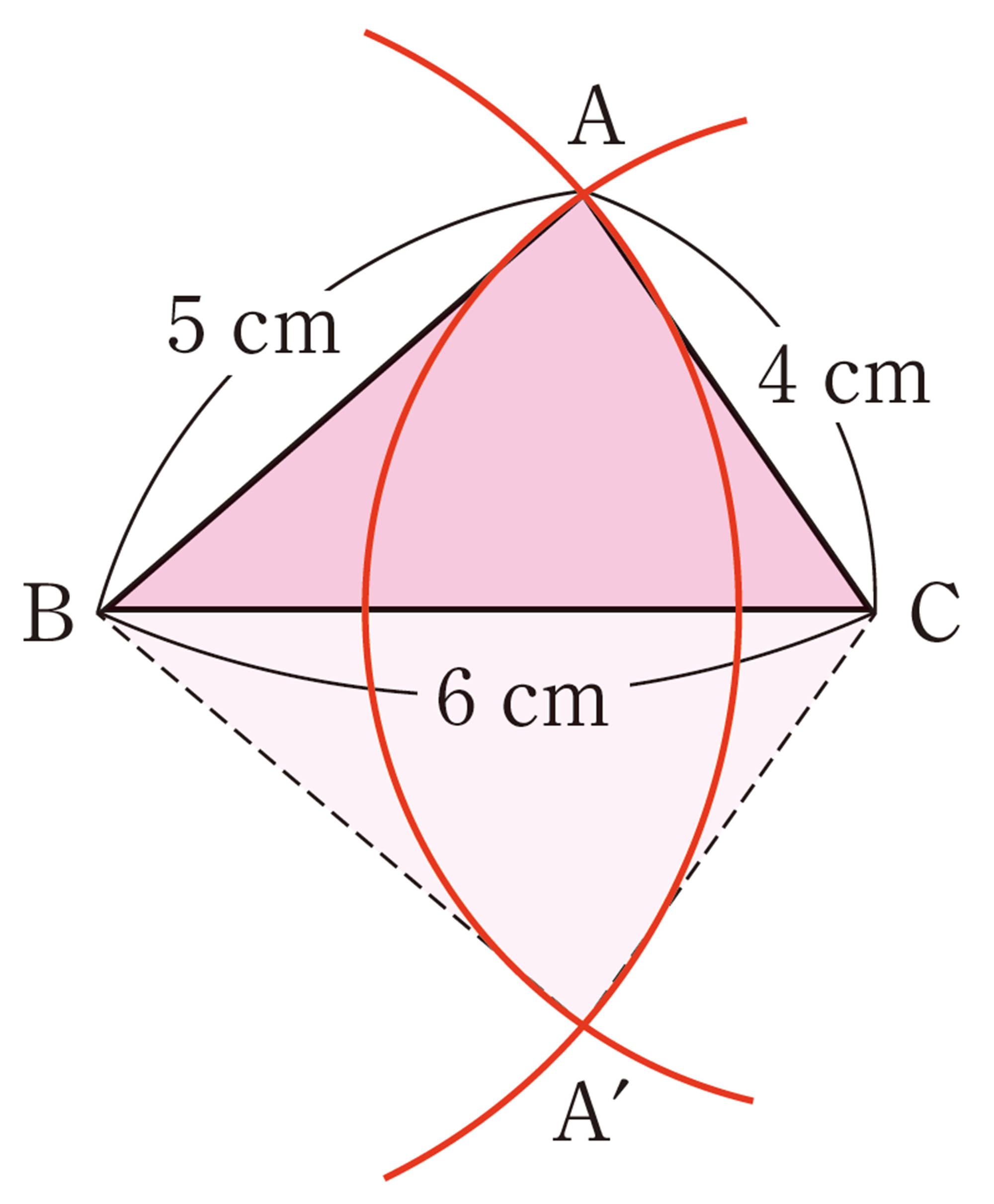
㋐ [mathjax]\(AB=5\)cm，[mathjax]\(BC=6\)cm，[mathjax]\(AC=4\)cm
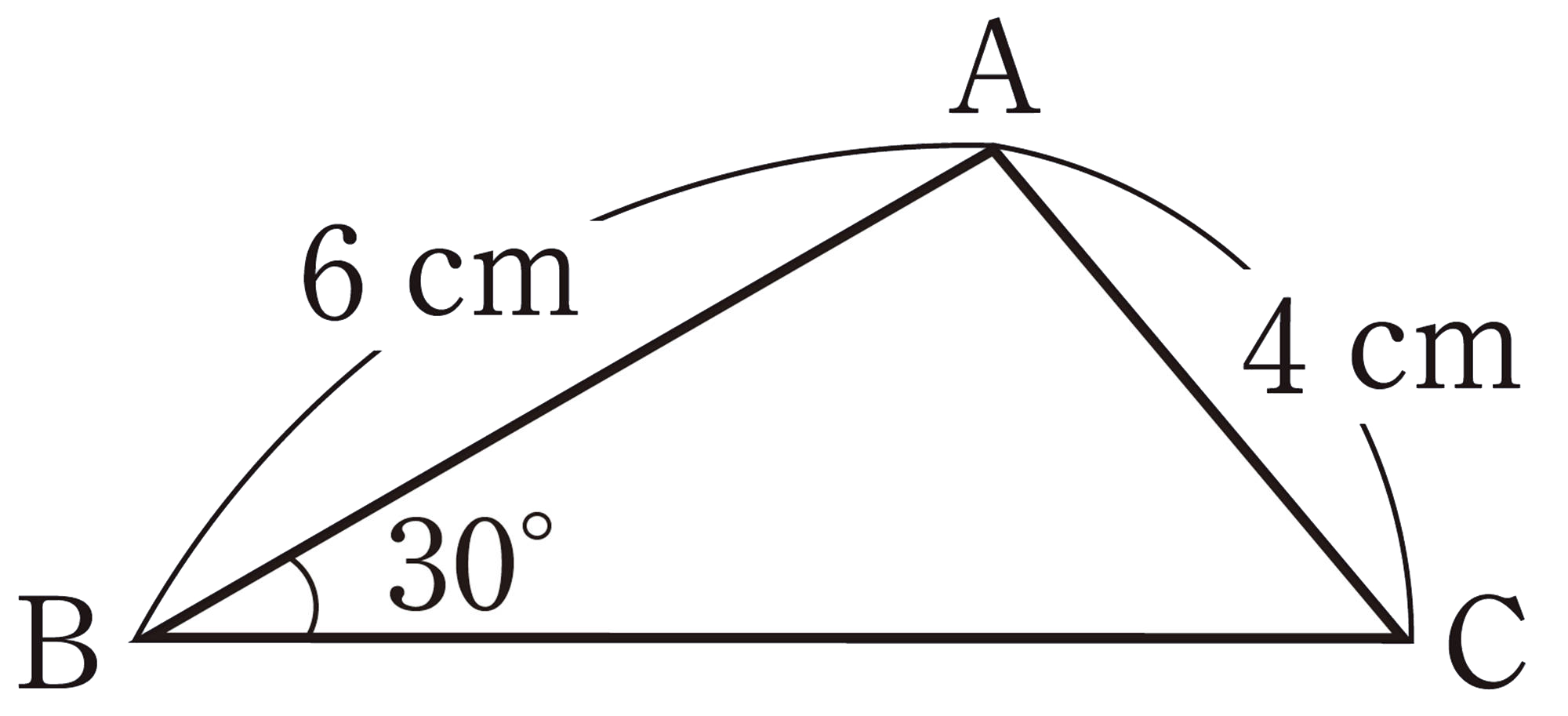
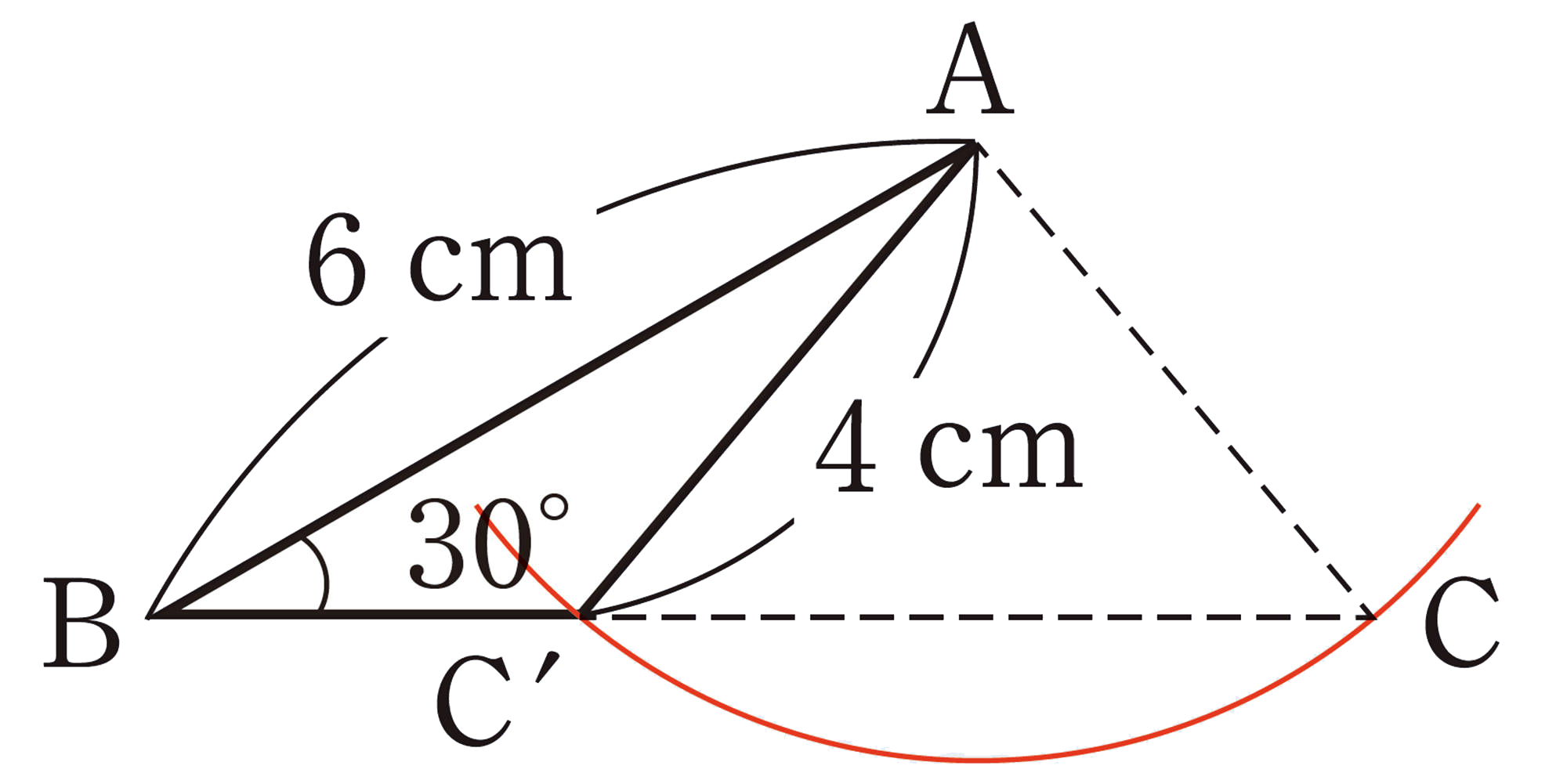
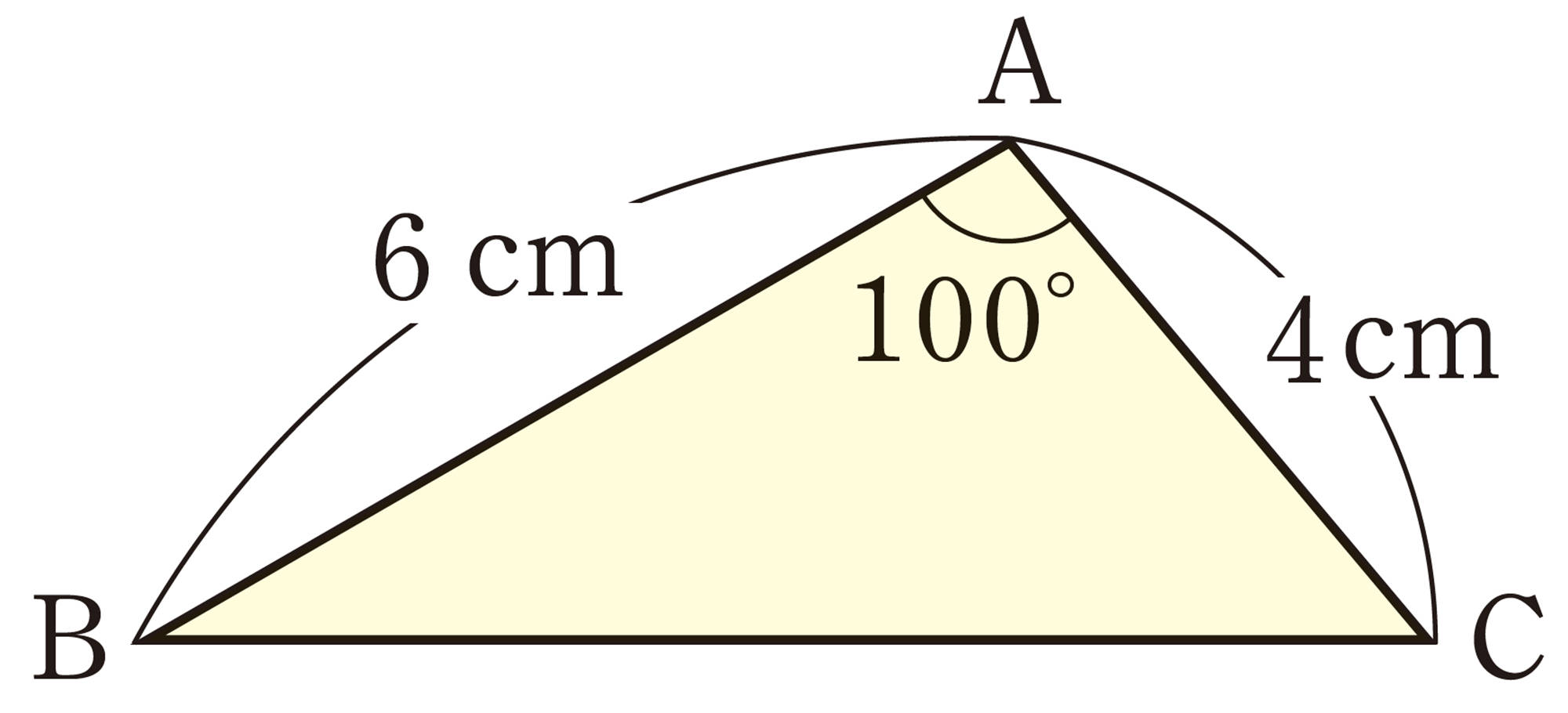
㋑ [mathjax]\(AB=6\)cm，[mathjax]\(\angle B=30^{ \circ }\)，[mathjax]\(AC=4\)cm
⑴ 美月さんと拓真さんは，㋑の[mathjax]\(\triangle ABC\) を次のようにかきました。
このことから，どんなことがいえるか話し合ってみましょう。
美月さんの考え
拓真さんの考え
⑵ ㋑の問題に，どのような条件をつけると三角形が1つに決まるといえるか，考えてみましょう。
[mathjax]\(\angle B\) ではなく，[mathjax]\(\angle A\)や[mathjax]\(\angle C\)の角度が決まっている場合はどうかな。
見方・考え方
条件が変わると，三角形は1つに決まるかな。
目標 ▷ 三角形が1つに決まるかき方について調べよう。
【Q】㋑のように，「2辺と1つの角」がわかっているという条件で[mathjax]\(\triangle ABC\) をかくと，【Q】⑴のように，2種類の三角形をかくことができる。したがって，三角形は1つに決まらない。
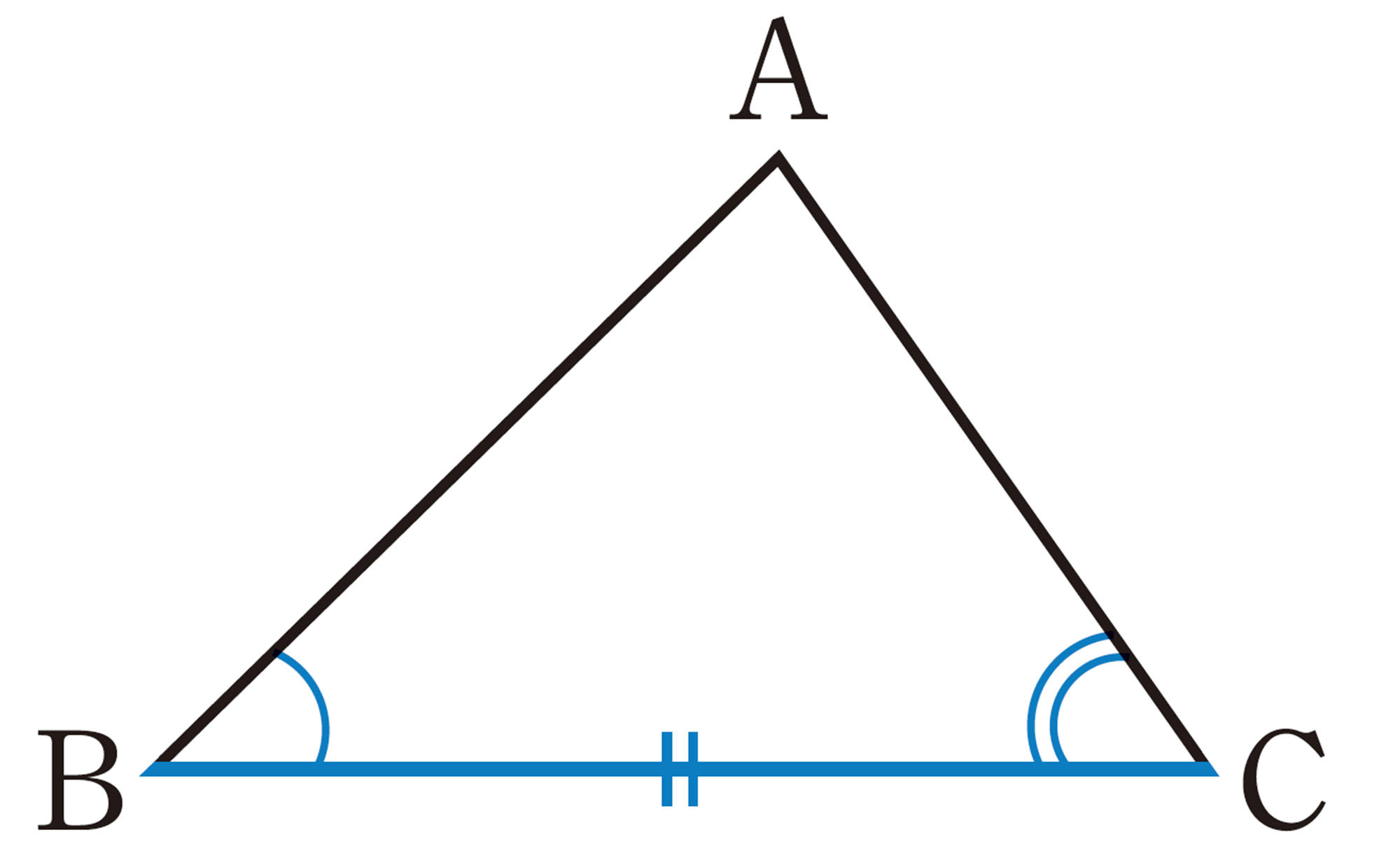
これに対し，右の図のように，「2辺と1つの角」に，さらに条件をつけて，「2辺とその間の角」にすると，三角形は1つに決まる。
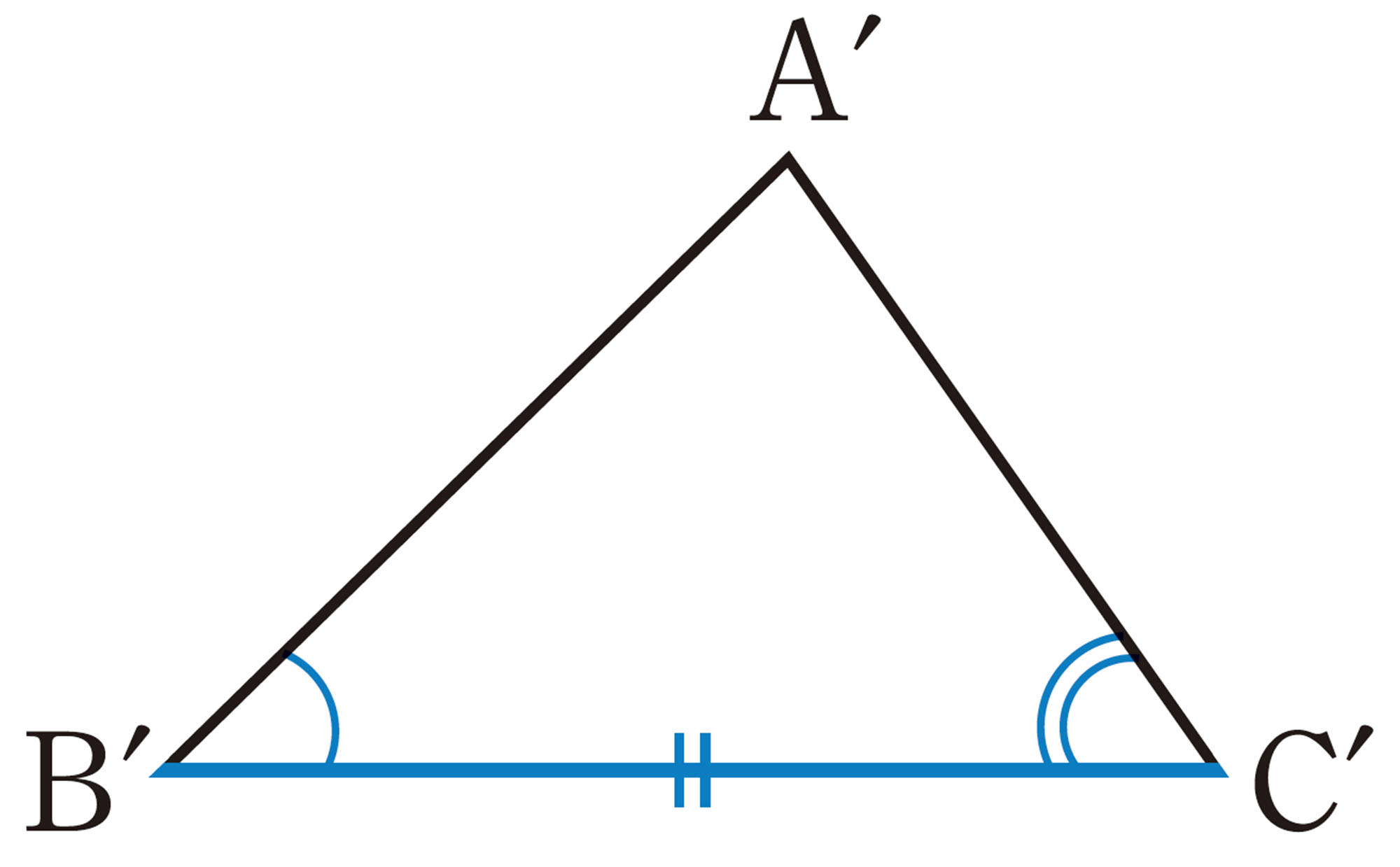
また，右の図のように，「3辺の長さ」がわかっているという条件で[mathjax]\(\triangle ABC\) をかくと，2つの三角形をかくことができるが， [mathjax]\(\triangle ABC\) をBCを対称の軸として対称移動すれば，[mathjax]\(\triangle A´BC\) にぴったり重ね合わせることができるので，三角形は1つに決まるといえる。
<2年p.128>
ほかにも，右の図のように，「1辺とその両端の角」がわかっているという条件で[mathjax]\(\triangle ABC\) をかくと，三角形は1つに決まる。
これまで調べたことから，次の条件のうちのどれか1つがわかっているとき，三角形は1つに決まるといえる。
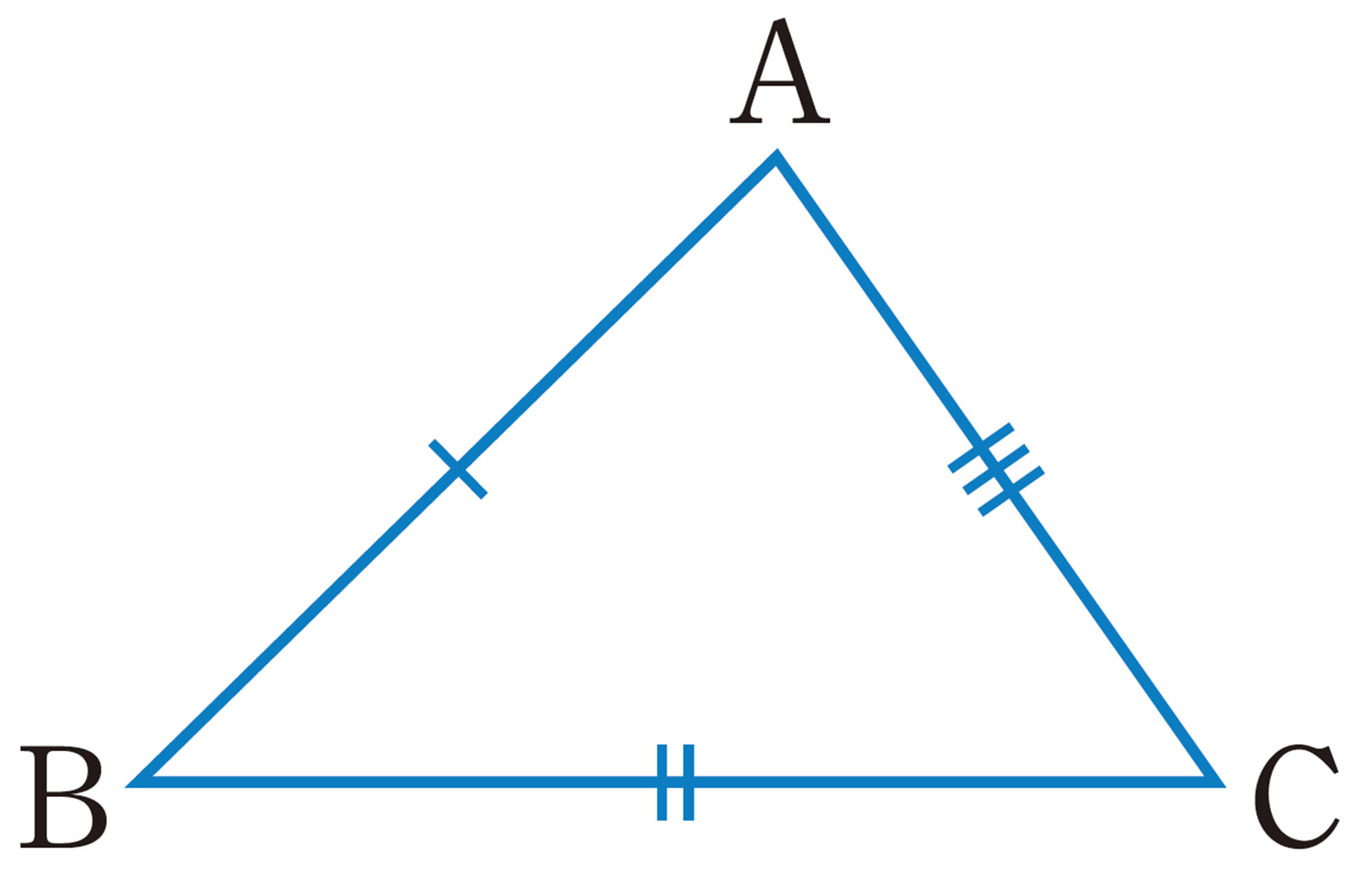
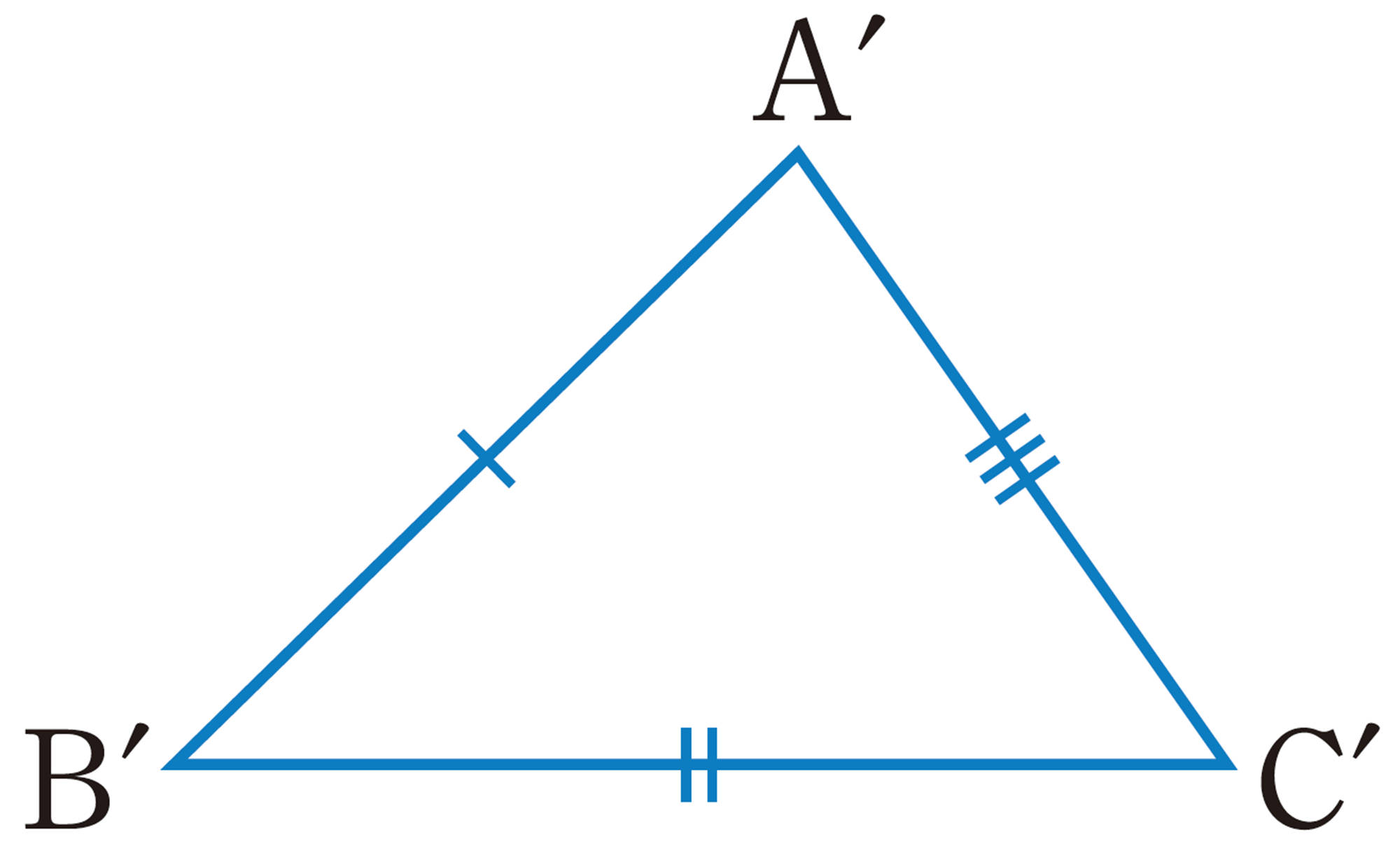
① 3辺
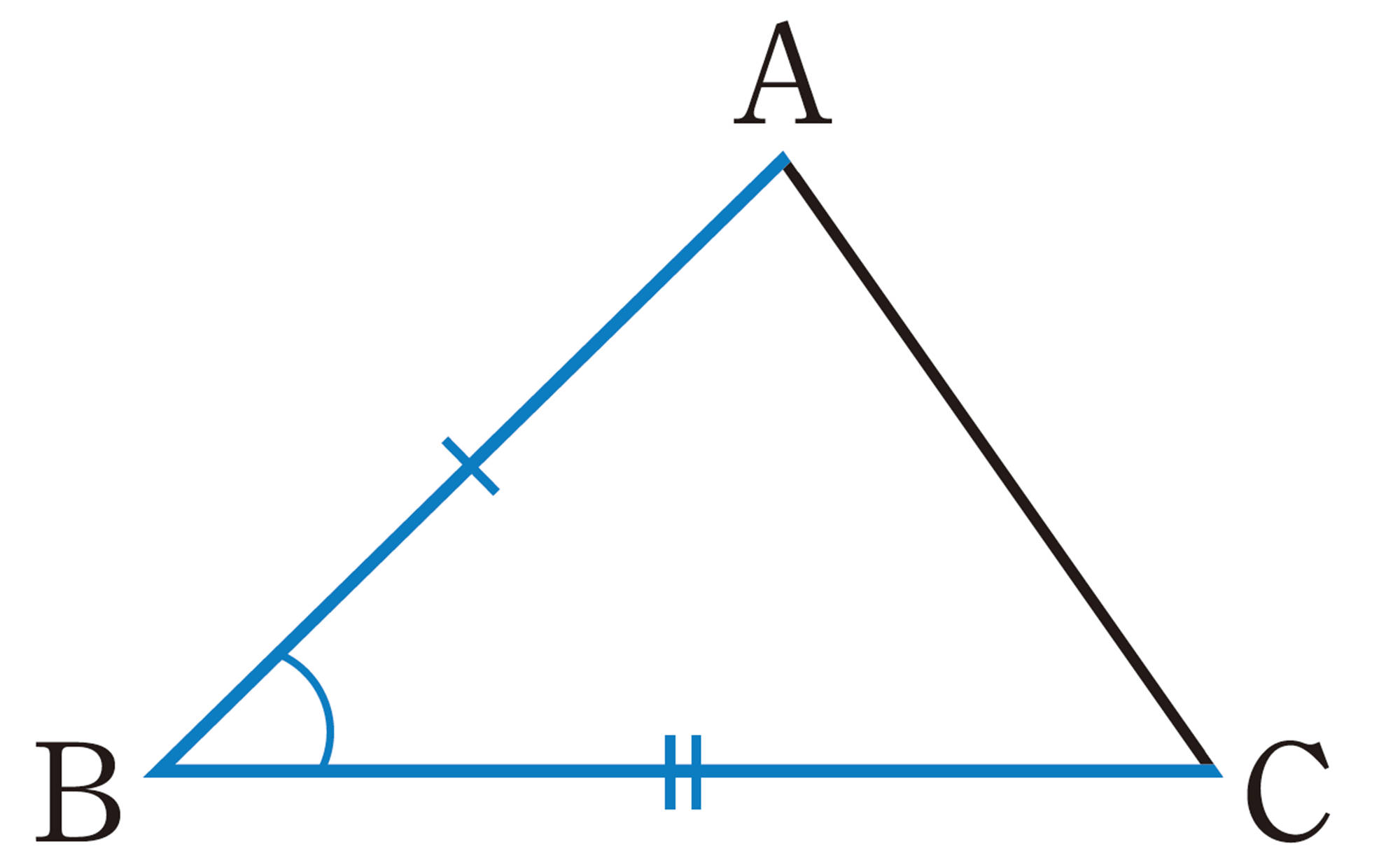
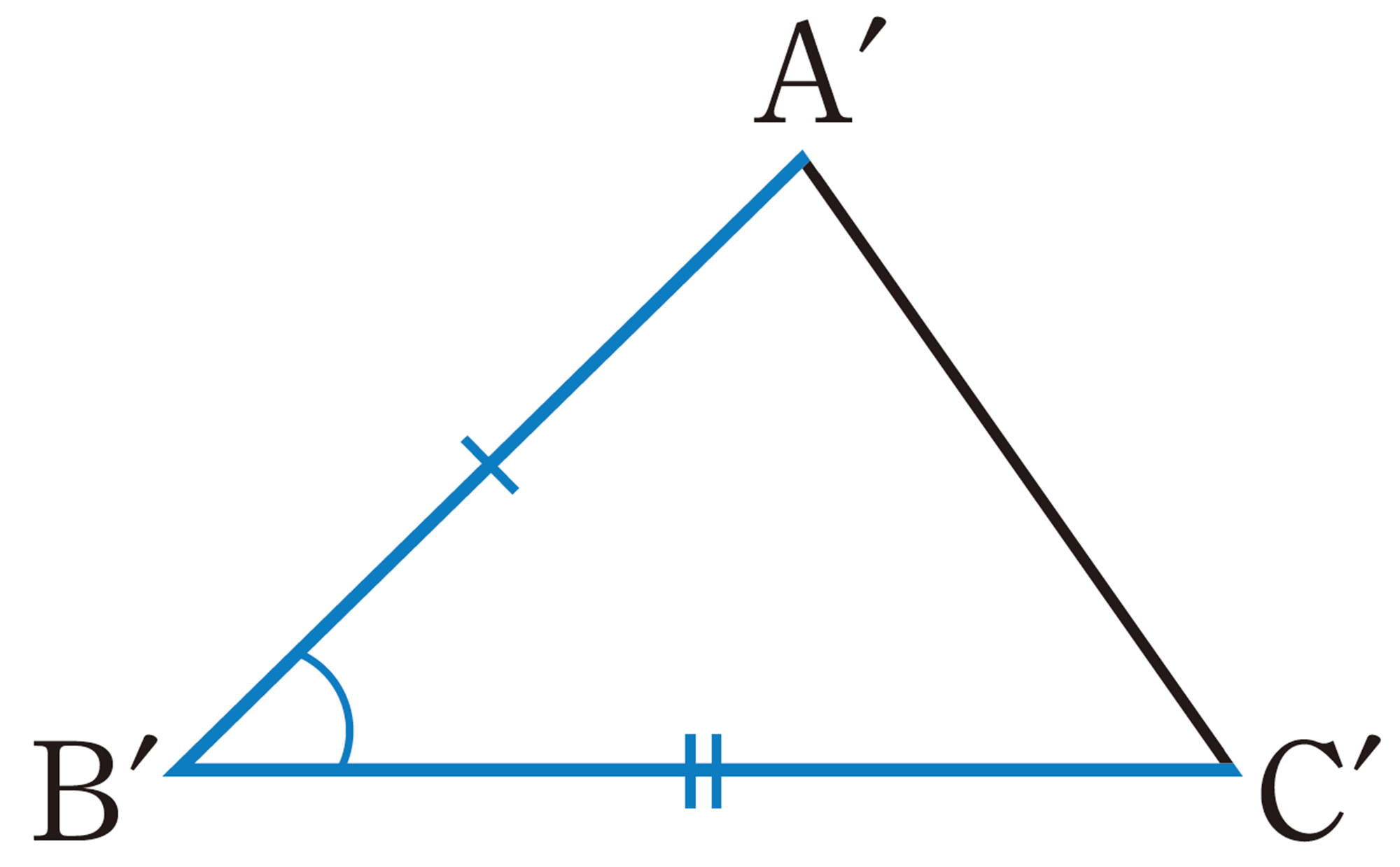
② 2辺とその間の角
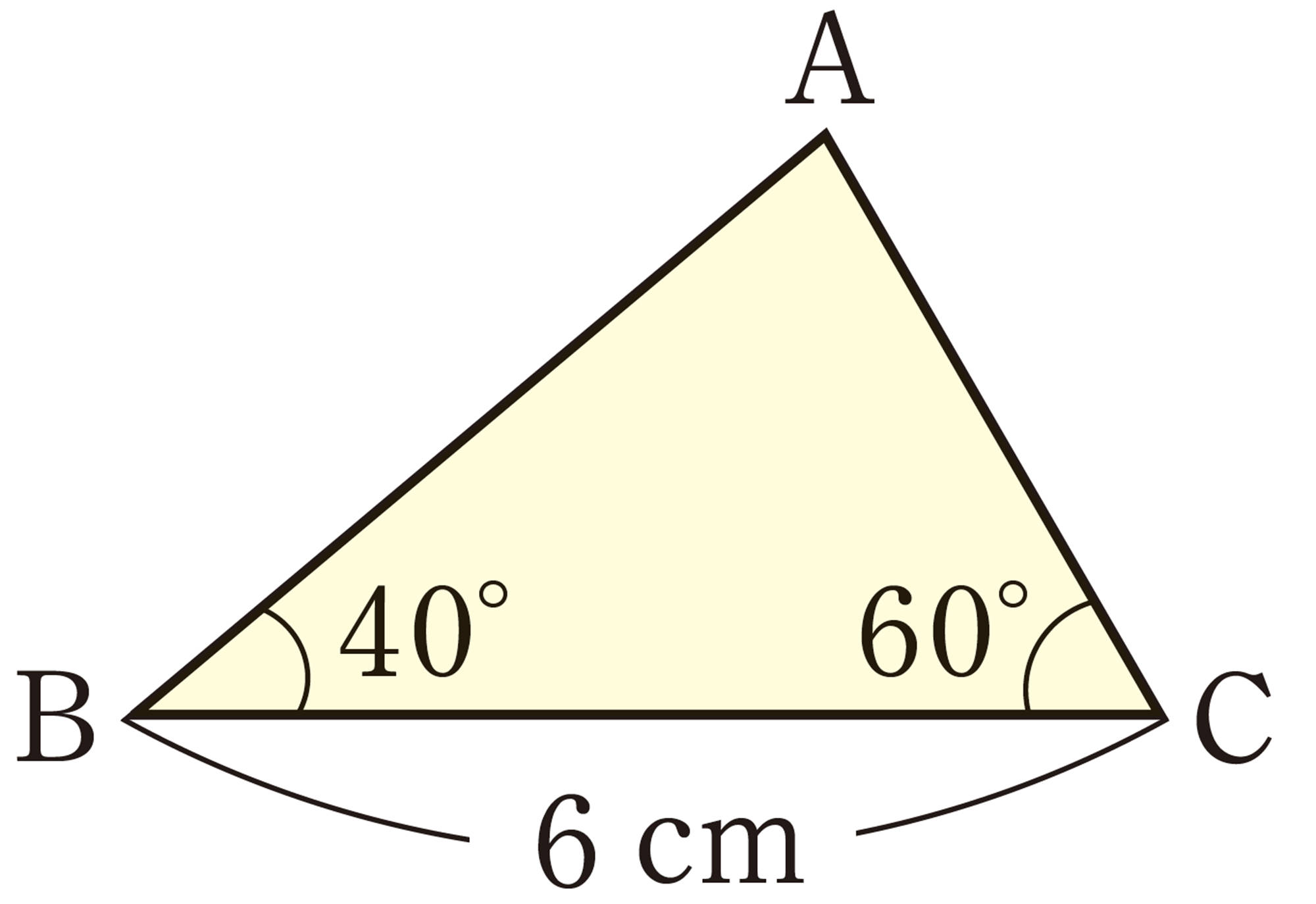
③ 1辺とその両端の角
したがって，2つの三角形が合同であることを確かめるには，それらを重ね合わせなくても，上の①〜③のうち，どれか1つについて，対応する辺や角が等しいかどうかを調べればよい。
これまで調べたことから，次のように，三角形の合同条件としてまとめることができる。
三角形の合同条件
2つの三角形は，次のどれか1つが成り立てば合同である。
① 3組の辺がそれぞれ等しい。
[mathjax]\(AB=A´B´\)
[mathjax]\(BC=B´C´\)
[mathjax]\(CA=C´A´\)
② 2組の辺とその間の角がそれぞれ等しい。
[mathjax]\(AB=A´B´\)
[mathjax]\(BC=B´C´\)
[mathjax]\(\angle B= \angle B´\)
③ 1組の辺とその両端の角がそれぞれ等しい。
[mathjax]\(BC=B´C´\)
[mathjax]\(\angle B= \angle B´\)
[mathjax]\(\angle C= \angle C´\)
<2年p.129>
例 １ 右の図の[mathjax]\(\triangle ABC\) と[mathjax]\(\triangle DEF\) では，
[mathjax]\(BC=EF\)
[mathjax]\(\angle B=\angle E\)
[mathjax]\(\angle C=\angle F\)
で，1組の辺とその両端の角がそれぞれ等しいから，[mathjax]\(\triangle ABC \equiv \triangle DEF\) である。
例1のように，三角形の合同条件を使えば，それらが合同であることを確かめることができる。
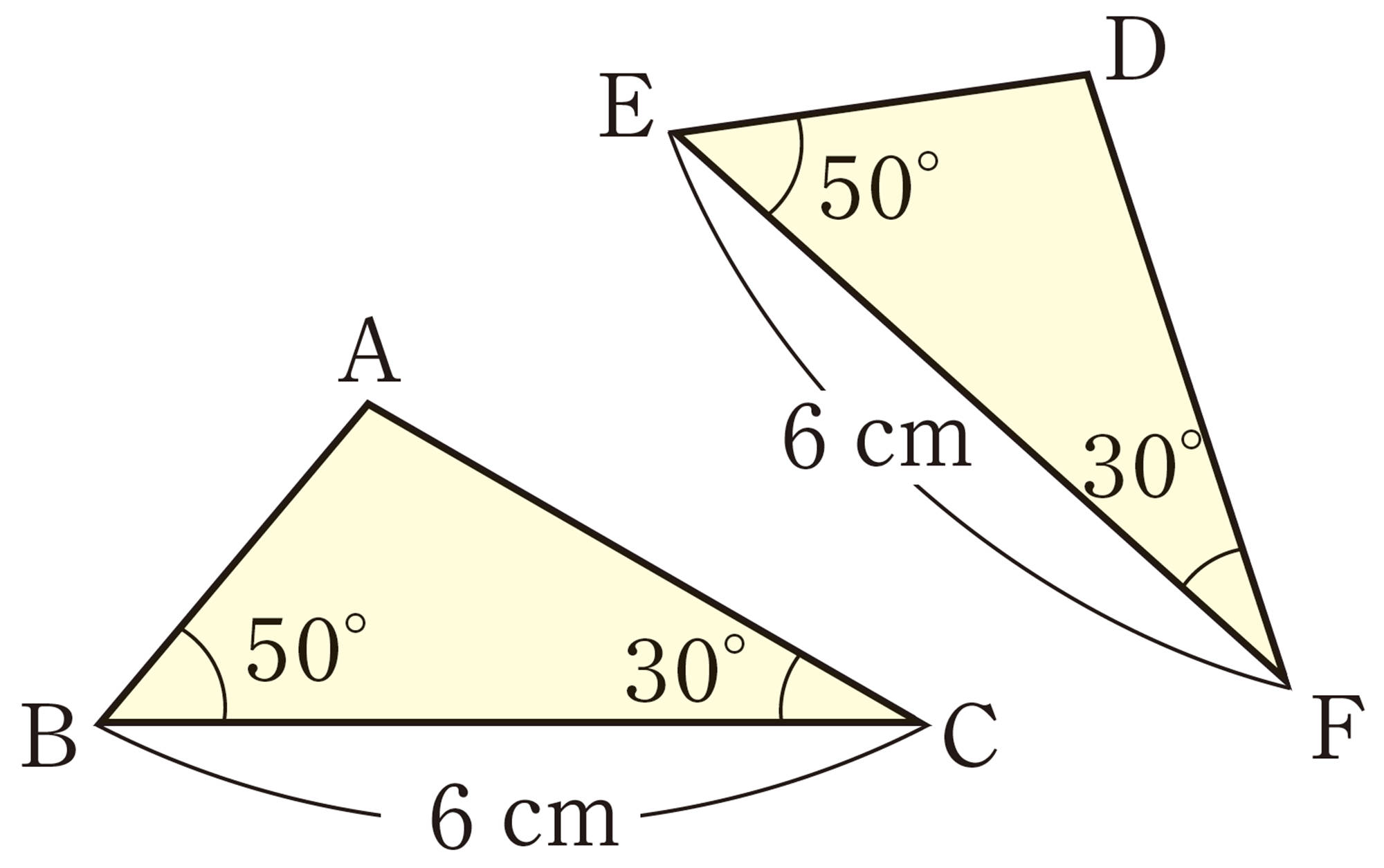
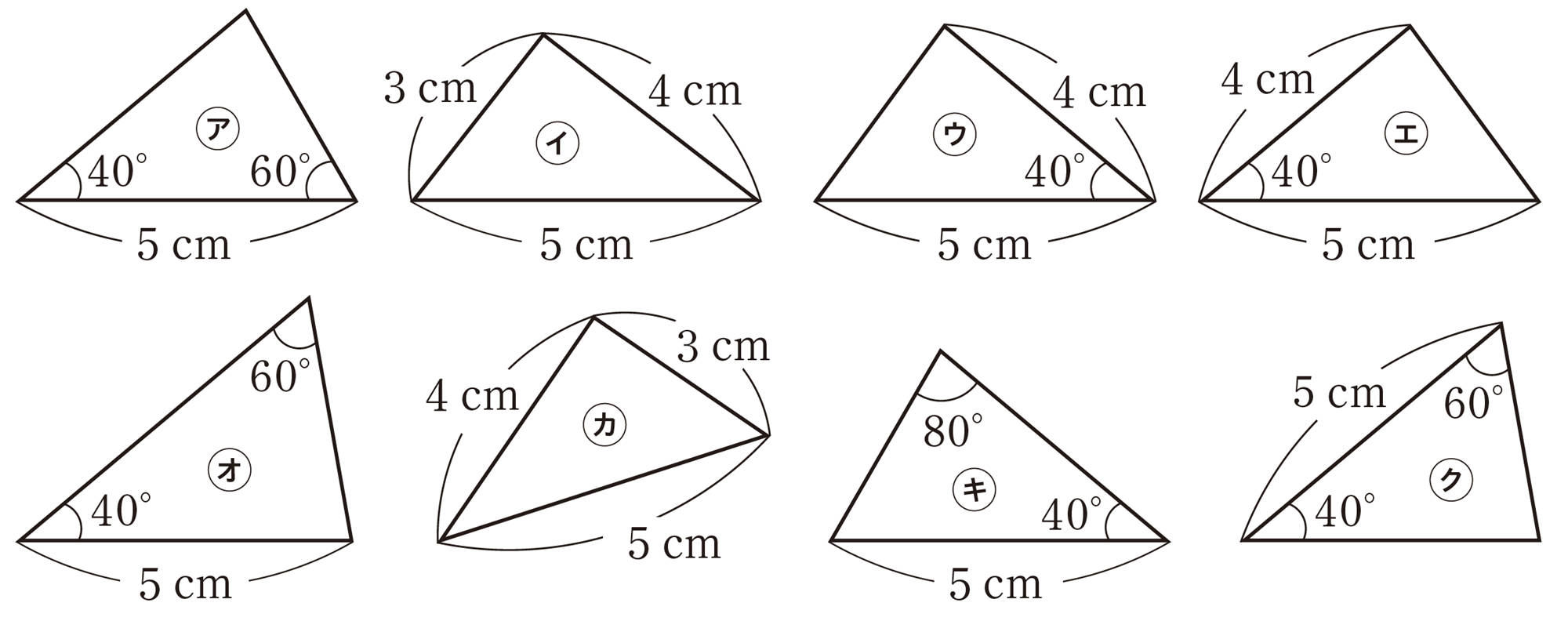
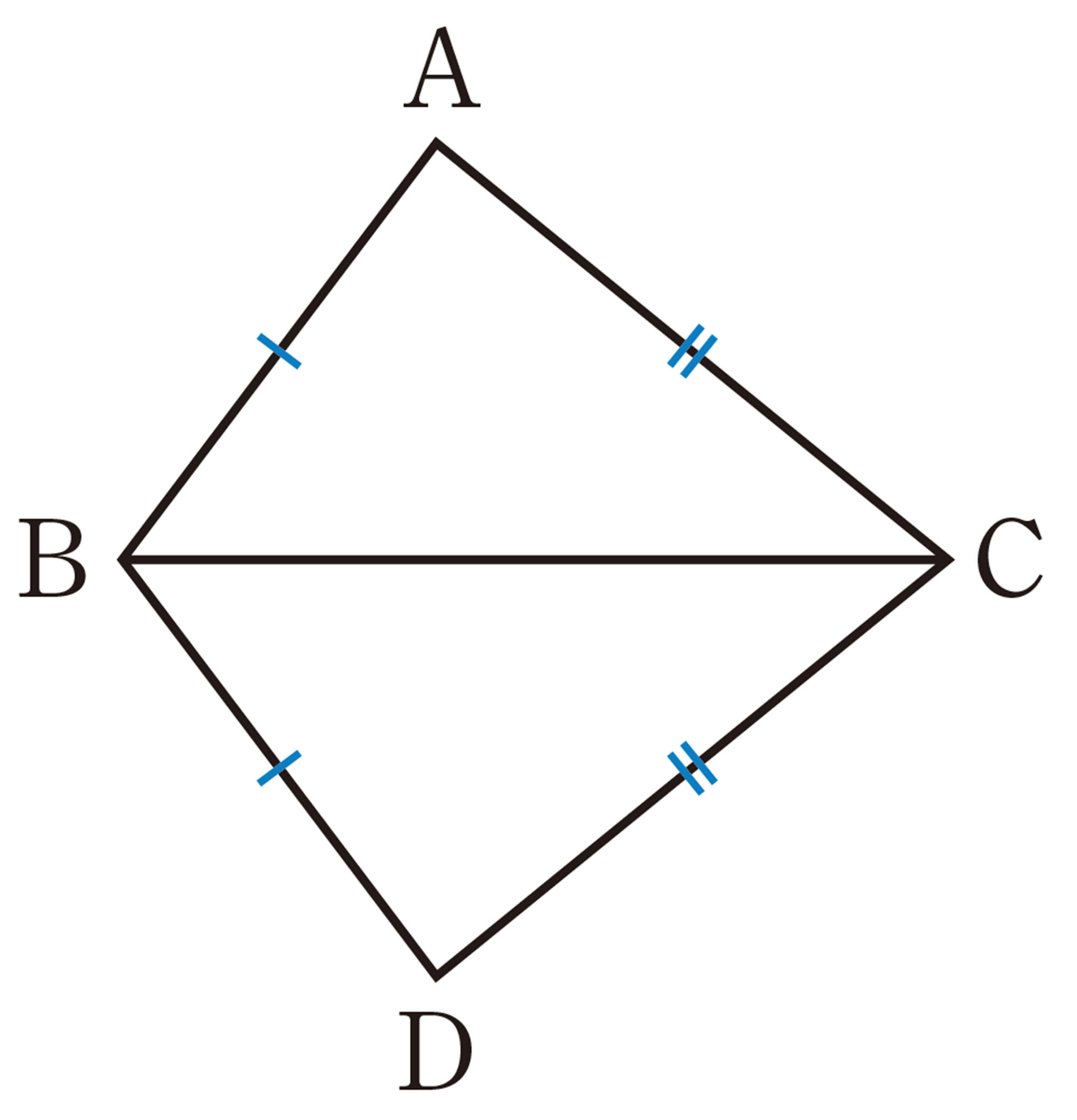
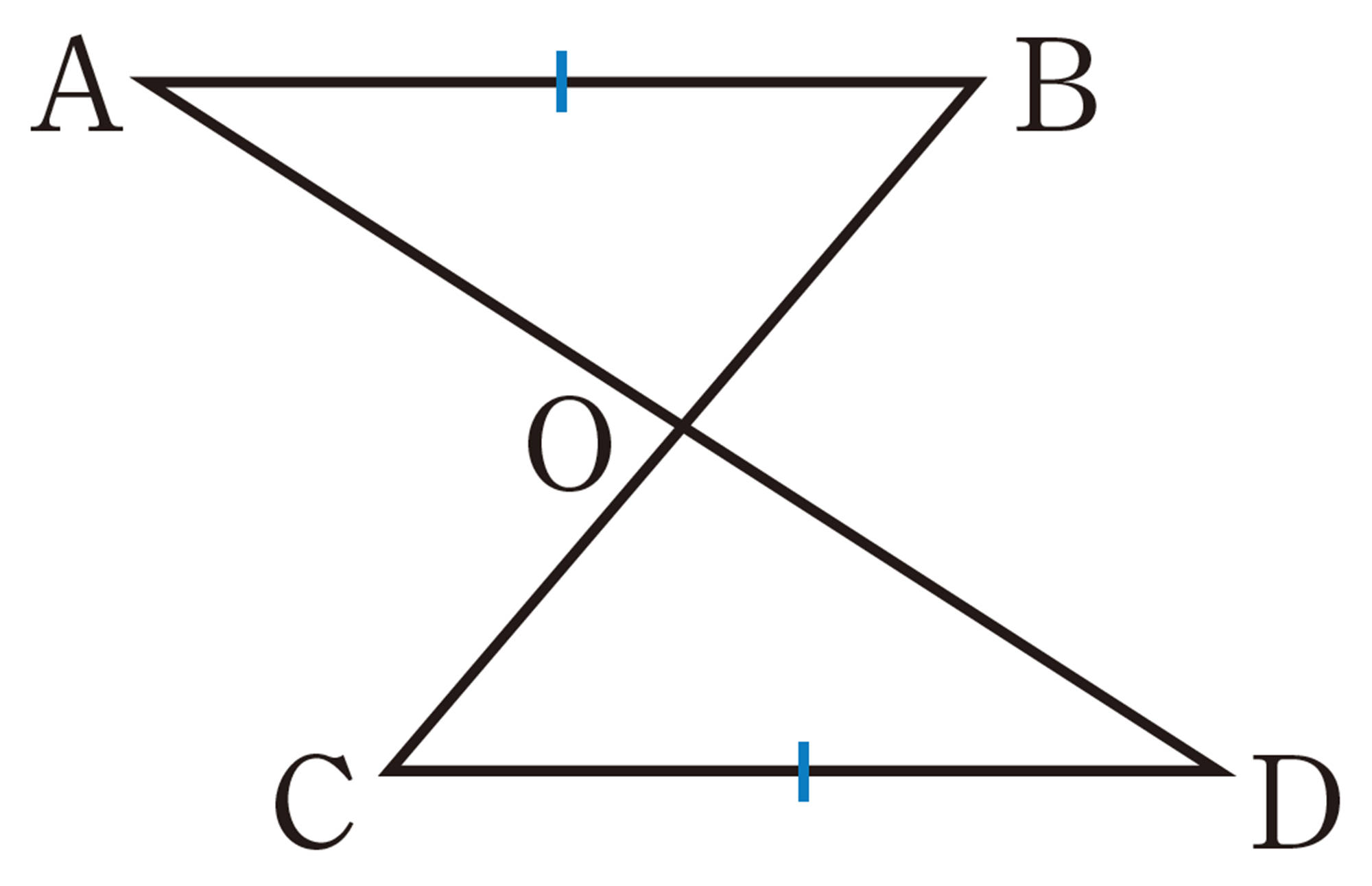
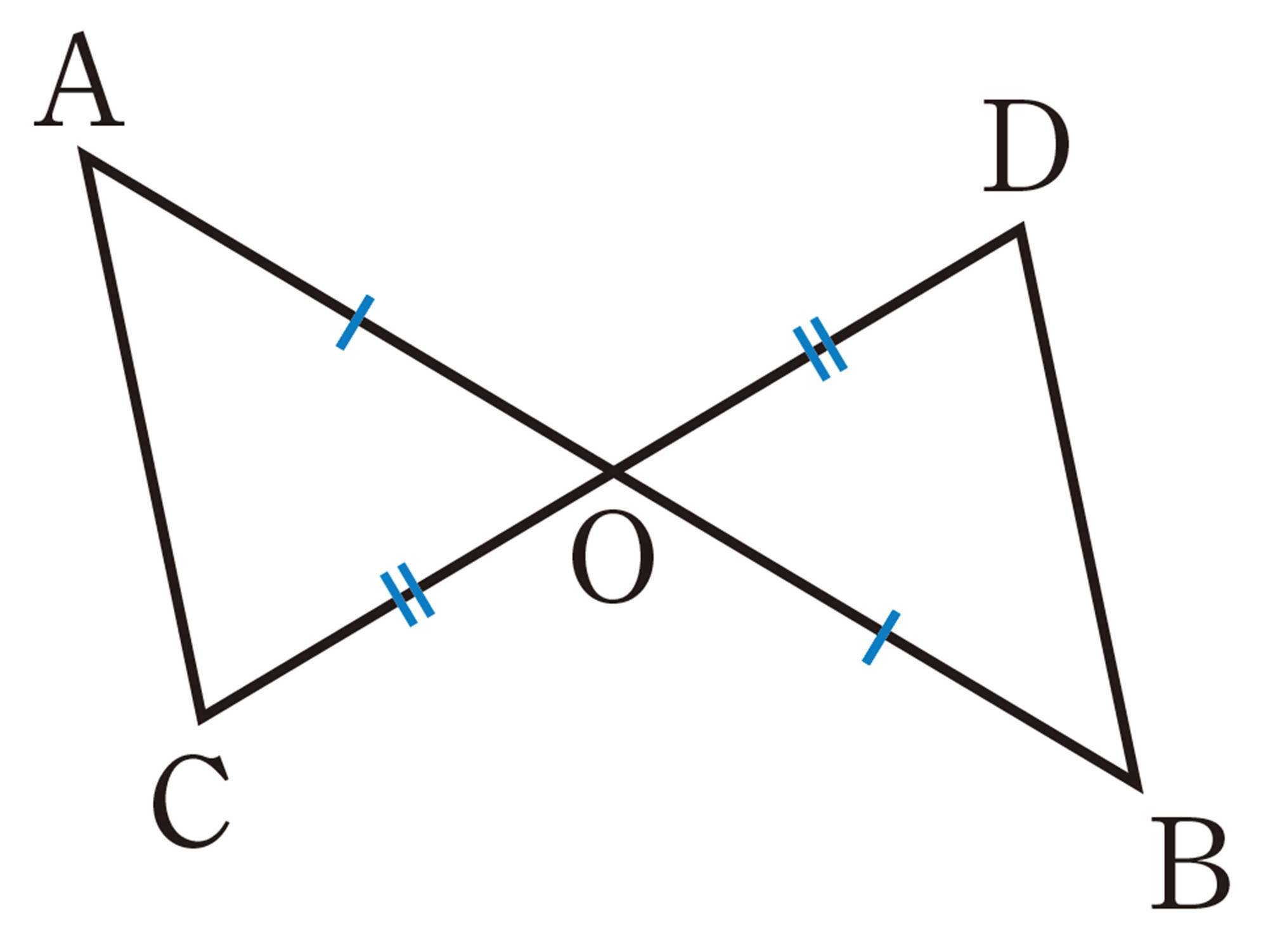
問 １ 次の図で，合同な三角形はどれとどれですか。また，そのときの合同条件をいいなさい。
問 ２ 次の図で，合同な三角形はどれとどれですか。記号 [mathjax]\(\equiv\) を使って表しなさい。また，そのときの合同条件をいいなさい。ただし，同じ印をつけた辺は等しいとします。
⑴
⑵
⑶ [mathjax]\(AB/\!/CD\)
どんなことがわかったかな
2つの三角形が合同であるかどうかは，三角形の合同条件を使えば確かめることができます。
次の課題へ！
確かめたことがらが正しいことを，どのように人に伝えたらいいのかな？
P.130
