<2年p.118>
３ 多角形の角
多角形の内角の和
Q Question
五角形の内角の和は何度になるでしょうか。また，どうやって求めたか説明してみましょう。
多角形の内角の和は，小学校でも求めたね。
いろいろな求め方で考えられるかな。
見方・考え方
根拠を明らかにして，説明できるかな。
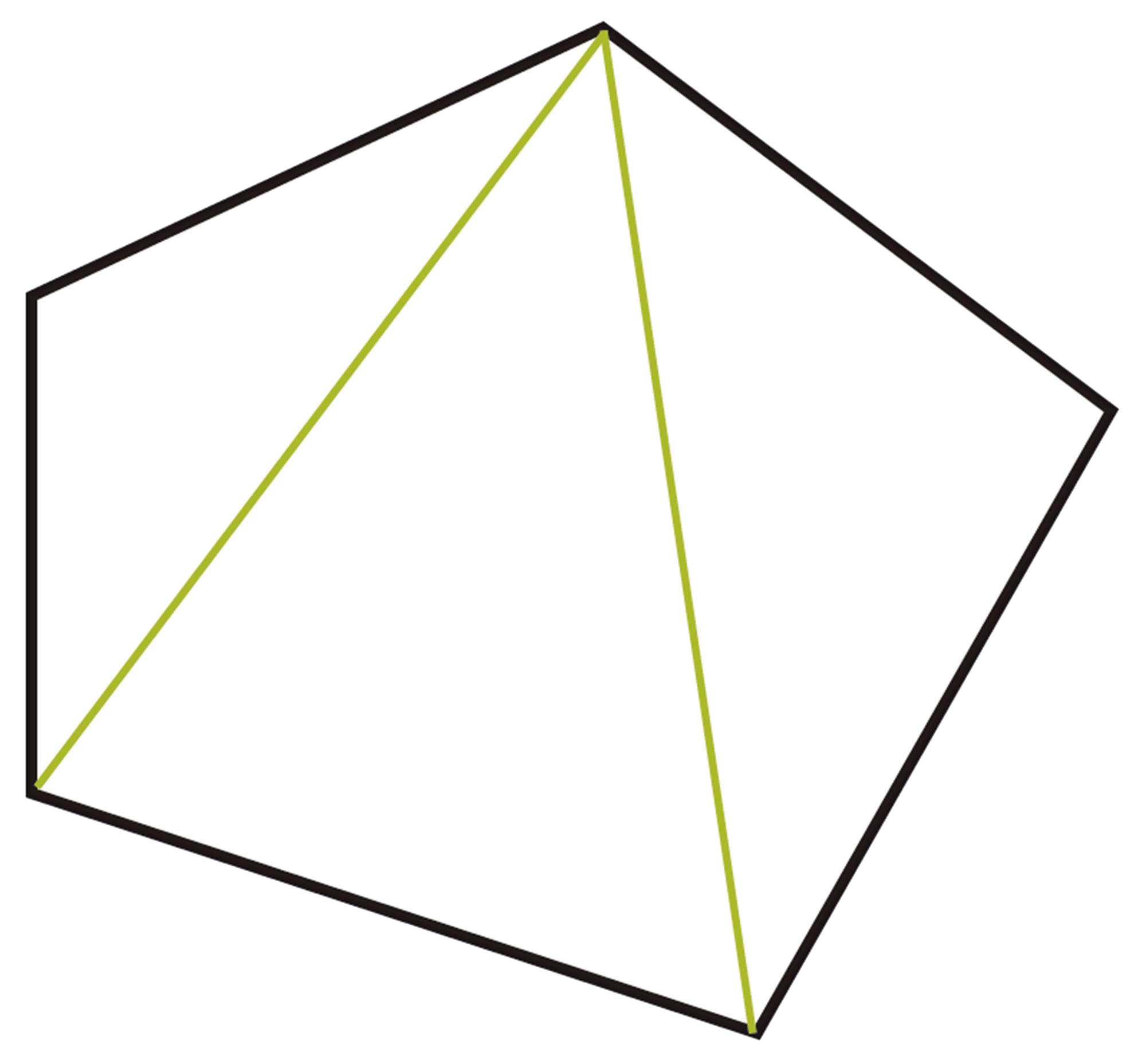
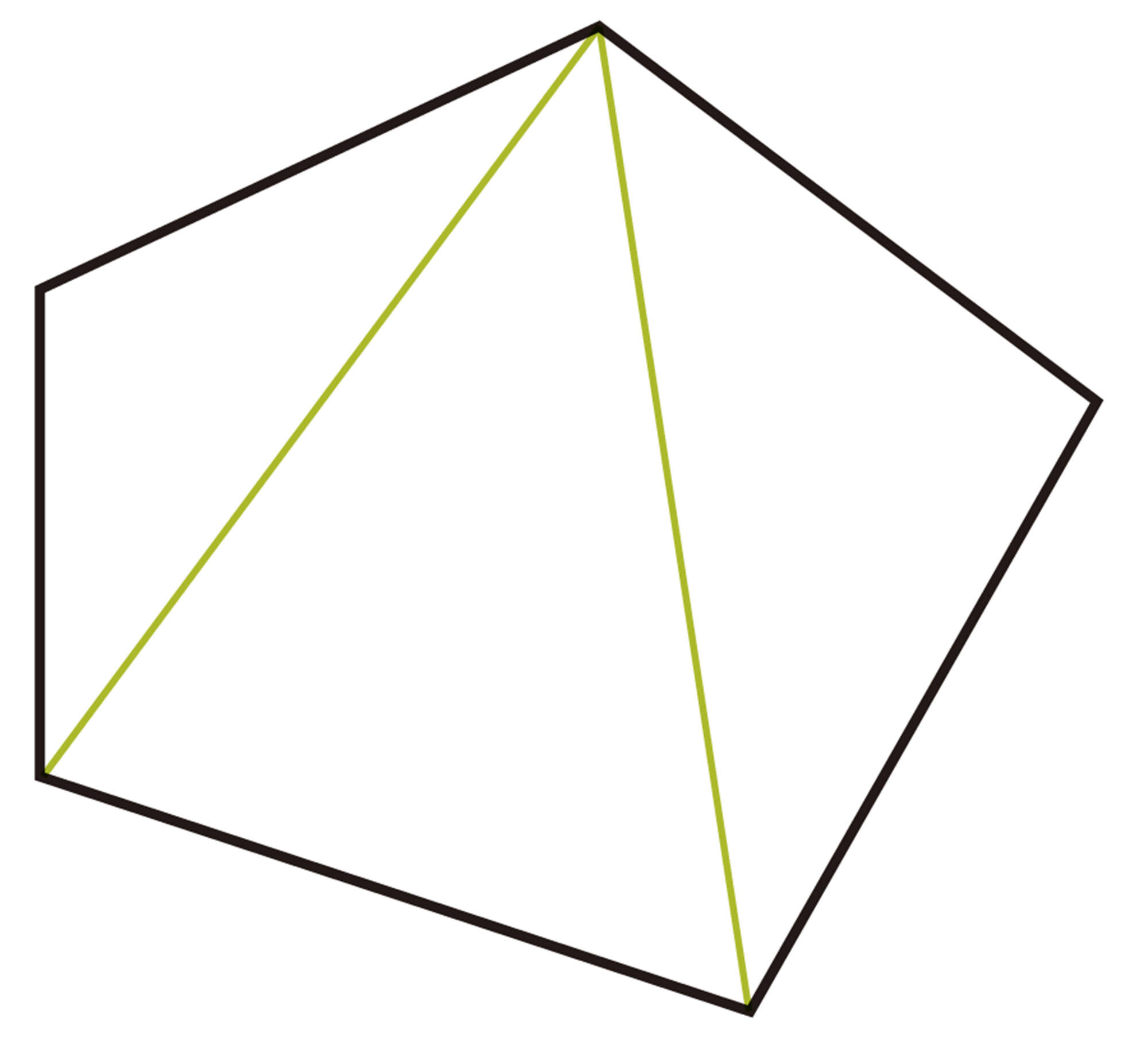
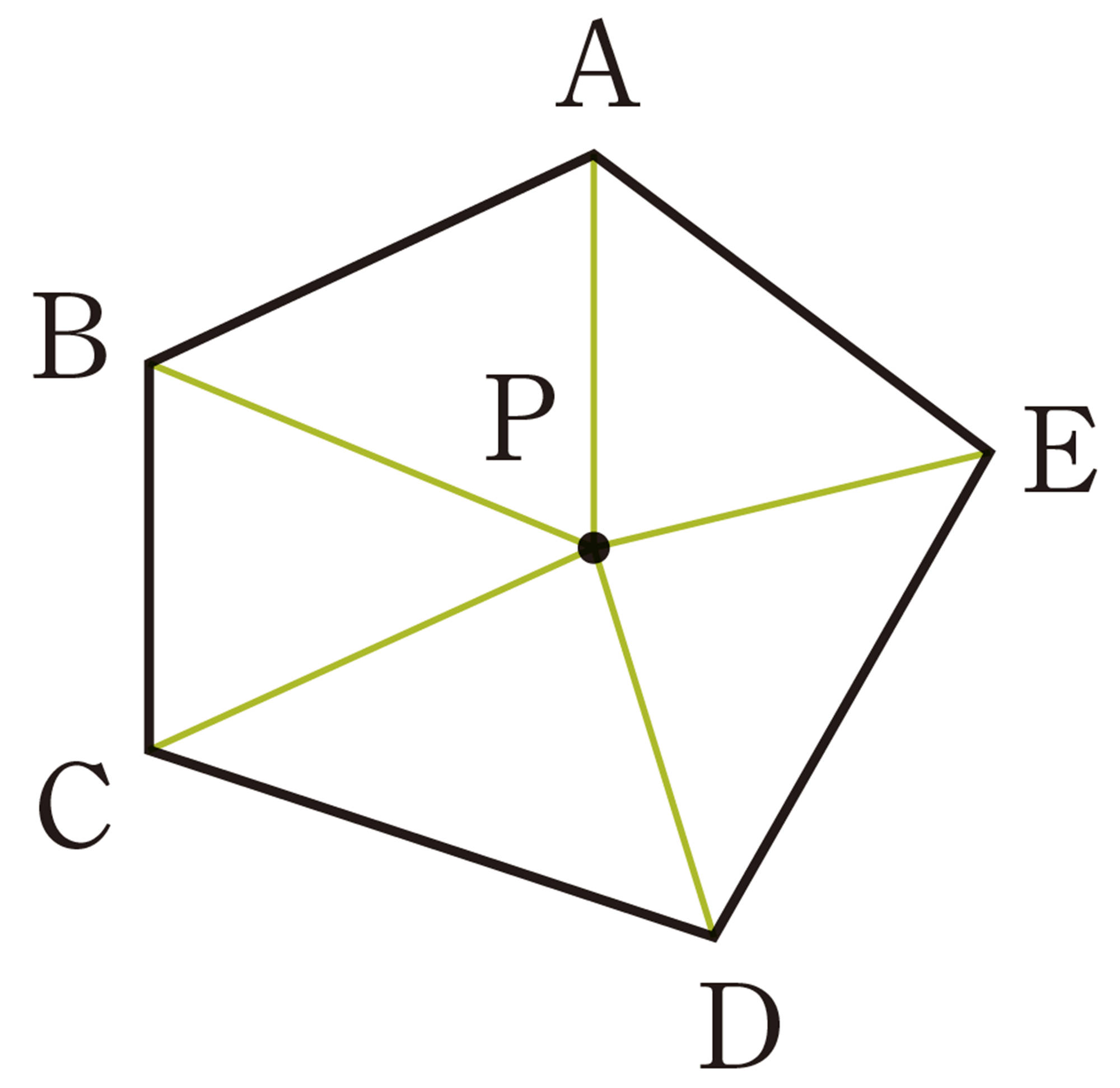
１ 【Q】について，拓真さんは，次のようにして五角形の内角の和を求めました。
拓真さんの考え
五角形は，1つの頂点から引いた対角線によって，3つの三角形に分けることができるから，内角の和は，
[mathjax]\( 180^{ \circ } \times 3=540^{ \circ } \)
となる。
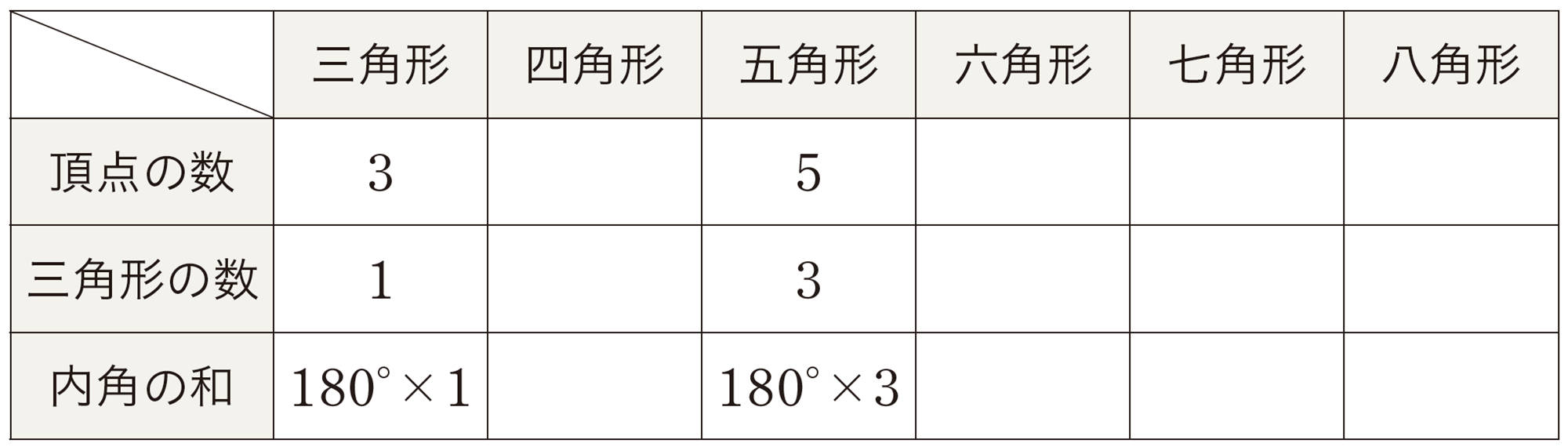
拓真さんの考え方を使って，いろいろな多角形の内角の和を求めて，次の表を完成させましょう。
目標 ▷ 多角形の内角の和の性質について調べよう。
多角形の内角の和には，共通のきまりがありそうだね。
いろいろな多角形の内角の和を求める式を，1つの式で表せないかな。
<2年p.119>
２ 前ページの1の表で，多角形の頂点の数をnとすると，内角の和はどんな式で求めることができるでしょうか。
頂点の数がn個のとき，三角形の数は何個になるかな。
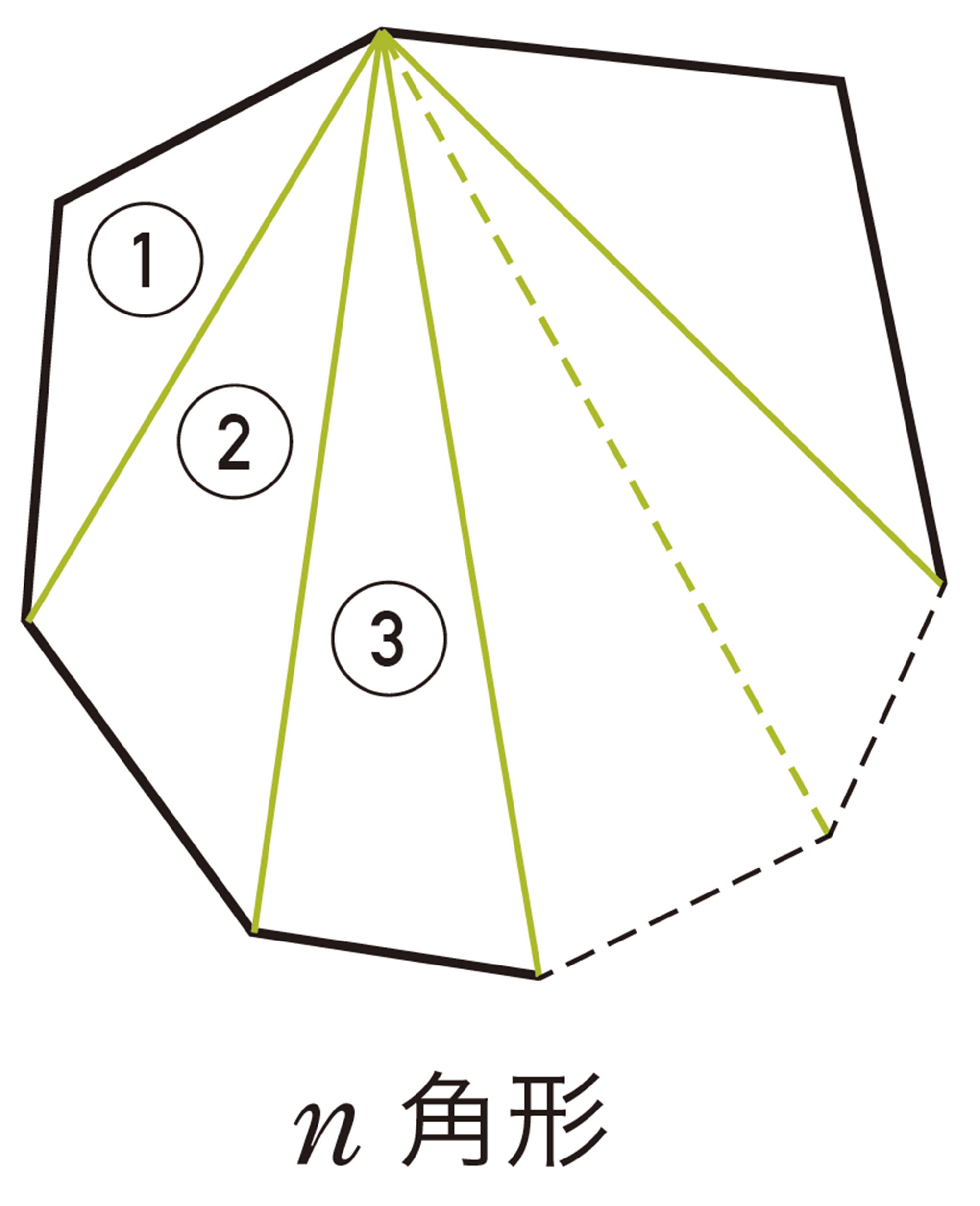
これまで調べたことから，n角形の内角の和は，次のようになる。
多角形の内角の和
n角形の内角の和は，[mathjax]\( 180^{ \circ } \times (n-2) \) である。
三角形に分ける方法は，ほかにもありそうだね。
どんな分け方をしても，結果は同じになるのかな。
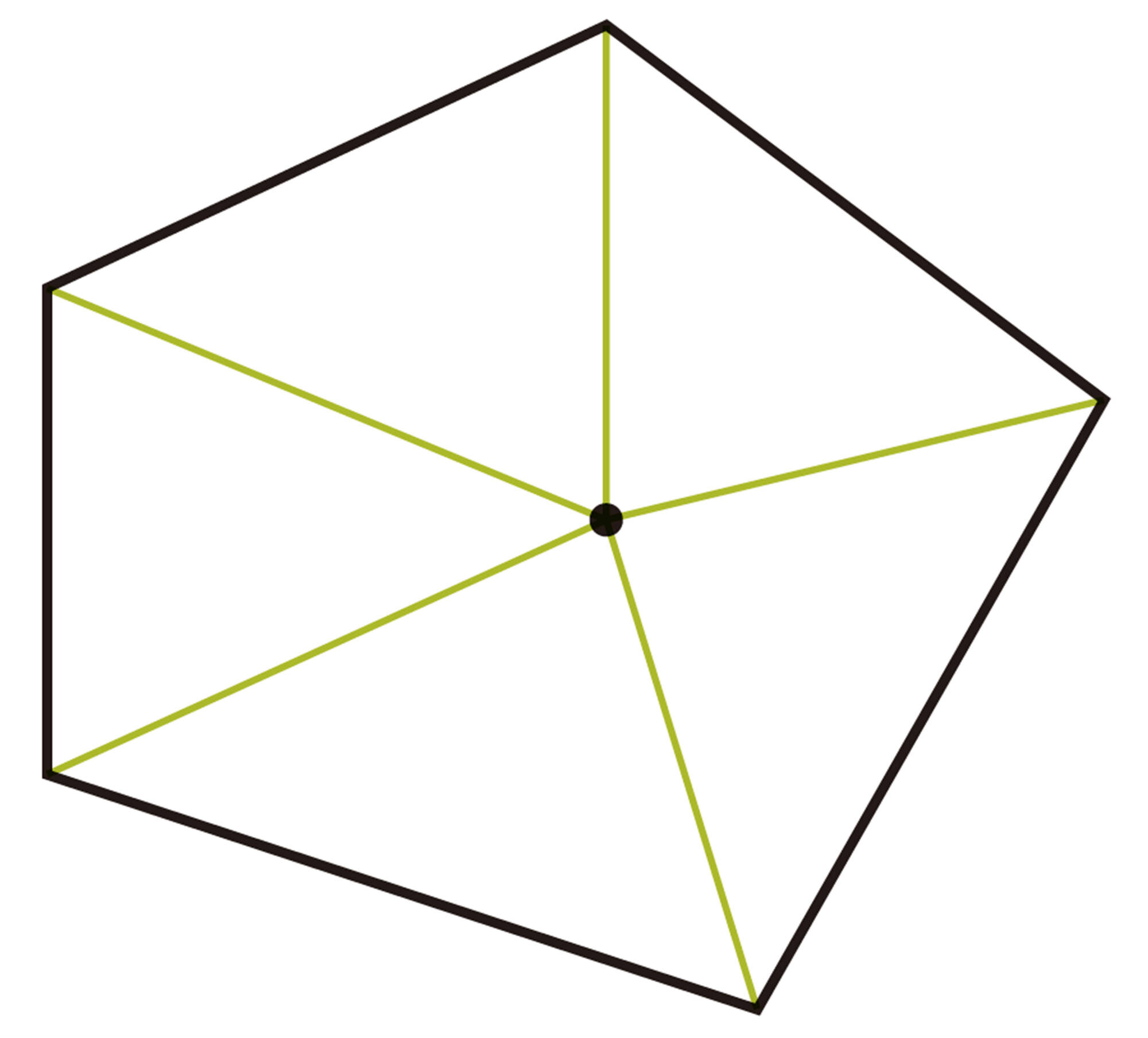
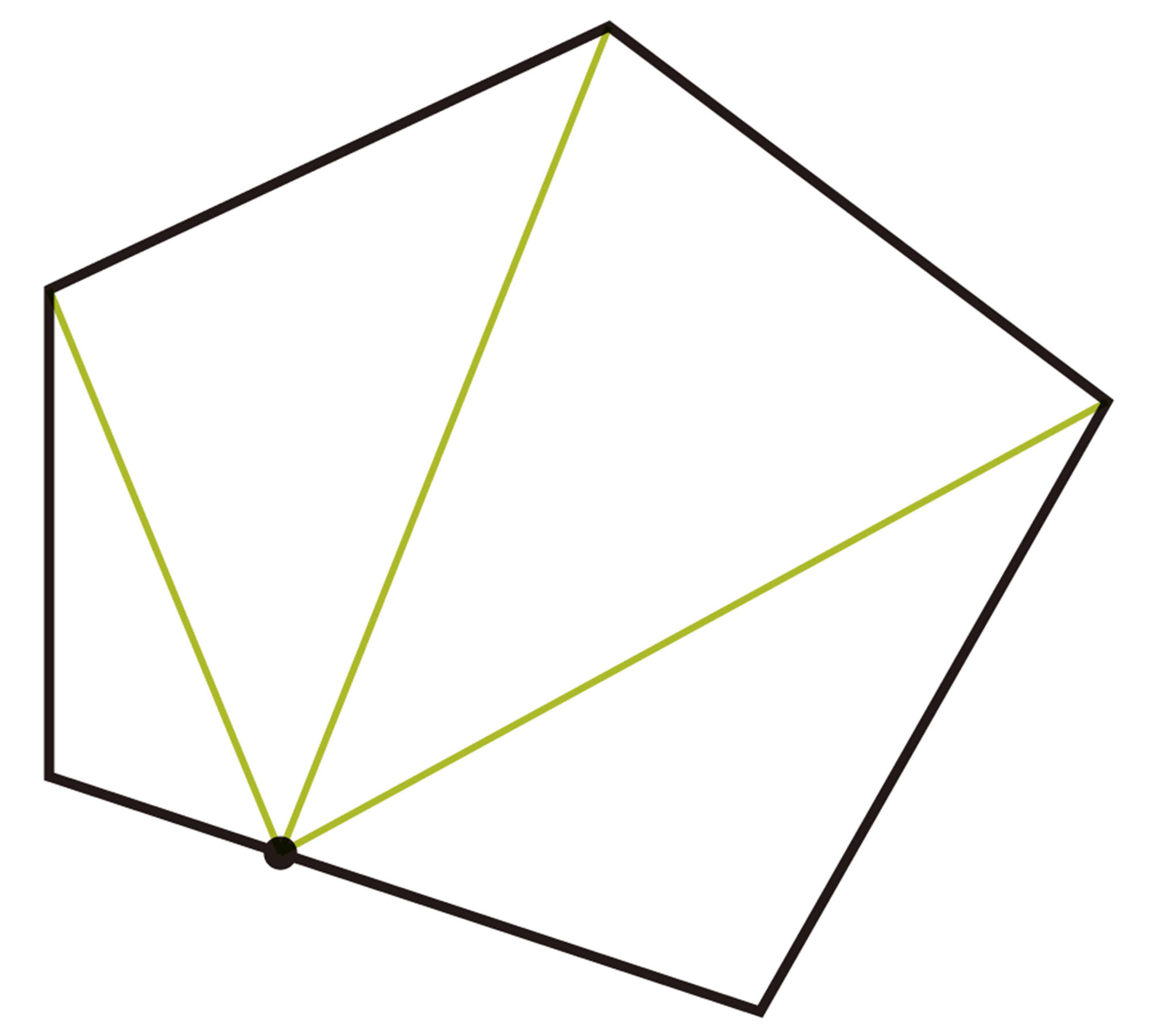
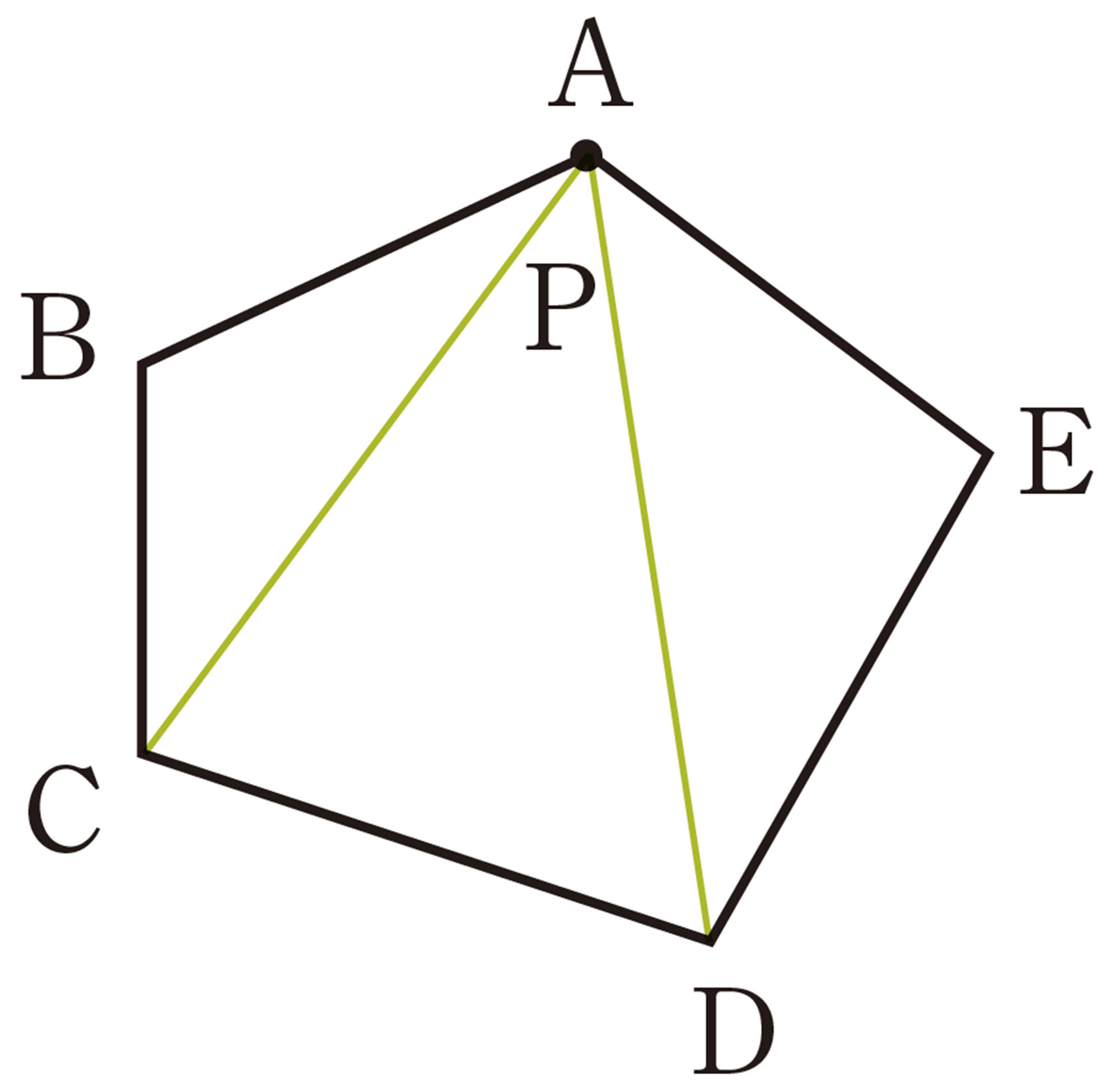
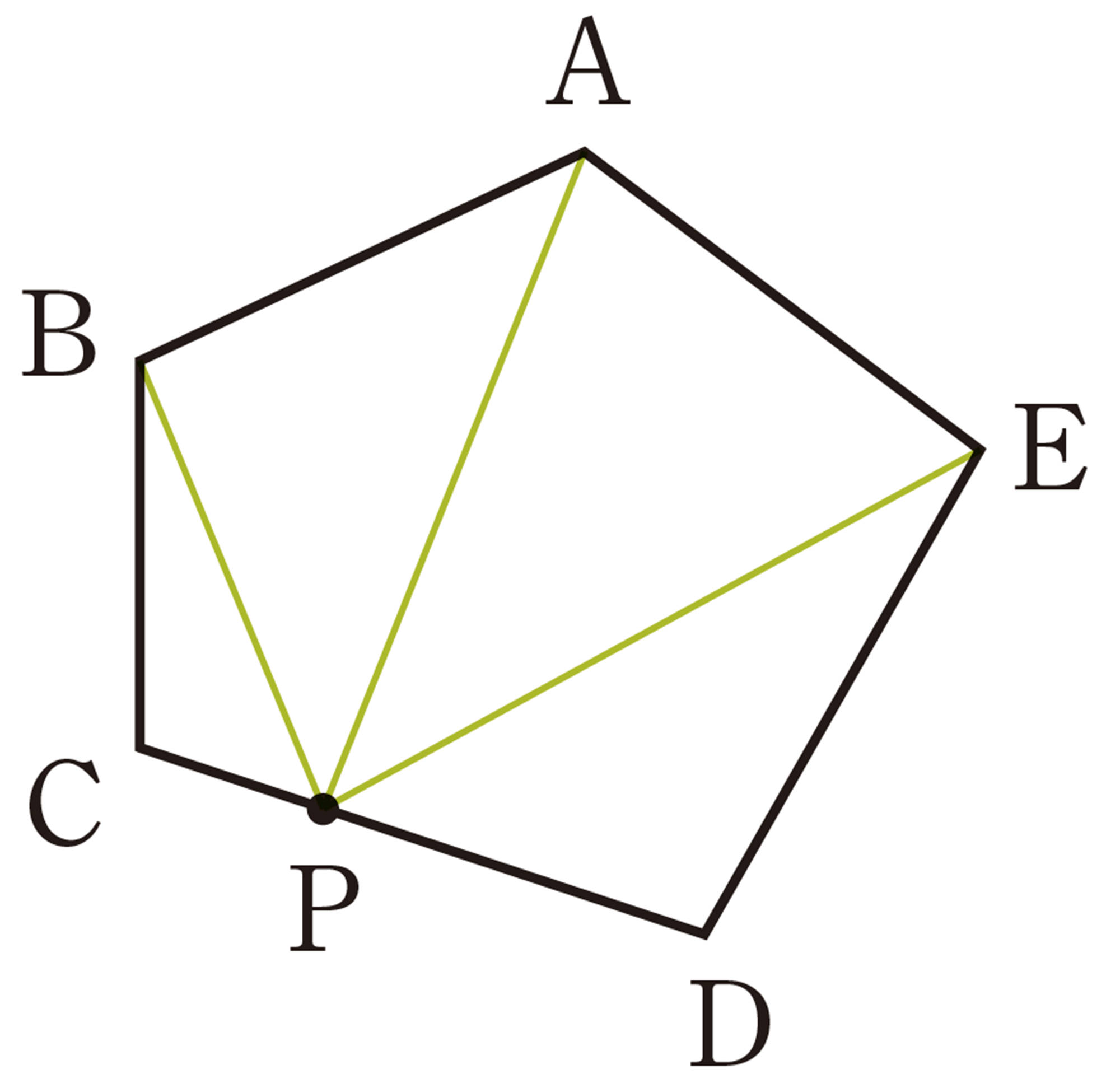
３ 前ページのQについて，美月さんは，次のようにして五角形の内角の和を求めました。美月さんの考え方を説明してみましょう。
美月さんの考え
五角形の内部に点Pをとり，Pと各頂点を結ぶと，内角の和は，
[mathjax]\( 180^{ \circ } \times 5-360^{ \circ }=540^{ \circ } \)
となる。
４ 美月さんの考え方でn角形の内角の和を求め，それが[mathjax]\( 180^{ \circ } \times (n-2) \) と等しいことを確かめてみましょう。
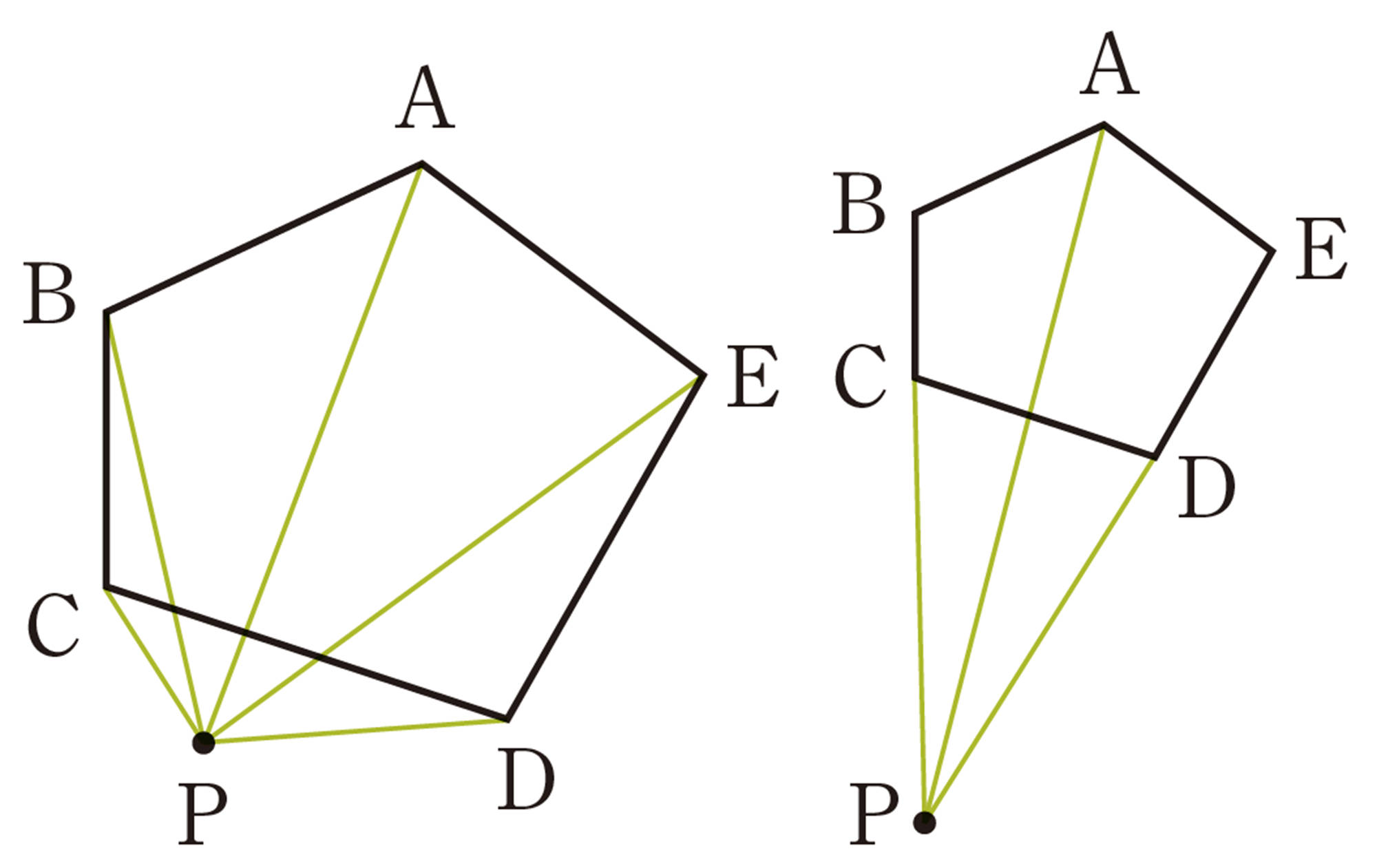
点Pを図形の内部にとっているけど，どこに点Pをとっても同じ結果になるのかな。
辺上や，五角形の外部にとっても同じことがいえるのかな。
関連 P.120
<2年p.120>
問 １ n角形の内角の和が [mathjax]\( 180^{ \circ } \times (n-2) \) であることを使って，次の問いに答えなさい。
⑴ 十二角形の内角の和は何度ですか。
⑵ 正十二角形の1つの内角の大きさは何度ですか。
⑶ 内角の和が [mathjax]\( 1260^{ \circ }\) になるのは何角形ですか。
点Pを動かして考えよう Tea Break
五角形の内角の和を求めるとき，五角形を三角形に分けるには，次のような方法があります。
これらの方法は，「適当な1点Pと五角形の各頂点を結び，Pをいろいろな場所に動かした」と考えると，統合的にみることができます。
上のような見方をすると，右の図のように，点Pを五角形の外部に動かした場合も考えることができます。
この図を使って，五角形の内角の和を求めてみましょう。
<2年p.121>
多角形の外角の和
Q Question
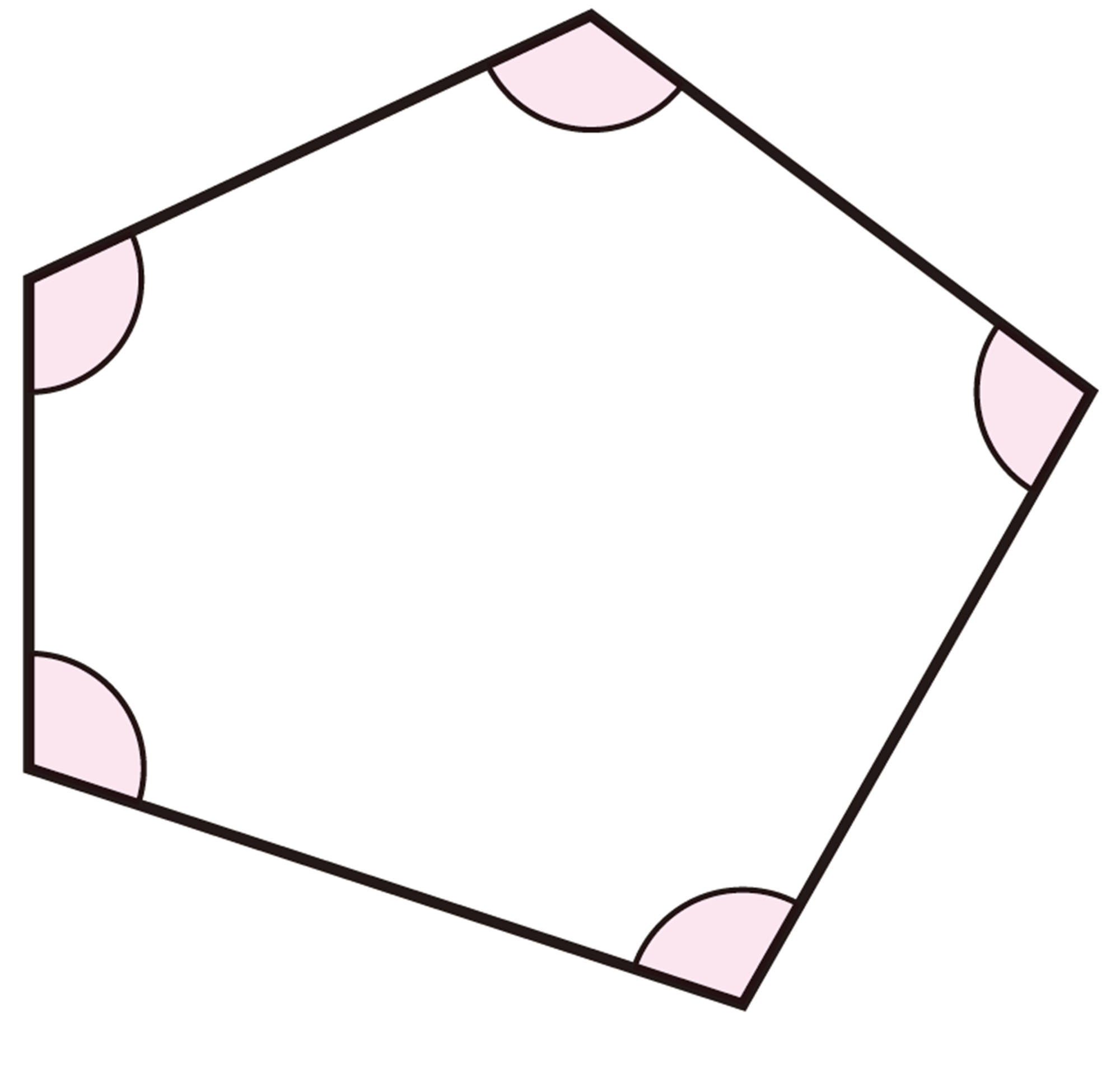
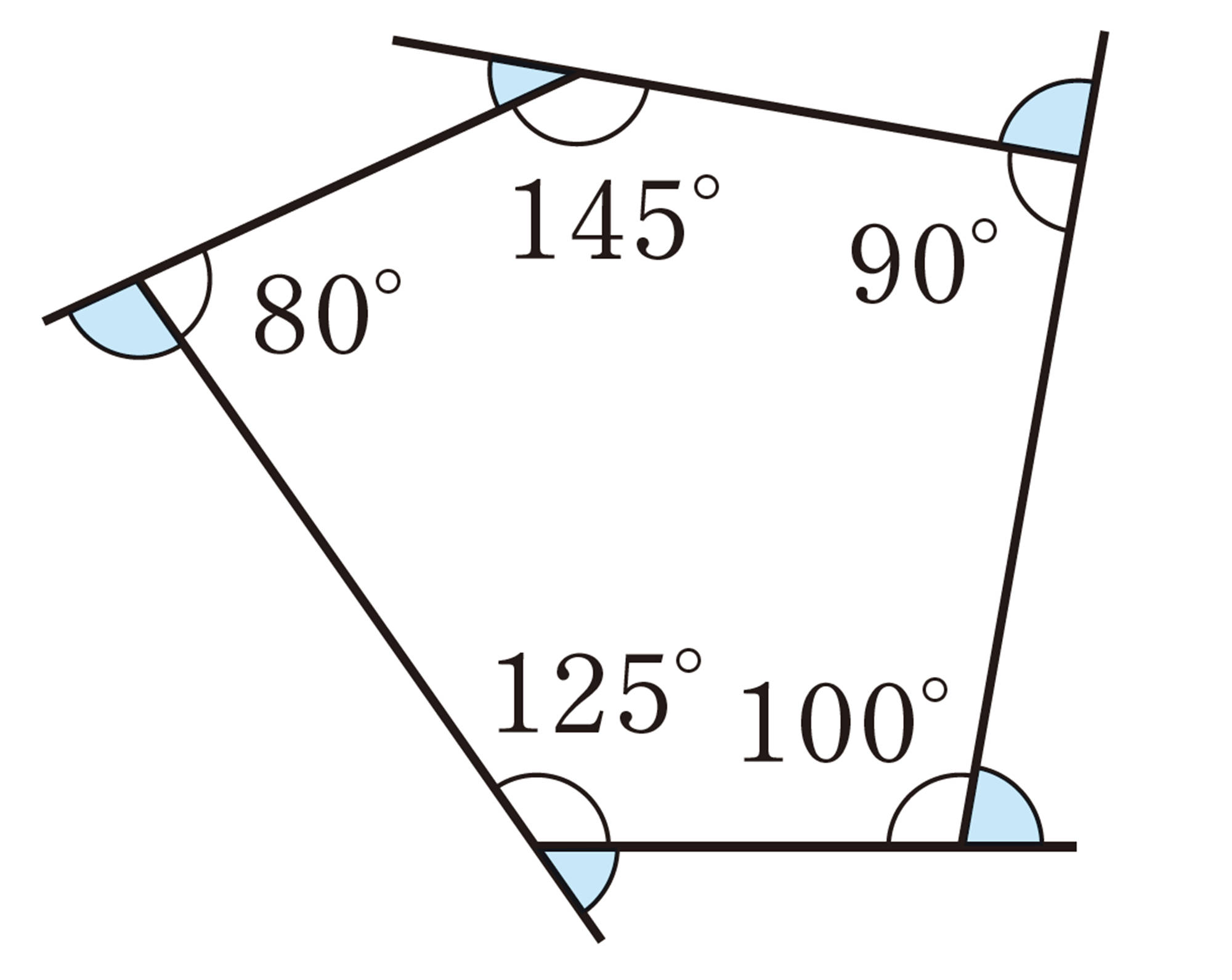
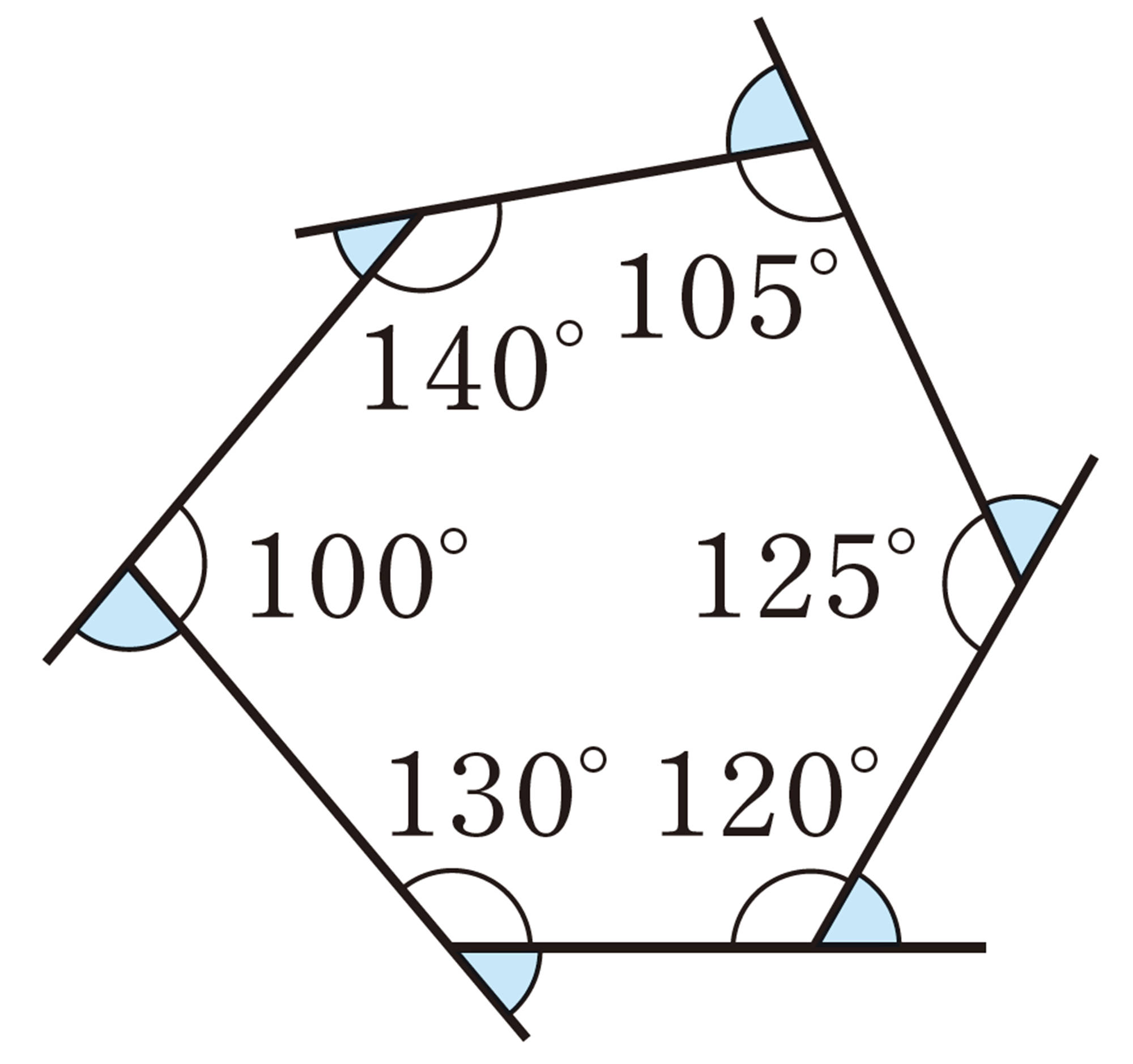
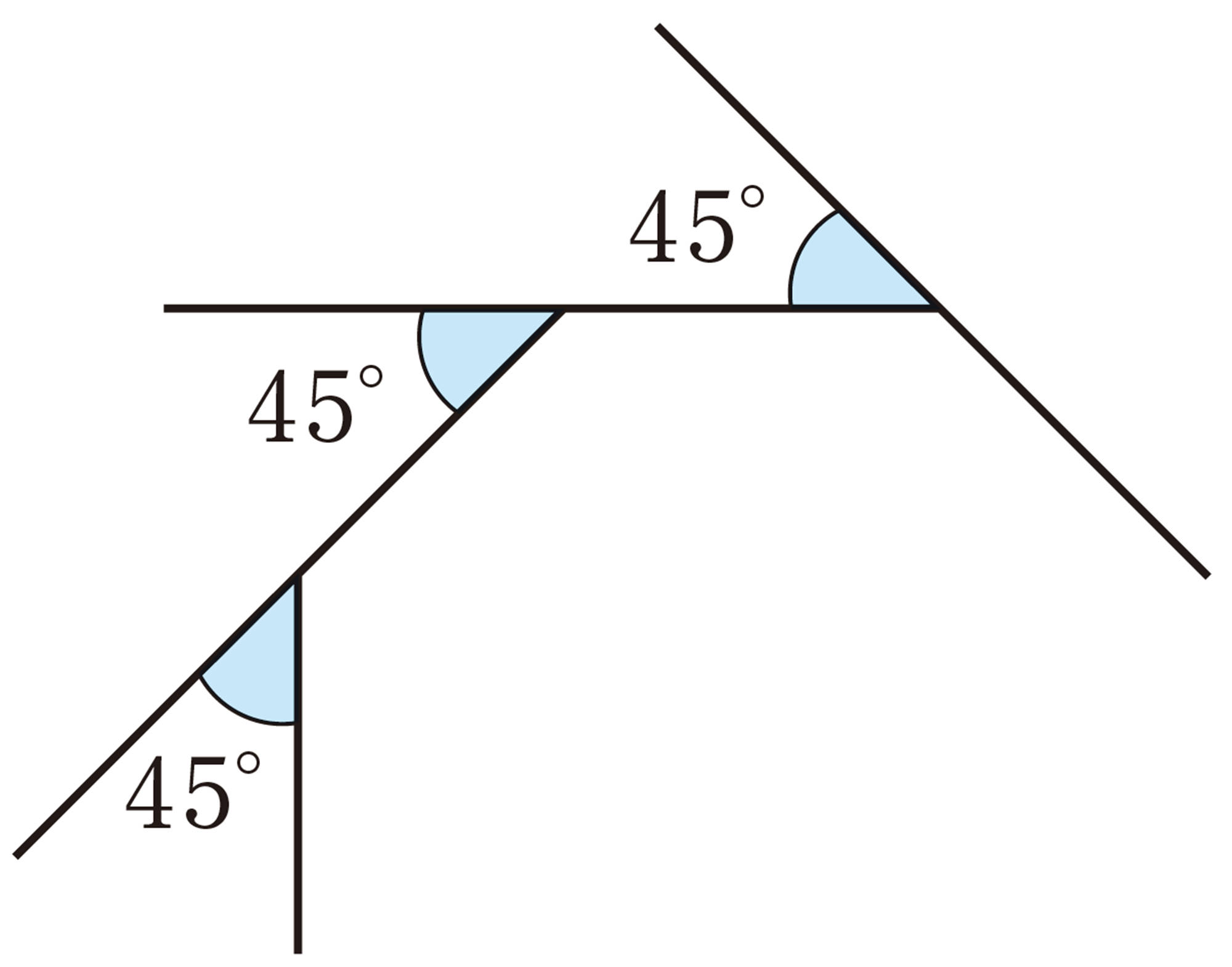
次の図は，四角形，五角形，六角形の各頂点の外角を表しています。これらの外角の和は，それぞれ何度になるでしょうか。また，その結果から，多角形の外角の和について，どんなことが予想できるでしょうか。
三角形の外角の和は [mathjax]\( 360^{ \circ }\) だったね。
ほかの多角形でも，同じようにいえるのかな。
見方・考え方
図をもとにして，どんな性質があるか見つけられるかな。
目標 ▷ 多角形の外角の和の性質について調べよう。
五角形の外角の和は，次のように求めることができる。
どの頂点でも，内角と外角の和は [mathjax]\( 180^{ \circ }\) である。したがって，5つの頂点における内角と1つの外角の和をすべて加えると，
[mathjax]\( 180^{ \circ } \times 5=900^{ \circ } \)
一方，五角形の内角の和は，
[mathjax]\( 180^{ \circ } \times (5-2)=540^{ \circ } \)
したがって，五角形の外角の和は，
[mathjax]\( 900^{ \circ }-540^{ \circ }=360^{ \circ } \)
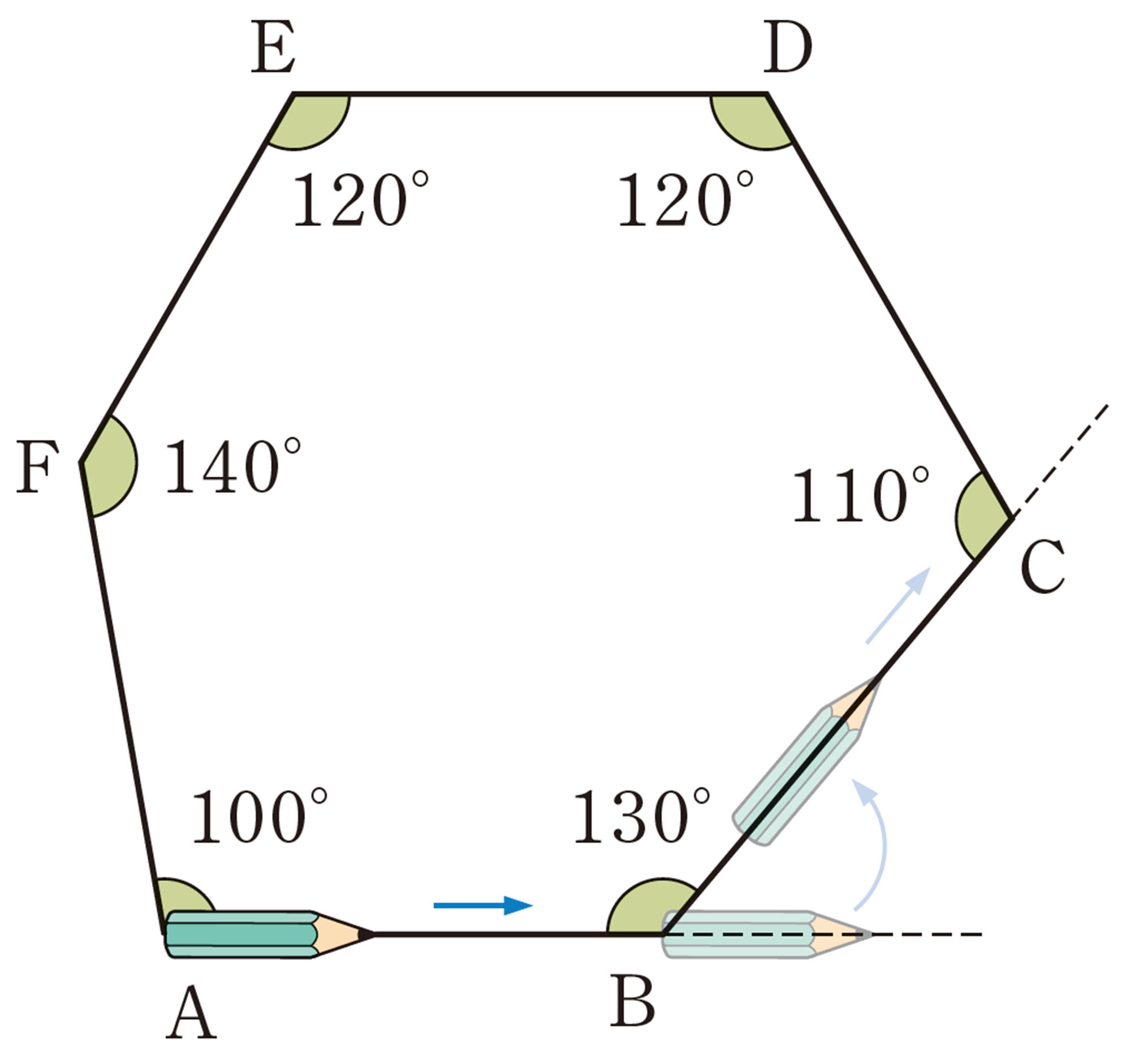
また，五角形の外角の和は，次の図のようにそれぞれの辺を平行移動して考えても， [mathjax]\( 360^{ \circ }\) であることがわかる。
<2年p.122>
問 ２ 八角形の外角の和を求めなさい。
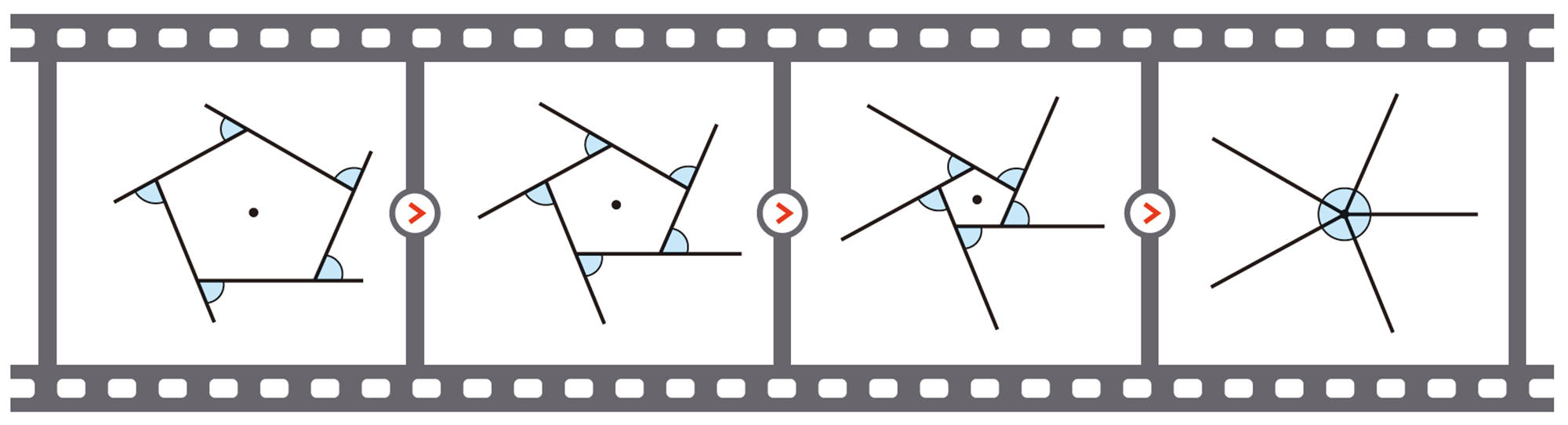
n角形の外角の和は，次のように求めることができる。
多角形の外角の和
多角形の外角の和は，[mathjax]\( 360^{ \circ } \) である。
問 ３ 次の問いに答えなさい。
⑴ 1つの外角が[mathjax]\( 45^{ \circ } \) になるのは，正何角形ですか。
⑵ 1つの内角が[mathjax]\( 160^{ \circ } \) になるのは，正何角形ですか。
鉛筆の回転角は何度？ Tea Break
右の図のような六角形があります。頂点Aのところに鉛筆を置いて多角形の辺にそって動かし，頂点で向きを変えて1周させてみましょう。
それぞれの頂点では，鉛筆を何度回転させればよいでしょうか。また，鉛筆がもとの位置にもどるまでに，合計何度回転したことになるでしょうか。さらに，このことからどんなことがいえるでしょうか。
<2年p.123>
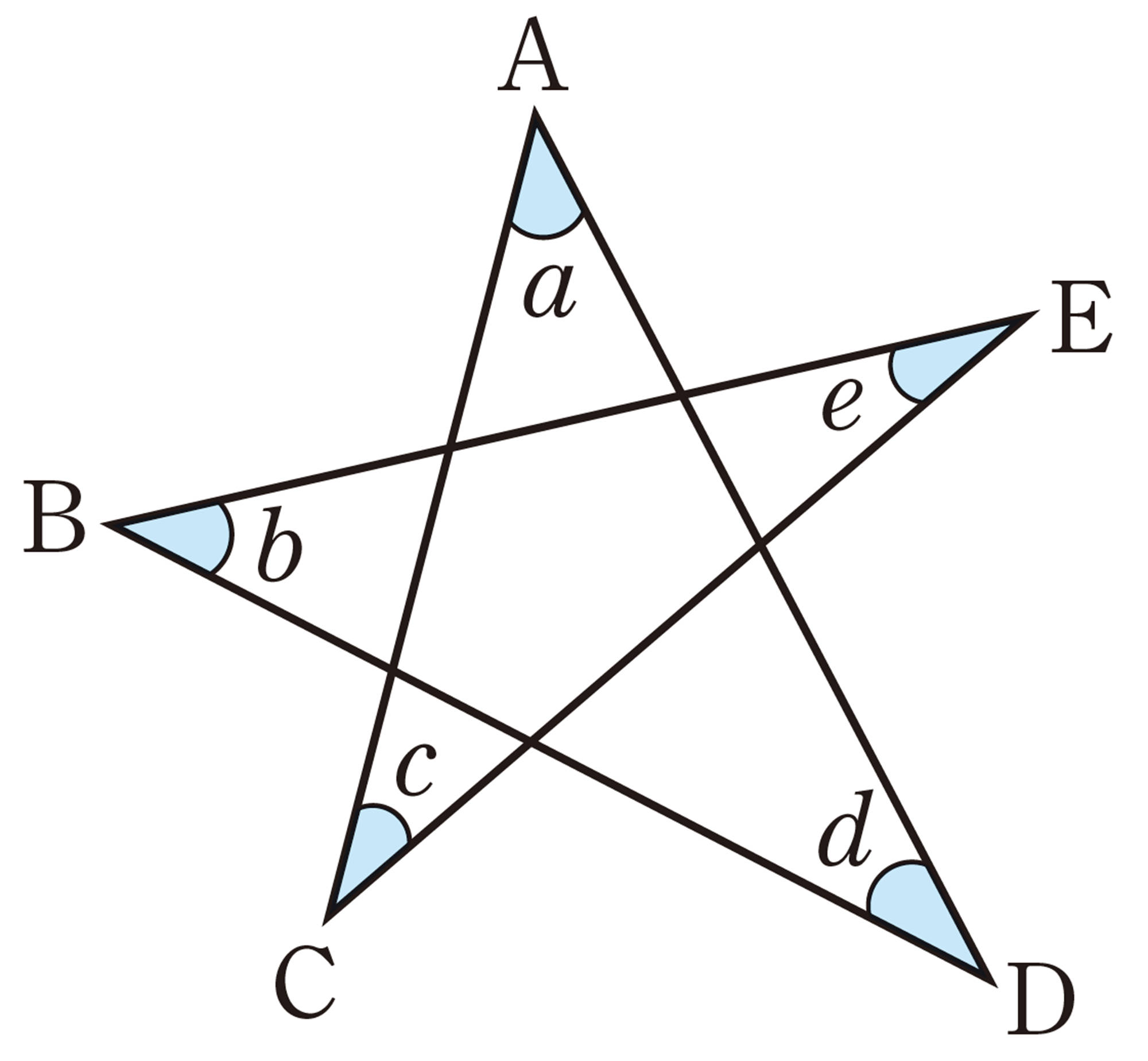
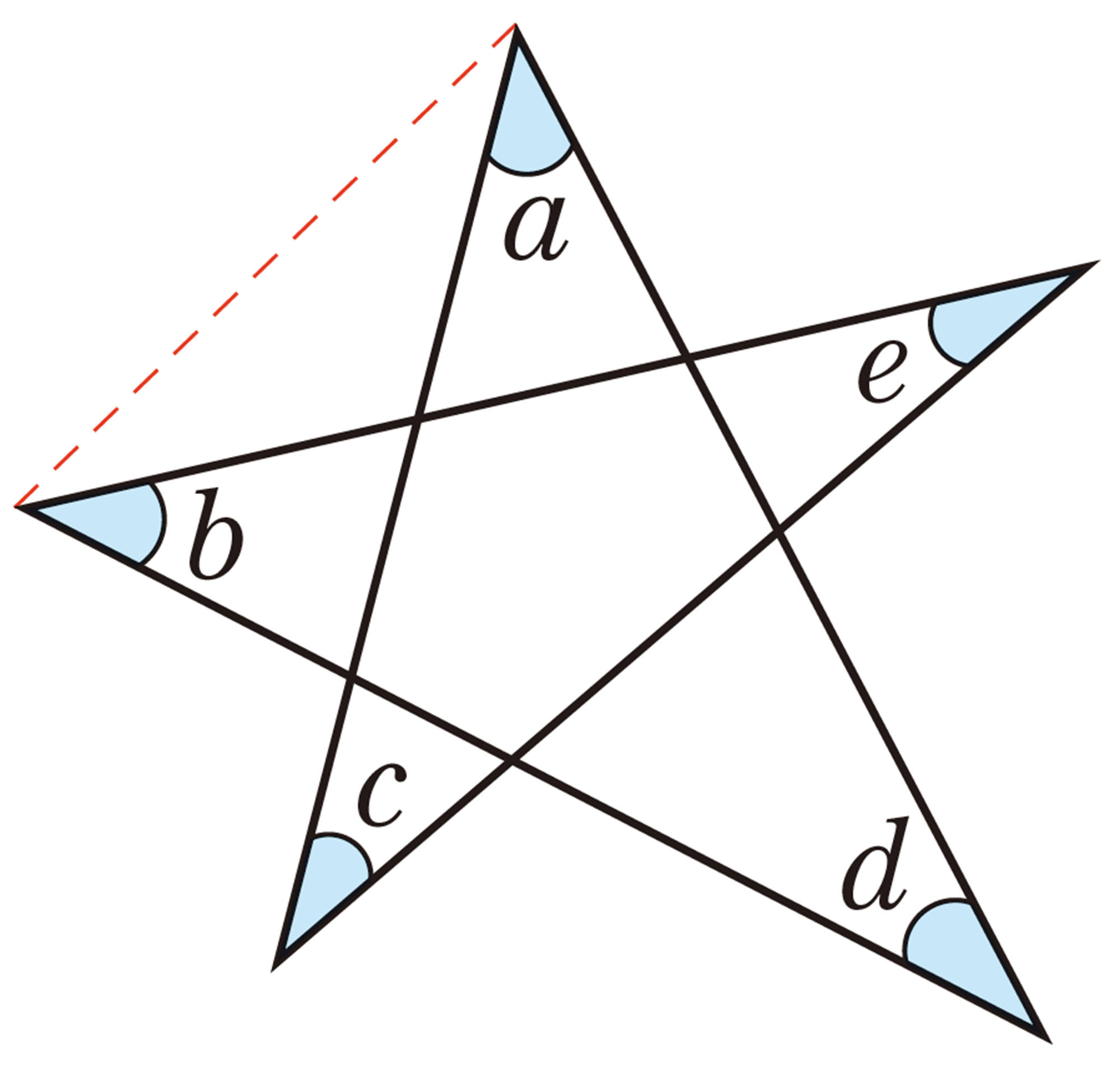
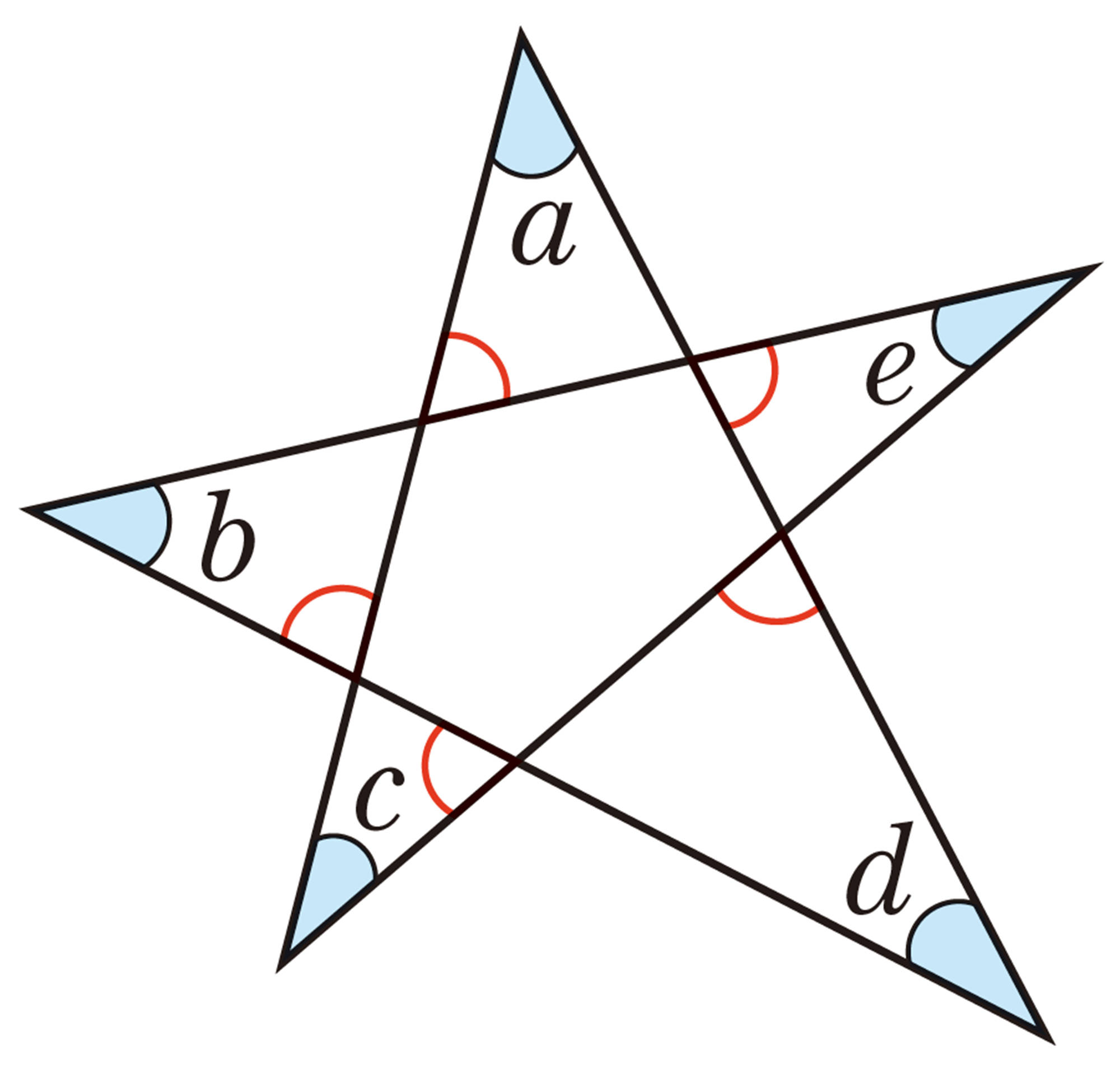
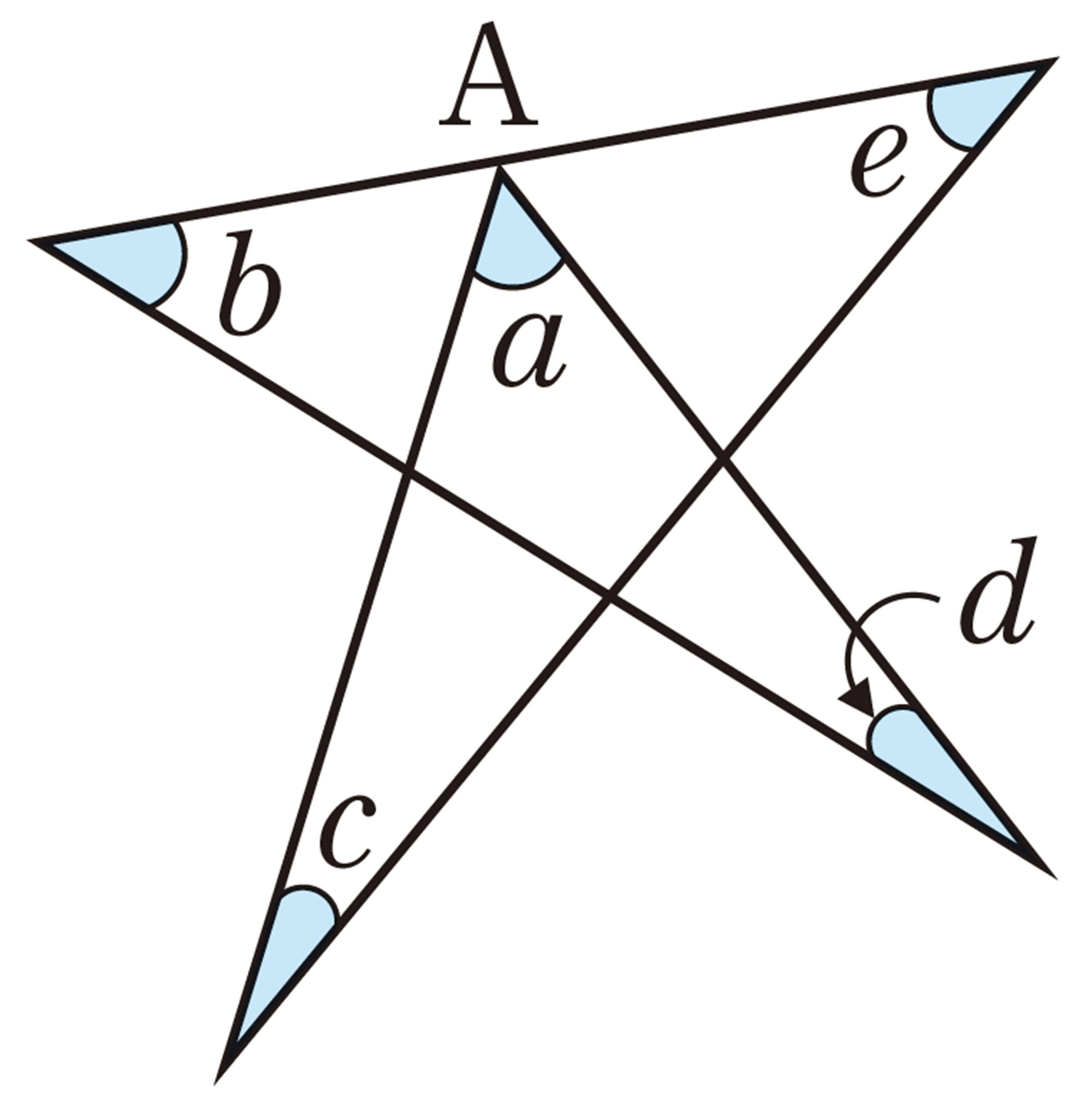
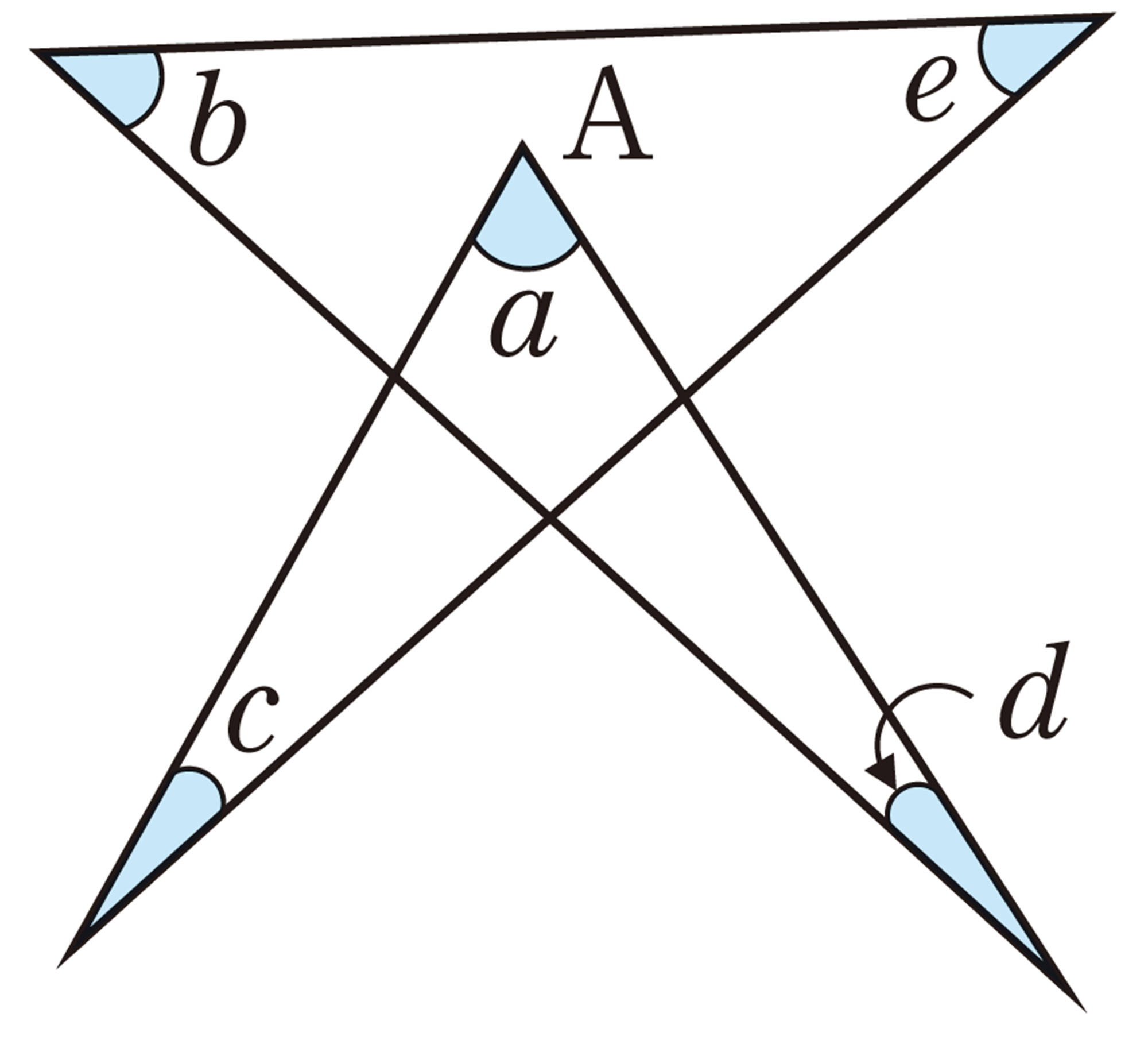
Q Question
[mathjax] \(108\)，[mathjax] \(109\)ページの星形五角形の先端部分の5つの角の和が [mathjax]\( 180^{ \circ }\) になることは，どのようにして説明すればよいか話し合ってみましょう。
三角形の角の性質が使えそうだね。
真ん中にある五角形の外角が使えないかな。
関連 P.145
見方・考え方
根拠を明らかにして，説明できるかな。
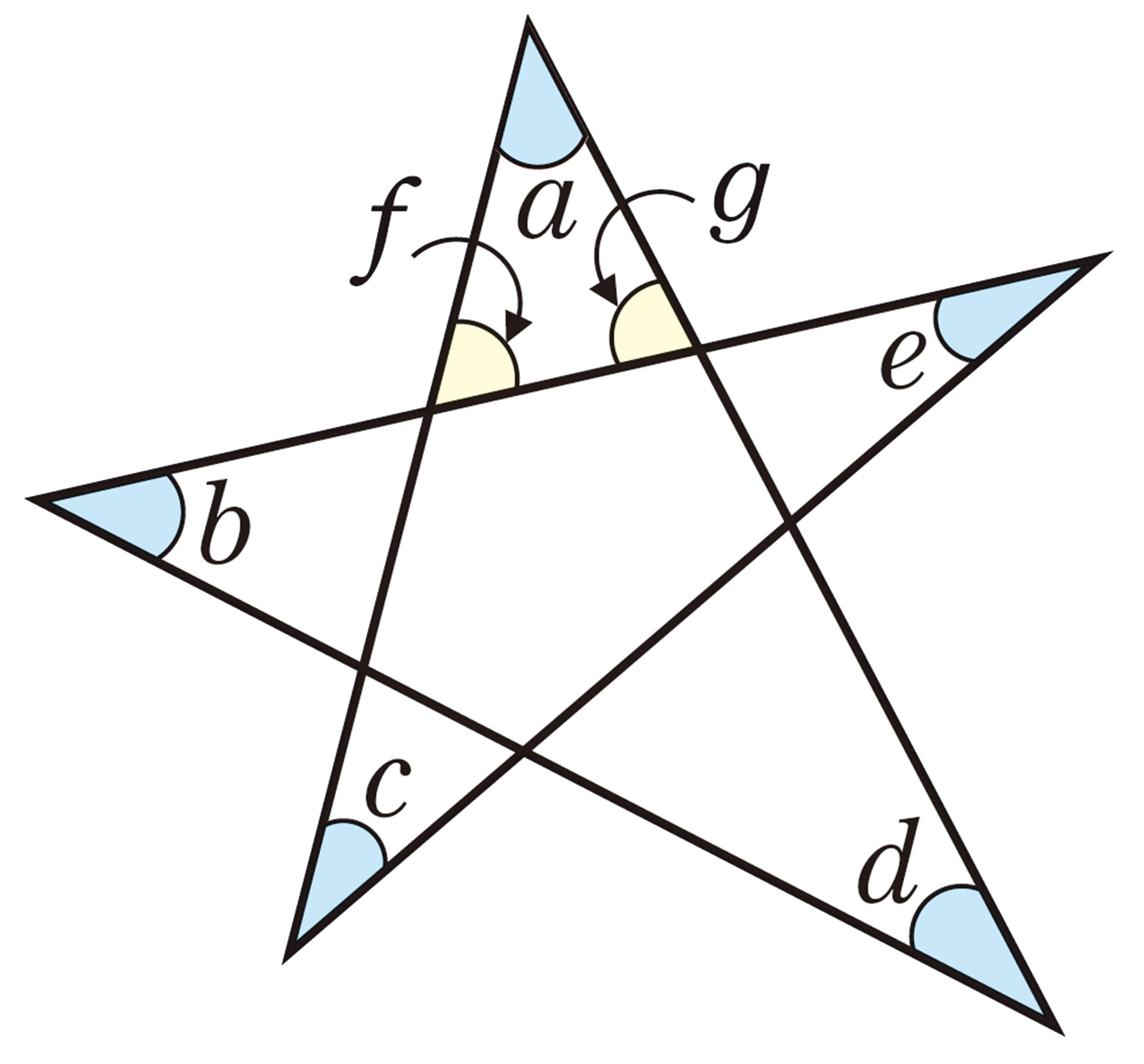
問 ４ Qについて，美月さんは，次のように考えました。美月さんの考え方を説明しなさい。
美月さんの考え
[mathjax]\(\angle c+\angle e=\angle f \) ，[mathjax]\(\angle b+\angle d=\angle g \)したがって，
問 ５ 星形五角形の5つの角の和を，問4の美月さんとはちがう方法で求めなさい。
▲トライ 点Aを右の図の位置に動かしても，[mathjax]\(\angle a+\angle b+\angle c+\angle d+\angle e=180^{ \circ } \)が成り立つか，確かめてみよう。
どんなことがわかったかな
n角形の内角の和が[mathjax]\( 180^{ \circ } \times (n-2) \) ，外角の和が [mathjax]\( 360^{ \circ }\) であることを利用すると，星形五角形の先端部分の5つの角の和が [mathjax]\( 180^{ \circ }\) になることを説明することができます。
<2年p.124>
確かめよう 1節 いろいろな角と多角形
１ 右の図について，次の問いに答えなさい。
⑴ [mathjax]\(\angle a\) と等しい角をいいなさい。
⑵ [mathjax]\(\angle h\) の対頂角，同位角，錯角をいいなさい。
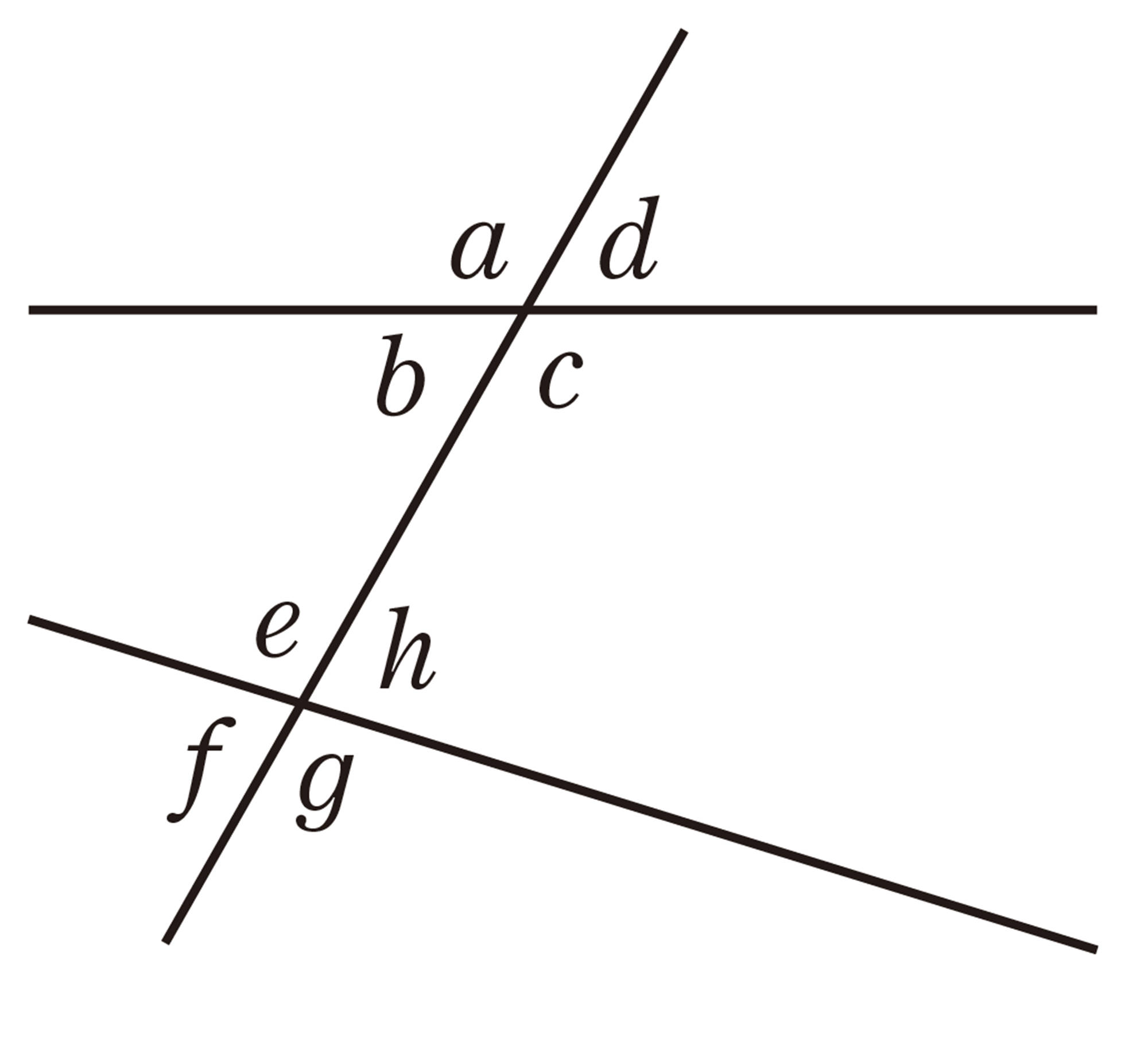
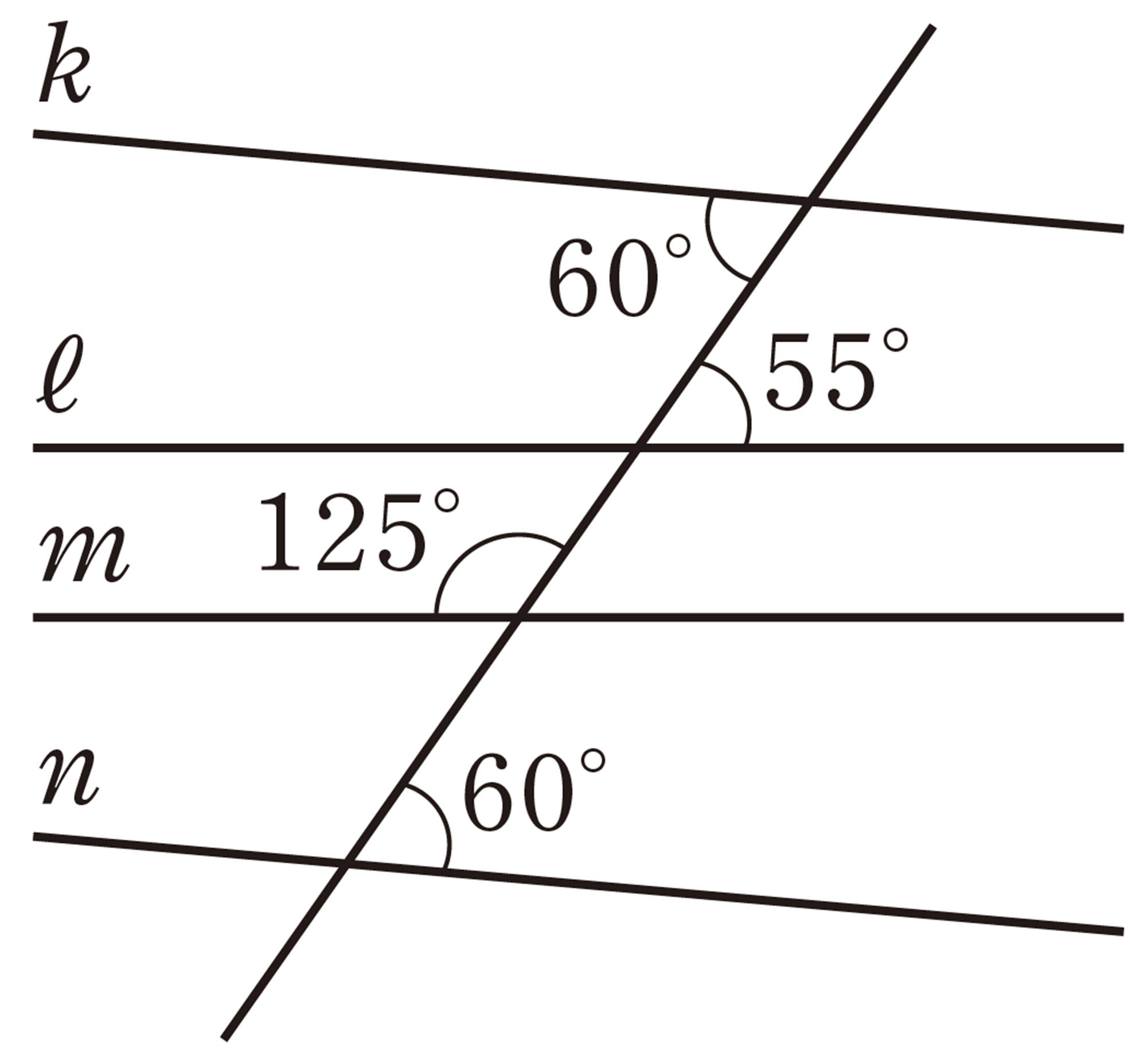
２ 次の⑴の図で，平行線はどれですか。
平行の記号を使って表しなさい。
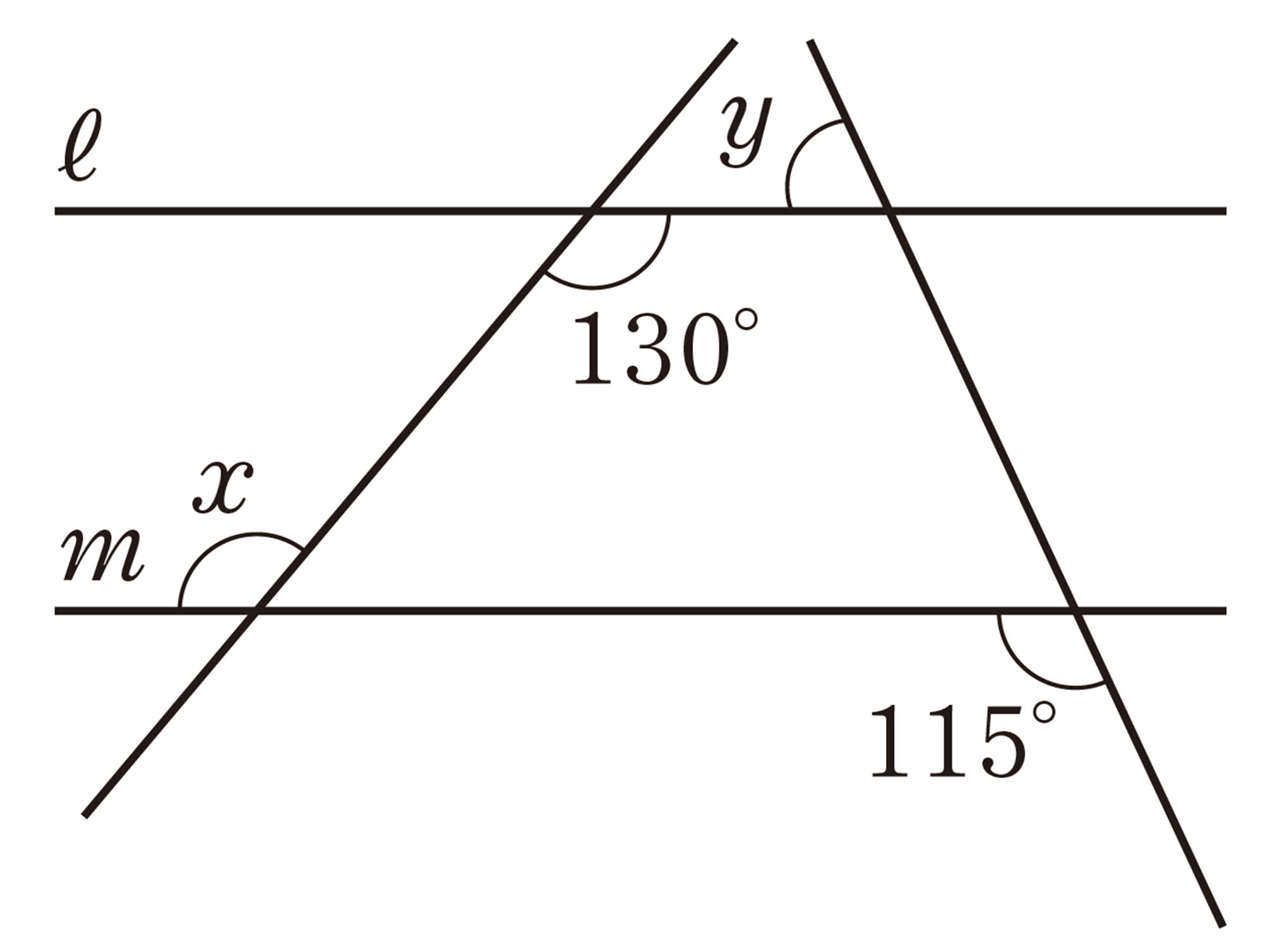
また，⑵の図で，[mathjax]\(ℓ/\!/m\) のとき，[mathjax]\(\angle x\)，[mathjax]\(\angle y\)の大きさを求めなさい。
⑴
⑵
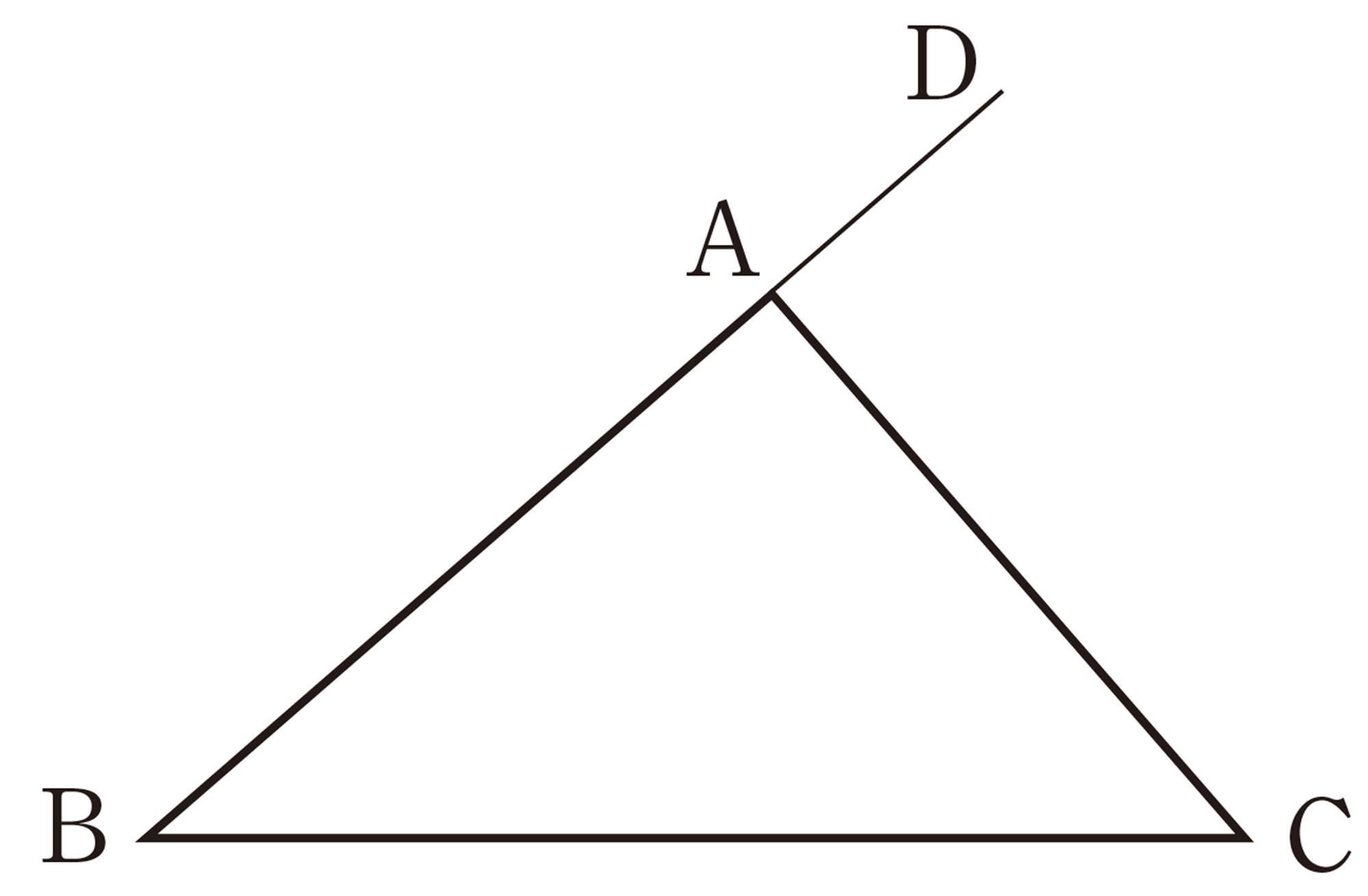
３ 右の図の [mathjax]\(\triangle ABC\) について，次の[mathjax]\(\boxed{\phantom{00}}\)にあてはまる数や角をいいなさい。
⑴ [mathjax]\(\angle BAC+\angle B+\angle C=\boxed{\phantom{00}}^{ \circ } \)
⑵ [mathjax]\(\angle DAC=\boxed{\phantom{000}}+\boxed{\phantom{000}} \)
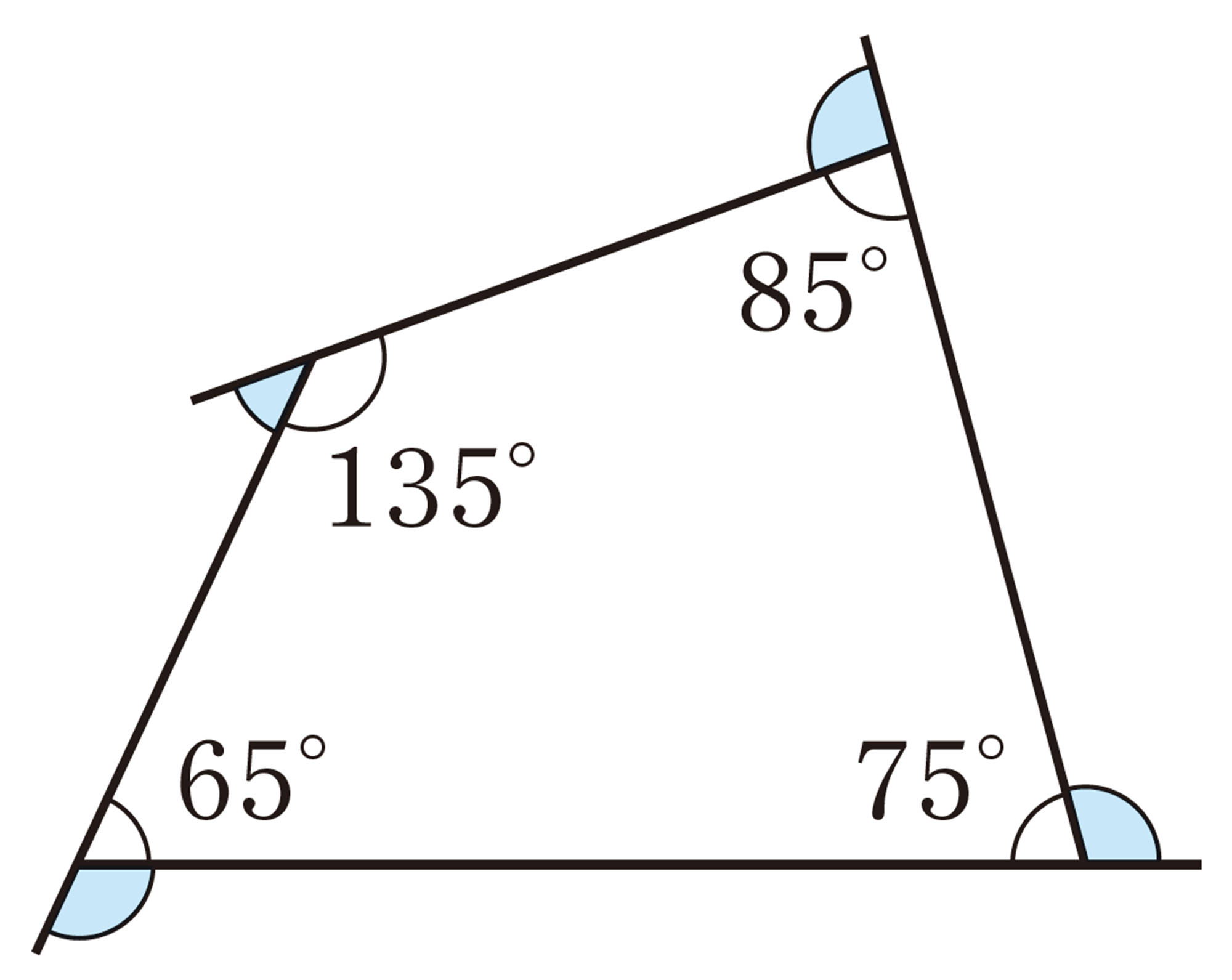
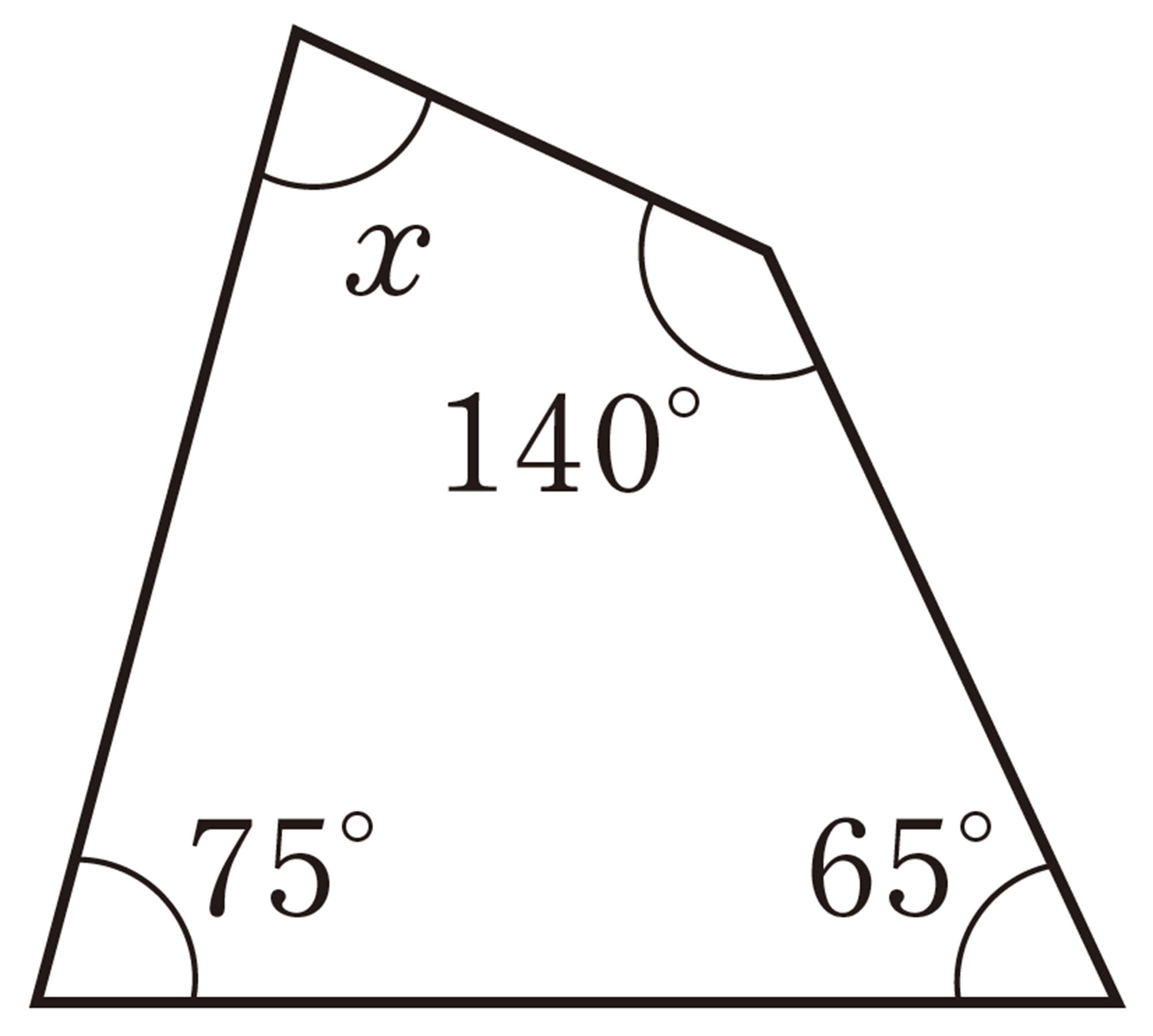
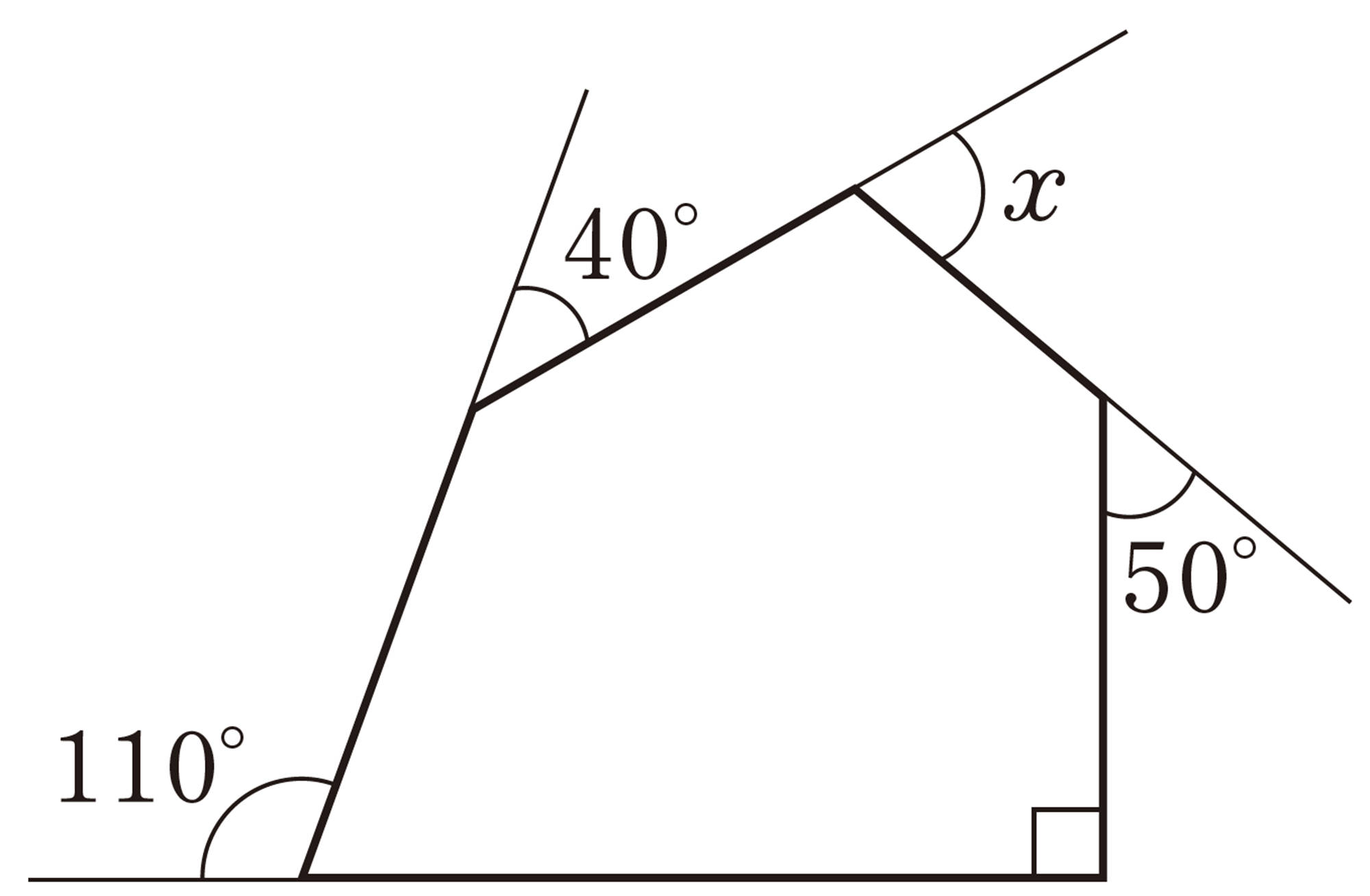
４ 次の図で，[mathjax]\( \angle x \) の大きさを求めなさい。
⑴
⑵
