<2年p.115>
2 三角形の角
三角形の角の性質
Q Question
目標 ▷ 三角形の角の性質について調べよう。
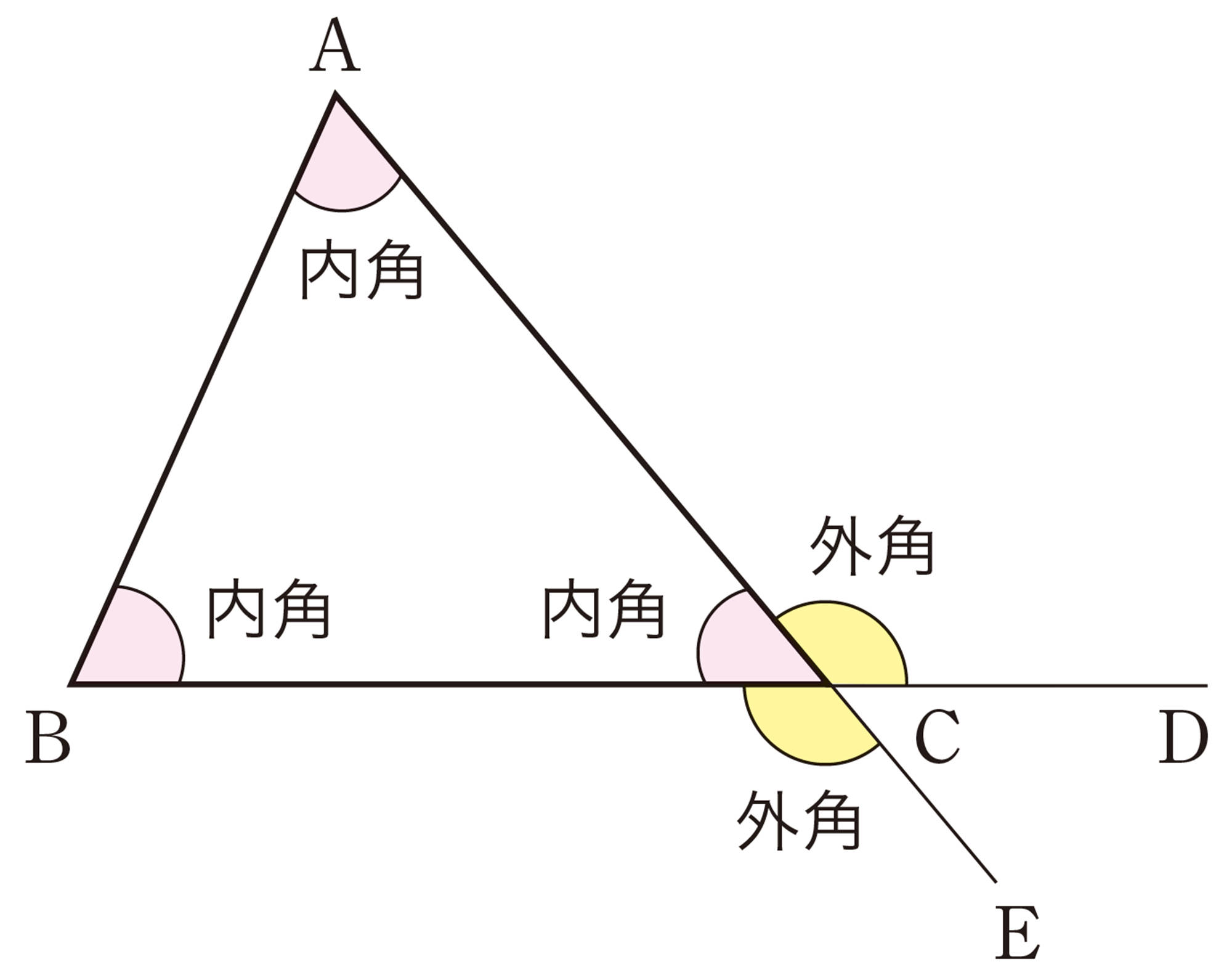
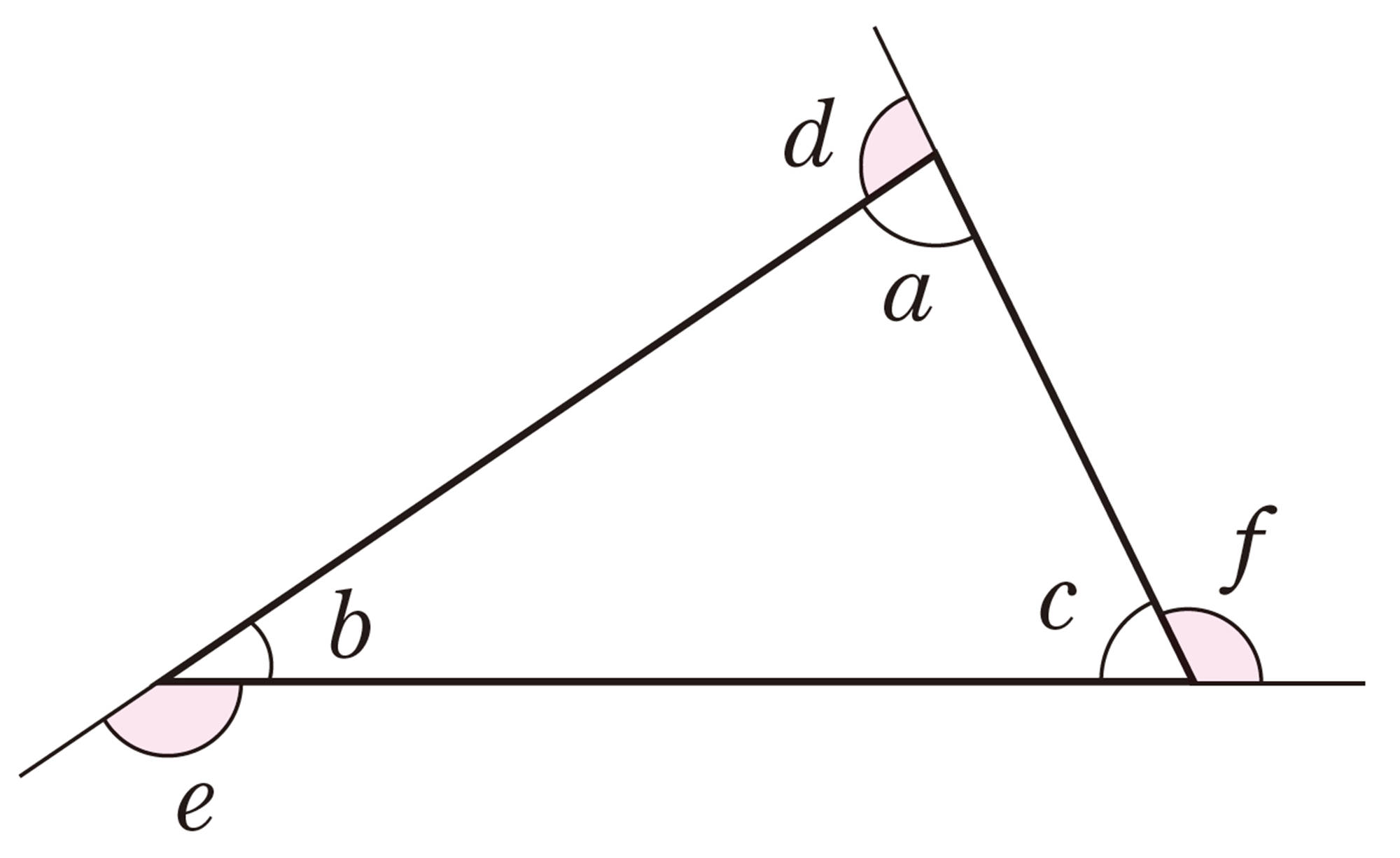
問 1 上の図の[mathjax]\(\triangle ABC\) で,頂点A,Bにおける外角を,それぞれ図に示しなさい。
<2年p.116>
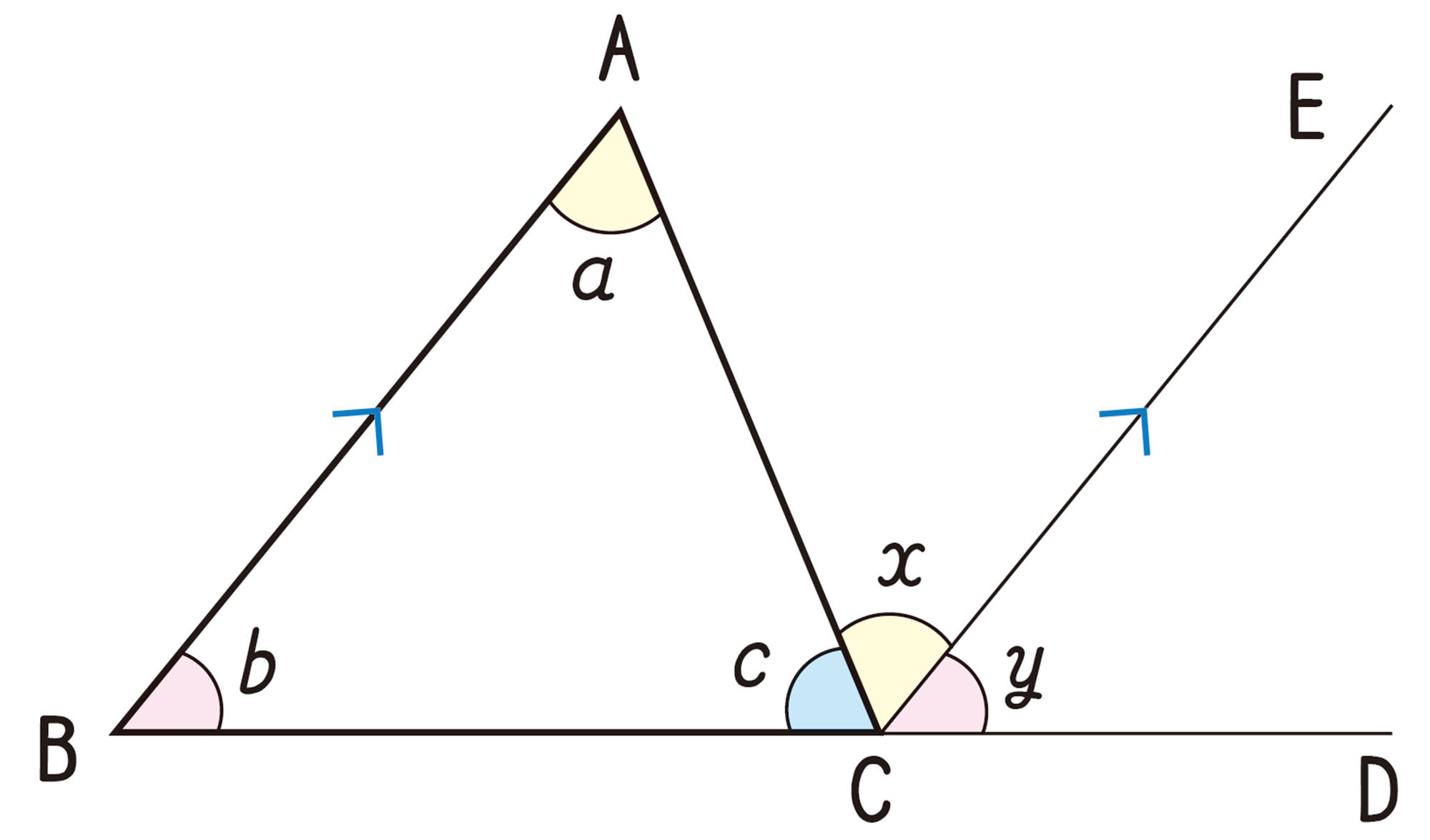
例 1 [mathjax]\(\triangle ABC\) の内角の和が[mathjax]\( 180^{ \circ }\) となる理由を説明しなさい。
解答
[mathjax]\(\triangle ABC\) の辺BCを延長してBDとし, 点Cを通り辺BAに平行な半直線CEを引く。
平行線の錯角は等しいから, [mathjax]\(BA/\!/CE\) より,
[mathjax] \(\angle a=\angle x\)
平行線の同位角は等しいから, [mathjax]\(BA/\!/CE\) より,
[mathjax] \(\angle b=\angle y\)
したがって,
注意 半直線CD,CEのように,考える手がかりとして引いた線を補助線という。
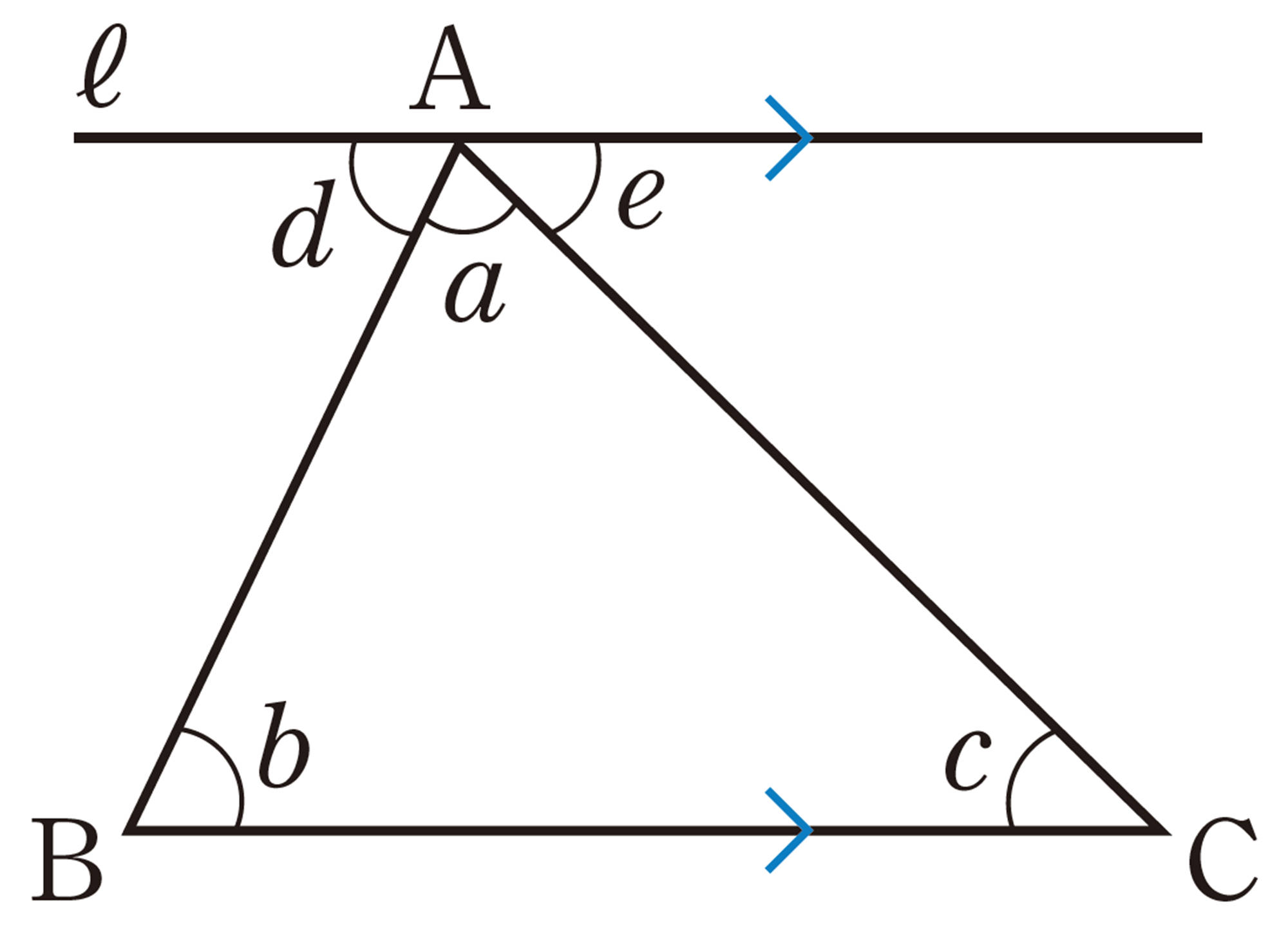
問 2 美月さんは,[mathjax]\(\triangle ABC\) の内角の和が[mathjax]\( 180^{ \circ }\)になることを,次の図のように,点Aを通り辺BCに平行な直線[mathjax]\( ℓ \) を引いて説明しました。次の図を使って,美月さんの考えを説明しなさい。
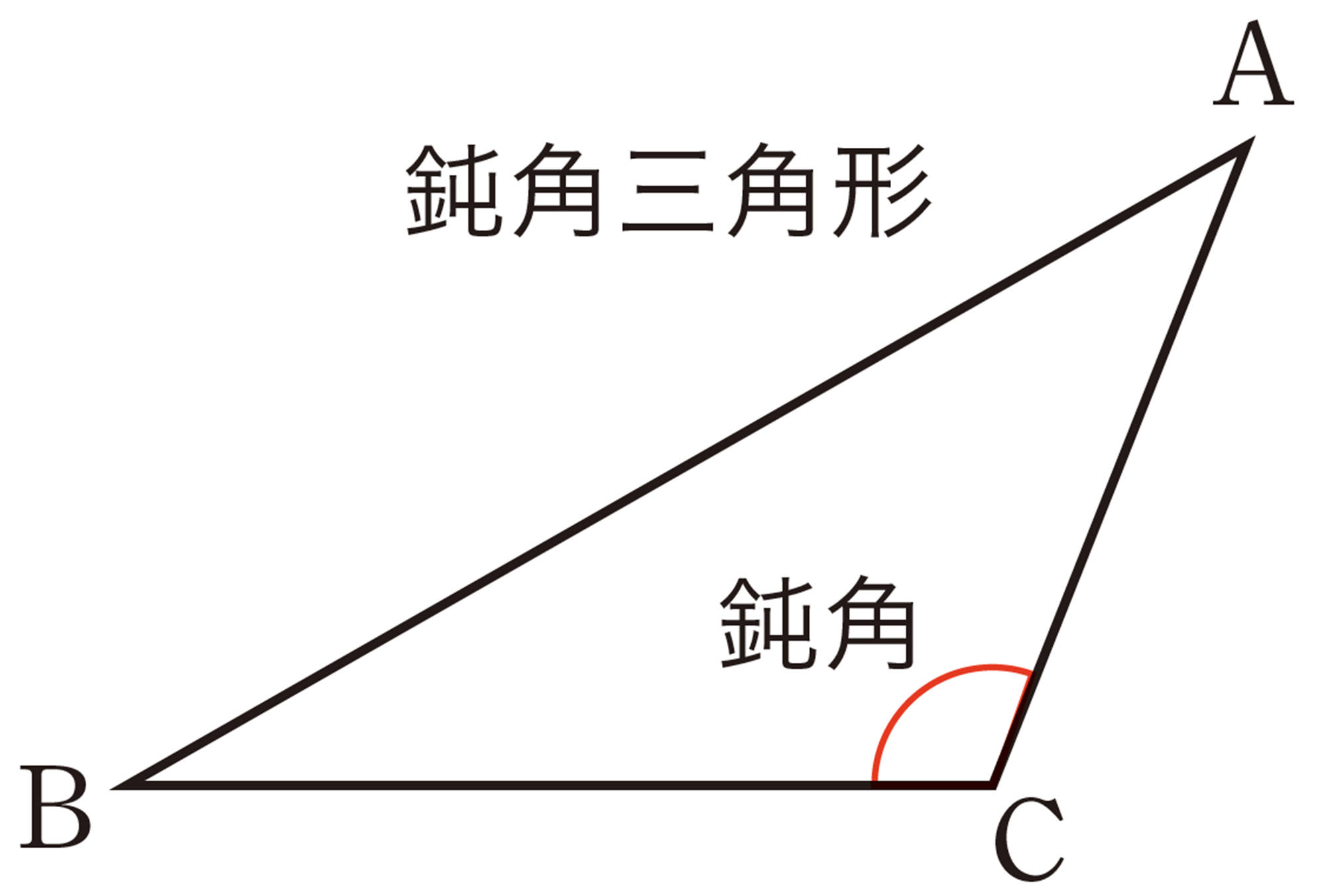
三角形は,内角の大きさによって,次の3つに分類できる。
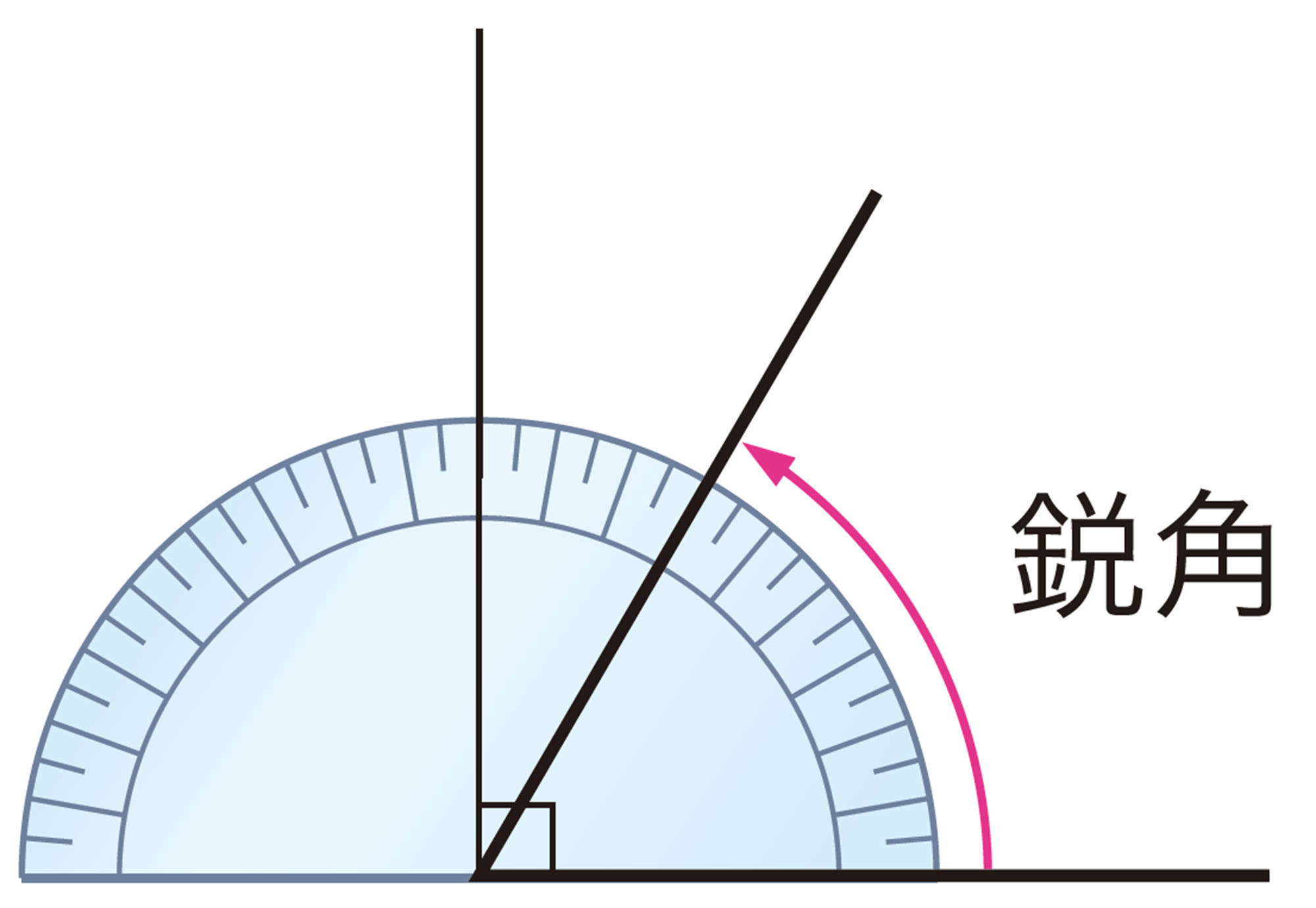
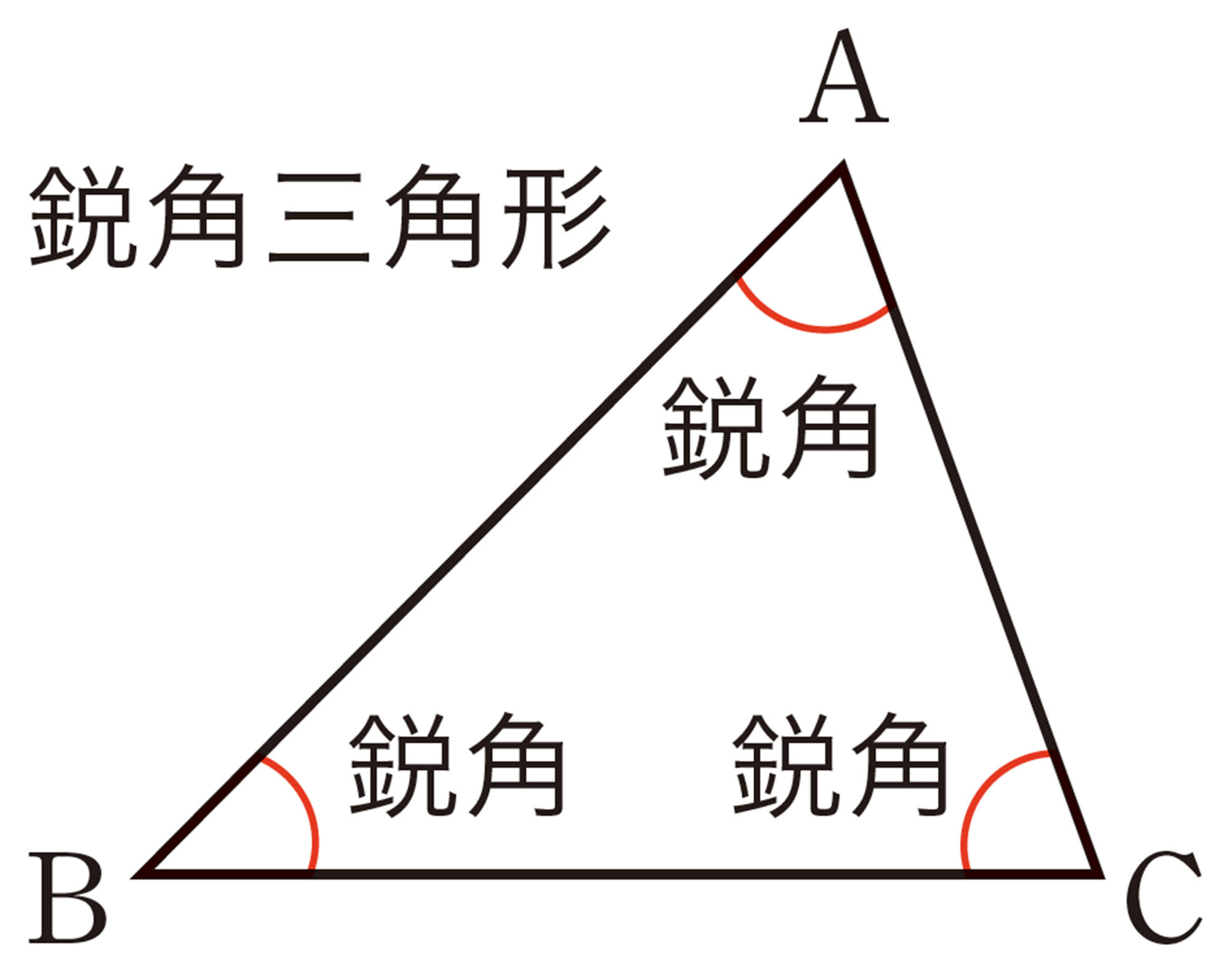
① 鋭角三角形 … 3つの内角がすべて鋭角である三角形
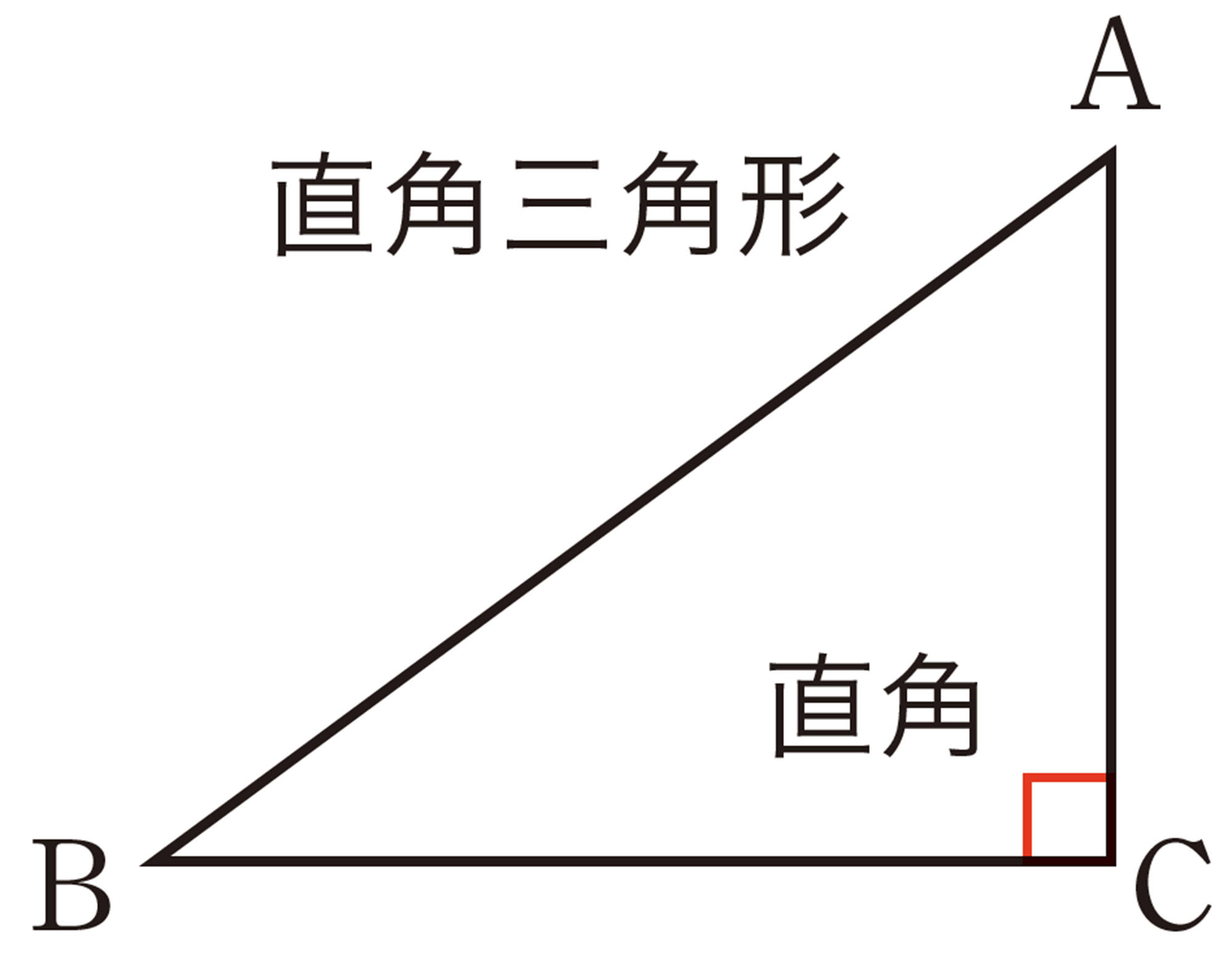
② 直角三角形 … 1つの内角が直角である三角形
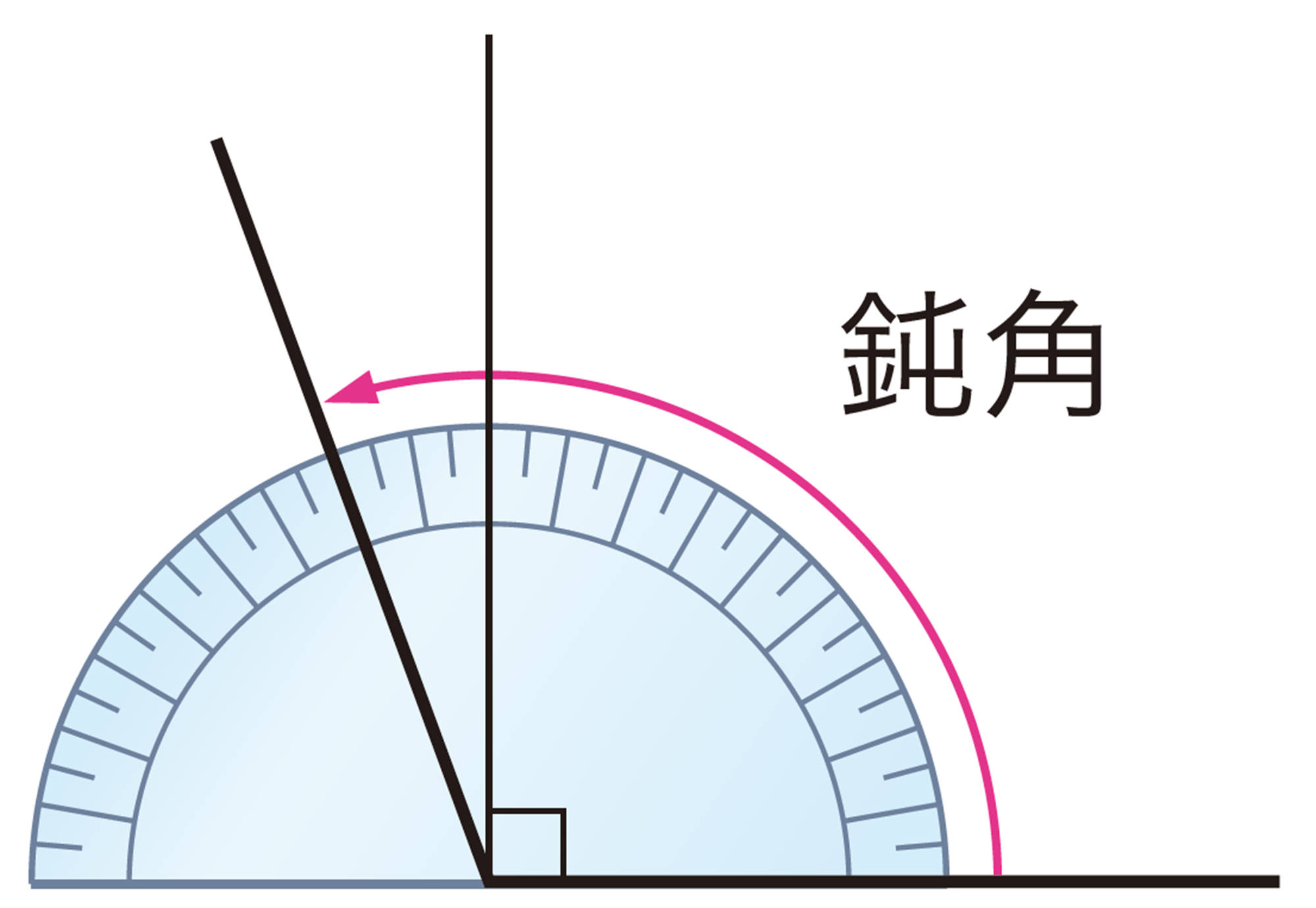
③ 鈍角三角形 … 1つの内角が鈍角である三角形
<2年p.117>
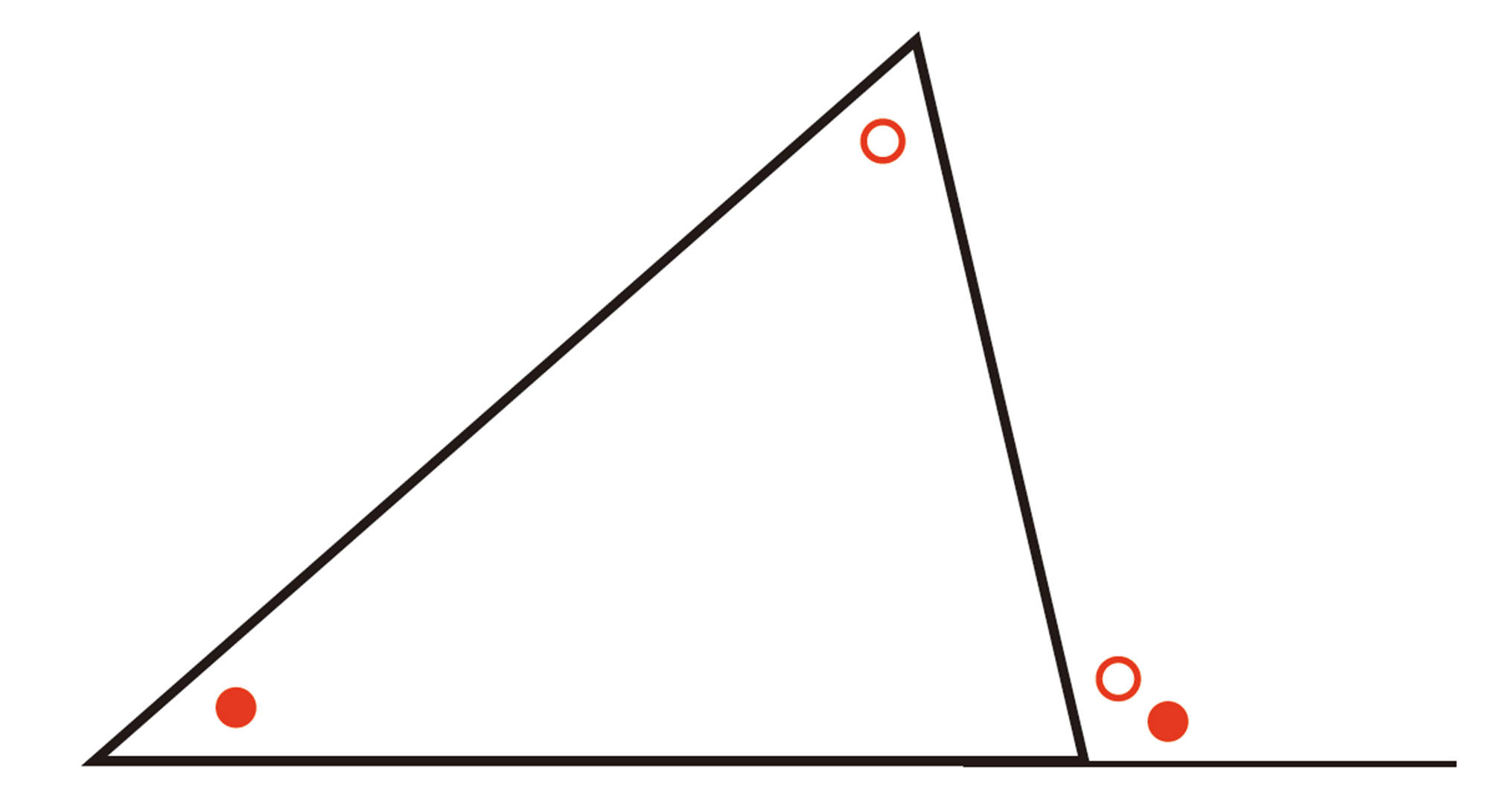
三角形の内角,外角について,次のようにまとめることができる。
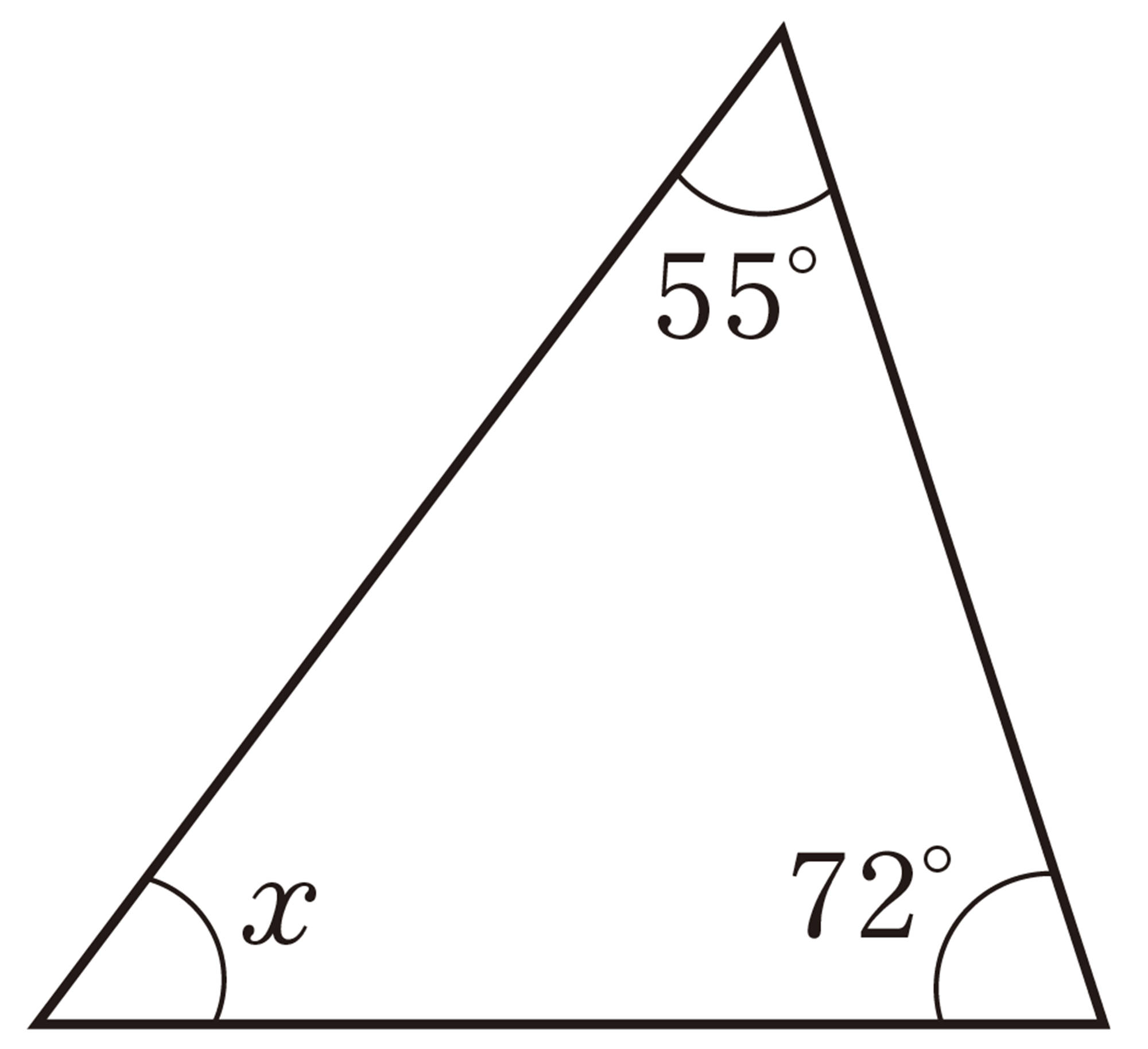
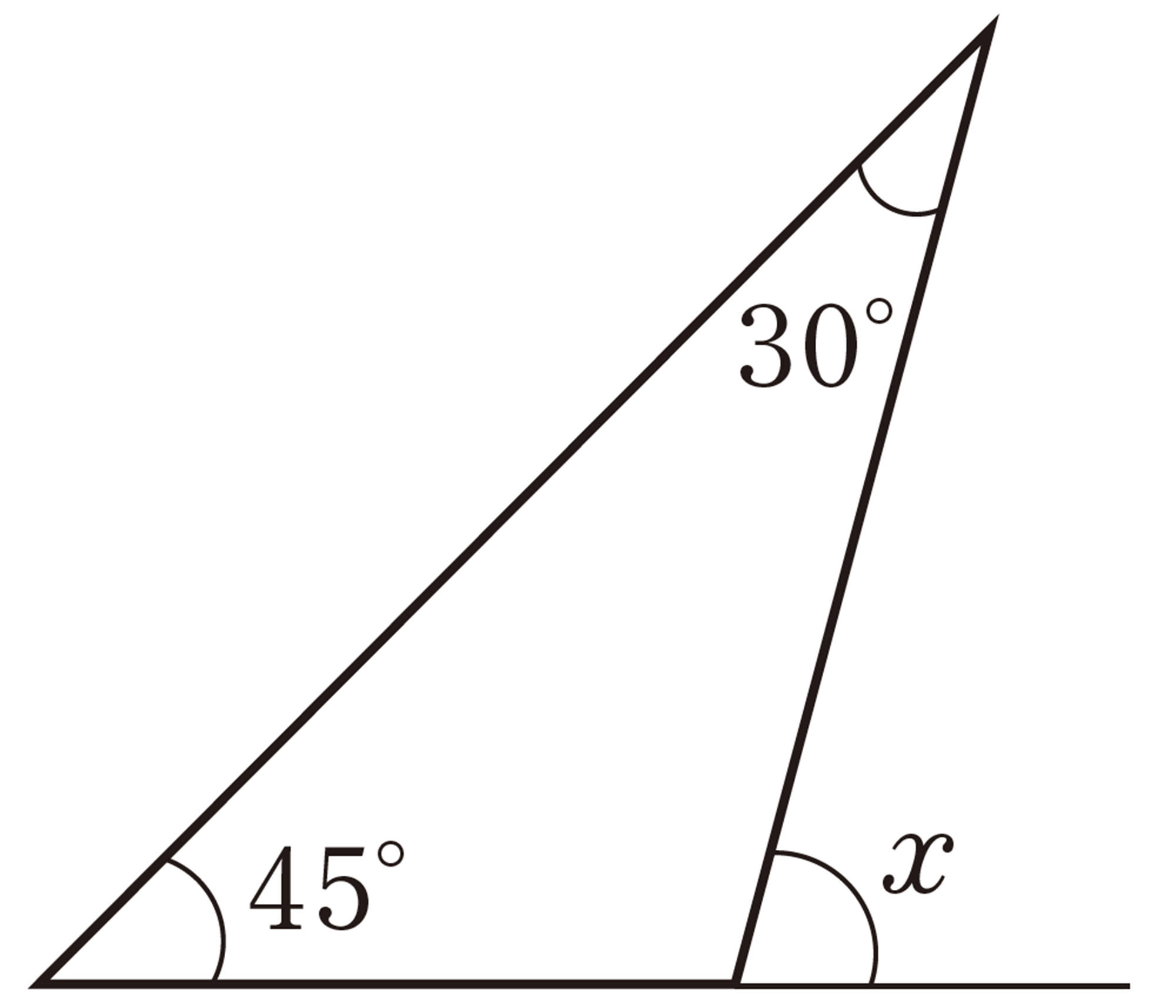
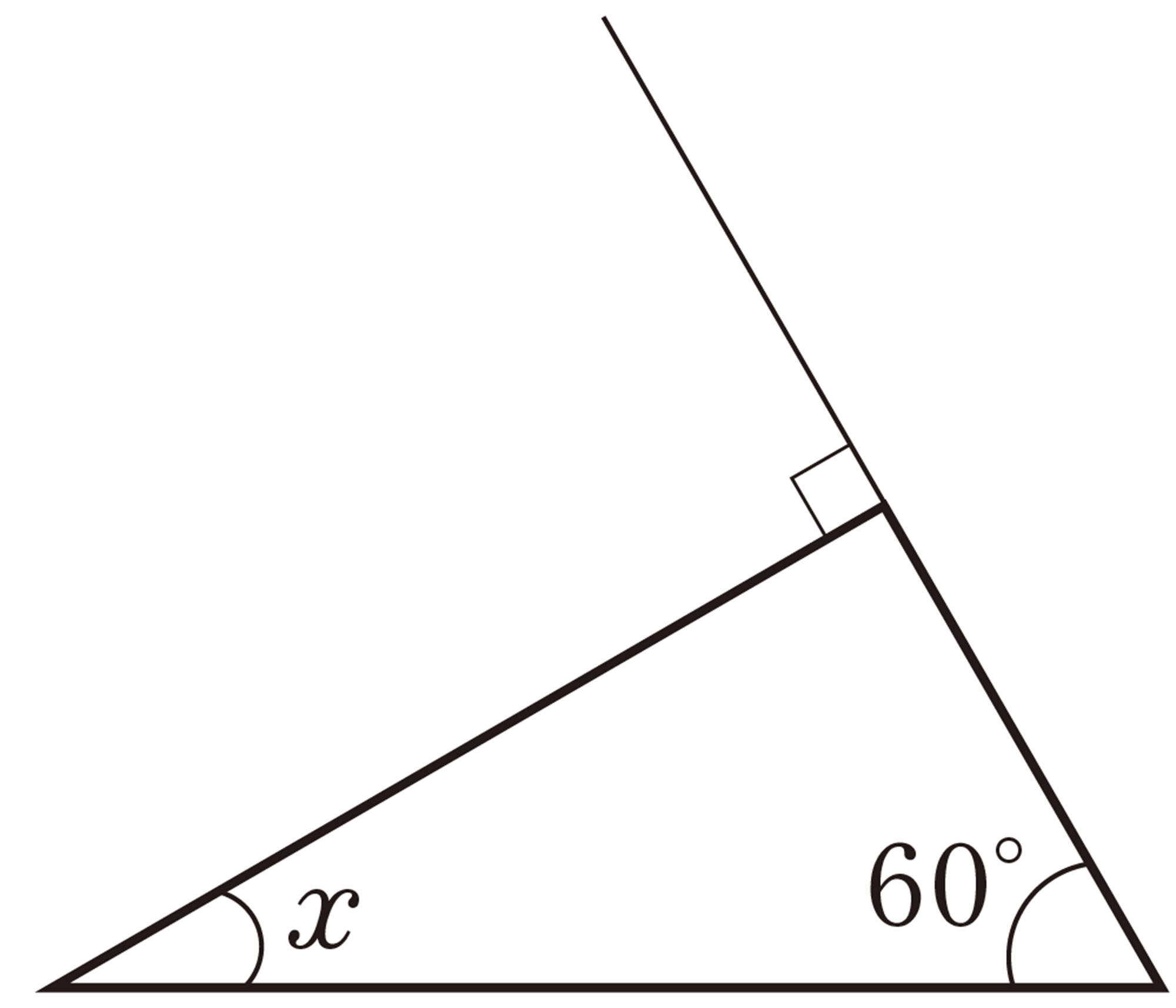
問 4 次の図で,[mathjax]\(\angle x\)の大きさを求めなさい。
問5で調べたことからわかるように,三角形の外角の和は,[mathjax]\( 360^{ \circ }\)である。
どんなことがわかったかな
どんな三角形でも,内角の和は[mathjax]\( 180^{ \circ }\),外角の和は[mathjax]\( 360^{ \circ }\)になることを説明することができます。
次の課題へ!
三角形以外の多角形でも,内角の和や外角の和は一定なのかな?
P.118, 121