[mathjax]\(\begin{eqnarray}
& & \angle a + \angle b + \angle c \\
&=& 180^{\circ}\end{eqnarray}\)
gkt-horizontal-line
<2年p.106>
ふりかえり
【合同】
2つの図形がぴったり重なるとき，2つの図形は合同であるという。
合同な図形をかくときは，辺の長さや角の大きさがすべてわからなくてもかけたね。
【二等辺三角形】
2つの辺の長さが等しい三角形を，二等辺三角形という。
いろいろな図形を観察すると，きまりが見えてきたね。
【正三角形】
3つの辺の長さが等しい三角形を，正三角形という。
図形は，辺の長さや角の大きさに着目すると，分類できたね。
【平行四辺形】
向かい合った2組の辺がそれぞれ平行な四角形を平行四辺形という。
二等辺三角形の条件を変えると，正三角形になることがあったね。
平行四辺形の条件を変えると，ひし形や長方形，正方形になったよ。
gkt-horizontal-line
<2年p.107>
４章 Chapter４ 図形の性質の調べ方
1節 いろいろな角と多角形
2節 図形の合同
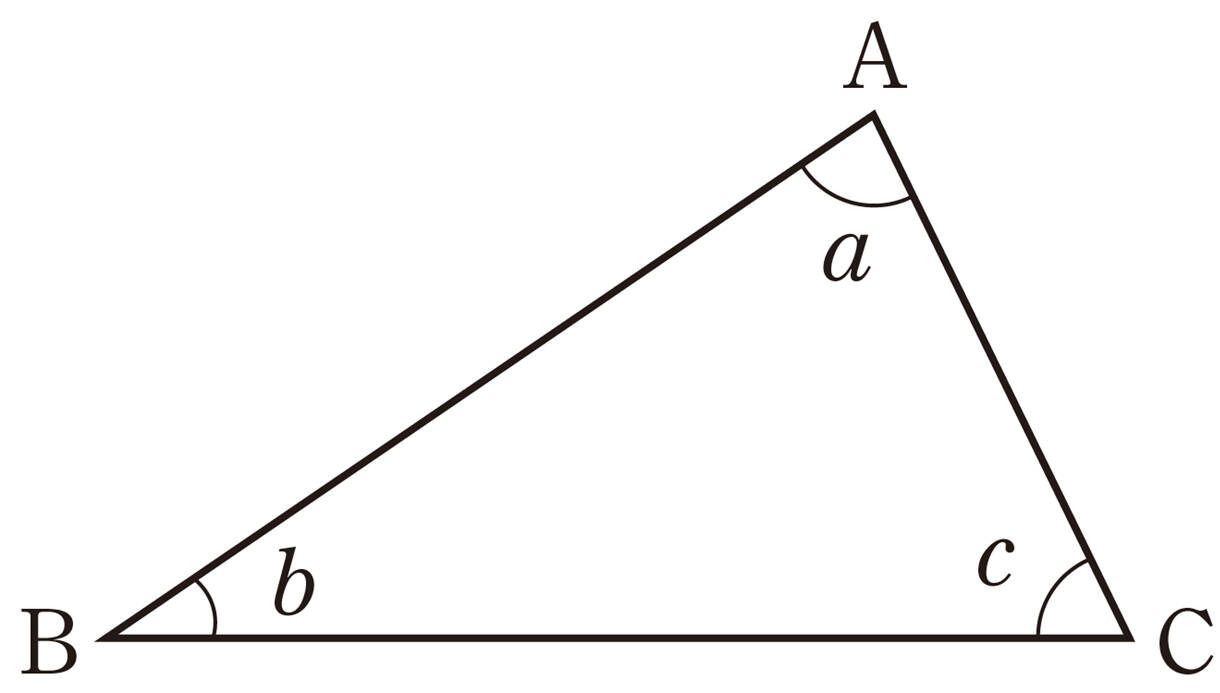
小学校のとき，三角形の3つの角の和が[mathjax]\(180^{\circ}\)になることを学んだよ。
いろいろな方法で，確かめたね。
本当に，どんな三角形でも3つの角の和が[mathjax]\(180^{\circ}\)になるといえるのかな。
いろいろな三角形があるから，1つずつ確かめるわけにはいかないよね。
？ 図形の性質がいつでも成り立つことを説明できるかな？
gkt-horizontal-line
<2年p.108>
1節 いろいろな角と多角形
全部で何度？
【１】 次の図形は，星形五角形と呼ばれています。いろいろな角の大きさを測って，気づいたことを話し合ってみましょう。
大きさが等しい角があるね。
ほかにもわかることはあるかな。
gkt-horizontal-line
<2年p.109>
【２】 左や下の2つの星形五角形の先端部分の5つの角の和を求めましょう。また，その結果から，どんなことが予想できるでしょうか。
【３】 2で予想したことがいつでも正しいといえるかどうか，どのように確かめればよいか話し合ってみましょう。
次の課題へ！
いろいろな角の大きさにはどんな関係があるのかな？
P.110
次の課題へ！
星形五角形の中には，三角形や五角形があるね。それらを使って先端部分の5つの角の和が求められないかな？
P.115
gkt-horizontal-line
<2年p.110>
１ いろいろな角
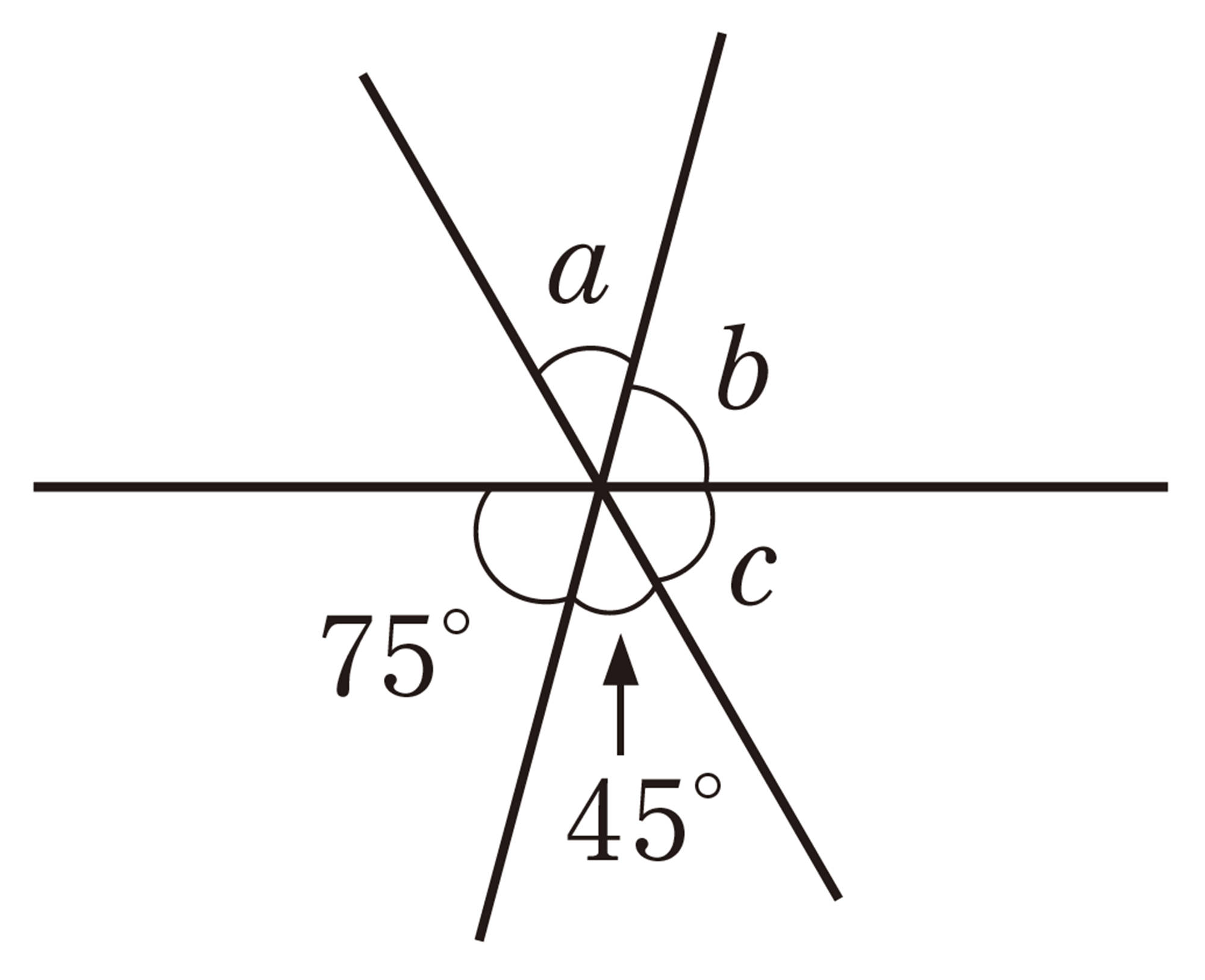
Q Question
右の図で，[mathjax]\(\angle a\)，[mathjax]\(\angle b\)，[mathjax]\(\angle c\)，[mathjax]\(\angle d\)の大きさを測って，気づいたことを話し合ってみましょう。
向かい合う角が同じ大きさになっているみたいだね。
ほかにも同じ大きさになるところはあるのかな。
見方・考え方
図をもとにして，どんな性質があるか見つけられるかな。
目標 ▷ いろいろな角の性質について調べよう。
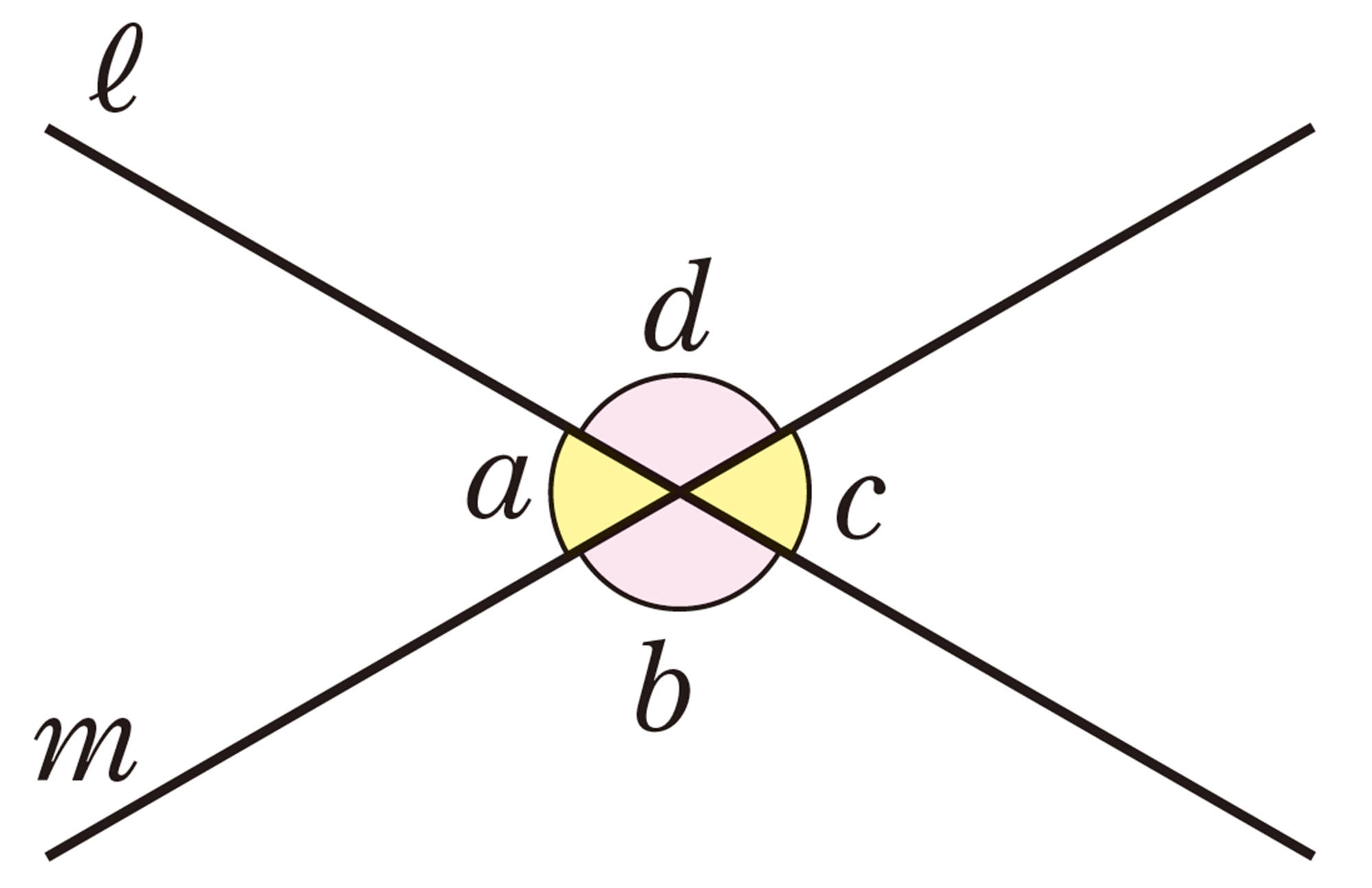
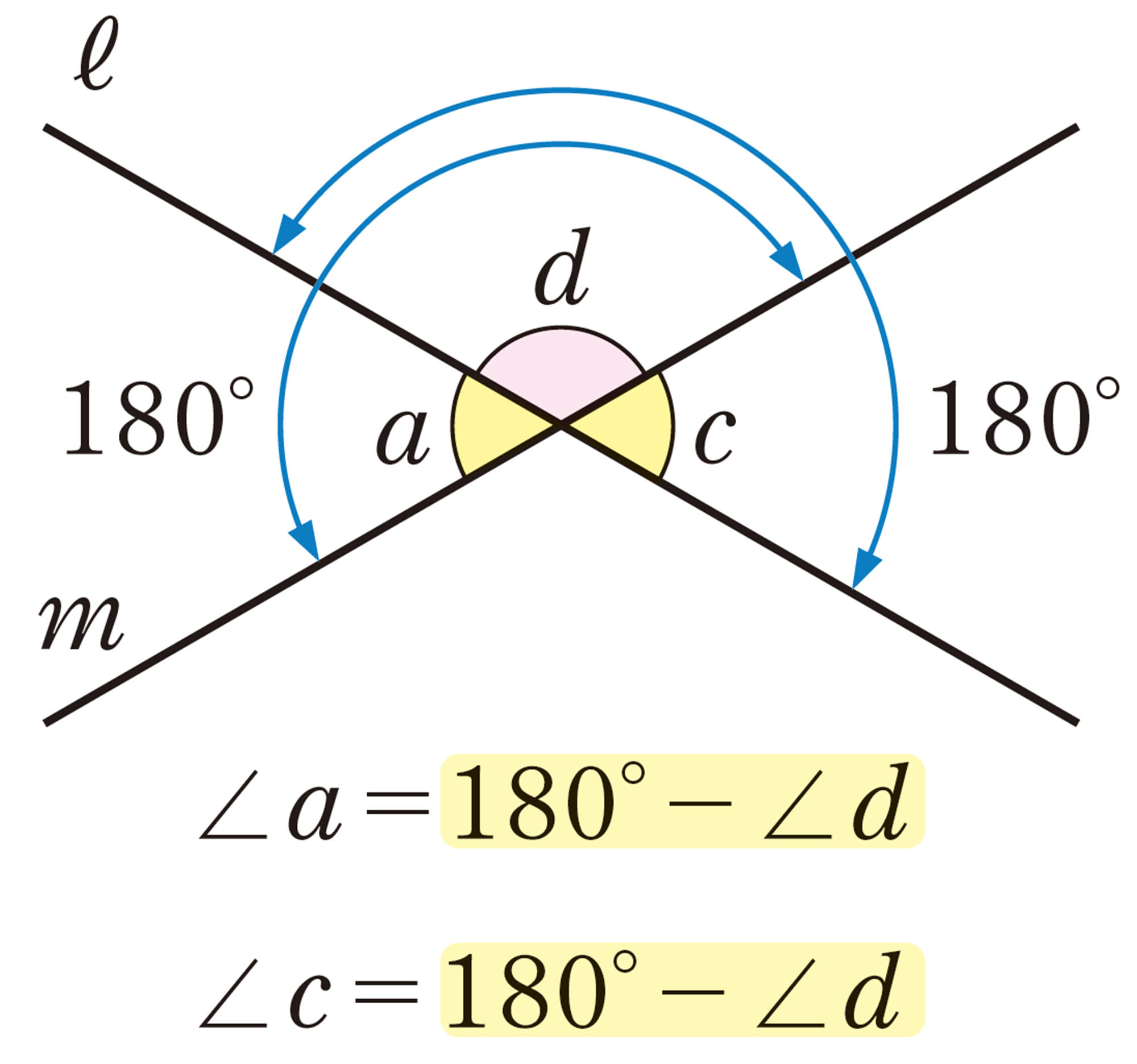
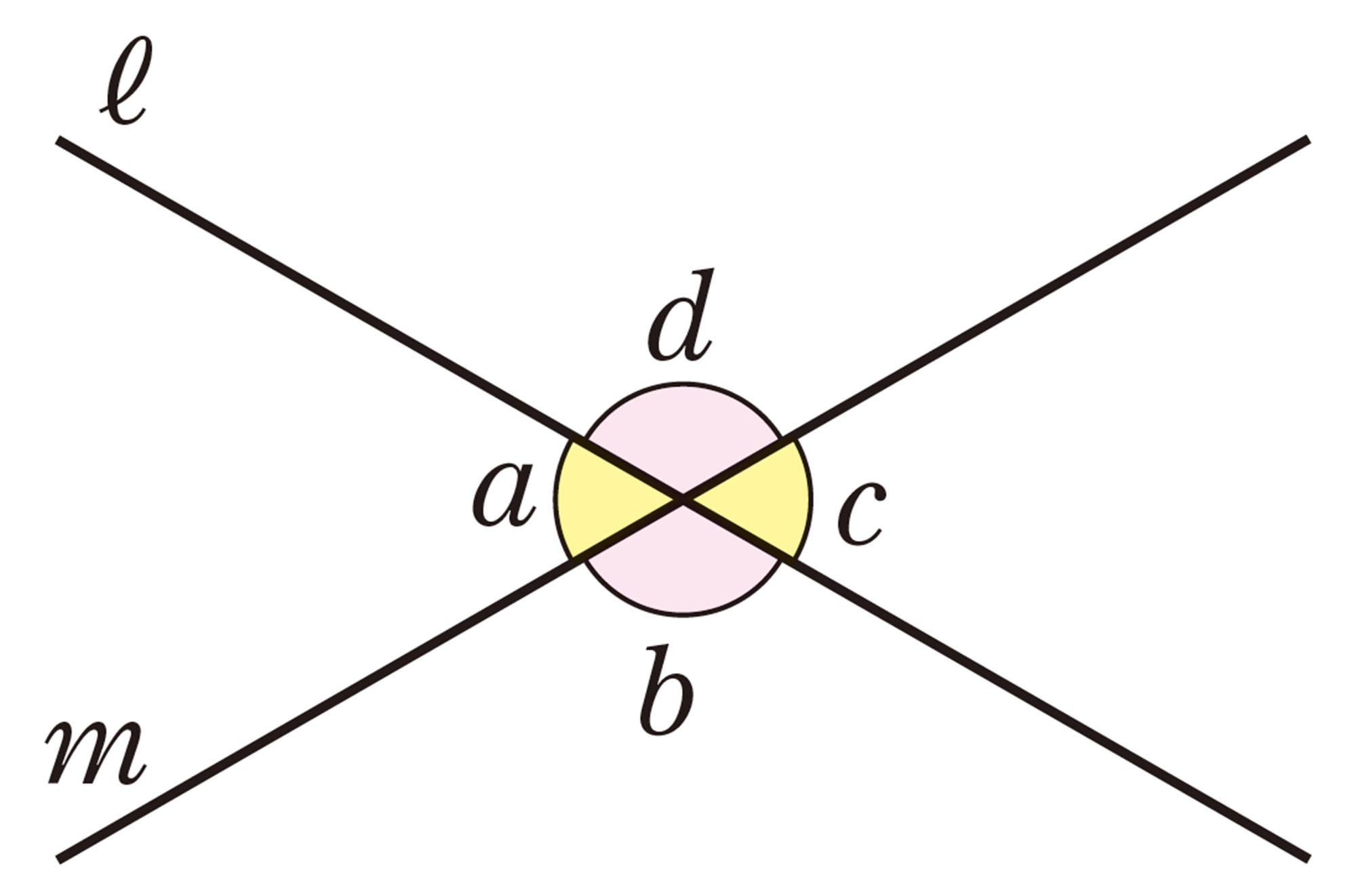
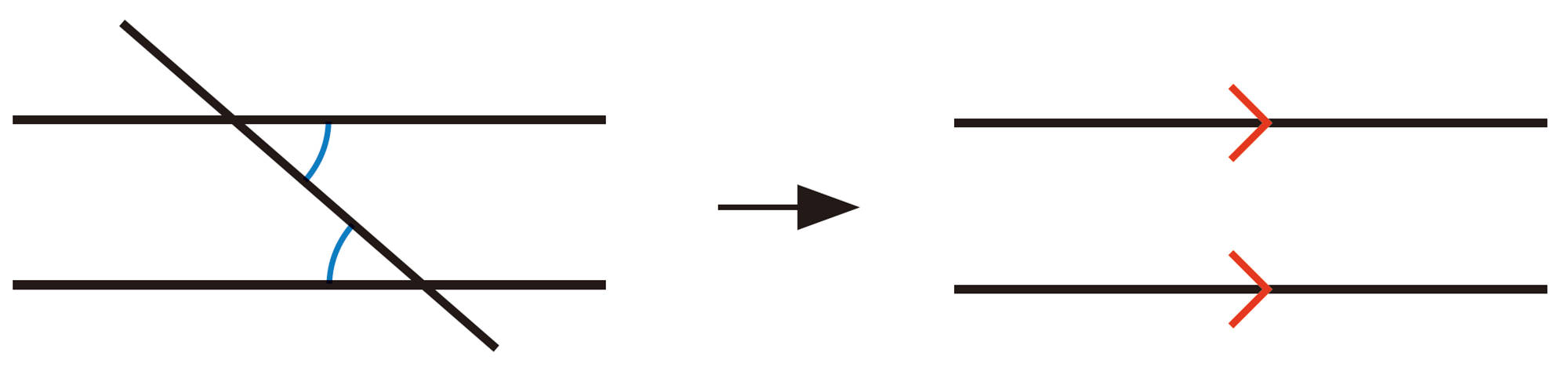
対頂角
右の図のように，2直線[mathjax]\(ℓ\)，[mathjax]\(m\)が交わってできる4つの角のうち，[mathjax]\(\angle a\)と[mathjax]\(\angle c\)，[mathjax]\(\angle b\)と[mathjax]\(\angle d\)のように，向かい合った2つの角を対頂角という。
右の図で，[mathjax]\(\angle d\)が何度であっても，
[mathjax]\(\angle a=180^{ \circ }-\angle d\)
[mathjax]\(\angle c=180^{ \circ }-\angle d\)
と表すことができる。
このことから，[mathjax]\(\angle a=\angle c\)であることがわかる。
問 １ 右の図で，[mathjax]\(\angle b=\angle d\)であることを説明しなさい。
gkt-horizontal-line
<2年p.111>
対頂角の性質
対頂角は等しい。
問 ２ 右の図のように，3直線が1点で交わっています。[mathjax]\(\angle a\)，[mathjax]\(\angle b\)，[mathjax]\(\angle c\)の大きさを求めなさい。
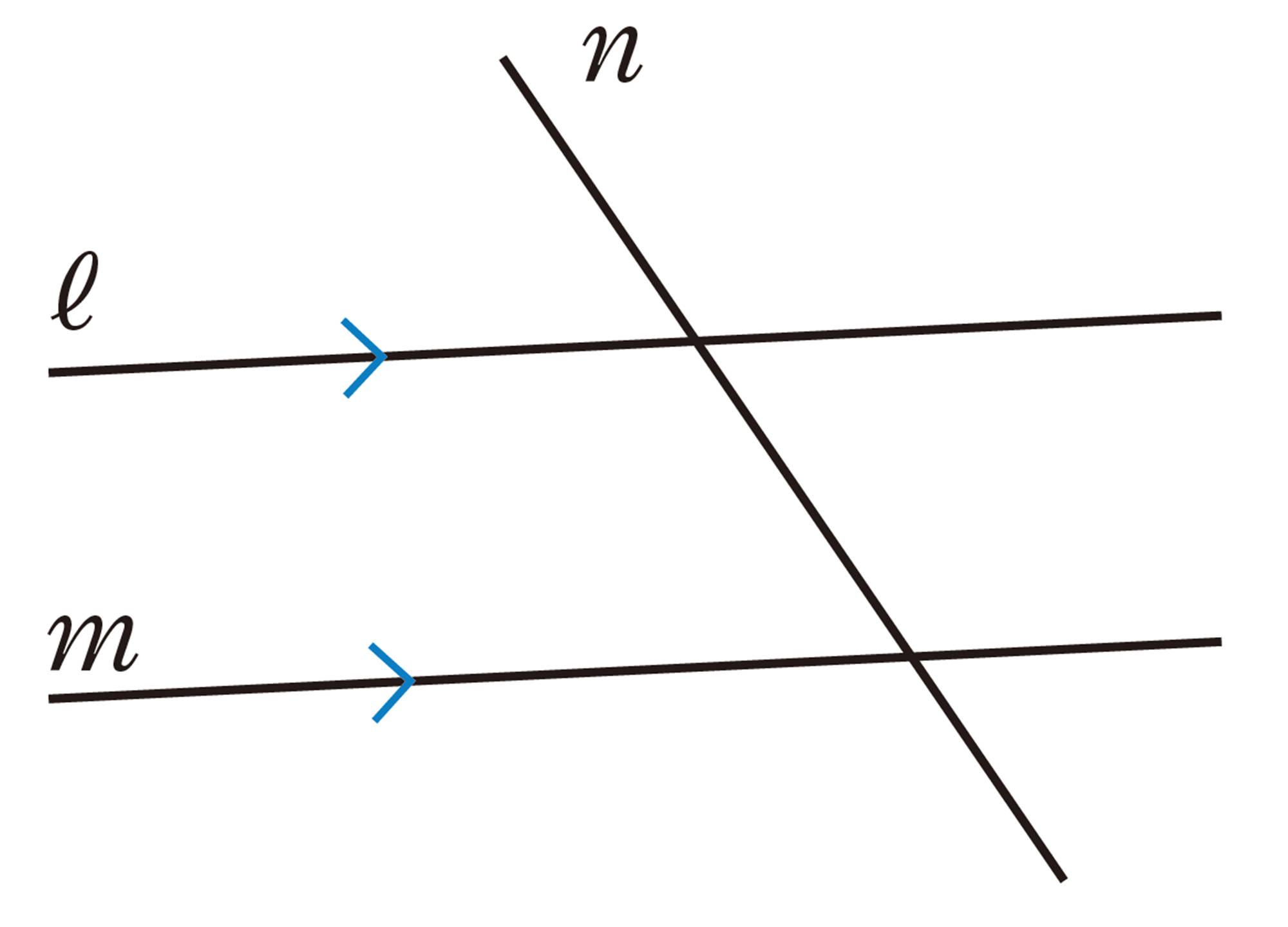
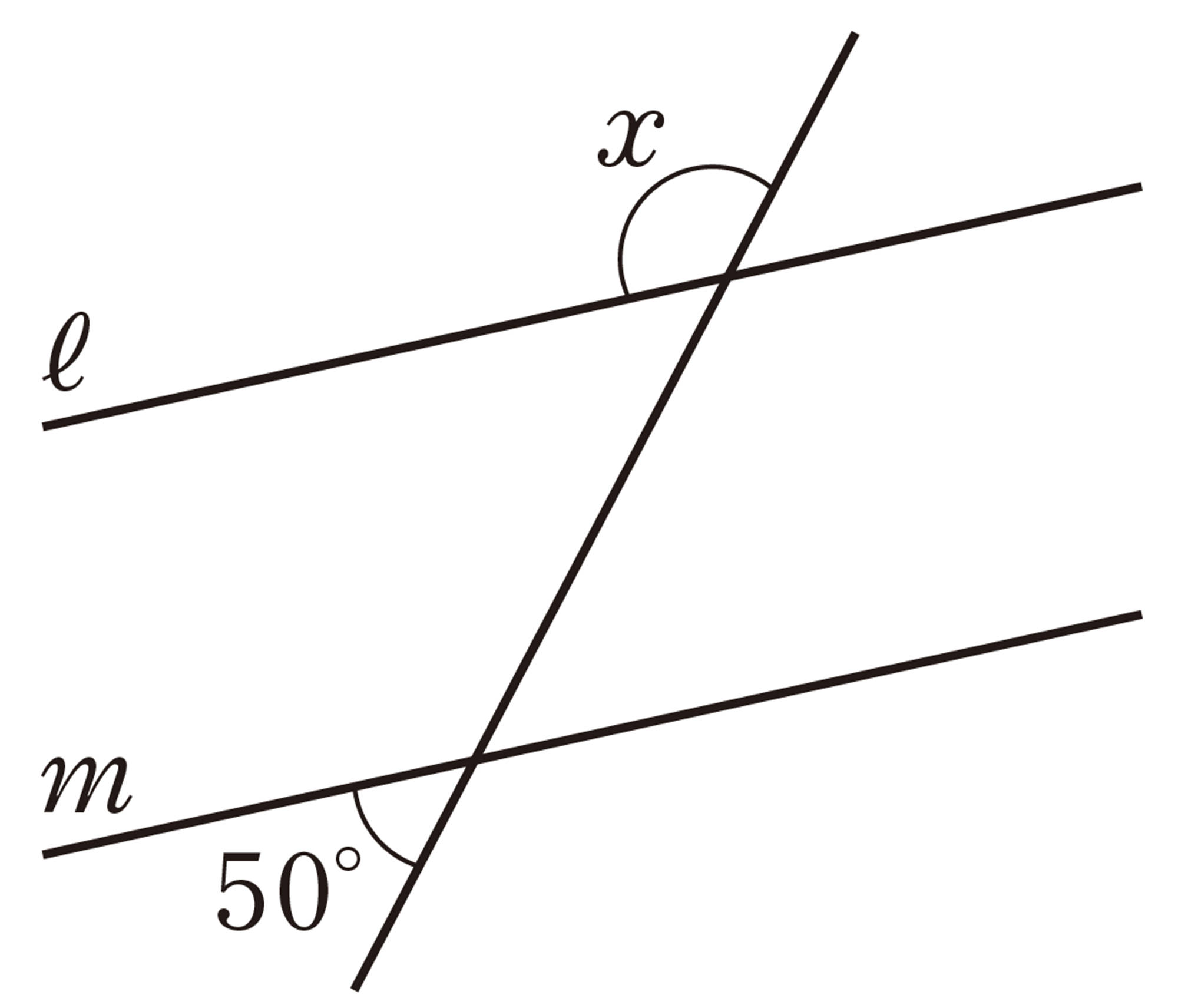
同位角と錯角
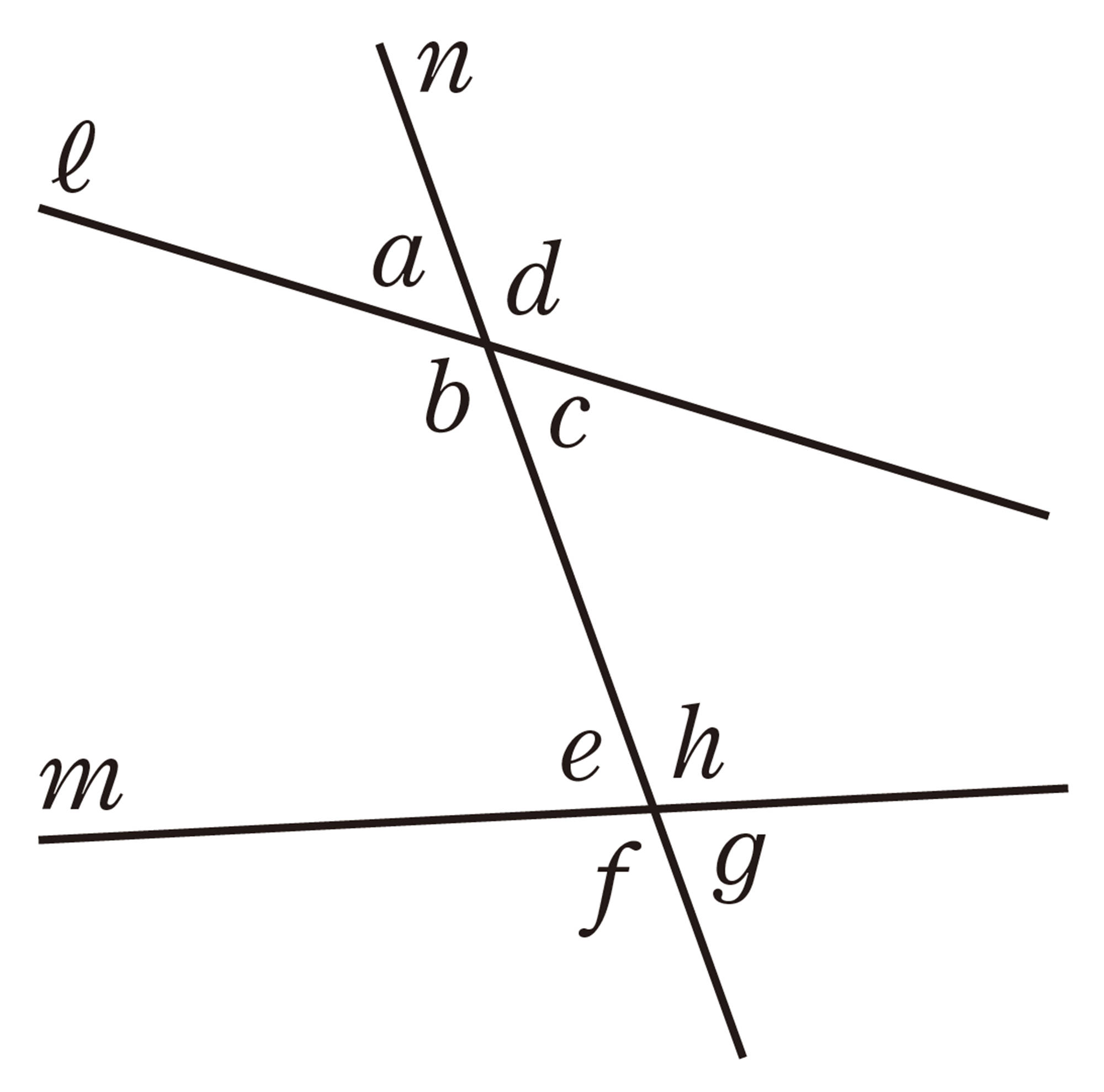
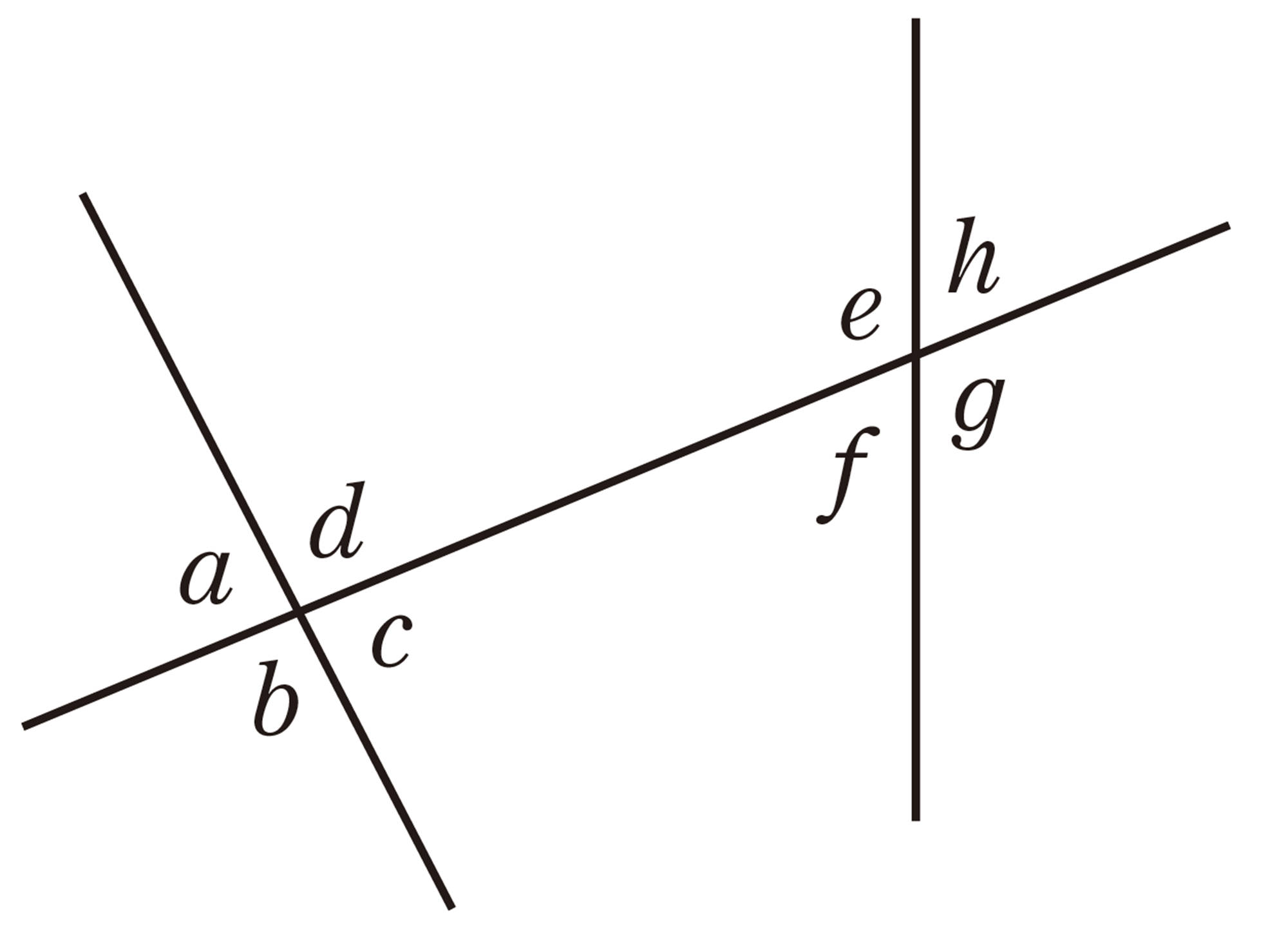
右の図のように，2直線[mathjax]\(ℓ\)，[mathjax]\(m\)に直線[mathjax]\(n\)が交わってできる角のうち，
[mathjax]\(\angle a\)と[mathjax]\(\angle e\)，[mathjax]\(\angle b\)と[mathjax]\(\angle f\)，
[mathjax]\(\angle c\)と[mathjax]\(\angle g\)，[mathjax]\(\angle d\)と[mathjax]\(\angle h\)
のような位置にある2つの角を同位角という。
また，
[mathjax]\(\angle b\)と[mathjax]\(\angle h\)，[mathjax]\(\angle c\)と[mathjax]\(\angle e\)
のような位置にある2つの角を錯角という。
問 ３ 右の図について， 次の問いに答えなさい。
⑴ [mathjax]\(\angle d\)の同位角をいいなさい。
⑵ [mathjax]\(\angle d\)の錯角をいいなさい。
gkt-horizontal-line
用語の由来「錯角」 Tea Break
“錯”の意味は，「まじること，入りまじること」です。英語では，錯角のことを，alternate interior angles(たがいちがいの内側の角)といいます。つまり，錯角とは，2直線に1つの直線が交わるとき， 2つの直線の内側にできる4つの角のうち，斜めに交差している角を意味しています。
gkt-horizontal-line
<2年p.112>
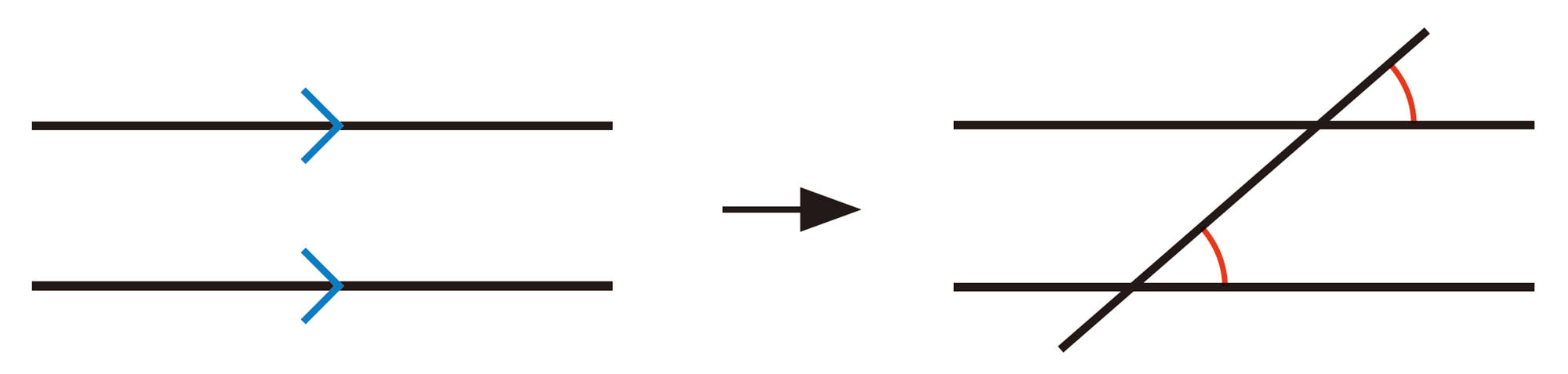
平行線と同位角
Q Question
右の図のように，三角定規を使って平行線を引いてみましょう。なぜこの方法で平行線が引けるのでしょうか。
小学校では，1つの直線に同じ角度で交わっている2つの直線は平行だと学んだね。
同位角が等しいときは，平行といえるのかな。
見方・考え方
根拠を明らかにして，説明できるかな。
直線 [mathjax]\(n\) に対して，同位角が等しくなるように2直線[mathjax]\(ℓ\)，[mathjax]\(m\)を引くと，[mathjax]\(ℓ\)と[mathjax]\(m\)は平行になる。すなわち，右の図で，次のことが゙成り立つ。
[mathjax]\(\angle a=\angle b\)ならば，[mathjax]\(ℓ/\!/m\)
直線 [mathjax]\(n\) に対して，同位角が等しくなるように2直線[mathjax]\(ℓ\)，[mathjax]\(m\)を引くと，[mathjax]\(ℓ\)と[mathjax]\(m\)は平行になる。すなわち，右の図で，次のことが゙成り立つ。
[mathjax]\(\angle a=\angle b\)ならば，[mathjax]\(ℓ/\!/m\)
問 ４ 右の図のように，平行な2直線[mathjax]\(ℓ\)，[mathjax]\(m\)に直線[mathjax]\(n\)が交わっているとき，同位角は等しくなるか調べなさい。
平行な2直線[mathjax]\(ℓ\)，[mathjax]\(m\)に交わる直線[mathjax]\(n\)を引くと，同位角は等しくなる。すなわち，右の図で，次のことが゙成り立つ。
[mathjax]\(ℓ/\!/m\)ならば，[mathjax]\(\angle a=\angle b\)
問 ５ 右の図で，平行線はどれで゙すか。平行の記号を使って表しなさい。また，[mathjax]\(\angle x\)，[mathjax]\(\angle y\)，[mathjax]\(\angle z\)のうち，等しい角はどれとどれですか。
gkt-horizontal-line
<2年p.113>
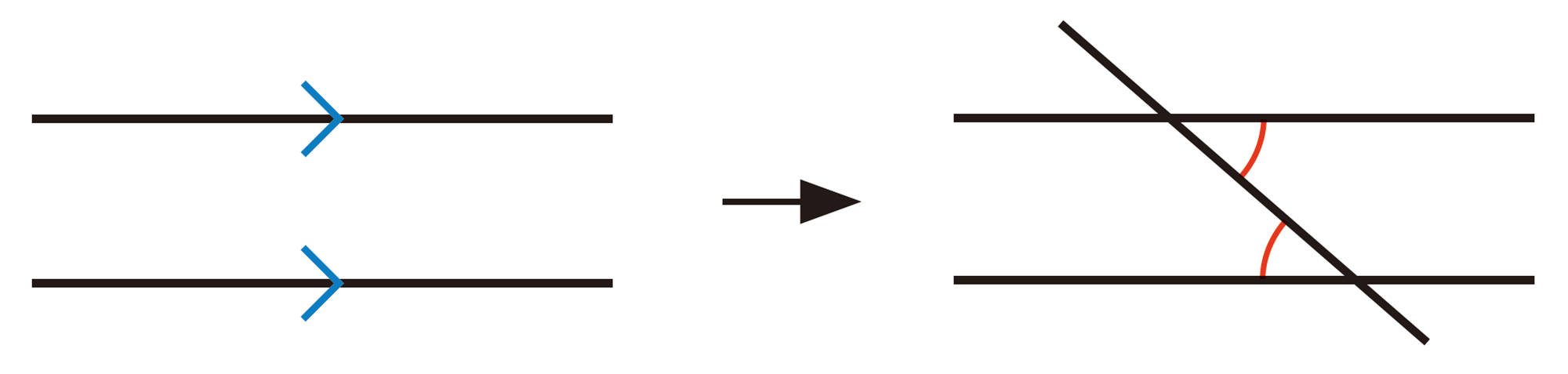
平行線と錯角
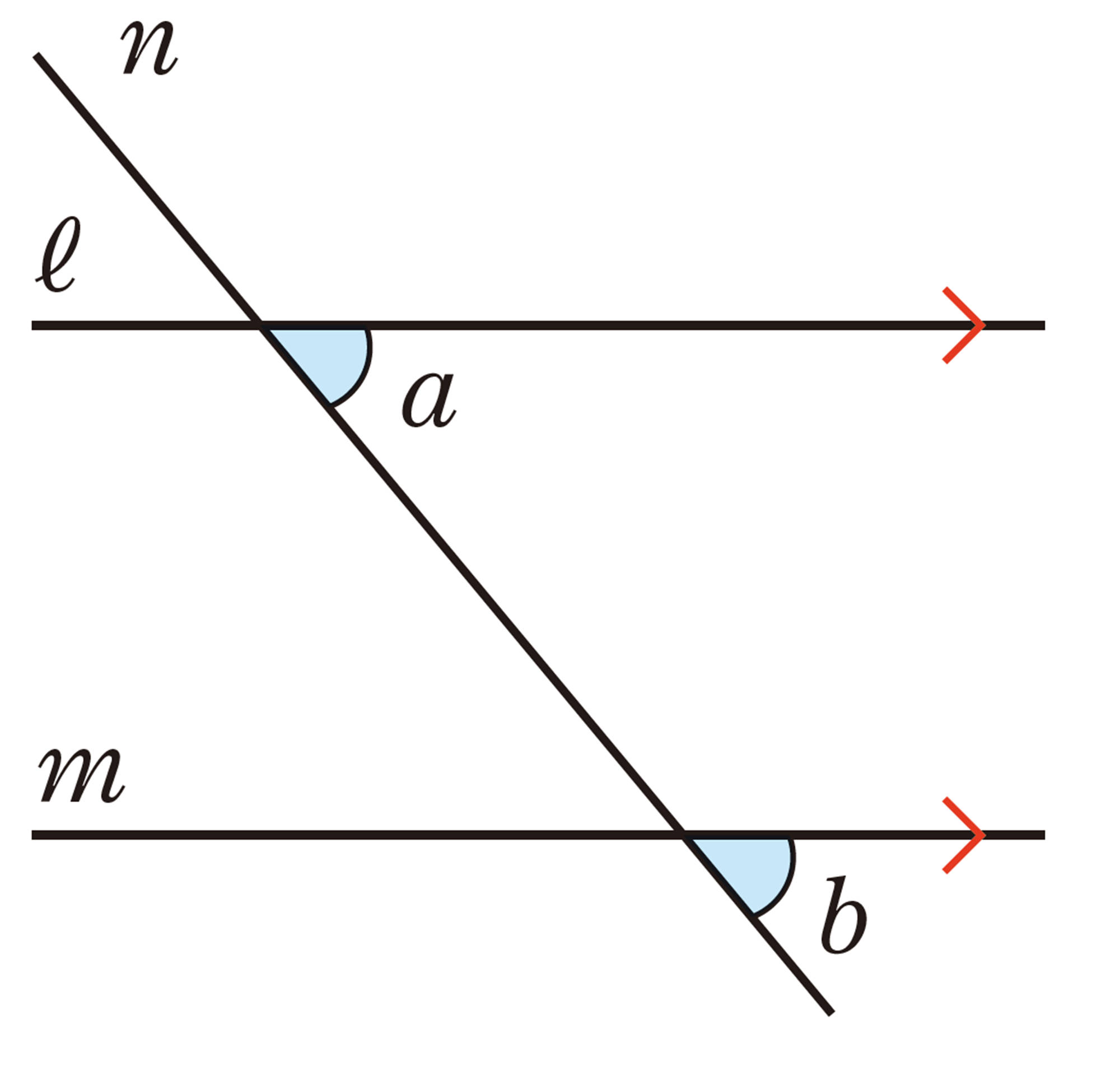
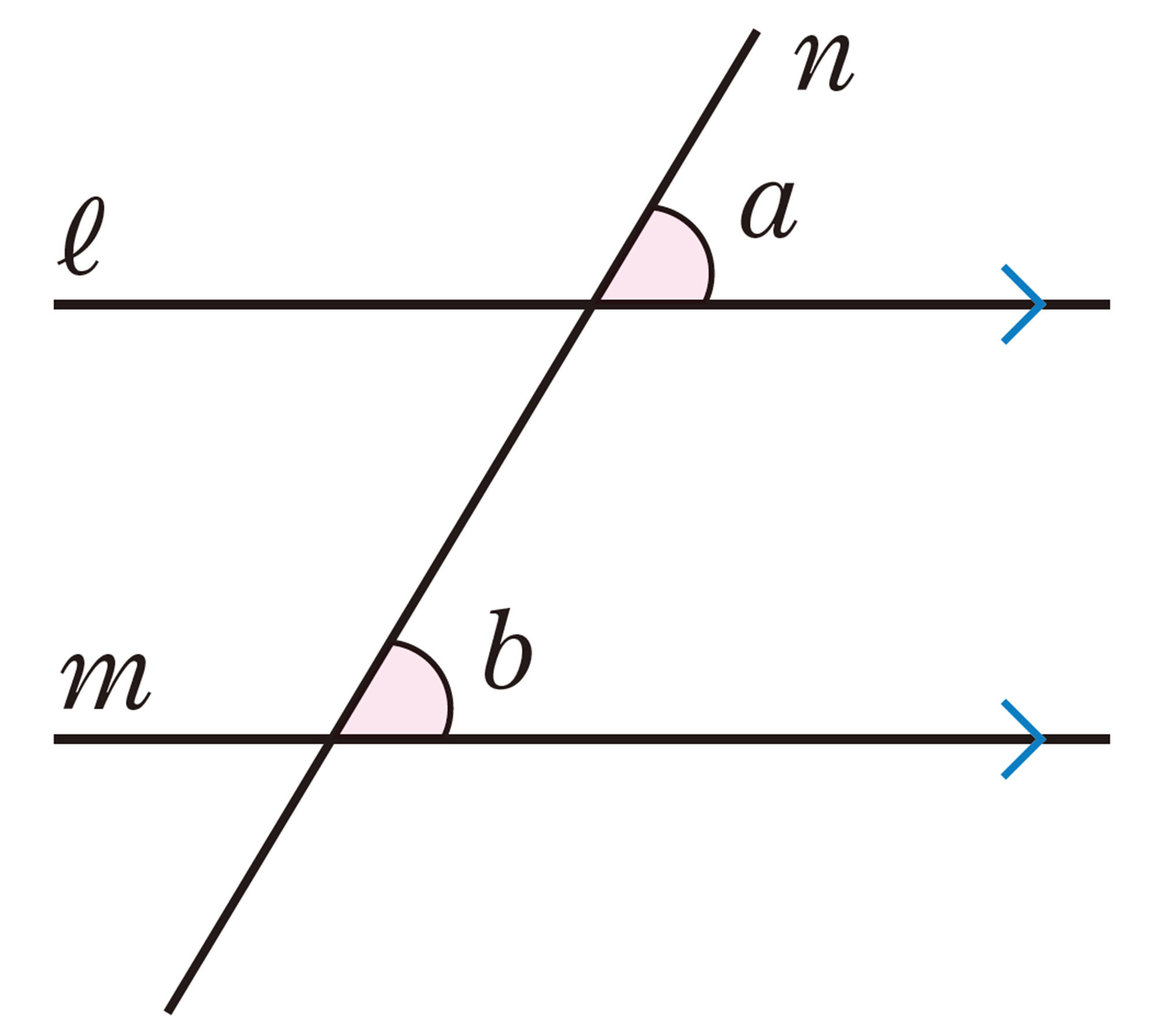
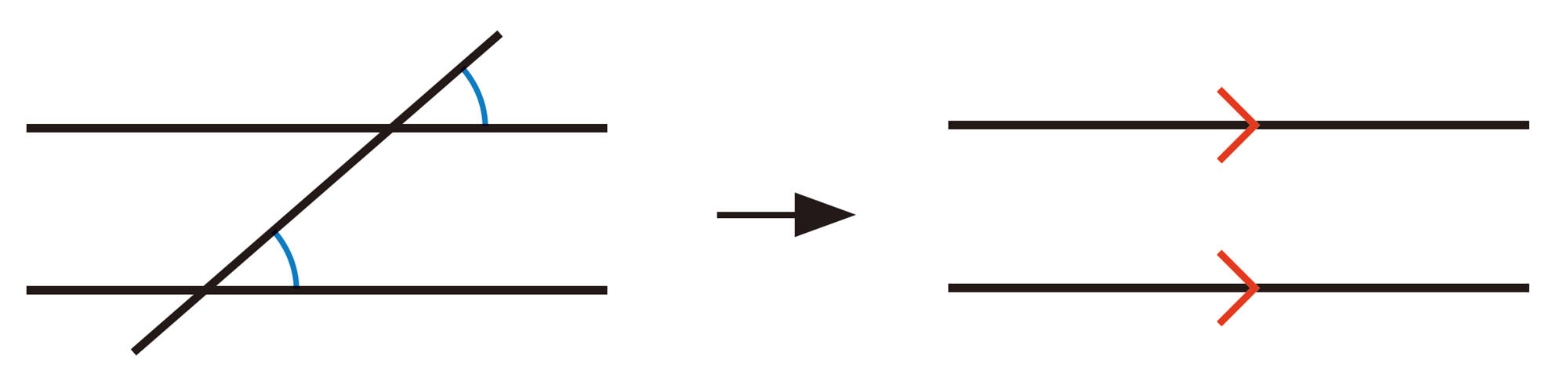
例 １ 右の図で，[mathjax]\(\angle a=\angle b\) のとき，[mathjax]\(ℓ/\!/m\) であることを，説明しなさい。
解答
[mathjax] \(
\begin{align}
&\quad & \angle a &=\angle b &\cdots \cdots ①\\
&\mathsf{対頂角は等しいから，}& \angle b &=\angle c &\cdots \cdots ②\\
&\mathsf{①，②より，}& \angle a&=\angle c \\
&\mathsf{同位角が等しいから，}& ℓ &/\!/ m
\end{align}\)
2直線[mathjax]\(ℓ\)，[mathjax]\(m\) に直線[mathjax]\(n\) が交わるとき，錯角が等しければ，[mathjax]\(ℓ\) と[mathjax]\(m\) は平行になる。すなわち，例1の図で，次のことが゙成り立つ。
[mathjax]\(\angle a=\angle b\) ならば，[mathjax]\(ℓ/\!/m\)
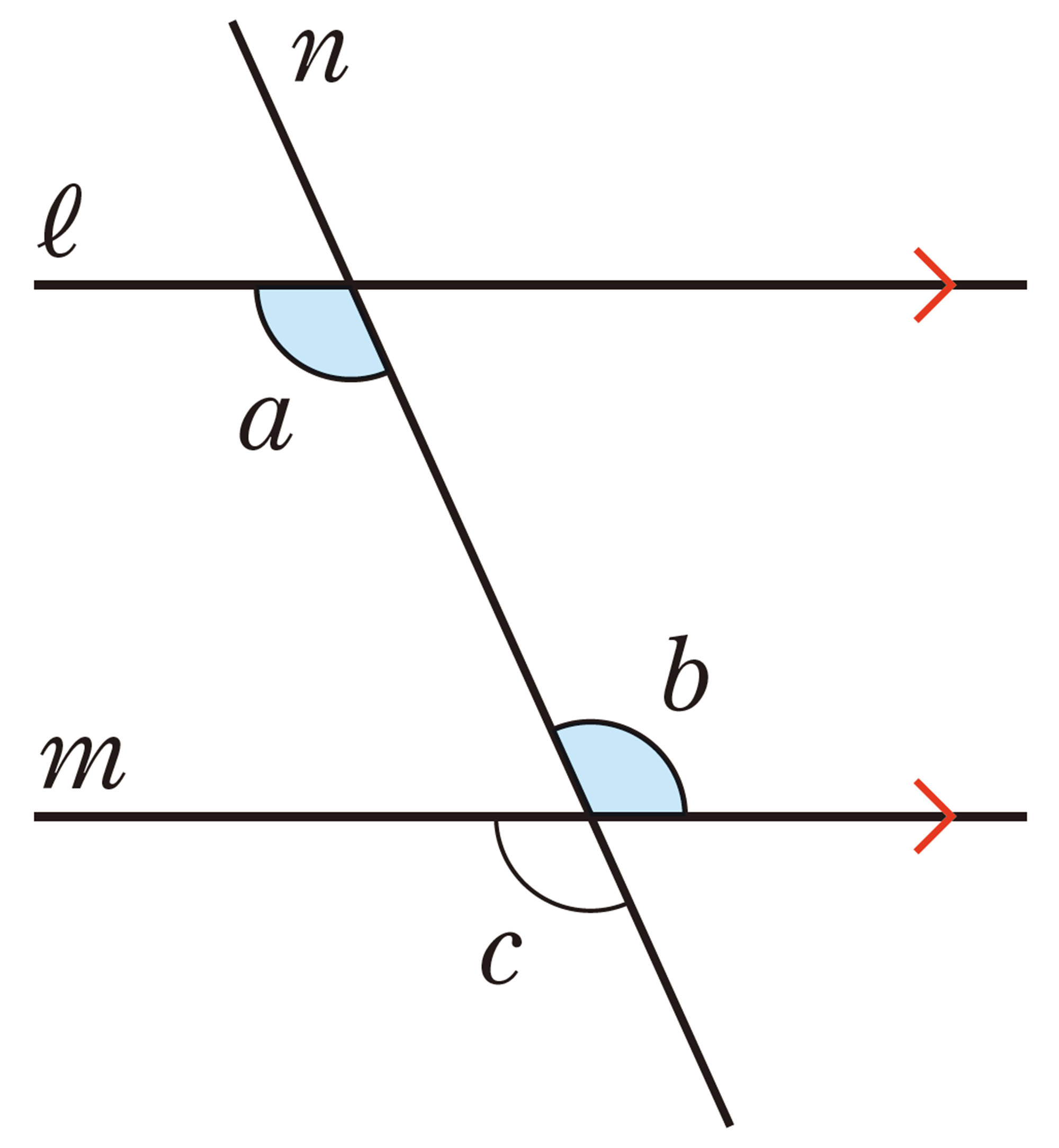
問 ６ 右の図で，[mathjax]\(ℓ/\!/m\) のとき，[mathjax]\(\angle a=\angle b\) となることを，次のように説明しました。[mathjax]\(\boxed{\phantom{00}}\) にあてはまる角を書き入れなさい。
[mathjax] \(
\begin{align}
&\mathsf{平行線の同位角は等しいから，}& \angle a &=\boxed{\phantom{00}} &\cdots \cdots ①\\
&\mathsf{対頂角は等しいから，}& \boxed{\phantom{00}} &=\angle b &\cdots \cdots ②\\
&\mathsf{①，②より，}& \boxed{\phantom{00}} &=\boxed{\phantom{00}} \end{align}\)
平行な2直線[mathjax]\(ℓ\)，[mathjax]\(m\) に交わる直線[mathjax]\(n\) を引くと，錯角は等しくなる。すなわち，問6の図で，次のことが成り立つ。
[mathjax]\(ℓ/\!/m\)ならば，[mathjax]\(\angle a=\angle b\)
問 ７ 右の図で，[mathjax]\(ℓ/\!/m\) のとき，[mathjax]\(\angle x\)，[mathjax]\(\angle y\) の大きさを求めなさい。
gkt-horizontal-line
<2年p.114>
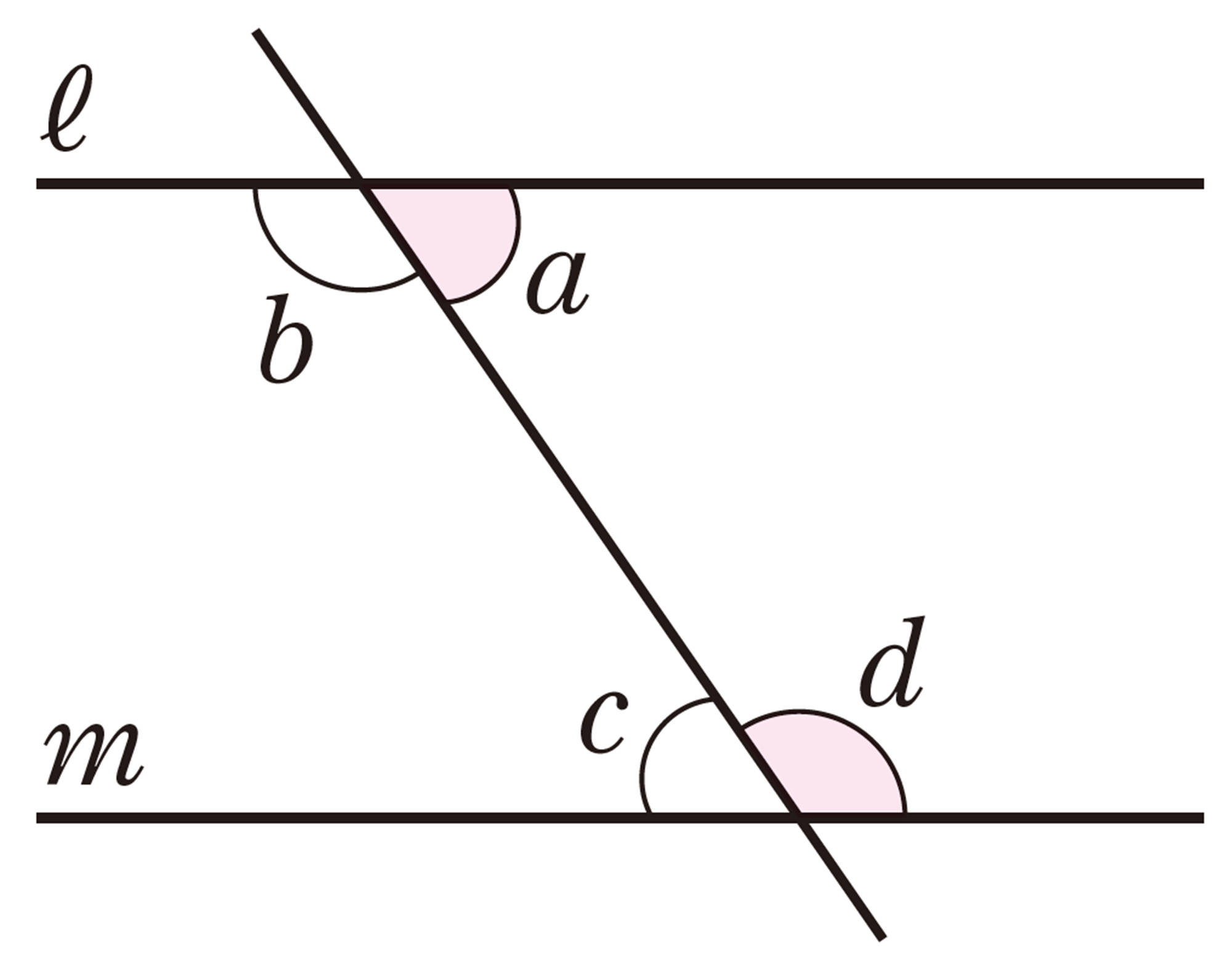
これまで調べたことは，次のようにまとめることができる。
平行線の性質
2直線に1つの直線が交わるとき，次のことが成り立つ。
① 2直線が平行ならば，同位角は等しい。
② 2直線が平行ならば，錯角は等しい。
平行線になるための条件
2直線に1つの直線が交わるとき，次のことが成り立つ。
① 同位角が等しいならば，2直線は平行である。
② 錯角が等しいならば，2直線は平行である。
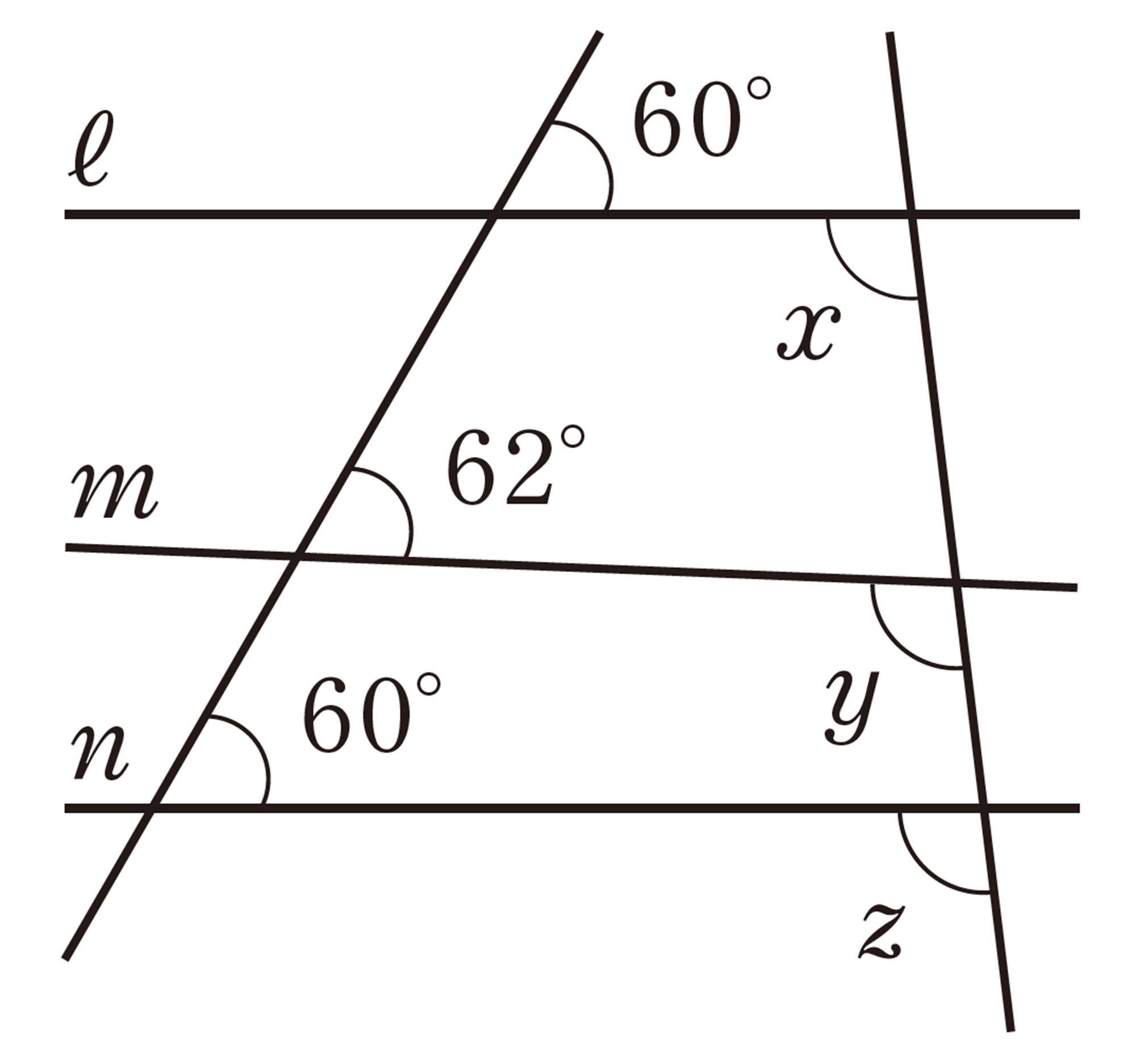
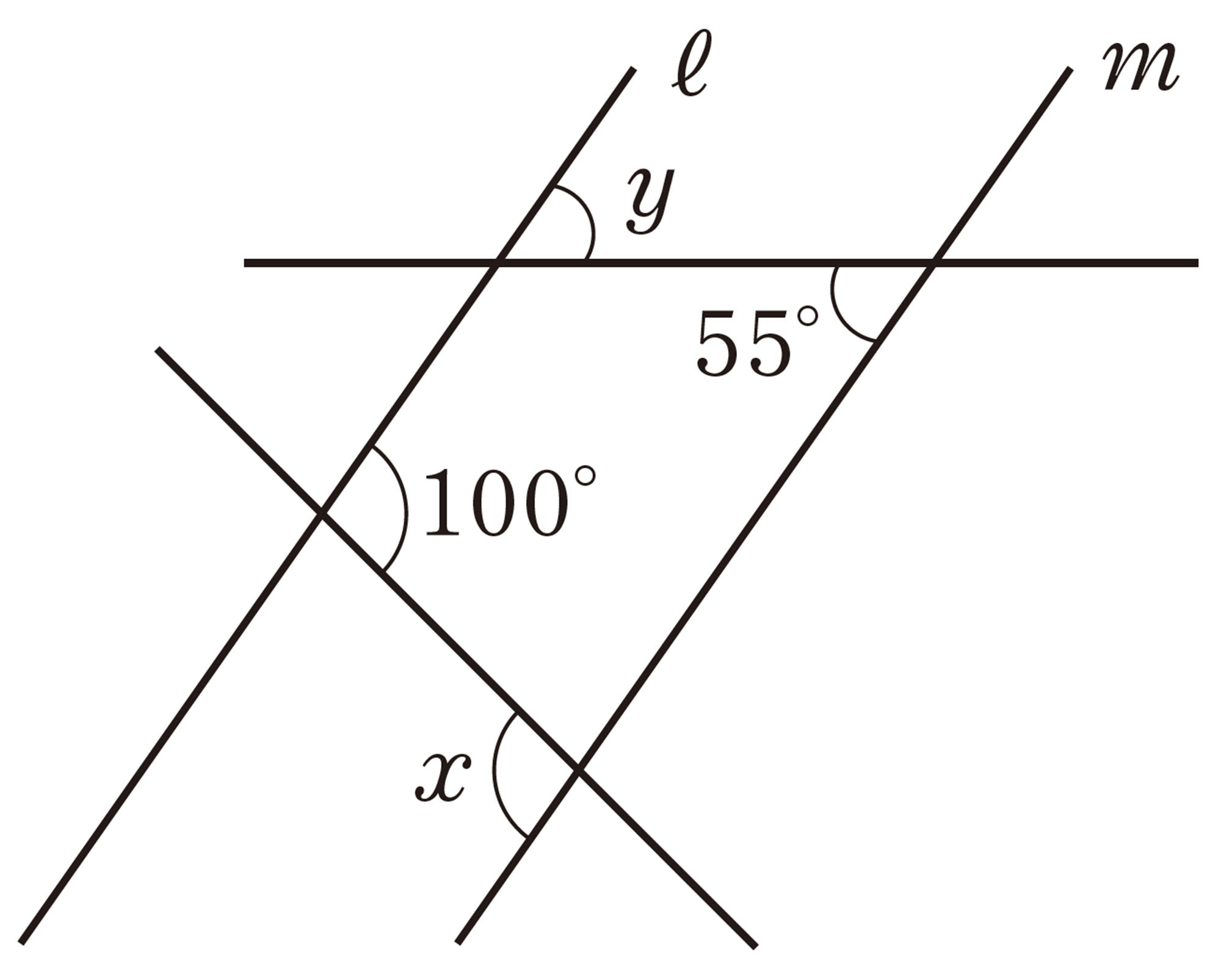
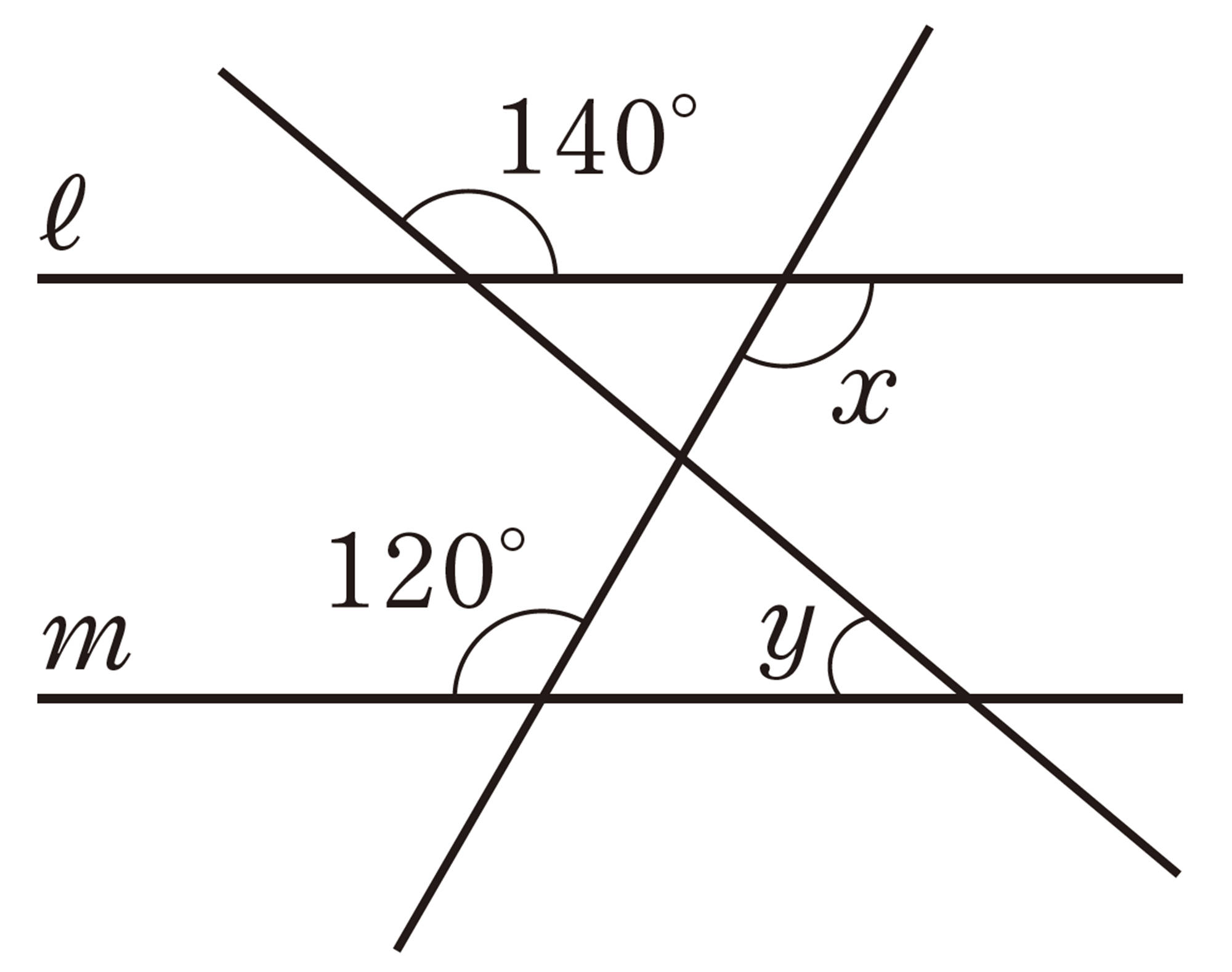
問 ８ 次の図で，[mathjax]\(ℓ/\!/m\) のとき，[mathjax]\(\angle x\)，[mathjax]\(\angle y\) の大きさを求めなさい。
⑴
⑵
問 ９ 右の図で，[mathjax]\(\angle a+\angle d=180^{ \circ }\) のとき，[mathjax]\(ℓ/\!/m\) となる理由を説明しなさい。
どんなことがわかったかな
対頂角が等しいことや，同位角，錯角と平行線の関係について説明することができます。
