<2年p.102>
３章のまとめの問題 解答 P.248〜249 基本
１ 次の式で表される関数のうち，yがxの1次関数であるものはどれですか。
㋐ [mathjax]\( y=15-2x \)
㋑ [mathjax]\( y=5x \)
㋒ [mathjax]\( y= \dfrac{12}{x} \)
㋓ [mathjax]\( y= \dfrac{3}{4}x-1 \)
２ 1次関数 [mathjax]\( y= \dfrac{2}{3}x+1 \) について，次の問いに答えなさい。
⑴ 変化の割合をいいなさい。
⑵ xの増加量が9のときのyの増加量を求めなさい。
⑶ xの変域が [mathjax]\( -6 \leqq x \lt 3 \) のときのyの変域を求めなさい。
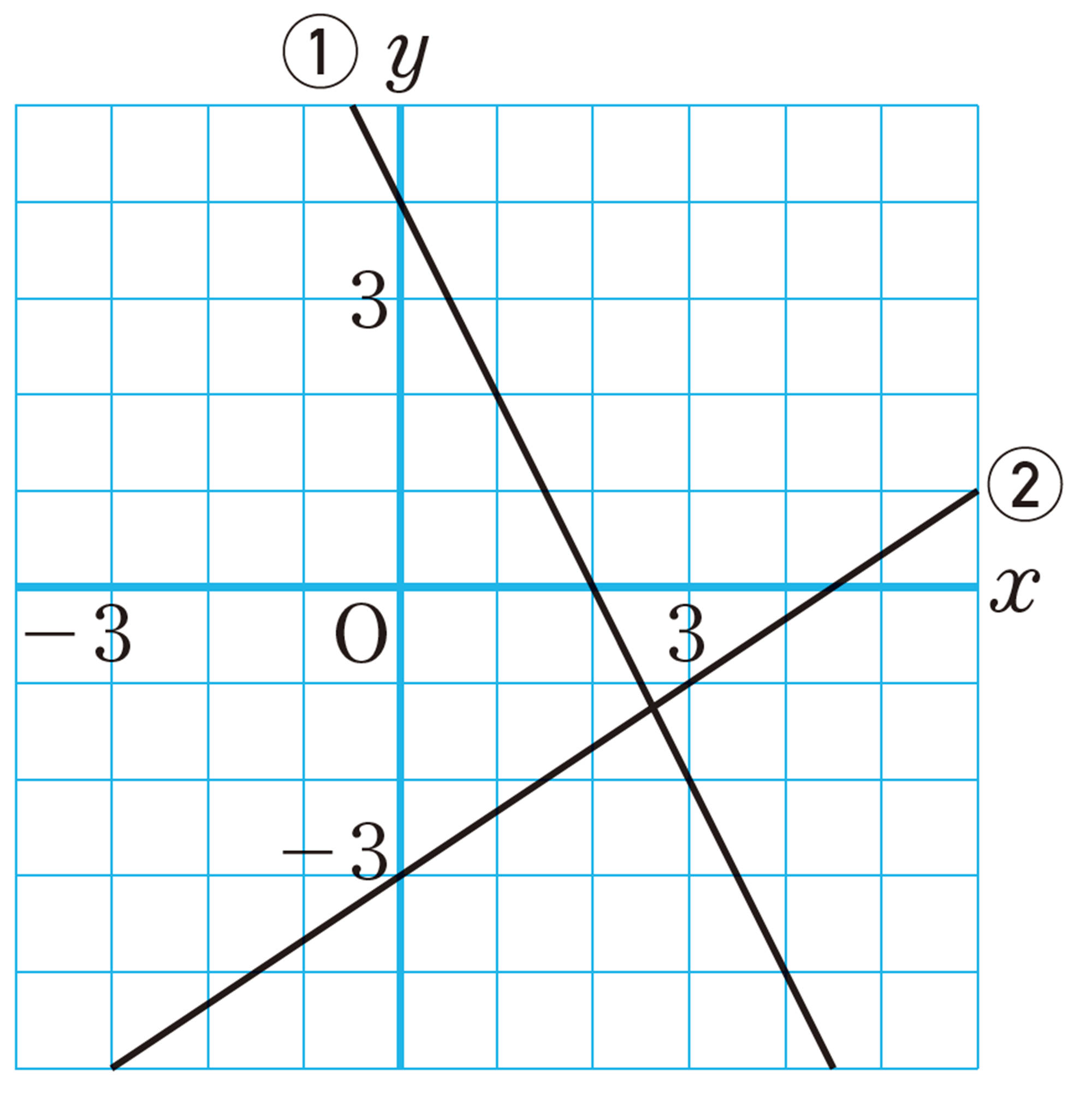
３ 次の1次関数や直線の式を求めなさい。
⑴ [mathjax]\( x=0 \) のとき [mathjax]\( y=-3 \) で，変化の割合が4である1次関数
⑵ 点 [mathjax]\( (1,7) \) を通り，直線 [mathjax]\( y=2x+3 \) に平行な直線
⑶ 2点 [mathjax]\( (3,2) \) ，[mathjax]\( (-1,4) \) を通る直線
４
左の図について，次の問いに答えなさい。
⑴ 直線①，②の式を求めなさい。
⑵ 直線①，②の交点の座標を求めなさい。
⑶ 方程式 [mathjax]\( 3x-2y=-2 \) のグラフを，左の図にかき入れなさい。
５ ろうそくに火をつけ，ろうそくの長さの変化を調べたところ，火をつけてから4分後には10cm，10分後には7cmになりました。ろうそくは一定の割合で短くなるとして，次の問いに答えなさい。
⑴ 火をつける前のろうそくの長さを求めなさい。
⑵ ろうそくが燃えつきるのは，火をつけてから何分後ですか。
<2年p.103>
応用
１ 右の図のように，2点 A[mathjax]\((-8,10)\) ，B[mathjax]\((4,1)\) がある。このとき，次の問いに答えなさい。ただし，座標の1目盛りは1cmとする。
⑴ [mathjax]\(\triangle OAB \) の面積を求めなさい。
⑵ 点Bを通り，[mathjax]\(\triangle OAB \) の面積を2等分する直線の式を求めなさい。
⑶ ABを延長して[mathjax]\( x \) 軸と交わった点をCとする。このとき，[mathjax]\(\triangle OBC \) をOCを軸として1回転してできる立体の体積を求めなさい。
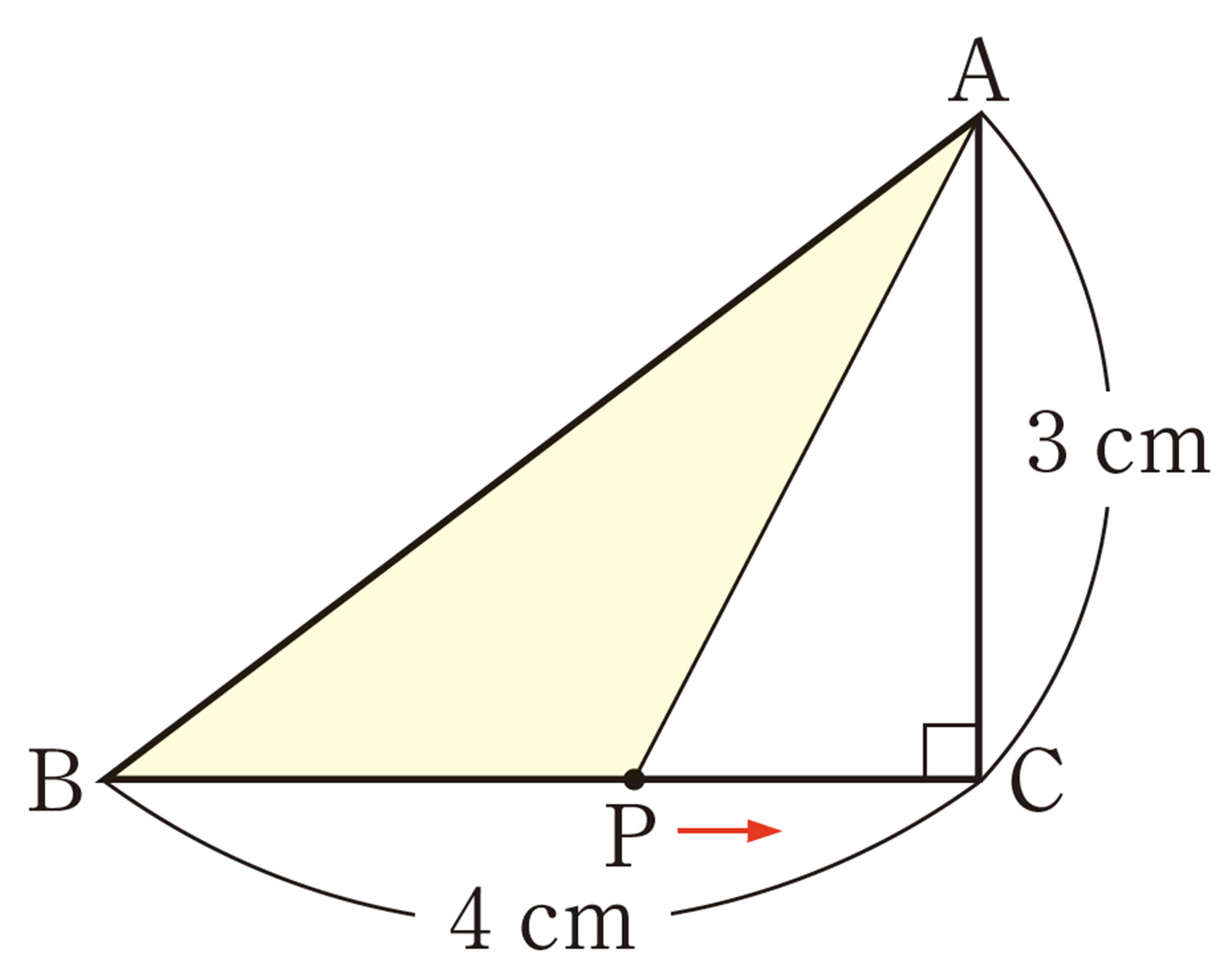
２ 右の図の[mathjax]\(\triangle ABC \) は，[mathjax]\(\angle C = 90^{\circ }\) の直角三角形です。点PはBを出発して，辺上をCを通ってAまで動きます。
点PがBから [mathjax]\( x \) cm動いたときの[mathjax]\(\triangle ABP \) の面積を [mathjax]\( y \) cm²とするとき，次の問いに答えなさい。
⑴ [mathjax]\( y \) を[mathjax]\( x \) の式で表しなさい。ただし，[mathjax]\( x \) の変域も示しなさい。
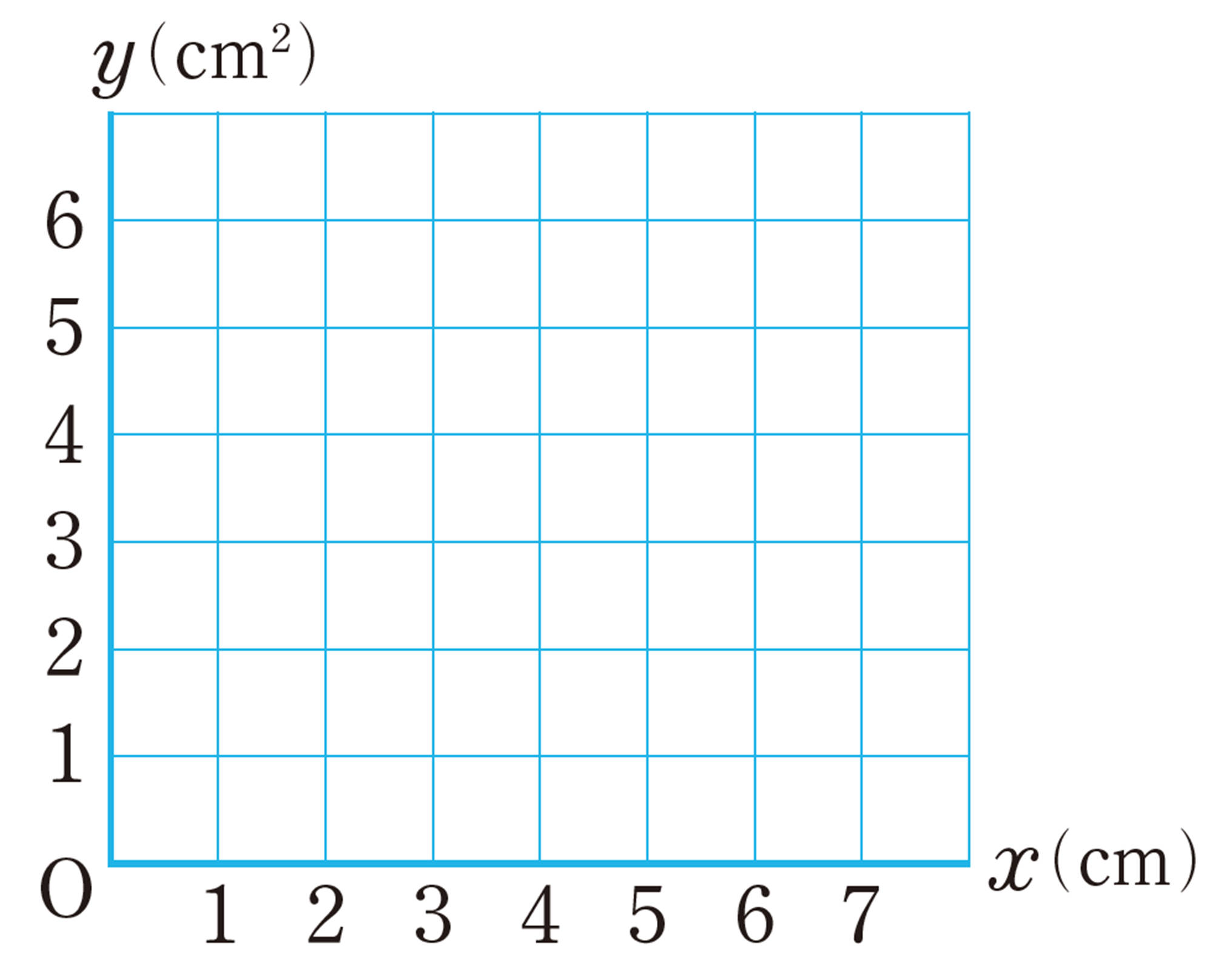
⑵ グラフを右の図にかき入れなさい。
<2年p.104>
3章のまとめの問題 活用
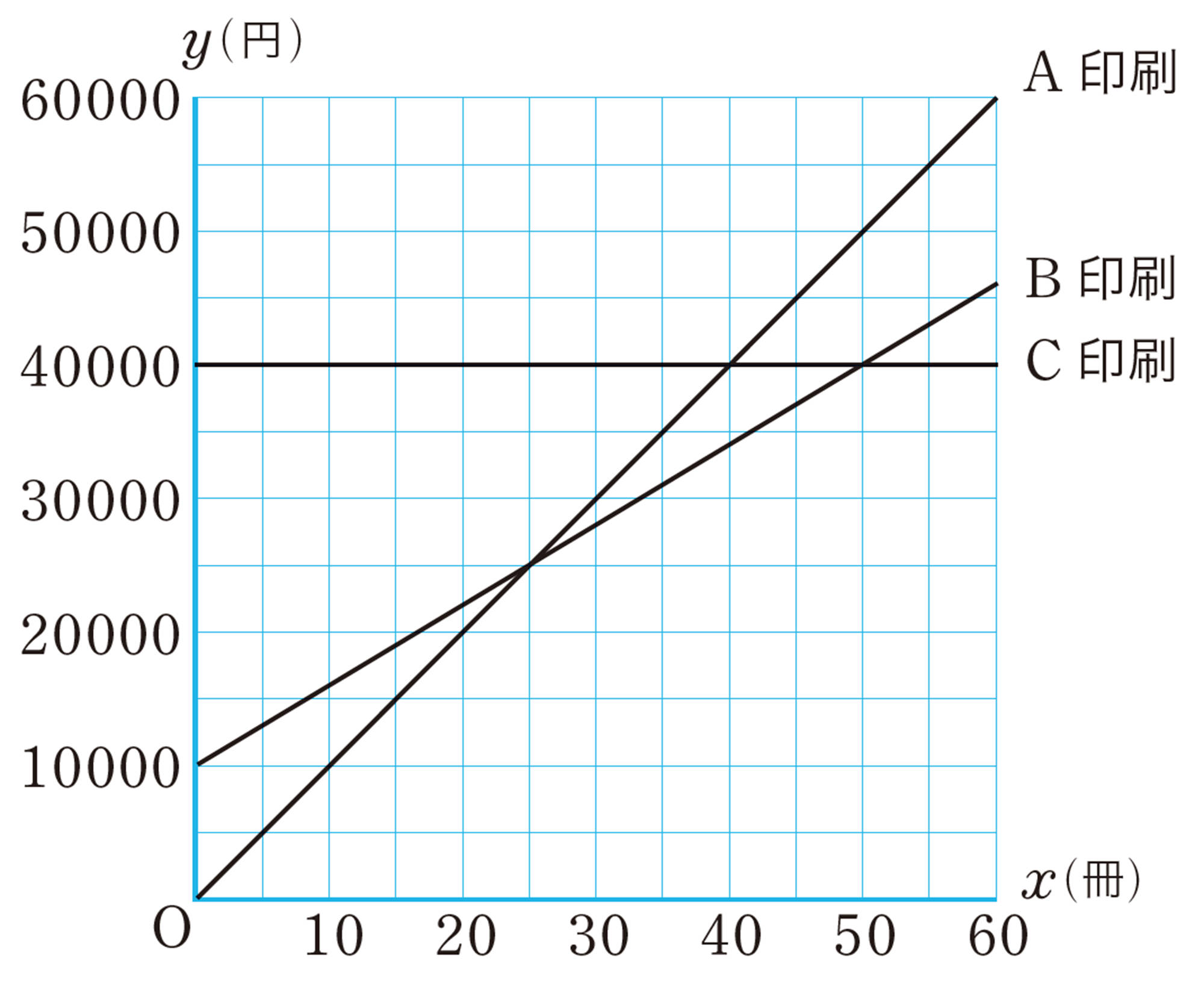
１ 学校で，文集をつくることになりました。そこで，印刷代がいくらになるか，3つの印刷所に問い合わせたところ，それぞれ次のような料金でした。
印刷する冊数によって，どの印刷所の料金が安くなるかを調べるために，文集をx冊印刷したときの印刷代をy円として，印刷所ごとのxとyの関係を，右のようにグラフに表しました。次の問いに答えなさい。
⑴ ある冊数の文集を印刷すると，B印刷とC印刷のどちらに頼んでも料金が同じになります。このとき，文集の冊数は，グラフ上のどの点の座標を見ればわかりますか。また，B印刷とC印刷の料金が同じになるのは，文集が何冊のときですか。
⑵ ⑴と同じように，グラフからA印刷とB印刷の料金が同じになる冊数を求めなさい。
⑶ それぞれの印刷所について，[mathjax]\( y \) を [mathjax]\( x \) の式で表しなさい。
⑷ 学校で文集の希望冊数を聞いたところ，全部で46冊でした。文集46冊の印刷代がもっとも安い印刷所を選ぶ方法を説明しなさい。ただし，実際に料金を求める必要はありません。
<2年p.105>
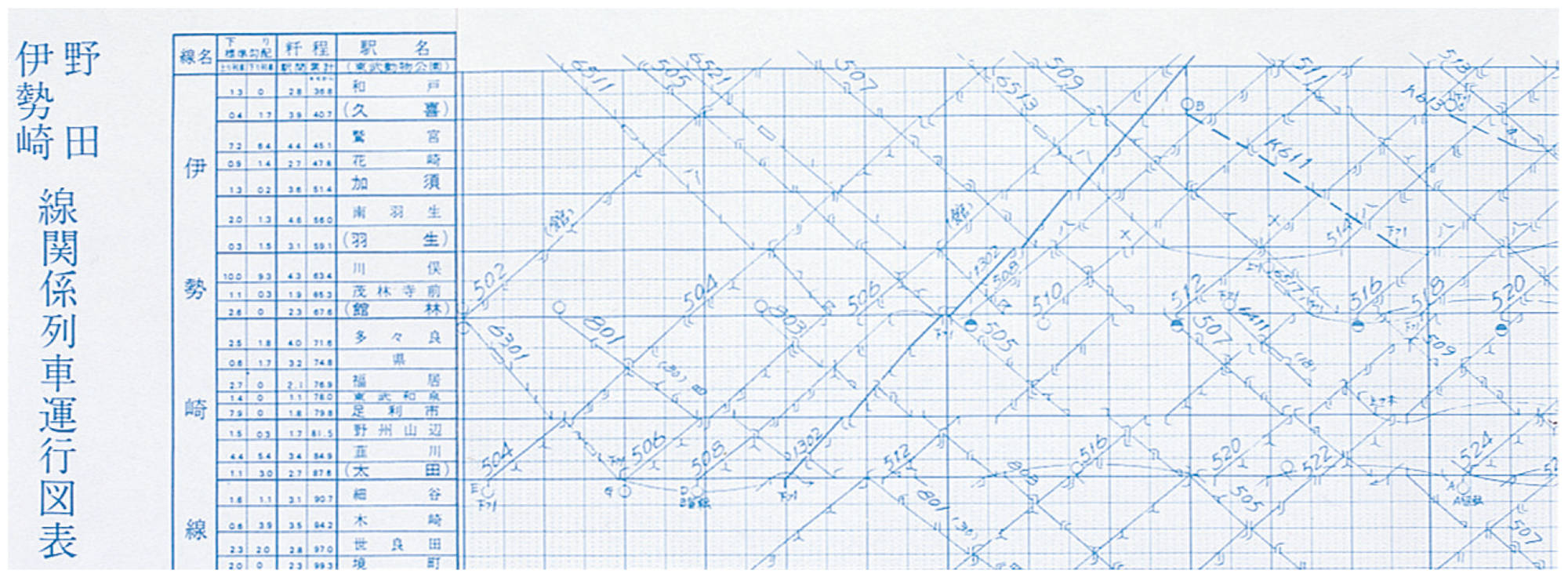
深めよう ダイヤグラム
列車の運行のようすが一目でわかるようにグラフに表したものを，ダイヤグラムといいます。ダイヤグラムを見ると，列車の出発時刻や到着時刻だけでなく，列車どうしがすれちがったり追い越したりする時刻や場所なども知ることができます。
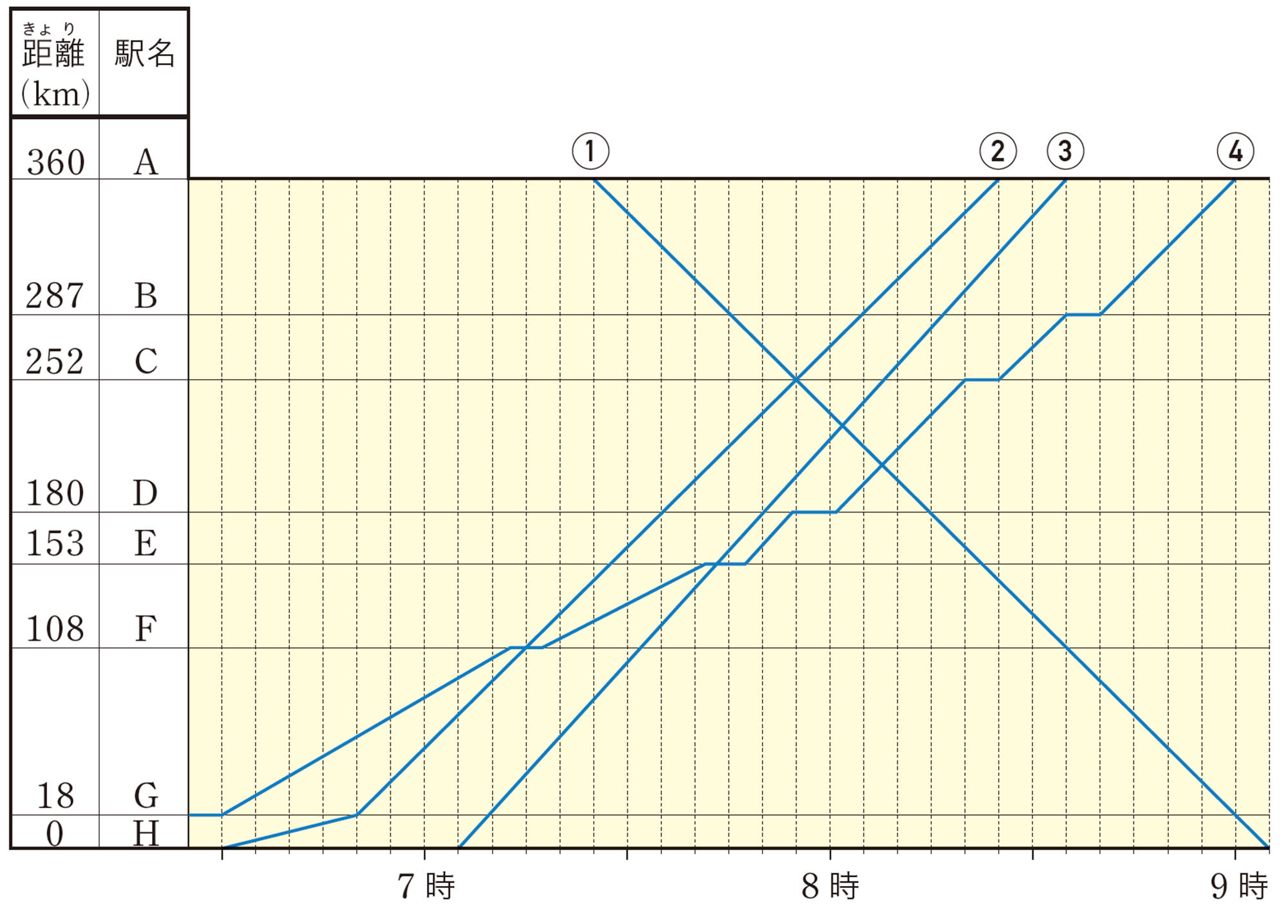
次のダイヤグラムを見て，下の❶～❺を考えてみましょう。
❶ ③の列車の速さを求めましょう。
❷ ③の列車がD駅を通過する時刻は，何時何分でしょうか。
❸ ②の列車が④の列車を追い越すのは，どの駅で何時何分でしょうか。
❹ ①のグラフと②のグラフの交点は何を表しているでしょうか。
❺ ④のグラフの平らなところは何を表しているでしょうか。
上のダイヤグラムから，ほかにどんなことがわかるか考えてみましょう。
＞＞ 関連する職業・仕事 ［鉄道会社］
