<2年p.95>
３節 1次関数の利用
関数を利用することができるかな？
美月さんは，おいしいお茶の入れ方を調べてみました。
おいしいお茶は，70℃から80℃の湯で入れるとよいそうです。
しかし，70℃の湯を沸かしたいとき，見ただけでは70℃になったかどうかがわかりません。
【１】 湯を沸かしているとき，湯の温度が70℃になったかどうかを知るにはどうしたらよいでしょうか。
水を熱するとき，時間がたつと，温度は高くなるね。
時間と温度はどんな関係になっているのかな。
どんな関係になっているか，実験して調べてみよう。
熱している時間と水の温度の関係を調べるんだね。
次の課題へ！
身のまわりのことがらで，2つの数量がどのような関係になっているかを調べて考察することができるかな？
P.96
<2年p.96>
１ １次関数の利用
Q Question
右の図のような装置で水を熱し，熱し始めてから [mathjax]\( x \) 分後の水温を [mathjax]\( y \) ℃として [mathjax]\( x \) と [mathjax]\( y \) の関係を調べたところ，次の表のようになりました。このとき，水が70℃になるのは何分後になると予測できるでしょうか。
変化の割合がばらばらだよ。
時間と温度には，関係があるのかな。
見方・考え方
時間と温度には，どんな関係があるとみなせるかな。
目標 ▷ 1次関数の関係を利用して，身のまわりの問題を解決しよう。
【１】
比例のときは，どうやって調べたかな。
[mathjax]\( x \) と [mathjax]\( y \) の値の組を座標とする点をとって，直線で結べるかどうかを調べたよ。
【Q】の [mathjax]\( x \) と [mathjax]\( y \) の関係はどのようなグラフになるでしょうか。表の対応する [mathjax]\( x \) ， [mathjax]\( y \) の値の組を座標とする点を，左の図にかき入れてみましょう。
7つの点から，どんなグラフがかけそうかな。
<2年p.97>
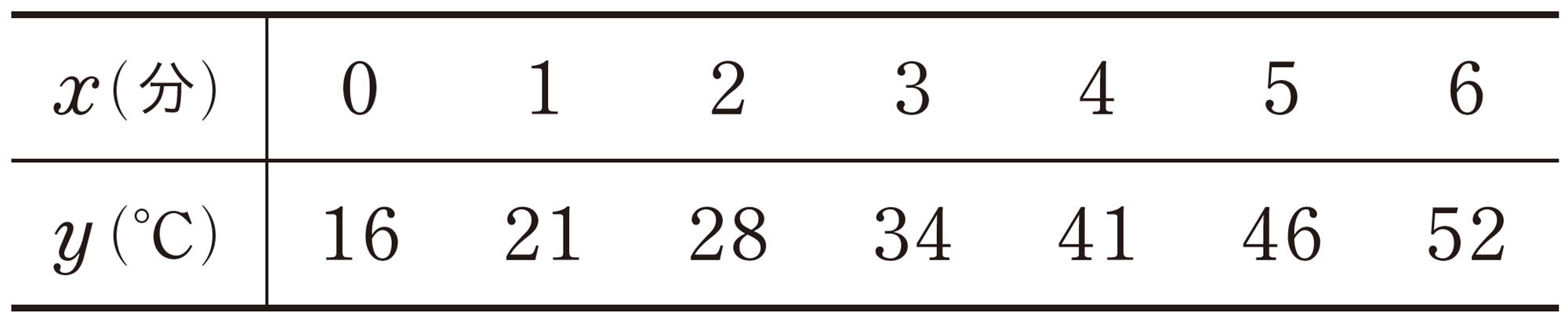
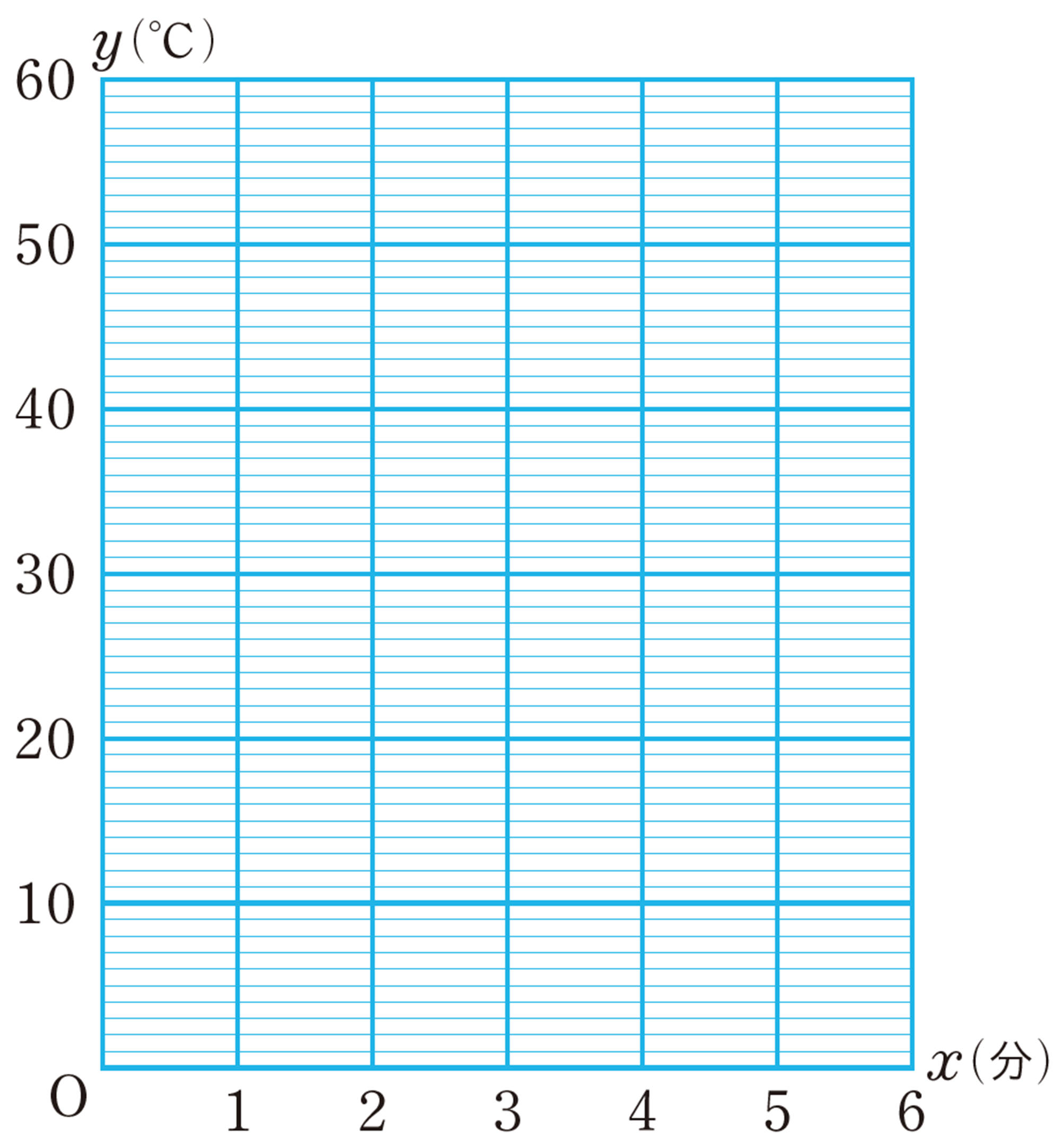
前ページの【１】では，7つの点はほぼ一直線上に並び，グラフは直線になるとみなすことができる。すなわち，[mathjax]\( y \) は [mathjax]\( x \) の1次関数であると考えられる。また，グラフをかくときには，できるだけ多くの点を通るか，点の近くを通るようにする。
【２】 このまま水を熱し続けたとき，水温が70℃になるのは，熱し始めてから何分後と考えられるでしょうか。その求め方を説明してみましょう。
70のところを見ればいいよ。
70といわれても， [mathjax]\( x \) か[mathjax]\( y \) かもわからないし，表にもグラフにもないよ。
求めたいのは [mathjax]\( y \) の値が70のときの [mathjax]\( x \) の値だよ。
そうなんだ。1次関数とみなして，式に表せばいいね。
比例のときのように，1組の [mathjax]\( x \) と [mathjax]\( y \) の値がわかれば，式が求められるかな。
直線が原点を必ず通るわけではないから，2組の [mathjax]\( x \) と [mathjax]\( y \) の値が必要だと思うな。
そうだね。2組の値がないと，直線が決まらないね。
求めたいのは70℃のときの時間だから，求めた式の [mathjax]\( y \) に70を代入すればいいね。
【３】 このグラフが，2点 [mathjax]\( (0,16) \) ，[mathjax]\( (6,52) \) を通る直線と考えて式に表し，水の温度が70℃になるのは熱し始めてから何分後かを求めてみましょう。
身のまわりのことがらを1次関数とみなすと，先のことが予測できるね。
お湯を冷ますときも1次関数になるといえるのかな。
これまで調べたように，実験結果から2つの数量の間の関係を読み取るには，グラフに表してみるとよい。また，それが1次関数であるとみなすことができれば，式をつくって調べたり結果を予測したりすることができる。
<2年p.98>
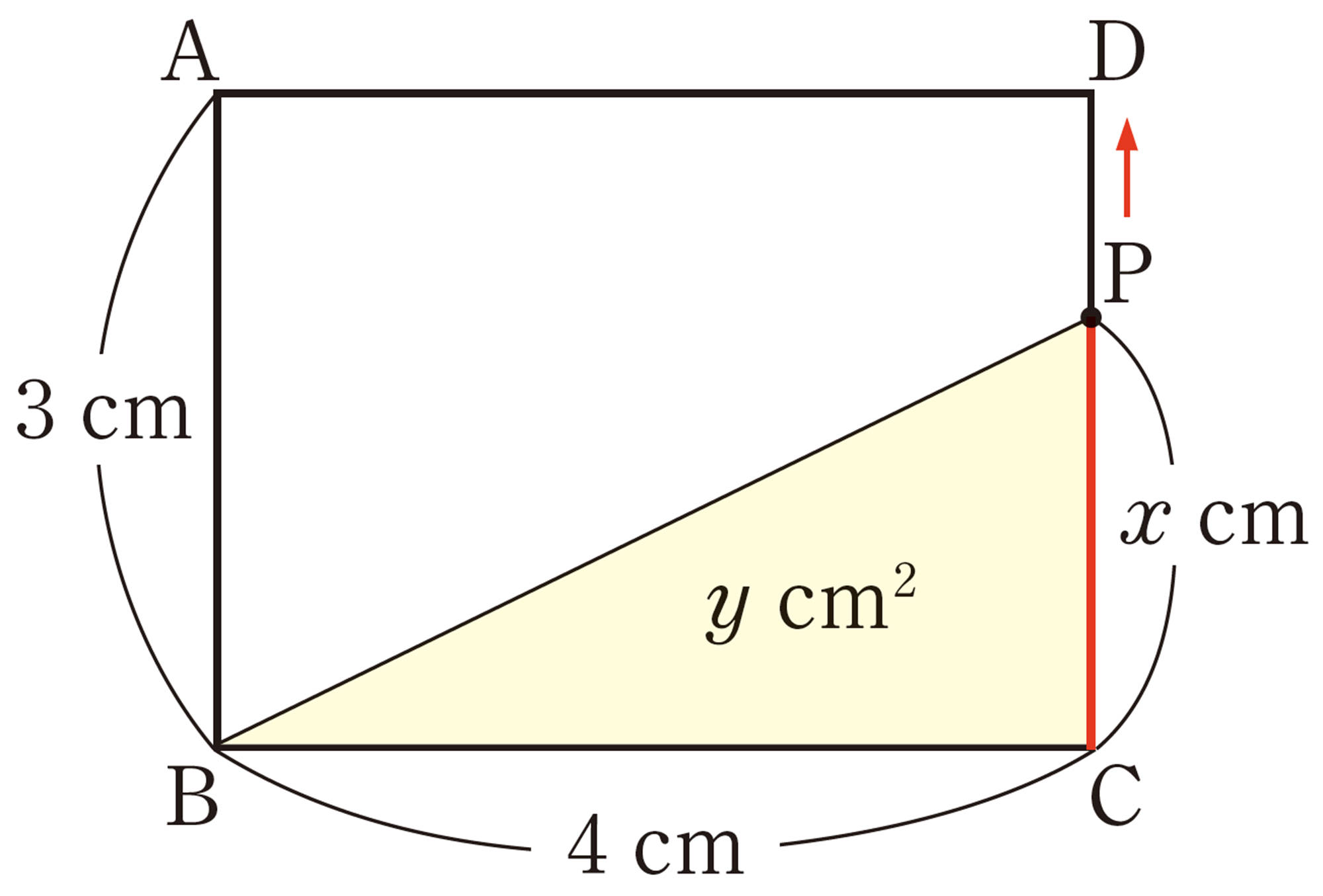
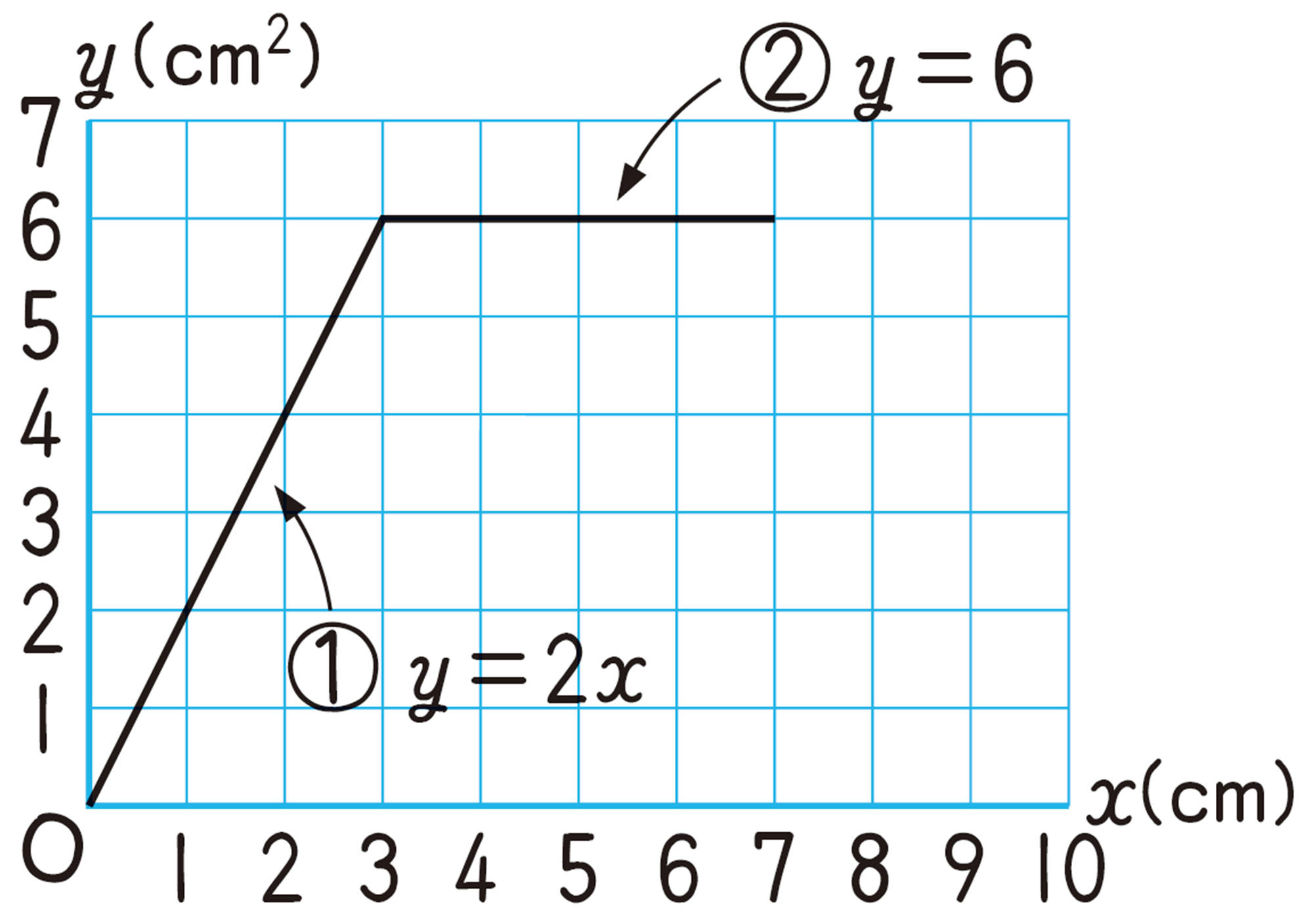
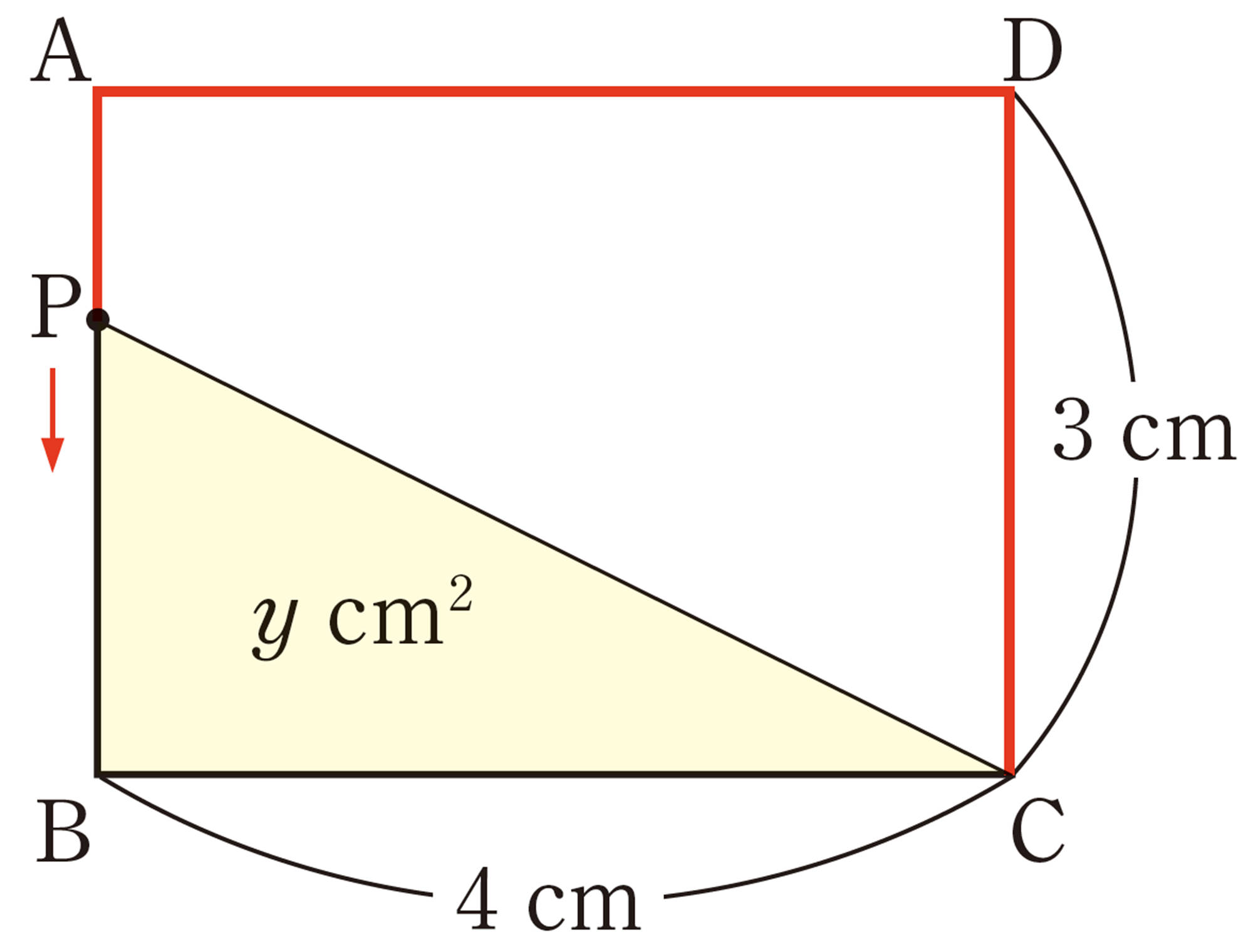
図形における利用
例 １ 右の図の長方形ABCDで，点PはCを出発して，辺上をDを通ってAまで動きます。点PがCから [mathjax]\( x \) cm動いたときの [mathjax]\(\triangle PBC\) の面積を [mathjax]\( y \) cm²とするとき， [mathjax]\( x \) と [mathjax]\( y \) の関係をグラフに表しなさい。
考え方 点Pの位置は，次の㋐，㋑の2つの場合に分けることができる。それぞれ [mathjax]\( x \) と [mathjax]\( y \) の関係を式で表し，それらのグラフをかく。
㋐ 辺CD上
㋑ 辺DA上
解答
問 １ 例1で，点PがAまで動いたあと， Aを通過してBまで動くとするとき，[mathjax]\( y \) を [mathjax]\( x \) の式で表し，グラフを上の図にかき入れなさい。
<2年p.99>
グラフの利用
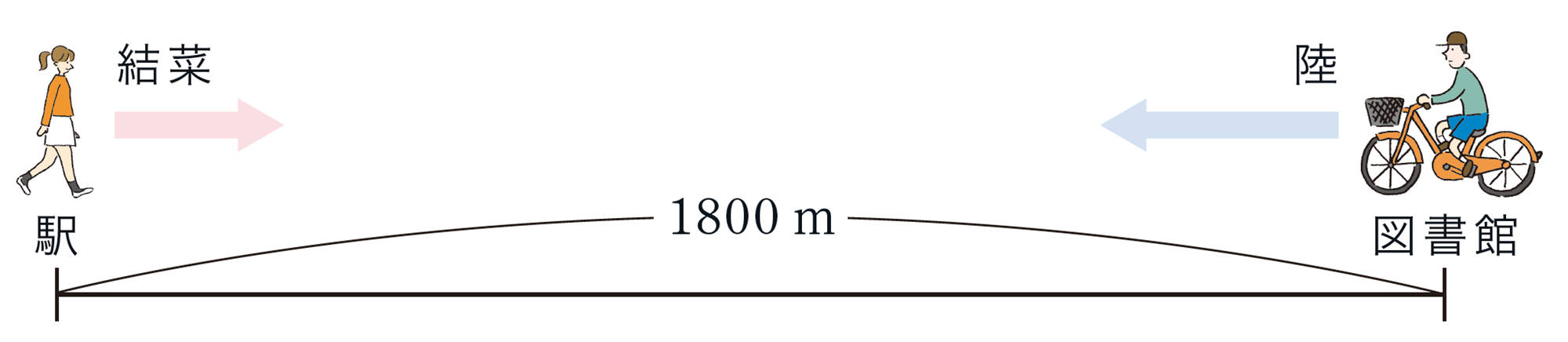
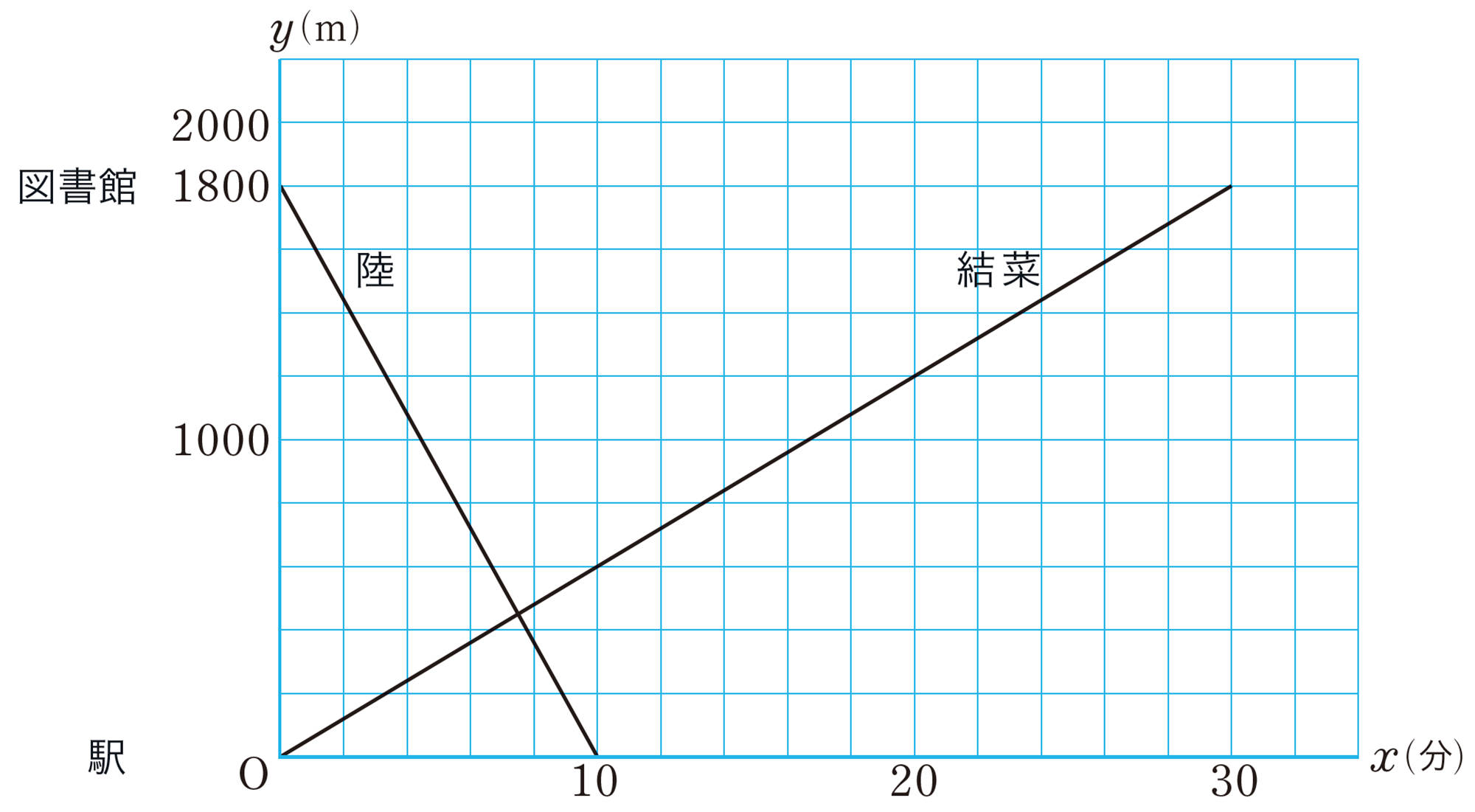
例 ２ 結菜さんは，駅から1800m離れた図書館に歩いて行き，陸さんは，同じ道を図書館から駅に自転車で行った。2人が同時に出発したとき，出発してからx分後の駅からの道のりをymとして，2人が進んだようすをグラフに表すと，下の図のようになる。
問 ２ 例2について，次の問いに答えなさい。
⑴ 結菜さんと陸さんの速さを，それぞれ求めなさい。
⑵ 陸さんが駅に着いたとき，結菜さんは駅から何mのところにいますか。
⑶ 2人が出会うのは出発してから何分後で，駅から何mのところですか。
⑷ 真央さんは，陸さんが駅に着いてから4分後に，分速150mで駅から図書館に自転車で向かいました。真央さんの進むようすを表すグラフを，上の図にかき入れなさい。また，真央さんが結菜さんを追い越すのは，駅から何mのところですか。
どんなことがわかったかな
身のまわりのことがらを1次関数とみなすと，未来を予測したり，グラフを使って量の変化や人の動きを表したりすることで，問題を解決できることがあります。
<2年p.100>
確かめよう 3節 1次関数の利用
１ 風呂を沸かそうとして，温め始めてからx分後の水温をy℃として，xとyの関係を調べると，次の表のようになりました。下の問いに答えなさい。
⑴ 上の表の対応するx，yの値の組を座標とする点を，右の図にかき入れなさい。
⑵ yはxの1次関数であるとみなすとき，そのグラフが 2点 [mathjax]\( (0,25.1) \) ， [mathjax]\( (25,37.6) \) を通ると考えて，直線の式を求めなさい。
⑶ 42℃になるのは約何分後か求めなさい。
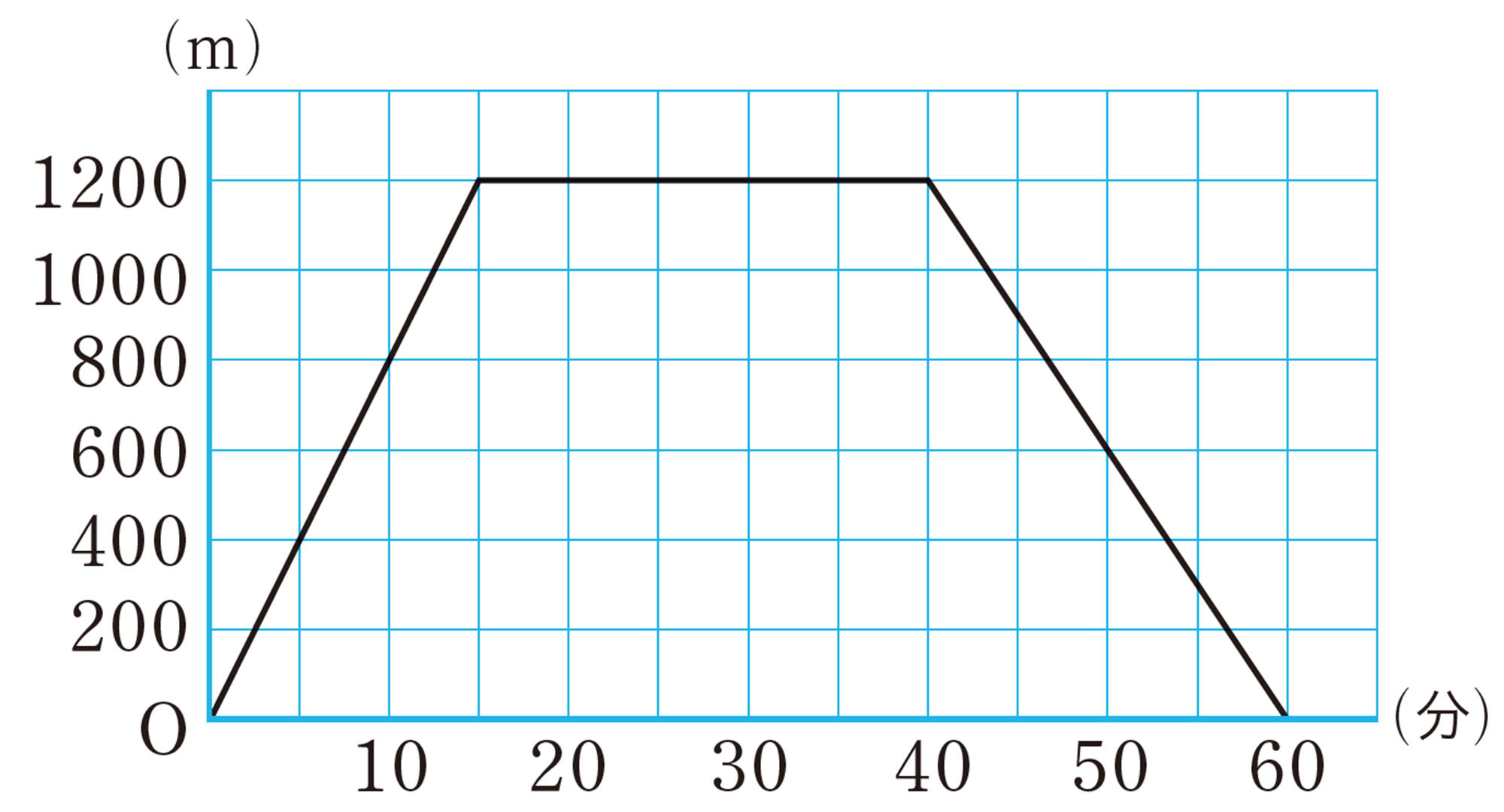
２ 大和さんは，家から1200m離れた図書館に行き，本を借りてから同じ道を通って家に帰りました。右の図は，大和さんが家を出てからの時間と，家からの道のりの関係を表したグラフです。次の問いに答えなさい。
⑴ 大和さんは図書館に何分間いましたか。
⑵ 大和さんの行きと帰りの速さを，それぞれ求めなさい。
<2年p.101>
3章 「1次関数」を学んで
できるようになったこと 身のまわりの課題へ ▷P.104，105
2つの数量xとyの関係が [mathjax]\( y=ax+b \) で表されるとき，yはxの1次関数であることが理解できる。
1次関数の変化の割合は一定で，グラフが直線になることを理解して，直線の式を求めることができる。
連立方程式の解は，2つの2元1次方程式をグラフに表し，そのグラフの交点から求めることができる。
身のまわりや数学の中から見つけた2つの数量の関係を，1次関数とみなして，解決に利用することができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない 気温とアイスクリームの売り上げ 発展 高等学校
1次関数を利用すると，身近な問題を考えるときに役立つことがあります。
たとえば，日ごとの最高気温をx℃，日ごとのアイスクリームの売り上げ個数をy個とします。このとき，yをxの1次関数と考えることで，最高気温から売り上げ個数をおおまかに予測することができます。
右のグラフは，最高気温とアイスクリームの売り上げ個数の関係を表した1つの例です。
明日の最高気温が30℃だとすると，あなたはアイスクリームを何個用意しますか。
実際には，ほかの要素も関わってくるので，正確な予測は難しいですが，1次関数は未来を予測する際に有効な手段の1つといえます。
