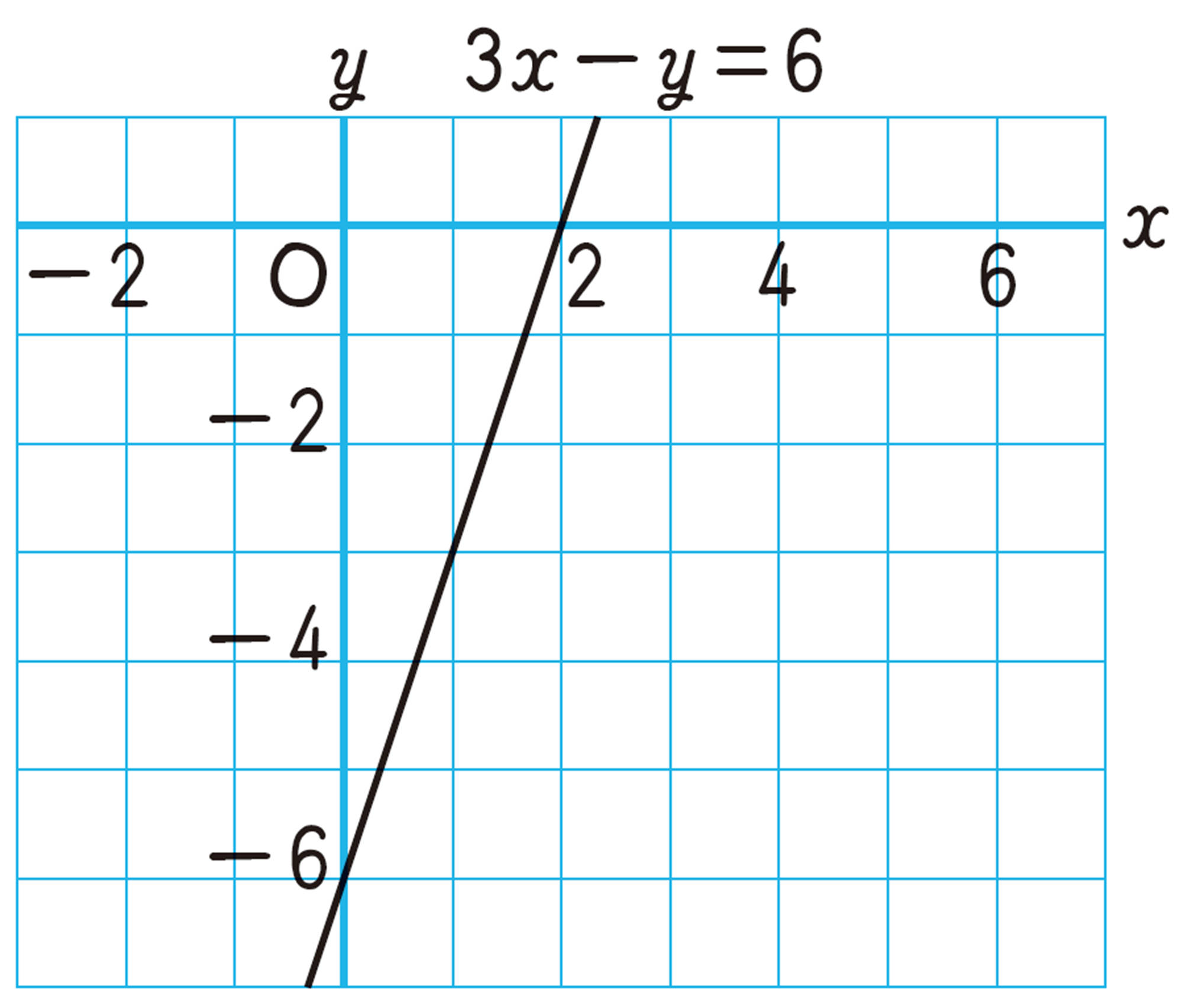<2年p.87>
2節 方程式と1次関数
2元1次方程式と1次関数の関係は？
拓真さんは，1次関数の式と2元1次方程式が似ていると考えました。
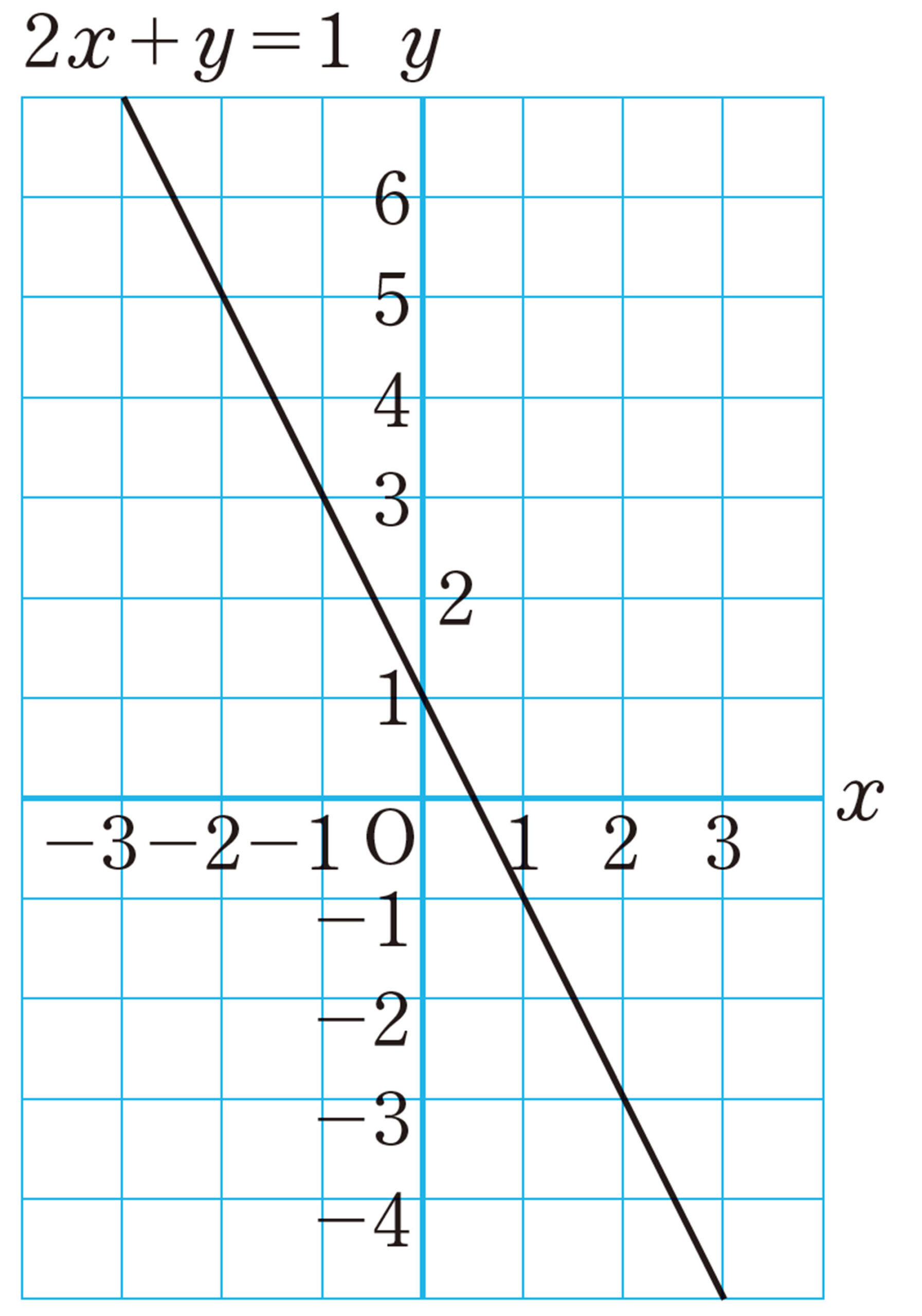
[mathjax]\( y=-2x+1 \) と [mathjax]\( 2x+y=1 \) 。 何か共通点があるのかな。
【１】 拓真さんは，2元1次方程式 [mathjax]\( 2x+y=1 \) の解を求めるために，次のような表を作りました。
⑴ 上の表を完成させましょう。
⑵ 対応する [mathjax]\( x \) ， [mathjax]\( y \) の値の組を座標とする点を，右の図にかき入れてみましょう。
⑶ [mathjax]\( x \) と [mathjax]\( y \) の間には，どんな関係があると考えられるか話し合ってみましょう。
もっと細かく点をとるとどうなるかな。
2元1次方程式の解を座標とする点の集合は，どんな形になるかな。
次の課題へ！
1次関数のグラフに似ているけど，1次関数とはどんな関係があるのかな？
P.88
<2年p.88>
１ 2元1次方程式のグラフ
目標 ▷ 2元1次方程式と1次関数の関係について調べよう。
[mathjax]\( x \) ， [mathjax]\( y \) の変域をすべての数とすると，2元1次方程式 [mathjax]\( 2x+y=1 \) の解は無数にある。
これらの解を座標とする点の集合は，右の図のような直線となる。
この直線を，2元1次方程式 [mathjax]\( 2x+y=1 \) のグラフという。
2元1次方程式 [mathjax]\( 2x+y=1 \) では， [mathjax]\( x \) の値を決めると，それに対応する [mathjax]\( y \) の値がただ1つ決まる。
また， [mathjax]\( 2x+y=1 \) を [mathjax]\( y \) について解くと，
[mathjax]\( y=-2x+1 \)
となる。したがって， [mathjax]\( y \) は [mathjax]\( x \) の1次関数とみることもできる。
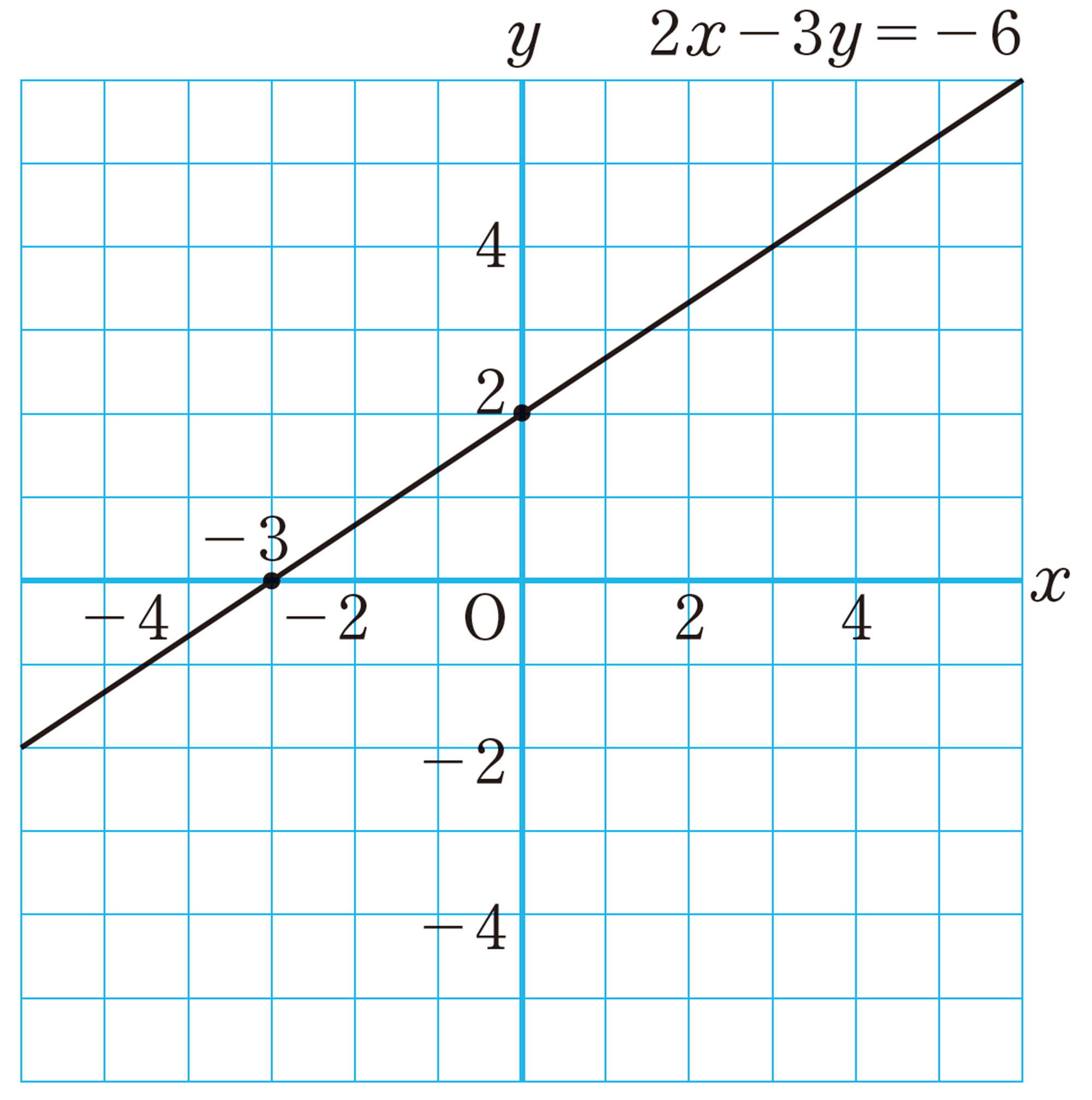
2元1次方程式のグラフのかき方
例 １ 方程式 [mathjax]\( 3x-y=6 \) のグラフをかきなさい。
解答
[mathjax] \( 3x-y=6 \) を [mathjax] \( y \) について解くと，
したがって，[mathjax] \( 3x-y=6 \) のグラフは，右の図のように， 傾きが3，切片が[mathjax] \(-6\)の直線となる。
<2年p.89>
問 １ 次の方程式のグラフを，右の図にかき入れなさい。
⑴ [mathjax] \( x+y=2 \)
⑵ [mathjax] \( 3x-2y=4 \)
例 ２ 方程式 [mathjax] \( 2x-3y=-6 \) で，
[mathjax] \( x=0 \) のとき [mathjax] \( y=2 \)
[mathjax] \( y=0 \) のとき [mathjax] \( x=-3 \)
したがって， [mathjax] \( 2x-3y=-6 \) のグラフは，2点 [mathjax] \( (0,2) \) ，[mathjax] \( (-3,0) \) を通る直線となる。
2元1次方程式のグラフは直線であるから，例2のように，グラフが通る適当な2点を決めてかくこともできる。
問 ２ 次の方程式のグラフを，適当な2点を決めて，右の図にかき入れなさい。
⑴ [mathjax] \( x-2y=4 \)
⑵ [mathjax] \( 4x+3y=12 \)
<2年p.90>
[mathjax] \( y=h \) ，[mathjax] \( x=k \) のグラフ
Q Question
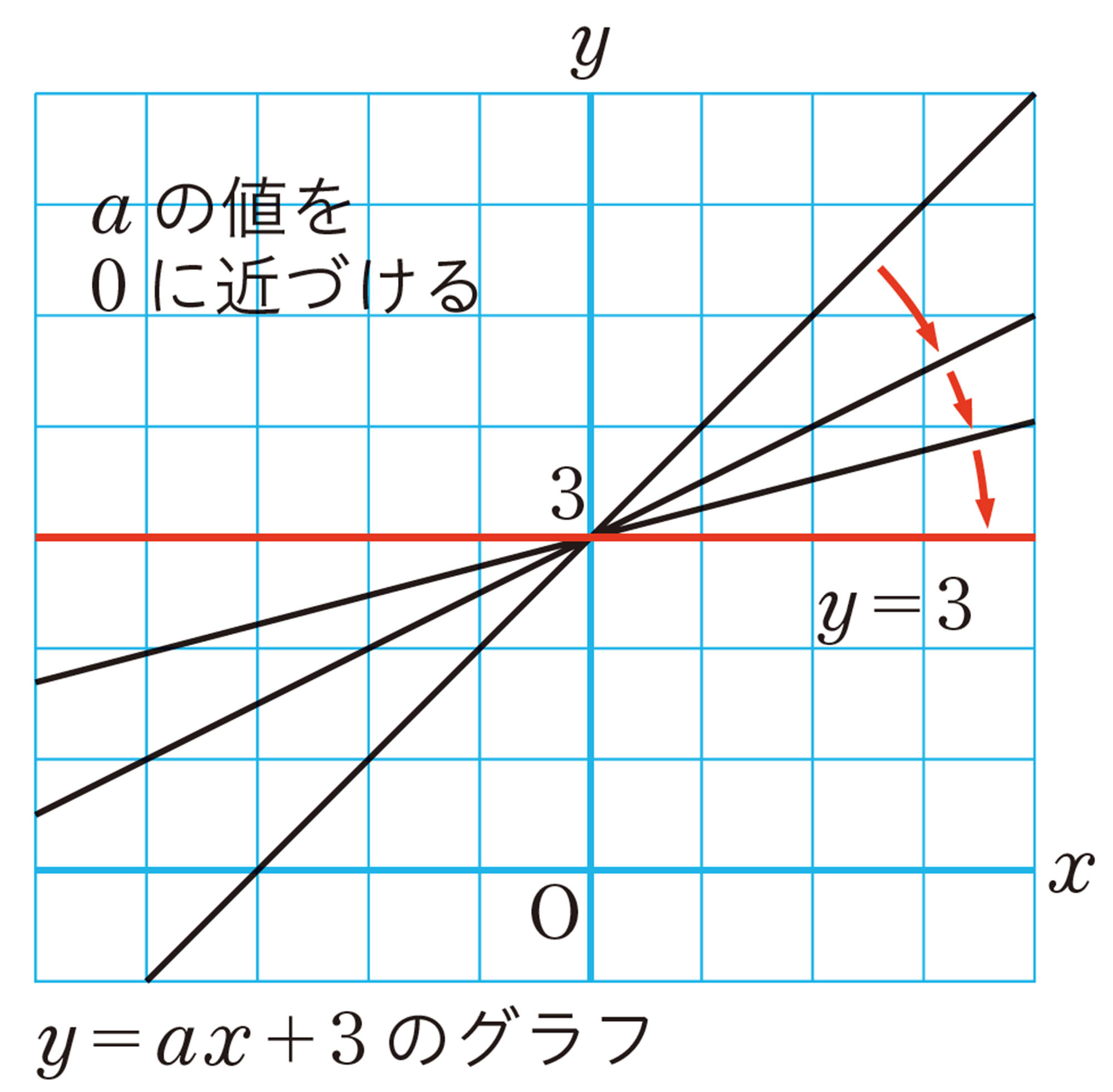
方程式 [mathjax] \( ax+by=c \) で， [mathjax] \( a \) ， [mathjax] \( b \) ， [mathjax] \( c \) の値が次の⑴，⑵のとき，どんなグラフになるか話し合ってみましょう。
⑴ [mathjax] \( a=0 \) ，[mathjax] \( b=1 \) ，[mathjax] \( c=3 \)
⑵ [mathjax] \( a=2 \) ，[mathjax] \( b=0 \) ，[mathjax] \( c=4 \)
[mathjax] \( ax+by=c \) の [mathjax] \( a \) が [mathjax] \( 0 \) だと [mathjax] \( x \) の項が，[mathjax] \( b \) が [mathjax] \( 0 \) だと [mathjax] \( y \) の項が消えてしまうね。
解を座標とする点はどんな集合になるのかな。
見方・考え方
特別な場合について考えられるかな。
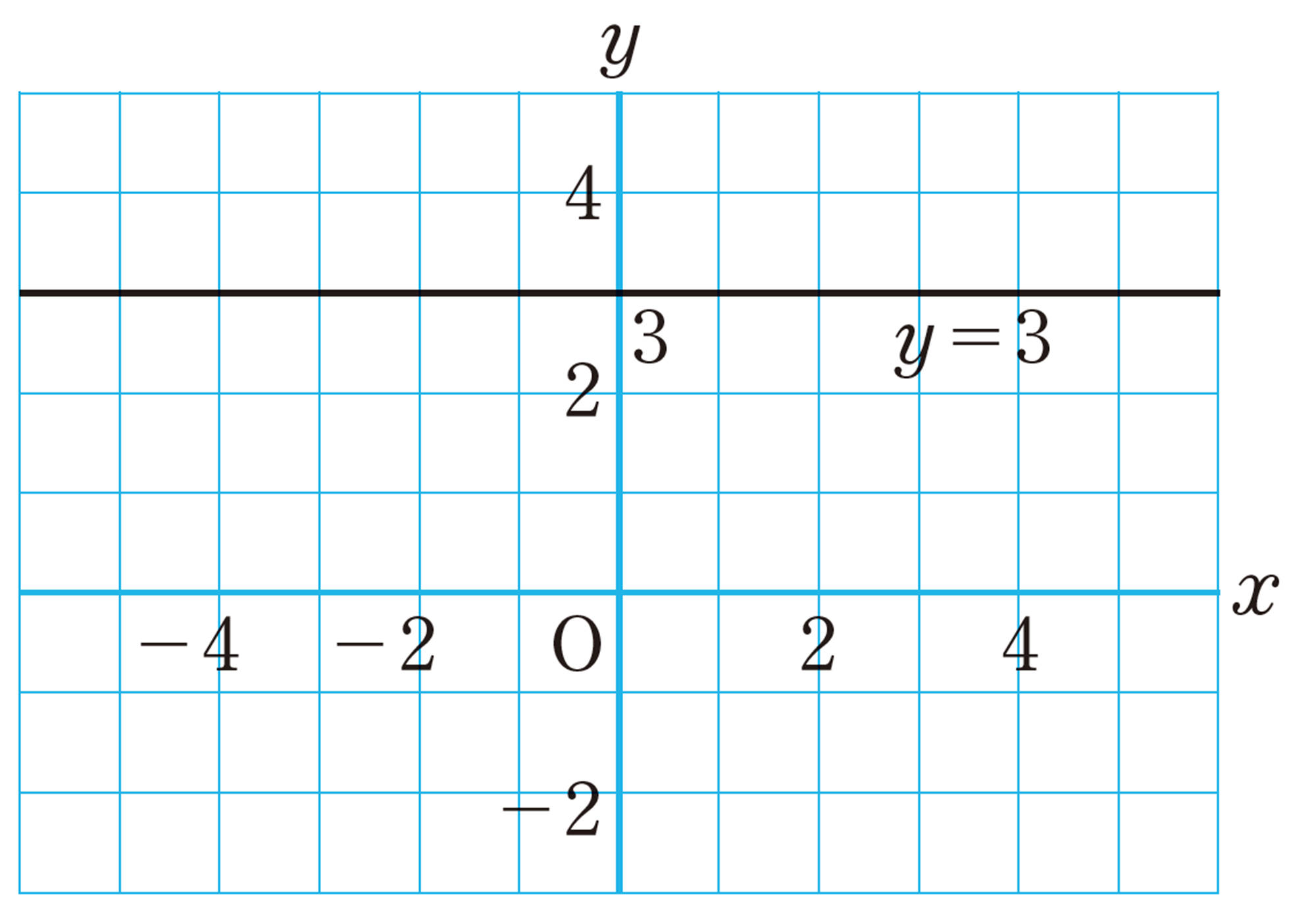
例 ３ 方程式 [mathjax] \( ax+by=c \) で， [mathjax] \( a=0 \) ， [mathjax] \( b=1 \) ， [mathjax] \( c=3 \) のときを考える。この方程式は，
となる。
このとき，[mathjax] \( x \) がどんな値をとっても，それに対応する[mathjax] \( y \) の値は3になる。
したがって，そのグラフは，点 [mathjax] \( (0,3) \) を通り，[mathjax] \( x \) 軸に平行な直線となる。
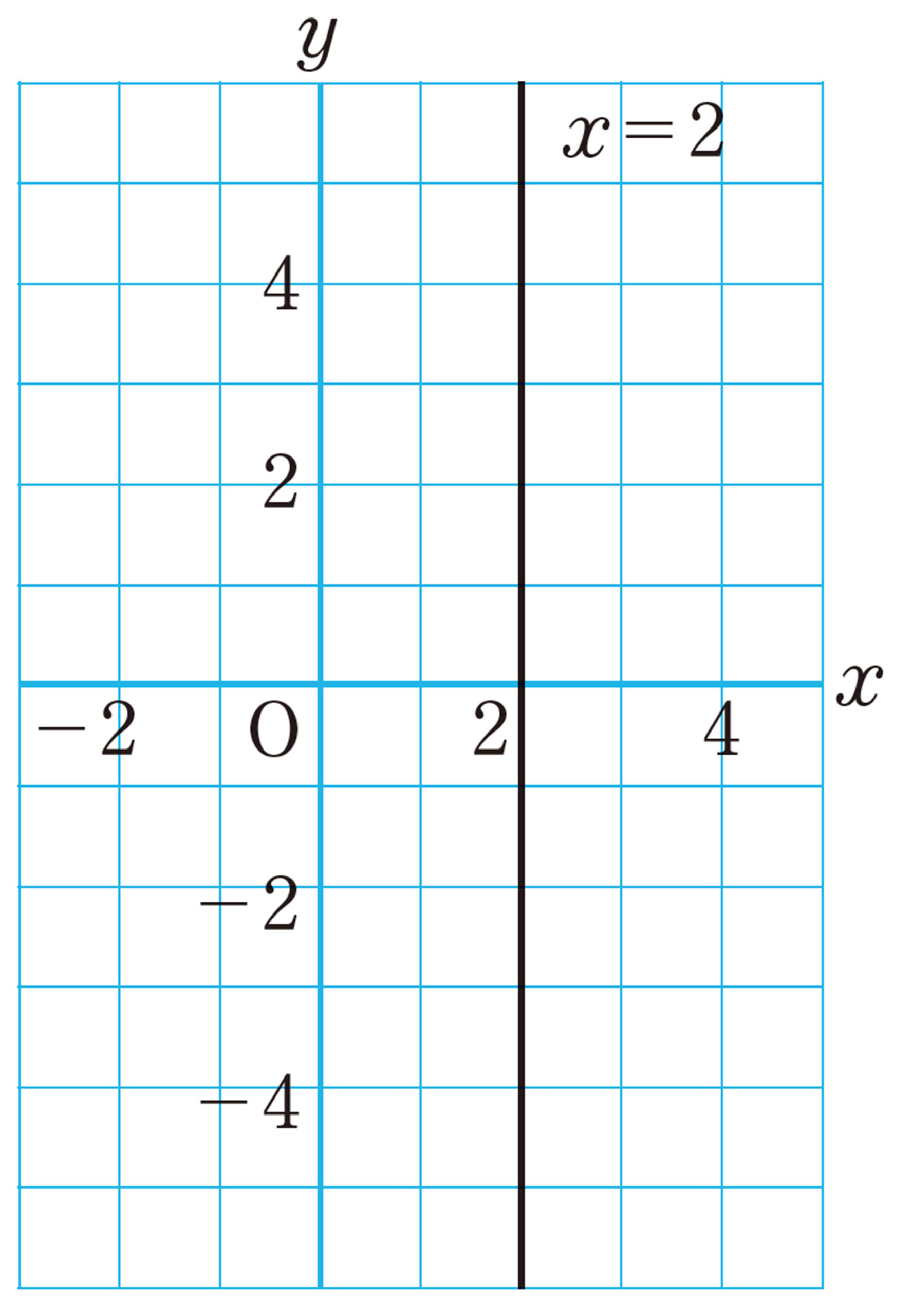
例 ４ 方程式 [mathjax] \( ax+by=c \) で，[mathjax] \( a=2 \) ， [mathjax] \( b=0 \) ， [mathjax] \( c=4 \) のときを考える。この方程式は，
となる。
このとき，[mathjax] \( y \) がどんな値をとっても，それに対応する [mathjax] \( x \) の値は2になる。したがって，そのグラフは，点 [mathjax] \( (2,0) \) を通り，[mathjax] \( y \) 軸に平行な直線となる。
<2年p.91>
問 ３ 次の方程式のグラフを，右の図にかき入れなさい。
⑴ [mathjax]\( y=4 \)
⑵ [mathjax]\( 3y=-6 \)
⑶ [mathjax]\( x=-3 \)
⑷ [mathjax]\( 2x-10=0 \)
⑸ [mathjax]\( x=0 \)
これまでのことから，次のようにまとめることができる。
2元1次方程式 [mathjax]\( ax+by=c \) のグラフについて，[mathjax]\( a=0 \) のときは [mathjax]\( x \) 軸に平行な直線，[mathjax]\( b=0 \) のときは [mathjax]\( y \) 軸に平行な直線となる。
どんなことがわかったかな
2元1次方程式の解を座標とする点の集合は，直線になります。
次の課題へ！
連立方程式の2つの2元1次方程式を，グラフに表すとどうなるのかな？
P.92
傾きが0の直線 Tea Break
1次関数 [mathjax]\( y=ax+3 \) で，[mathjax]\( a \) の値を0に近づけていくと，そのグラフはしだいに [mathjax]\( y=3 \) のグラフに近づいていきます。
このように，[mathjax]\( y=3 \) のグラフは，切片が3，傾きが0の直線とみることができます。
<2年p.92>
２ 連立方程式の解とグラフ
Q Question
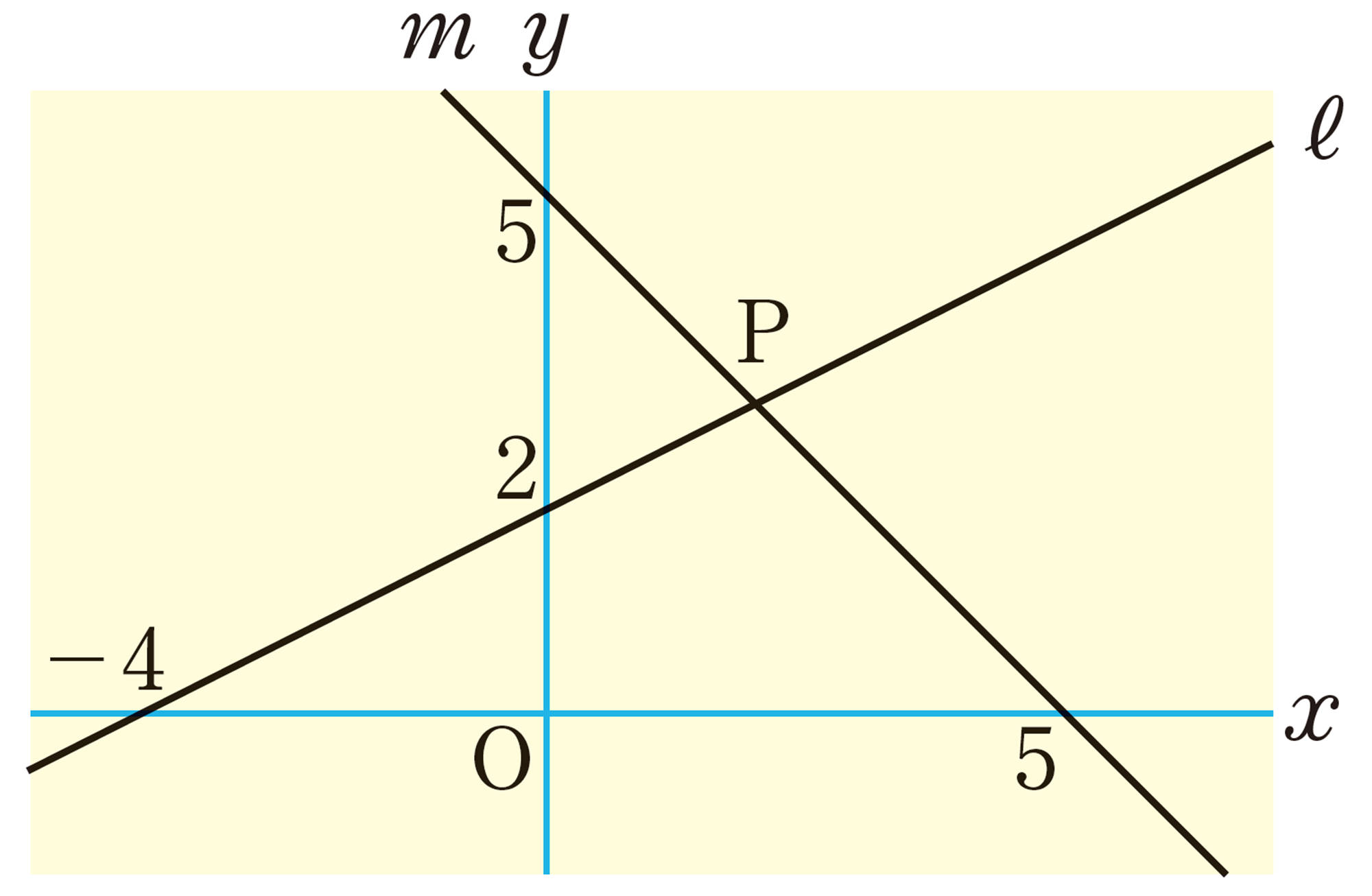
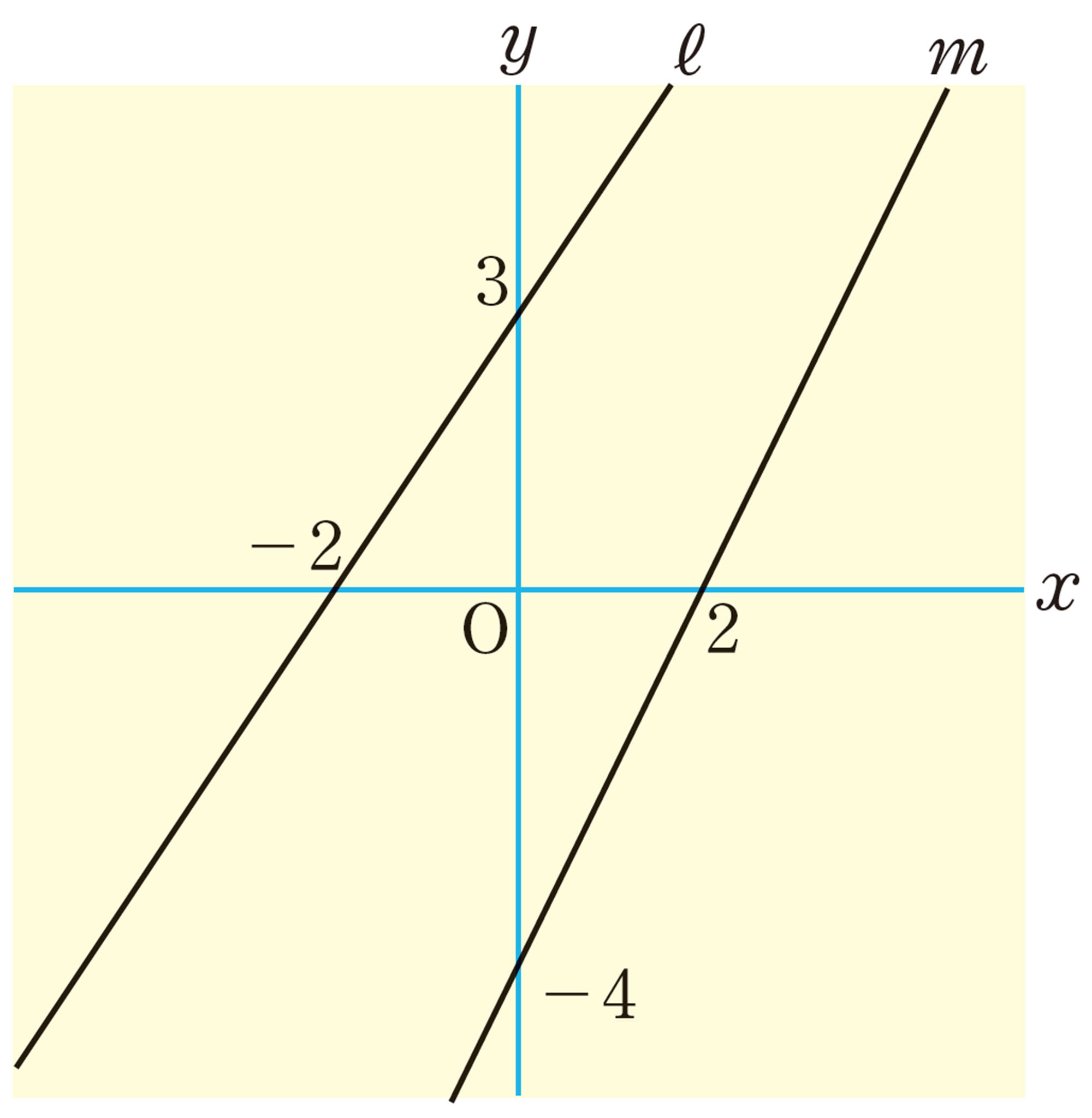
連立方程式
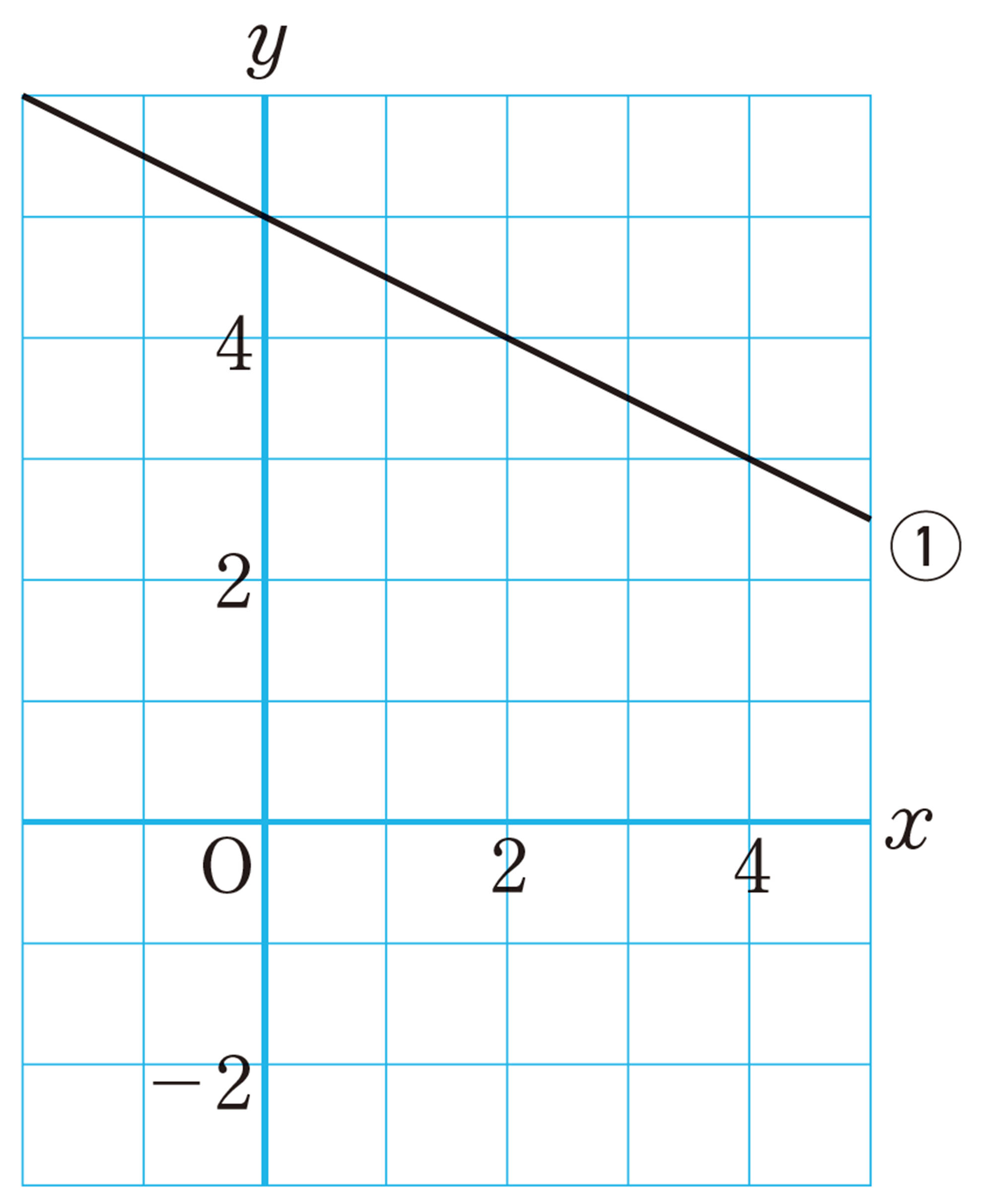
で，方程式①のグラフは，右の図の直線①になります。方程式②のグラフを，この図にかき入れてみましょう。また，2つのグラフの交点の座標を読み取ってみましょう。
連立方程式をグラフで表すと2本のグラフになるね。
グラフの交点にはどんな意味があるのかな。
見方・考え方
2元1次方程式のグラフを解の集合とみて考えられるかな。
目標 ▷ 2元1次方程式のグラフを使って，連立方程式の解を求めよう。
上の図で，直線①上の点の座標 [mathjax]\( (x,y) \) は，方程式①の解を表している。同様に，方程式②のグラフを直線②とすると，直線②上の点の座標 [mathjax]\( (x,y) \) は，方程式②の解を表している。
したがって，方程式①と②のグラフの交点の座標 [mathjax]\( (2,4) \) は，【Q】で示した
連立方程式の解
を表している。
グラフの交点の座標
[mathjax]\(\updownarrow \)
連立方程式の解
問 １ 【Q】で示した連立方程式の解を計算で求めなさい。また，その解がグラフの交点の座標と一致することを確かめなさい。
問 ２ 次の連立方程式を，グラフを使って解きなさい。
<2年p.93>
グラフの交点と連立方程式の解
2つの2元1次方程式のグラフの交点の [mathjax]\( x \) 座標， [mathjax]\( y \) 座標の組は，その2つの方程式を1組にした連立方程式の解である。
問 ３ 2直線 [mathjax]\( ℓ \) ，[mathjax]\( m \) が，右の図のように点Pで交わっています。このとき，点Pの座標を次の手順で求めなさい。
① 直線 [mathjax]\( ℓ \) ， [mathjax]\( m \) の式を求める。
② ①で求めた2つの式を，連立方程式として解く。
どんなことがわかったかな
連立方程式の解は，2つの2元1次方程式をグラフに表し，そのグラフの交点の座標から求めることができます。
次の課題へ！
身のまわりで，1次関数の関係にあることがらには，どんなものがあるのかな？
P.95
解が1組にならない連立方程式 Tea Break
次の連立方程式は計算で解けるでしょうか。また，グラフをかき，それぞれの解を調べてみましょう。
①
②
連立方程式には，①のように解がないものや，②のように解が無数にあるものがあります。
<2年p.94>
確かめよう 2節 方程式と1次関数
１
次の方程式のグラフを，左の図にかき入れなさい。
⑴ [mathjax]\( -2x+y=4 \)
⑵ [mathjax]\( 3x-5y=15 \)
⑶ [mathjax]\( y=-3 \)
⑷ [mathjax]\( x=4 \)
２
次の連立方程式を，グラフを使って解きなさい。
３ 右のような2直線 [mathjax]\( ℓ \) ，[mathjax]\( m \) があります。このとき，次の問いに答えなさい。
⑴ 直線 [mathjax]\( ℓ \) ，[mathjax]\( m \) の式を求めなさい。
⑵ [mathjax]\( ℓ \) ，[mathjax]\( m \) の交点の座標を求めなさい。
