<2年p.82>
３ 1次関数のグラフのかき方・式の求め方
Q Question
1次関数 [mathjax]\( y=- \dfrac{1}{2}x+3 \) のグラフについて，表を使わずにかく方法を考えてみましょう。
1次関数のグラフは直線だから，2点が決まればかけそうだね。
どうやって2点を決めればいいのかな。
見方・考え方
比例のグラフをかいたときと同じようにかけるかな。
目標 ▷ 1次関数のグラフのかき方を考えよう。
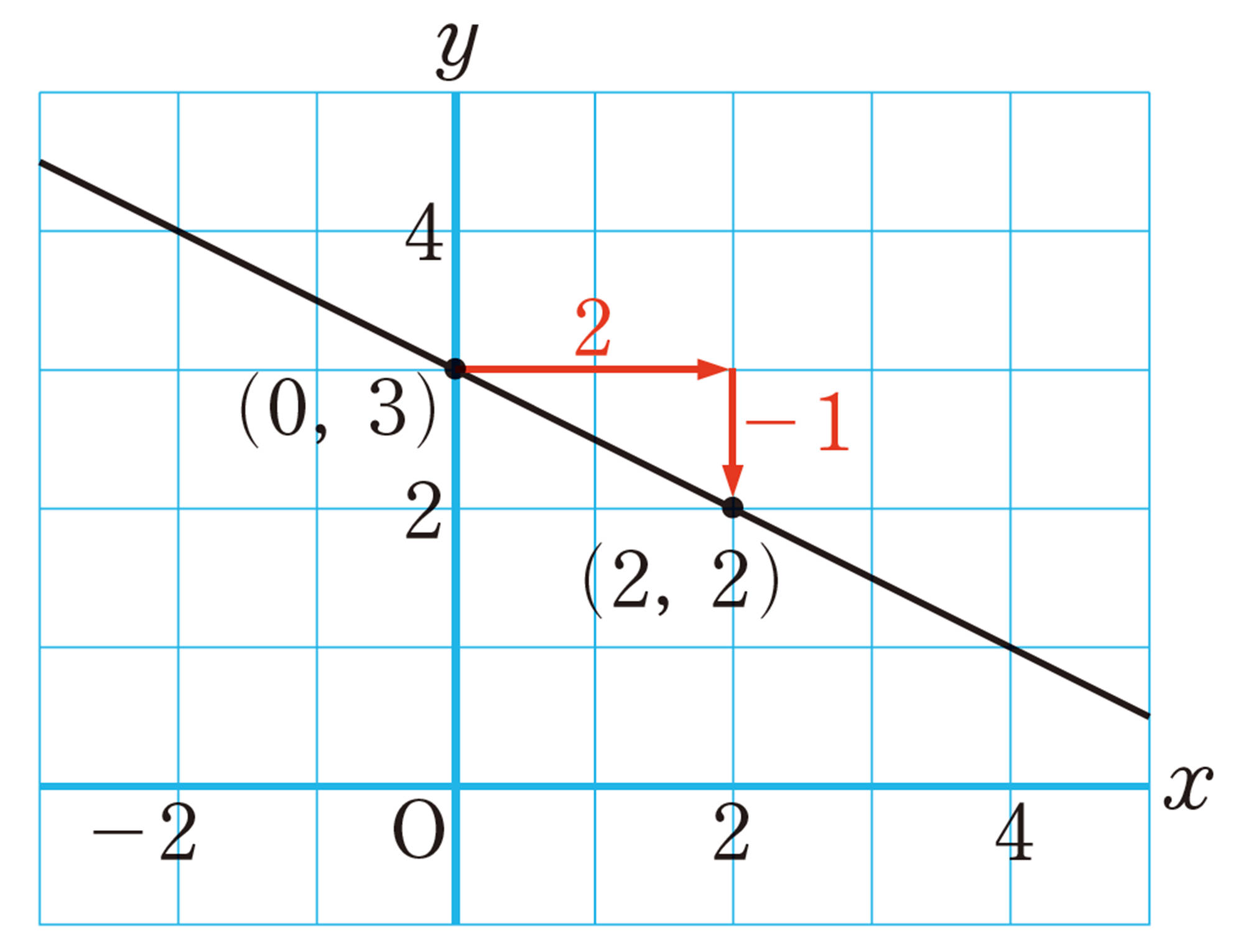
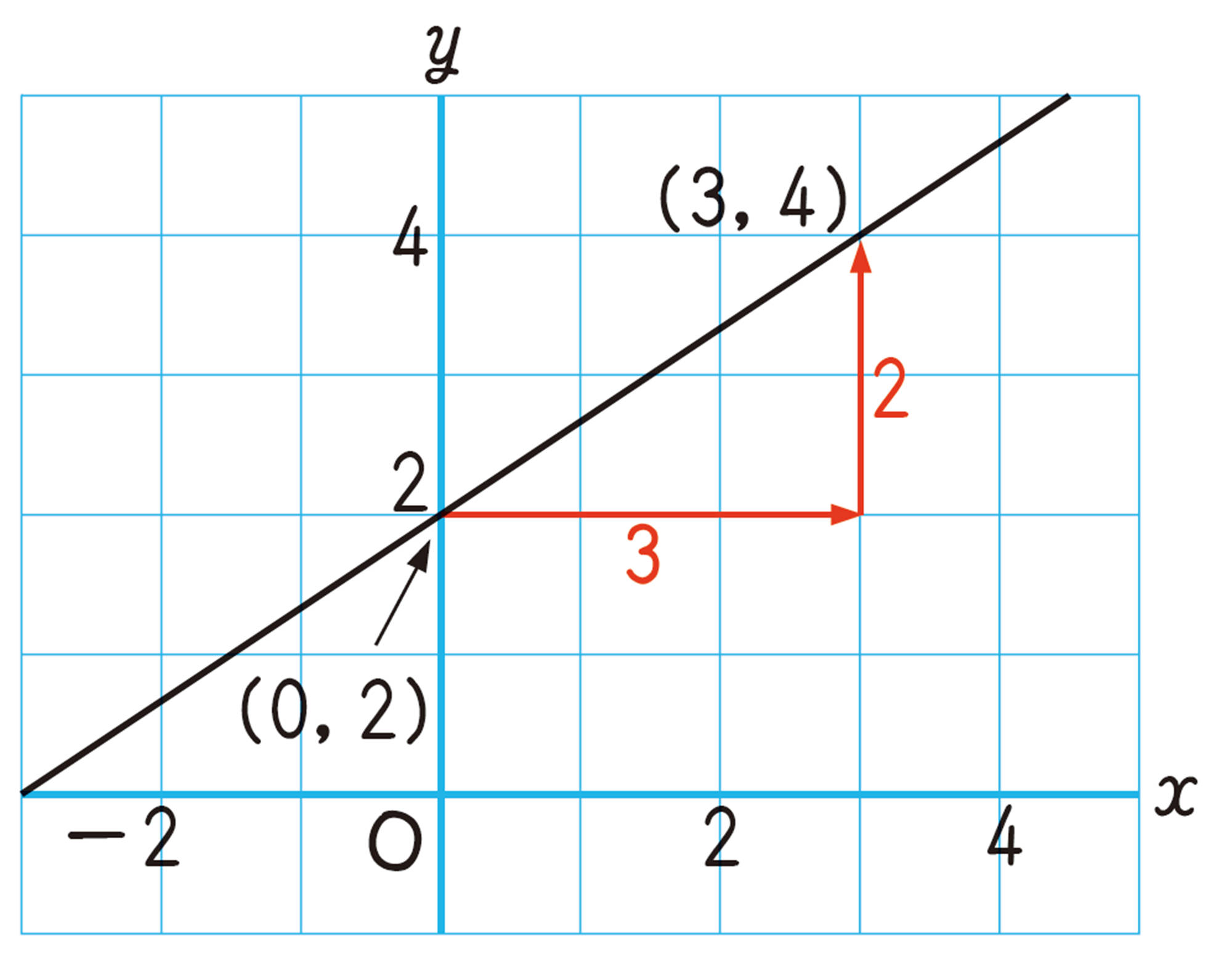
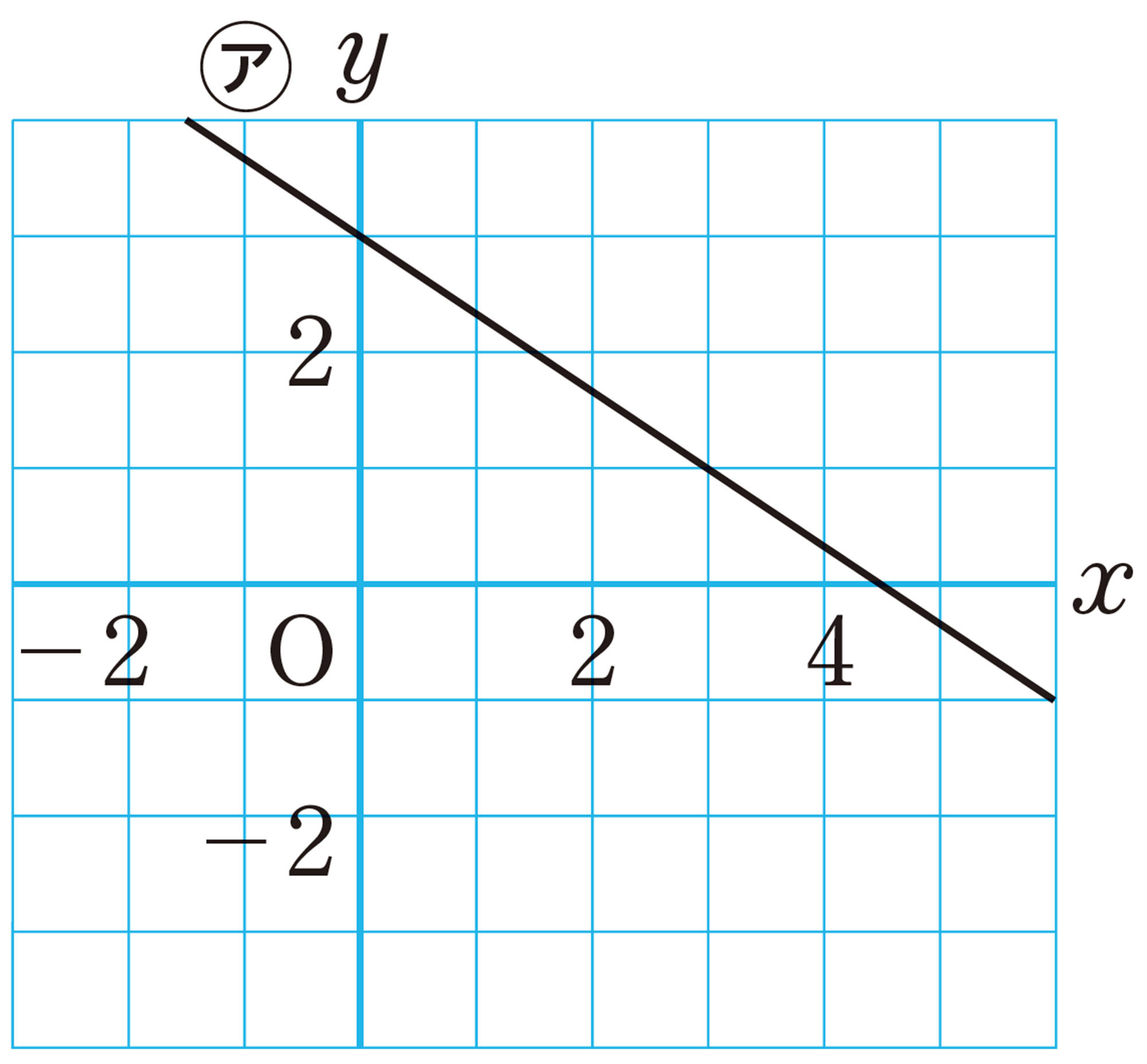
例 １ 1次関数 [mathjax]\( y=- \dfrac{1}{2}x+3 \) のグラフをかきなさい。
考え方 切片が3であるから， [mathjax]\( y \) 軸上の点 [mathjax]\( (0,3) \) を通る。また，傾きが [mathjax]\( – \dfrac{1}{2} \) であるから，点 [mathjax]\( (0,3) \) から，たとえば，右へ2，下へ1だけ進んだ点 [mathjax]\( (2,2) \) を通る。
解答
[mathjax]\( x \) ， [mathjax]\( y \) の値が整数になる点を見つけるとかきやすいね。
問 １
次の1次関数のグラフを，左の図にかき入れなさい。
⑴ [mathjax]\( y=2x-1 \)
⑵ [mathjax]\( y=-x+3 \)
⑶ [mathjax]\( y= \dfrac{1}{3}x+2 \)
⑷ [mathjax]\( y=- \dfrac{3}{4}x-2 \)
<2年p.83>
変域とグラフ
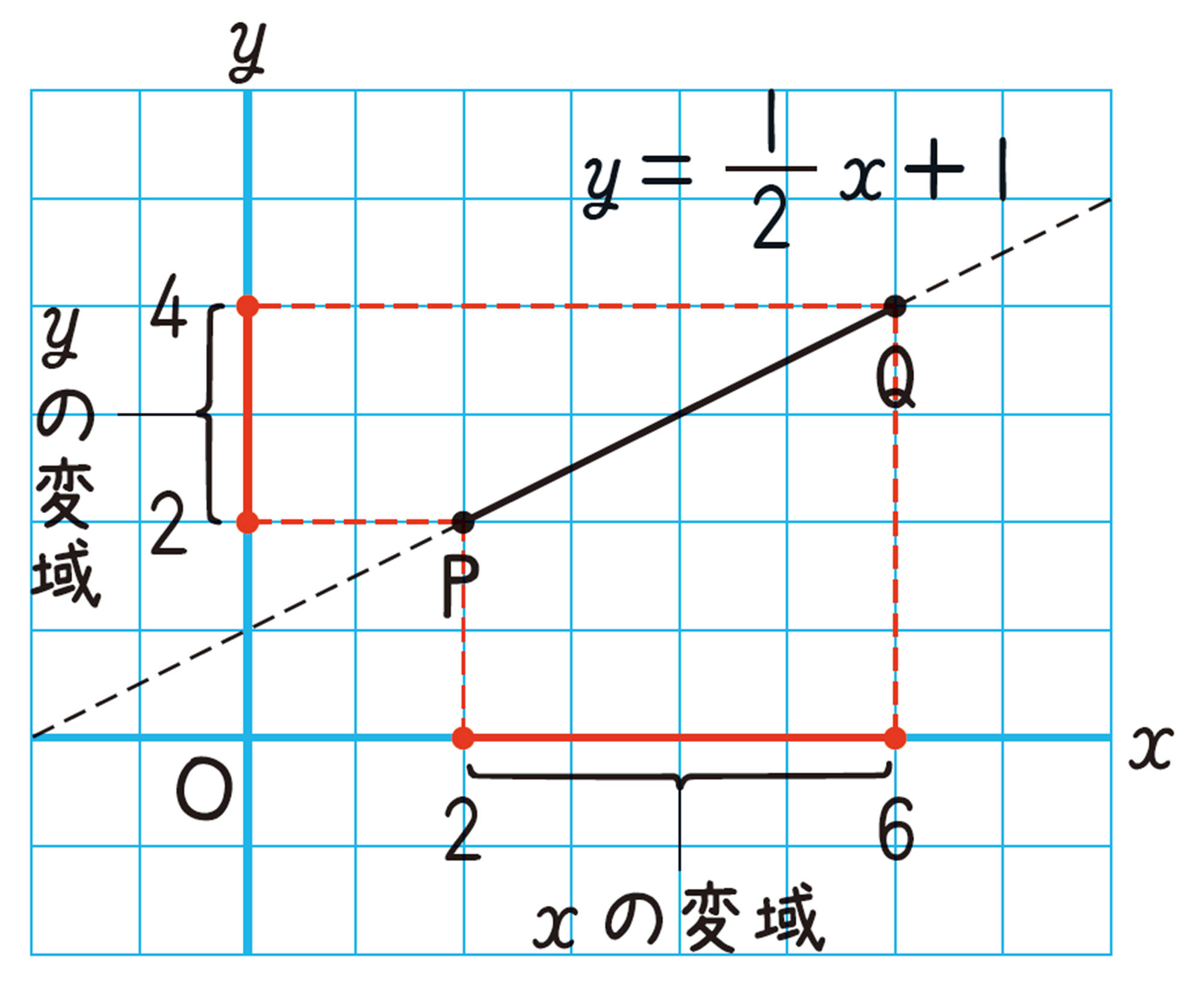
例 ２ [mathjax]\( x \) の変域が [mathjax]\( 2 \leqq x \leqq 6 \) のとき，1次関数 [mathjax]\( y= \dfrac{1}{2}x+1 \) のグラフをかきなさい。また， [mathjax]\( y \) の変域を求めなさい。
解答
[mathjax] \( x=2 \) のとき[mathjax] \( y=2 \)
[mathjax] \( x=6 \) のとき[mathjax] \( y=4 \)
したがって， グラフは， 2点P [mathjax]\( (2,2) \) ，Q [mathjax]\( (6,4) \) を結ぶ線分PQになる。
このグラフから， [mathjax] \(y\) の変域は，
[mathjax] \( 2 \leqq y \leqq 4 \)
であることがわかる。
答 [mathjax] \(2 \leqq y \leqq 4\)
問 ２ [mathjax] \( x \) の変域が [mathjax] \( -1 \lt x \leqq 3 \) のとき，1次関数 [mathjax] \( y=-2x+2 \) のグラフを，右の図にかき入れなさい。
また， [mathjax] \( y \) の変域を求めなさい。
直線の式の求め方
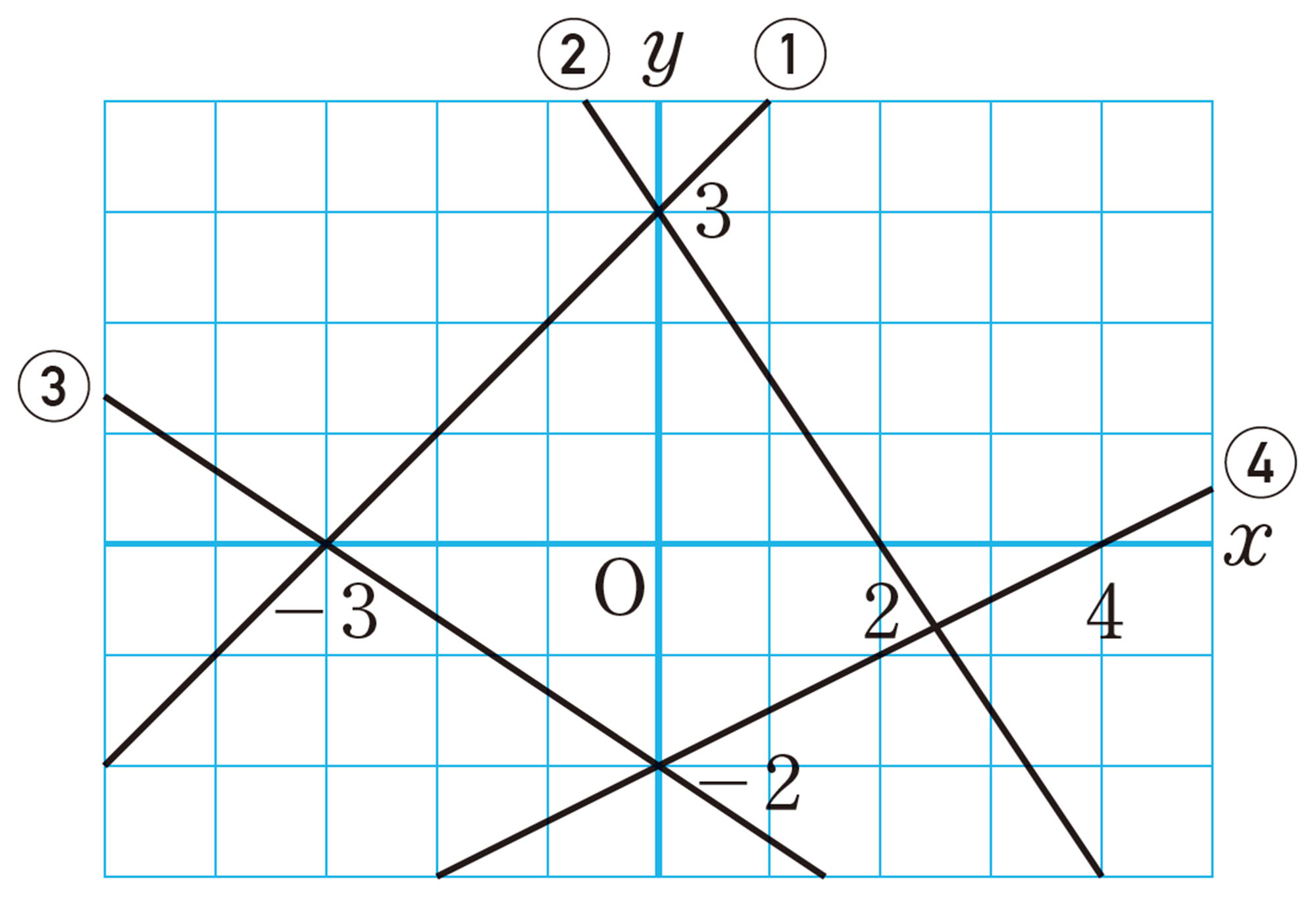
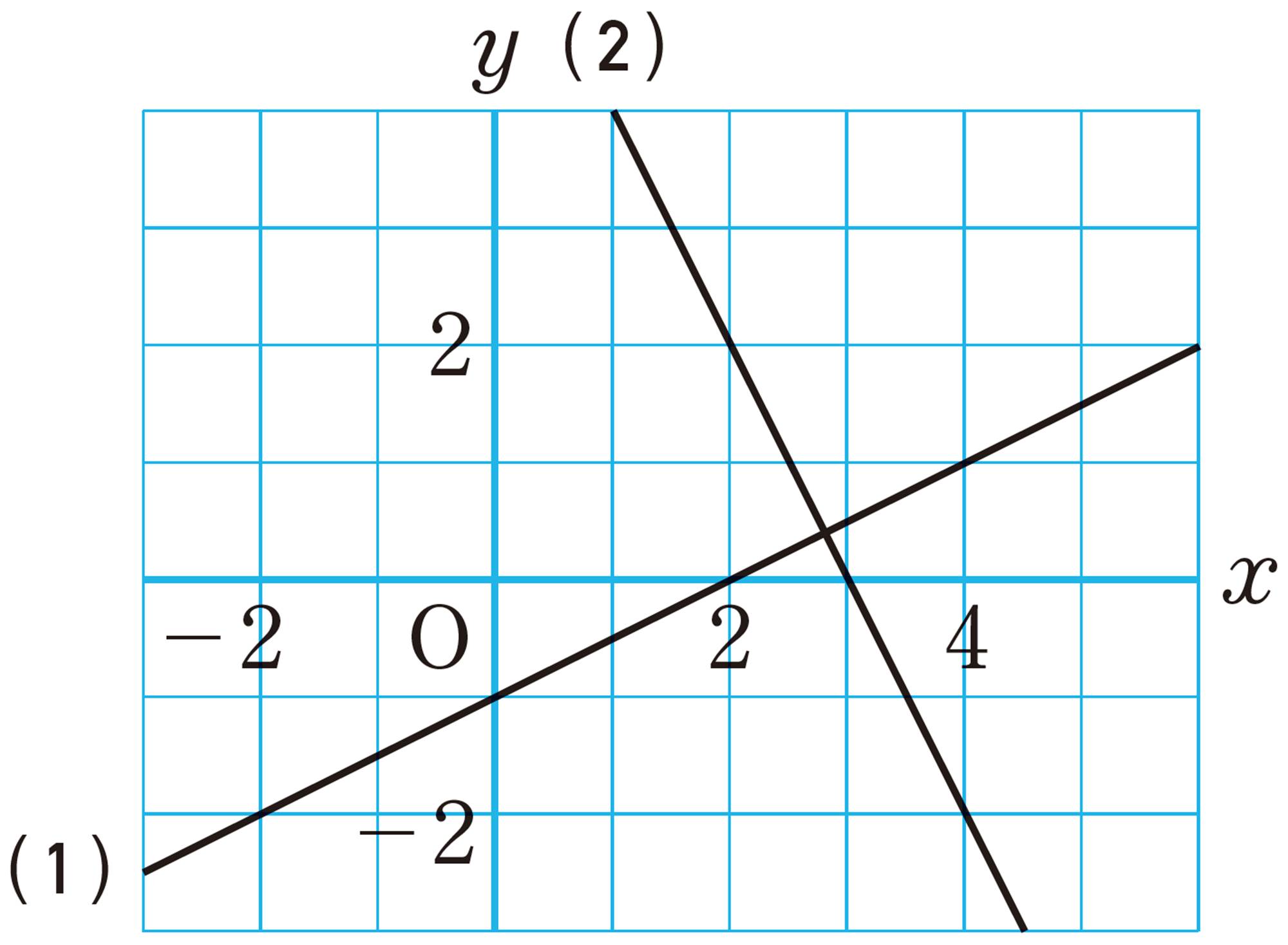
Q Question
右の直線をグラフとする1次関数の式を求める方法を考えてみましょう。
見方・考え方
どこに着目して考えればいいかな。
何がわかれば [mathjax] \( y \) を [mathjax] \( x \) の式で表せるかな。
<2年p.84>
例 ３ 前ページのQの直線をグラフとする1次関数の式を求めなさい。
考え方 求める式を [mathjax]\( y=ax+b \) として，傾き [mathjax]\( a \) ，切片 [mathjax]\( b \) の値をグラフから読み取る。
解答
求める式を[mathjax] \(y=ax+b\) とする。
グラフが点 [mathjax]\( (0,2) \) を通るから，
[mathjax]\( b=2 \)
また， グラフ上のある点から右へ3進むと上へ2進むから，
[mathjax]\( a= \dfrac{2}{3} \)
したがって， 求める1 次関数の式は，
[mathjax] \( y= \dfrac{2}{3}x+2 \)
答 [mathjax]\(y= \dfrac{2}{3}x+2\)
例3で求めたような1次関数の式を，直線の式ともいう。
問 ３ 右の図の直線①〜④の式を求めなさい。
1点の座標と傾きがわかっているときの直線の式を求めてみよう。
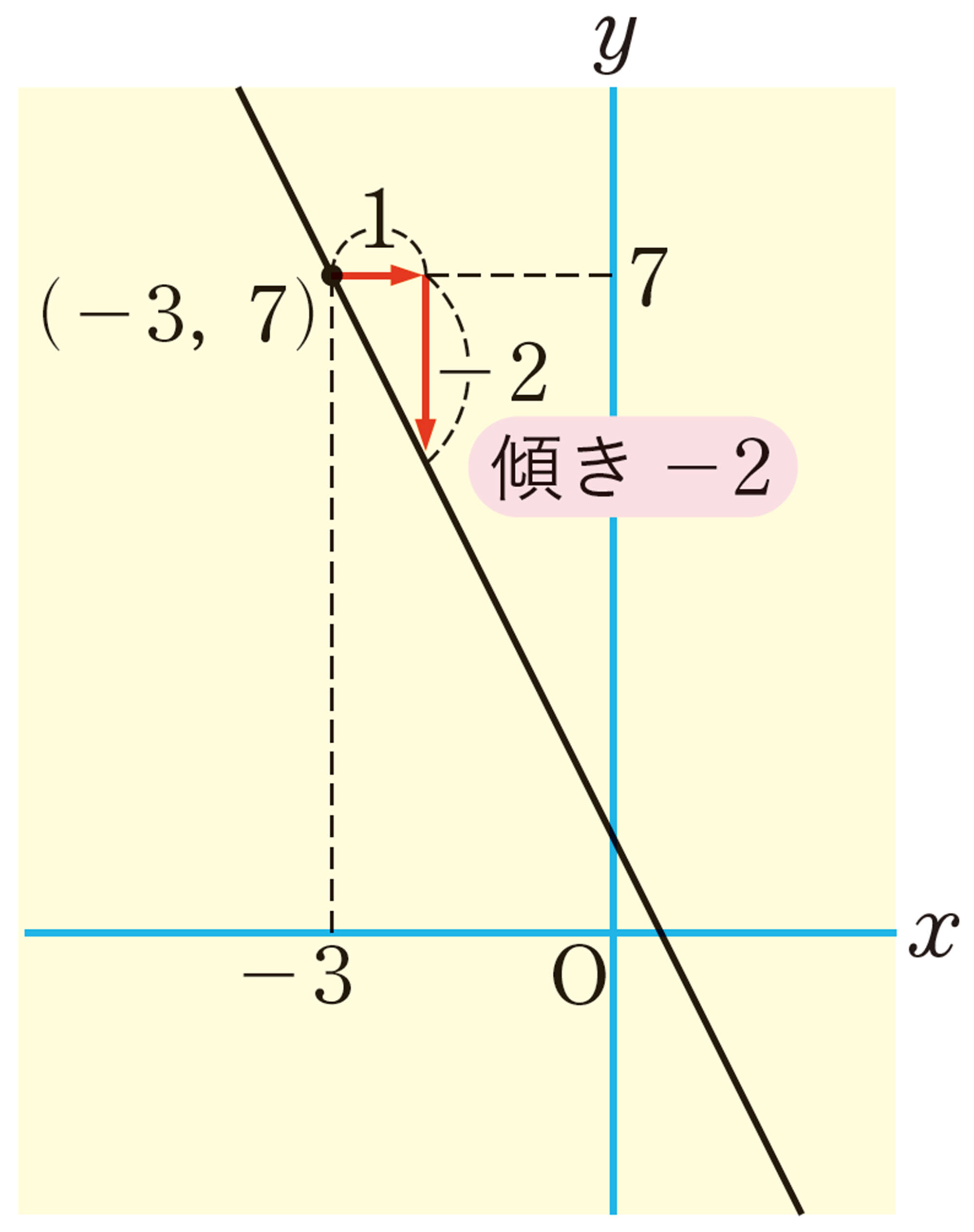
例 ４ 点 [mathjax] \( (-3,7) \) を通り，傾きが[mathjax] \( -2 \)の直線の式を求めなさい。
解答
求める直線の式を[mathjax] \( y=ax+b \) とする。
傾きが-2 より， [mathjax] \(a=-2 \) となるから，
[mathjax] \( y=-2x+b \)･･････①
この直線が点 [mathjax] \( (-3,7) \) を通るから，
[mathjax] \(x=-3 \) ，[mathjax] \(y=7 \) を①に代入すると，
[mathjax] \( 7=-2 \times (-3)+b \)
これを解くと，
[mathjax] \( b=1 \)
したがって， 求める直線の式は，
[mathjax] \( y=-2x+1 \)
答 [mathjax] \(y=-2x+1\)
<2年p.85>
問 ４ 次の直線の式を求めなさい。
⑴ 点 [mathjax] \( (2,4) \) を通り，傾きが3の直線
⑵ 点 [mathjax] \( (-1,2) \) を通り，傾きが [mathjax] \( – \dfrac{2}{3} \) の直線
⑶ 点 [mathjax] \( (3,5) \) を通り，直線 [mathjax] \( y=x \) に平行な直線
平行な2つの直線の傾きは，どうなっていたかな。
2点の座標がわかっているときの直線の式を求めてみよう。
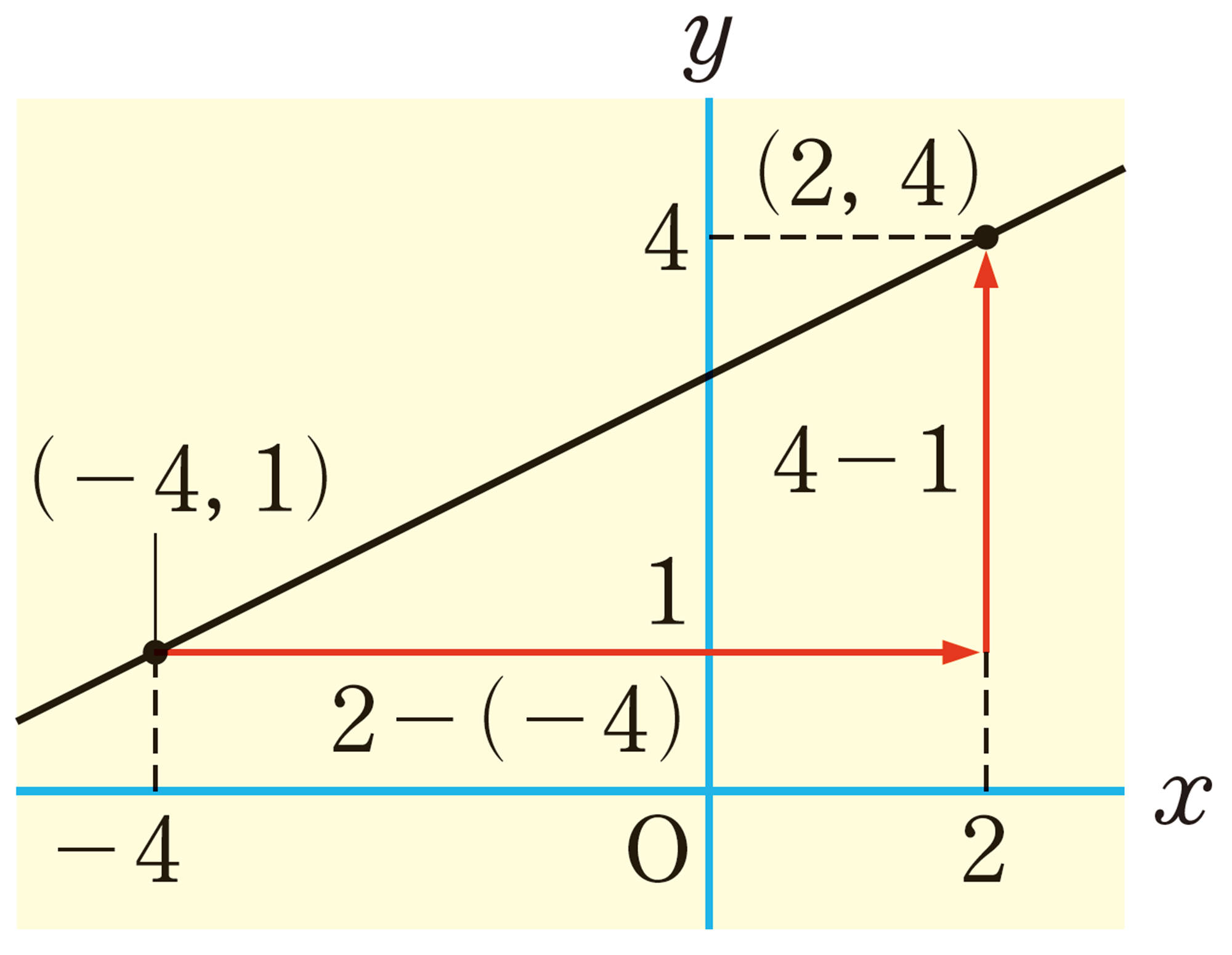
例 ５ 2点 [mathjax] \( (-4,1) \) ， [mathjax] \( (2,4) \) を通る直線の式を求めなさい。
解答
求める直線の式を[mathjax] \( y=ax+b \) とする。
この直線が2点 [mathjax] \( (-4, 1) \) ， [mathjax] \( (2, 4) \) を通るから， 直線の傾き[mathjax] \( a \) は，
[mathjax] \( a= \dfrac{4-1}{2-(-4)}= \dfrac{1}{2} \)
よって，[mathjax] \( y= \dfrac{1}{2}x+b \) ･･････①
[mathjax] \( x=-4 \) ， [mathjax] \( y=1 \) を①に代入すると，
[mathjax] \( 1= \dfrac{1}{2} \times (-4)+b \)
これを解くと， [mathjax] \( b=3 \)
したがって， 求める直線の式は，
[mathjax] \( y= \dfrac{1}{2}x+3 \)
答 [mathjax] \( y= \dfrac{1}{2}x+3 \)
[mathjax] \( y= \dfrac{1}{2}x+b \) に， [mathjax] \( x=2 \) ， [mathjax] \( y=4 \) を代入しても， [mathjax] \( b \) を求められるかな。
問 ５ 拓真さんは，例5について，次のように考えました。
求める直線の式を [mathjax] \( y=ax+b \) とする。
[mathjax] \( x=-4 \) のとき [mathjax] \( y=1 \) であるから， [mathjax] \( 1=-4a+b \) ･･････①
[mathjax] \( x=2 \) のとき [mathjax] \( y=4 \) であるから， [mathjax] \( 4=2a+b \) ･･････②
①，②を連立方程式として解き， [mathjax] \( a \) ， [mathjax] \( b \) の値を求めればよい。
拓真さんの考え方で，直線の式を求めなさい。
問 ６ 次の直線の式を求めなさい。
⑴ 2点 [mathjax] \( (-3,11) \) ， [mathjax] \( (4,-10) \) を通る直線
⑵ [mathjax] \( x=-3 \) のとき [mathjax] \( y=4 \) ， [mathjax] \( x=3 \) のとき [mathjax] \( y=1 \) の直線
<2年p.86>
問 7 次の図の直線の式を求めなさい。
どんなことがわかったかな
2点を決めてグラフをかいたり，傾きや切片から直線の式を求めたりすることができます。
次の課題へ！
1次関数の式 [mathjax]\( y=-2x+1 \) と2元 1次方程式 [mathjax]\( 2x+y=1 \) は似ているけど，共通点はあるのかな？
P.87
確かめよう 1節 1次関数
１ 音が空気中を伝わる速さは，気温によって変化します。次の表は，それらの関係を表したものです。このとき，下の問いに答えなさい。
⑴ 気温が1℃上がると，音の速さはどのように変化しますか。
⑵ 気温が [mathjax]\( x \) ℃のときの音の速さを [mathjax]\( y \) m/sとして， [mathjax]\( y \) を [mathjax]\( x \) の式で表しなさい。
２ 1次関数 [mathjax]\( y= \dfrac{1}{2}x-2 \) について，次の問いに答えなさい。
⑴ 変化の割合をいいなさい。
⑵ [mathjax]\( x \) の増加量が6のときの [mathjax]\( y \) の増加量を求めなさい。
⑶ グラフを，下の図にかき入れなさい。
３ 次の直線の式を求めなさい。
⑴ 左の図の直線㋐
⑵ 点 [mathjax]\( (-1,0) \) を通り，傾きが3の直線
⑶ 2点 [mathjax]\( (-2,4) \) ， [mathjax]\( (5,-3) \) を通る直線
