<2年p.64>
2章のまとめの問題 解答 P.247〜248 基本
1 2元1次方程式 [mathjax]\( 2x+y=8 \) について,次の問いに答えなさい。
⑴
は,この方程式の解といえますか。
⑵ [mathjax]\( x \) ,[mathjax]\( y \) を自然数とするとき,この方程式の解をすべて求めなさい。
2 次の連立方程式を解きなさい。
⑴
⑵
⑶
⑷
⑸
⑹
3 ある美術館の入館料は,大人1人と中学生3人では1550円,大人2人と中学生5人では2750円です。大人1人,中学生1人の入館料を,それぞれ求めなさい。
5 連立方程式の一方の方程式が [mathjax]\( x+y=9 \) になるような問題をつくりなさい。また,その問題を解いて答えを求めなさい。
<2年p.65>
応用
1 次の連立方程式を解きなさい。
⑴
⑵
⑶
⑷ [mathjax]\( 5x-3y+1=4x-2y=10-6x+3y \)
2 2組の連立方程式
が同じ解をもつとき,[mathjax]\( a \) ,[mathjax]\( b \) の値を求めなさい。
3 現在,父親の年齢は子どもの年齢の3倍ですが,15年後には,父親の年齢が子どもの年齢の2倍になります。現在の父親と子どもの年齢を,それぞれ求めなさい。
4 ある町の人口を調べたところ,5373人でした。これを昨年の調査と比べると,男性は2%減り,女性は4%増え,合計では48人増えています。この町の昨年の男性と女性の人口を,それぞれ求めなさい。
6 2桁の自然数があります。その十の位の数と一の位の数の和は12です。また,その十の位の数と一の位の数を入れかえてできる自然数は,もとの自然数より18大きくなります。もとの自然数を求めなさい。
<2年p.66>
活用
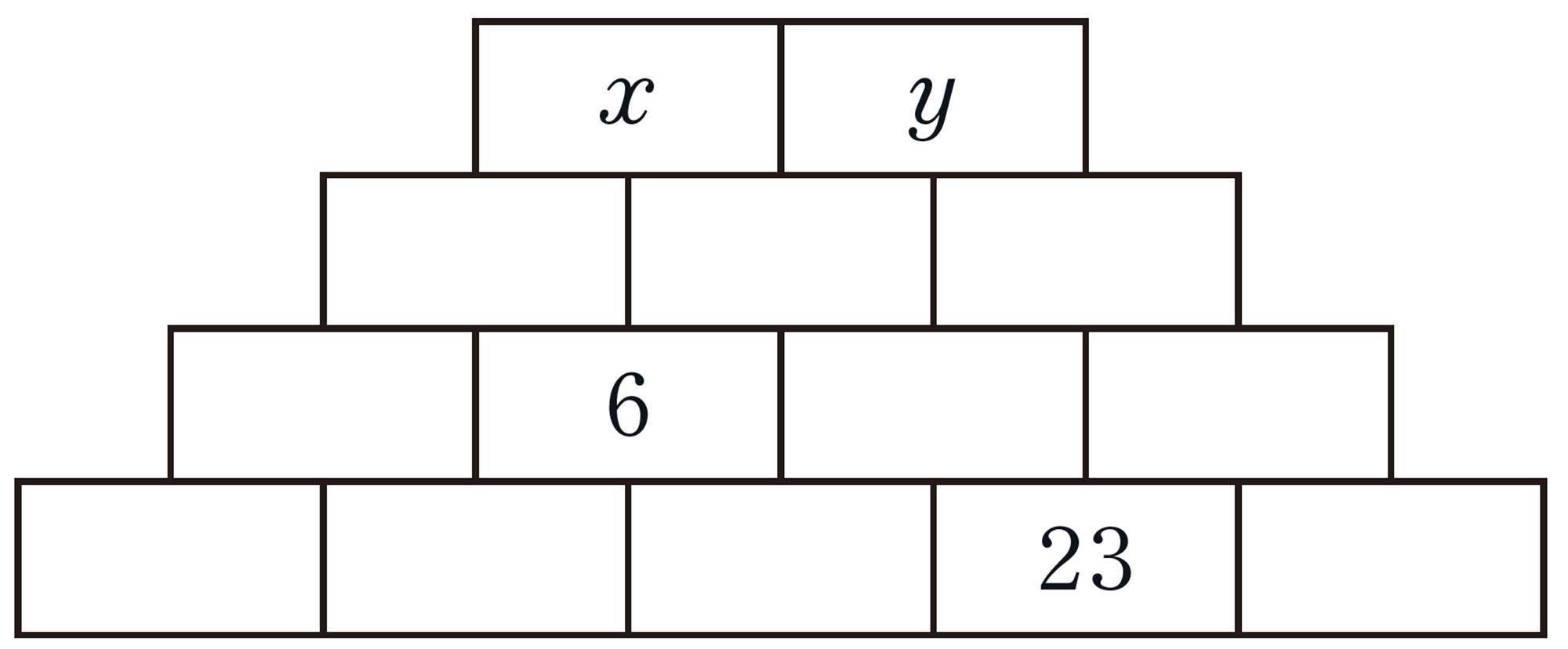
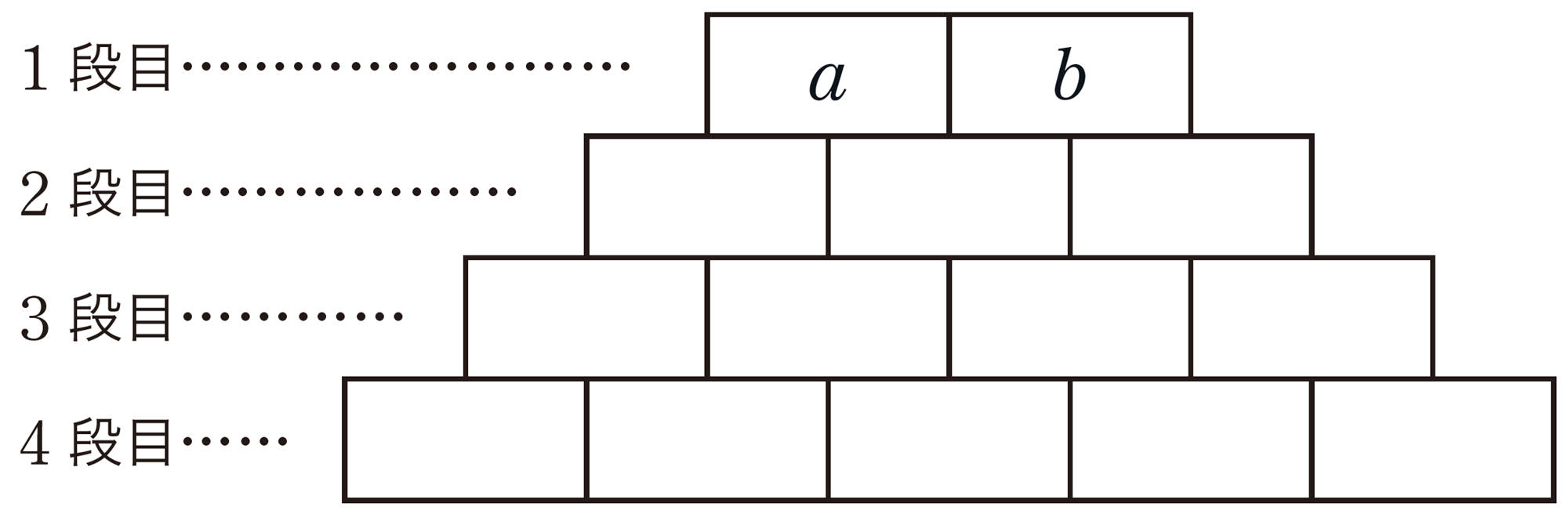
1 次の図のように,あるきまりにしたがって,数を上から順に並べました。
この図について,下の問いに答えなさい。
⑴ どんなきまりにしたがってつくられていますか。1段目に入る数を [mathjax]\(a \) ,[mathjax]\( b \) として,次の図を完成させなさい。
⑵ ⑴の図で,[mathjax]\( a \) ,[mathjax]\( b \) を整数とするとき,4段目の中央に入る数はどんな数だといえますか。次の㋐〜㋔で,正しいものをすべて選びなさい。
㋐ 偶数
㋑ 奇数
㋒ 3の倍数
㋓ 6の倍数
㋔ 1段目の2数の和の3倍の数
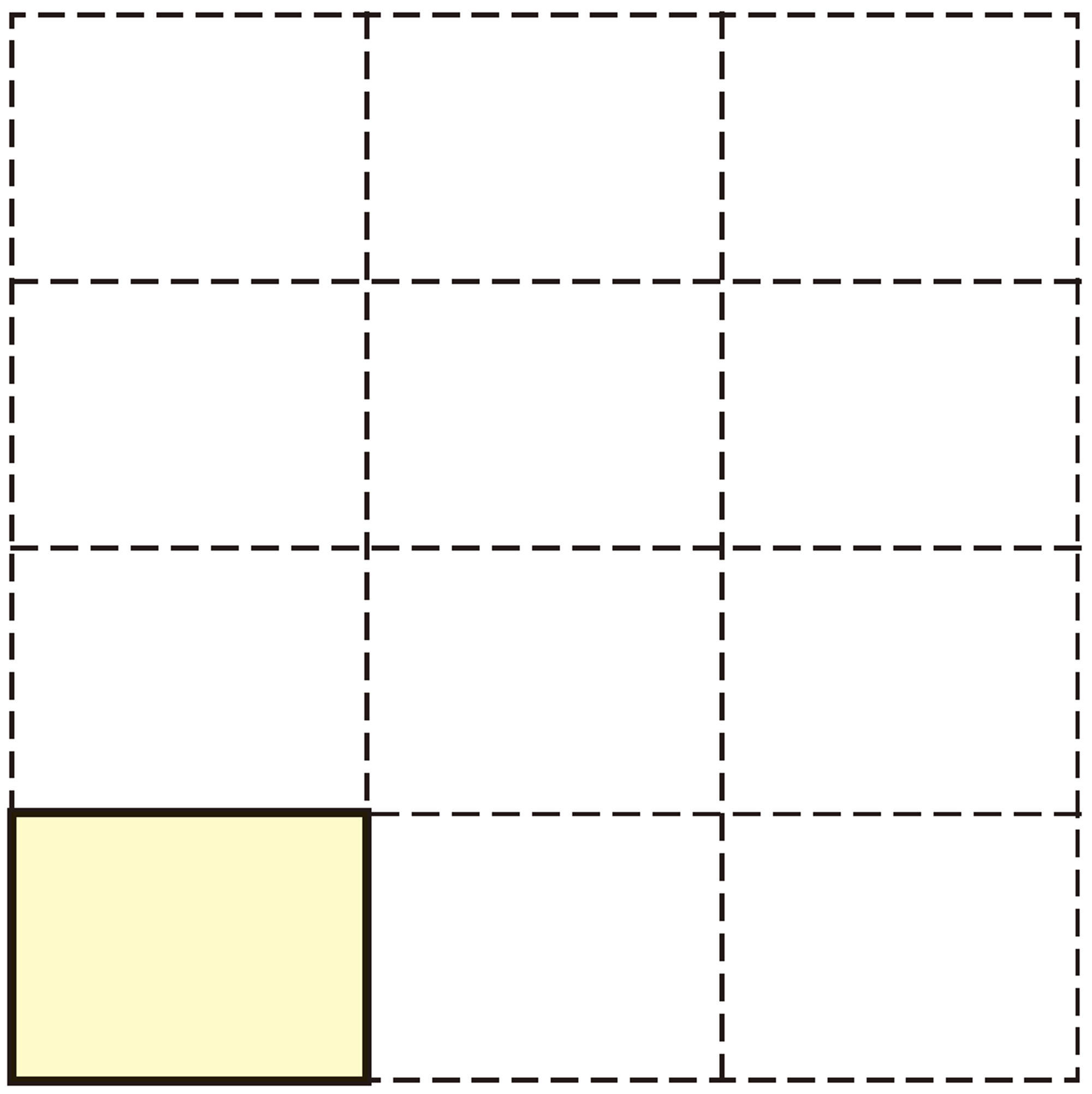
⑶ 次の図のように,2か所だけ数がわかっています。このとき,1段目に入る数を[mathjax]\( x \) ,[mathjax]\( y \) として,その値を求めなさい。
<2年p.67>
深めよう CTスキャンと数学 発展
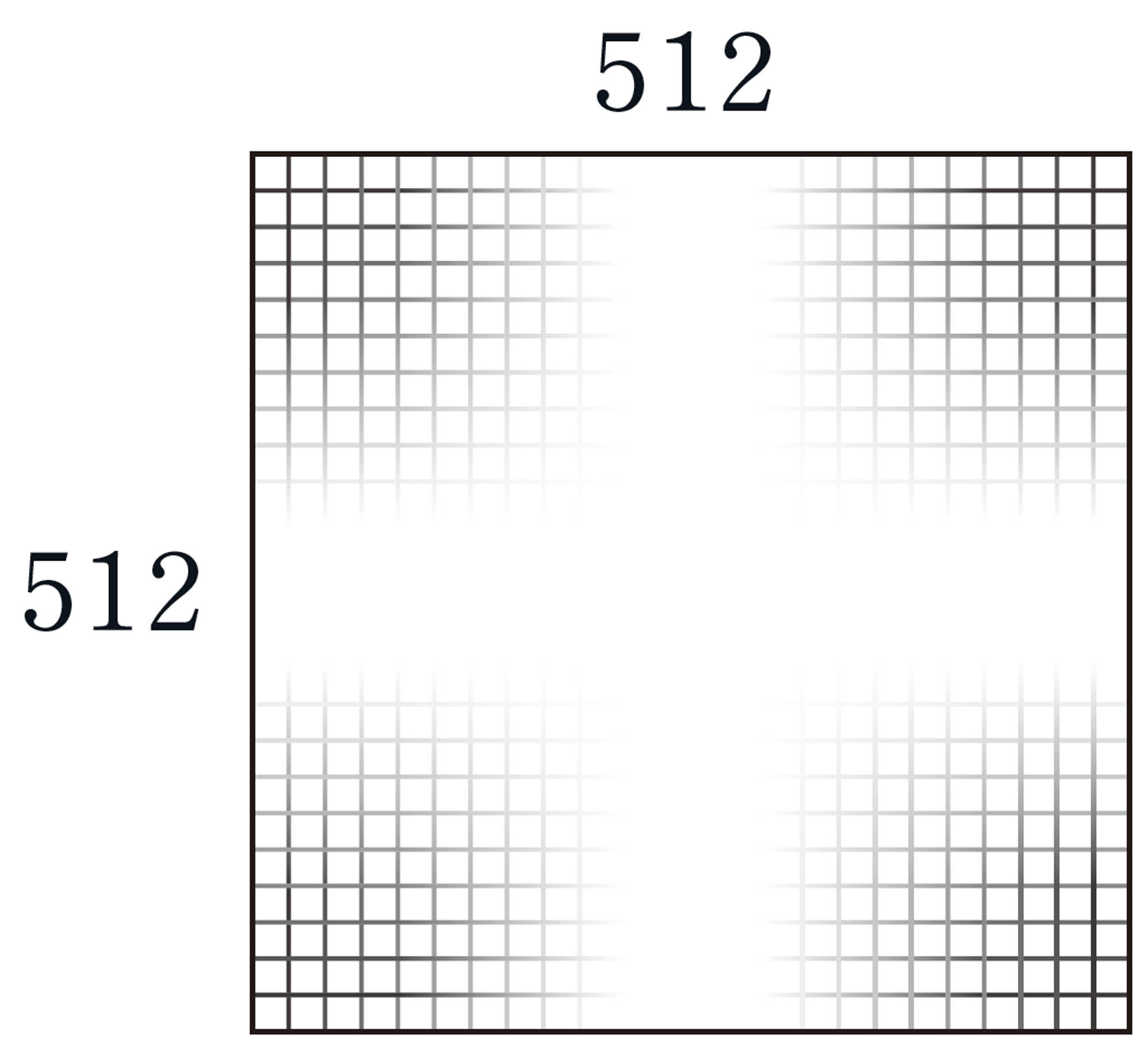
この場合,[mathjax]\( (512 \times 512) \) 個に分割して計算するのが一般的ですが,ここでは,簡単な例として,物体の断面を[mathjax]\( (2 \times 2) \) 個に分割した場合を考えてみましょう。
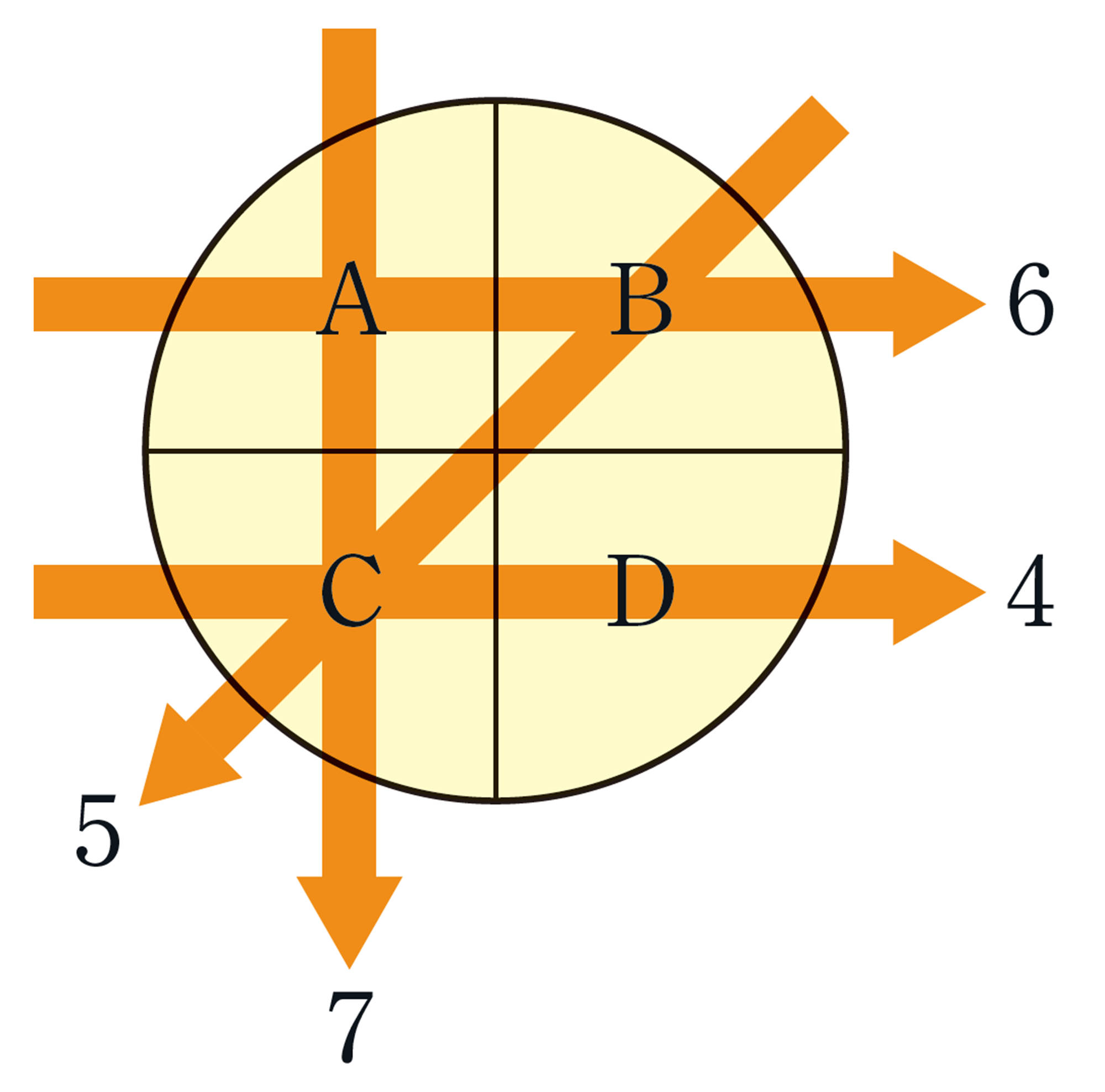
調べる部分をA,B,C,Dの4つとして,X線を右の図のようにあてたとき,それぞれ図のような値が出たとしてこの関係を連立方程式で表すと,次のようになります。
このような連立方程式を解くことで,各部分のX線の吸収率を求めることができます。
① 上の連立方程式をどのように解けばよいか考えてみましょう。
② X線をあてて出た数値を自分で決めて,A,B,C,Dそれぞれの値を連立方程式で解いて求めてみましょう。
>> 関連する職業・仕事 [医師,放射線技師]