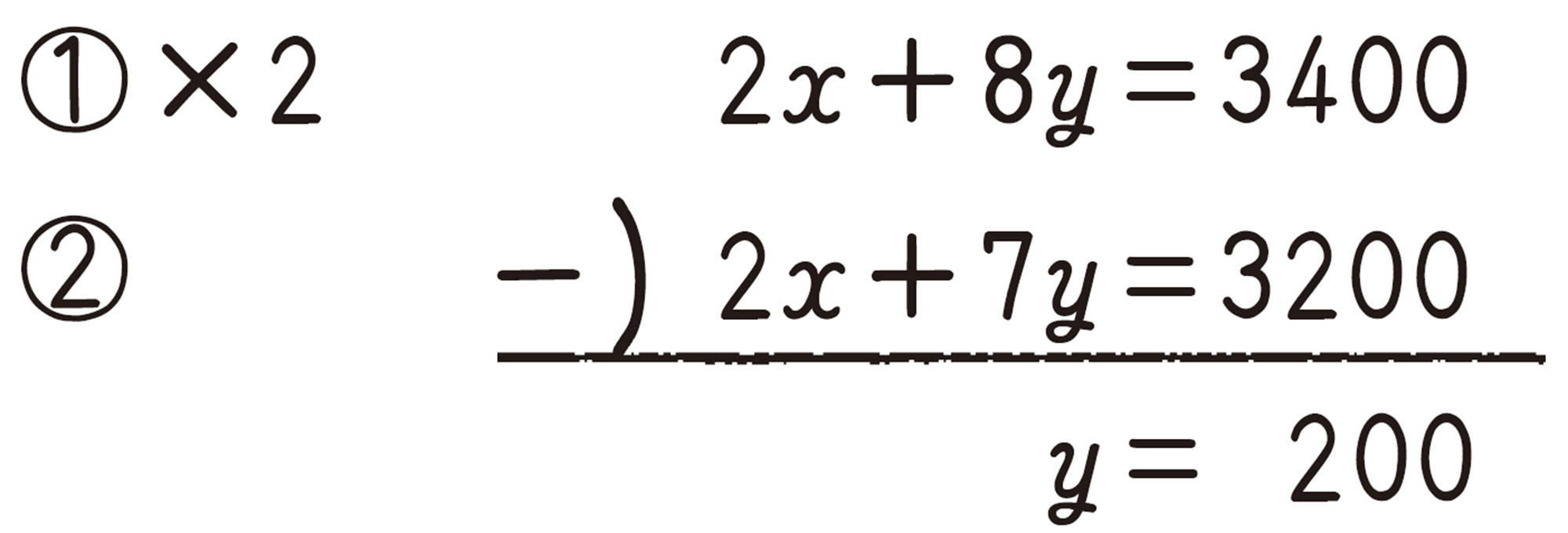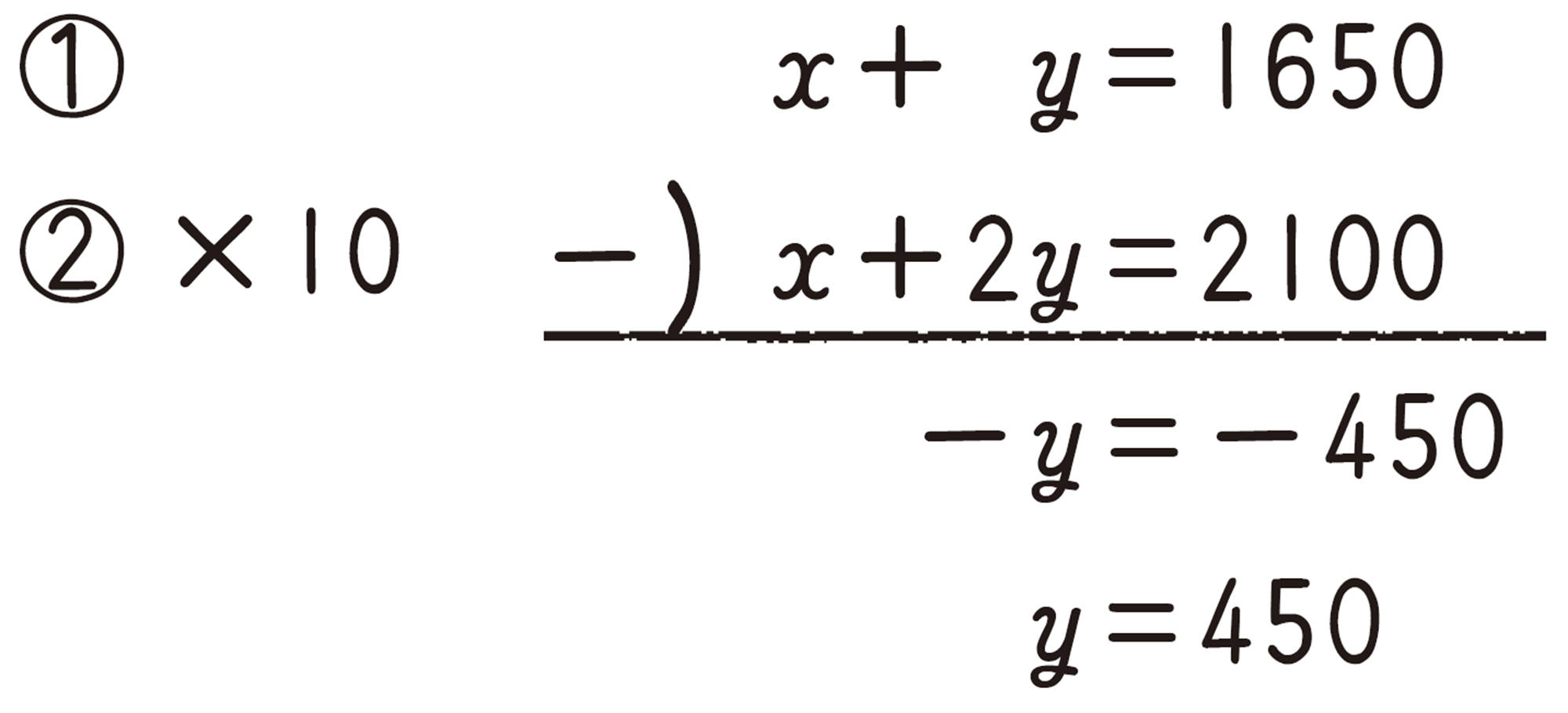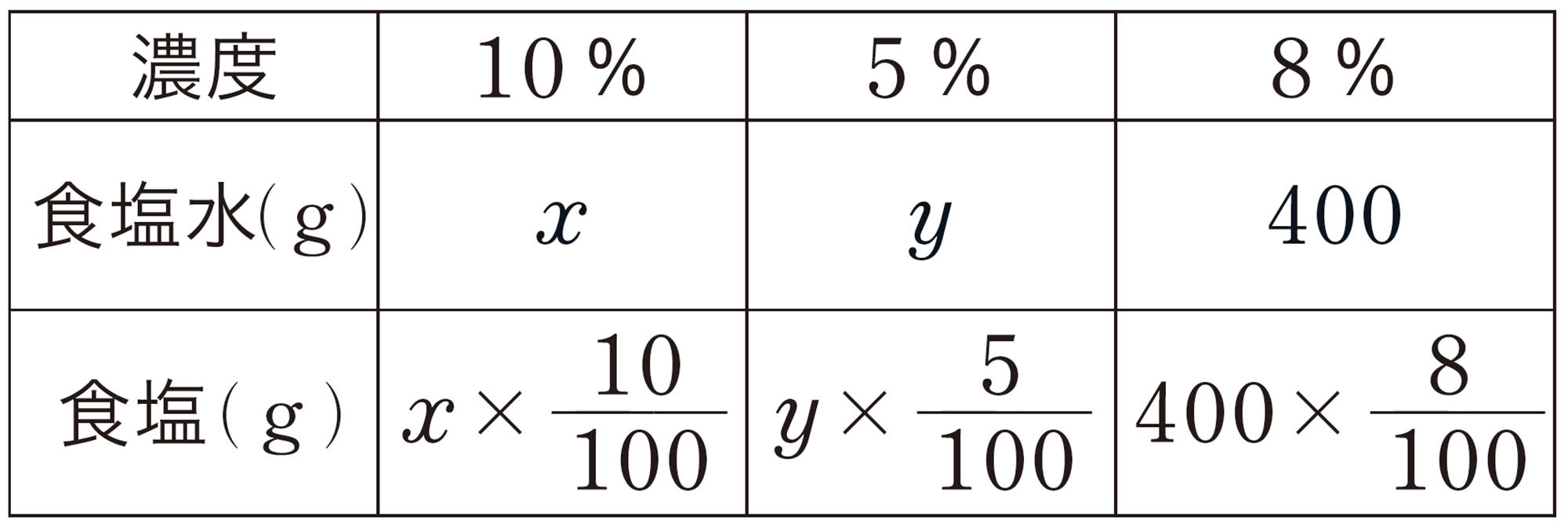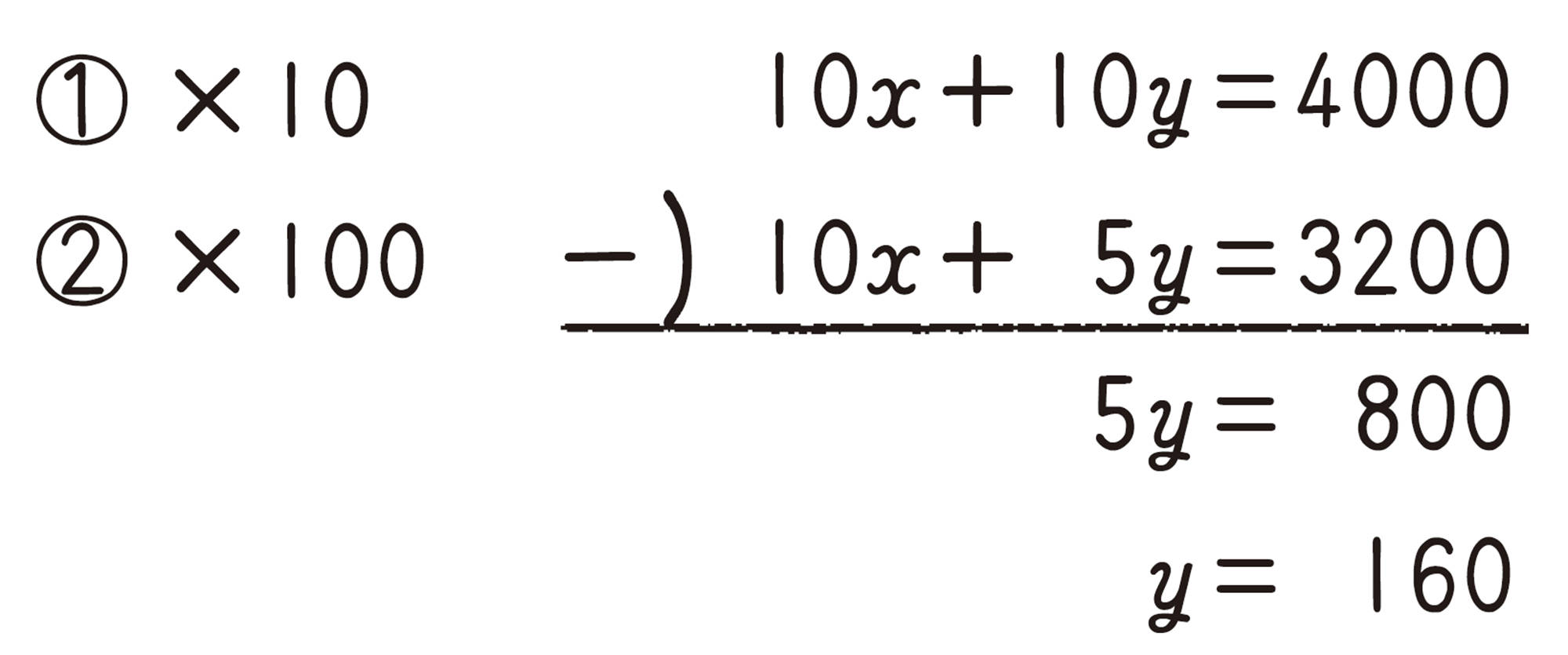教科書アドバイザー「マスマス！」

gkt-horizontal-line

<2年p.56>

２節　連立方程式の利用

連立方程式が使えるかな？

身のまわりの問題の解決のしかたを考えてみましょう。

avatar

具体的な場面で方程式を使ってみたいな。

　どんなふうに方程式を使えばいいのかな。

avatar

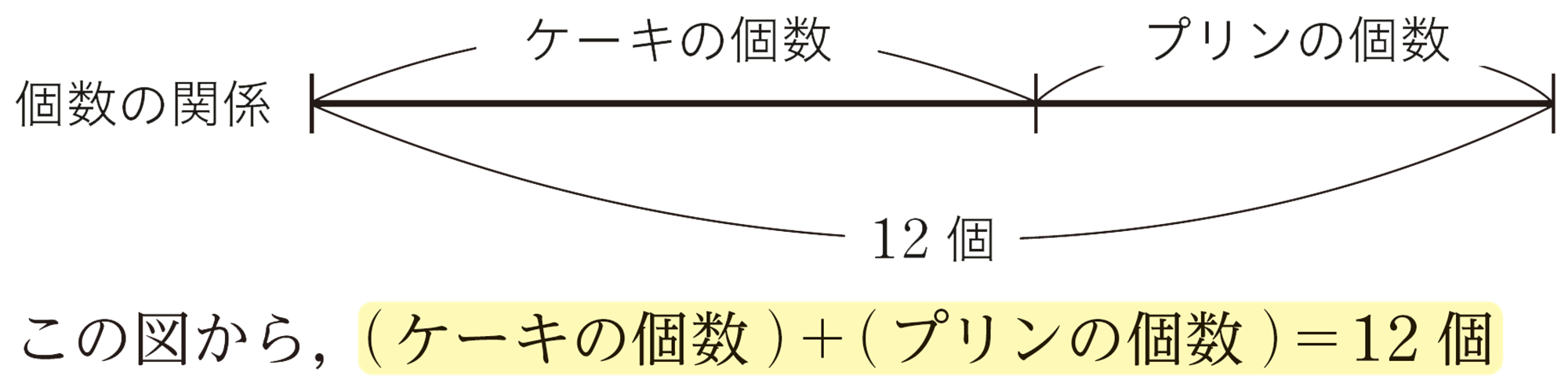
【１】　1個200円のケーキと1個120円のプリンを合わせて12個買い，代金の合計が2000円になるようにします。ケーキとプリンを，それぞれ何個買えばよいでしょうか。

avatar

　1元1次方程式でも，解けそうだね。

　連立方程式にした方が，式をつくりやすいと思う。

avatar

【２】　方程式を使って，問題を解決する手順を説明しましょう。

問題にふくまれている数量の関係を図やことばの式で表すと，次のようになる。

次の課題へ！
1次方程式のとき，どのような手順で問題を解いたかな？
P.57

<2年p.57>

１　連立方程式の利用

　目標　▷　連立方程式を利用して，身のまわりの問題を解決しよう。

　問１　　前ページの問題を，連立方程式をつくって解きなさい。また，その解が問題に適しているかどうかを確かめなさい。

おしえて！
P.62
解が問題に適しているか，いつも確かめないといけないのかな？

連立方程式を利用して問題を解く手順

❶ 図や表，ことばの式などを使って，数量の関係を見つける。
❷ 文字を使って連立方程式をつくる。
❸ 連立方程式を解く。
❹ 連立方程式の解が問題に適しているかどうかを確かめ，適していれば問題の答えとする。

　問２　　35人の生徒を5人の班と4人の班に分け，全部で8班とするとき，それぞれの班の数を求めます。このとき，次の問いに答えなさい。

⑴　数量の関係を，図とことばの式で表しなさい。

班の数の関係

人数の関係

⑵　⑴の図やことばの式から，連立方程式をつくりなさい。

⑶　⑵でつくった連立方程式を解きなさい。

⑷　⑶で求めた連立方程式の解が問題に適しているかどうかを確かめ，問題の答えを求めなさい。

gkt-horizontal-line

<2年p.58>

　例１　　ある公園の入園料は，大人1人と中学生4人では1700円，大人2人と中学生7人では3200円です。大人1人，中学生1人の入園料は，それぞれいくらですか。

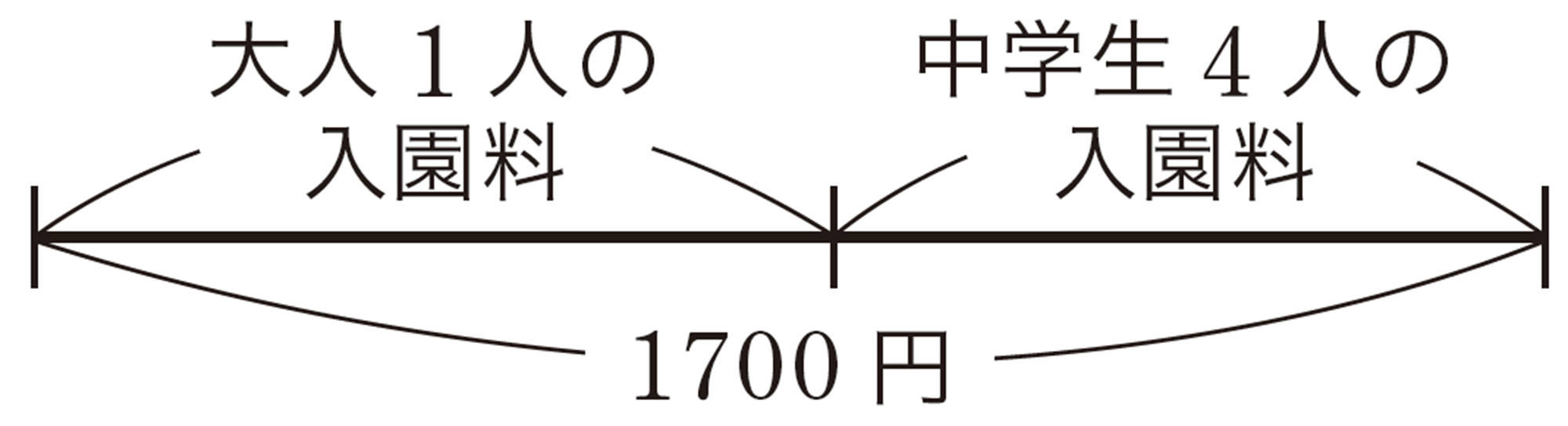
　考え方　　問題にふくまれている数量の関係は，次のようになる。

[mathjax]\( ( \mathsf{大人}1 \mathsf{人の入園料})+( \mathsf{中学生}4 \mathsf{人の入園料})=1700\)円
[mathjax]\( ( \mathsf{(大人}2 \mathsf{人の入園料})+( \mathsf{中学生}7 \mathsf{人の入園料})=3200\)円

解答

大人1人の入園料を [mathjax]\( x \) 円，中学生1人の入園料を [mathjax]\( y \) 円とすると，

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} x+4y=1700 & \cdots \cdots ①\\ 2x+7y=3200 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

[mathjax]\(\begin{array}{lr} ① \times 2 & 2x+8y=3400\\ ② &\underline{-\big{)}2x+7y=3200} \\ & y=\phantom{0}200 \end{array}\)

[mathjax]\( y=200 \) を①に代入すると，

[mathjax] \( \begin{eqnarray} x+4 \times 200 &=& 1700 \\ x &=& 900 \end{eqnarray} \)

大人1人の入園料900円，中学生1人の入園料200円は，問題に適している。

答　大人1 人900円，中学生1 人200円

　問３　　重さのちがうおもりA，Bがあります。A3個とB2個の重さの合計は190g，A4個と B6個の重さの合計は320gです。A1個，B1個の重さは，それぞれ何gですか。

gkt-horizontal-line

<2年p.59>

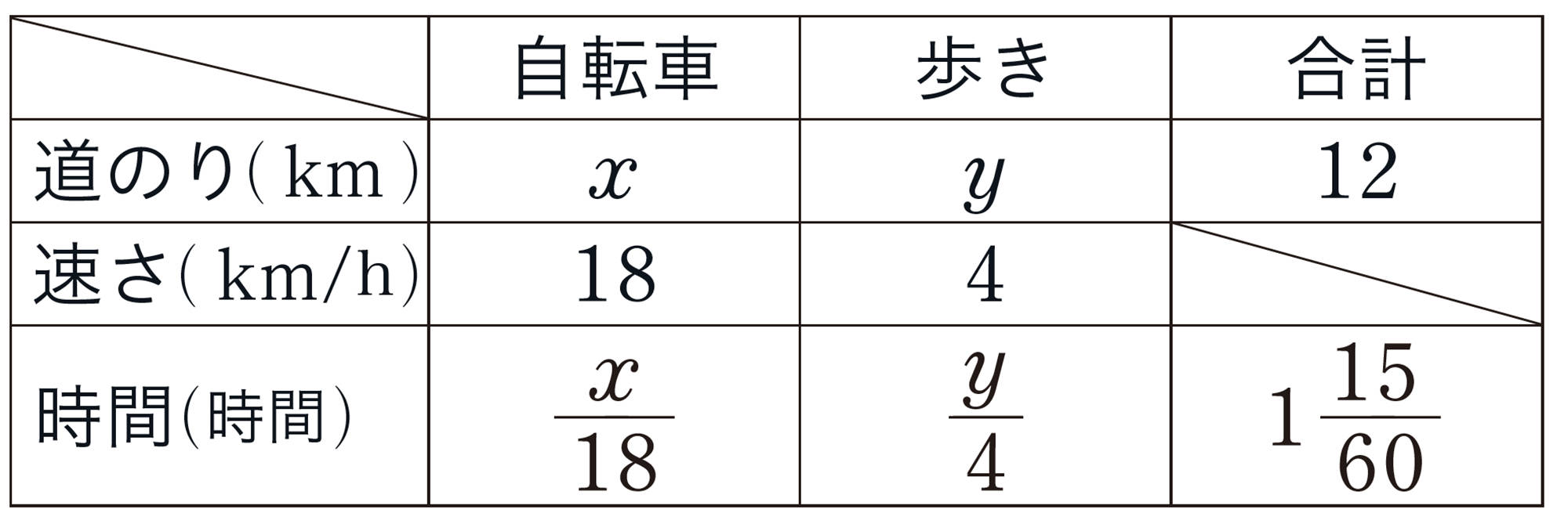
　例２　　家から12km離れた公園まで行きました。最初は自転車に乗って時速18kmで走っていましたが，途中でタイヤがパンクしたため，そこからは時速4 kmで自転車を押して歩き，全体で1時間15分かかりました。

自転車で走った道のりと歩いた道のりを求めなさい。

　考え方　　問題にふくまれている数量の関係は，次のようになる。

数量の関係をもとに，自転車で走った道のりを [mathjax] \( x \) km，歩いた道のりを [mathjax] \( y \) kmとして整理すると，次の表のようになる。

ふりかえり

小学校5年

[mathjax] \( ( \mathsf{時間})= \dfrac{( \mathsf{道のり})}{( \mathsf{速さ})} \)

解答

自転車で走った道のりを[mathjax] \( x \) km，歩いた道のりを [mathjax] \( y \) km とすると，

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} x+y=12 & \cdots \cdots ①\\ \dfrac{x}{18}+ \dfrac{y}{4}=1 \dfrac{15}{60} & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

[mathjax]\(\begin{array}{r} ①\times 2\phantom{000000} \ 2x+2y=24\\ \phantom{0} ②\times36\quad\underline{-\big{)} \phantom{0} 2x+9y=45\phantom{0}}\\ -7y=-21 \ y=3\phantom{00} \end{array}\)

[mathjax]\( \begin{eqnarray} \require{physics} \left(\dfrac{x}{18}+ \dfrac{y}{4}\right) \times 36 &=& 1 \dfrac{15}{60} \times 36 \\ \dfrac{x}{18} \times 36+ \dfrac{y}{4} \times 36 &=& \dfrac{75}{60} \times 36 \\ 2x+9y &=& \dfrac{5}{4} \times 36 \\ 2x+9y &=& 45 \end{eqnarray} \)

[mathjax]\( y=3 \) を①に代入すると，

[mathjax]\( \begin{eqnarray} x+3 &=& 12 \\ x &=& 9 \end{eqnarray} \)

自転車で走った道のり9 km，歩いた道のり3 kmは，問題に適している。

答　自転車で走った道のり9 km，歩いた道のり3 km

　問４　　例2で，自転車で走った時間を [mathjax]\( x \) 時間，歩いた時間を [mathjax]\( y \) 時間として連立方程式をつくり，問題の答えを求めなさい。

gkt-horizontal-line

<2年p.60>

　問５　　自動車に乗って，A町から90km離れたB町まで行きました。高速道路では時速80km，一般道路では時速50kmで走り，全体で1時間30分かかりました。高速道路を走った道のりと一般道路を走った道のりを求めなさい。

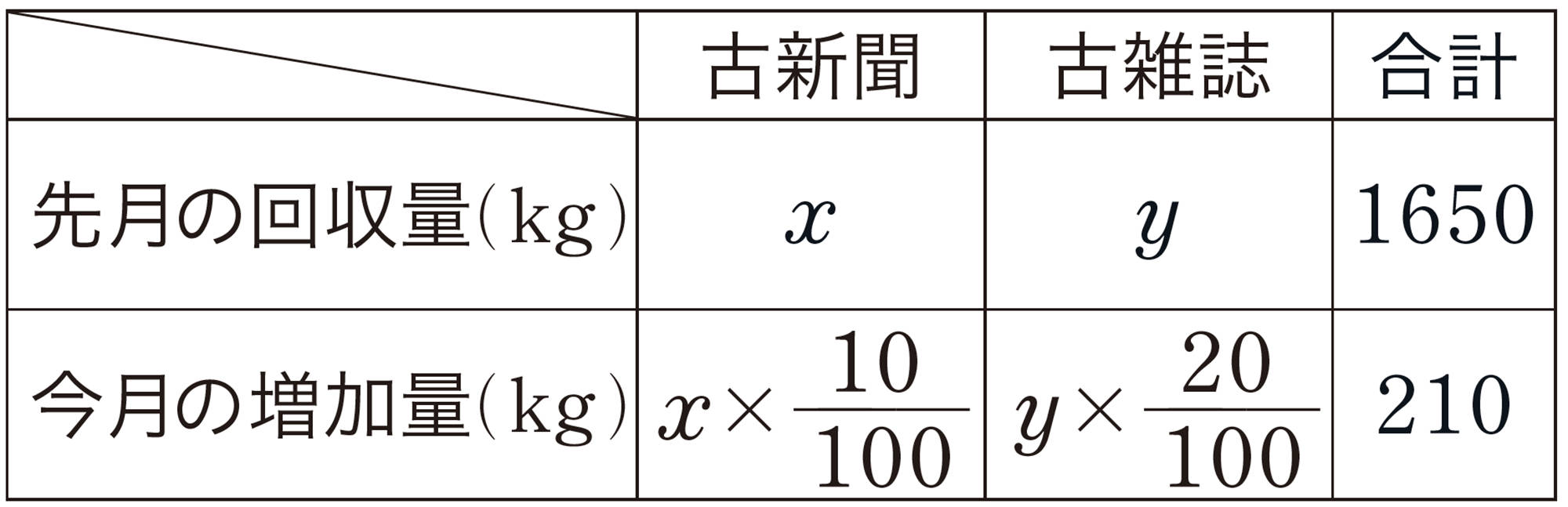
　例３　　資源回収のレポートに，先月は，古新聞と古雑誌を合わせて1650kg回収したと書かれていました。今月は，先月に比べ，古新聞が10％，古雑誌が20％それぞれ増え，合わせて210kg増えています。先月の古新聞と古雑誌の回収量は，それぞれ何kgですか。

　考え方　　数量の関係をもとに，先月回収した古新聞を [mathjax]\( x \) kg，古雑誌を [mathjax]\( y \) kgとして整理すると，右の表のようになる。

解答

先月回収した古新聞を [mathjax]\( x \) kg，古雑誌を [mathjax]\( y \) kgとすると，

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} x+y=1650 & \cdots \cdots ①\\ \dfrac{10}{100}x+ \dfrac{20}{100}y=210 & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

[mathjax]\(\begin{array}{lr} ① & x+\phantom{0}y=1650\\ ② \times 10 &\underline{-\big{)}x+2y=2100} \\ & -y=-450\\ & y=450\phantom{-} \end{array}\)

[mathjax]\( y=450 \) を①に代入すると，

[mathjax] \( \begin{eqnarray} x+450 &=& 1650 \\ x &=& 1200 \end{eqnarray}\)

先月回収した古新聞1200 kg，古雑誌450 kgは，問題に適している。

答　先月回収した古新聞1200kg，先月回収した古雑誌450kg

　問６　　ある中学校の昨年の全校生徒数は，男女合わせて220人でした。今年は，昨年と比べ，男子が5％増え，女子が2％減ったため，全体では4人増えています。次の問いに答えなさい。

⑴　昨年の男子と女子の人数を，それぞれ求めなさい。
⑵　今年の男子と女子の人数を，それぞれ求めなさい。

gkt-horizontal-line

<2年p.61>

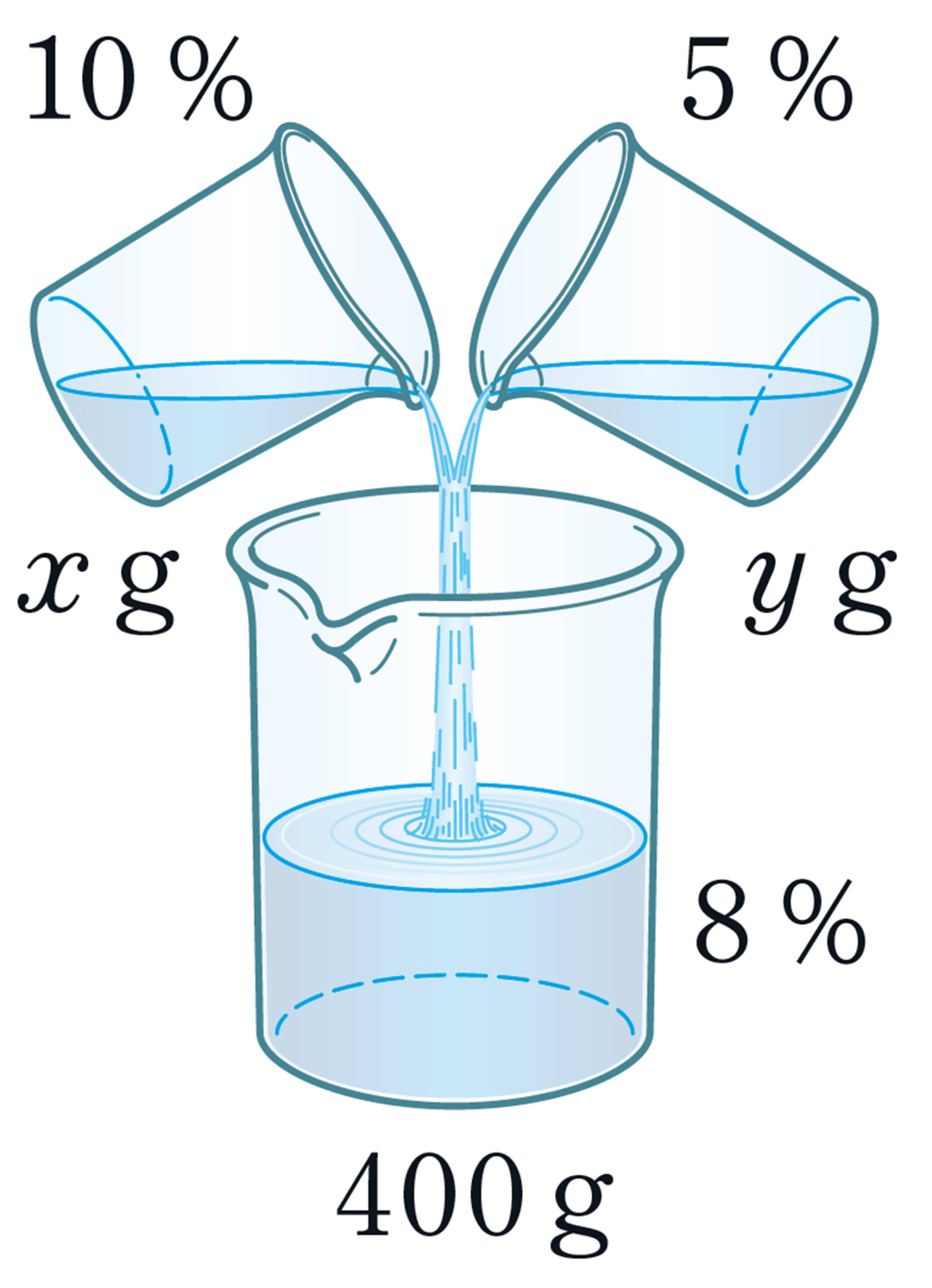
　例４　　10％の食塩水と5％の食塩水を混ぜて，8％の食塩水400gをつくります。それぞれ何gずつ混ぜればよいですか。

　考え方　　数量の関係をもとに，10％の食塩水を[mathjax]\( x \) g，5％の食塩水を [mathjax]\( y \) g混ぜるとして整理すると，次の表のようになる。

[mathjax]\(\begin{array}{|c|c|c|} \hline \mathsf{濃度}& 10\% & 5\% & 8\%\\ \hline \mathsf{食塩水}(g) & x & y & 400\\ \hline \mathsf{食塩}(g) & x \times \dfrac{10}{100} & y \times \dfrac{5}{100} & 400 \times \dfrac{8}{100}\\ \hline \end{array}\)

ふりかえり　

理科
[mathjax]\( \mathsf{食塩水の濃度}( \mathsf{％})= \dfrac{ \mathsf{食塩の量}( \text{g})}{ \mathsf{食塩水全体の量}( \text{g})} \times 100 \)

［例１］
水80gに食塩20gを溶かしたときの食塩水の濃度は20％になる。

［例２］
15％の食塩水200g中には，30gの食塩が溶けている。

解答

10％の食塩水を [mathjax]\( x \) g，5％の食塩水を [mathjax]\( y \) gとすると，

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} x+y=400 & \cdots \cdots ①\\ \dfrac{10}{100}x+ \dfrac{5}{100}y=400 \times \dfrac{8}{100} & \cdots \cdots ② \end{array} \right. \end{eqnarray} \)

[mathjax]\(\begin{array}{lr} ① \times 10 & 10x+10y=4000\\ ② \times 100 &\underline{-\big{)}10x+\phantom{0}5y=3200} \\ & 5y=\phantom{0}800\\ & y=\phantom{0}160 \end{array}\)

[mathjax]\( y=160 \) を①に代入すると，

[mathjax] \( \begin{eqnarray} x+160 &=& 400 \\ x &=& 240 \end{eqnarray} \)

10 ％の食塩水240 g，5 ％の食塩水160 gは，問題に適している。

答　10 ％の食塩水240 g，5 ％の食塩水160 g

　問７　　12％の食塩水と20％の食塩水を混ぜて，15％の食塩水200gをつくります。それぞれ何gずつ混ぜればよいですか。

gkt-horizontal-line

<2年p.62>

どんなことがわかったかな

身のまわりの問題の中には，数量の関係から2元1次方程式を2つつくれば，連立方程式を利用して解決することができる問題があります。ただし，方程式の解が問題に適しているかどうかを確かめる必要があります。

gkt-horizontal-line

確かめよう　2節　連立方程式の利用

□　連立方程式を利用して，問題を解くことができる。　連立方程式の利用　・P.57

１　郵便局で荷物を送るための料金が1180円かかります。50円切手と120円切手を合わせて11枚はり，合計の金額がちょうど1180円になるようにするには，それぞれの切手を何枚にするとよいか求めなさい。

□　連立方程式を利用して，問題を解くことができる。　連立方程式の利用　・P.57

２　2つの数があります。大きい方の数から小さい方の数をひいた差は40になります。また，小さい方の数の2倍に10を加えると大きい方の数と等しくなります。この2つの数を求めなさい。

gkt-horizontal-line

解の確かめはなぜ必要？　Tea Break

咲良さんは，次のような問題をつくりました。

1個240円のケーキと1個80円のシュークリームを合わせて12個買い，代金をちょうど2000円にしたいと思います。ケーキとシュークリームを，それぞれ何個買えばよいでしょうか。

[mathjax]\( x \) と [mathjax]\( y \) は，どんな数でなければならないのかな。

avatar

　ケーキを [mathjax]\( x \) 個，シュークリームを [mathjax]\( y \) 個買うとして連立方程式をつくり，それを解いてみましょう。

求めた解は，問題に適しているでしょうか。

また，このことから，解の確かめがなぜ必要なのか話し合ってみましょう。

gkt-horizontal-line

<2年p.63>

2章「連立方程式」を学んで

　できるようになったこと　　身のまわりの課題へ ▷ P.67

2元1次方程式の解は1つに決まらないが，2つの2元1次方程式を連立方程式として考えると，2つの式を同時に成り立たせる値の組が1つに決まり，解となることを理解できる。

連立方程式を，加減法や代入法を使って解くことができる。

身のまわりや数学の中から見つけた問題を，連立方程式を使って解決することができる。

　さらに学んでみたいこと　

これからもっと学んでみたいことや，疑問に思ったことを書いておこう。

gkt-horizontal-line

数学へのいざない　GPSと連立方程式の関係　発展

カーナビ(Car Navigation System)やスマートフォンなど，いろいろな機器にGPS(Global PositioningSystem)と呼ばれるシステムが搭載されています。GPSは，複数の衛星から電波を受信して，衛星との距離などを計算することで現在位置の座標を導き出しているシステムのことです。これには，連立方程式の考えが利用されています。
どのように連立方程式が利用されているのか調べてみましょう。

＞＞　　関連する職業・仕事　　［システムエンジニア］

２節　連立方程式の利用