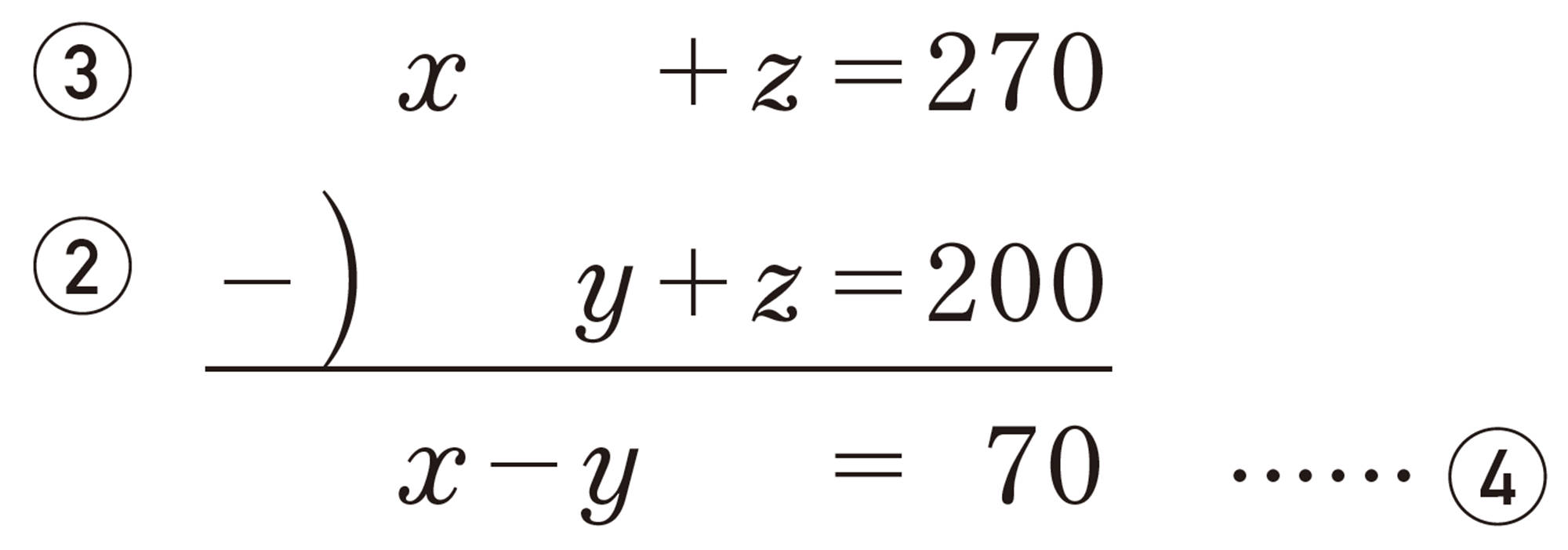教科書アドバイザー「マスマス！」

２年２章１節－３（親ページ）053-055

gkt-horizontal-line

<2年p.53>

計算力を高めよう 2　

家庭学習や計算練習で利用しましょう。

連立方程式　解答　▷P.247

次の連立方程式を解きなさい。

１　加減法

⑴

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 3x+y=17 \\ x-y=3 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 2x+5y=1 \\ 2x+y=5 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} -x+3y=-8\\ x-4y=9 \end{array} \right. \end{eqnarray} \)

⑷

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 2x+y=6 \\ x+3y=13 \end{array} \right. \end{eqnarray} \)

⑸

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x-2y=3\\ 5x-6y=7 \end{array} \right. \end{eqnarray} \)

⑹

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} -2x+5y=-15 \\ 4x-9y=27 \end{array} \right. \end{eqnarray} \)

⑺

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 3x-2y=-11 \\ 2x+3y=-3 \end{array} \right. \end{eqnarray} \)

⑻

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 4x+3y=0 \\ 5x-2y=-23 \end{array} \right. \end{eqnarray} \)

⑼

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 5x-7y=-16 \\ -4x-3y=30 \end{array} \right. \end{eqnarray} \)

２　代入法

⑴

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} y=x+2 \\ 3x+y=14 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x+5y=4 \\ x=-3y+3 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x=2y+6 \\ 2x+3y=5 \end{array} \right. \end{eqnarray} \)

⑷

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 9x-2y=-1 \\ y=3x+1 \end{array} \right. \end{eqnarray} \)

⑸

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} y=2x-1 \\ y=-3x+14 \end{array} \right. \end{eqnarray} \)

⑹

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 2x=3y-1\\ 2x=5y-7 \end{array} \right. \end{eqnarray} \)

３　いろいろな連立方程式

⑴

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 8x=5y+2\\ 5-3x=-4y \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 3(2x+1)+5y=-5\\ -7x-4(y+3)=-10 \end{array} \right. \end{eqnarray} \)

⑶

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 0.5x-1.4y=8\\ -x+2y=-12 \end{array} \right. \end{eqnarray} \)

⑷

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 0.35x-0.12y=-1.5\\ -2x+3y=-3 \end{array} \right. \end{eqnarray} \)

⑸

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} \dfrac{1}{6}x- \dfrac{1}{8}y=1 \\ 2x+y=2 \end{array} \right. \end{eqnarray} \)

⑹

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} 6x+5y=9\\ \dfrac{3x-2y}{6}=-1 \end{array} \right. \end{eqnarray} \)

⑺　[mathjax]\( 2x-y=3x+y=-10 \)

⑻　[mathjax]\( x-2y=4x+3y=1-4y \)

gkt-horizontal-line

<2年p.54>

3つの文字をふくむ方程式を解こう　発展　Tea Break

ある店で買い物をしたところ，次のような代金になりました。
①　りんごとみかんを1個ずつ買うと230円
②　みかんと柿を1個ずつ買うと200円
③　りんごと柿を1個ずつ買うと270円
このとき，りんご1個，みかん1個，柿1個の値段は，それぞれいくらでしょうか。

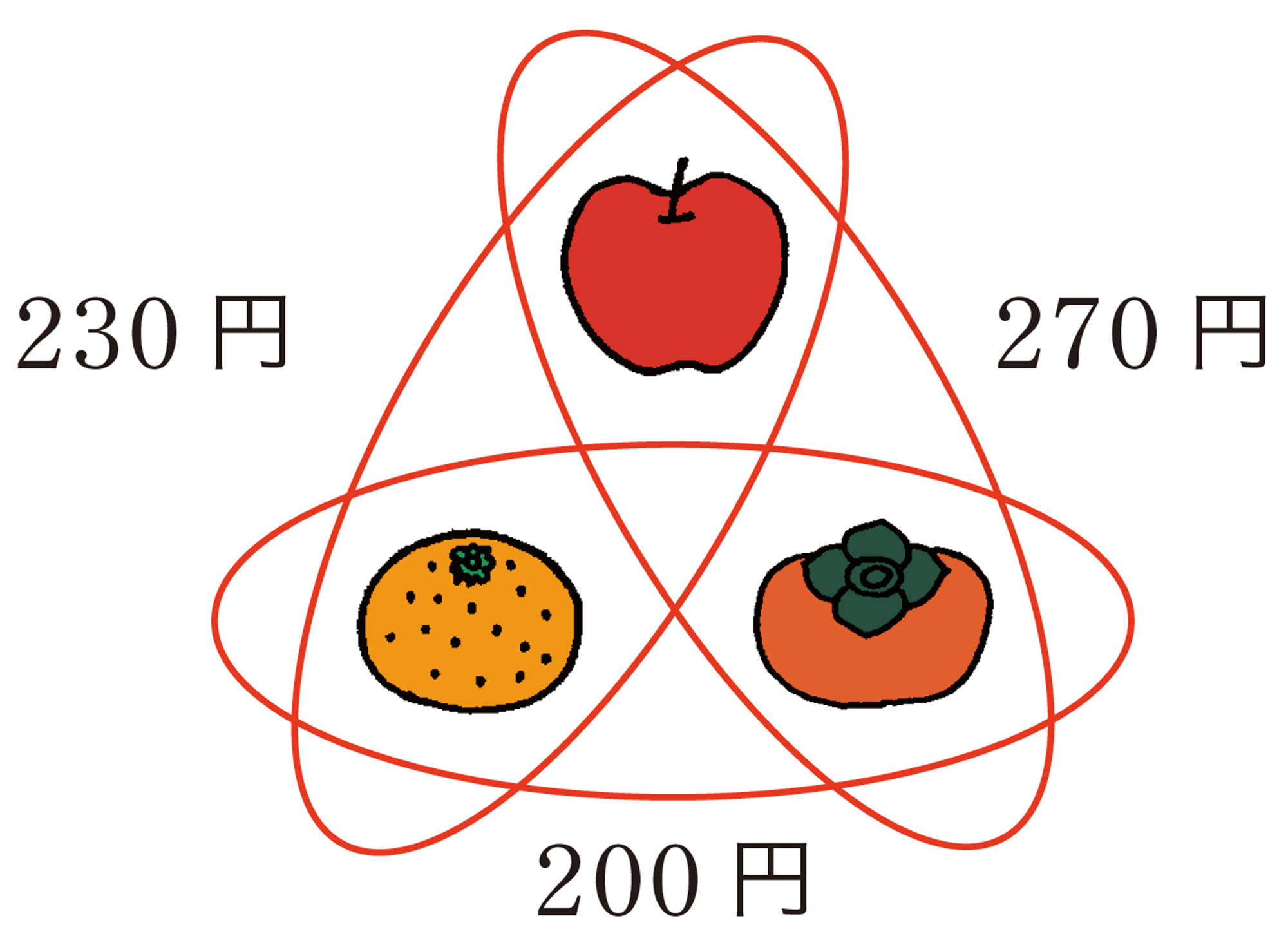
【１】　自分の考えた方法で，この問題の答えを求めてみましょう。

【２】　りんご1個の値段を [mathjax]\( x \) 円，みかん1個の値段を [mathjax]\( y \) 円，柿1個の値段を [mathjax]\( z \) 円とすると，数量の関係は，どんな式で表すことができるでしょうか。

【３】　2でつくった3つの式

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} x+y=230 & \cdots \cdots ① \\ y+z=200 & \cdots \cdots ② \\ x+z=270 & \cdots \cdots ③ \end{array} \right. \end{eqnarray} \)

を3つの文字をふくむ連立方程式と考えて，その解き方を次の（Ⅰ）〜（Ⅲ）の順に考えてみましょう。

（Ⅰ）③の両辺から②の両辺をそれぞれひいて [mathjax]\( z \) を消去し，[mathjax]\( x \) と [mathjax]\( y \) についての2元1次方程式をつくる。その式を④とする。

（Ⅱ）　①と④を連立方程式として解き，[mathjax]\( x \) ，[mathjax]\( y \) の値を求める。

（Ⅲ）　②に（Ⅱ）で求めた [mathjax]\( y \) の値を代入して，[mathjax]\( z \) の値を求める。

[mathjax]\(\begin{array}{lr} ③&x\phantom{000}+z=270 \\ ②&\underline{-\big{)}\phantom{0000}y+z=200} \\ & x-y\phantom{000}=\phantom{0}70 &\cdots\cdots ④\\ \end{array}\)

gkt-horizontal-line

<2年p.55>

前ページの3で調べたように，3つの文字をふくむ連立方程式は，加減法や代入法を使って1つの文字を消去し，連立2元1次方程式をつくって解くことができます。

【４】　次の連立方程式の解き方を考えてみましょう。

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{lr} x+y+z=2 & \cdots \cdots ① \\ 2x+3y-z=-1 & \cdots \cdots ② \\ x-2y+3z=10 & \cdots \cdots ③ \end{array} \right. \end{eqnarray} \)

⑴　①と②から [mathjax]\( z \) を消去するには，この2つの式にどんな操作をすればよいでしょうか。

⑵　②と③から [mathjax]\( z \) を消去するには，この2つの式にどんな操作をすればよいでしょうか。

⑶　⑴と⑵の考え方で [mathjax]\( z \) を消去し，この連立方程式を解いてみましょう。

⑵では，はじめに [mathjax]\( z \) の係数の絶対値をそろえる必要があるね。

avatar

4では，[mathjax]\( z \) を消去するのに，①と②，②と③を用いましたが，①と③を用いることもできます。また，はじめに [mathjax]\( x \) や [mathjax]\( y \) を消去して解くこともできます。

【５】　4の連立方程式を，はじめに [mathjax]\( y \) を消去して解いてみましょう。

[mathjax]\( x+y+z=2 \) のように，3つの文字をふくむ1次方程式を，3元1次方程式といいます。また，3つの3元1次方程式を1組と考えたものを，連立3元1次方程式といいます。

【６】　次の連立方程式を解いてみましょう。

⑴

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x+y+z=13 \\ x-y+2z=7 \\ 3x+y-z=23 \end{array} \right. \end{eqnarray} \)

⑵

[mathjax]\( \begin{eqnarray} \left\{\begin{array}{l} x+2y=6 \\ y=3z+8 \\ x-6z=2 \end{array} \right. \end{eqnarray} \)

計算力を高めよう 2

＜ミライ教科書３学年分もくじ＞

＜スグラパ＞

＜ドリルまとめ＞