<2年p.39>
２章 Chapter ２ 連立方程式
1節 連立方程式
2節 連立方程式の利用
[mathjax] \( 2x+13=25 \)
1年のとき，上のような文字が1つの式で，文字にあてはまる数を求めたね。
[mathjax] \( 2x+13 = 25 \\ \)
[mathjax] \( \phantom{+000}2x = 25-13 \\ \)
[mathjax] \( \phantom{+000}2x = 12 \\ \)
[mathjax] \( \phantom{+0000}x = 6 \)
文字が2つの式では，文字にあてはまる数を求めることができるかな。
[mathjax] \( 2x+13y=36 \)
文字に，いろいろな数をあてはめれば，わかりそうだけど…。
？ 文字が2つのとき，あてはまる数を求められるかな？
<2年p.40>
1節 連立方程式
何回ずつ乗った？
この遊園地には，チケット2枚で乗れる乗り物と，チケット1枚で乗れる乗り物があります。
【１】 11枚つづりのチケットを買ってすべて使い切ったとすると，チケット2枚で乗れる乗り物と，チケット1枚で乗れる乗り物に，それぞれ何回ずつ乗ったでしょうか。
A チケット2枚の乗り物
観覧車
ローラーコースター
お化け屋敷
フリーフォール
ジャングルカヌー
B チケット1枚の乗り物
メリーゴーラウンド
ゴーカート
スカイサイクル
ティーカップ
海賊船
<2年p.41>
次の課題へ！
答えが何通りもありそうだけど，式に表すことはできるのかな？
P.42
<2年p.42>
１ 連立方程式とその解
Q Question
遊園地で，チケット2枚で乗れる乗り物に [mathjax] \( x \) 回，チケット1枚で乗れる乗り物に[mathjax] \( y \) 回乗って，チケットを11枚使ったことを，式で表してみましょう。
また，それぞれの乗り物に何回乗ったでしょうか。
2枚の乗り物に5回，1枚の乗り物に1回乗れば使い切れるね。
ほかにもチケットを使い切れる場合があるよ。方程式にできれば求められるかな。
見方・考え方
式に表して考えられるかな。
【Q】で， [mathjax] \( x \) と [mathjax] \( y \) の関係を式で表すと，次のようになる。
[mathjax] \( 2x+y=11 \) ･･････①
①の式のように，2種類の文字をふくむ1次方程式を 2元1次方程式という。これに対して，1年で学んだ [mathjax] \( 3x+5=8 \) のように，1種類だけの文字をふくむ1次方程式を1元1次方程式という。
目標 ▷ 2元1次方程式について考えよう。
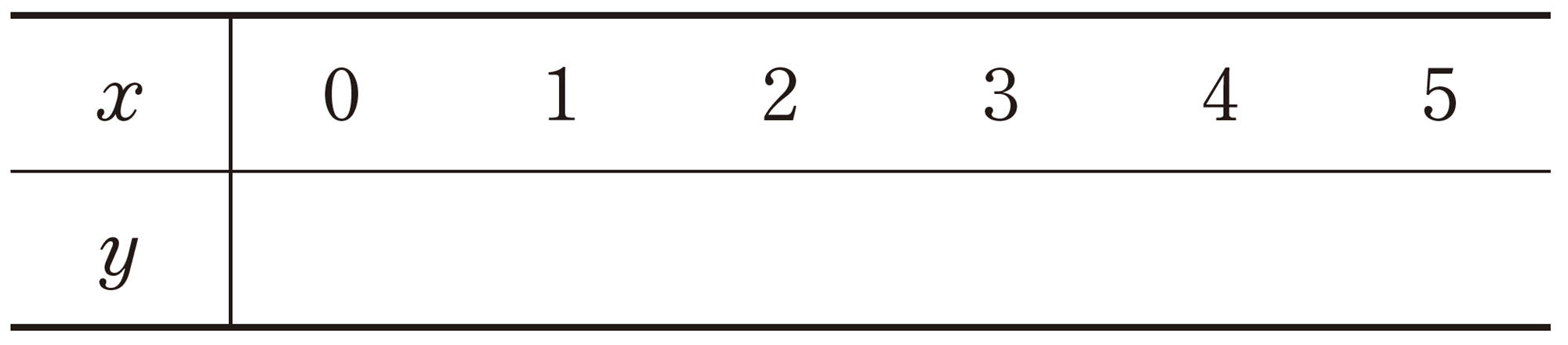
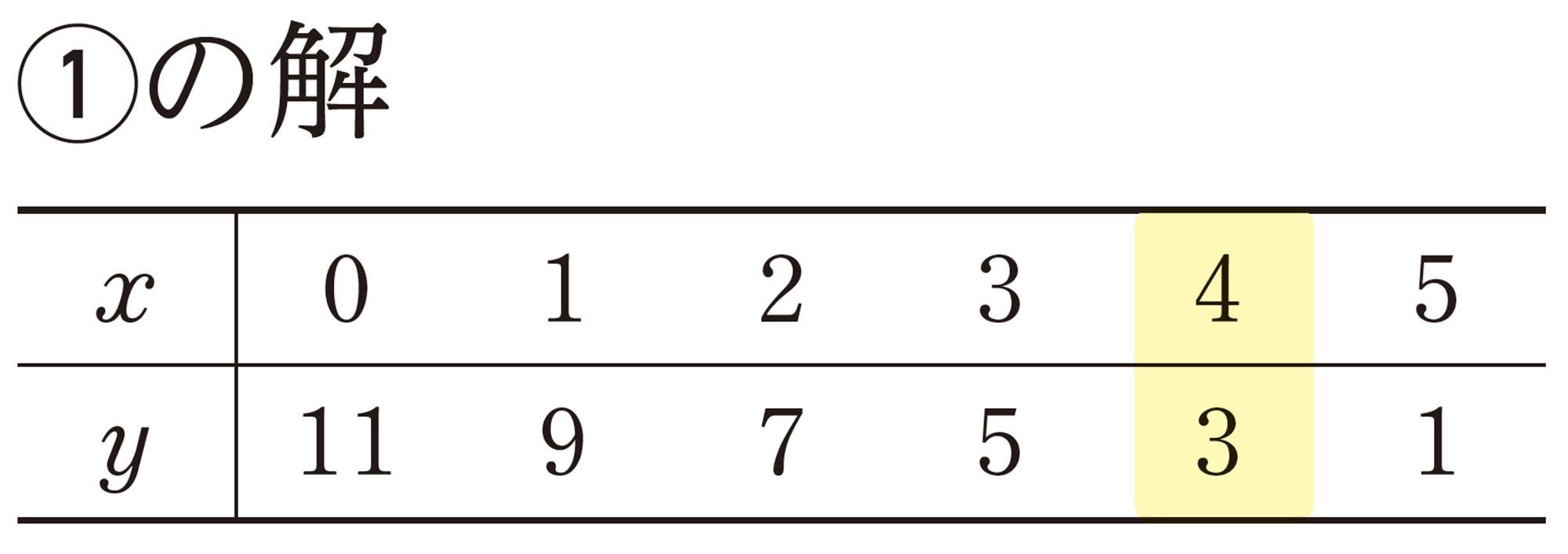
問 １ ①の式を成り立たせる [mathjax] \( x \) ， [mathjax] \( y \) の値の組を，次の表にまとめなさい。
2元1次方程式を成り立たせる [mathjax] \( x \) ， [mathjax] \( y \) の値の組を2元1次方程式の解という。
問1の表で，
，
，
，
…
などは，どれも2元1次方程式 [mathjax]\( 2x+y=11 \) の解である。
2元1次方程式の解は，1つではないんだね。
注意
を， [mathjax]\( x=0 \) ， [mathjax]\( y=11 \) や， [mathjax]\( (x, y)=(0, 11) \) のように表すこともある。
<2年p.43>
前ページの【Q】で，遊園地の乗り物に合計7回乗ったとすると， [mathjax] \( x \) と [mathjax] \( y \) の関係は，次の式で表すことができる。
[mathjax] \( x+y=7 \) ･･････②
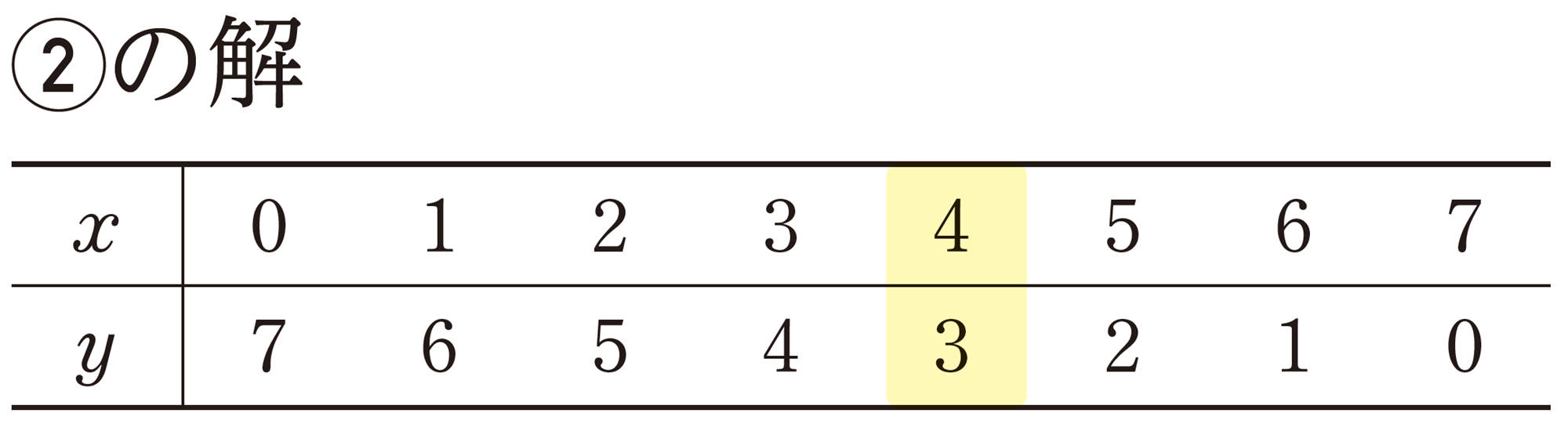
問 ２ ②の式の解を，次の表にまとめなさい。
問 ３ 前ページの問1と問2の表から，①，②を同時に成り立たせるx，yの値の組を求めなさい。
2つの2元1次方程式を1組と考えたものを 連立方程式 または連立2元1次方程式といい，次のように表す。
連立方程式で，2つの方程式を同時に成り立たせるx，yの値の組を，連立方程式の解といい，解を求めることを，連立方程式を解くという。
上の連立方程式の解は，
である。
問 ４ 次の㋐～㋒の中で，連立方程式
の解はどれですか。
㋐
㋑
㋒
どんなことがわかったかな
2元1次方程式の解はいくつもありますが，2つの2元1次方程式を連立方程式と考えると，連立方程式の解は1つに決まります。
次の課題へ！
文字に数を代入せずに連立方程式を解く方法はあるのかな？
P.44
