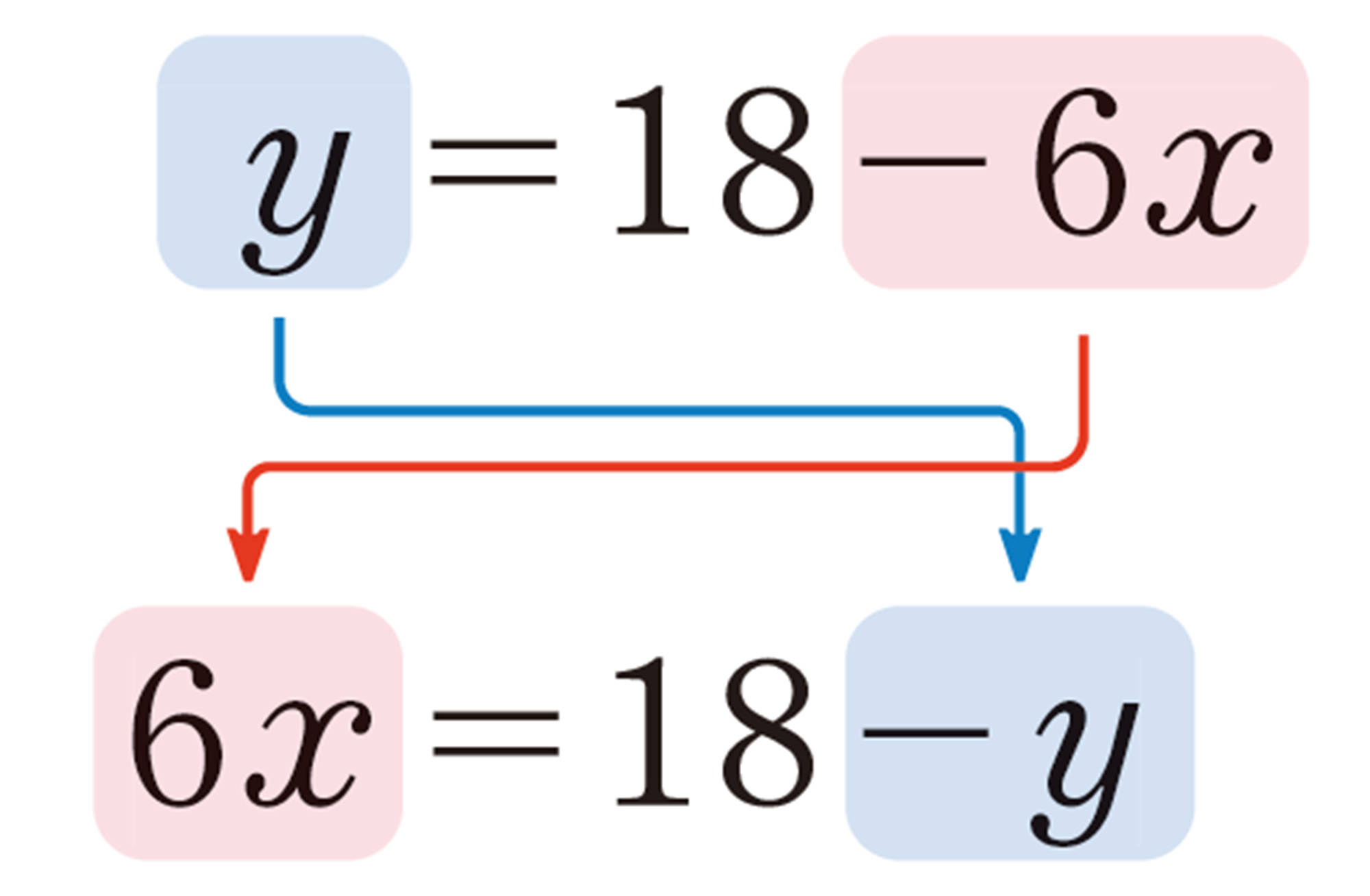<2年p.31>
２ 等式の変形
Q Question
次の⑴～⑶は，道のり，速さ，時間の関係を表したものです。 [mathjax] \( \boxed{\phantom{0}} \) にあてはまる記号を入れ，それぞれの式の関係について，話し合ってみましょう。
⑴ [mathjax] \( (\mathsf{道のり})=(\mathsf{速さ}) \boxed{\phantom{0}} (\mathsf{時間})\)
⑵ [mathjax] \( (\mathsf{速さ})=(\mathsf{道のり}) \boxed{\phantom{0}} (\mathsf{時間})\)
⑶ [mathjax] \( (\mathsf{時間})=(\mathsf{道のり}) \boxed{\phantom{0}} (\mathsf{速さ})\)
道のり，速さ，時間の関係を表しているね。
求めるものによって，式の形を変えているね。
見方・考え方
それぞれの式の関係をまとめて見ると，どんなことがわかるかな。
目標 ▷ 式の計算を利用して，等式を目的に応じた形に変形しよう。
いま，地上の気温を 18 ℃，地上 x km の気温を y ℃ とすると，xと y の関係は，[mathjax] \( y=18-6x \) と表すことができます。この式を，xを求める式に直しなさい。
解答
答 [mathjax]\(\underline{x=\dfrac{18-y}{6}}\)
例1のように，等式 [mathjax] \( y=18-6x \) を変形して [mathjax] \( x= \dfrac{18-y}{6} \) を導くことを，[mathjax] \( y=18-6x \) を [mathjax] \( x \) について解くという。
注意 [mathjax] \( x= \dfrac{18-y}{6} \) は，[mathjax] \( x=3- \dfrac{1}{6} y\) や，[mathjax] \( x=- \dfrac{1}{6}y+3 \) と表してもよい。
問 １ 例1で，気温が 6 ℃ ，[mathjax] \(-30\) ℃になるのは，それぞれ地上何kmですか。
問 ２ 次の等式を〔 〕内の文字について解きなさい。
⑴ [mathjax] \( x-y=8 \) 〔 [mathjax] \( x \) 〕
⑵ [mathjax] \( y=12-4x \) 〔[mathjax] \( x \) 〕
⑶ [mathjax] \( 6x+2y=10 \) 〔[mathjax] \( y \) 〕
⑷ [mathjax] \( 3x-y=5 \) 〔[mathjax] \( y \) 〕
<2年p.32>
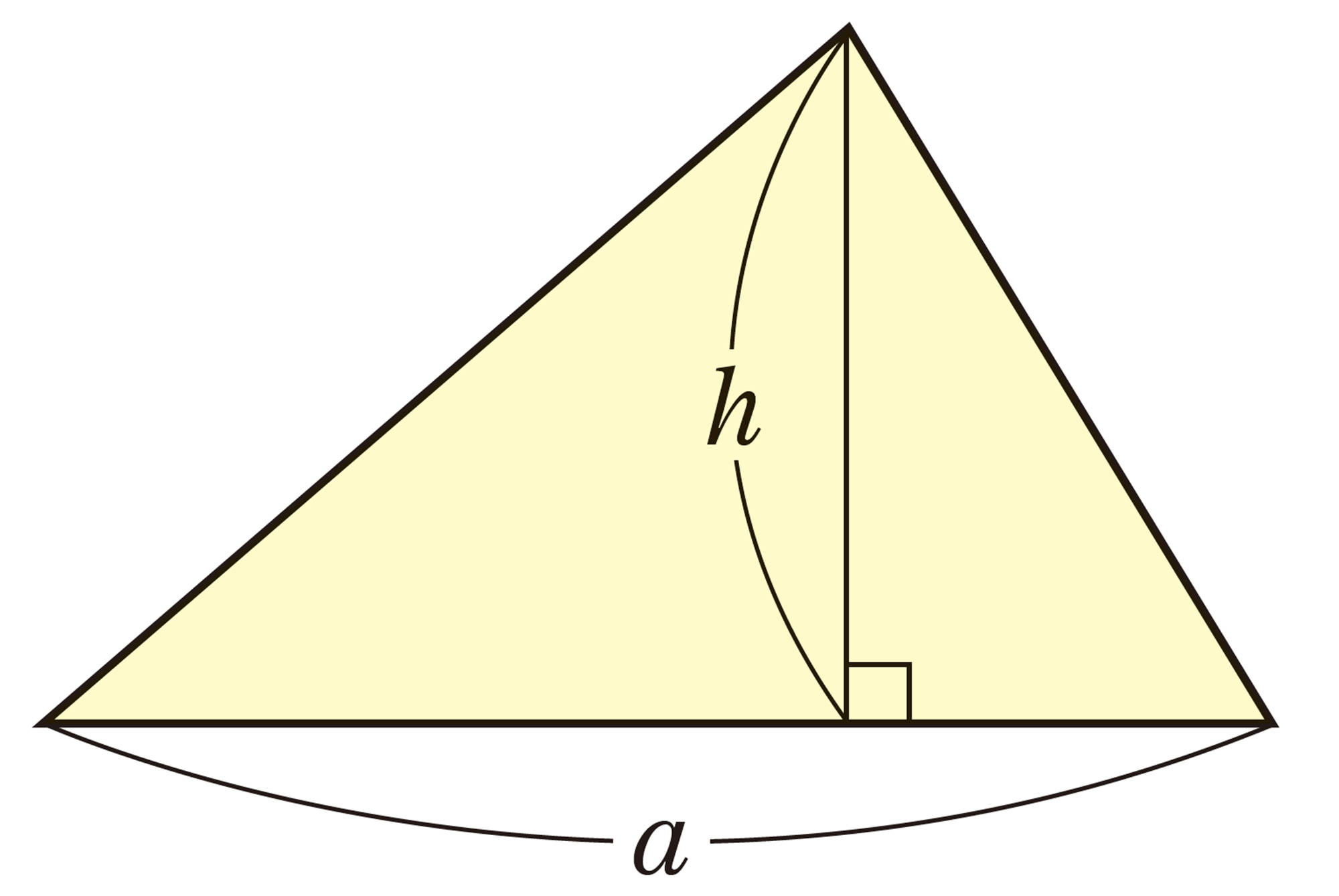
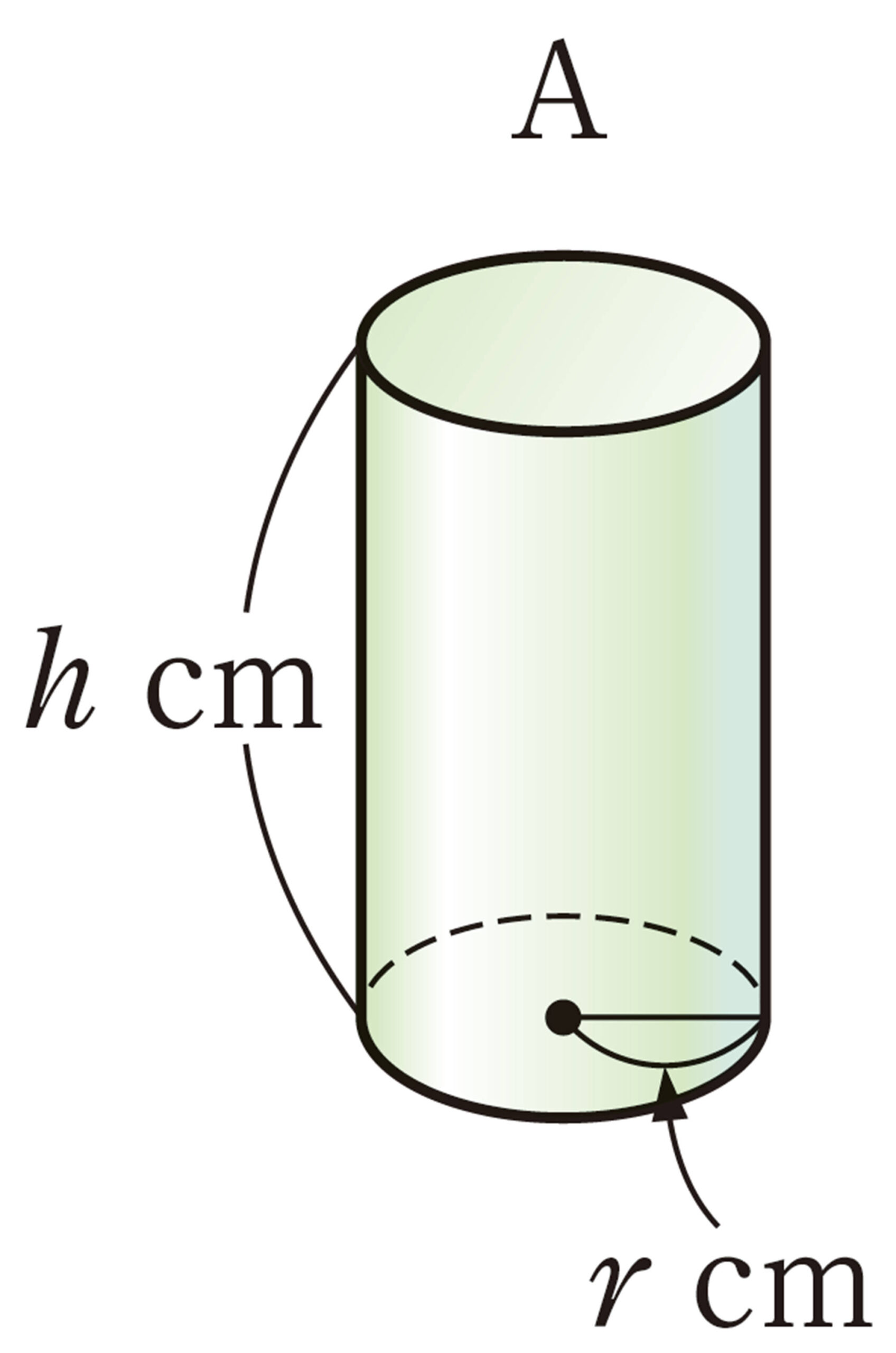
例 ２ 三角形の面積の公式 [mathjax] \( S= \dfrac{1}{2}ah \) を， [mathjax] \( h \) について解きなさい。
解答
答 [mathjax] \(\underline{h=\dfrac{2s}{a}}\)
高さが求めやすくなるように，変形しているね。
問 ３ 次の等式を〔 〕内の文字について解きなさい。
⑴ [mathjax] \( V= \dfrac{1}{3}Sh \) 〔[mathjax] \( h \) 〕
⑵ [mathjax] \( l=2(a+b) \) 〔[mathjax] \( a \) 〕
⑶ [mathjax] \( S= \dfrac{(a+b)h}{2} \) 〔[mathjax] \( a \) 〕
どんなことがわかったかな
何を求めたいかによって，等式を変形することができます。
確かめよう 2節 式の利用
１ [mathjax] \(5\)，[mathjax] \(7\)のような連続する2つの奇数の和は4の倍数になることを，文字式を使って説明しなさい。
２ 次の等式を〔 〕内の文字について解きなさい。
⑴ [mathjax] \( 4x-y=8 \) 〔[mathjax] \( x \) 〕
⑵ [mathjax] \( m= \dfrac{a+b}{2} \) 〔[mathjax] \( a \) 〕
<2年p.33>
1章 「式の計算」を学んで
できるようになったこと 身のまわりの課題へ ▷P.38
多項式の加法・減法や，単項式の乗法・除法の計算ができる。
文字を使って数量の関係や求めた結果を表したり，文字を使って表された数量の関係を読み取ったりすることができる。
身のまわりや数学の中から見つけた問題を，多項式や単項式の計算を使って解決することができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない 誕生日当て
生まれた月の数に7をかけて，生まれた日の数を加えてください。その答えに10をかけたものを㋐とします。次に，生まれた月の数に10をかけて，そこから生まれた日の数を3倍した数をひいてください。その答えをさらに3倍したものを㋑とします。最後に㋐と㋑を加えてください。答えはいくつになりましたか。
203です。
誕生日は2月3日ですね。
ある人が [mathjax] \( x \) 月 [mathjax] \( y \) 日生まれであるとして，文字を使って計算すると，答えは [mathjax] \( 100x+y \) となり，誕生日を当てられる理由が文字を使うことでひと目でわかります。
自分でもクイズをつくって，いろいろな人に出題してみましょう。
<2年p.34>
１章のまとめの問題 解答 P.246〜247 基本
１ 次の㋐～㋕の式について，下の問いに答えなさい。
㋐ [mathjax] \( 4x+7 \)
㋑ [mathjax] \( 2x² \)
㋒ [mathjax] \( 3x-5y \)
㋓ [mathjax] \( -8x \)
㋔ [mathjax] \( 6xy+9y \)
㋕ [mathjax] \( x²-6x+1 \)
⑴ 単項式はどれですか。
⑵ 2次式はどれですか。
２ 次の計算をしなさい。
⑴ [mathjax] \( 8a²+6a+a²-2a \)
⑵ [mathjax] \( -2x-8y+7y-3x+5 \)
⑶ [mathjax] \( (4a-9b)+(3a+5b) \)
⑷ [mathjax] \( (5x+2y)-(6x-4y) \)
３ 次の計算をしなさい。
⑴ [mathjax] \( (20x-4y) \div (-4) \)
⑵ [mathjax] \( (5a-8b)+3(-a+2b) \)
⑶ [mathjax] \( 5(x+3y)-4(2x-y) \)
⑷ [mathjax] \( \dfrac{3x+y}{4}- \dfrac{x-y}{6} \)
⑸ [mathjax] \( 7x \times 4y \)
⑹ [mathjax] \( 3a² \times (-2a) \)
⑺ [mathjax] \( (-9x)² \)
⑻ [mathjax] \( (-16a²) \div 4a \)
⑼ [mathjax] \( 6xy \div \dfrac{3}{7}x \)
⑽ [mathjax] \( 4x² \div 6x² \times 3x \)
４ 次の計算の誤りを直し，正しい答えを求めなさい。
⑴
⑵
５ [mathjax] \( x=6 \) ， [mathjax] \( y=-5 \) のとき，次の式の値を求めなさい。
⑴ [mathjax] \( 14xy² \div 7y \)
⑵ [mathjax] \( (3x+5y)-(x+6y) \)
<2年p.35>
６ [mathjax] \(1\)，[mathjax] \(4\)，[mathjax] \(7\)のような差が3の3つの整数の和は3の倍数であることを，文字式を使って説明しなさい。
７ 次の等式を〔 〕内の文字について解きなさい。
⑴ [mathjax] \( 3x+2y=10 \) 〔 [mathjax] \( y \) 〕
⑵ [mathjax] \( a= \dfrac{4b+3c}{7} \) 〔 [mathjax] \( c \) 〕
応用
１ 次の計算をしなさい。
⑴ [mathjax] \( \dfrac{1}{2}x+y- \require{physics} \left(\dfrac{2}{3}x- \dfrac{y}{2}\right) \)
⑵ [mathjax] \( x-y- \dfrac{3x-y}{4} \)
⑶ [mathjax] \( 3a² \div 6ab \times (-2a)² \)
⑷ [mathjax] \( 9x² \times (-xy) \div \dfrac{3}{5}y³ \)
２ [mathjax] \( A=x²-3x-5 \) ， [mathjax] \( B=-2x²+x+7 \)とするとき， [mathjax] \( A \) からどんな式をひくと，その差が [mathjax] \( B \) になりますか。
３ 底面の半径が [mathjax] \( r \) cm，高さが [mathjax] \( h \) cmの円柱Aと，底面の半径が Aの2倍で，高さがAの [mathjax] \( \dfrac{1}{2} \) の円柱Bがあります。このとき，Bの体積はAの体積の何倍になるかを，文字式を使って説明しなさい。
４ 右のカレンダーで，◯ で囲んだ3つの数[mathjax] \(2\)，[mathjax] \(9\)，[mathjax] \(16\)の和は，中央の数9の3倍に等しくなっています。ほかの場所でも，縦に並んだ3つの数の和について同じことがいえるかを，文字式を使って説明しなさい。
<2年p.36>
１章のまとめの問題 活用
１ 美月さんは，3桁の自然数と，その百の位の数と一の位の数を入れかえてできる自然数との差は，どんな数になるかを調べています。
[mathjax] \( 524 \) のとき， [mathjax] \( 524-425=99 \)
[mathjax] \( 937 \) のとき， [mathjax] \( 937-739=198 \)
[mathjax] \( 259 \) のとき， [mathjax] \( 259-952=-693 \)
これらの結果から，美月さんは次のことを予想し，それが正しいことを下のように説明しようとしています。美月さんの説明を完成させなさい。
美月さんの予想
3桁の自然数と，その百の位の数と一の位の数を入れかえてできる自然数との差は，99の倍数である。
3桁の自然数の百の位の数をa，十の位の数をb，一の位の数をcとすると，
3桁の自然数は， [mathjax] \( \boxed{\phantom{000000}} \)
百の位の数と一の位の数を入れかえてできる自然数は，
[mathjax] \( \boxed{\phantom{000000}} \)
と表される。この2数の差は，
[mathjax] \( \boxed{\phantom{000000000000000000000000000000}} \)
したがって，3桁の自然数と，その百の位の数と一の位の数を入れかえてできる自然数との差は，99の倍数である。
<2年p.37>
２ 美月さんの説明で求めた式から，「2数の差は99 の倍数である」ことのほかにわかることがあります。次の㋐～㋕の中から，あてはまるものをすべて選びなさい。
㋐ 2数の差は6の倍数である。
㋑ 2数の差は11の倍数である。
㋒ 2数の差は奇数である。
㋓ 2数の差は偶数である。
㋔ 2数の差は，もとの3桁の自然数の十の位の数には関係しない。
㋕ 2数の差は，もとの3桁の自然数の百の位の数から一の位の数をひいた差の99倍である。
３ これまでに，
「2桁の自然数と，その十の位の数と一の位の数を入れかえてできる自然数との差は，9の倍数である」
ことや，
「3桁の自然数と，その百の位の数と一の位の数を入れかえてできる自然数との差は，99の倍数である」
ことを学習しました。このことから，拓真さんは，
「4桁の自然数と，その千の位の数と一の位の数を入れかえてできる自然数との差は，999の倍数である」
と予想しました。このことは正しいですか。正しいと考える場合は，そのことを文字式で説明しなさい。また，正しくないと考える場合は，999の倍数にならない例を示しなさい。
<2年p.38>
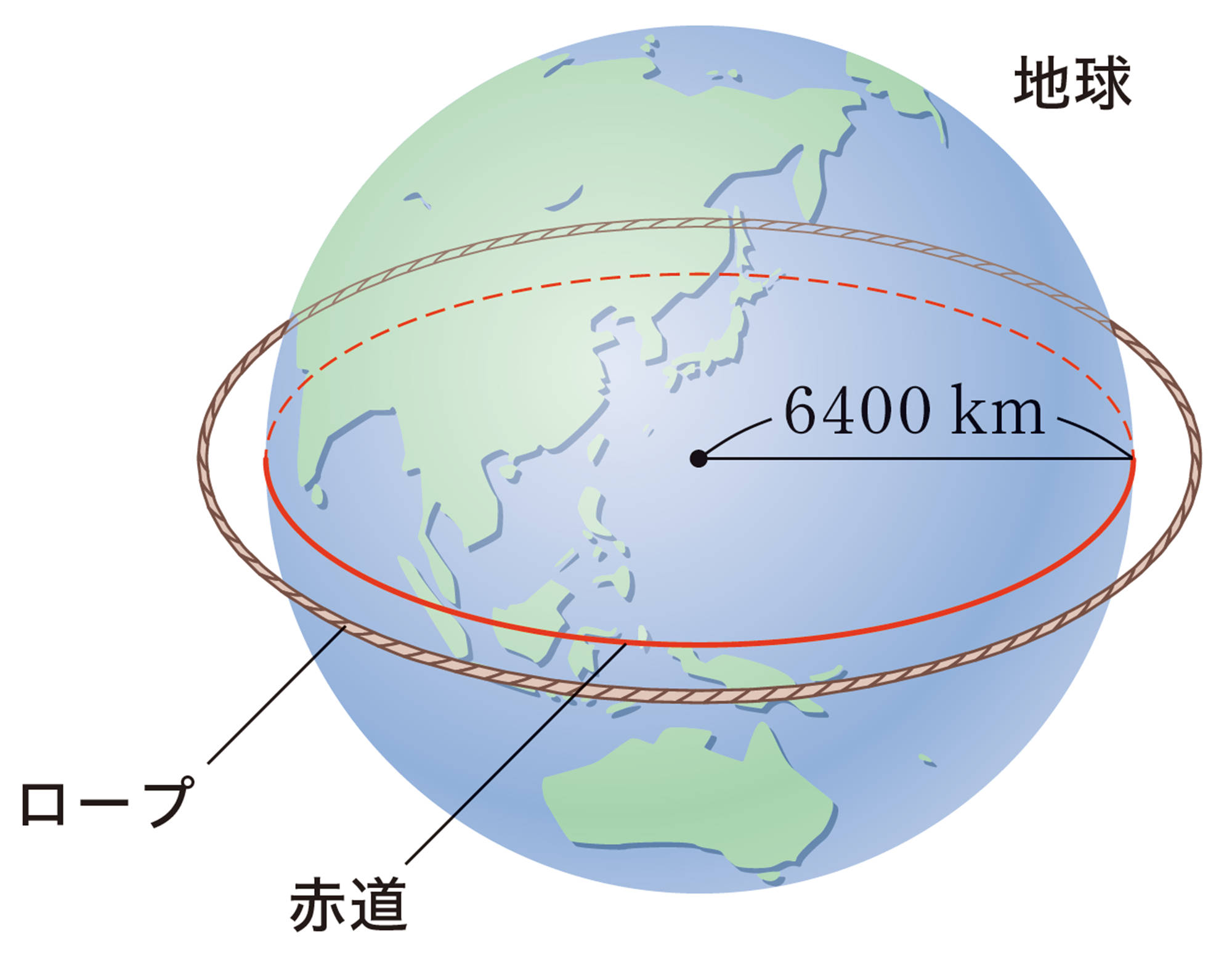
深めよう 赤道のまわりにロープを巻くと？
地球の半径は約6400kmです。いま，地球の赤道の長さよりも10m長いロープを用意し，赤道上空に一定の高さで円形に巻くことができたとします。 このとき，赤道とロープのすき間を通りぬけることができるのは，次の動物のうちのどれか予想してみましょう。
㋐ ネズミ( 高さ 約5cm )
㋑ ウシ( 高さ 約1m50cm )
㋒ ゾウ( 高さ 約3m )
① 地球の半径を [mathjax] \( r \)mとすると，赤道の長さは [mathjax] \( 2 \pi r \)mです。ロープの長さと，ロープでつくった円の半径を，それぞれ式で表してみましょう。
② ロープでつくった円の半径と地球の半径の差を求めてみましょう。また，円周率を[mathjax]\(3.14\)とすると，その値は約何mになるでしょうか。
すき間を通りぬけることができる動物はどれかな。
②の結果は，半径rには関係しません。したがって，上の問題では，地球を月や卓球のボールなど，ほかの球形のものにおきかえても同じ結果が得られます。
▷グラウンドに陸上競技のトラックをつくります。 トラックの曲線部分は半円です。このトラックを1周するとき，となり合うレーンとのスタート位置の差は，何mにすればよいでしょうか。 各レーンの幅を1m，円周率を[mathjax]\(3.14\)とします。
