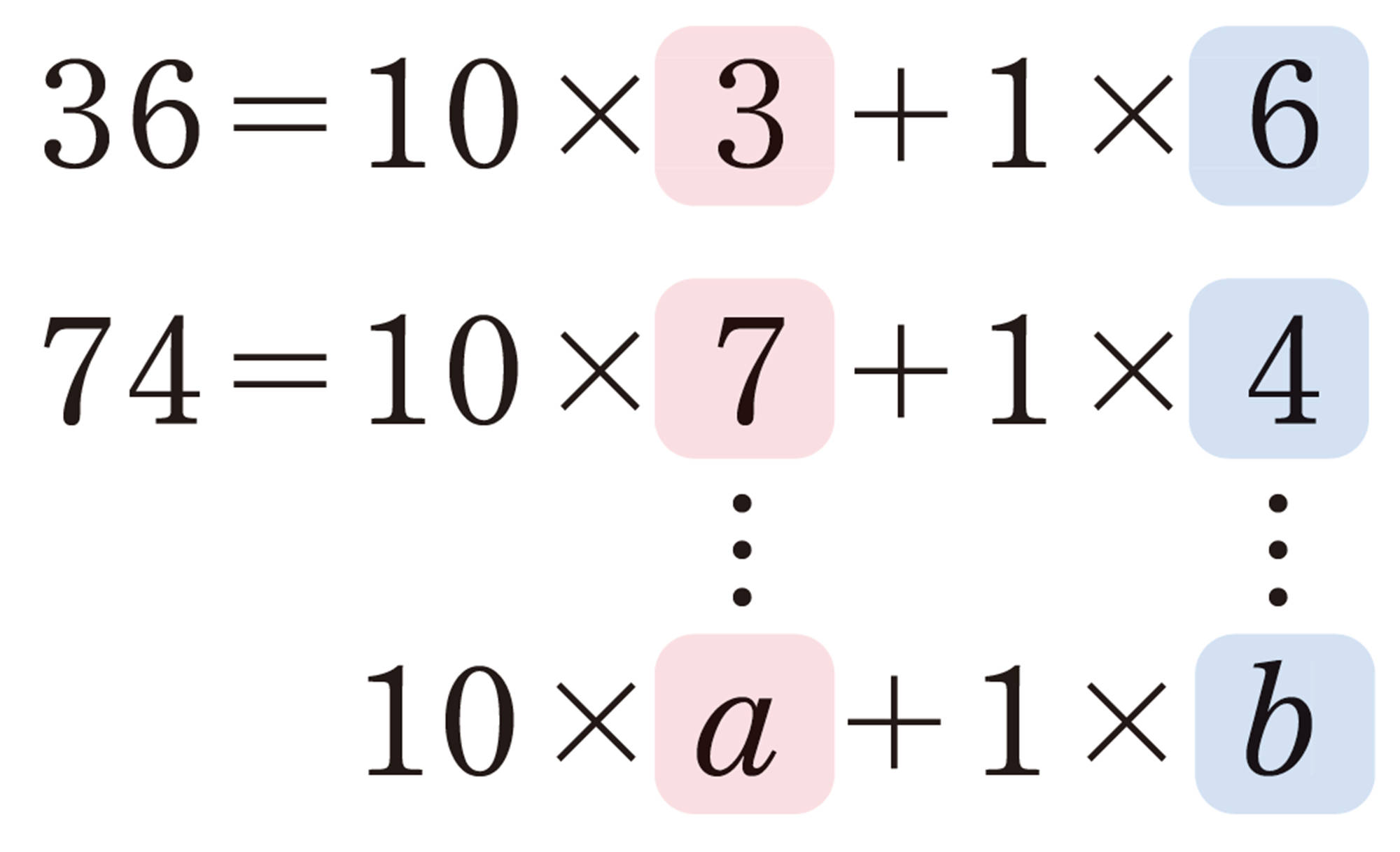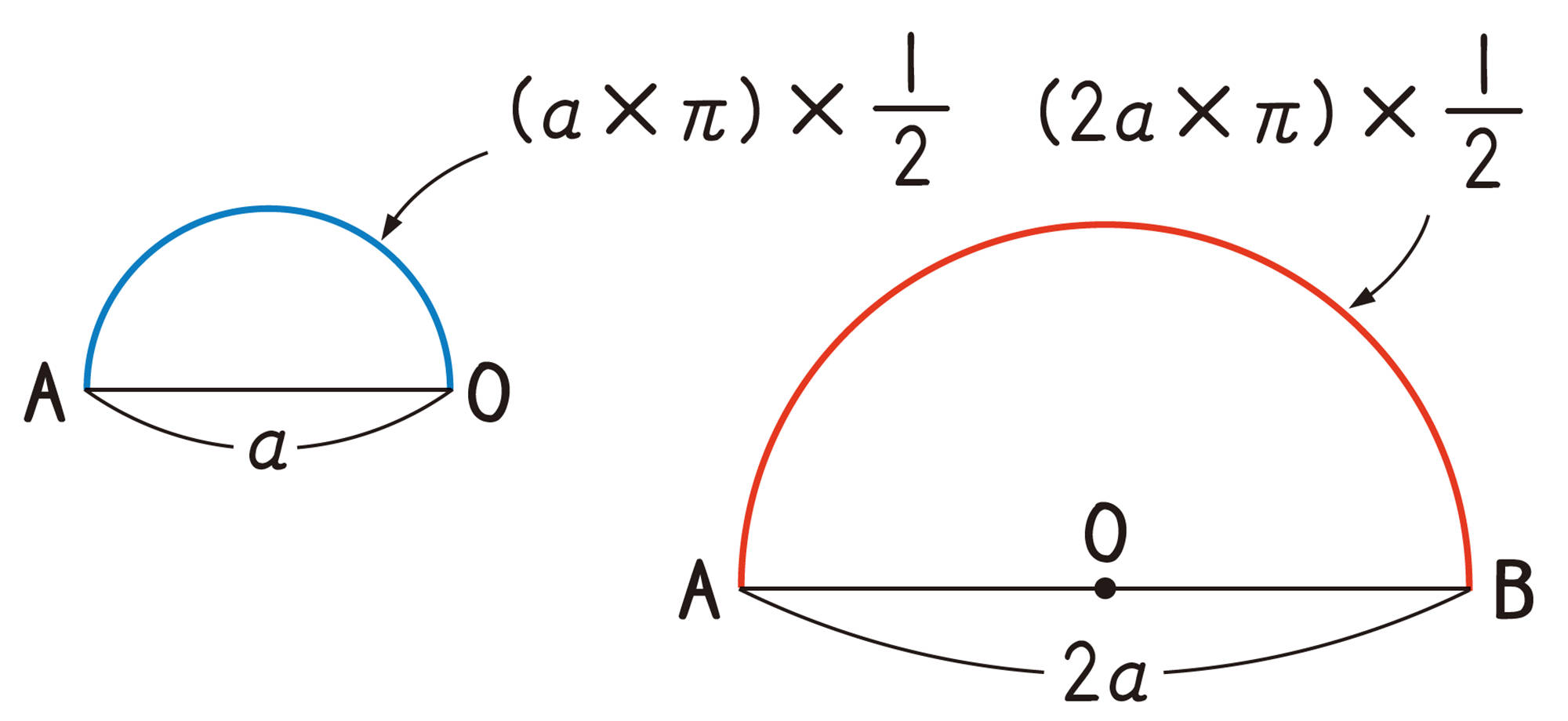<2年p.24>
2節 式の利用
文字を使って考えられるかな？
【１】 [mathjax] \(6\)，[mathjax] \(7\)，[mathjax] \(8\)のような連続する3つの整数の和を求めてみましょう。
それらの和には，共通する性質があるでしょうか。
どんな性質があるか予想してみましょう。
どうすれば共通する性質を見つけられるかな。
具体的な数で計算してみればいいね。
どんな性質があるかな。
[mathjax] \( 6+7+8=\boxed{\phantom{00}}\)
[mathjax] \( 10+11+12=\boxed{\phantom{00}}\)
[mathjax] \( 23+24+25=\boxed{\phantom{00}}\)
3つとも和は，3の倍数になっているね。
もっとほかの数でも，調べてみよう。
[mathjax] \( 111+112+113=\boxed{\phantom{00}}\)
[mathjax] \( 318+319+320=\boxed{\phantom{00}}\)
[mathjax] \( 2353+2354+2355=\boxed{\phantom{00}}\)
連続する3つの整数の和は，3の倍数になるといえそうだね。
【２】 「連続する3つの整数の和は，3の倍数になる」といえるか話し合ってみましょう。
どんな場合でも，3の倍数になるといえるのかな。
次の課題へ！
数の性質がいつでも成り立つことを説明するにはどうしたらいいのかな？
P.25
<2年p.25>
１ 文字式による説明
前ページの 1 のように，具体的な数で調べるだけでは，すべての数で成り立つかどうかを確かめることはできない。
しかし，文字式を利用することで，すべての数で成り立つかどうかを確かめることができる。
目標 ▷ 文字式を使って，数や図形の性質を説明しよう。
例 １ 連続する3つの整数の和は3の倍数であることを，文字式を使って説明しなさい。
考え方 連続する3つの整数を文字を使って表し，それらの和が [mathjax] \( 3 \times ( \mathsf{整数}) \) の形で表されることを示す。
解答
連続する 3 つの整数のうち， もっとも小さい整数を [mathjax] \( n \) とすると，
連続する 3 つの整数は， [mathjax] \( n \) ， [mathjax] \( n+1 \) ， [mathjax] \( n+2 \) と表される。 それらの和は，
目的に応じて，分配法則を使って[mathjax]\(3(n+1)\) の形に直す
[mathjax] \( n+1 \) は整数だから， [mathjax] \( 3(n+1) \) は 3 の倍数である。
したがって， 連続する 3 つの整数の和は 3 の倍数である。
注意 ある数の倍数というときには，その数に 0 や負の整数をかけた数も倍数と考えている。
問 １ 例1の解答で，連続する3つの整数の和が [mathjax] \( 3(n+1) \) となることから，3の倍数であることのほかに，どんなことがわかりますか。
どんな性質があるかわかるかな。
問 ２ 例1について，中央の数を [mathjax] \( n \) として説明しなさい。
<2年p.26>
Q Question
2桁の自然数と，その十の位の数と一の位の数を入れかえてできる自然数との和は，ある数の倍数になります。どんな数の倍数になるかを調べてみましょう。
文字式を使って説明できそうだね。
2桁の自然数は，文字を使ってabと表していいのかな。
見方・考え方
いろいろな数の場合を調べて，どんな性質があるか見つけられるかな。
2桁の自然数は，十の位の数を [mathjax] \( a \) ，一の位の数を [mathjax] \( b \) とすると，[mathjax] \( 10a+b \) と表すことができる。このことを利用して，Qで調べたことを確かめてみよう。
例 ２ 2桁の自然数と，その十の位の数と一の位の数を入れかえてできる自然数との和が11の倍数になることを，文字式を使って説明しなさい。
解答
2 桁の自然数の十の位の数を [mathjax] \( a \) ， 一の位の数を [mathjax] \( b \) とすると，
もとの数は， [mathjax] \( 10a+b \)
入れかえてできる数は， [mathjax] \( 10b+a \)
と表される。 この 2 数の和は，
[mathjax] \( a+b \) は整数だから， [mathjax] \( 11(a+b) \) は 11 の倍数である。
したがって， 2 桁の自然数と， その十の位の数と一の位の数を入れかえてできる自然数との和は， 11 の倍数である。
[mathjax] \( (a+b) \)の倍数にもなっているね。
問 ３ 2桁の自然数と，その十の位の数と一の位の数を入れかえてできる自然数との差について，どんなことがいえますか。また，そのことを文字式を使って説明しなさい。
<2年p.27>
Q Question
次の2数の和は，偶数，奇数のどちらでしょうか。
⑴ [mathjax] \( ( \mathsf{偶数})+( \mathsf{奇数}) \)
⑵ [mathjax] \( ( \mathsf{偶数})+( \mathsf{偶数}) \)
⑶ [mathjax] \( ( \mathsf{奇数})+( \mathsf{奇数}) \)
いろいろな数で確かめてみればわかりそうだね。
いつでもそれが成り立つことをいうには，どうすればいいのかな。
見方・考え方
根拠を明らかにして，説明できるかな。
偶数は，2でわりきれる数，つまり2の倍数であるから， [mathjax] \( m \) を整数とすると， [mathjax] \( 2m \) と表すことができる。
また，奇数は2でわりきれない数，つまり偶数に1を加えた数であるから， [mathjax] \( n \) を整数とすると， [mathjax] \( 2n+1 \) と表すことができる。
[mathjax] \( m \) ， [mathjax] \( n \) は整数だから，0や負の数を代入してもいいんだね。
【１】 いろいろな数で， [mathjax] \( ( \mathsf{偶数})+( \mathsf{奇数}) \) の和を求めてみましょう。それらの和には，共通する性質があるか考えてみましょう。
【２】 大和さんは，次のような性質が成り立ちそうだと考えました。
「偶数と奇数の和は奇数になる。」
そこで文字式を用いて，上の性質が成り立つ理由を次のように説明しました。この説明は正しいといえるか，話し合ってみましょう。
これでいいのかな？
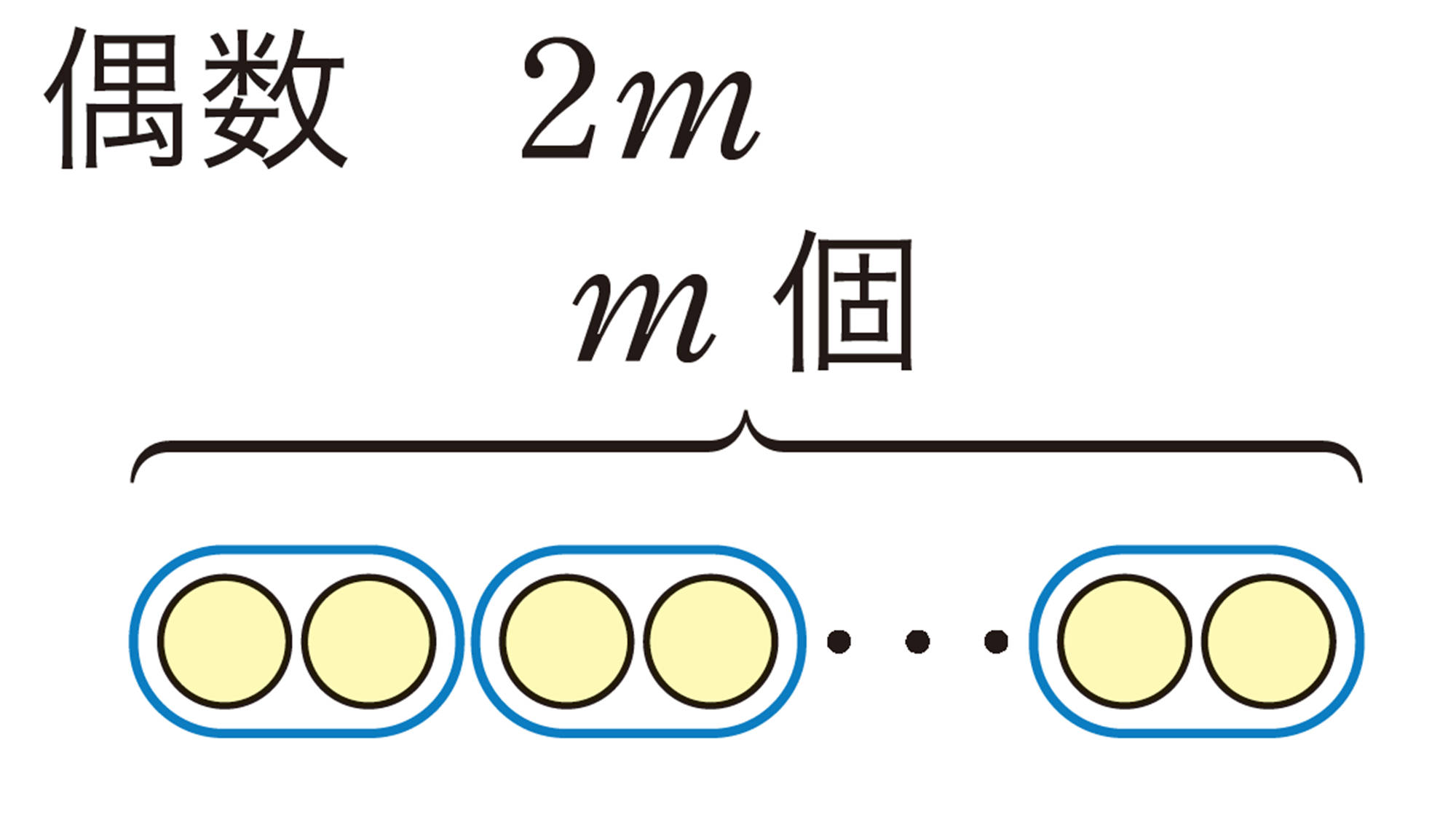
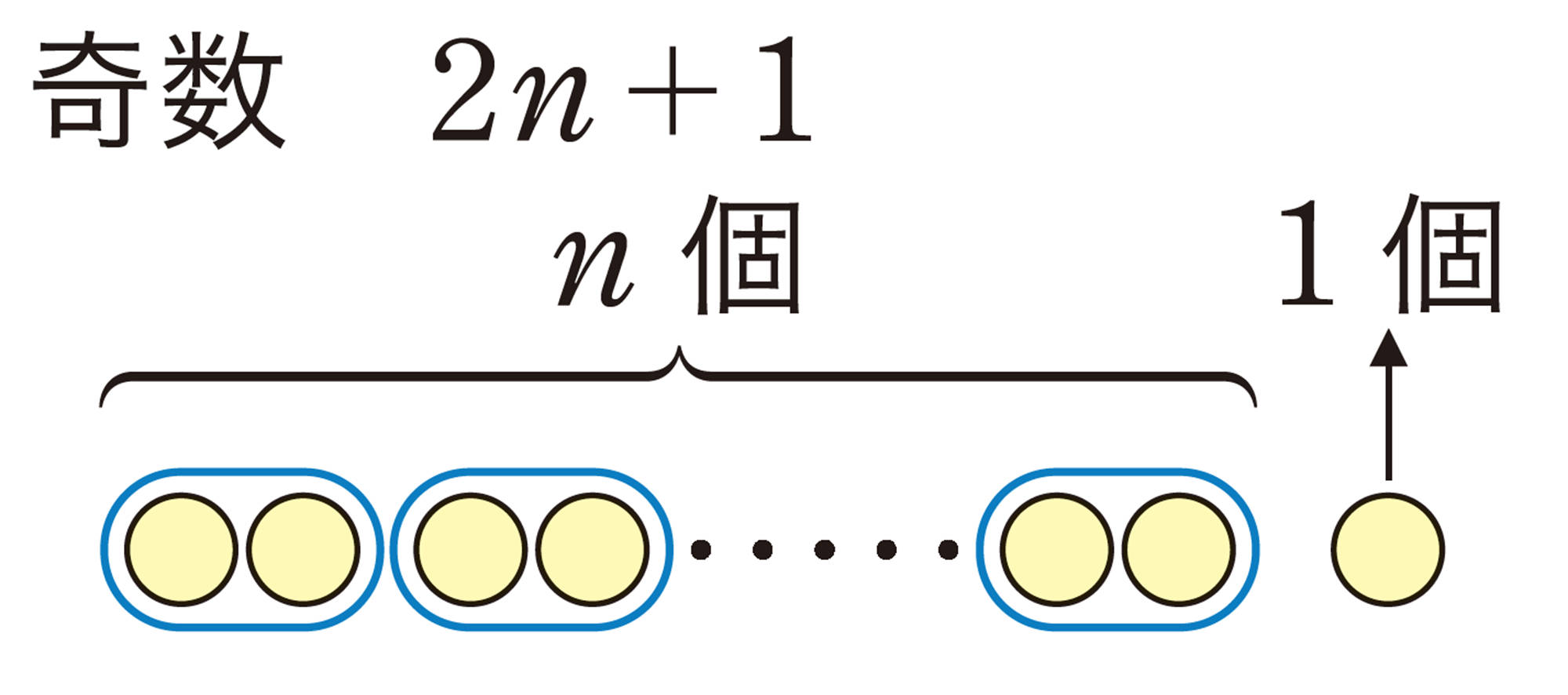
[mathjax] \( n \) を整数とすると，偶数は [mathjax] \( 2n \) ，奇数は [mathjax] \( 2n+1 \) と表される。
偶数と奇数の和は，
[mathjax] \( 4n \) は4の倍数なので偶数になり，それに1をたすので [mathjax] \( 4n+1 \) は奇数である。したがって，偶数と奇数の和は奇数になる。
<2年p.28>
[mathjax] \( 2n \) と [mathjax] \( 2n+1 \) の [mathjax] \( n \) に整数を代入してみると，連続した偶数と奇数になってしまうよ。
連続していない偶数と奇数の和についても，考えないといけないね。
大和さんは，前の説明を次のように修正しました。
これでいいのかな？
[mathjax] \( m \)， [mathjax] \( n \) を整数とすると，偶数は[mathjax] \( 2m \) ，奇数は[mathjax] \( 2n+1 \) と表される。
偶数と奇数の和は，
[mathjax] \( 2m+2n \) は偶数と偶数の和なので偶数になり，それに1をたすので [mathjax] \( 2m+2n+1 \) は奇数である。
したがって，偶数と奇数の和は奇数になる。
【３】 大和さんがどのように説明を修正したかを話し合ってみましょう。また，なぜそのように修正したのかも考えてみましょう。
この説明だと最後の部分で，「偶数と偶数の和は偶数になる」ということを使っているね。でも，そのことはまだ確かめていないよね。「偶数と偶数の和が偶数になる」ことを使わないで説明することはできないのかな。
[mathjax] \( 2 \times (\textsf{整数})+1 \) と表すことができれば，奇数だとわかるよね。[mathjax] \( 2m+2n+1 \) をこの形に直せないかな。
【４】 上の説明に出てくる「[mathjax] \( 2m+2n+1 \) 」を「[mathjax] \( 2 \times (\textsf{整数})+1 \) 」の形に直して，「偶数と奇数の和は奇数になる」という性質がいつでも成り立つ理由を，ほかの人にもわかりやすく説明してみましょう。
【５】 前ページのQの⑵，⑶の2数の和は，偶数，奇数のどちらでしょうか。
また，そうなる理由を文字式を使って，ノートに書き，それをもとに友だちに説明してみましょう。
⑵ [mathjax] \( ( \textsf{偶数})+( \textsf{偶数}) \)
⑶ [mathjax] \( ( \textsf{奇数})+( \textsf{奇数}) \)
<2年p.29>
問 ４ 真央さんは，2の倍数と3の倍数の和は5の倍数になると考え，右のように文字式を使って説明しました。この説明は正しいですか。 正しくない場合は，その理由を説明しなさい。
正しいかな？
2の倍数を[mathjax] \( 2a \) ，3の倍数を[mathjax] \( 3a \) とすると，2の倍数と3の倍数の合計は，
[mathjax] \( 2a+3a=5a \)
と表せるから，5の倍数になるといえる。
あることがらが成り立たないことを示すには，成り立たない例を1つあげればよい。たとえば，問4の場合，2の倍数4と3の倍数9の和は13となり，2の倍数と3の倍数の和は5の倍数になるとはいえないことがわかる。
問 ５ [mathjax] \(10\)，[mathjax] \(11\)ページの問題について，次の問いに答えなさい。
⑴ 6桁の自然数を，[mathjax] \( 100000a+10000b+1000c+100a+10b+c \) と表したとき，7でわり切れることを説明しなさい。
⑵ 7以外の数でわり切れる数はありますか。
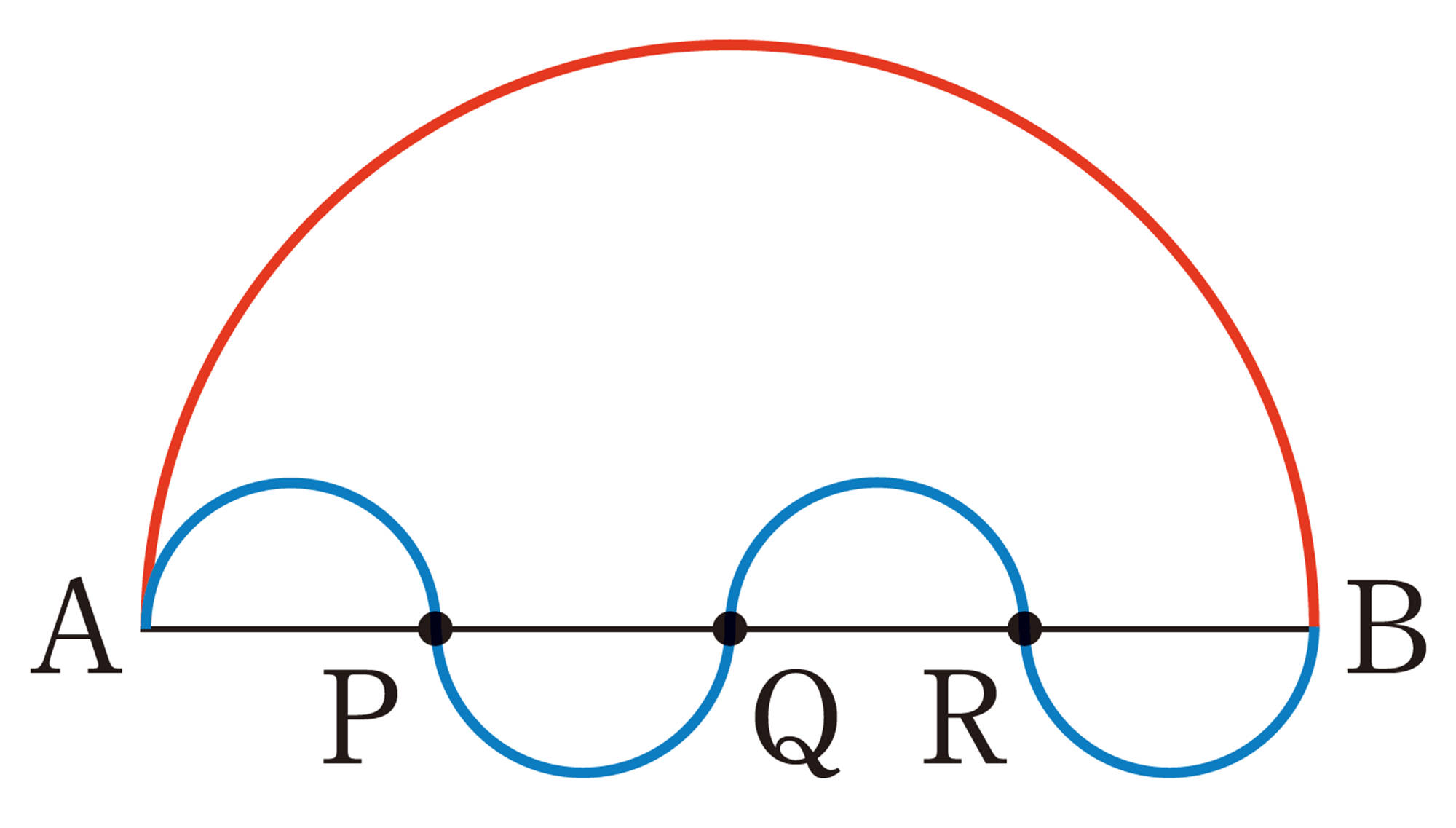
17列目の数の不思議 Tea Break
【１】 右の表を使って，次のような計算をしてみましょう。その結果から，どんなことがわかるでしょうか。
① 1列目に，1〜9までの好きな数を書く。
② 3列目に，1列目の数と2列目の数5の和を書く（和が2桁の数になったときは一の位の数だけを書く）。
③ 4列目は，2列目と3列目の数の和を書く。
以下同じようにして，直前の2列の数の和を求め，17列目の数まで求める。
【２】 2列目の数を5以外の数に変えるとどうなるでしょうか。結果を予想して，調べてみましょう。
【３】 [mathjax] \(1\)，[mathjax] \(2\)で調べたことを，文字を使って説明してみましょう。
<2年p.30>
例 ３ 右の図で，点 O は線分 AB の中点です。
このとき，AO，BO をそれぞれ直径とする2つの半円の弧の長さの和は，AB を直径とする半円の弧の長さと等しくなります。
このことを，文字式を使って説明しなさい。
考え方 [mathjax] \( AO=a \) として，それぞれの弧の長さを求めて考える。
解答
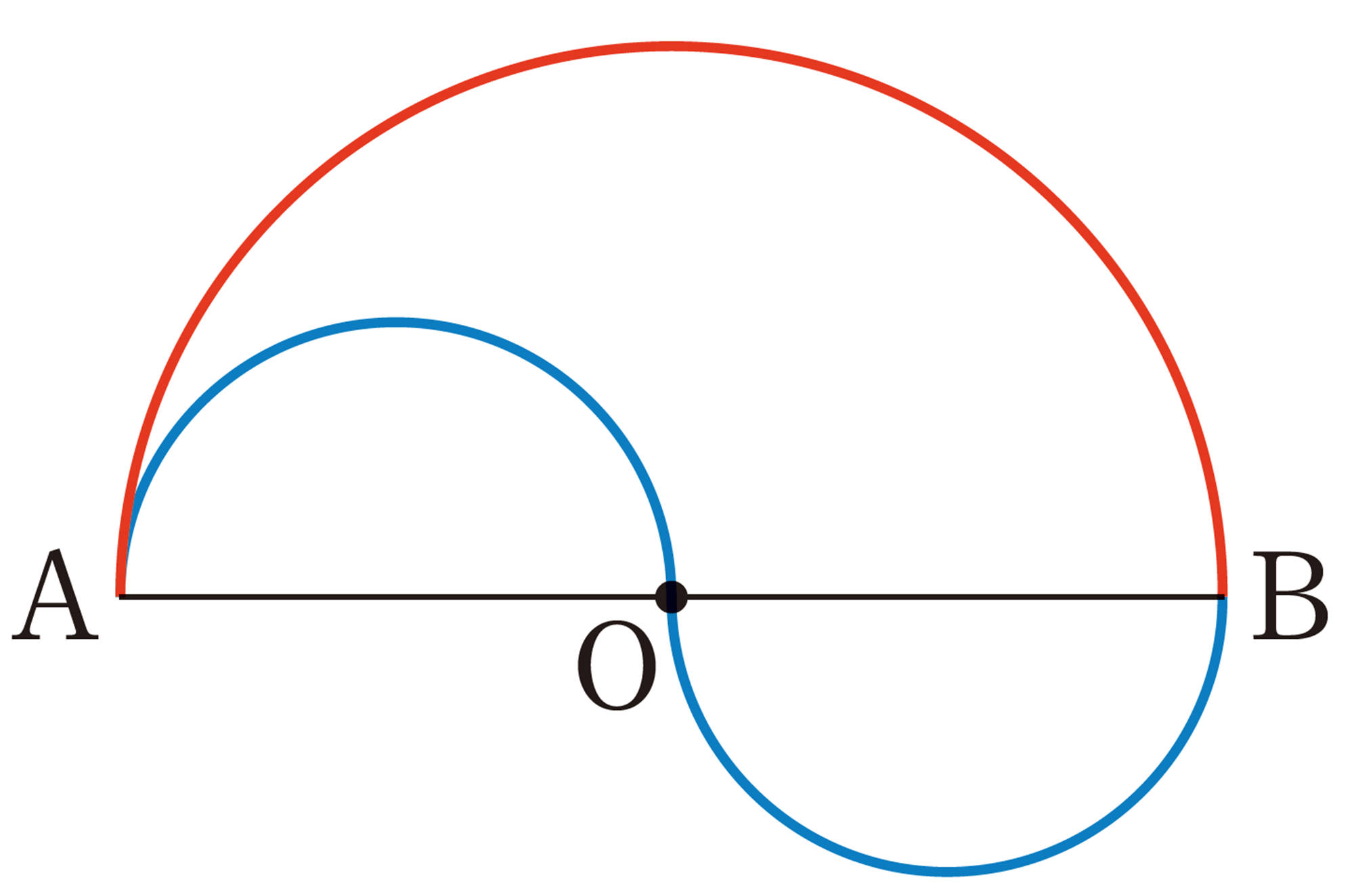
[mathjax] \(AO=a\) とすると， AO を直径とする
半円の弧の長さは，
[mathjax] \( ( a \times \pi ) \times \dfrac{1}{2} \)
点O は， 線分AB の中点であるから，
[mathjax] \(AO=BO\)
したがって， AO， BO をそれぞれ直径とする
2 つの半円の弧の長さは等しく， それらの和は，
[mathjax] \( ( a \times \pi ) \times \dfrac{1}{2} \times 2= \pi a \)･･････①
また，[mathjax]\(AB=2a \) であるから， AB を直径とする半円の弧の長さは，
[mathjax] \( (2a \times \pi ) \times \dfrac{1}{2}= \pi a \) ･･････②
①と②より， AO， BO をそれぞれ直径とする2つの半円の弧の長さの和は， AB を直径とする半円の弧の長さと等しい。
説明をわかりやすくするために，図をきちんとかいておこう。
分数は2行使って書こう。
問 ６ 右の図で， [mathjax] \(AP=PQ=QR=RB\) のとき，AP，PQ，QR，RB をそれぞれ直径とする4つの半円の弧の長さの和は，AB を直径とする半円の弧の長さと等しくなることを，文字式を使って説明しなさい。
どんなことがわかったかな
文字式を利用することで，数や図形の性質がいつでも成り立つことを説明することができます。
