<1年p.302 >
1章 正の数・負の数 [解答]
トライ P.29
表の左から順に, [mathjax]\(-79\) , [mathjax]\(-33\) , [mathjax]\(+59\) , [mathjax]\(+92\)
計算力を高めよう1 P.34
1
⑴ [mathjax]\(+15\)
⑵ [mathjax]\(-18\)
⑶ [mathjax]\(+7\)
⑷ [mathjax]\(-7\)
⑸ [mathjax]\(0\)
⑹ [mathjax]\(-5\)
⑺ [mathjax]\(+4\)
⑻ [mathjax]\(-1.2\)
⑼ [mathjax]\(-6.2\)
⑽ [mathjax]\(+\dfrac{1}{6}\)
⑾ [mathjax]\(-\dfrac{7}{6}\)
2
⑴ [mathjax]\(+4\)
⑵ [mathjax]\(-6\)
⑶ [mathjax]\(+7\)
⑷ [mathjax]\(+13\)
⑸ [mathjax]\(-9\)
⑹ [mathjax]\(-8\)
⑺ [mathjax]\(+13\)
⑻ [mathjax]\(-3.3\)
⑼ [mathjax]\(+\dfrac{2}{3}\)
⑽ [mathjax]\(-\dfrac{9}{14}\)
⑾ [mathjax]\(+\dfrac{4}{3}\)
3
⑴ [mathjax]\(-6\)
⑵ [mathjax]\(0\)
⑶ [mathjax]\(-2\)
⑷ [mathjax]\(-5\)
⑸ [mathjax]\(3\)
⑹ [mathjax]\(-11\)
⑺ [mathjax]\(0\)
⑻ [mathjax]\(-14\)
⑼ [mathjax]\(-4\)
⑽ [mathjax]\(-7\)
⑾ [mathjax]\(6\)
⑿ [mathjax]\(-4\)
⒀ [mathjax]\(-1.5\)
⒁ [mathjax]\(1.4\)
⒂ [mathjax]\(-1\)
⒃ [mathjax]\(-\dfrac{7}{18}\)
⒄ [mathjax]\(-18\)
⒅ [mathjax]\(13\)
⒆ [mathjax]\(-3\)
⒇ [mathjax]\(-0.4\)
(21) [mathjax]\(\dfrac{1}{2}\)
計算力を高めよう2 p.53
1
⑴ [mathjax]\(10\)
⑵ [mathjax]\(-24\)
⑶ [mathjax]\(-36\)
⑷ [mathjax]\(42\)
⑸ [mathjax]\(-120\)
⑹ [mathjax]\(48\)
⑺ [mathjax]\(81\)
⑻ [mathjax]\(-81\)
⑼ [mathjax]\(-64\)
⑽ [mathjax]\(0.49\)
⑾ [mathjax]\(-\dfrac{3}{8}\)
⑿ [mathjax]\(14\)
2
⑴ [mathjax]\(2\)
⑵ [mathjax]\(-5\)
⑶ [mathjax]\(-3\)
⑷ [mathjax]\(\dfrac{21}{2}\)
⑸ [mathjax]\(0\)
⑹ [mathjax]\(-0.4\)
⑺ [mathjax]\(-\dfrac{1}{9}\)
⑻ [mathjax]\(21\)
⑼ [mathjax]\(-\dfrac{5}{6}\)
3
⑴ [mathjax]\(14\)
⑵ [mathjax]\(12\)
⑶ [mathjax]\(-10\)
⑷ [mathjax]\(\dfrac{3}{2}\)
⑸ [mathjax]\(-\dfrac{3}{2}\)
⑹ [mathjax]\(-\dfrac{32}{27}\)
⑺ [mathjax]\(\dfrac{4}{9}\)
4
⑴ [mathjax]\(-10\)
⑵ [mathjax]\(-26\)
⑶ [mathjax]\(26\)
⑷ [mathjax]\(-36\)
⑸ [mathjax]\(7\)
⑹ [mathjax]\(-15\)
⑺ [mathjax]\(9\)
⑻ [mathjax]\(-6\)
⑼ [mathjax]\(0\)
⑽ [mathjax]\(10\)
⑾ [mathjax]\(2\)
⑿ [mathjax]\(19\)
⒀ [mathjax]\(\dfrac{5}{12}\)
⒁ [mathjax]\(\dfrac{2}{3}\)
1章のまとめの問題 P.61〜63
1
⑴ [mathjax]\(-1\),[mathjax]\(+2\)
⑵ [mathjax]\(+5\) 年
⑶ [mathjax]\(+7\) ,[mathjax]\(-7\)
⑷ 小さく,大きく
2
⑴ [mathjax]\(-3 \lt 1\)
⑵ [mathjax]\(-6 \gt -7\)
⑶ [mathjax]\(-5 \lt -2 \lt 4\)
3
⑴ [mathjax]\(2\)
⑵ [mathjax]\(-10\)
⑶ [mathjax]\(-15\)
⑷ [mathjax]\(-\dfrac{1}{3}\)
⑸ [mathjax]\(6\)
⑹ [mathjax]\(8\)
⑺ [mathjax]\(-16\)
⑻ [mathjax]\(\dfrac{9}{16}\)
⑼ [mathjax]\(-0.08\)
⑽ [mathjax]\(7\)
⑾ [mathjax]\(-\dfrac{3}{4}\)
⑿ [mathjax]\(-\dfrac{3}{4}\)
4
⑴ [mathjax]\(90\)
⑵ [mathjax]\(-4\)
⑶ [mathjax]\(3\)
⑷ [mathjax]\(8\)
⑸ [mathjax]\(-9\)
⑹ [mathjax]\(-4\)
⑺ [mathjax]\(-5\)
⑻ [mathjax]\(1\)
5
⑴ 最大公約数・・・[mathjax]\(8\),最小公倍数・・・[mathjax]\(160\)
⑵ 最大公約数・・・[mathjax]\(18\),最小公倍数・・・[mathjax]\(108\)
6
⑴ 1月6日
⑵ 1月7日
応用
1
⑴ [mathjax]\(-45\)
⑵ [mathjax]\(15\)
⑶ [mathjax]\(-\dfrac{1}{14}\)
⑷ [mathjax]\(\dfrac{7}{12}\)
⑸ [mathjax]\(-\dfrac{1}{16}\)
⑹ [mathjax]\(-14\)
2
⑴ 表の左から順に,[mathjax]\(-3\),[mathjax]\(+5\),[mathjax]\(-8\)
⑵ [mathjax]\(55+(-3+1+0+5-8) \div 5=54\)
答 [mathjax]\(54\)点
3
⑴ [mathjax]\(8\),[mathjax]\(16\),[mathjax]\(32\)
⑵ [mathjax]\(49\),[mathjax]\(94\)
活用
1
⑴ 太陽光が太陽電池に当たっていない時間帯だから,発電した電力が[mathjax]\(0\) kWhになる。
⑵ 表の左から順に,
[mathjax]\(0.6\),[mathjax]\(-0.78\),[mathjax]\(3.1\),[mathjax]\(2.41\),[mathjax]\(0.83\),[mathjax]\(0\)
<1年p.303 >
⑶ もっとも小さい時間帯・・・ 20時 〜 22 時
もっとも大きい時間帯・・・ 12時 〜14時
⑷ 余剰電力の合計を求めて,それが正の数か負の数かを調べれば,どちらが大きいかがわかる
時刻がもどる? P.64
① ドーハ・・・ [mathjax]\(+3\) ,ホノルル・・・ [mathjax]\(-10\)
② 3月3日3時55 分, [mathjax] \(-17\)
③ 11 時間55分
2章 文字式 [解答]
1
⑴ [mathjax]\(7a\)
⑵ [mathjax]\(2a\)
⑶ [mathjax]\(-6x\)
⑷ [mathjax]\(-a\)
⑸ [mathjax]\(5x\)
⑹ [mathjax]\(5a+9\)
⑺ [mathjax]\(-2x+1\)
⑻ [mathjax]\(-9a+13\)
⑼ [mathjax]\(1.3x\)
⑽ [mathjax]\(\dfrac{3}{2}y\)
2
⑴ [mathjax]\(8x-7\)
⑵ [mathjax]\(3x-2\)
⑶ [mathjax]\(x-\dfrac{1}{3}\)
⑷ [mathjax]\(2x+5\)
⑸ [mathjax]\(-5y+2\)
⑹ [mathjax]\(23\)
⑺ [mathjax]\(\dfrac{3}{4}y+9\)
3
⑴ [mathjax]\(27a\)
⑵ [mathjax]\(-40x\)
⑶ [mathjax]\(-2.4y\)
⑷ [mathjax]\(16a\)
⑸ [mathjax]\(3y\)
⑹ [mathjax]\(-7a\)
⑺ [mathjax]\(-\dfrac{1}{3}x\)
⑻ [mathjax]\(36a\)
⑼ [mathjax]\(-3a-21\)
⑽ [mathjax]\(24x-20\)
⑾ [mathjax]\(4a-3\)
⑿ [mathjax]\(24x-10\)
⒀ [mathjax]\(2x-7\)
⒁ [mathjax]\(2a-3\)
⒂ [mathjax]\(2x-\dfrac{5}{2}\)
⒃ [mathjax]\(18x+6\)
4
⑴ [mathjax]\(14x-35\)
⑵ [mathjax]\(-4a+5\)
⑶ [mathjax]\(-a+8\)
⑷ [mathjax]\(7x+16\)
⑸ [mathjax]\(y-10\)
⑹ [mathjax]\(-13x+1\)
⑺ [mathjax]\(20a\)
⑻ [mathjax]\(\dfrac{3}{4}x-4\)
⑼ [mathjax]\(\dfrac{1}{9}\)
2章のまとめの問題 P.91〜93
1
⑴ [mathjax]\(8x²\)
⑵ [mathjax]\(\dfrac{7}{x}\)
⑶ [mathjax]\(5a+b\)
⑷ [mathjax]\(\dfrac{x-1}{2}\)
2
⑴ [mathjax]\((7a+3b)\) 円
⑵ [mathjax]\(\dfrac{1}{5}x\) L ( [mathjax]\(0.2x\) L )
⑶ [mathjax]\((10-3x)\) km
⑷ [mathjax]\(\dfrac{a}{b}\) m
3
⑴ [mathjax]\(-10\)
⑵ [mathjax]\(324\)
⑶ [mathjax]\(-17\)
⑷ [mathjax]\(21\)
4
⑴ [mathjax]\(2x\)
⑵ [mathjax]\(-3x+8\)
⑶ [mathjax]\(\dfrac{3}{5}a\)
⑷ [mathjax]\(-a+3\)
⑸ [mathjax]\(-2x+3\)
⑹ [mathjax]\(-56a\)
⑺ [mathjax]\(0.6x\)
⑻ [mathjax]\(-6x\)
⑼ [mathjax]\(-x+4\)
⑽ [mathjax]\(2x-5\)
⑾ [mathjax]\(a-2\)
⑿ [mathjax]\(4x-2\)
5
⑴ 図形の面積
⑵ 図形のまわりの長さ
応用
1
⑴ [mathjax]\(-0.8x+0.6\)
⑵ [mathjax]\(\dfrac{7}{6}x-\dfrac{9}{4}\)
⑶ [mathjax]\(-8x+\dfrac{1}{2}\)
⑷ [mathjax]\(-x+12\)
2
⑴ [mathjax]\(27\)
⑵ [mathjax]\(10\)
活用
1
⑴ [mathjax]\((6n-6)\) 本
⑵ [mathjax]\(61\) 本
カレンダーの数の秘密を考えよう P.94
① 略
② 略
③ [mathjax]\(7\) ,[mathjax]\(7\) ,[mathjax]\(7\) ,[mathjax]\(7\)
④ 上の数・・・ [mathjax]\(a-7\) ,下の数・・・ [mathjax]\(a+7\) ,[mathjax]\(3\) つの数の和は,中央の数 [mathjax]\(a\) の [mathjax]\(3\) 倍の数といえる。
⑤ 略
3章 1次方程式 [解答]
計算力を高めよう4 P.112
1
⑴ [mathjax]\(x=4\)
⑵ [mathjax]\(x=11\)
⑶ [mathjax]\(x=-8\)
⑷ [mathjax]\(x=1\)
⑸ [mathjax]\(x=6\)
⑹ [mathjax]\(x=-9\)
⑺ [mathjax]\(x=7\)
⑻ [mathjax]\(x=-\dfrac{5}{3}\)
⑼ [mathjax]\(x=20\)
⑽ [mathjax]\(x=-6\)
2
⑴ [mathjax]\(x=3\)
⑵ [mathjax]\(x=-1\)
⑶ [mathjax]\(x=6\)
⑷ [mathjax]\(x=3\)
⑸ [mathjax]\(x=0\)
⑹ [mathjax]\(x=-3\)
⑺ [mathjax]\(x=-2\)
⑻ [mathjax]\(x=-7\)
⑼ [mathjax]\(x=\dfrac{4}{5}\)
⑽ [mathjax]\(x=6\)
<1年p.304 >
⑾ [mathjax]\(x=1\)
⑿ [mathjax]\(x=-\dfrac{14}{3}\)
⒀ [mathjax]\(x=-\dfrac{2}{3}\)
⒁ [mathjax]\(x=2\)
⒂ [mathjax]\(x=\dfrac{3}{2}\)
3
⑴ [mathjax]\(x=-8\)
⑵ [mathjax]\(x=\dfrac{1}{2}\)
⑶ [mathjax]\(x=4\)
⑷ [mathjax]\(x=-2\)
4
⑴ [mathjax]\(x=-5\)
⑵ [mathjax]\(x=\dfrac{15}{2}\)
⑶ [mathjax]\(x=-5\)
⑷ [mathjax]\(x=8\)
5
⑴ [mathjax]\(x=\dfrac{2}{5}\)
⑵ [mathjax]\(x=4\)
⑶ [mathjax]\(x=-7\)
⑷ [mathjax]\(x=1\)
トライ P.115
くりの個数を [mathjax]\(x\) 個とすると,
答 班の人数 [mathjax]\(7\) 人,くりの個数 [mathjax]\(60\) 個
3章のまとめの問題 P.124〜P.126
1
⑴ [mathjax]\(10x+200=1300\)
⑵ [mathjax]\(2x-3 \gt x+5\)
2
① [mathjax]\(\mathsf{㋐,}m=5 ( \mathsf{㋑,} m=-5)\)
② [mathjax]\(\mathsf{㋓ ,}m=3 \require{physics} \left( \mathsf{㋒,}m=\dfrac{1}{3}\right) \)
3
⑴ [mathjax]\(x=28\)
⑵ [mathjax]\(x=-3\)
⑶ [mathjax]\(x=1\)
⑷ [mathjax]\(x=-9\)
⑸ [mathjax]\(x=6\)
⑹ [mathjax]\(x=1\)
⑺ [mathjax]\(x=\dfrac{15}{2}\)
⑻ [mathjax]\(x=\dfrac{1}{2}\)
⑼ [mathjax]\(x=20\)
⑽ [mathjax]\(x=8\)
⑾ [mathjax]\(x=28\)
⑿ [mathjax]\(x=\dfrac{20}{3}\)
4
⑴ 兄の年齢
⑵ 兄 [mathjax]\(12\) 歳,弟 [mathjax]\(9\) 歳
5
移した水の量を [mathjax]\(x\) Lとすると,
答 [mathjax]\(3\) L
6
この機械を [mathjax]\(x\) 時間作動させたとすると,
答 [mathjax]\(5\) 時間
応用
1
⑴ [mathjax]\(x=\dfrac{3}{5}\)
⑵ [mathjax]\(x=14\)
⑶ [mathjax]\(x=16\)
⑷ [mathjax]\(x=-2\)
⑸ [mathjax]\(x=-7\)
⑹ [mathjax]\(x=1\)
2
[mathjax]\(a=-2\)
3
A市とB市の間の道のりを [mathjax]\(x\) kmとすると,
答 [mathjax]\(120\) km
4
真央さんが [mathjax]\(x\) 個買う予定だったとすると,
答 [mathjax]\(2400\) 円
活用
1
⑴ 約 [mathjax]\(161\) g
⑵ トラックの輸送距離を [mathjax]\(x\) kmとすると,
答 トラック [mathjax]\(1566\) km,船[mathjax]\(8882\) km
⑶ ㋑
カーボンニュートラルを目指して P.127
① [mathjax]\(2016\) 年の温室効果ガス排出量を [mathjax]\(x\) 万 t とすると,
答 約 [mathjax]\(1193\) 万 t
② [mathjax]\(1193 \times 0.95¹⁴=581.79\cdots\cdots \)
答 約 [mathjax]\(582\) 万 t で,目標を達成できない
③ [mathjax]\(1193 \times 0.95³⁴=208.56\cdots\cdots \)
答 約 [mathjax]\(209\) 万 t
④ [mathjax]\(2090000 \div 8.8=237500\)
答 約 [mathjax]\(237500\) ha
⑤ [mathjax]\(71372 \times 8.8=628073.6\)
答 約 [mathjax]\(63\)万 t
4章 比例と反比例 [解答]
<1年p.305 >
4章のまとめの問題 P.166〜168
1
⑴ 関数
⑵ [mathjax]\(3\) ,減少
⑶ 比例定数
2
⑴ [mathjax]\(y=\dfrac{3}{2}x\),[mathjax]\(y=6\)
⑵ [mathjax]\(y=-\dfrac{4}{x}\),[mathjax]\(y=-1\)
3
⑴ [mathjax]\(y=3x\)
⑵ [mathjax]\(0 \leqq y \leqq 12\)
4
⑴ [mathjax]\(y=\dfrac{28}{x}\)
⑵ [mathjax]\(56\) mm
5
正しくない
(例) [mathjax]\(y=-\dfrac{6}{x}\) のように,比例定数が負の数のとき,[mathjax]\(x\) の値が増加すると[mathjax]\(y\) の値も増加するから。
応用
1
㋐比例定数・・・[mathjax]\(3\) ,[mathjax]\(y=3x\)
㋑比例定数・・・[mathjax]\(-\dfrac{1}{2}\),[mathjax]\(y=-\dfrac{1}{2}x\)
㋒比例定数・・・[mathjax]\(6\) ,[mathjax]\(y=\dfrac{6}{x}\)
㋓比例定数・・・[mathjax]\(-4\) ,[mathjax]\(y=-\dfrac{4}{x}\)
2
⑴ [mathjax]\(48\) cm²
⑵ [mathjax]\(y=16x\)
⑶ [mathjax]\(0 \leqq x \leqq 6\),[mathjax]\(0 \leqq y \leqq 96\)
活用
1
⑴ ペットボトルのキャップの個数と重さは比例するから,ペットボトルのキャップ [mathjax]\(1\) 個の重さと全体の重さを量り,全体の個数を [mathjax]\(x\) 個として,比を利用する。
⑵ [mathjax]\(y=\dfrac{1}{860}x\)
⑶ 約 [mathjax]\(86000\) 個
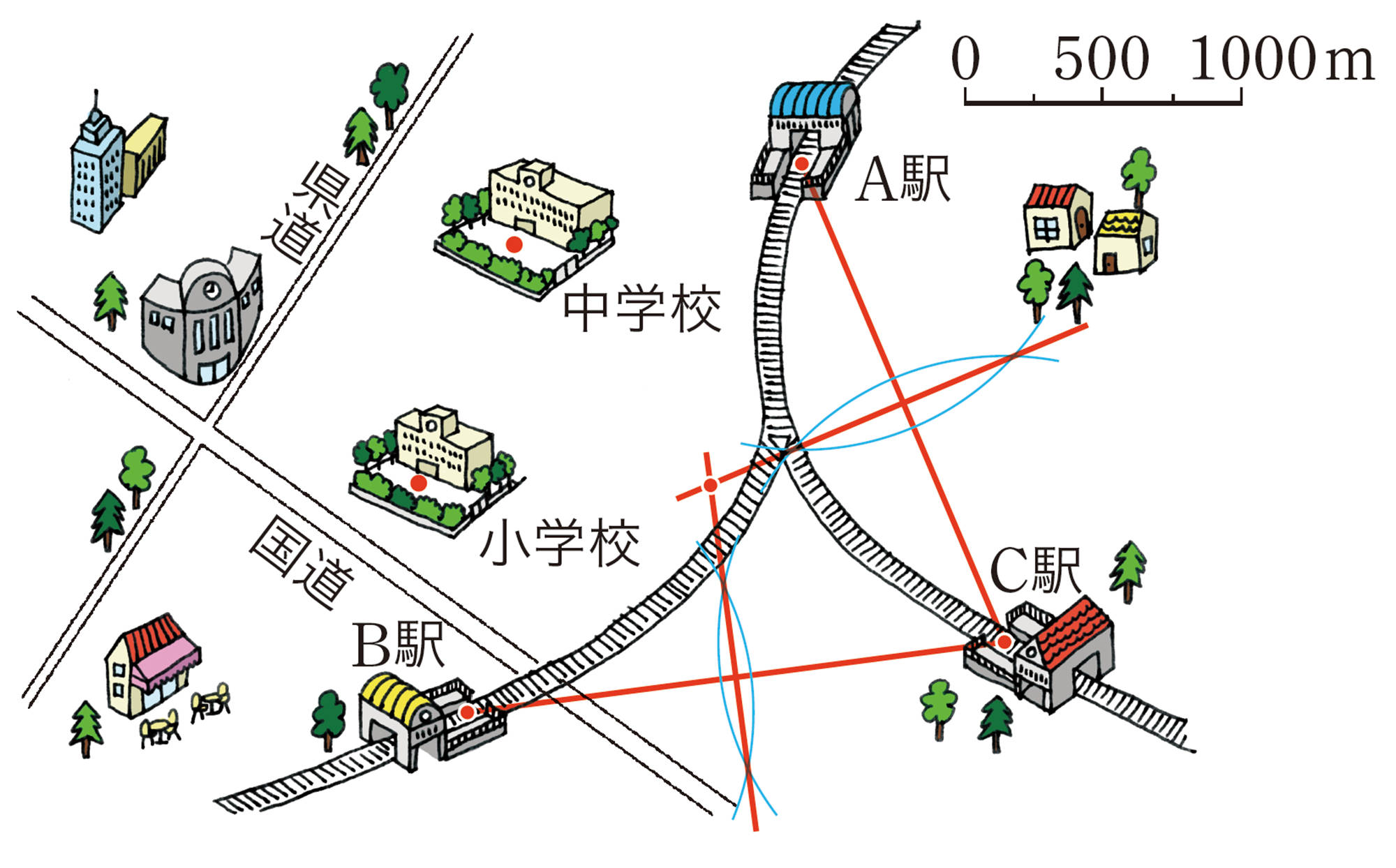
震源までの距離は? P.169
① 比例の関係 [mathjax]\((y=7.5x)\)
② 約 [mathjax]\(16.1\) km
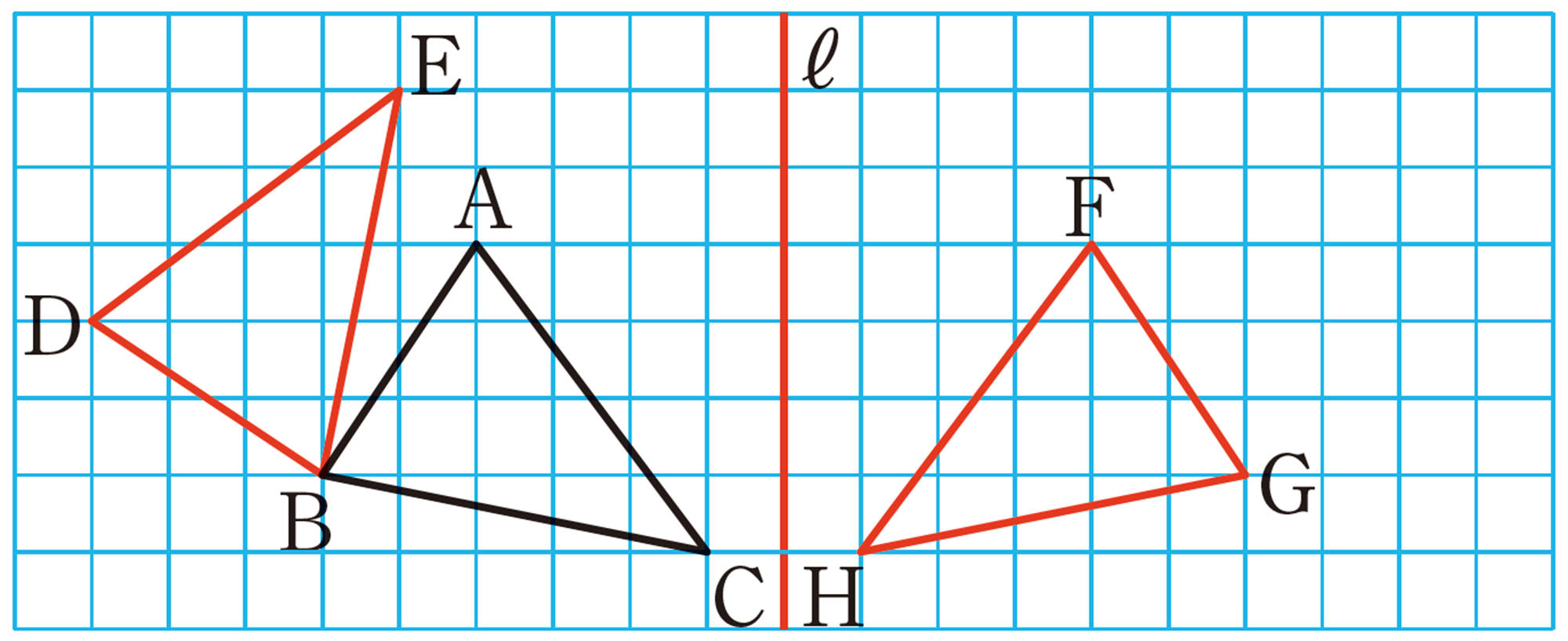
5章 平面図形 [解答]
<1年p.306 >
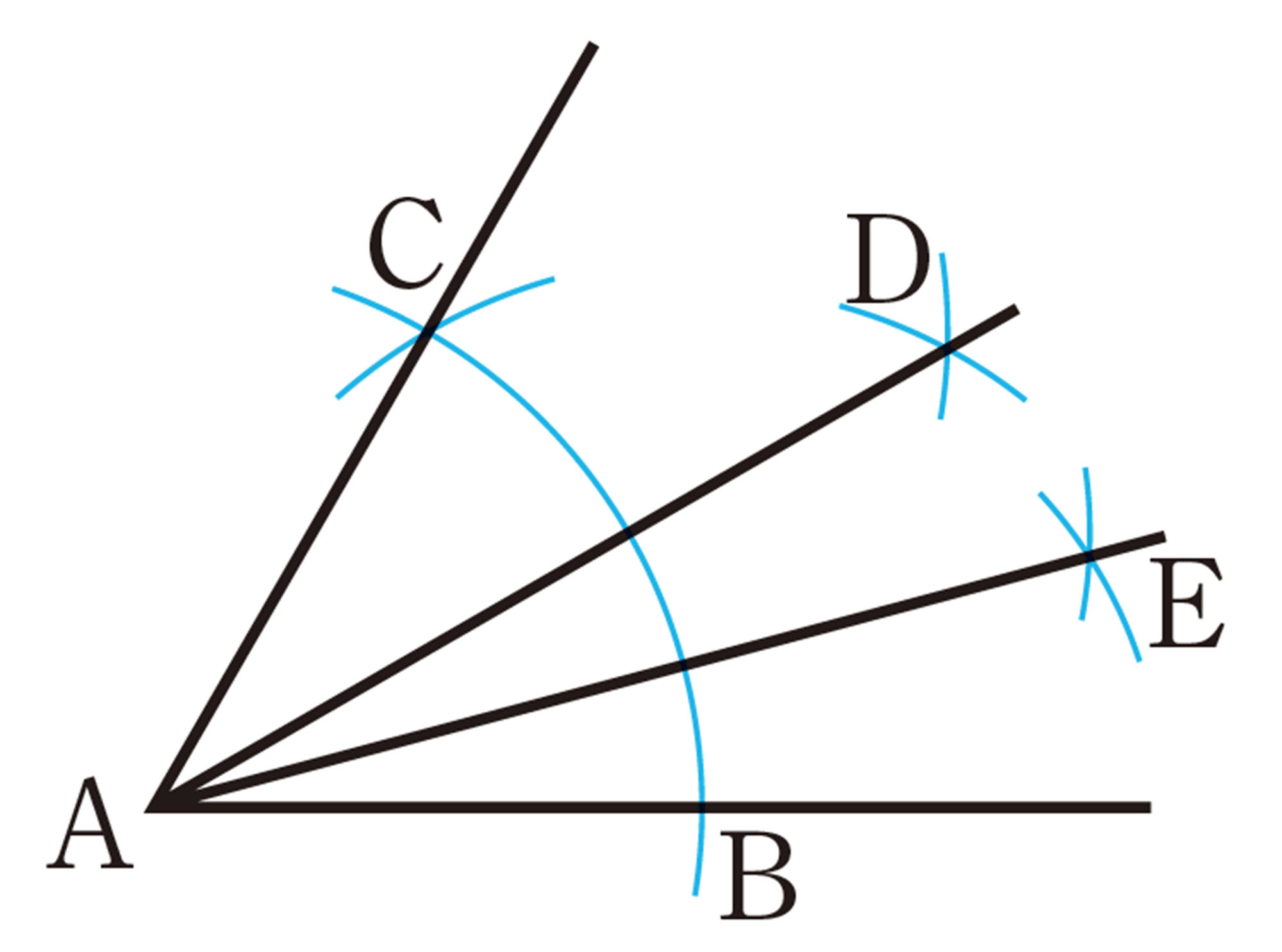
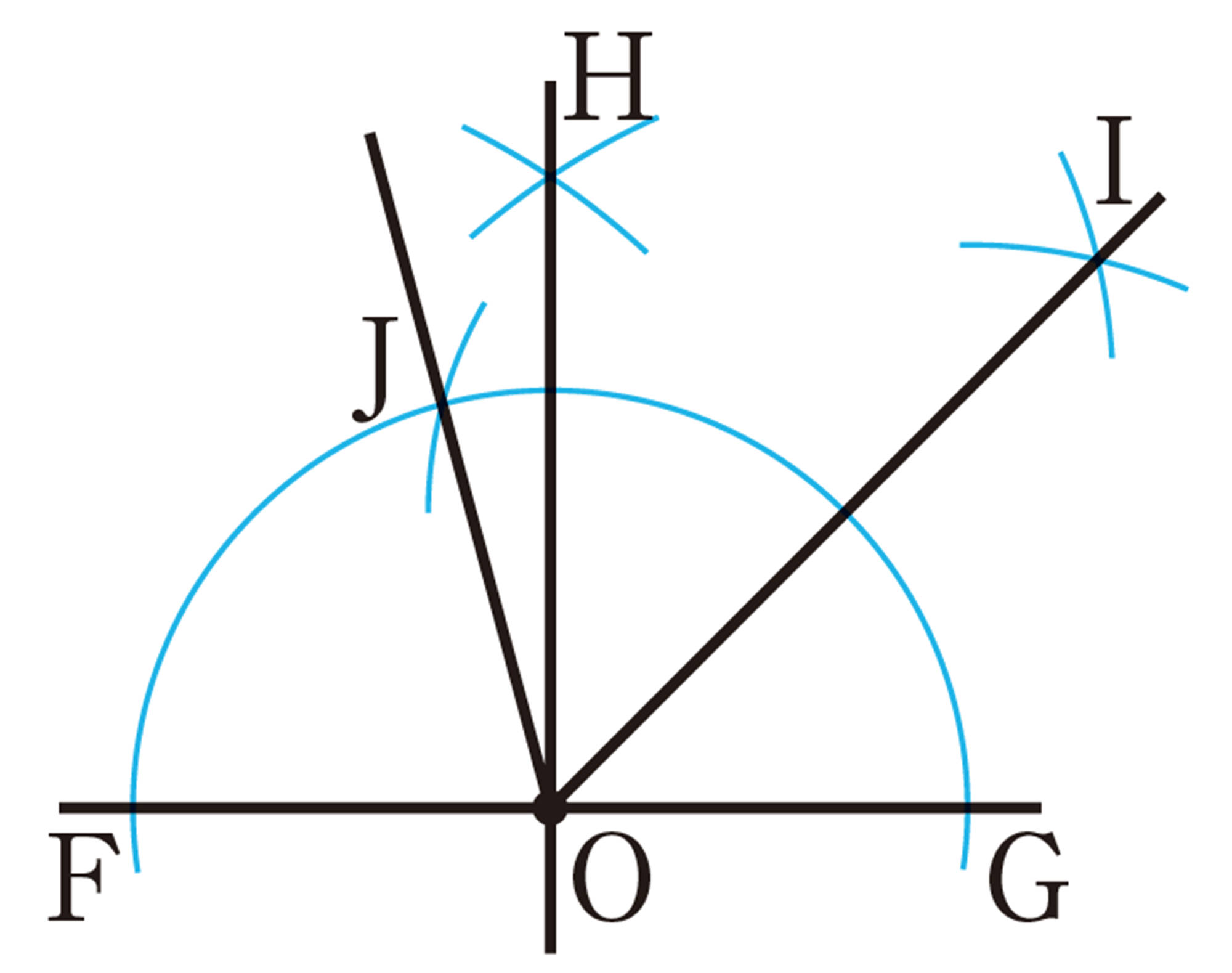
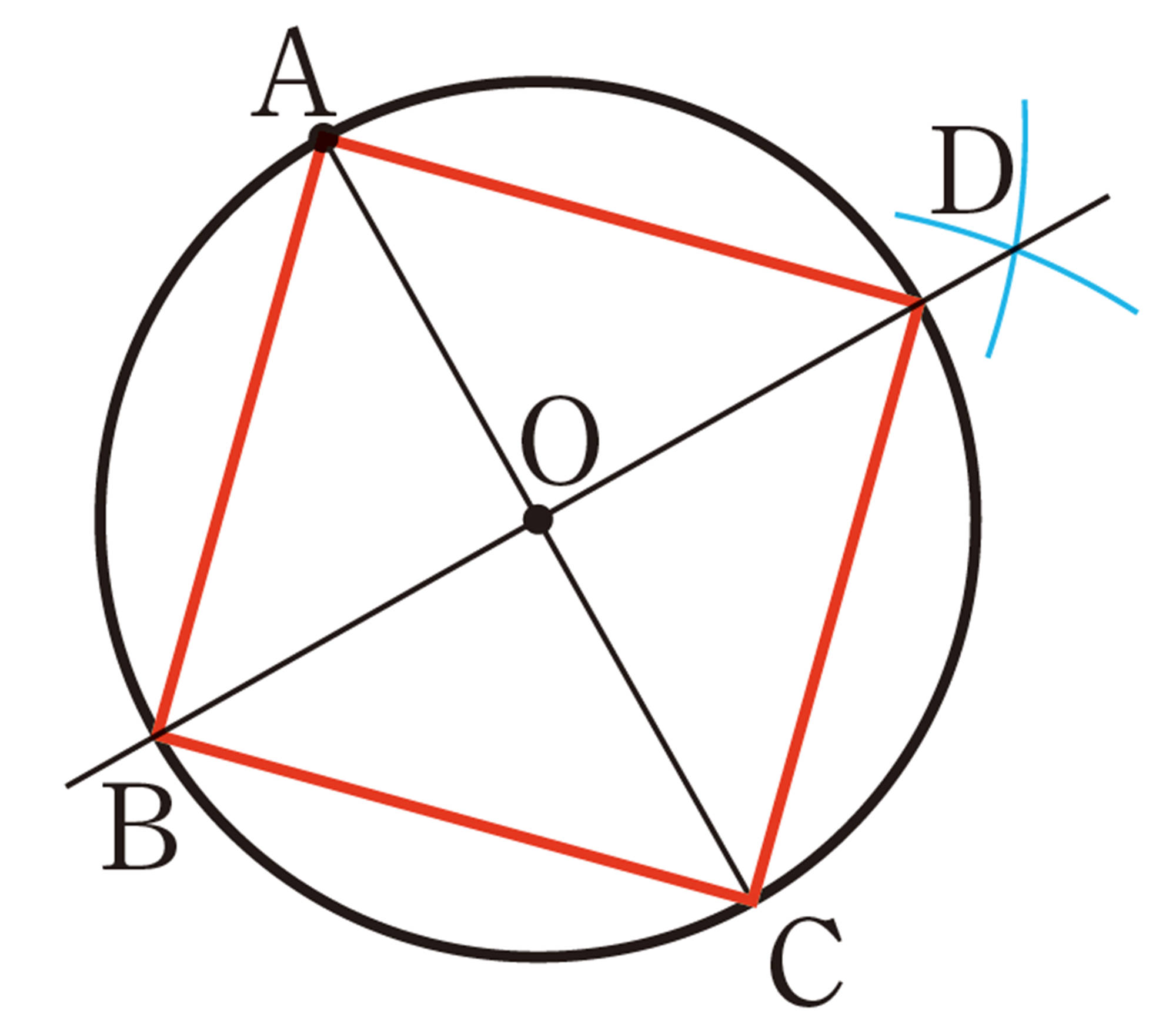
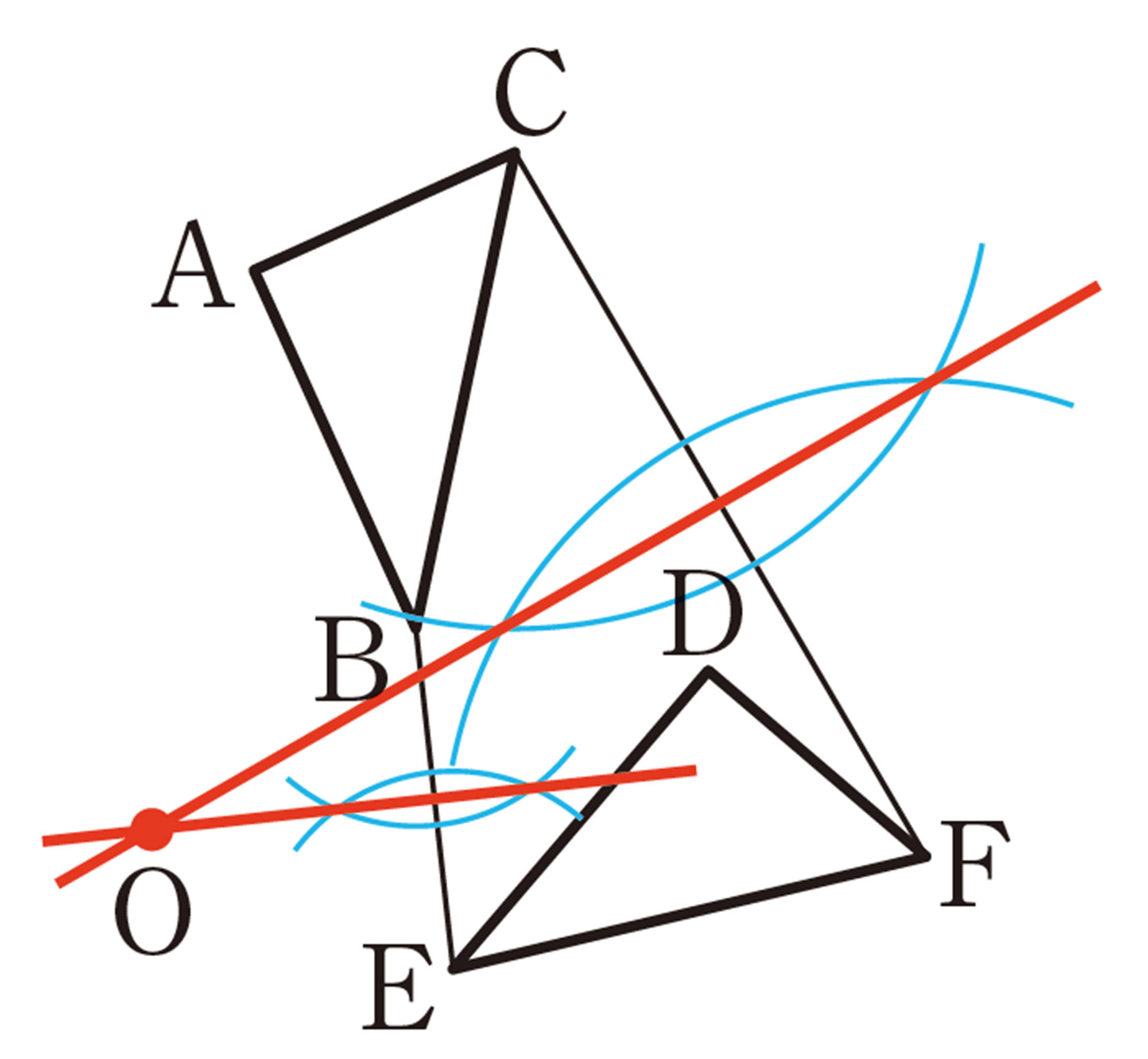
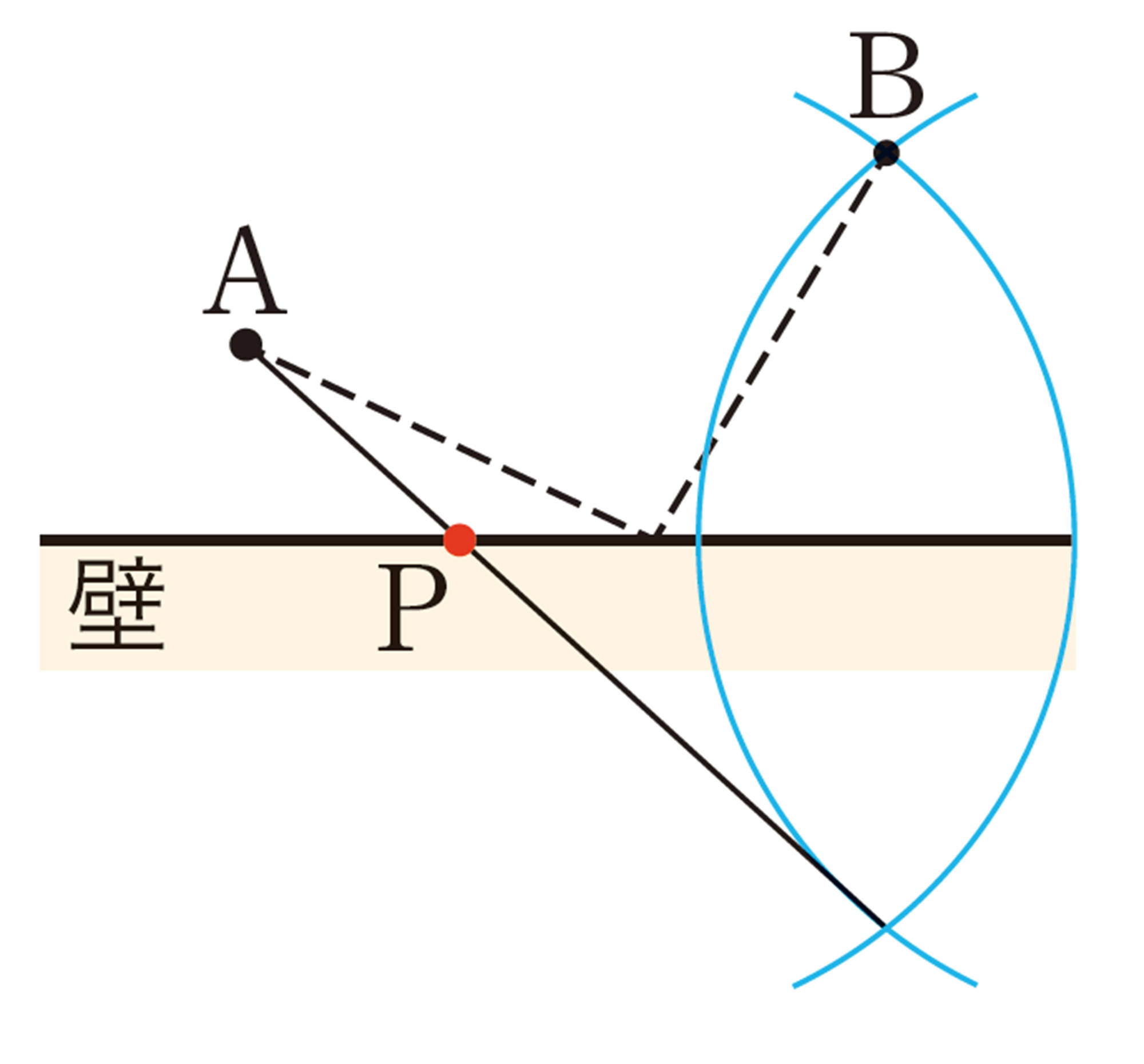
三角形に接する円を作図しよう P.201〜202
❶ 略
❷
① 点Oは辺ABの垂直二等分線上の点だから,[mathjax]\(OA=OB\) である。
② 点Oは辺ACの垂直二等分線上の点だから,[mathjax]\(OA=OC\) である。
③ ①,② から,[mathjax]\(OA=OB=OC\) となり,円Oは [mathjax]\(3\) つの頂点A,B,Cを通る。
❸ 略
❹ 略
❺ 略
❻ 点Iから辺AC,ABに垂線IE,IFを引くと,AI は [mathjax]\(\angle A\) の二等分線だから,[mathjax]\(IE=IF\)
BI は [mathjax]\(\angle B\) の二等分線だから,[mathjax]\(IF=ID\)
これより,[mathjax]\(ID=IE=IF\)
したがって,円Iは [mathjax]\(\triangle ABC\) の [mathjax]\(3\) つの辺に接する。
❼ 略
6章 空間図形 [解答]
トライ P.236
⑴ ㋑ [mathjax]\(2\) ㋒ [mathjax]\(3\)
⑵ ㋑,㋒ともに [mathjax]\(100 \pi\) cm²で,面積は等しい。
6章のまとめの問題 P.238〜240
1
⑴ 多面体
⑵ 平行,ねじれの位置
⑶ [mathjax]\(\pi\),[mathjax]\(2 \pi r\),[mathjax]\(\pi r²\)
2
⑴ 辺BE,CF
⑵ 辺BC,EF
⑶ 面DEF
⑷ 面ABED,BCFE,ACFD
活用
1
⑴ [mathjax]\(544 \pi\) cm²
⑵ [mathjax]\(35\) 人
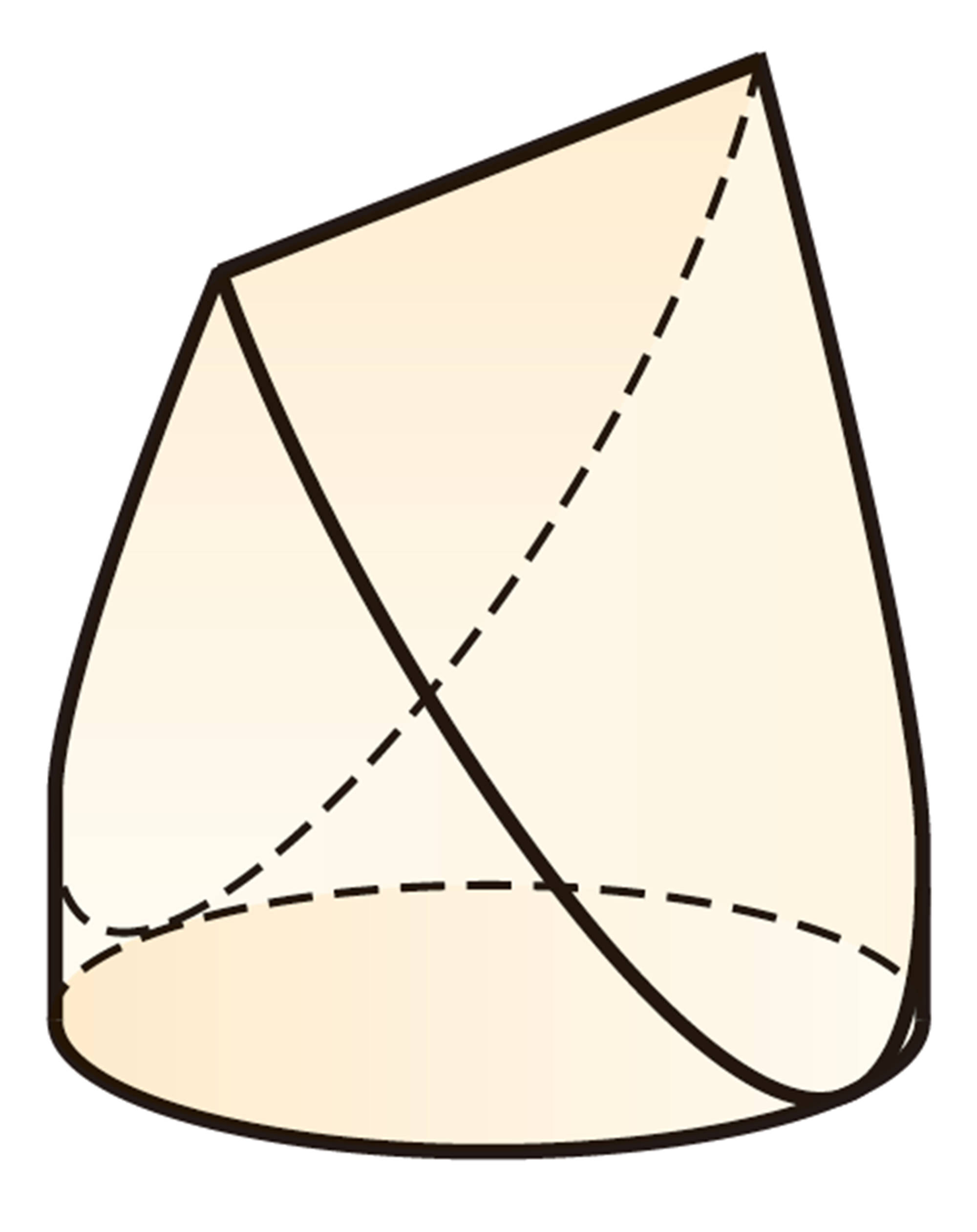
体積や表面積を比べよう P.241
❶ピラミッドの体積は,約 [mathjax]\(2570000\) m³となる。これは,東京ドームの容積の約 [mathjax]\(2\) 倍である。
❷
⑴ 略
⑵ Bの方が多く入る
7章 データの活用 [解答]
7章のまとめの問題 P.269〜271
1
⑴ 最頻値
(例) 今年もっとも多く売れたサイズが,来年ももっとも多く売れると考えられるから,最頻値を用いる。
⑵ 平均値
(例)メンバーの記録の平均値がよいチームが,リレーの合計タイムもよくなると
<1年p.307 >
考えられるから,平均値を用いる。
⑶ 中央値
(例)この場合,中央値はよい方から [mathjax]\(8\) 番目の記録である。自分の記録が中央値より上ならば,上位[mathjax]\(7\) 位以内と判断できるから,中央値を用いる。
2
上向きが出る確率・・・ [mathjax]\(0.53\)
下向きが出る確率・・・ [mathjax]\(0.47\)
活用
1
⑴ [mathjax]\(20\) 回
⑵ (A選手)平均値・・・ [mathjax]\(112\) m
(B選手)平均値・・・ [mathjax]\(118\) m
⑶
A選手を選んだ場合
(例)記録にばらつきはあるものの,最大値が大きく,より遠くへ飛べる可能性があると考えられるから。
B選手を選んだ場合
(例)平均値がA選手よりよいため,安定してよい成績が見込めると考えられるから。
POSデータとABC分析 P.272
❶ 略
小学校の計算・1年の復習 [解答]
小学校の計算 P.294
1
⑴ [mathjax]\(63\)
⑵ [mathjax]\(94\)
⑶ [mathjax]\(125\)
⑷ [mathjax]\(23\)
⑸ [mathjax]\(27\)
⑹ [mathjax]\(7\)
2
⑴ [mathjax]\(84\)
⑵ [mathjax]\(290\)
⑶ [mathjax]\(588\)
⑷ [mathjax]\(864\)
⑸ [mathjax]\(28000\)
⑹ [mathjax]\(6\)
⑺ [mathjax]\(7\)
⑻ [mathjax]\(4\)
⑼ [mathjax]\(8\)
3
⑴ [mathjax]\(7.9\)
⑵ [mathjax]\(6.3\)
⑶ [mathjax]\(12\)
⑷ [mathjax]\(3.3\)
⑸ [mathjax]\(4.8\)
⑹ [mathjax]\(4.6\)
4
⑴ [mathjax]\(27.2\)
⑵ [mathjax]\(10.8\)
⑶ [mathjax]\(6.08\)
⑷ [mathjax]\(0.6\)
⑸ [mathjax]\(6\)
⑹ [mathjax]\(3\)
<1年p.308 >
5
⑴ [mathjax]\(1\)
⑵ [mathjax]\(\dfrac{8}{15}\)
⑶ [mathjax]\(\dfrac{1}{2}\)
⑷ [mathjax]\(\dfrac{23}{12} \require{physics} \left(1\dfrac{11}{12}\right)\)
⑸ [mathjax]\(\dfrac{1}{2}\)
⑹ [mathjax]\(\dfrac{13}{6} \left(2\dfrac{1}{6}\right)\)
⑺ [mathjax]\(\dfrac{11}{18}\)
⑻ [mathjax]\(\dfrac{29}{30}\)
6
⑴ [mathjax]\(\dfrac{7}{4} \left(1\dfrac{3}{4}\right)\)
⑵ [mathjax]\(\dfrac{1}{14}\)
⑶ [mathjax]\(\dfrac{1}{3}\)
⑷ [mathjax]\(\dfrac{2}{3}\)
⑸ [mathjax]\(\dfrac{1}{10}\)
⑹ [mathjax]\(10\)
⑺ [mathjax]\(\dfrac{7}{5} \left(1\dfrac{2}{5}\right)\)
⑻ [mathjax]\(\dfrac{2}{3}\)
1章 正の数・負の数 P.295
1
⑴ [mathjax]\(-7 \lt -3 \lt +2\)
⑵ [mathjax]\(-2\) ,[mathjax]\(-1\) ,[mathjax]\(0\) ,[mathjax]\(+1\) ,[mathjax]\(+2\)
2
⑴ [mathjax]\(-7\)
⑵ [mathjax]\(-18\)
⑶ [mathjax]\(-17\)
⑷ [mathjax]\(4\)
⑸ [mathjax]\(\dfrac{11}{12}\)
⑹ [mathjax]\(-3.7\)
⑺ [mathjax]\(-7\)
⑻ [mathjax]\(-5\)
⑼ [mathjax]\(-\dfrac{7}{6}\)
3
⑴ [mathjax]\(-35\)
⑵ [mathjax]\(-12\)
⑶ [mathjax]\(\dfrac{4}{5}\)
⑷ [mathjax]\(70\)
⑸ [mathjax]\(-16\)
⑹ [mathjax]\(9\)
⑺ [mathjax]\(-6\)
⑻ [mathjax]\(-30\)
⑼ [mathjax]\(\dfrac{18}{5}\)
4
⑴ [mathjax]\(-23\)
⑵ [mathjax]\(\dfrac{1}{4}\)
⑶ [mathjax]\(9\)
⑷ [mathjax]\(-36\)
⑸ [mathjax]\(\dfrac{1}{4}\)
⑹ [mathjax]\(-\dfrac{1}{8}\)
⑺ [mathjax]\(-7\)
⑻ [mathjax]\(\dfrac{1}{16}\)
⑼ [mathjax]\(-6\)
⑽ [mathjax]\(\dfrac{1}{3}\)
⑾ [mathjax]\(-4\)
⑿ [mathjax]\(-23\)
5
⑴ ア・・・[mathjax]\(+9\),イ・・・[mathjax]\(-12\)
⑵ [mathjax]\(122\) 人
6
[mathjax]\(3\)
2章 文字式 P.296
1
⑴ [mathjax]\(-2ab\)
⑵ [mathjax]\(3x²y\)
⑶ [mathjax]\(\dfrac{a+b}{7}\)
⑷ [mathjax]\(4x-\dfrac{y}{5}\)
2
⑴ [mathjax]\((1000-2x)\) 円
⑵ [mathjax]\(\require{physics} \left(\dfrac{a}{70}+\dfrac{a}{60}\right)\) 分
3
⑴ [mathjax]\(19\)
⑵ [mathjax]\(14\)
4
⑴ [mathjax]\(-3a\)
⑵ [mathjax]\(-6.1x\)
⑶ [mathjax]\(-\dfrac{5}{12}x\)
⑷ [mathjax]\(-5x+1\)
⑸ [mathjax]\(-a-0.9\)
⑹ [mathjax]\(12x-12\)
⑺ [mathjax]\(-\dfrac{1}{2}x-\dfrac{8}{7}\)
⑻ [mathjax]\(-4a-4\)
⑼ [mathjax]\(-\dfrac{7}{6}x+11\)
⑽ [mathjax]\(-8y+20\)
⑾ [mathjax]\(-\dfrac{27}{5}x\)
⑿ [mathjax]\(2x-3\)
⒀ [mathjax]\(-a+6\)
⒁ [mathjax]\(-17x+15\)
⒂ [mathjax]\(-7x-6\)
⒃ [mathjax]\(13a-8\)
5
⑴ [mathjax]\(21\) 個
⑵ [mathjax]\(3(a-1)\) 個
3章 1次方程式 P.297
1
⑴ [mathjax]\(38-5x=3\)
⑵ [mathjax]\(0.8x \lt 5000\)
2
⑴ [mathjax]\(x=2\)
⑵ [mathjax]\(x=3\)
⑶ [mathjax]\(x=-2\)
⑷ [mathjax]\(x=-6\)
⑸ [mathjax]\(x=5\)
⑹ [mathjax]\(x=-3\)
⑺ [mathjax]\(x=-\dfrac{15}{2}\)
⑻ [mathjax]\(x=9\)
⑼ [mathjax]\(x=\dfrac{45}{2}\)
3
⑴ [mathjax]\(x=-5\)
⑵ [mathjax]\(x=4\)
⑶ [mathjax]\(x=-2\)
⑷ [mathjax]\(x=-9\)
⑸ [mathjax]\(x=30\)
⑹ [mathjax]\(x=7\)
⑺ [mathjax]\(x=-6\)
⑻ [mathjax]\(x=2\)
⑼ [mathjax]\(x=-2\)
⑽ [mathjax]\(x=11\)
⑾ [mathjax]\(x=8\)
⑿ [mathjax]\(x=12\)
4
[mathjax]\(a=-8\)
5
りんご [mathjax]\(1\) 個の値段を [mathjax]\(x\) 円とすると,
[mathjax]\( 140+60=200 \)
答 りんご [mathjax]\(1\) 個 [mathjax]\( 140\) 円,もも [mathjax]\(1\) 個 [mathjax]\(200\) 円
6
箱が [mathjax]\(x\) 箱あるとすると,
[mathjax]\(90 \times 11+17=1007\)
答 [mathjax]\(1007\) 個
7
[mathjax]\(x\) mLの水で薄めればよいとすると,
答 [mathjax]\(130\) mL
<1年p.309 >
4章 比例と反比例 P.298
1
⑴ [mathjax]\(y=80x\)
⑵ [mathjax]\(y=\dfrac{10}{x}\)
⑶ [mathjax]\(y=3x\)
比例・・・ ⑴,⑶ 反比例・・・⑵
2
⑴ [mathjax]\(y=3x\),[mathjax]\(y=9\)
⑵ [mathjax]\(y=-\dfrac{12}{x}\),[mathjax]\(y=3\)
3
⑴ [mathjax]\(y=\dfrac{120}{x}\)
⑵ [mathjax]\(2\) 時間 [mathjax]\(24\) 分
⑶ 時速 [mathjax]\(60\) km
4
⑴ [mathjax]\(18\) km
⑵ A・・・[mathjax]\(y=18x\),B・・・[mathjax]\(y=10x\)
⑶ Bの方が [mathjax]\(12\) L多い
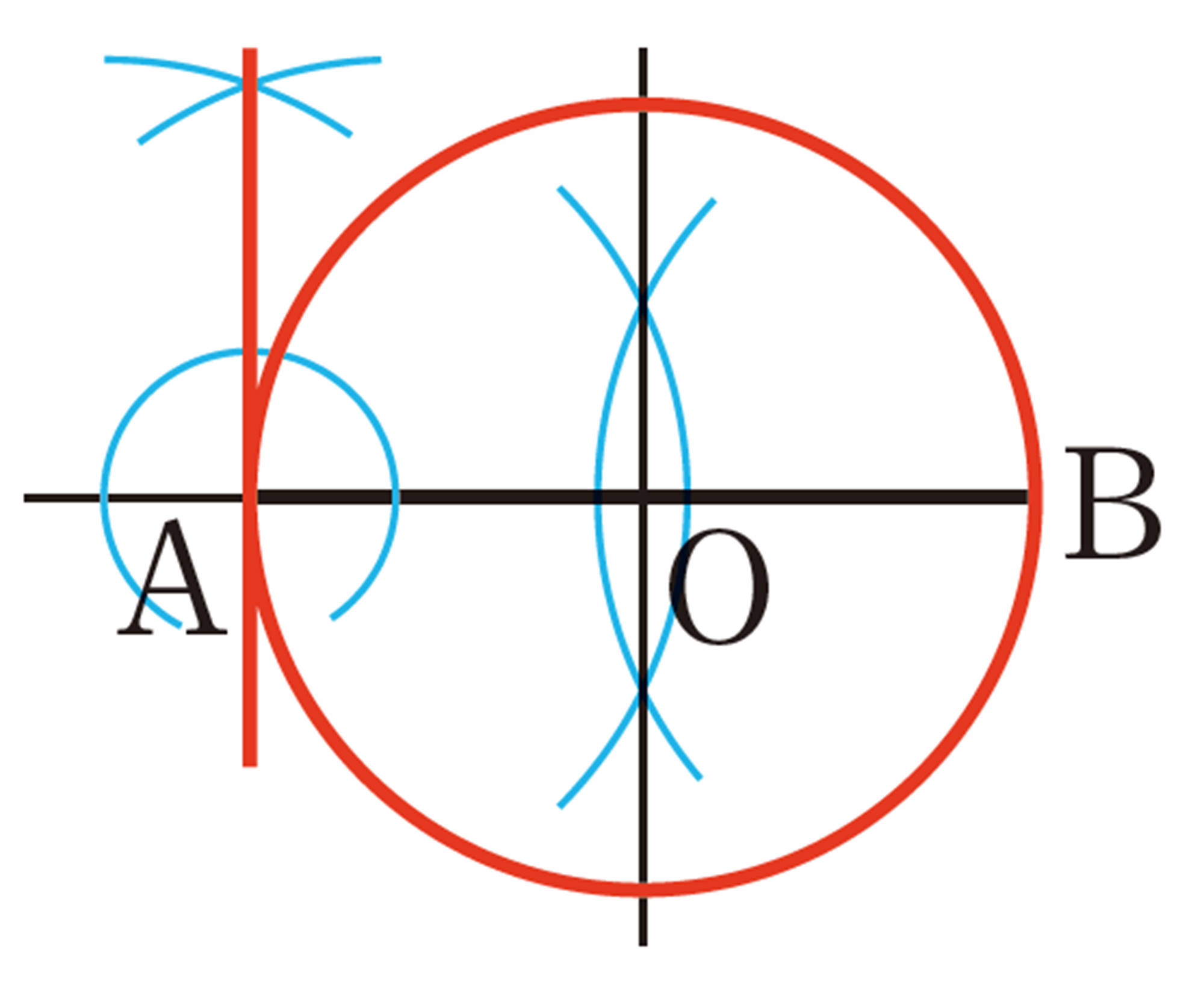
5章 平面図形 P.299
6章 空間図形 P.300
1
⑴ 辺FG,GH,HI,IJ,JF
⑵ 辺DI,EJ,AF,BG
⑶ 面ABCDE,FGHIJ
⑷ 辺FG,GH,HI,IJ,BG,CH,DI
2
⑴ [mathjax]\(144^{ \circ }\)
⑵ [mathjax]\(90 \pi\) cm²
⑶ [mathjax]\(126 \pi\) cm²
7章 データの活用 P.301
1
⑴ [mathjax]\(34\) 人
⑵ [mathjax]\(6.5\) 点
⑶ [mathjax]\(6.5\) 点
2
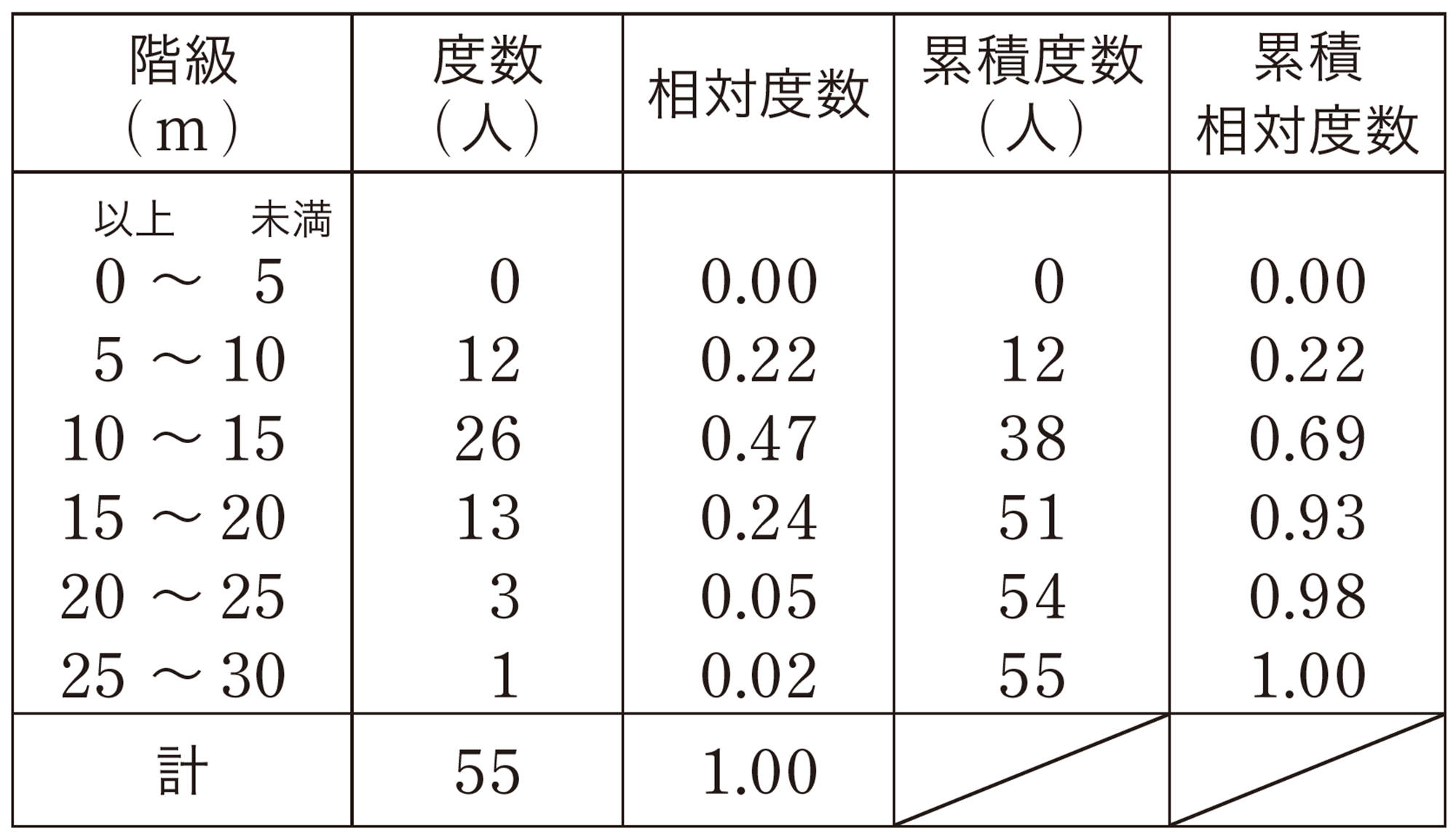
⑴ ア・・・[mathjax]\(28\),イ・・・[mathjax]\(5\)
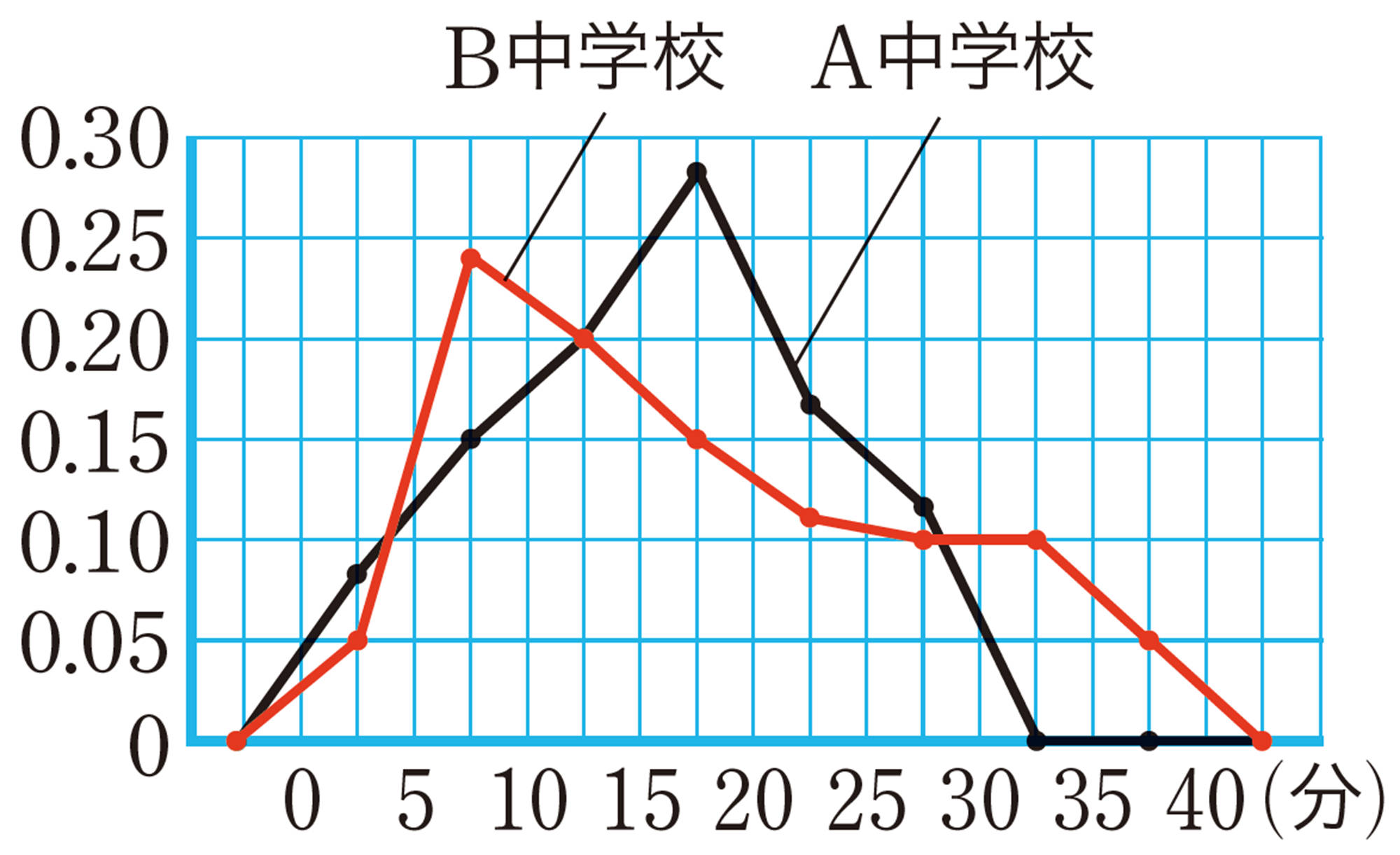
⑵ [mathjax]\(18\) m以上 [mathjax]\(22\) m未満
⑶ [mathjax]\(24\) m
⑷ [mathjax]\(( \mathsf{階級値} ) \times ( \mathsf{度数} )\)・・・上から順に,
[mathjax]\( 36,80,120,168,84,32 \),計 [mathjax]\(520\)
平均値・・・[mathjax]\(20.8\) m
⑸ 相対度数・・・上から順に,
[mathjax]\(0.12\),[mathjax]\(0.20\),[mathjax]\(0.24\),[mathjax]\(0.28\),[mathjax]\(0.12\),[mathjax]\(0.04\),
計 [mathjax]\(1.00\)
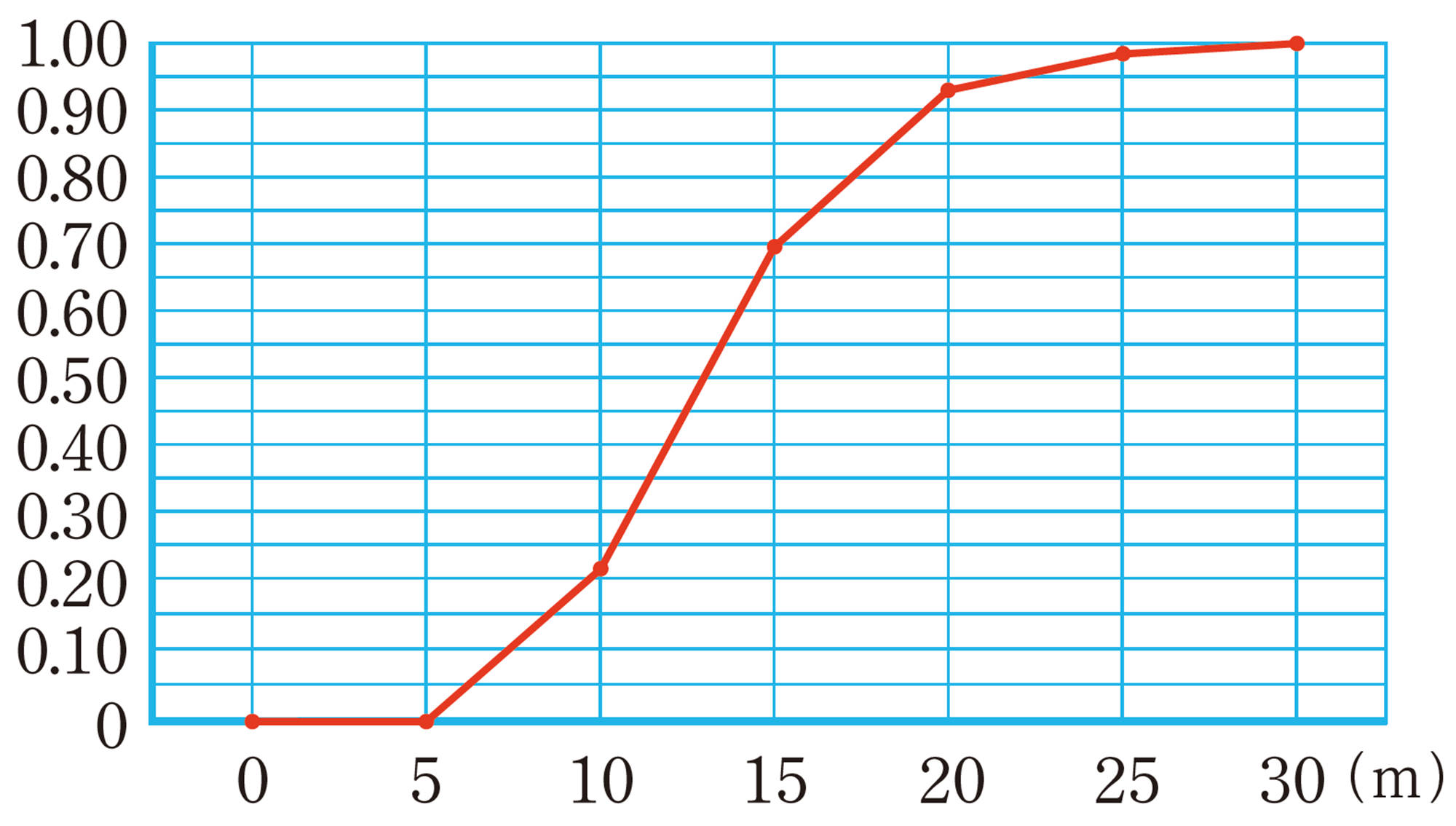
累積相対度数・・・上から順に,
[mathjax]\(0.12\),[mathjax]\(0.32\),[mathjax]\(0.56\),[mathjax]\(0.84\),[mathjax]\(0.96\),[mathjax]\(1.00\)
⑹ [mathjax]\(22\)m未満
3
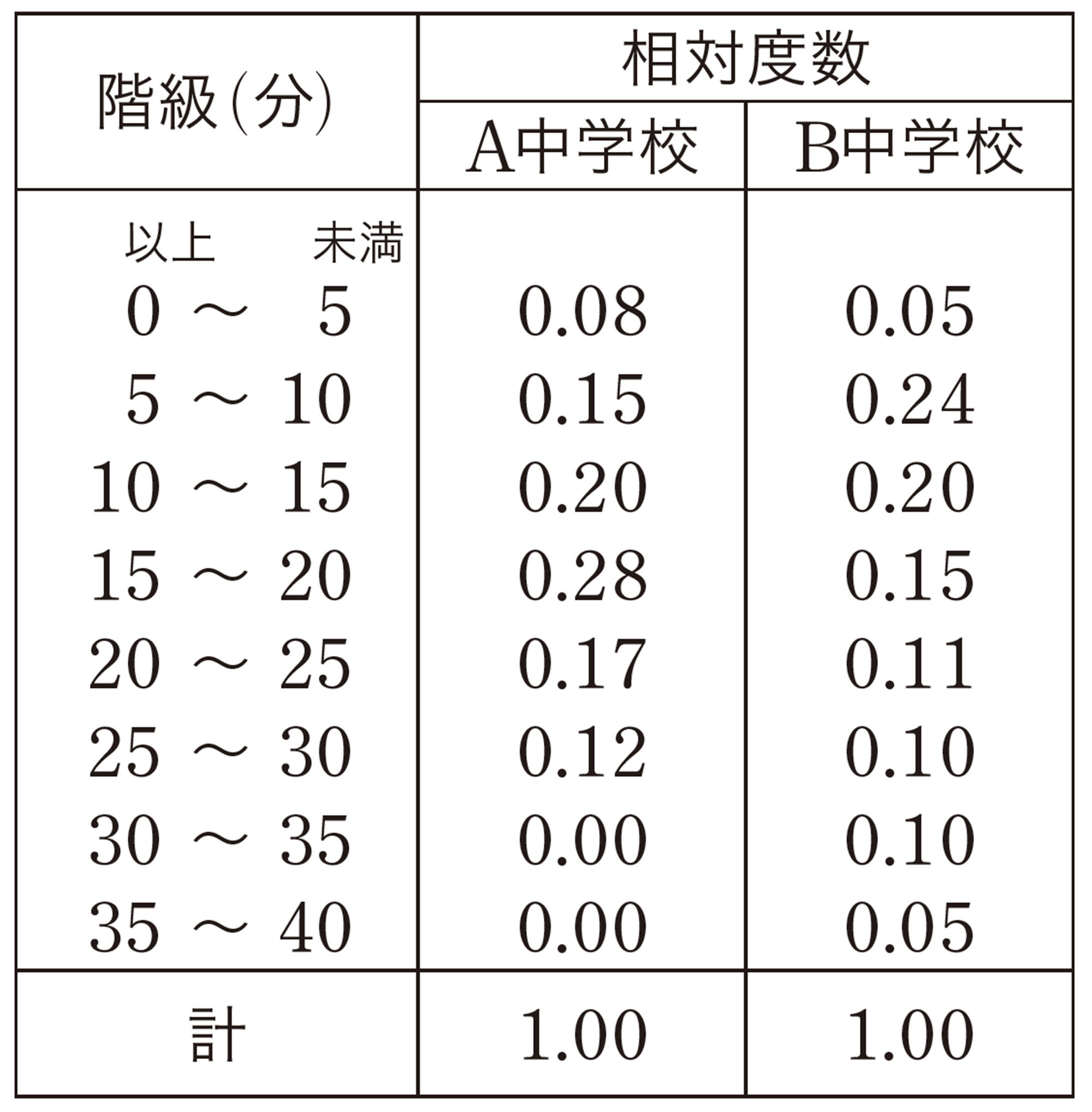
左から順に,[mathjax]\(0.11\),[mathjax]\(0.13\),[mathjax]\(0.13\),[mathjax]\(0.13\),[mathjax]\(0.12\),[mathjax]\(0.12\),[mathjax]\(0.12\)
将棋の駒が立つ確率・・・[mathjax]\(0.12\)
<1年p.⑧>
数学の力
~RSA暗号~
「暗号」というと,スパイ小説や映画が思い浮うかびますか?
現在でも,インターネット上で交換されるクレジットカードなどの情報が盗み見されないように,暗号が日常的に大活躍しています。
暗号技術自体も発展してきました。暗号には,暗号化するための鍵( 暗号化鍵) と,暗号を復号するための鍵( 復号鍵) が必要です。第二次世界大戦頃までの暗号は,「合言葉方式」,つまり,暗号文の送り手と受け手が同じ秘密の鍵( 暗号化鍵と復号鍵が共通) を知っていることが前提でした。
1976 年に,暗号化鍵と復号鍵が異なる「公開鍵暗号方式」が考案されました。公開鍵といわれる暗号化鍵を公開しても,暗号が解読されない方式が,数学を活用して研究されています。
この暗号をつくるためには,公開鍵を使って変換( 暗号化) は簡単にできるけど,その逆変換( 復号) をするのは難しいという,「一方向性」のある変換が必要になります。ここで,「素因数分解の難しさ」に着目したのが「RSA暗号」です。
このRSA暗号は,2 つの素数の積を求めるのは簡単だけど,この積を2 つの素数に素因数分解するのは難しいという性質を使っています。たとえば,300 桁くらいの2 つの素数の積はパソコンを使って一瞬で計算できるが,600 桁の積を2 つの素数に素因数分解するにはスーパーコンピュータでも何万年もかかるといわれています。そこで,RSA暗号では,2 つの素数を復号鍵,その積を公開鍵としました。これなら,公開鍵を公開しても,復号鍵はばれないですよね。
私は,大学で数学を勉強し,就職してRSA暗号に出会い,その数学的な美しさに衝撃を受けました。また,暗号が,IT社会の安心・安全を支える縁の下の力持ちであることにも気づきました。それからずっと,暗号を活用したセキュリティやプライバシー保護の研究を続け,どうしたらもっと使いやすく,公平で,安心・安全なシステムを設計できるかを生活者目線で考えています。
数学的な思考をもとに,実現したいことをモデル化し,これなら大丈夫と検証できることは,社会をデザインするときの要になります。実際,公平なネット抽選方式や電子投票システムを考案してきました。これからも数学を活用して,私たちの社会が健全に機能するような,みんなにとって有用なしくみや技術を生み出していきたいと思っています。