<1年p.275>
さらなる数学へ
協働学習のページ
1年間で学んだ数学をもう1歩進めてみましょう。数学の問題を解決するとき，どんな「見方・考え方」をしてきたでしょうか。どのくらい，数学の力がついたでしょうか。これから，身についた力を確認していきましょう。
276 「見方・考え方」をまとめよう
278 今の自分を知ろう
282 表現する力を身につけよう
282 レポートの作成
283 発表のしかた
284 レポート例
286 疑問を考えよう
286 米は何粒？
【関連】 文字式
288 複雑な形の面積は？
【関連】 比例
289 道路のカーブの半径は？
【関連】 平面図形
290 立方体の切り口の形は？ 発展
【関連】 空間図形
291 数学の歴史の話
291 ディオファントスと方程式
292 円周率[mathjax]\(\pi\)の話
<1年p.276>
Theme 「見方・考え方」をまとめよう
中学校1年の数学の学習では，新しいことを学び，いろいろなことができるようになりました。数学の学習を進めていくにあたって，どんな「見方・考え方」をしてきたかまとめてみましょう。
「見方・考え方」はここにあるだけでなく，いろいろな場面でいろいろな「見方・考え方」を使います。
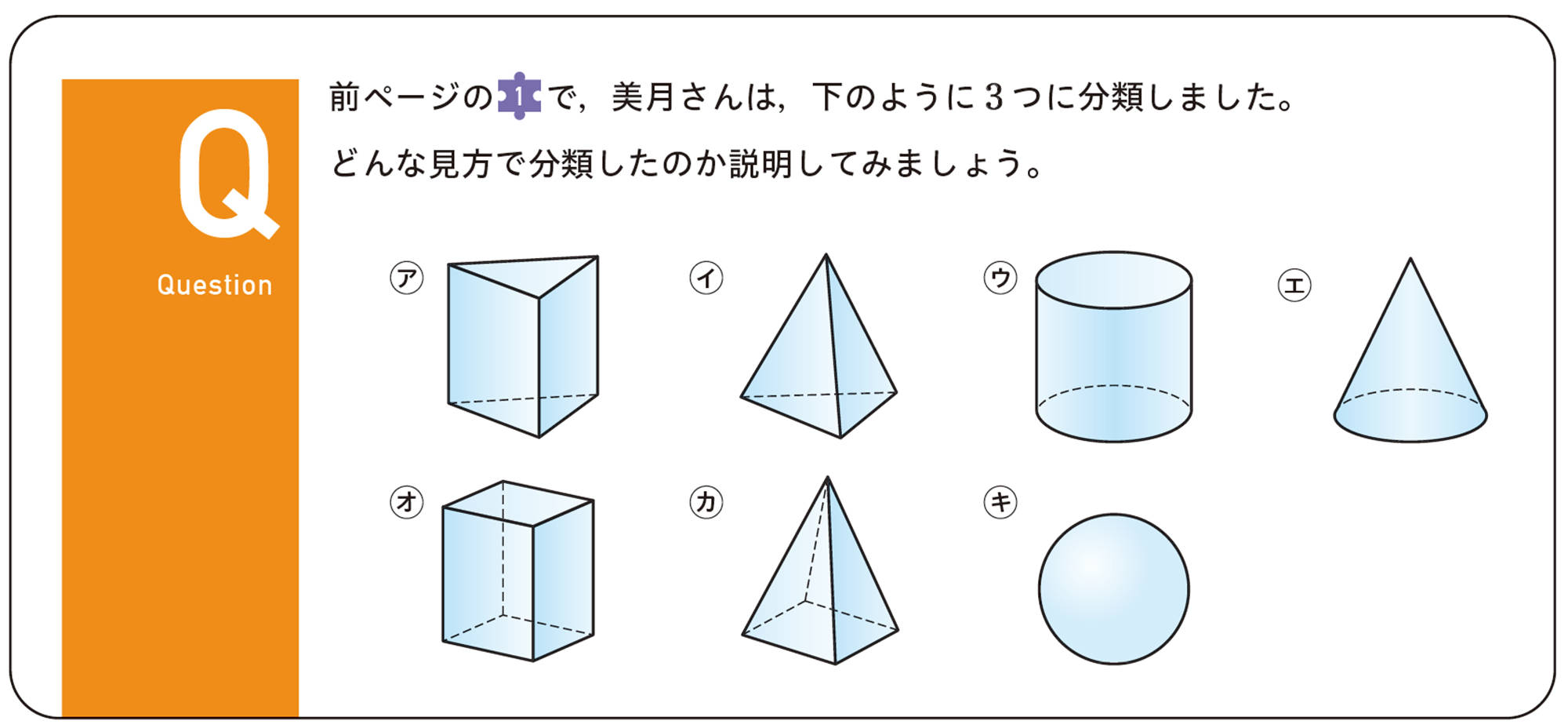
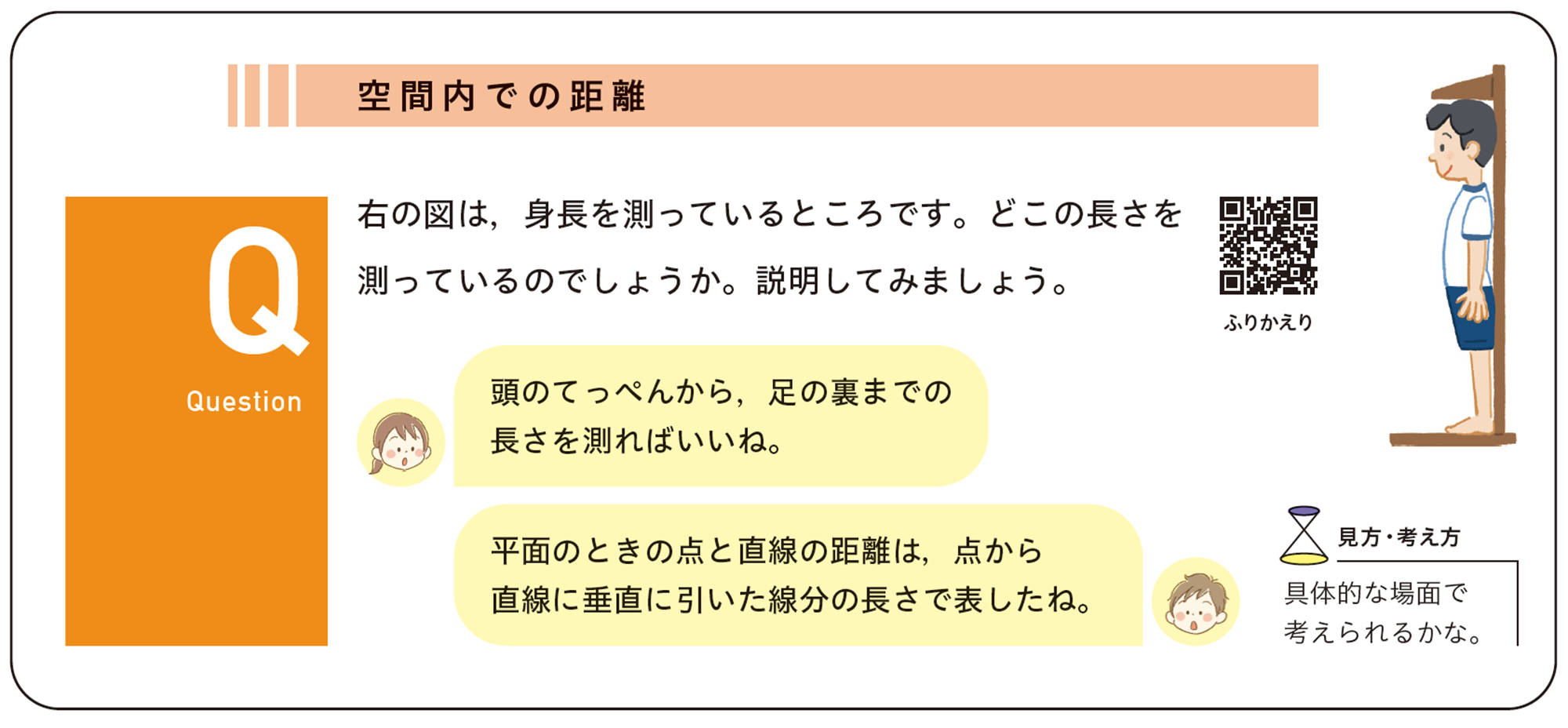
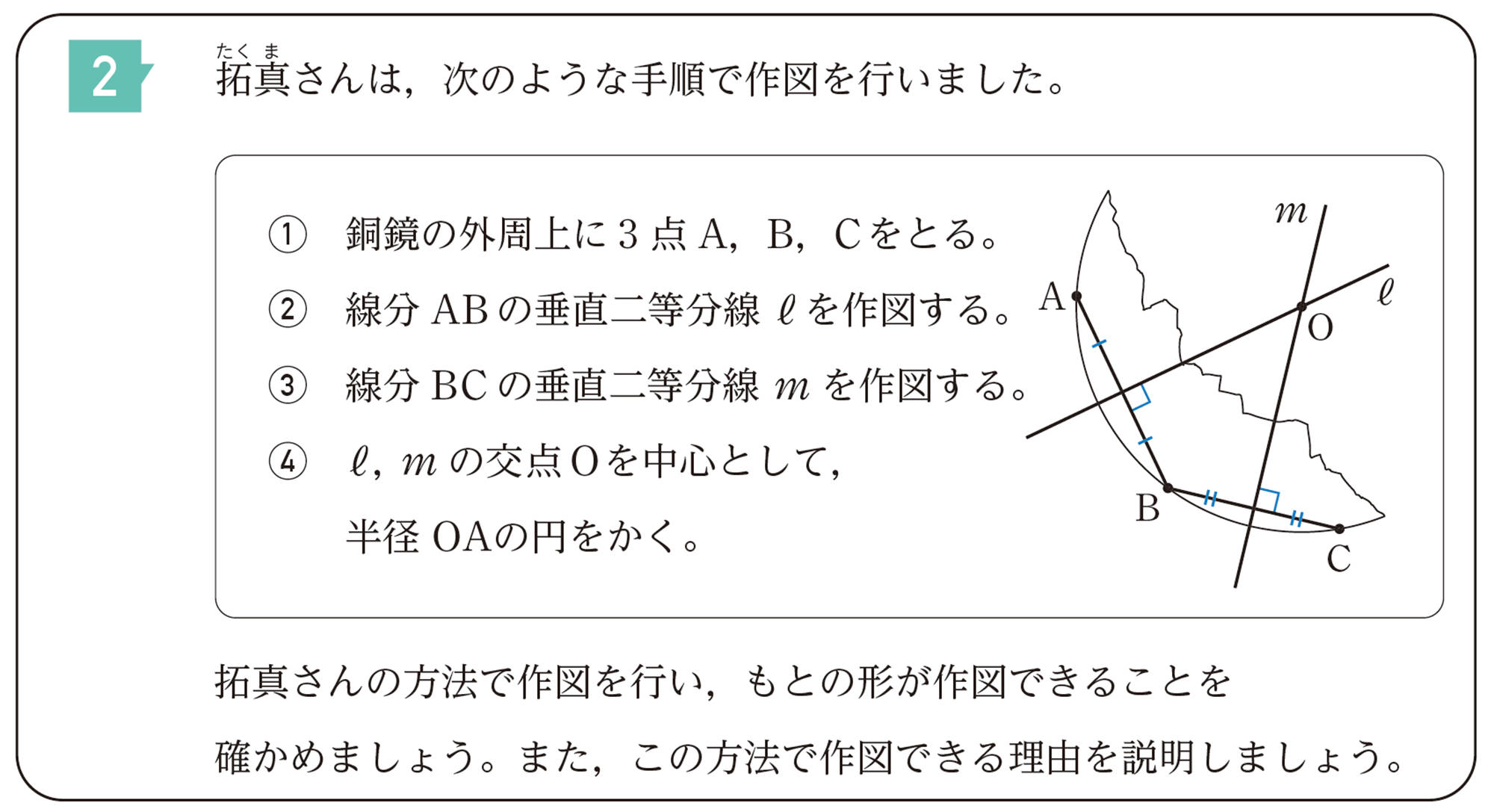
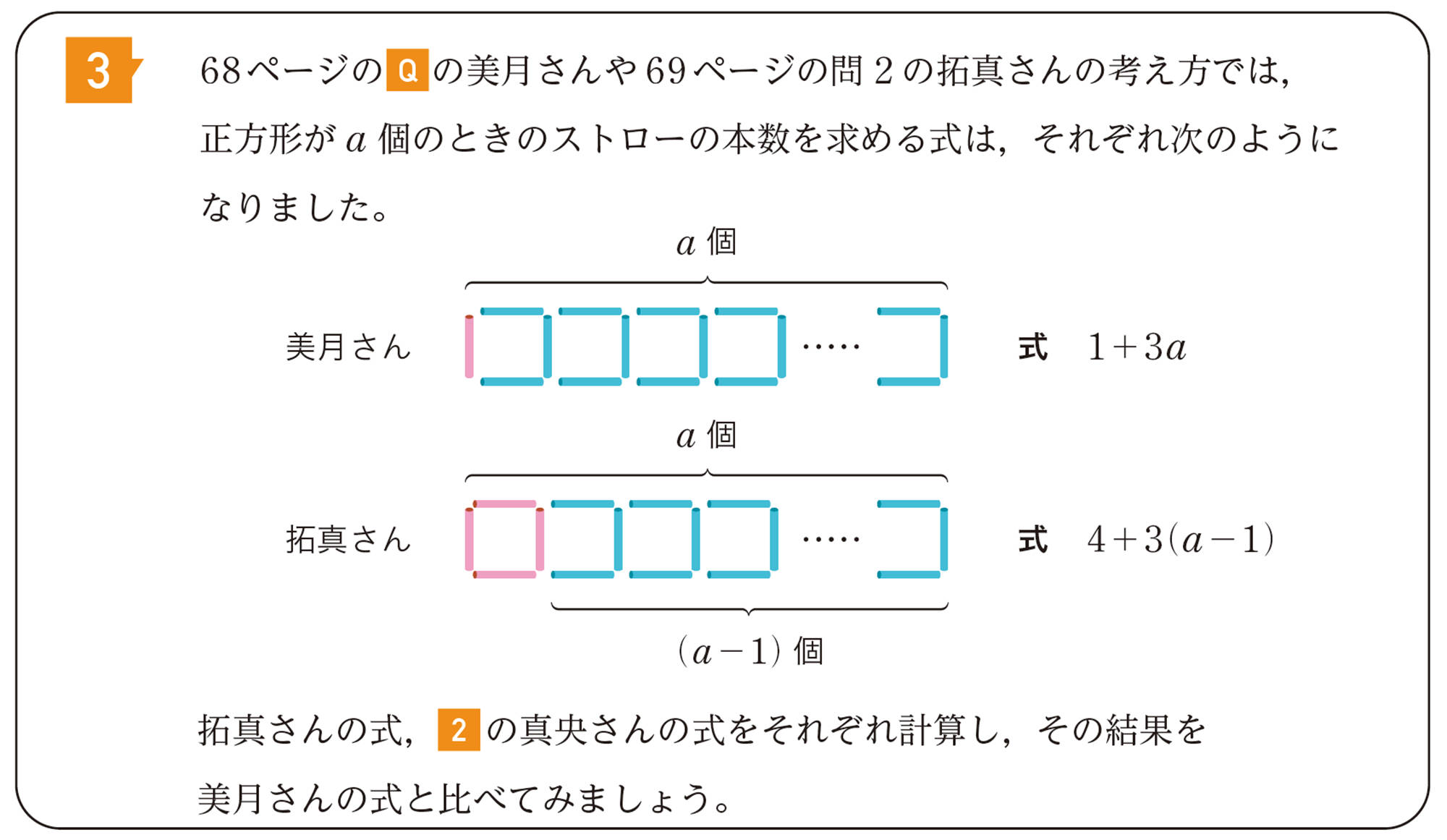
1 身のまわりや数学の中から問題を発見しよう
見方
数量や図形に着目する
P.206
立体を分類するとき，面や辺に着目して考えました。
2 数学の問題として考えよう
具体化する・抽象化する
具体的な場面で考える
P.216
具体的な場面で距離を考えました。
理想化する・単純化する
みなして考える
P.156
測定した値でも，関数関係にあるとみなして考えました。
<1年p.277>
3 解決しよう
ほかにも，いろいろなところで，「見方・考え方」を見つけてみよう！
類推的に考える
同じように考える
P.24
小学校の計算と同じようにできるか考えました。
帰納的に考える
きまりや性質を考える
P.40
いくつかの計算から，きまりを考えました。
演繹的に考える
根拠をもとに理由を考える
P.189
根拠を明らかにして理由を説明できるか考えました。
4 新たな問題を見つけよう
統合させる
関連づけて考える
P.87
同じ数を表していることから，関連づけて考えました。
発展させる
範囲・条件を変えて考える
P.140
数直線をもとに，負の数を表せる図を考えました。
<1年p.278>
Theme 今の自分を知ろう
SDGs（Sustainable Development Goals）とは，2015年9月の国連サミットで採択された2016年から2030年までの国際目標です。持続可能な世界を実現するための17のゴール・169のターゲットから構成され，地球上の誰一人として取り残さない（leave no one behind）ことを誓っています。SDGsは発展途上国のみならず，先進国自身が取り組むユニバーサル（普遍的）なものであり，日本としても積極的に取り組んでいます。
SDGsの17の目標のうち，これまで身につけた数学の力を使って，自分たちにできることがないか調べて，取り組んでみましょう。
地球温暖化って聞いたことがあるよ。
気温が上昇することで，海面水位が上昇してしまう可能性があるらしいよ。
場所によっては，沈んでしまうところもあるみたいだね。
どのくらい気温や海面水位が上昇するのかな。
<1年p.279>
海面水位の上昇を抑えるためにできることを考えよう
Mission
地球温暖化の問題点の1つに，気温が上昇することによる海面水位の上昇があります。海面水位が上昇することで，これまで陸であった場所が海になってしまい，そこに住んでいる人々の生活を脅かす可能性があります。
いろいろなデータをもとにして，これからどのような環境が予想されるか，また，そうならないために自分たちに何ができるか考えて，まとめてみましょう。
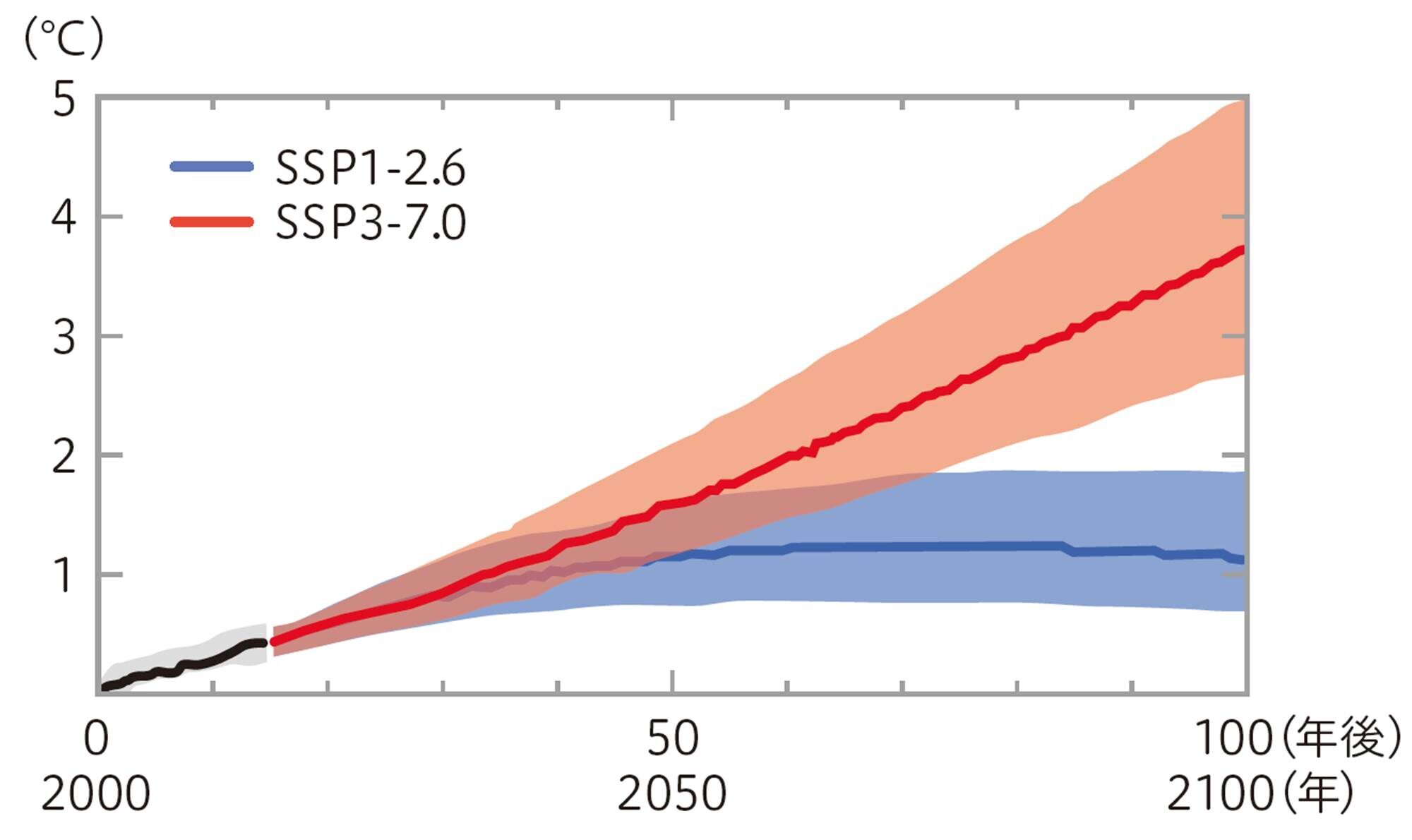
注意 SSPのシナリオは，気候変動を予測するシナリオのことで，数値が小さいほど，温暖化対策をしっかり行ったシナリオを表している。
Data_1
次の図は，世界平均気温の変化と，世界平均海面水位の変化について，SSP[mathjax]\(1-2.6\)とSSP[mathjax]\(3-7.0\)のそれぞれの場合をシミュレーションした１つのグラフです。これらのグラフは，2000年の値を0として示してあります。グラフが0年後(2000年)の値と100年後(2100年)の値を結んだ直線になるとみなしたとき，どんなことが予想できるでしょうか。
注意 実線が予測値，色で塗られた範囲は予測の幅を表している。
<1年p.280>
Data_2
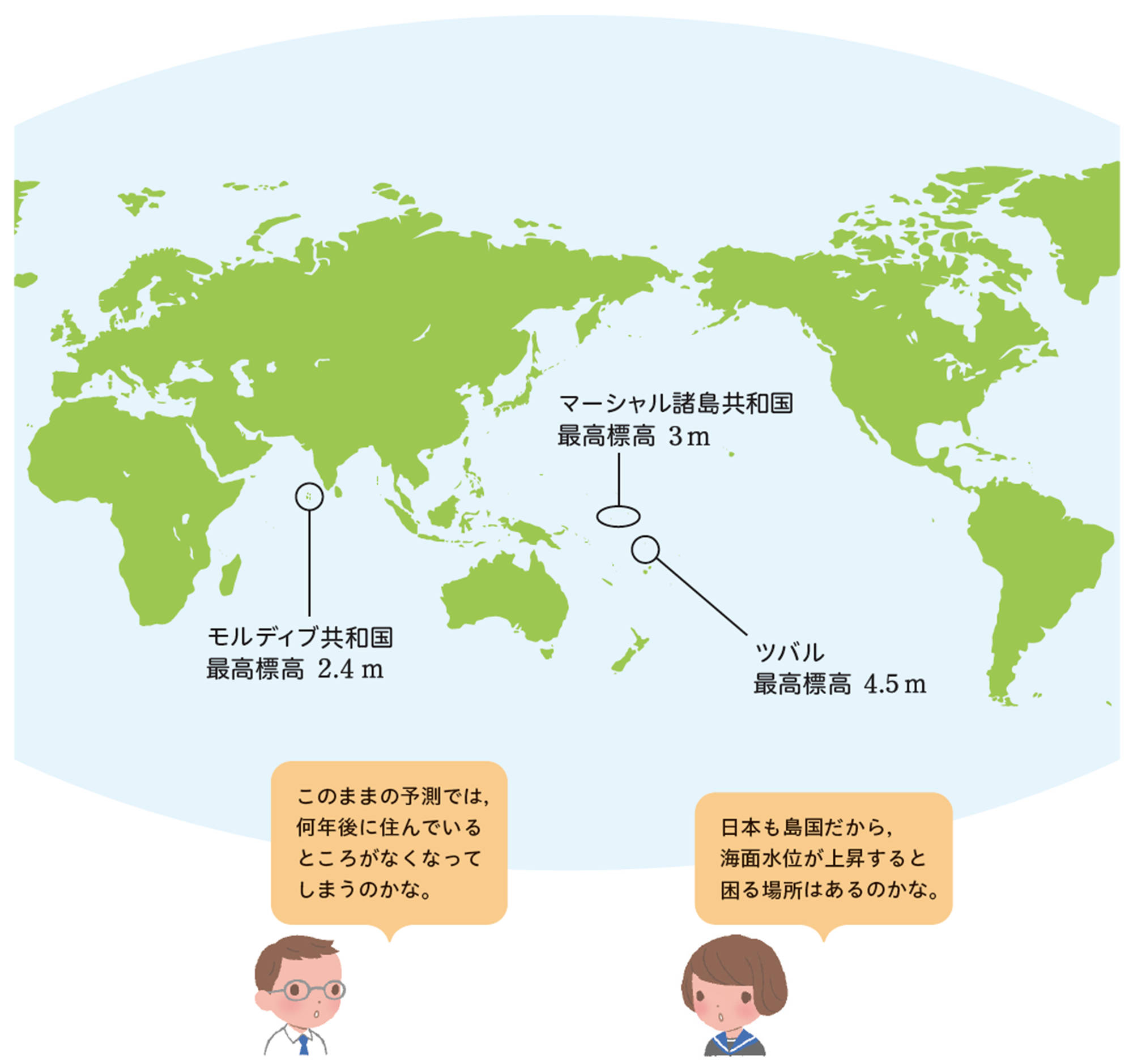
次の図は，最高標高が低い主な国や島を表したものです。前ページの【 Data_1 】で考えたことと合わせて，どんなことがいえるか考えてみましょう。
マーシャル諸島共和国最高標高 3m
モルディブ共和国最高標高 [mathjax]\(2.4\)m
ツバル最高標高 [mathjax]\(4.5\)m
このままの予測では，何年後に住んでいるところがなくなってしまうのかな。
日本も島国だから，海面水位が上昇すると困る場所はあるのかな。
Report
これまで調べたことから，気温上昇による海面水位の上昇がどのような危険性があるかまとめてみましょう。
また，そうならないように，自分たちでできることを調べたり考えたりして，レポートにまとめましょう。
日本の標高を調べるサイトや，地球温暖化についてまとめたサイトにリンクしています。
<1年p.281>
海面水位の上昇を抑えるためにできることを考えよう
学びに向かう力
問題意識をもって取り組むことができた
学習したことを役立てることができた
自分の考えをくふうしてまとめることができた
とてもそう思う
少しそう思う
あまりそう思わない
考える力，決める力，表す力
グラフを読み取るとき，これまで学んだ数学の使い方を見つけることができた
予測が正しいかどうか確かめることができた
自分なりに，調べたり考えたりしたことを図や表で表すことができた
とてもそう思う
少しそう思う
あまりそう思わない
知っていることやできるようになったこと
自分たちで，海面水位の上昇を抑えるためにできることを見つけることができた
身のまわりのことがらについて考えることで数学の知識の理解が深まった
とてもそう思う
少しそう思う
あまりそう思わない
もっと調べたいと思ったこと
自分の住んでいるところや，近くの標高の低いところを探してみよう。
<1年p.282>
Theme 表現する力を身につけよう
〜自分の考えをまとめよう〜
自分の考えをまとめたり伝えたりするために，レポートをつくってみましょう。レポートにまとめることで，学習したこと以外に新たな発見をしたり，疑問が生まれたりします。それこそが，本当の数学のおもしろさです。
レポートの作成
1 興味や関心をもったことをテーマにしよう
数学の学習のときやふだんの生活の中で， 「なぜだろう」，「別の条件ならどうだろう」，「もっと知りたい」と感じたことをレポートのテーマにしましょう。ふだんから気になったことをノートなどに記録しておくと，テーマを決めるときに役立ちます。
2 資料の収集方法の計画を立てよう
自分で考えるだけでなく，
・実験や観察，調査などをする
・アンケート調査をする
・図書館の本や新聞記事，インターネット等で調べる
など，目的に合わせた資料の収集方法を計画することが大切です。
3 資料を集め，整理して分析しよう
調べた情報やデータを分析して，資料の特徴を見つけましょう。収集した情報やデータは，何を参考にしたのかわかるように記録しておきましょう。また，インターネットで検索するとたくさんの情報が得られますが，信頼できる情報かどうかに注意する必要があります。
4 自分の考えを整理してまとめよう
レポートの作成を通して， 調べた内容や調査過程，そのおもしろさや価値などが友だちにわかりやすく伝わるように， 整理してまとめましょう。レポートという形にこだわらず，新聞やポスターなど，発表のしかたに合わせて形式を選ぶと，さらによいものをつくることができます。
<1年p.283>
発表のしかた
発表する人は…
自分の考えや思いがどうやったらうまく伝わるかを考えて発表しよう
- 何について調べて，何を伝えたいのかをはっきりさせておこう。
- 話す順序を事前に考えておこう。
- 聞く人にレポートを配ったり，よく見えるようにレポートを置いたりしよう。
- 相手にわかりやすいことばを使ったり，声の大きさやスピードに注意したりしよう。
- 自分で考えた部分と，調べてわかった部分を区別して話そう。
- どんなところで数学を使ったかわかるようにしよう。
発表を聞く人は…
発表している人の考えや思いをくみ取りながら聞こう
- 調べたことの目的や内容を理解しよう。
- 内容やまとめ方について，よかった点を参考にしよう。
- 表やグラフの扱い方が適切かどうかに注目しよう。
- 自分の考えと同じ点やちがう点がないかに注意して聞こう。
- わからないことがあったら質問しよう。
<1年p.284>
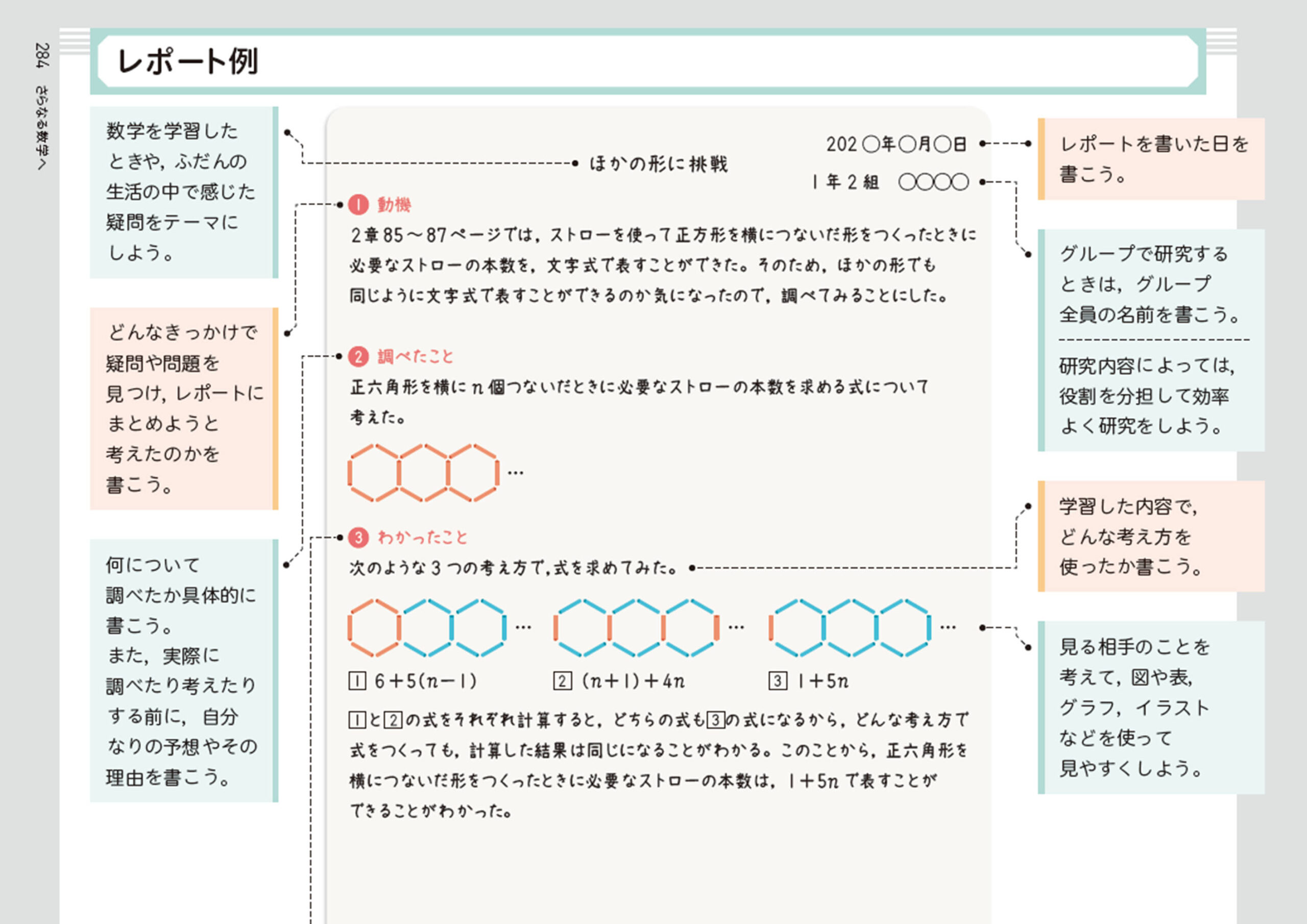
レポート例
ほかの形に挑戦
202◯年◯月◯日
1 年 2 組 ◯◯◯◯
1 動機
2章85〜87ページでは，ストローを使って正方形を横につないだ形をつくったときに必要なストローの本数を，文字式で表すことができた。そのため，ほかの形でも同じように文字式で表すことができるのか気になったので，調べてみることにした。
2 調べたこと
正六角形を横にn個つないだときに必要なストローの本数を求める式について考えた。
3 わかったこと
次のような3つの考え方で，式を求めてみた。
1 [mathjax]\(6+5(n-1)\)
2 [mathjax]\((n+1)+4n\)
3 [mathjax]\(1+5n\)
1と2の式をそれぞれ計算すると，どちらの式も3の式になるから，どんな考え方で式をつくっても，計算した結果は同じになることがわかる。このことから，正六角形を横につないだ形をつくったときに必要なストローの本数は，1+5nで表すことができることがわかった。
数学を学習したときや，ふだんの生活の中で感じた疑問をテーマにしよう。
どんなきっかけで疑問や問題を見つけ，レポートにまとめようと考えたのかを書こう。
何について調べたか具体的に書こう。また，実際に調べたり考えたりする前に，自分なりの予想やその理由を書こう。
レポートを書いた日を書こう。
グループで研究するときは，グループ全員の名前を書こう。
研究内容によっては，役割を分担して効率よく研究をしよう。
学習した内容で，どんな考え方を使ったか書こう。
見る相手のことを考えて， 図や表，グラフ，イラストなどを使って見やすくしよう。
<1年p.285>
また，これまでのことから，いろいろな正多角形についても，同じように必要なストローの本数を文字式で簡単に表すことができると予想できる。
4 わからなかったこと
今回，正多角形について考えたけど，ストローを使って立体をつくったときにも，同じように，必要なストローの本数を文字式で表すことができるのか疑問がわいたので，さらに調べてみることにした。
立方体を横につないだ形をつくったときに必要なストローの本数を文字式で表すために，ストローを使って正多角形と同じように立体をつくることにした。しかし，ストローだけでは立体を組み立てることができなかったので，図をかいて考えてみたけど文字式で表すことができなかった。
5 感想
正多角形のときはストローを並べやすくて，いろいろな式を考えることができました。しかし，立体になると，組み立てることが難しくて図をかいて考えたけど，式を見つけることができませんでした。今後，実際に立体を組み立てて，今回できなかった立方体を横につないだときの文字式も考えてみようと思います。
調べたり考えたりしたことをふりかえって，わかったことをまとめよう。
わからなかったことがあれば，どんな点がわからなかったのかを書こう。
新たに知ったことや今後調べてみたいことなどを書こう。
くふうしたことや難しかったことなどを書こう。
引用した資料や参考にした文献があるときは，最後に示しておこう。
例│参考文献 著者名(発行年)『書名』出版社名
総務省統計局
283ページの発表のしかたを参考にして，グループ内で発表しよう！
