<1年p.231>
２ 立体の体積
角柱，円柱の体積
問 １ 次の四角柱，円柱の体積を求めましょう。
⑴ 四角柱
⑵ 円柱
小学校で学んだように，角柱や円柱の体積は，(底面積)[mathjax]\(\times\)(高さ)で求めることができる。
角柱，円柱の体積
底面積[mathjax] \( S \) cm²，高さ[mathjax]\(h\) cmの角柱，円柱の体積を[mathjax] \( V \) cm³とすると，
[mathjax]\(V=Sh\)
注意 [mathjax]\(h\) はheight(高さ)，[mathjax]\(V\) はvolume(体積)の頭文字である。
問 ２ 次の立体の体積を求めなさい。
⑴ 四角柱
⑵ 底面が半円の立体
<1年p.232>
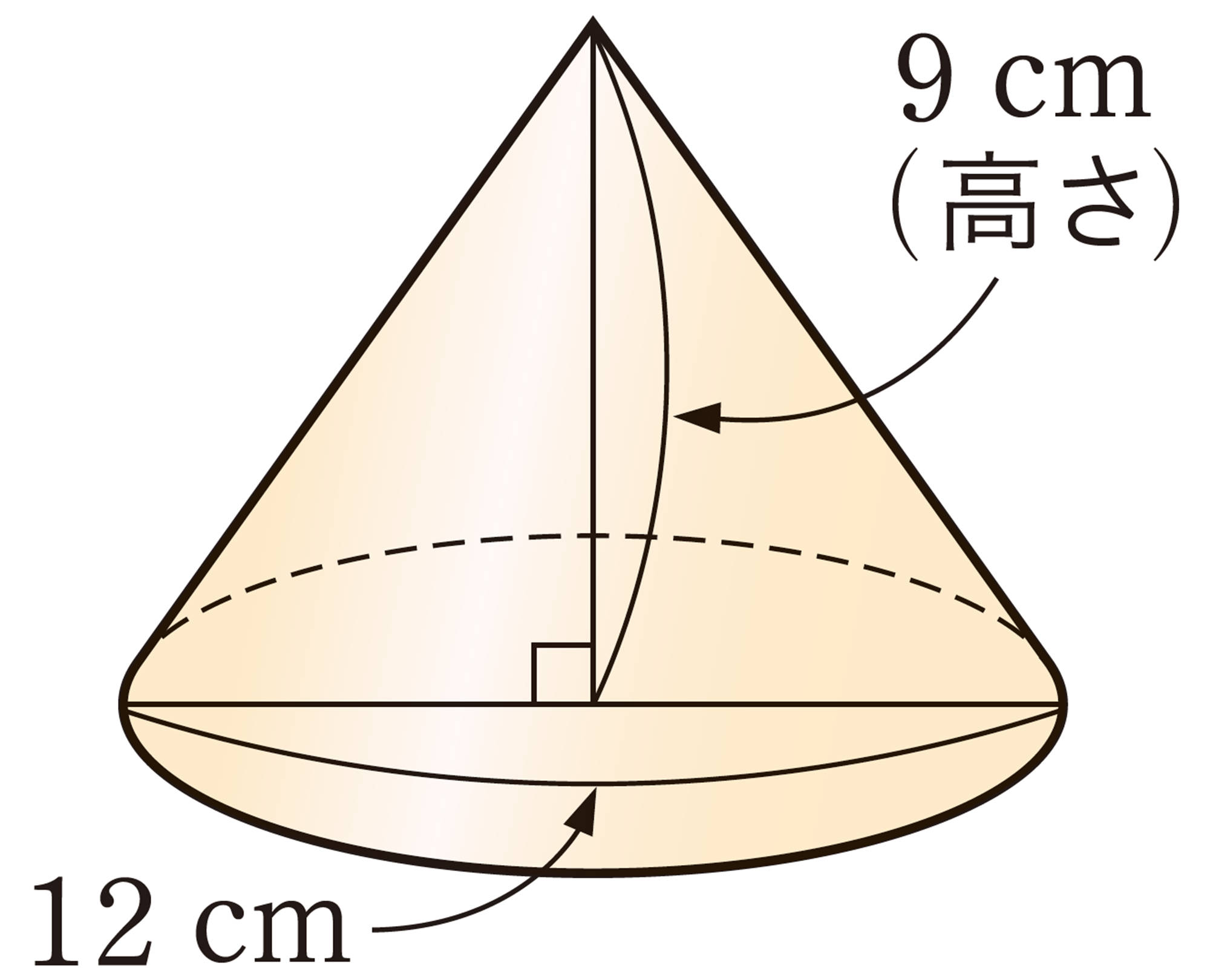
角錐，円錐の体積
Q Question
底面積が等しく高さも等しい角柱と角錐，円柱と円錐の容器を使って，2つの体積を比べてみましょう。どんなことがわかるでしょうか。
見方・考え方
実験をもとに，それぞれの立体の体積の関係を考えられるかな。
角錐や円錐に入れた水は，角柱や円柱に何杯入るかな。
目標 ▷ 角錐，円錐の体積について調べよう。
【Q】の結果から，角錐，円錐の体積は，それぞれ底面積が等しく高さも等しい角柱，円柱の体積の[mathjax] \( \dfrac{1}{3}\)であることがわかる。
角錐，円錐の体積
底面積[mathjax] \( S \) cm²，高さh cmの角錐，円錐の体積を[mathjax] \( V \)cm³ とすると，
[mathjax] \( V=\dfrac{1}{3}Sh\)
問３ 次の立体の体積を求めなさい。
⑴ 正四角錐
⑵ 円錐
どんなことがわかったかな
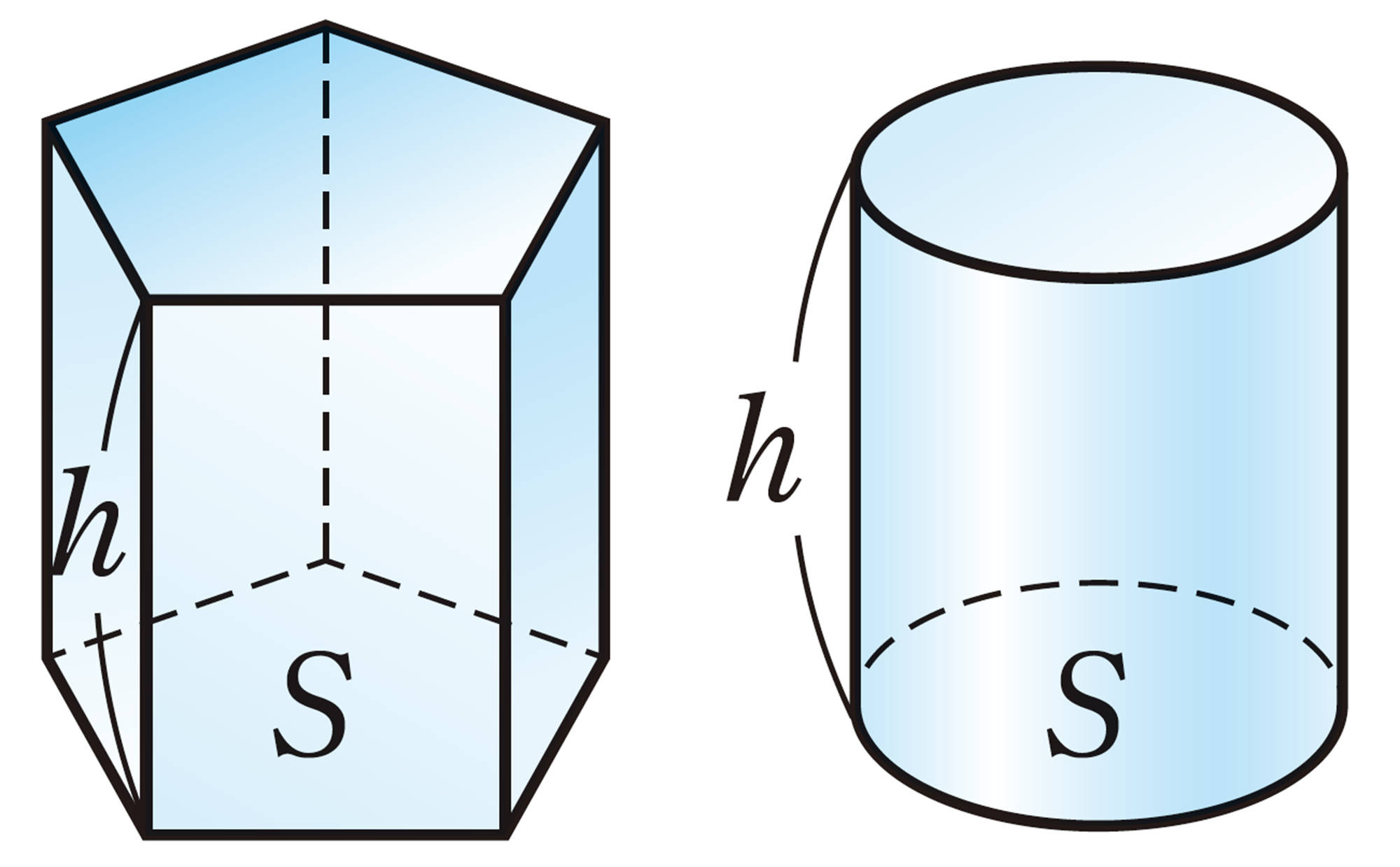
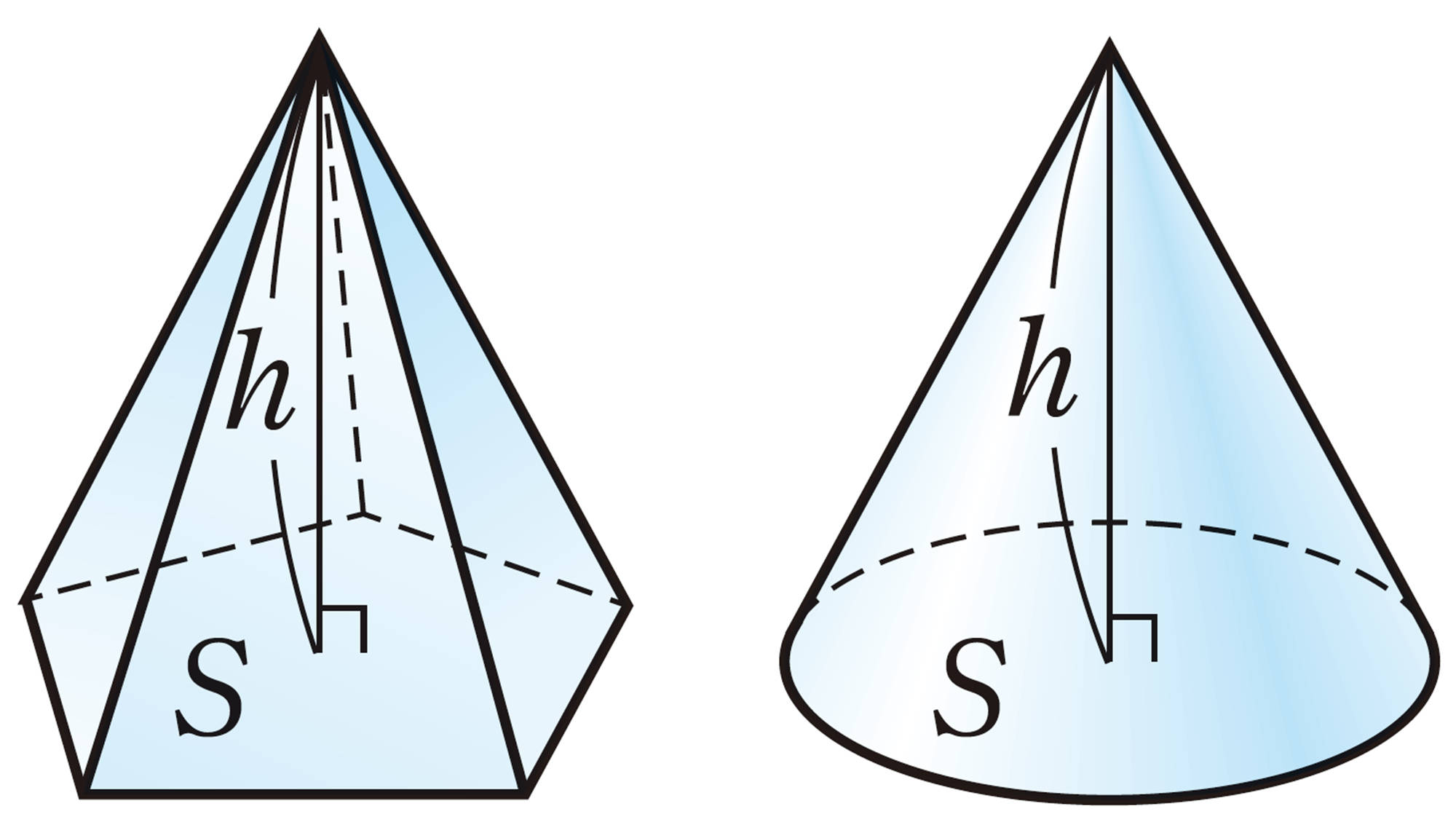
底面積[mathjax] \(S\)，高さ[mathjax] \(h\)の角錐，円錐の体積をVとすると，[mathjax] \(V=\dfrac{1}{3}Sh\) で求めることができます。
次の課題へ！
球の体積も同じように求めることができるのかな？
↓P.235
<1年p.233>
模型で考える角錐の体積 Tea Break
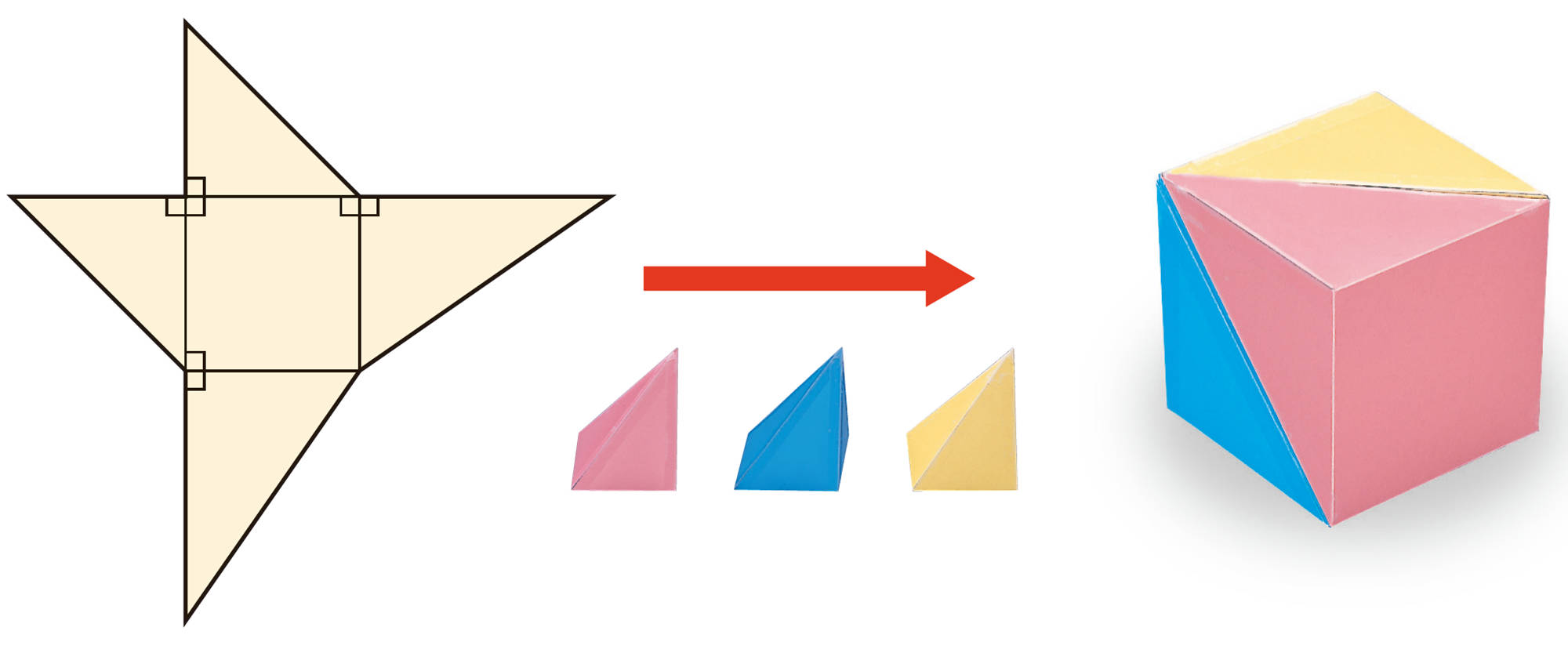
【１】 巻末②にある展開図を使って，四角錐を3個つくり，それらを組み合わせて立方体をつくってみましょう。
【１】から，上の四角錐の体積は，その底面を1つの面とする立方体の体積の[mathjax] \( \dfrac{1}{3}\) であることがわかります。
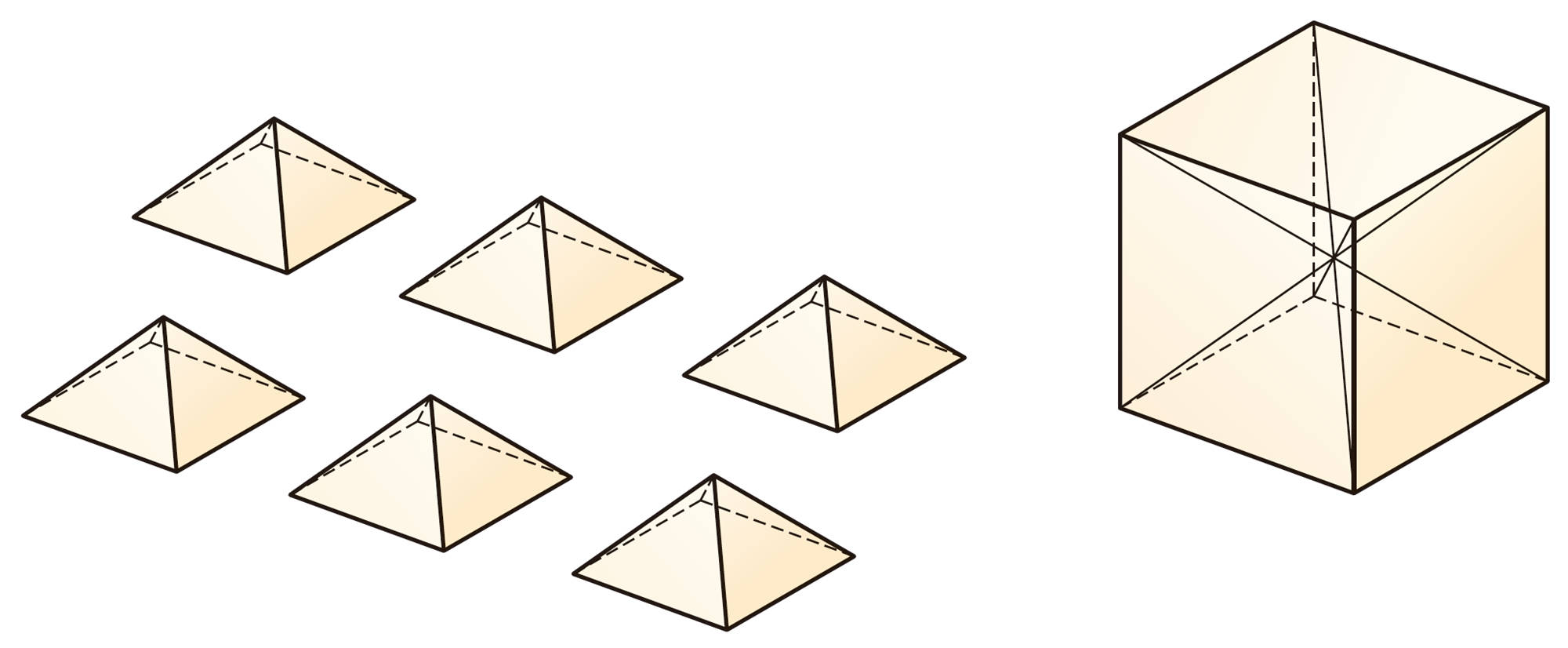
【２】 巻末②にある展開図を使って，正四角錐を6個つくり，それらを組み合わせて立方体をつくってみましょう。
【２】から，上の正四角錐の体積は，その底面を1つの面とした，高さが2倍の立方体の体積の[mathjax] \( \dfrac{1}{6}\) であることがわかります。
【３】 【１】，【２】から，四角錐の体積が，それぞれ底面積と高さが等しい四角柱の体積の[mathjax] \( \dfrac{1}{3}\) であることを説明してみましょう。
<1年p.234>
３ 球の表面積と体積
球の表面積
Q Question
半径5 cmの球の表面に，右の写真のように，ひもを全体にすき間なく巻いたものをほどいて，円になるように巻き直すと，半径10 cmの円になりました。球の表面積について，どんなことがわかるか話し合ってみましょう。
球の表面積と，円の面積は同じになるといっていいのかな。
ほかの立体のように，面積を求める公式がつくれるかな。
見方・考え方
球の表面積を円の面積におきかえて考えられるかな。
目標 ▷ 球の表面積や体積について調べよう。
一般に，半径[mathjax]\(r\) cmの球の表面積は，半径[mathjax]\(2r\) cmの円の面積と等しくなる。したがって，半径[mathjax]\(r\) cmの球の表面積は，次のようになる。
[mathjax] \(= 4\pi r²\) (cm²)
球の表面積
半径r cmの球の表面積を[mathjax] \( S \)cm²とすると，
[mathjax] \( S=4\pi r²\)
問 １ 半径4 cmの球の表面積を求めなさい。
問 ２ 右の図のような半径3 cm，中心角[mathjax]\(90^{\circ}\)のおうぎ形を，直線 ℓ を軸として1回転してできる立体の表面積を求めなさい。
<1年p.235>
球の体積
Q Question
半径5 cmの半球の容器Aと，底面の半径が5 cm，高さが10 cmの円柱の容器Bを使って，2つの体積を比べてみましょう。球の体積について，どんなことがわかるでしょうか。
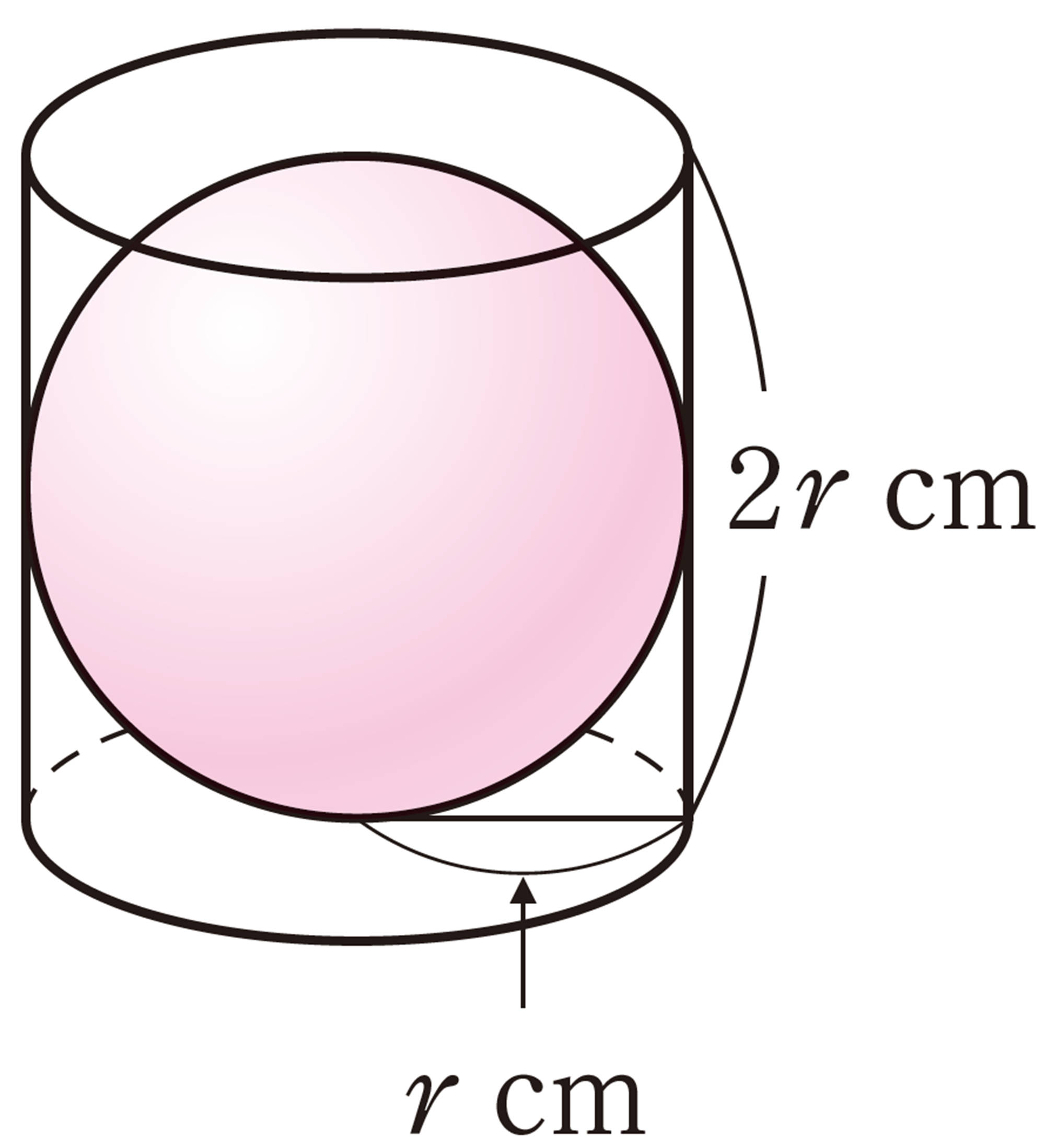
半球と円柱の体積にはどんな関係があるのかな。
半球に入れた水は，円柱に何杯入るのかな。
見方・考え方
角錐や円錐の体積を考えたときと同じように考えられるかな。
【Q】から，半球Aの体積は，円柱Bの体積の[mathjax] \( \dfrac{1}{3}\) になることがわかる。このことから，半径r cmの球の体積を[mathjax] \( V \)cm³とすると，半径r cm，高さ2r cmの円柱をもとにして，次のように考えることができる。
球の体積
半径r cmの球の体積を[mathjax] \( V \) cm³とすると，
[mathjax] \( V=\dfrac{4}{3}\pi r³\)
問 ３ 半径4 cmの球の体積を求めなさい。
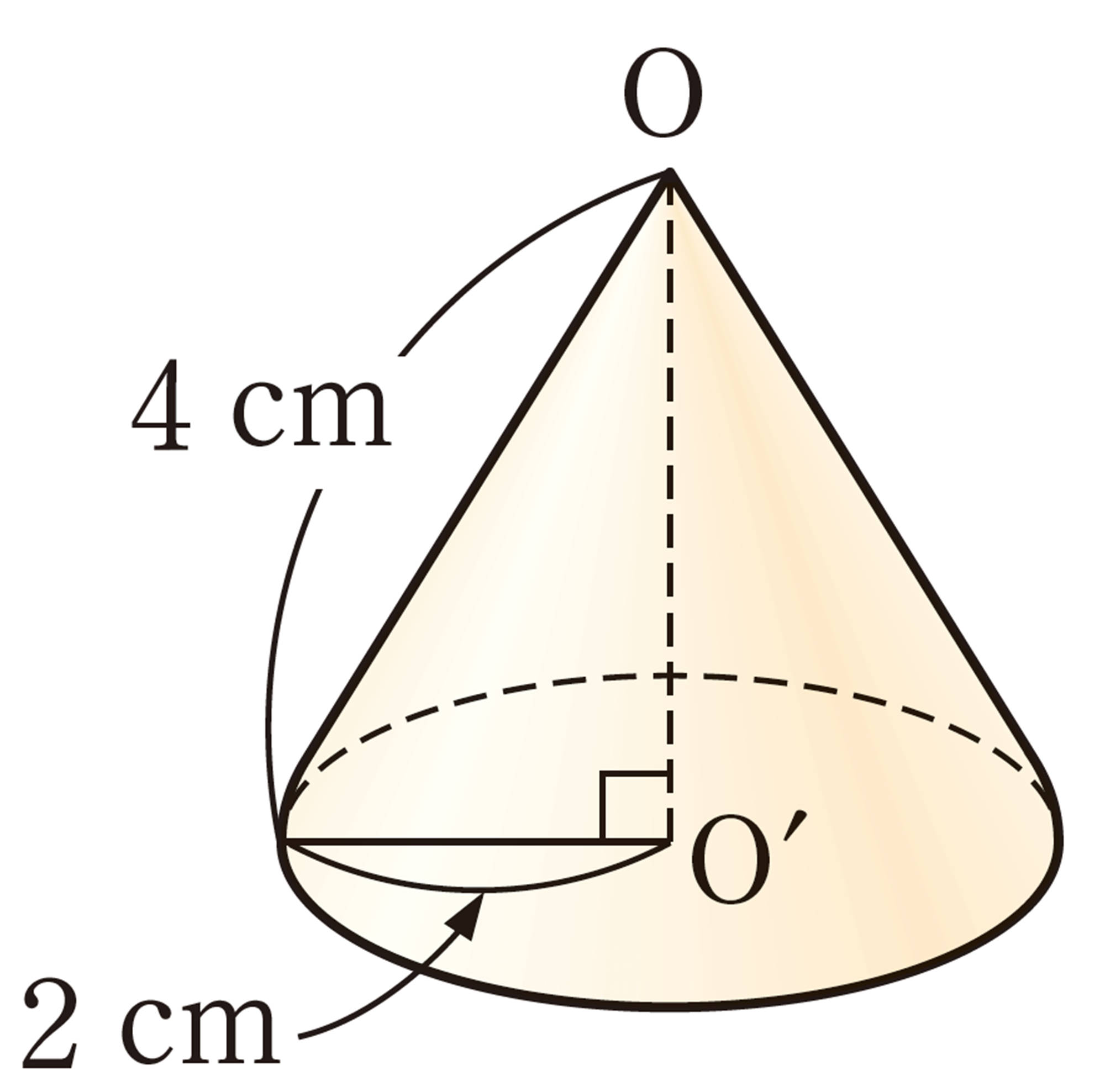
問 ４ 前ページの問2の立体について，その体積を求めなさい。
<1年p.236>
㋐底面の半径が5 cm，高さが10 cmの円錐
㋑半径5 cmの球
㋒底面の半径が5 cm，高さが10 cmの円柱
⑴ ㋐の体積を1とすると，㋑，㋒の体積はいくらになるでしょうか。
⑵ ㋑の表面積と㋒の側面積を比べてみましょう。
どんなことがわかったかな
半径[mathjax] \(r\)の球の表面積を[mathjax] \(S\)とすると，[mathjax] \( S=4\pi r²\)で求めることができます。
半径[mathjax] \(r\)の球の体積を[mathjax] \(V\)とすると， [mathjax] \( V=\dfrac{4}{3}\pi r³\)で求めることができます。
確かめよう 2節 立体の表面積・体積
１ 半径12 cm，中心角[mathjax]\(240^{\circ}\)のおうぎ形の弧の長さと面積を求めなさい。
２ 右の図の円錐の底面積，側面積，表面積を求めなさい。
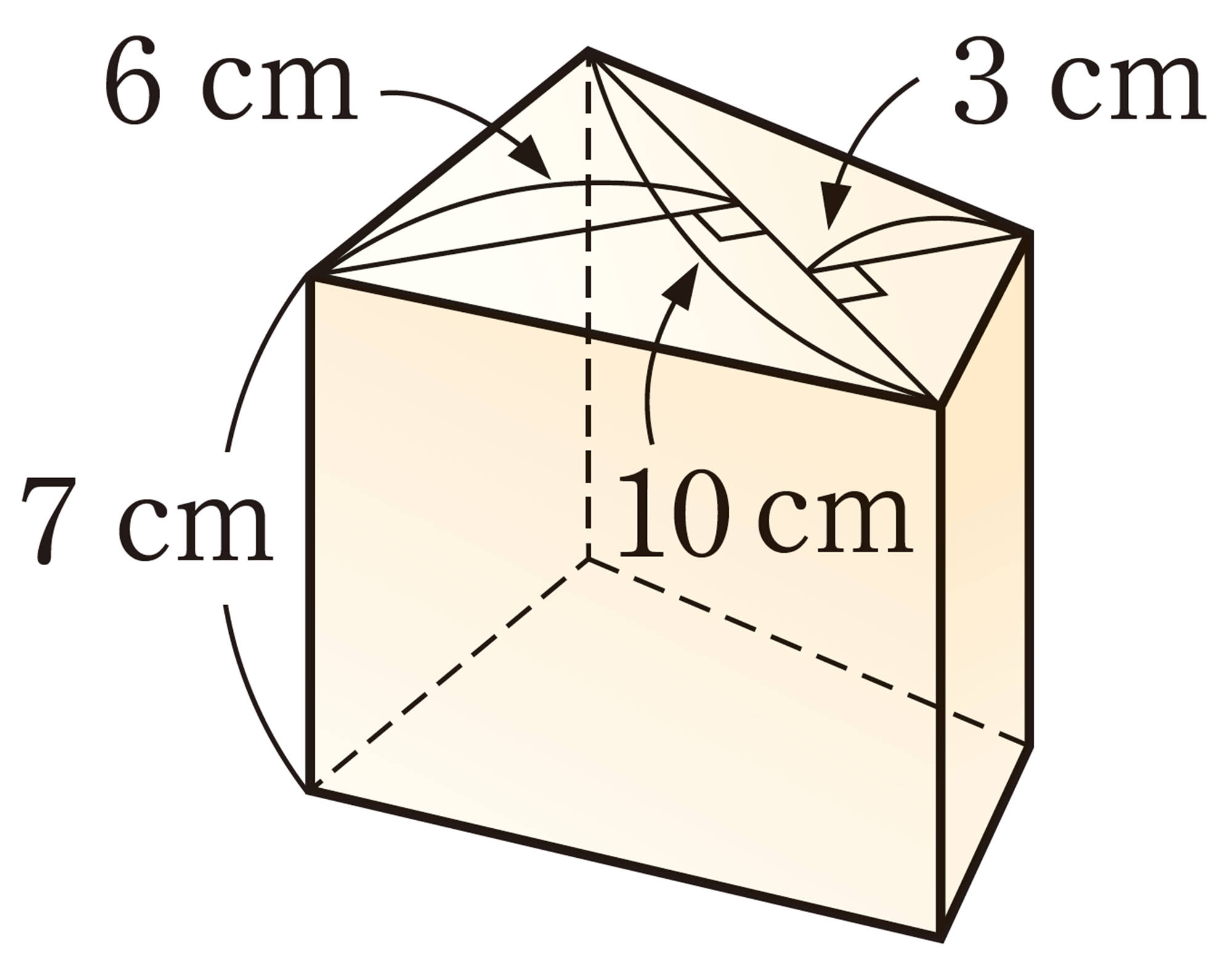
３ 次の立体の体積を求めなさい。
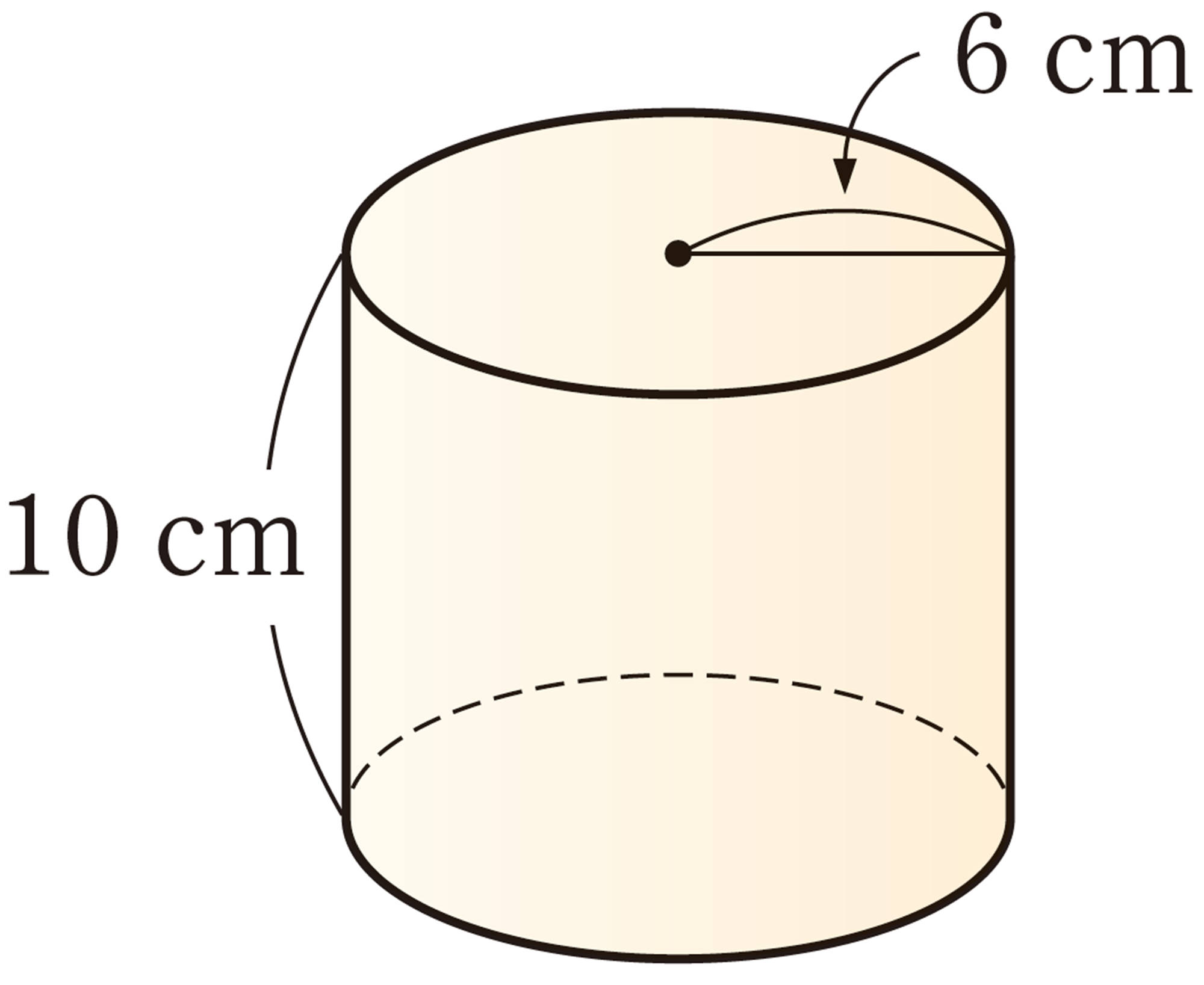
⑴ 底面の半径が10 cm，高さが15 cmの円柱
⑵ 底面積が60 cm²，高さが8 cmの五角錐
□ 球の表面積や体積を求めることができる。 球の表面積と体積 P.234 問1 P.235 問3
４ 直径6 cmの球の表面積と体積を求めなさい。
<1年p.237>
6章 「空間図形」を学んで
できるようになったこと 身のまわりの課題へ P.240，241
空間内の直線や平面の性質を理解することができる。
立体を投影図，展開図，見取図で表したり，面が動いてできる図形とみたりすることができる。
立体の表面積や体積を，小学校で学んだことを生かしたり，実験から求め方を導いたりして求めることができる。
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない オイラーの多面体定理 発展
へこみのない多面体の頂点の数，辺の数，面の数の関係について，次のようなオイラーの多面体定理と呼ばれるものがあります。頂点の数をt，辺の数をs，面の数をmとすると，次の式が成り立ちます。
[mathjax] \(t-s+m=2\)
いろいろな多面体で，確かめてみましょう。この定理の名前にあるレオンハルト・オイラー（1707〜1783）は，スイスの数学者で，数学のさまざまな分野で業績を残しています。オイラーの定理，オイラーの公式と呼ばれるものは，ほかにもたくさんあります。どんなものがあるか調べてみましょう。
